A&A 369, 826-850 (2001)
DOI: 10.1051/0004-6361:20010240
H. Böhringer1 - P. Schuecker1 - L. Guzzo2 -
C. A. Collins3 - W. Voges1 - S. Schindler 3 -
D. M. Neumann 4 -
R. G. Cruddace 5 - S. De Grandi 2 -
G. Chincarini 2,6 - A. C. Edge 7 - H. T. MacGillivray 8 -
P. Shaver 9
1 - Max-Planck-Institut für extraterr. Physik,
D 85740 Garching, Germany
2 -
Osservatorio Astronomico di Brera, Merate, Italy
3 -
Liverpool John Moores University, Liverpool,UK
4 -
CEA Saclay, Service d`Astrophysique, Gif-sur-Yvette, France
5 -
Naval Research Laboratory, Washington, USA
6 -
Dipartimento di Fisica, Universita degli Studi di Milano, Italy
7 -
Physics Department, University of Durham, UK
8 -
Royal Observatory, Edinburgh, UK
9 -
European Southern Observatory, Garching, Germany
Received 29 August 2000 / Accepted 7 February 2001
Abstract
We discuss the construction of an X-ray flux-limited sample of
galaxy clusters, the REFLEX survey catalogue, to be used for cosmological
studies. This cluster identification and redshift survey was conducted
in the frame of an ESO key programme and is based on
candidates selected from the southern part of the ROSAT All-Sky
Survey (RASS). For the first cluster candidate selection from
a flux-limited RASS source list, we make use of optical data
from the COSMOS digital catalogue produced from the scans of
the UK-Schmidt plates. To ensure homogeneity of the sample
construction process, this selection is based only on this one
well-defined optical data base.
The nature of the candidates selected in this process is subsequently
checked by a more detailed evaluation of the X-ray and optical source
properties and available literature data. The final identification and
the redshift is then based on optical spectroscopic
follow-up observations.
In this paper we document the process by which the primary cluster
candidate catalogue is constructed prior to the optical follow-up
observations. We describe the reanalysis of the RASS source catalogue
which enables us to impose a proper flux limit cut to the X-ray source list
without introducing a severe bias against extended sources. We discuss the
correlation of the X-ray and optical (COSMOS) data to find galaxy density
enhancements at the RASS X-ray source positions and the further evaluation of
the nature of these cluster candidates. Based also on the results of the
follow-up observations we provide
a statistical analysis of the completeness and contamination of the
final cluster sample and show results on the cluster number counts.
The final sample of identified X-ray clusters reaches a flux
limit of
3 10-12 ergs-1 cm-2 in the 0.1-2.4 keV band
and comprises 452 clusters in an area of 4.24 ster.
The results imply a completeness of the REFLEX cluster sample
well in excess of 90%. We also derive for the first time an
upper limit of less than 9% for the number of clusters which may
feature a dominant contribution to the X-ray emission
from AGN. This accuracy is sufficient
for the use of this cluster sample for cosmological tests.
Key words: cosmology: miscellaneous - galaxies: clusters - X-rays: galaxies
![]() An effective selection
by mass (with a known dispersion which can be taken into account in any
corresponding modeling).
An effective selection
by mass (with a known dispersion which can be taken into account in any
corresponding modeling).
![]() The X-ray background originates mostly from distant point
sources which are very homogeneously distributed (e.g. Soltan & Hasinger 1994).
Therefore the X-ray background is very much easier to subtract from the cluster
emission than the optical galaxy background distribution.
The X-ray background originates mostly from distant point
sources which are very homogeneously distributed (e.g. Soltan & Hasinger 1994).
Therefore the X-ray background is very much easier to subtract from the cluster
emission than the optical galaxy background distribution.
![]() The X-ray surface brightness is much more concentrated towards
the cluster centre as compared to the galaxy distribution.
Therefore the effect of overlaps along the line of sight is minimized.
The X-ray surface brightness is much more concentrated towards
the cluster centre as compared to the galaxy distribution.
Therefore the effect of overlaps along the line of sight is minimized.
![]() For an X-ray flux-limited survey the survey volume
as a function of X-ray luminosity can exactly be calculated
(e.g. for the construction of the X-ray luminosity or mass function).
For an X-ray flux-limited survey the survey volume
as a function of X-ray luminosity can exactly be calculated
(e.g. for the construction of the X-ray luminosity or mass function).
The construction of statistically complete samples of X-ray clusters
started with the completion of the first all-sky
X-ray surveys by the HEAO-1 and ARIEL V satellites
(Piccinotti et al. 1982; Kowalski et al. 1984). With additional observations from EINSTEIN and EXOSAT
a cluster sample of the ![]() 50 X-ray brightest objects with more
detailed X-ray data was compiled (Lahav et al. 1989; Edge et al. 1990)
and with the analysis of deeper EINSTEIN observations
the first deep X-ray cluster survey, within the EMSS, has been obtained
(Gioia et al. 1990; Henry et al. 1992). The latter
survey allowed in particular to address the question of the evolution of
cluster abundance with redshift (e.g. Henry et al. 1992; Nichol et al. 1997).
The ROSAT All-Sky Survey (RASS), the first X-ray all-sky survey conducted
with an X-ray telescope (Trümper 1992, 1993) provides an ideal basis
for the construction of a large X-ray cluster sample for cosmological studies.
Previous cluster surveys based on the RASS include: Romer et al. (1994);
Pierre et al. (1994); Burns et al. (1996);
Ebeling et al. (1996, 1998, 2000a, 2000b); De Grandi (1999);
Henry et al. (1997); Ledlow et al. (1999); Böhringer et al. (2000);
and Cruddace et al. (2000). Two of these surveys are pilot projects
to REFLEX concentrating on the South Galactic Pole and the Hydra
regions with results reported in Romer et al. (1994, see also
Cruddace 2001) and Pierre et al. (1994), respectively. The sample
described by De Grandi et al. (1999) was compiled from an
earlier version of the current cluster sample based on X-ray
data from the first processing of the RASS and a significantly
shallower correlation with the COSMOS data base as well
as correlations with a variety of optical cluster catalogues.
It constitutes a subsample of the present cluster sample
comprising 130 clusters at a flux limit of
3-4 10-12 ergs-1 cm-2 (as measured in the
0.5-2 keV energy band) in 2.5 sr of the southern sky.
The work reported in Cruddace et al. (2001) uses the same
starting material as the present work with a
slightly different cluster search method applied to the COSMOS
data and goes deeper in flux in an area limited to 1.013 ster around
the South Galactic Pole. The cluster samples described in
Ebeling et al. (1996); Burns et al. (1996), and Ledlow et al. (1999)
are derived from correlations of the cluster catalogue by Abell et al. (1989)
with the RASS data. The work described in Henry et al. (1997) concentrates
on a small area around the North Ecliptic Pole with the special feature of
this survey that all X-ray sources, not only the clusters, are identified
up the flux-limit of the sample. The northern BCS survey (Allen et al. 1992;
Crawford et al. 1995, 1999; Ebeling et al. 1998, 2000a) is optimising
the search for clusters by combining the correlation with several optical
catalogues, by relying on X-ray extent information, and by combining
two different detection algorithms - the standard RASS processing for
the complete region and the Voronoi Tesselation
and Percolation method covering about one seventh of the survey area.
The price payed for the application of several, partly inhomogeneous
selection processes in parallel is an inhomogeneous selection function
which is very hard to specify and no details have been published up to date.
50 X-ray brightest objects with more
detailed X-ray data was compiled (Lahav et al. 1989; Edge et al. 1990)
and with the analysis of deeper EINSTEIN observations
the first deep X-ray cluster survey, within the EMSS, has been obtained
(Gioia et al. 1990; Henry et al. 1992). The latter
survey allowed in particular to address the question of the evolution of
cluster abundance with redshift (e.g. Henry et al. 1992; Nichol et al. 1997).
The ROSAT All-Sky Survey (RASS), the first X-ray all-sky survey conducted
with an X-ray telescope (Trümper 1992, 1993) provides an ideal basis
for the construction of a large X-ray cluster sample for cosmological studies.
Previous cluster surveys based on the RASS include: Romer et al. (1994);
Pierre et al. (1994); Burns et al. (1996);
Ebeling et al. (1996, 1998, 2000a, 2000b); De Grandi (1999);
Henry et al. (1997); Ledlow et al. (1999); Böhringer et al. (2000);
and Cruddace et al. (2000). Two of these surveys are pilot projects
to REFLEX concentrating on the South Galactic Pole and the Hydra
regions with results reported in Romer et al. (1994, see also
Cruddace 2001) and Pierre et al. (1994), respectively. The sample
described by De Grandi et al. (1999) was compiled from an
earlier version of the current cluster sample based on X-ray
data from the first processing of the RASS and a significantly
shallower correlation with the COSMOS data base as well
as correlations with a variety of optical cluster catalogues.
It constitutes a subsample of the present cluster sample
comprising 130 clusters at a flux limit of
3-4 10-12 ergs-1 cm-2 (as measured in the
0.5-2 keV energy band) in 2.5 sr of the southern sky.
The work reported in Cruddace et al. (2001) uses the same
starting material as the present work with a
slightly different cluster search method applied to the COSMOS
data and goes deeper in flux in an area limited to 1.013 ster around
the South Galactic Pole. The cluster samples described in
Ebeling et al. (1996); Burns et al. (1996), and Ledlow et al. (1999)
are derived from correlations of the cluster catalogue by Abell et al. (1989)
with the RASS data. The work described in Henry et al. (1997) concentrates
on a small area around the North Ecliptic Pole with the special feature of
this survey that all X-ray sources, not only the clusters, are identified
up the flux-limit of the sample. The northern BCS survey (Allen et al. 1992;
Crawford et al. 1995, 1999; Ebeling et al. 1998, 2000a) is optimising
the search for clusters by combining the correlation with several optical
catalogues, by relying on X-ray extent information, and by combining
two different detection algorithms - the standard RASS processing for
the complete region and the Voronoi Tesselation
and Percolation method covering about one seventh of the survey area.
The price payed for the application of several, partly inhomogeneous
selection processes in parallel is an inhomogeneous selection function
which is very hard to specify and no details have been published up to date.
The most important final goal of the present survey is the statistical and cosmographical characterisation of the large-scale structure of the present day Universe. This requires a large enough sample by number and volume and a nearly homogeneous and well controlled selection function in order to minimize and correct for any artificial fluctuations in the cluster density. The first condition is not provided by the above surveys concentrating on a small sky area while the latter point is not fulfiled by the surveys based on optical catalogues (e.g. the Abell catalogue) with known selection problems and inhomogeneous source detection as featured by the early RASS processing or reanalysis covering only part of the sky. Therefore, with the current survey (and its complement in the South Galactic Pole region by Cruddace et al.), we are following a completely new avenue using a highly homogeneous sampling of information from the X-ray RASS II data and the COSMOS optical data base. The importance and success of this new approach is demonstrated, for example, by preempting the results derived in this paper and comparing the sky surface density of the present cluster sample with the northern BCS sample: at the flux-limit of BCS, the BCS sample reaches 78% of the surface density of clusters in the present sample (see Sect. 11 for details). This reduction in incompleteness is expected to go along with an increase in homogeneity.
For the construction of the present cluster sample optical, follow-up
observations, in addition to the X-ray analysis and X-ray/optical correlations,
are necessary to clearly identify the nature of the X-ray sources
and to determine the cluster redshifts.
To this aim we have conducted an intensive follow-up optical survey project
as an ESO key program from 1992 to 1999
(e.g. Böhringer 1994; Guzzo et al. 1995; Böhringer et al. 1998;
Guzzo et al. 1999) which has been termed REFLEX
(ROSAT-ESO-Flux-Limited-X-ray) Cluster Survey.
Within this program the identification of all the cluster candidates
at
![]() and
down to a flux limit of
3 10-12 ergs-1 cm-2
in the ROSAT band (0.1 to 2.4 keV) has been completed. This
sample includes 452 identified galaxy clusters, 449 of which have a measured
redshift. An extension of the identification programme
down to a lower flux limit has been started and a large number of redshifts
for this extension has already been secured.
and
down to a flux limit of
3 10-12 ergs-1 cm-2
in the ROSAT band (0.1 to 2.4 keV) has been completed. This
sample includes 452 identified galaxy clusters, 449 of which have a measured
redshift. An extension of the identification programme
down to a lower flux limit has been started and a large number of redshifts
for this extension has already been secured.
A complementary RASS cluster
redshift survey programme is conducted for the northern celestial hemisphere
in a collaboration by MPE, STScI, CfA, and ESO, the Northern ROSAT All-Sky
Cluster Survey (NORAS; e.g. Böhringer 1994; Burg et al. 1994)
and a first catalogue containing 483 identified X-ray galaxy clusters
has recently been published (Böhringer et al. 2000).
It is the future aim to combine the northern and southern surveys
which in our ongoing program are based on
slightly different identification strategies, mostly
due to the different optical data available. Work on homogenization
of this is in progress.
We have also successfully extended the cluster search into
the region close to the galactic plane covering about 2/3 of the region
with galactic latitude
![]() (Böhringer et al. 2001b).
In this paper, we describe the selection of the cluster candidate sample
for the REFLEX Survey.
The layout of the paper is as follows. In Sect. 2 we characterize
the depth and the sky area of the study and in Sect. 3 the basic RASS data
used as input. It was found that a reanalysis of the X-ray properties of the
clusters in the RASS was necessary for the project. This new reanalysis
technique and its results are presented in Sect. 4.
The selection of the galaxy cluster candidates by means of a correlation
of the X-ray source positions with the optical
data base from COSMOS is described in Sects. 5 and 6. The further X-ray source
classification is discussed in Sect. 7. Section 8 provides tests of the
sample completeness. The resulting REFLEX cluster sample for a flux limit
of
3 10-12 ergs-1 cm-2 (0.1-2.4 keV)
and some of its characteristics
is described in Sect. 9. Further statistics of the X-ray properties
of the REFLEX clusters and the contamination of the sample by non-cluster
sources is discussed in Sect. 10, and Sect. 11 provides a summary
and conclusions.
(Böhringer et al. 2001b).
In this paper, we describe the selection of the cluster candidate sample
for the REFLEX Survey.
The layout of the paper is as follows. In Sect. 2 we characterize
the depth and the sky area of the study and in Sect. 3 the basic RASS data
used as input. It was found that a reanalysis of the X-ray properties of the
clusters in the RASS was necessary for the project. This new reanalysis
technique and its results are presented in Sect. 4.
The selection of the galaxy cluster candidates by means of a correlation
of the X-ray source positions with the optical
data base from COSMOS is described in Sects. 5 and 6. The further X-ray source
classification is discussed in Sect. 7. Section 8 provides tests of the
sample completeness. The resulting REFLEX cluster sample for a flux limit
of
3 10-12 ergs-1 cm-2 (0.1-2.4 keV)
and some of its characteristics
is described in Sect. 9. Further statistics of the X-ray properties
of the REFLEX clusters and the contamination of the sample by non-cluster
sources is discussed in Sect. 10, and Sect. 11 provides a summary
and conclusions.
The total survey area after this excision amounts to 4.24 ster or 13924 deg2 which corresponds to 33.75% of the sky. This survey covers the largest area for which currently a homogeneous combined optical/X-ray survey is possible, since there is no optical survey covering both hemispheres simultaneously. The observational goal of this survey programme is the identification and redshift determination of all galaxy clusters in the study area above a given flux limit. In a first step, within the ESO key programme, we have completed the observations for a sample of 452 galaxy cluster (with redshifts for 449 clusters) above a limiting flux of 3 10-12 ergs-1 cm-2 (0.1-2.4 keV). In addition we have already secured many redshifts at lower fluxes and we plan to extend the redshift survey to flux limit of 1.6-2 10-12 ergs-1 cm-2. This corresponds to a count rate limit in the hard ROSAT band of about 0.08-0.1 cts s-1. With a typical exposure in the southern part of the RASS of about 330 sec this yields about 25-30 photons for the fainter sources. This is still just enough to determine a flux within uncertainty limits of typically less than 30% and provides some leverage for the determination of some source properties. At this flux limit we expect between 700 and 1000 galaxy clusters in the survey area (based on the number counts of previous surveys e.g. Gioia et al. 1990; Rosati et al. 1998).
For the preparation of the candidate sample we have therefore chosen
to start with a source sample with a count rate limit of 0.08 cts s-1
in the hard ROSAT band (channel 52 to 201 corresponding approximately to
an energy range of 0.5 to 2.0 keV). Note that all the fluxes quoted in
this paper refer to the total ROSAT energy band (0.1-2.4 keV) in
contrast to the more restricted band of pulse high channels chosen
for the determination of the count rate.
This count rate limit translates into
a flux limit for cluster type spectra of
1.55-1.95 10-12 ergs-1 cm-2, a range determined mainly by
variations of the interstellar HI column density in the REFLEX area
(20% in the range
1-10 1020 cm-2).
Weaker dependences on the cluster temperature (e.g. ![]() 1.4%
in the range 3-8 keV, see Fig. 8 in Böhringer et al. 2000)
and redshift (in analogy to the optical K-correction,
0.5% in the range z = 0 to z = 0.2) are found.
(Below about 2 keV the temperature
dependence is stronger, however.) We will be quoting
unabsorbed flux values in
the ROSAT energy band (defined as 0.1 to 2.4 keV) throughout this paper
since the results in this energy band are less dependent on the
spectral model assumptions for the sources compared to any other
significantly wider band definition.
Further assumptions or information on the source spectrum (e.g. intracluster
plasma temperatures) are
needed to subsequently convert these primary data to other energy
bands or to bolometric fluxes and luminosities.
1.4%
in the range 3-8 keV, see Fig. 8 in Böhringer et al. 2000)
and redshift (in analogy to the optical K-correction,
0.5% in the range z = 0 to z = 0.2) are found.
(Below about 2 keV the temperature
dependence is stronger, however.) We will be quoting
unabsorbed flux values in
the ROSAT energy band (defined as 0.1 to 2.4 keV) throughout this paper
since the results in this energy band are less dependent on the
spectral model assumptions for the sources compared to any other
significantly wider band definition.
Further assumptions or information on the source spectrum (e.g. intracluster
plasma temperatures) are
needed to subsequently convert these primary data to other energy
bands or to bolometric fluxes and luminosities.
For the calculations of the fluxes, the luminosities, and some other physical
parameters in this paper we have made the following assumptions. A first
approximate unabsorbed flux is calculated for each
X-ray source from the observed count rate,
prior to any knowledge about its nature and redshift by assuming a thermal
spectrum with a temperature of 5 keV, a metallicity of 0.3 solar
(with abundances taken from Anders & Grevesse (1989). A redshift of zero,
and an interstellar column density of hydrogen as obtained from Dickey
& Lockman (1990) & Stark et al. (1992) for the X-ray source position
is adopted.
This nominal flux is used to impose the flux limit on the X-ray source sample.
After a cluster has been identified and its redshift secured
a better temperature estimate is obtained by means of the
temperature/X-ray luminosity relation (Markevitch 1998)![]() ,
and a corrected flux
and X-ray luminosity is calculated taking the new estimated temperature,
the K-correction for the observed redshift, and the dependence on the
interstellar absorption into account. The X-ray luminosities are always
calculated in the ROSAT band in the cluster restframe, while the fluxes
are given in the ROSAT band for the observer frame as unabsorbed fluxes.
The calculations are performed within the EXSAS software system
(Zimmermann et al. 1994) with the spectral code from John Raymond
(Raymond & Smith 1977). Instead of using the standard codes of EXSAS
for the count rate-flux conversion we are using our own macros, which
have been tested against XSPEC and show a general agreement within less
than 3%. For the calculations of the luminosities and
other physical properties of the clusters we assume a standard cosmology
with H0 = 50 kms-1 Mpc-1,
,
and a corrected flux
and X-ray luminosity is calculated taking the new estimated temperature,
the K-correction for the observed redshift, and the dependence on the
interstellar absorption into account. The X-ray luminosities are always
calculated in the ROSAT band in the cluster restframe, while the fluxes
are given in the ROSAT band for the observer frame as unabsorbed fluxes.
The calculations are performed within the EXSAS software system
(Zimmermann et al. 1994) with the spectral code from John Raymond
(Raymond & Smith 1977). Instead of using the standard codes of EXSAS
for the count rate-flux conversion we are using our own macros, which
have been tested against XSPEC and show a general agreement within less
than 3%. For the calculations of the luminosities and
other physical properties of the clusters we assume a standard cosmology
with H0 = 50 kms-1 Mpc-1,
![]() and
and
![]() .
While the basis of the source detections is the standard analysis
of the RASS (Voges et al. 1999), we have reanalysed the source count rates
and other source properties as described in Sect. 4 with the growth
curve analysis technique. Note that previous
comparisons of the results of this technique with deeper pointed
ROSAT observations show that the measured flux underestimates the total
cluster flux, typically by an amount of 7-10%
(Böhringer et al. 2000).
The fluxes and luminosities quoted here are the measured values
without a correction for the possibly missing flux.
.
While the basis of the source detections is the standard analysis
of the RASS (Voges et al. 1999), we have reanalysed the source count rates
and other source properties as described in Sect. 4 with the growth
curve analysis technique. Note that previous
comparisons of the results of this technique with deeper pointed
ROSAT observations show that the measured flux underestimates the total
cluster flux, typically by an amount of 7-10%
(Böhringer et al. 2000).
The fluxes and luminosities quoted here are the measured values
without a correction for the possibly missing flux.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{aa10210f1.ps} %
\end{figure}](/articles/aa/full/2001/15/aa10210/Timg27.gif) |
Figure 1: Exposure time distribution of the ROSAT All-Sky Survey as analyzed in RASS II in the area of the REFLEX survey |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=13.3cm,clip]{aa10210f2.ps} %
\end{figure}](/articles/aa/full/2001/15/aa10210/Timg28.gif) |
Figure 2:
Exposure distribution in the area of the REFLEX survey. Four grey levels
have been used for the coding of the exposure times, with increasing intensity
for
|
| Open with DEXTER | |
For each source GCA returns (among other
information) the following most important parameters which will be
used in the source selection work:
![]() observed source count rate (background subtracted)
observed source count rate (background subtracted)
![]() Poisson error (photon statistics) for the count rate
Poisson error (photon statistics) for the count rate
![]() locally redetermined center of the source
locally redetermined center of the source
![]() mean exposure for the source region
mean exposure for the source region
![]() significance of the source detection
significance of the source detection
![]() estimate of the radius out to which the source emission
is significantly detected
estimate of the radius out to which the source emission
is significantly detected
![]() extrapolated source count rate (obtained by model fitting to
the source emission distribution)
extrapolated source count rate (obtained by model fitting to
the source emission distribution)
![]() hardness ratio characterizing the source spectrum and
its photon statistical error
hardness ratio characterizing the source spectrum and
its photon statistical error
![]() fitted source core radius
fitted source core radius
![]() Kolmogorov-Smirnov test probability that the source shape
is consistent with a point source
The basic parameters are derived for the photon distribution
in the three energy bands "hard'' (0.5 to 2.0 keV, channels 52-201),
"broad'' (0.1 to 2.4 keV, channels 11-240), and "soft'' (0.1 to 0.4 keV, channel 11-40). The band definitions are the same as those used
in the standard analysis (Voges et al. 1999).
Here we are only using the hard band results, since the clusters
are detected in this band with the highest signal to noise ratio.
An exception is the hardness ratio which
requires the results from the hard and soft bands.
Kolmogorov-Smirnov test probability that the source shape
is consistent with a point source
The basic parameters are derived for the photon distribution
in the three energy bands "hard'' (0.5 to 2.0 keV, channels 52-201),
"broad'' (0.1 to 2.4 keV, channels 11-240), and "soft'' (0.1 to 0.4 keV, channel 11-40). The band definitions are the same as those used
in the standard analysis (Voges et al. 1999).
Here we are only using the hard band results, since the clusters
are detected in this band with the highest signal to noise ratio.
An exception is the hardness ratio which
requires the results from the hard and soft bands.
![\begin{figure}
\par\includegraphics[width=5.8cm,clip]{aa10210f3.ps} %
\end{figure}](/articles/aa/full/2001/15/aa10210/Timg30.gif) |
Figure 3:
Example of the set-up of the source characterization method used
in the GCA technique. The image shows the hard band photon distribution from
an area of the RASS in a 1.5 degree box around the X-ray source.
The outer two circles enclose the area of the background
determination. This background area is divided into 12 sectors. The
two sectors marked by a cross are discarded from the background
determination. They are flagged by a |
| Open with DEXTER | |
The count rate is determined in two alternative ways. In the first
determination an outer radius of significant X-ray emission,
![]() ,
is determined
from the point where the increase in the
,
is determined
from the point where the increase in the ![]() error is larger
than the increase of the source signal. The integrated count rate
is then taken at this radius. In the second method a horizontal
level is fitted to the outer region of the growth curve (at
error is larger
than the increase of the source signal. The integrated count rate
is then taken at this radius. In the second method a horizontal
level is fitted to the outer region of the growth curve (at
![]() ),
and this plateau is adopted as the source flux. We use the second
approach as the standard method but use also the first method as a check,
and a way to estimate systematic uncertainties in the count rate
determination in addition to the pure photon statistical errors.
We also determine a fitted total count rate by means of a
),
and this plateau is adopted as the source flux. We use the second
approach as the standard method but use also the first method as a check,
and a way to estimate systematic uncertainties in the count rate
determination in addition to the pure photon statistical errors.
We also determine a fitted total count rate by means of a ![]() -model
as described below.
For sources where close neighbours disturb the count rate
measurement we run a separate deblending analysis.
-model
as described below.
For sources where close neighbours disturb the count rate
measurement we run a separate deblending analysis.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{aa10210f4.ps} %
\end{figure}](/articles/aa/full/2001/15/aa10210/Timg34.gif) |
Figure 4:
Integrated count rate profile for the source shown in Fig. 3.
The integrated count rate profile is background subtracted. The two
dashed curves give the photon statistical error ( |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14.5cm,clip]{aa10210f18a.ps}\end{figure}](/articles/aa/full/2001/15/aa10210/Timg35.gif) |
Figure 5: Flow diagram illustrating the major data reduction steps conducted in the construction of the REFLEX sample. Also shown are two side branches of the data analysis used to test the sample completeness based on a separate search for X-ray emission in RASS II for the clusters of Abell et al. (1989) and an inspection of all extended X-ray sources in the REFLEX area above the REFLEX flux-limit |
| Open with DEXTER | |
The two most important source quality parameters determined within GCA are the
spectral hardness ratio and the source extent.
The hardness ratio, HR, is defined as
![]() where H is the hard band and S the soft band source count rate
(both determined for the same outer radius limit).
where H is the hard band and S the soft band source count rate
(both determined for the same outer radius limit).
The source extent is investigated in two ways.
In the first analysis a ![]() -model profile (Cavaliere & Fusco-Femiano 1976)
convolved with the averaged survey PSF
(G. Hasinger, private communication) is fitted to the differential
count rate profile (using a fixed value of
-model profile (Cavaliere & Fusco-Femiano 1976)
convolved with the averaged survey PSF
(G. Hasinger, private communication) is fitted to the differential
count rate profile (using a fixed value of ![]() of 2/3) yielding
a core radius,
of 2/3) yielding
a core radius, ![]() ,
and a fitted total count rate. Secondly, a
Kolmogorov-Smirnov test is used to estimate the probability that
the source is consistent with a point source. The source is flagged to
be extended when the KS probability is less than
0.01. Tests with X-ray sources which have been identified with
stars or AGN show a false classification rate as extended sources
of about 5% (these results will be discussed in detail in a
subsequent paper).
,
and a fitted total count rate. Secondly, a
Kolmogorov-Smirnov test is used to estimate the probability that
the source is consistent with a point source. The source is flagged to
be extended when the KS probability is less than
0.01. Tests with X-ray sources which have been identified with
stars or AGN show a false classification rate as extended sources
of about 5% (these results will be discussed in detail in a
subsequent paper).
All 54076 RASS II sources in the REFLEX study region were subjected to the
GCA reanalysis. All sources with a count rate ![]() ctss-1were retained for the primary sample.
ctss-1were retained for the primary sample.
For the first sample cut in count rate we have been very conservative.
In addition to selecting all sources with a count rate
![]() ctss-1 as measured at
ctss-1 as measured at
![]() we have also retained
all sources featuring a fitted total source count rate above this
value in the
we have also retained
all sources featuring a fitted total source count rate above this
value in the ![]() -model fit and a
significance for the source detection
-model fit and a
significance for the source detection
![]() .
While this leads
to the inclusion of a significant fraction of sources below the count
rate cut (due to less successful
.
While this leads
to the inclusion of a significant fraction of sources below the count
rate cut (due to less successful ![]() -model fits) it also ensures
that sources with pathological count rate profiles featuring an
underestimate of
-model fits) it also ensures
that sources with pathological count rate profiles featuring an
underestimate of
![]() are not lost before all sources can individually
be inspected in the GCA diagnostic plots.
A comparison of the GCA determined
count rate (first method) and the fitted count rate
is shown in Fig. 6.
There is a good correlation of the two count rate values above a measured count
rate of about 0.1 ctss-1. At low values of
the GCA count rate, the fitted count rates show a large scatter. This
is mostly due to the poor photon statistics providing not enough
constraints on the source shape for a good enough
are not lost before all sources can individually
be inspected in the GCA diagnostic plots.
A comparison of the GCA determined
count rate (first method) and the fitted count rate
is shown in Fig. 6.
There is a good correlation of the two count rate values above a measured count
rate of about 0.1 ctss-1. At low values of
the GCA count rate, the fitted count rates show a large scatter. This
is mostly due to the poor photon statistics providing not enough
constraints on the source shape for a good enough ![]() -model fit.
A closer inspection of the results shows that at low count rates the
fitted results give overestimates in more than one fourth of the sources,
leading to an oversampling of about 20%. Simulations have shown
that the reason for this is an overestimate of the core radius
for sources with small photon numbers. This is one reason why it
is preferable not to use model fits or the SRT method described
in De Grandi et al. (1997) for sources with low photon statistics.
The oversampling is of no harm to
the final sample construction, since the final REFLEX sample is
obtained by another cut in flux well above this limit.
-model fit.
A closer inspection of the results shows that at low count rates the
fitted results give overestimates in more than one fourth of the sources,
leading to an oversampling of about 20%. Simulations have shown
that the reason for this is an overestimate of the core radius
for sources with small photon numbers. This is one reason why it
is preferable not to use model fits or the SRT method described
in De Grandi et al. (1997) for sources with low photon statistics.
The oversampling is of no harm to
the final sample construction, since the final REFLEX sample is
obtained by another cut in flux well above this limit.
In total the first count rate cut leads to a sample of 6593 sources.
This sample contains still a large number of original multiple detections
of extended sources by the RASS II standard analysis. The new
analysis method offers an efficient way
of removing most of these multiple detections.
In the redetermination of the source center in the GCA analysis,
the technique usually finds a common center for the multiple detection
of clusters within small numerical
differences in the position (generally < 1 arcmin).
Since at a separation of
2 arcmin also point sources are already overlapping, we have used
a maximal separation of 2 arcmin to identify
these multiple detections as a single structure in the further identification process.
Removing the redundant detections
the source list shrinks to 4410 sources.
This is the sample that was subjected to the first X-ray optical
correlation as described in the next section.
Further screening revealed another 204 redundant detections in very extended
clusters where the method has settled in different local maxima
(with a separation larger than 2 arcmin), but
which are easily recognized visually
as continuous patches in the photon distribution.
Figure 5 summarizes the
number of sources obtained in the subsequent
steps of the X-ray source sample construction as well as
the further data reduction steps described in the following.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{aa10210f5.ps} %
\end{figure}](/articles/aa/full/2001/15/aa10210/Timg40.gif) |
Figure 6: Comparison of the count rates determined for the RASS sources in the REFLEX study area with both techniques, the "measured'' count rate out to the radius of significant X-ray emission and the count rate obtained by fitting a King profile to the source count rate profile shape. The diagonal line gives the location of the points for which both measures are equal. The vertical and horizontal line give the count rate cut values for the two techniques, respectively. The data for which the significance of the detected signal is found to be greater than 3 are marked by heavy dots, while the data below this significance threshold are plotted by light dots. In the graph for clarity only the first 5000 sources of the total sample of 54076 sources are shown |
| Open with DEXTER | |
Figure 8 shows in a similar way the typical signal-to-noise
ratio (
![]() ,
where
,
where ![]() are the
source counts and
are the
source counts and ![]() are the background counts in the source
region) for the flux measurement of a source as a function
of the X-ray flux. Again there are some sources with a low
significance for the source flux determination, which come from the
low exposure areas.
are the background counts in the source
region) for the flux measurement of a source as a function
of the X-ray flux. Again there are some sources with a low
significance for the source flux determination, which come from the
low exposure areas.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{aa10210f6.ps}\end{figure}](/articles/aa/full/2001/15/aa10210/Timg44.gif) |
Figure 7: Distribution of the number of source photons (background subtracted) obtained as a function of the X-ray flux |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{aa10210f7.ps}\end{figure}](/articles/aa/full/2001/15/aa10210/Timg45.gif) |
Figure 8: Distribution of the signal-to-noise of the flux determination as a function of the X-ray flux. For the definition of the significance parameter see the text |
| Open with DEXTER | |
Since the X-ray properties which are described above do not allow by themselves an identification of the X-ray sources associated to clusters, we have to include information from an optical data base in the further identification process. For this we are using the most comprehensive optical data base covering the southern sky and the area of the REFLEX survey: the COSMOS scans of the UK-Schmidt survey plates (MacGillivray & Stobie 1984). There are also the complementary APM scans of the same photographic survey material, but the galaxy classification in the APM survey concentrates on the southern part of the sky south of the galactic plane (Maddox et al. 1990) which covers only about 2/3 of the REFLEX region.
The UK-Schmidt survey has been performed using IIIa-J photographic
plates at the 1.2m UK-Schmidt-telescope.
The plates were scanned
within a sky area of about
![]() per plate
with the fast COSMOS scanning machine and subsequently analysed
yielding 32 parameters for the source characterization
per object. These parameters describe the object position,
intensity, shape, and classify the type of object.
Object images are recognized down to about
per plate
with the fast COSMOS scanning machine and subsequently analysed
yielding 32 parameters for the source characterization
per object. These parameters describe the object position,
intensity, shape, and classify the type of object.
Object images are recognized down to about
![]() mag.
This allows a subsequent star/galaxy separation which
has been estimated to be about 95% complete with about 5% contamination
to
mag.
This allows a subsequent star/galaxy separation which
has been estimated to be about 95% complete with about 5% contamination
to
![]() mag and about 90% complete with about 10%
contamination to
mag and about 90% complete with about 10%
contamination to
![]() mag (Heydon-Dumbleton et al. 1989; Yentis et al. 1992; MacGillivray et al. 1994,
and Mac Gillivray priv. communication). The galaxy magnitudes were
intercalibrated between the different plates using the substantial
plate overlaps and absolutely calibrated by CCD sequences
(Heydon-Dumbleton et al. 1989; MacGillivray et al. 1994).
mag (Heydon-Dumbleton et al. 1989; Yentis et al. 1992; MacGillivray et al. 1994,
and Mac Gillivray priv. communication). The galaxy magnitudes were
intercalibrated between the different plates using the substantial
plate overlaps and absolutely calibrated by CCD sequences
(Heydon-Dumbleton et al. 1989; MacGillivray et al. 1994).
Here we should make some remarks about the strategy behind the choice of the present cluster search algorithm. As mentioned before it is difficult to devise a good algorithm to select the most massive clusters of galaxies from optical sky survey images. We use a comparatively simple algorithm (aperture counts as compared to e.g. matched filter techniques). This simple technique seems well adapted to our needs and the depth of the COSMOS data set: (i) the technique is used to only flag the candidates and there is no need to determine a cluster richness, since we use the X-ray emission for a quantitative measure of the clusters; (ii) while matched filter techniques may introduce a bias, since a priori assumptions are made about the shape of an idealized, azimuthally symmetric cluster, we are interested in introducing as little bias and as few presumptions as possible; (iii) the actual numbers in the galaxy counts are limited and therefore the shape matching is not precise and is affected by low number statistical noise. Therefore our technique is not seen as a perfect and objective cluster characterization algorithm. The cluster selection should primarily depend on the X-ray criteria. We have chosen a very low cut for the optical selection which results in a substantially larger candidate sample compared to the expected number of clusters, with an estimated contamination of as much as 30-40%. But it assures on the other hand that we have a highly complete candidate sample. This overabundance of candidates is thus a necessary condition to obtain an essentially X-ray selected sample for our survey.
The galaxy counts are performed for 5 different radial aperture sizes: 1.5, 3, 5, 7.5, and 10 arcmin radius with no magnitude limit for the galaxies selected. Since an aperture size of about 0.5h50-1 Mpc in physical scale corresponding to about two core radii of a rich cluster provides a good sampling of the high signal-to-noise part of the galaxy overdensity in a cluster, the chosen set of apertures gives a good redshift coverage in the range from about z = 0.02 to 0.3 as shown by the values given in Table 4. With this choice and the depth limit of the COSMOS data set we are aiming at a high completeness in the cluster search out to a redshift of about z = 0.3. For this goal the chosen flux limit and the depth of the COSMOS data base are quite well matched as the richest and most massive clusters are still detected in both data sets out to this redshift.
The galaxy counts around the given
X-ray source positions are compared with the number count distributions
for 1000 random positions for each photographic plate.
With this comparison we are also accounting for plate to plate variations
in depth as explained below. The number count
histograms for the random positions have been generated at the
Naval Research Laboratory in preparation of a COSMOS galaxy cluster catalogue,
the SGP pilot study (Yentis et al. 1992; Cruddace et al. 2000), and for
this ESO key program. The results of the random
counts yield a differential probability density distribution,
![]() ,
of finding a number
of
,
of finding a number
of
![]() galaxies at random positions. An example for the distribution
galaxies at random positions. An example for the distribution
![]() for an average of 5 randomly selected plates is shown in
Fig. 9 for all five aperture sizes. (Note that
for an average of 5 randomly selected plates is shown in
Fig. 9 for all five aperture sizes. (Note that
![]() is defined here as a normalized probability density distribution
function while in Fig. 9 we show histograms of the form
is defined here as a normalized probability density distribution
function while in Fig. 9 we show histograms of the form
![]() ).
The distribution functions resemble
Poisson distributions (The possible theoretical description of the functions
is not further pursued here since we are only interested in the purely
empirical application to the following statistical analysis). In Fig. 10
the random count histogram for aperture 2 (3 arcmin radius) is
compared to the counting results for the 4206 X-ray source positions.
We note the large number of sources with significant galaxy
overdensities in the X-ray source sample compared to the random counts,
and expect to find the X-ray clusters in this high count tail
of the distribution.
).
The distribution functions resemble
Poisson distributions (The possible theoretical description of the functions
is not further pursued here since we are only interested in the purely
empirical application to the following statistical analysis). In Fig. 10
the random count histogram for aperture 2 (3 arcmin radius) is
compared to the counting results for the 4206 X-ray source positions.
We note the large number of sources with significant galaxy
overdensities in the X-ray source sample compared to the random counts,
and expect to find the X-ray clusters in this high count tail
of the distribution.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{aa10210f8.ps} %
\end{figure}](/articles/aa/full/2001/15/aa10210/Timg52.gif) |
Figure 9:
Example of the distributions of galaxy number counts,
|
| Open with DEXTER | |
These results for
![]() are then used
in the form of cumulative probability distribution functions
are then used
in the form of cumulative probability distribution functions
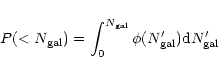 |
(1) |
Going back to the random sample, taking each of the values of
![]() assigned to each counting result, and plotting
the distribution function
assigned to each counting result, and plotting
the distribution function
![]() we will find that this function is a constant. This follows
simply from the chain rule of differentiation in the following
way
we will find that this function is a constant. This follows
simply from the chain rule of differentiation in the following
way
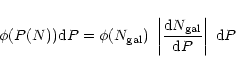 |
(2) |
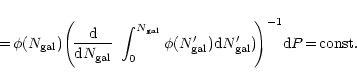 |
(3) |
For the further evaluation of this type of diagrams we make the following
simplifying assumptions: i) the distribution function is composed of
two types of counting results, results obtained for cluster
X-ray sources and results obtained for other sources, and ii) the
non-cluster X-ray sources are not correlated to the galaxy
distribution in the COSMOS data base and thus constitute effectively
a set of random counts. This latter assumption is of course not strictly
true for all the non-cluster X-ray sources. While it may be justified to
treat stars and other galactic sources as well as distant quasars
as independent of the nearby galaxy distribution, there is also a population
of extragalactic sources like low redshift AGN and starburst-galaxies
that we know are correlated to the
large-scale structure in the galaxy distribution.
However, the practical assumption that this correlation
is weak in comparison to the galaxy density enhancements in clusters of
galaxies is generally well justified.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{aa10210f9.ps}\end{figure}](/articles/aa/full/2001/15/aa10210/Timg62.gif) |
Figure 10: Example of the distributions of galaxy number counts in a circular aperture with 3 arcmin radius for an average of five UK Schmidt plates and 1000 random positions per plate (thin line). This distribution is compared to the results of the galaxy number counts for the 4206 X-ray sources of the sample for the same aperture radius. The histogram for the random position counts has been normalized to the histogram of the X-ray source counts so that the peaks have the same hight |
| Open with DEXTER | |
With this assumption we expect to find a distribution function
![]() composed of a constant function and a peak at
high P-values. Subtracting the constant function
leaves us with the cluster sources. This is
schematically illustrated in Fig. 12.
For the selection of the cluster candidates we can now either select
the sources which feature a high value of
composed of a constant function and a peak at
high P-values. Subtracting the constant function
leaves us with the cluster sources. This is
schematically illustrated in Fig. 12.
For the selection of the cluster candidates we can now either select
the sources which feature a high value of
![]() or a high
value of
or a high
value of
![]() .
We choose to use
.
We choose to use
![]() for the
sample selection (as justified further below) in such a way that most
of the cluster peak is included in the extracted sample (that is
choosing
for the
sample selection (as justified further below) in such a way that most
of the cluster peak is included in the extracted sample (that is
choosing
![]() such that the fraction C in Fig. 12
of cluster lost from the sample is small or negligible).
such that the fraction C in Fig. 12
of cluster lost from the sample is small or negligible).
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{aa10210f10.ps} %
\end{figure}](/articles/aa/full/2001/15/aa10210/Timg63.gif) |
Figure 11:
Histogram of the galaxy excess probabilities, |
| Open with DEXTER | |
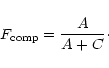 |
(4) |
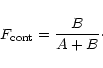 |
(5) |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{aa10210f11.ps} %
\end{figure}](/articles/aa/full/2001/15/aa10210/Timg70.gif) |
Figure 12:
Sketch of the typical result of the distribution function
|
| Open with DEXTER | |
 |
In total 452 stars with clearly visible diffraction spikes, 32
nearby galaxies, and 204 redundant detections of diffuse X-ray
sources were removed from the sample. With the cleaned sample
we can now repeat the statistical analysis with
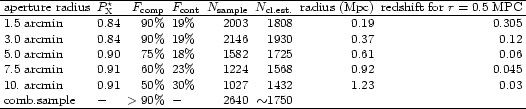
results given in Table 4. The sample selection cut
is kept the same as above. (Note that in this statistics there are
about 8% of the sources missing which leads to a lower normalization
but has no effect on the conclusions drawn in the following).
We note that this time the statistics indicates a number
of about 800-900 for the expected number of
clusters in the sample which is close to our expectations
based on a comparison with cluster number counts found
in deeper surveys (e.g. Gioia et al. 1990; Rosati 1998) as discussed
in Sect. 2. We also note, that for the combined sample of
candidates from the different aperture sizes,
we obtain a total sample size which is about a factor of ![]() 1.5
larger than the estimated number of true clusters. Thus we expect
a level of contamination of non-cluster sources
around
1.5
larger than the estimated number of true clusters. Thus we expect
a level of contamination of non-cluster sources
around ![]() .
This implies a
laborious further identification work to clean the sample from
the contamination, a price to be paid for the high completeness level
aimed for.
.
This implies a
laborious further identification work to clean the sample from
the contamination, a price to be paid for the high completeness level
aimed for.
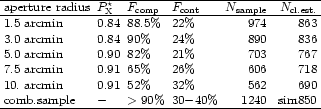 |
To analyse how well the cluster selection has worked we anticipate
the results of the REFLEX survey and the final identification
of the cluster candidates.
We repeat the statistical analysis including all the sources from
the starting sample with a flux in excess of
3 10-12 ergs-1 cm-2, corresponding to the flux limit of the REFLEX sample
(1417 sources without the multiple detections) except for the
stars with diffraction spikes, and the nearby galaxies (1169 X-ray sources).
The results of the cluster search for this high-flux sample
(with the same values for the selection parameter,
![]() as used
before) and the comparison with the final REFLEX
sample is given in Table 5.
as used
before) and the comparison with the final REFLEX
sample is given in Table 5.
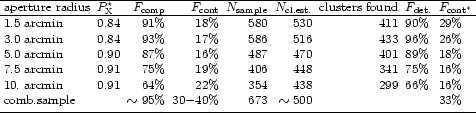 |
We note from the results given in Table 5 that the predictions are
very close to the actual
findings. One has to be careful, however, in the interpretation of this
comparison. In fact the general agreement should not be surprising as we
have used the same statistics to select the sample and we have
not yet used any independent means to include clusters missed by
our search to check the incompleteness independently.
Nevertheless a few results are striking. The number
of clusters predicted to be found is close to the number actually
identified. This shows that the signal observed in the diagnostic
plots of the type of Fig. 12 is indeed due to galaxy clusters
and there is no large contamination by other objects.
Had we found for example much less clusters
than predicted, we would be forced to speculate on the
presence of another source population
that mimics clusters in our analysis. This is obviously not the case
and the high
![]() signal is correctly representing the clusters
in the REFLEX sample.
Also the trend in the efficiency
of the different apertures in finding the clusters is predicted
roughly correctly. There are only small differences, as for example
that the total number of clusters and the contamination predicted from
the results of the first two apertures are too high and too low,
respectively.
signal is correctly representing the clusters
in the REFLEX sample.
Also the trend in the efficiency
of the different apertures in finding the clusters is predicted
roughly correctly. There are only small differences, as for example
that the total number of clusters and the contamination predicted from
the results of the first two apertures are too high and too low,
respectively.
Most of the clusters identified in the REFLEX survey (96%)
are detected in the search with aperture 2 with a radius of 3 arcmin.
That this ring size is the most effective is also shown in Fig. 13
where we compare the distribution of the probability values
![]() for
the source sample and for
the subsample which was identified as clusters in the course of
the REFLEX Survey. Only 16 additional clusters are found in aperture
1 with 1.5 arcmin radius and only 3 in the last three apertures.
The peak of the cluster signal is less constrained in the apertures
1, 3, 4, and 5 as shown in Fig. 13.
The large overlap in the detection of the clusters with the different
apertures is illustrated in Fig. 14 for
apertures 2, 3, and 4. Compared to the statistics in the starting sample
the predicted completeness has increased for the high flux sample
mostly due to the fact that the cluster signal in the statistical
analysis becomes better defined with increasing flux limit. Thus
the statistics of aperture 2 alone gives an internal completeness
estimate of 93%. Since the results of the different searches
are highly correlated (see Fig. 14) we cannot easily combine the
results in a statistically strict sense. A rough estimate is given
by a simple extrapolation from the completeness and the sample size
found for aperture 2 (93% for 433 clusters)
and the additional number of 19 clusters found
exclusively in other rings yielding a formal value of 97%.
for
the source sample and for
the subsample which was identified as clusters in the course of
the REFLEX Survey. Only 16 additional clusters are found in aperture
1 with 1.5 arcmin radius and only 3 in the last three apertures.
The peak of the cluster signal is less constrained in the apertures
1, 3, 4, and 5 as shown in Fig. 13.
The large overlap in the detection of the clusters with the different
apertures is illustrated in Fig. 14 for
apertures 2, 3, and 4. Compared to the statistics in the starting sample
the predicted completeness has increased for the high flux sample
mostly due to the fact that the cluster signal in the statistical
analysis becomes better defined with increasing flux limit. Thus
the statistics of aperture 2 alone gives an internal completeness
estimate of 93%. Since the results of the different searches
are highly correlated (see Fig. 14) we cannot easily combine the
results in a statistically strict sense. A rough estimate is given
by a simple extrapolation from the completeness and the sample size
found for aperture 2 (93% for 433 clusters)
and the additional number of 19 clusters found
exclusively in other rings yielding a formal value of 97%.
The latter number should be treated with care, however, as an internal
completeness check. This statistics would be more reliable if we had
one homogeneous population of clusters. Since our clusters cover a wide
range of richnesses and redshifts we cannot assume that all subsamples
contribute to the cluster signal in Fig. 12 in the same way.
If for example
no significant galaxy overdensity could be detected for the high redshift
clusters, this subsample would not enter into the statistics at all.
Likewise, galaxy clusters for which the X-ray detections are missed
in the basic source detection process are also not included in this
prediction.
Therefore the good agreement between the above predictions and
the final results
supports our confidence in the high quality of the sample but it is not
a sufficient test for completeness. We discuss further
external tests in Sect. 8.
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{aa10210f12.ps} %
\end{figure}](/articles/aa/full/2001/15/aa10210/Timg77.gif) |
Figure 13: Results for the cluster search with four of the five different circular apertures for the flux limit of the REFLEX sample. The thin (upper) line shows the statistics for the input sample and the thick (lower) line the results for the REFLEX clusters. The probability values plotted are defined by Eq. (1) |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{aa10210f16.ps}\end{figure}](/articles/aa/full/2001/15/aa10210/Timg78.gif) |
Figure 14: Number of cluster candidates selected by means of the aperture counts in rings 1 to 3 (3, 5, 7.5 arcmin, respectively) and number of clusters found in the REFLEX Survey (values in brackets) |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{aa10210f17.ps}\end{figure}](/articles/aa/full/2001/15/aa10210/Timg79.gif) |
Figure 15: Distribution of the numbers of galaxies detected in rings 1-3 for the clusters in the REFLEX sample. Thin line: 1.5 arcmin aperture, thick line: 3 arcmin aperture, broken line: 5 arcmin aperture |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{aa10210f18.ps}\end{figure}](/articles/aa/full/2001/15/aa10210/Timg80.gif) |
Figure 16: Distribution of the significance values of the detections of galaxy overdensities in rings 1-3 for the clusters in the REFLEX sample |
| Open with DEXTER | |
Another useful illustration concerns the question of how well defined
the galaxy overdensity signal is for an individual cluster. An answer
is given in Figs. 15 and 16 where
we show the number
of galaxies (above the background density) for the galaxy
counts in aperture 1, 2, and 3 for the clusters of the REFLEX sample.
For aperture 2 we find for example that the typical count result
is about 20 galaxies per cluster providing a signal of about ![]() .
Thus in general the overdensity signal is very well defined. There
is a tail to low number counts and significances which involves
only a few clusters, however. For aperture 1 we note that the number counts
and significance values are substantially less. Increasing the aperture
size beyond 3 arcmin increases the mean significance of the galaxy
counts, as seen in the results for aperture 3. But what is more
important: the tail towards low significance values is not reduced
if we compare aperture 3 to aperture 2. This once again shows the effectiveness
of aperture 2. One should also note the strong overlap of the results of
the different apertures as illustrated in Fig. 14 which
is reenforcing the significance of the selection results. In fact,
about 60% of all the REFLEX clusters are flagged in the counting results
for all five apertures. It is not surprising that the second aperture
with a 3 arcmin radius features as best adapted for our survey, since 3 arcmin
corresponds to a physical scale of about
370 h50-1 kpc at the
median distance of the REFLEX clusters,
.
Thus in general the overdensity signal is very well defined. There
is a tail to low number counts and significances which involves
only a few clusters, however. For aperture 1 we note that the number counts
and significance values are substantially less. Increasing the aperture
size beyond 3 arcmin increases the mean significance of the galaxy
counts, as seen in the results for aperture 3. But what is more
important: the tail towards low significance values is not reduced
if we compare aperture 3 to aperture 2. This once again shows the effectiveness
of aperture 2. One should also note the strong overlap of the results of
the different apertures as illustrated in Fig. 14 which
is reenforcing the significance of the selection results. In fact,
about 60% of all the REFLEX clusters are flagged in the counting results
for all five apertures. It is not surprising that the second aperture
with a 3 arcmin radius features as best adapted for our survey, since 3 arcmin
corresponds to a physical scale of about
370 h50-1 kpc at the
median distance of the REFLEX clusters,
![]() ,
(see also Table 3).
This corresponds to about 1.5 core radii,
a good sample radius to capture the high surface density part of the clusters.
,
(see also Table 3).
This corresponds to about 1.5 core radii,
a good sample radius to capture the high surface density part of the clusters.
In Figs. 17 to 19 we show the galaxy number
counts and significances
for aperture 2 as a function of flux
and redshift. While there is no striking correlation with flux we clearly
note the decrease of the number counts and significance values
even for the richest clusters with redshift.
In Fig. 18 we also show the expected number counts for a rich
cluster (with an Abell richness of 100, which is the number of galaxies
within
r = 3h50-1 Mpc and a magnitude interval ranging from the third
brightest galaxy to a limit 2 magnitudes deeper) as a function of redshift
for three magnitude limits for the galaxy detection on the plates of
![]() ,
21, 22 mag. Galaxies are still classified in the COSMOS
data base down to 22nd magnitude but the completeness is decreasing
continuously over the magnitude range from
,
21, 22 mag. Galaxies are still classified in the COSMOS
data base down to 22nd magnitude but the completeness is decreasing
continuously over the magnitude range from
![]() -22. For the calculation
we assume a Schechter function for the galaxy luminosity function with a slope
of -1.2 and
-22. For the calculation
we assume a Schechter function for the galaxy luminosity function with a slope
of -1.2 and
![]() ,
a cluster shape characterized by a King model
with a core radius of
0.5 h50-1 Mpc, and a K-correction of
,
a cluster shape characterized by a King model
with a core radius of
0.5 h50-1 Mpc, and a K-correction of
![]() (see e.g. Efstathiou et al. 1988; Dalton et al. 1997). The dashed curves in
Fig. 18 give then the number of galaxy counts expected for the various
magnitude limits. We note that the distribution of the data points
are well described by the theoretical curves with a steep rise at low
redshift which is due to an increasing part of the cluster being covered by the
aperture and the decrease at high redshift when only the very brightest
cluster galaxies are detected. We also not the increasing difficulty to
recognize clusters above a redshift of z = 0.3.
(see e.g. Efstathiou et al. 1988; Dalton et al. 1997). The dashed curves in
Fig. 18 give then the number of galaxy counts expected for the various
magnitude limits. We note that the distribution of the data points
are well described by the theoretical curves with a steep rise at low
redshift which is due to an increasing part of the cluster being covered by the
aperture and the decrease at high redshift when only the very brightest
cluster galaxies are detected. We also not the increasing difficulty to
recognize clusters above a redshift of z = 0.3.
Tests based on the comparison of the cluster
redshift distribution with simulations involving the REFLEX X-ray luminosity
and selection function (in right ascension, declination and redshift)
and assuming no evolution of the cluster population with redshift
show that there is no significant deficit of clusters
in the sample out to a redshift z = 0.3 (e.g. Fig. 8 in Schuecker et al. 2000).
Even beyond a redshift of 0.3 where the detection of clusters in the
COSMOS data becomes more difficult, we note no deficit in the
cluster population. Calculations based on a no-evolution assumption, in the
X-ray luminosity function as derived in the forthcoming paper (Böhringer et al.
2001a), and on the selection function derived here, lead to the prediction
of an expectation value for the detection at redshifts beyond z = 0.3 of
12 clusters, where 11 have been found. This indicates
that the most distant clusters in REFLEX are optically rich enough to
just be captured by the galaxy count technique applied to the COSMOS data.
Even the most distant clusters in the sample, which have independently
been found as extended RASS sources, are detected and selected
by the correlation based on the COSMOS data. The actual significance
value of ![]() for the extreme case of the most distant REFLEX
cluster at z=0.45, RXCJ1347.4-1144, (
for the extreme case of the most distant REFLEX
cluster at z=0.45, RXCJ1347.4-1144, (![]() for
aperture 3) and
for
aperture 3) and
![]() for the second most distant cluster
at z=0.42(found in aperture 1 with a
for the second most distant cluster
at z=0.42(found in aperture 1 with a ![]() signal) are quite low
for aperture 2, however. Still, the significance in the optimal aperture
is surprisingly good for the high redshifts of these clusters.
signal) are quite low
for aperture 2, however. Still, the significance in the optimal aperture
is surprisingly good for the high redshifts of these clusters.
In summary, we conclude that our combined use of X-ray and optical
data leads to a very
successful selection of cluster candidates without an introduction
of a significant optical bias, and we expect to be over
90% complete for the chosen X-ray flux limit.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{aa10210f19.ps}\end{figure}](/articles/aa/full/2001/15/aa10210/Timg90.gif) |
Figure 17: Distribution of the number of galaxies counted in aperture 2 versus X-ray flux. The background galaxy density has been subtracted from the aperture counts |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{aa10210f20.ps}\end{figure}](/articles/aa/full/2001/15/aa10210/Timg91.gif) |
Figure 18:
Distribution of the number of galaxies counted in aperture 2
versus redshift. Also shown are the expected number counts for this aperture
for a cluster with an Abell richness of 100 for the optical magnitude limits
of |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{aa10210f21.ps}\end{figure}](/articles/aa/full/2001/15/aa10210/Timg92.gif) |
Figure 19: Distribution of the significance of the galaxy overdensity for the galaxies found in aperture 2 versus redshift. Note that the significance can get negative if the number of galaxies counted in the aperture is less than the background value |
| Open with DEXTER | |
After this anticipation of the final results we return to the sequence of the REFLEX sample construction. Up to this point we have compiled a sample of cluster candidates relying only on machine based algorithms (except for the manual exclusion of obvious pathological cases like the bright diffraction spike stellar images and the multiple detections). The only two selection criteria are the X-ray flux limit for the X-ray sources and a signal of a galaxy overdensity in the optical data. This sample has still an estimated contamination of non-cluster X-ray sources of 30-40% (as discussed in the previous section). For the identification work that follows we treat each source individually, compile as much information as possible, and try to arrive at a safe classification in each case. The types of information used are the X-ray properties of the source, optical images (from the STScI scans of the POSS and UK Schmidt plates or CCD images if available), and literature information (including previous X-ray source identifications).
The basic X-ray source parameters used to assess the source properties
are the probability
for an extension of the X-ray emission (from the Kolmogorov-Smirnov
test mentioned above) and the spectral hardness ratio. The
hardness ratio and its photon statistical error is compared
to the expected hardness ratio for a thermal cluster spectrum
for a temperature of 5 keV and the absorbing interstellar column
density at the source position (Dickey & Lockman 1990), for
details see Böhringer et al. (2000). As a measure of the
consistency of the observation with X-ray emission from the
intracluster plasma of a cluster, we take the deviation of the
predicted and observed hardness ratio in units of the statistical error
(in ![]() units).
units).
In a first step we are discarding all sources that can be unambiguously classified as non-cluster objects. As a safe exclusion criterion we have either accepted a well documented previous identification or combined at least two quality criteria which exclude the identification as a cluster. Thus the following information leads to discarding a cluster candidate source:
i) Positive identification as a non-cluster X-ray source in the literature.
ii) The X-ray source is both well consistent with a point source
and deviates by more than ![]() from the theoretically
predicted hardness ratio of an X-ray cluster. In addition we
find no indication of a cluster in the optical images.
from the theoretically
predicted hardness ratio of an X-ray cluster. In addition we
find no indication of a cluster in the optical images.
iii) The X-ray source is point-like and there is an AGN spectrum observed for a galaxy or a point-like optical object at the X-ray source position.
iv) A point-like X-ray source coincides with a
![]() mag star
(within a radius of about 30 arcsec) and there is
no cluster visible in the optical image.
mag star
(within a radius of about 30 arcsec) and there is
no cluster visible in the optical image.
A large part of the contamination fraction can be removed from the source list by use of these criteria. The positive identifications are given simply by the observation of a clearly extended X-ray source and a galaxy cluster in the optical images. For all the X-ray sources for which no clear classifications can be obtained and also for all clusters that have not been identified previously and for which no redshift is available, further spectroscopic and if necessary imaging observations were conducted. In total 431 targets were observed by us within the ESO key programme for this project (including candidates with X-ray fluxes below the current flux limit of the REFLEX survey) as well as additional targets in related programmes (e.g. Cruddace et al. 2000 in preparation).
The identification strategy in the optical follow-up observations is similar to the scheme given above. We either try to establish the existence of a galaxy cluster as the counterpart of the X-ray source by securing several coincident galaxy redshifts in the X-ray source field or by arriving at an alternative identification of the X-ray source which is in general an AGN. AGN are found for about 10% of the sources for which spectra were taken. More details about the identification process and the different types of non-cluster sources found within the ESO key programme will be given in a subsequent paper which will also provide the object catalogue. Here we concentrate on discussing the statistics of some X-ray properties of the cluster and non-cluster X-ray sources in Sect. 10.
To further test the completeness of the REFLEX sample we have conducted two additional searches for clusters. The first search is based on the X-ray source extent and the second on a systematic search for X-ray emission from Abell clusters.
In the search for clusters among the extended RASS sources we have
inspected all sources in the flux limited sample
(
![]() ergs-1 cm-2)
which feature a KS-probability less than 0.01 of being point-like
and which are not already included in the REFLEX sample.
In total 48 additional extended sources are found (after removal
of strange detections at exposure edges and fragments of larger
clusters already included in REFLEX). 35 of these sources are
identified with bright stars and QSO and we notice that they
are often borderline cases concerning the extent significance; another
fraction of these sources feature an extent in the analysis
without deblending because they are close
pairs of point sources with identifications other than clusters.
The remaining objects for which a cluster identification cannot
be ruled out are in total 13 X-ray sources: 8 certain clusters,
2 good looking cluster candidates and 3 fields with no indication for
a galaxy cluster and no obvious other identification. We
are planning further deeper imaging for the latter sources.
Thus we have found about 10
objects in this search which have been missed in the REFLEX
compilation. The above result can also be used for another
interesting and useful statistic. The 35 partly spuriously extended
sources among the non-cluster candidates (plus the 28 extended
non-cluster sources mentioned in Sect. 10) if compared to an
initial sample of 1050 sources (above the REFLEX cut with extended
cluster sources subtracted) implies a failure rate of flagging
non-extended X-ray sources erroneously as extended of less than 6%.
ergs-1 cm-2)
which feature a KS-probability less than 0.01 of being point-like
and which are not already included in the REFLEX sample.
In total 48 additional extended sources are found (after removal
of strange detections at exposure edges and fragments of larger
clusters already included in REFLEX). 35 of these sources are
identified with bright stars and QSO and we notice that they
are often borderline cases concerning the extent significance; another
fraction of these sources feature an extent in the analysis
without deblending because they are close
pairs of point sources with identifications other than clusters.
The remaining objects for which a cluster identification cannot
be ruled out are in total 13 X-ray sources: 8 certain clusters,
2 good looking cluster candidates and 3 fields with no indication for
a galaxy cluster and no obvious other identification. We
are planning further deeper imaging for the latter sources.
Thus we have found about 10
objects in this search which have been missed in the REFLEX
compilation. The above result can also be used for another
interesting and useful statistic. The 35 partly spuriously extended
sources among the non-cluster candidates (plus the 28 extended
non-cluster sources mentioned in Sect. 10) if compared to an
initial sample of 1050 sources (above the REFLEX cut with extended
cluster sources subtracted) implies a failure rate of flagging
non-extended X-ray sources erroneously as extended of less than 6%.
The Abell and ACO catalogues (Abell 1958; Abell et al. 1989) contain about 5 times as many objects as the REFLEX sample in the study area. Even so we do not expect a very close match of the two samples, since e.g. the correlation of X-ray luminosity and optical richness is quite weak (see e.g. Ebeling et al. 1993), the large overabundance of Abell clusters provides a good check regarding problems in the recognition of clusters by the galaxy count technique based on COSMOS. To search systematically for X-ray emission from all ACO and ACO supplementary clusters we run the GCA algorithm on all ACO positions allowing for a recentering of the method within a radius of 10 arcmin of the input position. We find only one ACO supplementary cluster that was not flagged by the galaxy counts and should be included in REFLEX given its GCA flux. This cluster was already found in the above discussed additional cluster search at the positions of the extended RASS X-ray sources. It happens that this cluster is actually close to the boundary to the Large Magellanic Cloud which might explain the deficiency in counted galaxies at this position.
Since the search for X-ray emission from ACO clusters is independent of the previous source detection in the RASS II primary source list, we are not only testing the completeness of the cluster finding by the optical galaxy counts but also the source detection in the RASS II standard analysis (Voges et al. 1999). Since we find no ACO cluster missing in REFLEX due to its non-detection in RASS II, we can conclude that missing of sources in RASS II is not a significant problem for the completeness of the REFLEX sample. Such completeness of the primary source detection will be studied further by simulations of the source detection efficiency in the RASS data.
In summary, from the available material we find a missing fraction of clusters of about 2-3% in REFLEX which can be recovered as described in this section. This small fraction is still well consistent with the internal estimate of a completeness of over 90% and further supports the quality of the REFLEX sample. Note that the additional cluster detections are not integrated into the REFLEX sample to conserve its homogeneity but will be listed as REFLEX supplementary clusters in forthcoming catalogue publications.
Figure 20 shows the distribution of the X-ray luminosities and redshifts for the 449 clusters with redshift information. Details on the way the fluxes and luminosities of the clusters are calculated can be obtained from Böhringer et al. (2000, 2001a). The parabolic boundary in the plot reflects the flux limit of the sample. The sample is covering a luminosity range from about 1 1042 ergs-1to 6 1045 ergs-1. The objects with luminosities below 1043 ergs-1 are Hickson type groups and even smaller units down to elliptical galaxies with extended X-ray halos. In the latter objects the extended X-ray emission is still tracing a massive dark matter halo which is in principle not different from a scaled down cluster. Therefore we have included them in the cluster sample with the caveat that we are not certain at present how well the population of these objects below a luminosity of 1043 ergs-1 is sampled in this project. This is because some of them feature a very small membership number which may not always guarantee that they are detected by the galaxy count search.
At high redshifts, beyond z = 0.3, only exceptionally luminous objects
are observed, with X-ray luminosities of several 1045 ergs-1.
Even in this simple distribution plot we can recognize inhomogeneities
in the cluster distribution which can be attributed in a more detailed
analysis to the large-scale structure of the Universe
(Collins et al. 2000; Schuecker et al. 2000).
The paucity of the data
at very low redshifts in Fig. 20 is an effect of the small
sampling volume. The
apparent deficiency of clusters with
![]() erg s-1in the redshift interval
z = 0-0.15 is certainly an effect of large-scale
structure. Only about 3 such X-ray luminous clusters are expected in this
region. While we do not expect the sample to be complete above a redshift
of z = 0.3, the expected number of objects at these high redshifts is
indeed very small in a no-evolution model. We explore this further in a
forthcoming paper.
erg s-1in the redshift interval
z = 0-0.15 is certainly an effect of large-scale
structure. Only about 3 such X-ray luminous clusters are expected in this
region. While we do not expect the sample to be complete above a redshift
of z = 0.3, the expected number of objects at these high redshifts is
indeed very small in a no-evolution model. We explore this further in a
forthcoming paper.
Figure 20 also shows which of the clusters in the luminosity
redshift distribution are clusters already catalogued by Abell et al. (1989)
and which are mostly new. Since the difference of the two
different populations is not so easily recognized in this figure
we have plotted the non-Abell clusters separately in Fig. 21.
One notes that the non-ACO clusters are distributed over the whole
range of parameters covered by the total REFLEX sample. As we had
expected, many non-ACO clusters are found among the
nearby low luminosity, poor clusters which fail Abell's richness threshold
and among the most distant clusters, which are not covered well
in the optical plates. To our surprise there is also a large fraction
of non-ACO clusters found in the intermediate redshift range with
X-ray luminosities implying more typical Abell type cluster masses.
These latter clusters indicate an incompleteness effect in the
Abell catalogue. A similar result was found for the northern
BCS sample as shown in Ebeling et al. (1998).
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{aa10210f22.ps}\end{figure}](/articles/aa/full/2001/15/aa10210/Timg97.gif) |
Figure 20: Distribution of the REFLEX sample clusters in redshift and X-ray luminosity. The clusters catalogued by Abell et al. (1989) and the non-ACO clusters are marked differently. The luminosities are calculated for a Hubble constant of 50 km s-1 Mpc-1 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{aa10210f23.ps}\end{figure}](/articles/aa/full/2001/15/aa10210/Timg98.gif) |
Figure 21: Distribution of the non-ACO clusters in the REFLEX sample in redshift and X-ray luminosity. These clusters cover practically the whole distribution range of all REFLEX clusters. The clusters catalogued by Abell et al. (1989) are also shown as very light points |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=13.6cm,clip]{aa10210f24.ps} %
\end{figure}](/articles/aa/full/2001/15/aa10210/Timg99.gif) |
Figure 22: Sensitivity map of RASS II in the area of the REFLEX survey. Five levels of increasing grey scale have been used for the coding the sensitivity levels given in units of the number of photons detected at the flux limit: > 60 , 30-60 , 20-30, 15-20, and < 15, respectively. The coordinate system is equatorial for the epoch J2000 |
| Open with DEXTER | |
Since we do not have a homogeneous exposure coverage of the REFLEX survey
area as described in Sect. 3 we have to apply a corresponding correction
to any statistical study of the REFLEX sample. The best way to take the effect
of the varying exposure and the effect of the interstellar absorption
into account is to calculate for each sky position the number of photons
needed to reach a certain flux limit. This includes both the exposure
and the sensitivity modification by interstellar extinction.
In total the sensitivity variation due to extinction is less than
a factor of 1.25 in the REFLEX survey area (see also Böhringer
et al. 2000 for details and numerical values). The so defined
sensitivity distribution across the REFLEX study region is shown
in Fig. 22.
Since for the relatively
short exposures in the RASS the source detection process is practically
always source photon limited and not background limited (except for
the most diffuse, low-surface brightness structures) the success rate
of detection depends mostly on the number of photons.
The use of the ROSAT hard band to characterize the cluster emission
further reduces the background which is a great advantage for this
analysis. Thus fixing a
minimum number of photons per source we can calculate the effective
survey depth in terms of the flux limit at any position on the sky.
The integral of this survey depth versus sky coverage is shown in
Fig. 23 for the three cases of a minimum detection of 10, 20, and 30
photons. Also shown is the nominal flux limit of
3 10-12 ergs-1 cm-2. We note that for a detection requirement of
10 photons the sky coverage is 97% at a flux limit of
3 10-12 ergs-1 cm-2. For the much more conservative requirement
of at least 30 photons per source the sky coverage for the nominal flux
limit of the survey is about 78%. For the remaining part of the
survey area the flux limit is slightly reduced.
Since the sensitivity map is available for the whole study
area (Fig. 22) we can
for any choice of the minimum number of photons calculate the
correction for the missing sky coverage as a function of flux also
for the three-dimensional analyses e.g. the determination of the
correlation function and the power spectrum of the cluster density
distribution (see Collins et al. 2000; Schuecker et al. 2000).
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{aa10210f25.ps} %
\end{figure}](/articles/aa/full/2001/15/aa10210/Timg101.gif) |
Figure 23:
Effective sky coverage
of the REFLEX sample. The thick line gives the effective sky area
for the nominal flux limit of
3 10-12 erg s-1 cm-2and a minimum number of 30 photons per source as used e.g. for the correction
of the
|
| Open with DEXTER | |
In Fig. 24 we give the integral surface number counts of clusters
for the REFLEX sample as a function of X-ray flux
(
![]() -curve). For this determination we have chosen the
conservative requirement of a minimum of 30 counts. The figure also
shows the result of a maximum likelihood fit of a power law function
to the data for the corrected fluxes.
The likelihood analysis takes the uncertainties of
the flux measurement (analogous to the description of
Murdoch et al. 1973) and the variations of the effective
sky coverage for a count limit of 30 photons (as given in Fig. 23)
into account. The resulting power law index is constraint to the range
-1.39 with a 1
-curve). For this determination we have chosen the
conservative requirement of a minimum of 30 counts. The figure also
shows the result of a maximum likelihood fit of a power law function
to the data for the corrected fluxes.
The likelihood analysis takes the uncertainties of
the flux measurement (analogous to the description of
Murdoch et al. 1973) and the variations of the effective
sky coverage for a count limit of 30 photons (as given in Fig. 23)
into account. The resulting power law index is constraint to the range
-1.39 with a 1![]() error of
error of ![]() .
The normalization in Fig. 24 is fixed
to be consistent with the total number of clusters found.
This result is in good
agreement within the errors with other determinations of the
cluster number counts as the results
by Ebeling et al. (1998); De Grandi et al. (1999) and Rosati et al. (1998).
Note that the flux values used correspond to the observed fluxes.
The currently best estimate for the total flux implies an average
correction by a factor of about 1.1.
The fact that the observed
.
The normalization in Fig. 24 is fixed
to be consistent with the total number of clusters found.
This result is in good
agreement within the errors with other determinations of the
cluster number counts as the results
by Ebeling et al. (1998); De Grandi et al. (1999) and Rosati et al. (1998).
Note that the flux values used correspond to the observed fluxes.
The currently best estimate for the total flux implies an average
correction by a factor of about 1.1.
The fact that the observed
![]() -distribution follows
the straight line so closely down to the lowest fluxes shows clearly that
there is no significant incompleteness effect close to the flux limit.
-distribution follows
the straight line so closely down to the lowest fluxes shows clearly that
there is no significant incompleteness effect close to the flux limit.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{aa10210f26.ps}\end{figure}](/articles/aa/full/2001/15/aa10210/Timg103.gif) |
Figure 24:
Log N-Log S-distribution of the REFLEX sample clusters. The solid
line shows the
|
| Open with DEXTER | |
Given the
![]() -distribution corrected for the varying flux limit
as shown in Fig. 24, we can now also calculate the number of clusters
we expect to be detected with a certain number of counts. This
distribution is shown in Fig. 25. Here we are first of all
interested in checking the completeness of the sample concerning
detections at low photon numbers (< 30 photons). Since the
-distribution corrected for the varying flux limit
as shown in Fig. 24, we can now also calculate the number of clusters
we expect to be detected with a certain number of counts. This
distribution is shown in Fig. 25. Here we are first of all
interested in checking the completeness of the sample concerning
detections at low photon numbers (< 30 photons). Since the
![]() -distribution was constructed based on clusters with
more than 30 counts only, it provides an independent check on the
relative completeness of the sample for low compared to high photon numbers.
We note that the number of
clusters to be detected with low photon numbers is quite small and
also that there is no striking deficit of clusters at low counts.
Below a detection with 10 counts 3.8 clusters are expected and
1 is detected. In the interval between a detection of 10 to 20
counts there is no deficit and for the interval between 10 and 30 counts the expectation is about 37 clusters compared to 26 found,
a
-distribution was constructed based on clusters with
more than 30 counts only, it provides an independent check on the
relative completeness of the sample for low compared to high photon numbers.
We note that the number of
clusters to be detected with low photon numbers is quite small and
also that there is no striking deficit of clusters at low counts.
Below a detection with 10 counts 3.8 clusters are expected and
1 is detected. In the interval between a detection of 10 to 20
counts there is no deficit and for the interval between 10 and 30 counts the expectation is about 37 clusters compared to 26 found,
a ![]() deviation. Therefore we expect very little difference
for the statistical analyses using different cuts in count rate,
as long as the corresponding sky coverage is taken into account.
In fact in the construction of the luminosity function we find
only a difference of less than 2 percent
(in the fitting parameters for an analysis using a 10 photon count
and a 30 photon count limit, respectively (Böhringer et al. 2001a).
The proper corrections for the effective sky area will become increasingly
important, however, when the sample is extended to lower flux limits.
deviation. Therefore we expect very little difference
for the statistical analyses using different cuts in count rate,
as long as the corresponding sky coverage is taken into account.
In fact in the construction of the luminosity function we find
only a difference of less than 2 percent
(in the fitting parameters for an analysis using a 10 photon count
and a 30 photon count limit, respectively (Böhringer et al. 2001a).
The proper corrections for the effective sky area will become increasingly
important, however, when the sample is extended to lower flux limits.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{aa10210f27.ps}\end{figure}](/articles/aa/full/2001/15/aa10210/Timg105.gif) |
Figure 25:
Distribution of the number of source counts per cluster for the
REFLEX sample. The numbers are given as the number of objects per bin of ten
photons width. The solid line gives the expected numbers as calculated
from the
|
| Open with DEXTER | |
The GCA X-ray source analysis returns two source quality parameters,
the spectral hardness ratio and the source extent. These two parameters
are not used for the selection of the candidate sample. We have
only used this information in conjunction with optical data
as a justification to remove a number of obviously contaminating
sources. Therefore the distribution of these source properties
gives a practically independent information on the nature of the REFLEX cluster
sample and it is interesting to study them in comparison to
the properties of the non-cluster sources. (The results for the
spectral hardness ratios are used here in comparison to the expected
values that can be well calculated for cluster type spectra (5 keV)
and given interstellar HI column density in the light of sight.
The parameter quoted is the difference between the measurement
and the prediction in units of ![]() of the measurement uncertainty).
In Fig. 27 we show
the distribution of the two X-ray parameters for the 452
REFLEX clusters. The figure also shows the boundaries used
for the decision as dotted lines: a source is considered to
be very likely extended if it has a Kolmogorov-Smirnov probability
of less than 0.01 (
of the measurement uncertainty).
In Fig. 27 we show
the distribution of the two X-ray parameters for the 452
REFLEX clusters. The figure also shows the boundaries used
for the decision as dotted lines: a source is considered to
be very likely extended if it has a Kolmogorov-Smirnov probability
of less than 0.01 (
![]() ); and a deviation from the expected
hardness ratio of more than 3
); and a deviation from the expected
hardness ratio of more than 3![]() (to the soft side)
is considered as an
argument against a cluster identification. Based on these cuts
we find that 81% of the REFLEX clusters feature an X-ray
source extent. (This sample fraction of course depends on the
threshold value used in the KS-test. For a less stringent threshold
value of 0.05 for the probability of a source to be point-like
we could characterize more than 90% of the sources as extended.
The merits of relaxing the threshold condition are currently tested
with Monto Carlo simulations and will be described in a following paper.)
How the non-extended sources and their
fraction as compared to the REFLEX total are distributed
in redshift is shown in Fig. 26. While among nearby
objects only for a very small number of groups no significant
extent was found, the extent fraction is increasing clearly
with redshift. At high redshifts, where only the most
luminous clusters are found, still more than half of the
clusters feature a measurable extent.
Only 6% of all the sources have an observed
spectral parameter which appears too soft (Fig. 27).
This is a small
failure rate which is partly due to statistical fluctuations,
possibily due to an inaccurate acount of the interstellar
absorption for some of the sources, and also partly due to
the contamination of an AGN in the cluster for some of these
few sources. But since the overall deviation is only significant
for 6% of the sources the contamination by AGN which might
be indicated here is not a problem for the statistical use
of the overall sample.
(to the soft side)
is considered as an
argument against a cluster identification. Based on these cuts
we find that 81% of the REFLEX clusters feature an X-ray
source extent. (This sample fraction of course depends on the
threshold value used in the KS-test. For a less stringent threshold
value of 0.05 for the probability of a source to be point-like
we could characterize more than 90% of the sources as extended.
The merits of relaxing the threshold condition are currently tested
with Monto Carlo simulations and will be described in a following paper.)
How the non-extended sources and their
fraction as compared to the REFLEX total are distributed
in redshift is shown in Fig. 26. While among nearby
objects only for a very small number of groups no significant
extent was found, the extent fraction is increasing clearly
with redshift. At high redshifts, where only the most
luminous clusters are found, still more than half of the
clusters feature a measurable extent.
Only 6% of all the sources have an observed
spectral parameter which appears too soft (Fig. 27).
This is a small
failure rate which is partly due to statistical fluctuations,
possibily due to an inaccurate acount of the interstellar
absorption for some of the sources, and also partly due to
the contamination of an AGN in the cluster for some of these
few sources. But since the overall deviation is only significant
for 6% of the sources the contamination by AGN which might
be indicated here is not a problem for the statistical use
of the overall sample.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{aa10210f27a.ps}\end{figure}](/articles/aa/full/2001/15/aa10210/Timg107.gif) |
Figure 26: Redshift distribution of the non-extended X-ray cluster sources in the REFLEX sample (solid line). The fraction of non-extended sources compared to the total REFLEX sample for each redshift bin is shown as dashed line (in units of percent) |
| Open with DEXTER | |
It is interesting to compare these source parameters with
those for non-cluster sources. In Fig. 28 we show the distribution
of the hardness ratio deviations and the source extent probabilities
for the sample of 221 cluster candidates flagged by the galaxy counts
but excluded from the sample in the subsequent identification
process. (Note that this sample has some bias in comparison
to a random non-cluster sample since e.g. (i) in some cases the optical
selection may be due an extended object falsely split up into galaxies
(ii) contaminating sources may be preferentially recognized if
they have a soft spectrum).
There is a large fraction of much softer sources.
About 13% percent feature an apparent extent, however
(after a few spurious sources located at exposure edges were
removed).
This is more than the failure rate typically found in the
analysis of a test sample of already identified AGN
which are known point sources and the statistics of the falsely
flagged extended sources shown in Sect. 8 (<6%).
The higher rate of detection
of extended sources among these non-cluster sources as compared
to the false classification rate found in Sect. 8 is partly
due to really extended
X-ray emission from nearby galaxies and due to close, blended
double sources. The latter two source types are easily
recognized by inspection and therefore the actual false
classification rate of point sources as extended including
the inspection is at most about half of these 13%.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{aa10210f28.ps}\end{figure}](/articles/aa/full/2001/15/aa10210/Timg108.gif) |
Figure 27: Hardness ratio deviation and extent probability distribution of the REFLEX clusters. The vertical axis gives the deviation of the measured hardness ratio from the theoretically calculated value in units of the standard deviation. For the detailed definition of the parameters and the threshold values see the text |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{aa10210f29.ps}\end{figure}](/articles/aa/full/2001/15/aa10210/Timg109.gif) |
Figure 28: Hardness ratio deviation and extent probability distribution of stars and AGN excluded from the REFLEX sample clusters |
| Open with DEXTER | |
We can use the difference in the spectral hardness ratio distribution of the two samples of cluster and non-cluster sources to test for the possible contamination of the REFLEX cluster sample by AGN which are producing the dominant X-ray emission in a cluster. First of all the high fraction of extended sources guarantees that the emission of most of these 81% of the X-ray sources is extended emission from the intracluster medium of a cluster. The question is more critical for the non-extended sources. One way of checking the AGN contamination among them is to make a statistical comparison between the spectral parameters of the extended and non-extended cluster sources in REFLEX. This is done in the form of histograms for the deviation of the measured and expected hardness ratio for the two REFLEX subsamples in Fig. 29. We note that the two distributions are very similar, quite in contrast to the very different distribution of the non-cluster sources shown in the same figure. Thus there is no indication that the point-like REFLEX clusters are spectrally significantly different from the extended ones.
This can be more critically tested with cumulative and normalized plots of
these same distributions as shown in Fig. 30. Here we note again the
similarity of the distributions for the two REFLEX subsamples. They have
the same median and the only difference is a slightly broader distribution
for the extended cluster sources. We noted this behaviour already for the
NORAS cluster sample (Böhringer 2000) and it is most probably due to
the fact that the extended sources contain many more photons on average
and therefore systematic deviations play an increasing role compared
to the pure photon statistics which is the only aspect included in the
error calculation. The non-cluster sources labeled c have a completely
different distribution. To test the sensitivity of this comparison
we have artificially contaminated the point-like X-ray source cluster
sample by 20 randomly selected non-cluster sources. The resulting
distribution function is labeled with an asterisk in Fig. 30. This
sample is significantly different from the cluster distribution
and such a deviation would easily be recognized. Thus the contamination
in the total sample as introduced by the false identification
of non-extended REFLEX sources is less than 4%.
To this we have to add the possible contamination in the sample
of extended sources which could in principle be due to non-cluster
sources falsely flagged as extended. Making the following very extreme
assumptions: (i) there are as many non-cluster sources as cluster sources
in the candidate sample, (ii) the false classification rate is as high
as 6% as found in Sect. 8, (iii) all these falsely classified objects
have escaped our careful inspection in the sample cleaning process,
we find an upper limit for the possible contamination of this
part of the sample of less than 5%. Therefore
the overall contamination cannot be larger than
9% and is probably much less.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{aa10210f30.ps}\end{figure}](/articles/aa/full/2001/15/aa10210/Timg110.gif) |
Figure 29: Distribution of the significance of the deviation of the measured from the expected hardness ratio: extended REFLEX clusters (thin line), REFLEX clusters with no significant extent (thick line), non-cluster sources excluded from the REFLEX sample (dashed line). The plot shows that the extended and non-extended REFLEX clusters do belong to the same spectral class of X-ray sources. Note that the amplitudes of the extended cluster source and non-cluster source histograms have been scale down by a factor of 2 for better comparison with the smaller cluster point source sample |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{aa10210f31.ps}\end{figure}](/articles/aa/full/2001/15/aa10210/Timg111.gif) |
Figure 30: Cumulative distribution of the significance of the deviation of the measured from the expected hardness ratio: extended REFLEX clusters (dashed line, b), REFLEX clusters with no significant extent (thick line, a), non-cluster sources excluded from the REFLEX sample (c), non-extended REFLEX clusters artificially contaminated by 20 non-cluster sources (*) |
| Open with DEXTER | |
The main aim of the construction of this X-ray flux-limited galaxy cluster sample is its application to measure the large-scale structure of the Universe and to obtain constraints on cosmological models. To this end the sample has to be very homogenous in all its selection parameters in particular in its coverage of the sky. The unavoidable inhomogeneities have to be well quantified and modeled. Here, we described the construction of the cluster sample and the selection function (shown in Fig. 22) and have given the first demonstration that we have achieved our initial goal.
The primary candidate sample has been constructed from the refined second
analysis of RASS II and we have used a starting list of detections
that includes an overabundance of sources almost down to the ![]() detection limit. To ensure that we do not introduce a bias against the
flux measurement of extended sources we have reanalysed the sample with
the GCA method which accounts for this difficulty (see Böhringer et al. 2000 for checks of this method with deeper X-ray observations). Independent
checks for X-ray cluster sources which might have been missed by the
source detection in the standard analysis of the RASS
by means of the Abell catalogues have not shown a single
case of a failed detection.
detection limit. To ensure that we do not introduce a bias against the
flux measurement of extended sources we have reanalysed the sample with
the GCA method which accounts for this difficulty (see Böhringer et al. 2000 for checks of this method with deeper X-ray observations). Independent
checks for X-ray cluster sources which might have been missed by the
source detection in the standard analysis of the RASS
by means of the Abell catalogues have not shown a single
case of a failed detection.
The second selection is based on a correlation with the galaxy distribution
in the COSMOS data base. Alternatively we could have used a combined means
of identification of the X-ray sources by correlating also with other galaxy
or cluster catalogues to enhance the findings of clusters. The selection
based on only one criterion was deliberately chosen because it is the best
means to guarantee a fairly homogeneous sampling and to have some control
on possible selection effects which can be tested (e.g. we did not find a signature
in the correlation of the cluster density with the quality of the plate
material to be shown in a following paper in this series).
We have actually found an additional small fraction (![]() 2%) of clusters
which would fulfill the X-ray criteria of the sample as described
in Sect. 8, but they are not part of the REFLEX sample to preserve the
homogeneity of the present cluster catalogue. The second important point in
the optical selection is the achievement of a high completeness. The smaller the
missing fraction, the smaller is the imprint of the optical selection criteria
on the overall sample. With an estimated completeness in excess of 90%
the imprint should be negligible resulting in an effectively X-ray selected sample
of galaxy clusters. This is another important feature of the catalogue since
in the following application we will build on the close correlation between
X-ray luminosity and cluster mass. The high estimated completeness of the catalogue
is to a large part the result of a substantial oversampling of cluster candidates
in the correlation process as described in Sects. 5 and 6.
(At present we like to limit the statement about the high completeness
of the sample to the luminosity range
2%) of clusters
which would fulfill the X-ray criteria of the sample as described
in Sect. 8, but they are not part of the REFLEX sample to preserve the
homogeneity of the present cluster catalogue. The second important point in
the optical selection is the achievement of a high completeness. The smaller the
missing fraction, the smaller is the imprint of the optical selection criteria
on the overall sample. With an estimated completeness in excess of 90%
the imprint should be negligible resulting in an effectively X-ray selected sample
of galaxy clusters. This is another important feature of the catalogue since
in the following application we will build on the close correlation between
X-ray luminosity and cluster mass. The high estimated completeness of the catalogue
is to a large part the result of a substantial oversampling of cluster candidates
in the correlation process as described in Sects. 5 and 6.
(At present we like to limit the statement about the high completeness
of the sample to the luminosity range
![]() ergs-1and redshifts
ergs-1and redshifts ![]() until these regimes are explored with further
studies.) The price to be paid for this was
the large contamination fraction by non-cluster sources of about 30-40%,
which required a comprehensive follow-up observation programme.
until these regimes are explored with further
studies.) The price to be paid for this was
the large contamination fraction by non-cluster sources of about 30-40%,
which required a comprehensive follow-up observation programme.
The following identification work, necessary to remove this substantial contamination has to be very rigorous not to introduce an uncontrolled bias at this step. Therefore the strategy was adopted that either a clear identification could be achieved or in the case of a classification by selection in parameter space at least two strong selection parameters (failure rate not larger than 10% for each) were required to rule out a cluster identification.
All these measures taken together are the base of the quality of the present sample and its high completeness. The improvement that has been achieved over previous samples can for example be illustrated by a comparison with the northern BCS and extended BCS samples (Ebeling et al. 1998, 2000a). At the flux-limit of BCS, the mean sky surface density of REFLEX clusters is 62.3 ster-1 compared to 48.5 ster-1 for BCS (78% of the REFLEX value). At the REFLEX flux-limit the two parameters are 101.3 ster-1 (REFLEX) and 70.5 ster-1 (extented BCS, 69.5% of the REFLEX value).
There is still the question of sample contamination. It is for example difficult to rule out in each case that the cluster contains an AGN which is producing the majority of the measured X-ray flux. For this case the standard optical identification, to secure several coincident galaxy redshifts to prove the presence of a cluster, does not help to resolve the situation. The high fraction of true source extents that could be established by our reanalysis and the further tests based on the statistics of the spectral parameter distribution (Sect. 10) show that this is not a serious problem compromising the statistical use of the sample.
We conclude that we have reached the aim of the project to establish a cluster catalogue which can be used for a variety of cosmological studies. Part of these are described in a series of papers already submitted or in preparation covering further tests and the construction of the correlation function (Collins et al. 2000), the power spectrum of the cluster density distribution (Schuecker et al. 2000) the clustering on very large scales (Guzzo et al. 2000), and the X-ray luminosity function (Böhringer et al. 2001a).
Acknowledgements
We thank Joachim Trümper and the ROSAT team providing the RASS data fields and the EXSAS software, Rudolf Dümmler, Harald Ebeling, Andrew Fabian, Herbert Gursky, Silvano Molendi, Marguerite Pierre, Thomas Reiprich, Giampaolo Vettolani, Waltraut Seitter, and Gianni Zamorani for their help in the optical follow-up observations at ESO and for their work in the early phase of the project, and Kathy Romer for providing some unpublished redshifts. We also thank Daryl Yentis and the team at NRL for providing some of the software used in connection with the analysis of the COSMOS data. We have in particular benefited from the use of the COSMOS digitized optical survey of the southern sky, operated by the Royal Observatory Edinburgh. This work has made use of the SIMBAD database operated at CDS, Strasbourg, and of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology under contract with NASA. P. S. acknowledges the support by the Verbundforschung under the grant No.50OR970835, H. B. the Verbundforschung under the grand No.50OR93065. L. G. acknowledges financial support by A.S.I. We thank the anonymous referee for helpful comments on the presentation.