Oscillations in hot sdB stars have now been well established by observations (see O'Donoghue et al. 1998 and references therein). Potentially, this allows analysis of the internal structure of sdB stars by comparison of the observed frequencies with those corresponding to stellar models with different physical assumptions. Some work has already been done in this direction (see, e.g., Charpinet et al. 1997; Billeres et al. 1998; or Ulla et al. 1999).
Here we compare the frequency peaks reported in the previous section and
those found by Piccioni et al. (2000)
with theoretical frequencies based on stellar structure
models compatible with the surface parameters of PG 0856+121.
We have computed stellar structure models of different masses, suitable
for the sdB star PG 0856+121. The equation of state, opacity and nuclear reactions are briefly described in Jiménez & MacDonald (1996). An
additional change is the use of OPAL95 opacity tables (Iglesias & Rogers
1996). These models have helium cores and thin H-rich envelopes. A summary of the models here considered is given in Table 2.
To produce surface abundances similar to those in PG 0856+121, we have
included gravitational settling and element diffusion (Iben & MacDonald
1985) in models 4, 6 and 8.
The envelope compositions for models 1 and 2 are X=0.71, Y=0.29, Z=0.0001and for models 3, 5 and 7 X=0.60, Y=0.38, Z=0.02. For the models with
diffusion the initial envelope composition is also X=0.60, Y=0.38, Z=0.02. Gravitational settling causes helium
and heavy elements to quickly
sink below the photosphere. The outer layers are then pure hydrogen.
The fact that
![]() in PG 0856+121 and other sdBs can be
explained by the presence of a wind that counters the effects of
gravitational settling. The wind mass loss rates required to do this
are quite small (10-15-
in PG 0856+121 and other sdBs can be
explained by the presence of a wind that counters the effects of
gravitational settling. The wind mass loss rates required to do this
are quite small (10-15-
![]() /year) and completely undetectable up to date with ordinary techniques and instrumentation.
/year) and completely undetectable up to date with ordinary techniques and instrumentation.
| Model | Mass | log g | Envlp. Mass | Radius | Central |
|
Luminosity |
| nr. | x109 cm | x104 gr/cm3 | x104 K | ||||
| 1 | 0.3999 | 5.843 | 3.18 10-3 | 8.724 | 3.329 | 2.641 | 6.891 |
| 2 | 0.4517 | 5.644 | 6.46 10-3 | 11.69 | 2.550 | 2.642 | 12.42 |
| 3 | 0.5563 | 5.401 | 6.1 10-3 | 17.12 | 1.699 | 2.651 | 26.94 |
| 4 | 0.5563 | 5.340 | 5.0 10-3 | 18.37 | 1.699 | 2.560 | 26.97 |
| 5 | 0.7941 | 4.862 | 2.43 10-2 | 38.05 | 0.941 | 2.696 | 142.4 |
| 6 | 0.7941 | 4.821 | 2.07 10-2 | 39.88 | 0.941 | 2.644 | 144.7 |
| 7 | 1.0608 | 4.390 | 5.06 10-2 | 75.75 | 0.611 | 2.629 | 510.6 |
| 8 | 1.0608 | 4.312 | 4.53 10-2 | 82.83 | 0.612 | 2.541 | 532.7 |
The models eigenfrequencies were computed in the
adiabatic approximation, using the code developed by
Christensen-Dalsgaard (see Christensen-Dalsgaard & Berthomieu 1991).
For models with similar internal structure, as in the present case, the
dynamical time scale
![]() dominates the
variation of the oscillation frequencies. Thus it is convenient to
compare our results in terms of dimensionless frequencies
dominates the
variation of the oscillation frequencies. Thus it is convenient to
compare our results in terms of dimensionless frequencies
![]() ,
defined by
,
defined by
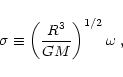 |
(1) |
In Fig. 4 we show the theoretical dimensionless frequencies,
computed by using Eq. (1). Only modes with
![]() are considered since
modes of higher degree can hardly be observed for point-like stars.
For the model with
are considered since
modes of higher degree can hardly be observed for point-like stars.
For the model with
![]() ,
the 6 p-mode frequencies shown in
Fig. 4 correspond to the fundamental and first overtone of
the
,
the 6 p-mode frequencies shown in
Fig. 4 correspond to the fundamental and first overtone of
the
![]() degrees. For other models, the p-mode spectrum is more complex due to
the presence of g-like modes.
As it can be seen in the figure, the dimensionless frequencies decrease with mass and increase when diffusion is considered.
degrees. For other models, the p-mode spectrum is more complex due to
the presence of g-like modes.
As it can be seen in the figure, the dimensionless frequencies decrease with mass and increase when diffusion is considered.
![\begin{figure}
\includegraphics[width=8.8cm,clip]{fig5.ps}
\end{figure}](/articles/aa/full/2001/15/aa10085/Timg35.gif) |
Figure 4: Dimensionless frequencies for PG 0856+121. Only 5 models, of those in Table 2, are shown for clarity |
The dimensionless frequencies corresponding to the observational periods are
usually estimated by expressing ![]() in terms of
in terms of
![]() ,
,
![]() and the luminosity L of the stars.
However, for this kind of star it seems better to use some estimate of the
mass rather than of L. In fact, the distance quoted in Table 1 was obtained
by assuming the canonical mass for sdB stars.
The relations are
and the luminosity L of the stars.
However, for this kind of star it seems better to use some estimate of the
mass rather than of L. In fact, the distance quoted in Table 1 was obtained
by assuming the canonical mass for sdB stars.
The relations are
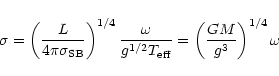 |
(2) |
In particular, for PG 0856+121,
we have used the value
![]() (Saffer et al. 1994).
For the mass we use the canonical value
(Saffer et al. 1994).
For the mass we use the canonical value
![]() (Saffer et al. 1994).
In addition, the observational frequencies have associated errors, but they
are negligible when compared to those of
(Saffer et al. 1994).
In addition, the observational frequencies have associated errors, but they
are negligible when compared to those of ![]() and M.
The resulting dimensionless frequencies for the observed frequency peaks
reported here are shown at the top of Fig. 4 as horizontal
continuous lines. Use of the results of Piccioni et al. (2000) instead
of those shown in the figure, does not change the following discussion.
The horizontal dashed lines in Fig. 4 were obtained by assuming the
same uncertainty in
and M.
The resulting dimensionless frequencies for the observed frequency peaks
reported here are shown at the top of Fig. 4 as horizontal
continuous lines. Use of the results of Piccioni et al. (2000) instead
of those shown in the figure, does not change the following discussion.
The horizontal dashed lines in Fig. 4 were obtained by assuming the
same uncertainty in ![]() as quoted above but for a mass range of
as quoted above but for a mass range of
![]() .
This allows us to explore the possibility that PG 0856+121
has a mass substantially larger than the canonical one.
.
This allows us to explore the possibility that PG 0856+121
has a mass substantially larger than the canonical one.
In the previous analysis the frequency splittings caused by rotation have
been neglected. Although we do not know the rotational velocity of this
particular star, we shall consider the value 90 kms-1 as an upper limit. This
follows from the work by Saffer et al. (1994; and a private communication), who measured this quantity for about 50 sdB stars and none was found to be rotating faster than about 90 kms-1. Then, by
using the stellar radii given in Table 2, it can be seen that the value of the
rotational frequency is, at most, ![]() that of the observational frequencies
and, hence, first order corrections for the frequency splitting will be enough for
our purposes. By using the values of M and R in Table 2, a rotational
frequency splitting
that of the observational frequencies
and, hence, first order corrections for the frequency splitting will be enough for
our purposes. By using the values of M and R in Table 2, a rotational
frequency splitting
![]() (here m is the azimuthal
order,
(here m is the azimuthal
order,
![]() the dimensionless rotational angular frequency and
the parameter
the dimensionless rotational angular frequency and
the parameter
![]() )
smaller than
0.25 is found for modes with
)
smaller than
0.25 is found for modes with
![]() .
Considering this additional
uncertainty in Fig. 4 also does not change the conclusions given below.
From Fig. 4 it follows that the peak at 3.3 mHz can be either a g mode
or a p mode. Since in other sdB stars only p modes are detected (see e.g.
Billeres et al. 1998; Koen et al. 1998b) in agreement with the theoretical
expectations of Fontaine et al. (1998) for the EC14026 stars, the latter
possibility can be considered with preference. In this case, and
assuming the canonical mass, the peak at 3.3 mHz would be a fundamental
p-mode with degree
.
Considering this additional
uncertainty in Fig. 4 also does not change the conclusions given below.
From Fig. 4 it follows that the peak at 3.3 mHz can be either a g mode
or a p mode. Since in other sdB stars only p modes are detected (see e.g.
Billeres et al. 1998; Koen et al. 1998b) in agreement with the theoretical
expectations of Fontaine et al. (1998) for the EC14026 stars, the latter
possibility can be considered with preference. In this case, and
assuming the canonical mass, the peak at 3.3 mHz would be a fundamental
p-mode with degree ![]() ,
or 2.
On the other hand, if any of the peaks at 1.9 and 2.1 mHz are real and the photometric value
of
,
or 2.
On the other hand, if any of the peaks at 1.9 and 2.1 mHz are real and the photometric value
of ![]() is correctly determined, from
Fig. 4 it follows that these peaks must be g-modes of low
order. It is important to note that this conclusion does not depend on the details
of the model structure, but only on the stellar parameters.
The basic reason is that the dimensionless frequencies
is correctly determined, from
Fig. 4 it follows that these peaks must be g-modes of low
order. It is important to note that this conclusion does not depend on the details
of the model structure, but only on the stellar parameters.
The basic reason is that the dimensionless frequencies ![]() of the p-modes
are, in a first approximation, independent of such details.
of the p-modes
are, in a first approximation, independent of such details.
Copyright ESO 2001