A&A 369, 706-728 (2001)
DOI: 10.1051/0004-6361:20010157
S. E. Caunt - M. J. Korpi
Astronomy Division, Department of Physical Sciences, PO Box 3000, 90014 University of Oulu, Finland
Received 22 December 2000 / Accepted 24 January 2001
Abstract
In this paper we describe a numerical method designed for
modelling different kinds of astrophysical flows in three
dimensions. Our method is a standard explicit finite difference method
employing the local shearing-box technique.
To model the features of astrophysical systems, which are usually
compressible, magnetised and turbulent, it is desirable to have high
spatial resolution and large domain size to model as many features as
possible, on various scales, within a particular system. In addition, the
time-scales involved are usually wide-ranging also requiring
significant amounts of CPU time.
These two limits (resolution and time-scales) enforce huge limits on
computational capabilities. The model we have developed therefore uses
parallel algorithms to increase the performance of standard serial
methods. The aim of this paper is to report the numerical methods we
use and the techniques invoked for parallelising the code. The
justification of these methods is given by the extensive tests
presented herein.
Key words: magnetohydrodynamics - turbulence - shock waves - methods: numerical - galaxies: ISM - accretion, accretion disks
Magnetic fields are present everywhere in the universe, for example in planets, stars, accretion disks around compact objects, galaxies of various kinds and even in the intergalactic medium. Most of these systems are characterised by large kinetic and magnetic Reynolds numbers, indicating that they are highly turbulent, and also that magnetic fields are dynamically significant. In many cases the observed magnetic field has, in addition to a random small-scale component, coherent magnetic field structures on large scales. For example the Sun has a mean magnetic field of dipolar structure, whereas numerous spiral galaxies posses a mean field of spiral shape often following the optical spiral arms. One of the fundamental questions in astrophysics is how the order seen in the large scale magnetic field structures can arise in the turbulent media they are embedded within.
The most plausible mechanism suggested to explain this phenomenon is the hydromagnetic dynamo (Parker 1955; Steenbeck et al. 1966), according to which large-scale magnetic fields can be generated and maintained by the combination of turbulence and large-scale shearing motions. Based on this theory, a vast number of mean-field dynamo models, which solve for the large scale magnetic field with turbulence remaining a parameterised quantity, have been developed for practically all astrophysical objects. Since the form and magnitude of the turbulent quantities are relatively unknown, this parameterisation is usually kept as simple as possible. The information lacking from these models can be obtained by studying the non-linear evolution of a magnetised turbulent flow in a fully 3D numerical simulation. These kind of simulations (e.g. Balsara & Pouquet 1999; Brandenburg 2000) have revealed that in the presence of helical turbulence, magnetic field energy can be transferred from the smallest scales to the larger ones, known as inverse cascade (Frisch et al. 1975; Pouquet et al. 1976). These simulations, however, have not yet developed to the stage where a realistic physical setup for a particular object could be studied.
On the other hand, when the magnetic field becomes strong enough it
can influence the fluid motions through the Lorentz force suppressing
turbulence and thereby quenching the generation of magnetic field,
known as ![]() -quenching in the mean field dynamo theory. Recent
numerical simulations (Cattaneo & Hughes 1996) have
indicated that the dynamo
-quenching in the mean field dynamo theory. Recent
numerical simulations (Cattaneo & Hughes 1996) have
indicated that the dynamo ![]() is dramatically quenched implying
that dynamo action cannot occur in high Reynolds number
flows. However, this result is still debatable and requires
investigation under more realistic physical setups (see for example
Brandenburg 2000).
is dramatically quenched implying
that dynamo action cannot occur in high Reynolds number
flows. However, this result is still debatable and requires
investigation under more realistic physical setups (see for example
Brandenburg 2000).
Modelling these kinds of systems provides a wide range of numerical challenges. One challenge that can never be overcome satisfactorily is the need for the highest possible spatial resolution to model turbulence. In some cases even the turbulent forcing occurs at very small scales, for example in galaxies where turbulence is mainly driven by dying stars exploding as supernovae (hereafter SNe). On the other extreme, one would also like to include the largest possible scales to study not only the generation of large-scale magnetic field, but also large-scale vertical structures such as chimneys or fountains observed in galaxies (e.g. Koo et al. 1992; Normandeau et al. 1996) and azimuthal features such as field reversals in accretion disks (e.g. Brandenburg et al. 1995; hereafter BNST). Another important feature of astrophysical flows which has to be taken into account is their compressible nature. With the violent physical processes active in these flows, such as SNe in galaxies and rapidly growing instabilities like the Balbus-Hawley instability in accretion disks (Balbus & Hawley 1991), shocks are commonly formed. Since the physical viscosity in the flow is negligible and the physical quantities become discontinuous, additional numerical techniques are required to resolve them (von Neumann & Richtmyer 1950 hereafter vNR). Once the flow has become turbulent, the time-scales involved in these turbulent motions is usually much shorter than the orbital period or decay time-scale of the magnetic field. To study the long-term evolution of the system a huge number of time-steps may be required. This all implies the need for efficient algorithms along with high resolution and large domain size.
A number of numerical models of this type have been developed being either specifically designed for a particular object (for solar corona e.g. Galsgaard & Nordlund 1996, for stellar convection e.g. Stein & Nordlund 1998, for accretion disks e.g. Hawley et al. 1995; BNST, for the interstellar matter e.g. Rosen & Bregman 1995; Vàzquez-Semadeni et al. 1995; Mac Low 1999; Korpi et al. 1999) or being more general (Stone & Norman 1992a, 1992b), and more recently global models are starting to appear (e.g. for the accretion disks Hawley & Krolik 2000). Our method is based on the standard local Cartesian shearing-box simulation (e.g. Wisdom & Tremaine 1988) and uses explicit finite differences on an Eulerian grid, discretising physical quantities onto a uniform mesh, ideal for data parallelisation. The methods are in principle very simple and therefore easy to implement and allow for rapid development. Shock viscosities (vNR) and further diffusive techniques (Nordlund & Galsgaard 1997 hereafter NG; Stein & Nordlund 1998) require additional effort but are however necessary to stabilise the numerics.
This paper is structured as follows. Section 2 describes the essential physics behind our model. Section 3 provides details of the numerical methods we use to model the fluid including the artificial viscosity employed to resolve shocks and reduce unphysically generated waves and the treatment of the boundaries of the box. The parallelisation of the code is discussed in Sect. 4 and finally the test suite used to verify the accuracy and acceptability of the code is covered in Sect. 5. Finally in Sect. 6 we summarise.
In this section we discuss the partial differential equations (PDEs) solved for in all astrophysical systems under consideration. These equations describe the flow of a magnetically conducting fluid within a differentially rotating body. Other, more specific, models include extra terms to model effects such as heating by supernovae (hereafter SNe) or stellar winds (hereafter SWs), and suitable cooling functions for various systems.
We solve the standard non-ideal MHD equations in three dimensions
using the standard shearing-box technique similar to those used by e.g. BNST and Hawley et al. (1995). The equations are solved in
a computational domain representing a small volume within a
differentially rotating cosmic object. The coordinate system is
reduced to Cartesian with x representing radial, y azimuthal and
z vertical direction, the dimensions of the box being
![]() .
The centre of the box is located at distance
R from the centre of rotation, which is much larger than any
dimension of the domain. This reference point is moving on a circular
orbit with angular velocity
.
The centre of the box is located at distance
R from the centre of rotation, which is much larger than any
dimension of the domain. This reference point is moving on a circular
orbit with angular velocity ![]() around the centre. As the fluid
is rotating differentially, the angular velocity is changing as
function of distance from the centre of rotation. In the local frame
of reference the equations of motion can be linearised relative to the
reference point (e.g. Spitzer & Schwarzschild 1953; Julian &
Toomre 1966) yielding a solution which can be interpreted to
have two contributions: the circular motion given by
around the centre. As the fluid
is rotating differentially, the angular velocity is changing as
function of distance from the centre of rotation. In the local frame
of reference the equations of motion can be linearised relative to the
reference point (e.g. Spitzer & Schwarzschild 1953; Julian &
Toomre 1966) yielding a solution which can be interpreted to
have two contributions: the circular motion given by
![]() and the epicyclic motion which yields a term
and the epicyclic motion which yields a term
![]() ,
where
,
where
![]() is equivalent for the Oort constant. For disk systems,
for example, for which the rotation law is of the form
is equivalent for the Oort constant. For disk systems,
for example, for which the rotation law is of the form
![]() ,
the Oort constant A can be written as
,
the Oort constant A can be written as
![]() ,
yielding the general form
,
yielding the general form
![]() for the shear flow and
for the shear flow and
![]() for the epicyclic
motion. Our velocity field then consists of two parts, the shear flow
for the epicyclic
motion. Our velocity field then consists of two parts, the shear flow
![]() discussed above, and deviations
discussed above, and deviations ![]() from it, the
total velocity field being
from it, the
total velocity field being
![]() .
In the
following we solve for
.
In the
following we solve for ![]() .
.
We choose to solve for the magnetic vector potential, ![]() ,
for
which
,
for
which
![]() is a natural consequence. We solve for
the internal energy e, which is related to temperature by
is a natural consequence. We solve for
the internal energy e, which is related to temperature by
![]() under the assumption of the perfect gas law
under the assumption of the perfect gas law
![]() with
with
![]() .
Finally we solve for the logarithm of
density
.
Finally we solve for the logarithm of
density ![]() ,
which is numerically convenient, since the
density range can be several orders of magnitude in many
models. However, this is not a conservative form of the continuity
equation, but the extensive tests have shown this not to be a major
disadvantage. Other factors, such as open boundaries and numerical
diffusion, would destroy the conservative nature of the continuity
equation even if
,
which is numerically convenient, since the
density range can be several orders of magnitude in many
models. However, this is not a conservative form of the continuity
equation, but the extensive tests have shown this not to be a major
disadvantage. Other factors, such as open boundaries and numerical
diffusion, would destroy the conservative nature of the continuity
equation even if ![]() was solved for. The basic equations we solve
are
was solved for. The basic equations we solve
are
The term ![]() in the momentum equation describes the external
gravitational potential. For accretion disks, for example, we estimate
the gravity by linearising the equation of motion, which yields gravity
in the vertical direction
in the momentum equation describes the external
gravitational potential. For accretion disks, for example, we estimate
the gravity by linearising the equation of motion, which yields gravity
in the vertical direction
![]() .
We neglect
self-gravity for the time being.
.
We neglect
self-gravity for the time being.
Additional specific terms to Eqs. (3) to (4) are included for different simulations, for example, inclusion of turbulent forcing mechanisms and appropriate cooling functions. However, the equations above are common throughout the models and lay the foundations for all future calculations.
In the azimuthal, y, direction we adopt periodic boundary conditions
since this lies in the direction of the shearing flow. In the radial
direction, the differential rotation and therefore shearing boundaries
need to be accounted for. For the linear shear we therefore adopt
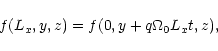 |
(5) |
In the vertical direction we have two schemes available. Since these
boundaries are the hardest to model since they are not "true''
boundaries in a physical system, we must chose conditions which best
suit the particular physical situation to be modeled. We always,
however, assume stress-free, electrically insulating boundary
conditions (BNST), such that
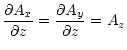 |
= | 0, | (6) |
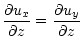 |
= | 0, | (7) |
| = | 0. | (8) |
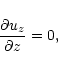 |
(9) |
| uz = 0, | (10) |
Our code is based on explicit finite difference calculations
using an array of data of size
![]() uniformly
spaced gridpoints. We numerically solve for the eight primary
variables
uniformly
spaced gridpoints. We numerically solve for the eight primary
variables ![]() ,
e and components of
,
e and components of ![]() and
and ![]() which represent the logarithm of density, energy per unit mass,
velocity and the magnetic vector potential.
which represent the logarithm of density, energy per unit mass,
velocity and the magnetic vector potential.
We use the logarithm of density for a number of reasons. It ensures
that we never obtain negative densities, it allows us to cope with
physical situations that require a large number of pressure scale
heights and finally the functional form of ![]() is much smoother
than that of
is much smoother
than that of ![]() ,
hence numerical derivatives are more accurately
calculated (Nordlund & Stein 1990).
,
hence numerical derivatives are more accurately
calculated (Nordlund & Stein 1990).
The discretisation of the partial derivatives in x, y and z are done using centred, 6th order accurate, explicit finite differences for both first and second derivatives. The exact form of these is included in Appendix A. These operators are highly non-dissipative with well defined waves retaining their original form over long periods of time.
Time-stepping is performed by a third order accurate Adams-Bashforth-Moulton predictor-corrector method, which is described in Appendix B. The accuracy of this scheme has been compared to other methods of advancing PDEs as discussed in Sect. 3.5.
The methods described above for solving the system of PDEs are inadequate alone to cope with strong discontinuities in the flow, such as shock waves, and are susceptible to low-level numerical noise. We therefore employ artificial viscosities to diffuse the discontinuities to be resolved by the finite computational grid and add stability to the numerical methods.
The methods we use generate viscosities that are localised at discontinuities or in regions of unresolved waves. This means that we are able to apply the minimum amounts of viscosity to those areas in which we would like the flow to remain unchanged. We use two techniques to account for these different numerical problems: a shock viscosity (vNR) and hyperdiffusion (NG).
We use artificial counterparts to the physical quantities of ![]() ,
,
![]() and
and ![]() being the kinematic viscosity, magnetic diffusivity
and thermal diffusivity, respectively. The numerical equivalent of
being the kinematic viscosity, magnetic diffusivity
and thermal diffusivity, respectively. The numerical equivalent of
![]() is incorporated into the stress tensor and viscous heating as
discussed in Sect. 3.2.3, and
is incorporated into the stress tensor and viscous heating as
discussed in Sect. 3.2.3, and ![]() and
and ![]() are the numerical
equivalents of quantities in the Eqs. (1) and (4).
are the numerical
equivalents of quantities in the Eqs. (1) and (4).
The shock viscosity is only applied to regions that are undergoing
compression, i.e. in regions which are characterised by
![]() .
The numerical equivalent of the kinematic
viscosity
.
The numerical equivalent of the kinematic
viscosity ![]() therefore takes the form of
therefore takes the form of
A similar shock viscosity is required for the magnetic resistivity,
however we wish to ensure that diffusion only occurs from the
components of velocity perpendicular to the field lines,
![]() ,
given by
,
given by
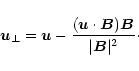 |
(13) |
Hyperdiffusion is incorporated to add numerical stability to the code. Small scale oscillations (around Nyquist frequency) need to be damped and the hyperdiffusive methods described by NG provide an efficient method while leaving resolved features practically undamped.
This is strongest for rapid (grid-scale) oscillations. In an implementation termed "positive definite quenching'' by NG the hyperdiffusion always has physically meaningful values such that the dissipation of energy is positive definite and always acts to stabilise the flow. For a detailed description of the hyperdiffusive techniques, we refer the reader to their article and Nordlund & Stein (1990). Our implementation of the techniques is discussed below.
Written in terms of viscosity, hyperdiffusion of a variable,
f, can be expressed as
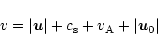 |
(16) |
Here ![]() represents a general viscosity term, and one can
equally substitute
represents a general viscosity term, and one can
equally substitute ![]() or
or ![]() for the energy and induction
equations, respectively, and mass diffusion in the continuity equation.
for the energy and induction
equations, respectively, and mass diffusion in the continuity equation.
Equations (1) to (4) all have additional diffusive terms in order to stabilise the code. For the momentum equation, this can be performed by replacing the stress tensor by a diffusive operator (retaining the essential form of the stress tensor but using numerical equivalents for viscosity). The magnetic diffusion similarly is replaced by a numerical equivalent as does the thermal diffusion. Mass diffusion however has no physical counterpart and is included purely for stability (Nordlund & Stein 1990).
The diffusive terms are calculated on a staggered mesh which provides a more accurate method of determining grid-scale structures. This is used in conjunction with second-order operators for determining highly localised structures. This combination allows high wavenumber noise to be detected more easily and discontinuities to be dealt with more efficiently.
The diffusion of the scalar quantities e and ![]() ,
represented by f below, in the ith-direction can be written as
,
represented by f below, in the ith-direction can be written as
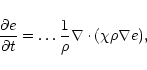 |
(18) |
The diffusion of the vector quantities is a more complex operation. In
the case of velocity, the diffusion is implemented in a way that
closely resembles the stress-tensor form of molecular viscosity
following the implementation illustrated by NG. In the momentum
equation we add a term of the form:
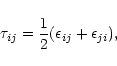 |
(20) |
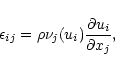 |
(21) |
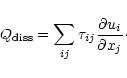 |
(22) |
The magnetic diffusion is defined as
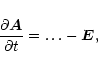 |
(23) |
| = | |||
| = | |||
| = | |||
| (24) |
Finally, we have the additional term in the energy equation to account
for the losses in magnetic energy
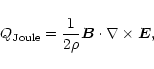 |
(25) |
The boundary conditions of Sect. 2.3 are incorporated directly into the derivative operators at the boundaries and need to account for sliding boundaries in the x direction, periodic in yand symmetric/antisymmetric in z with additional density boundary conditions also in the vertical direction. The y boundary is fairly trivial (the derivatives at the three points closest to each y-boundary are defined such that they use points at the opposite end of the box as well) however x and z boundaries are more complex and are discussed below.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{H2618F1.eps}
\end{figure}](/articles/aa/full/2001/14/aah2618/Timg103.gif) |
Figure 1: Calculations of derivatives at boundaries require interpolation in the y-direction to determine values at intermediate points. The figure shows one such y-interpolation required |
| Open with DEXTER | |
Figure 1 shows a typical situation where interpolation is
required to calculate the position at an intermediate point (i.e. between gridpoints). This must be performed
![]() times for each of the x boundaries to be used with the sixth
order centred differences. The procedure also takes into account that
the points require for a particular interpolation may lie in adjacent
boxes in the y-direction.
times for each of the x boundaries to be used with the sixth
order centred differences. The procedure also takes into account that
the points require for a particular interpolation may lie in adjacent
boxes in the y-direction.
For the velocity, magnetic vector potential and energy we desire that either the function value is equal to zero or the first derivative in the z direction is zero. These can be implemented using symmetric and antisymmetric boundary conditions, respectively, to mimic points outside the numerical domain as described by NG.
Figure 2 shows that by specifying the points outside the
boundary such that, if we assume that the index of the boundary grid
point is b, then for a symmetric boundary condition
| |
Figure 2:
Calculations of derivatives at vertical boundaries can be
performed by specifying the function to be symmetric or antisymmetric
to produce
|
| Open with DEXTER | |
The density boundaries are calculated from the hydrostatic equilibrium
condition Eq. (11) by setting
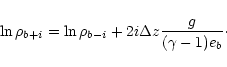 |
(28) |
The time-step is limited by the Courant-Friedrichs-Lewy condition
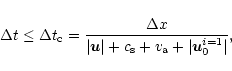 |
(29) |
A radiative time-scale is included by taking the thermal conduction as
the relevant quantity. Taking a similar form the the above expression
we express this as
The final time-step is then derived from the minimum value of these three time-scales and we find that this is adequate to ensure that the code remains stable in all conditions.
As mentioned earlier, we use an Adams-Bashforth-Moulton third order predictor corrector scheme to advance the equations in time. We have tested the performance of this compared a number of different methods and found that it behaves favourably compared to them.
We have used the standard one-dimensional shock tube test (described in more detail in Sect. 5.1) as a check on the accuracy of the scheme since an exact analytical solution to this problem can be found. This has been chosen as an adequate method of determining the accuracy of a combination of different elements of the code (namely the differencing operators in conjunction with the time stepping). For reliable test results the resolution of the numerical domain is varied and the time-step adjusted accordingly to more realistically match the resolution (but fixed for the duration of the test). In other words when the resolution is doubled, the time-step is halved.
From the initial condition, the equations are advanced using a
constant time-step to a time of t=0.256. The error between the true
(analytical) and numerical results is calculated as a sum for density,
velocity and energy and averaged over the total number of
gridpoints. Hence the error, ![]() ,
is given by
,
is given by
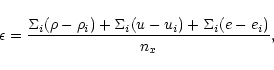 |
(33) |
As well as the third order Adams-Bashforth-Moulton method we have performed the test on the second order Adams-Bashforth-Moulton method, second and fourth order Runge-Kutta methods and the third order predictor-corrector method of Hyman (Hyman 1979).
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{H2618F3.eps}
\end{figure}](/articles/aa/full/2001/14/aah2618/Timg124.gif) |
Figure 3: Errors incurred by the different schemes for the Sod tube test using different resolutions and time-step sizes |
| Open with DEXTER | |
The results of this test are shown in Fig. 3. Here we see very clearly that as the resolution is increased and the time-step shortened the higher order schemes produce smaller errors and in all cases the errors from the Adams-Bashforth-Moulton third order scheme are the smallest. It is for this reason that we have chosen this method of advancing the equations. The exact algorithm used for this scheme is given in Appendix B.
 |
Figure 4: Data distribution over different numbers of dimensions. From left to right these are one-dimensional, or slab distribution, two-dimensional or column distribution and three-dimensional or block distribution |
| Open with DEXTER | |
We chose to use High Performance Fortran (HPF) due to its simplicity of implementing parallelisation methods and being ideally suited to data parallelisation. The finite difference model itself is ideal for running on a number of processors supporting the Single Instruction Multiple Data (SIMD) programming style where data is distributed onto the local memory of each processor. The operations at a particular grid-point are highly localised with data from only three nearest-neighbour points being involved in any particular operation. This results in a situation in which the data can be split between a large number of processors, with communication between processors only occurring at their common data boundaries. Hence, the efficiency of the parallelisation should theoretically improve for large data sets for which the boundary region size becomes small in comparison to the size of the inner data region on a particular processor (this fact is illustrated from the tests shown later in this section). In effect, the data set on each processor can be operated on virtually independently of all the other processors.
HPF directs the processor to distribute and align all the data variables over a number of processors, effectively splitting the domain into a number of smaller sub-domains. The communication calls are automatically determined by the compiler. This provides a particularly flexible approach to parallelisation since it can be easily altered to match the relative number of gridpoints in different dimensions.
Many test have been performed to produce the most optimal parallelisation results. Most of the tests have been performed on the Cray T3E supercomputer at the Centre for Scientific Computing (CSC) in Espoo, Finland. These include coding of derivative routines, calculations of the shearing boundary conditions, ghostzone boundaries and calculations of array operations. However, the most striking results were determined for how best to distribute the data over a number of processors. In theory the best distribution occurs for the smallest surface area of boundaries between processors since communication is at a minimum in this situation. However, our timings indicate that this is not necessarily the best option with timings widely varying between different distributions for the same calculations.
To test the effectiveness of the different options available for
distributing data (one-dimensional slabs, two-dimensional columns or
three-dimensional blocks as illustrated in Fig. 4) we
use a simple test code that calculates derivatives 1000 times in all
three directions (assuming periodic boundaries) using a block of data
of equal dimensions (
![]() ). This data is
distributed over 8 processors chosen as it allows the processors to be
arranged in a cube when distributed in three dimensions for which the
communication should be minimised. Results for this test are given in
Table 1 and shown in Fig. 5 for the total
times taken of all three derivatives. Following the notation of HPF
directives, distribution over a particular dimension is labeled as "B''
for "BLOCK'' (data is distributed as a block onto a particular
processor in this direction) and "*'' if distribution does not occur
along this particular direction.
). This data is
distributed over 8 processors chosen as it allows the processors to be
arranged in a cube when distributed in three dimensions for which the
communication should be minimised. Results for this test are given in
Table 1 and shown in Fig. 5 for the total
times taken of all three derivatives. Following the notation of HPF
directives, distribution over a particular dimension is labeled as "B''
for "BLOCK'' (data is distributed as a block onto a particular
processor in this direction) and "*'' if distribution does not occur
along this particular direction.
| Distribution | x-der. | y-der. | z-der. | total |
| (B, *, *) | 194.52 | 49.65 | 49.52 | 293.69 |
| (*, B, *) | 26.62 | 9.64 | 27.53 | 66.79 |
| (*, *, B) | 29.34 | 27.56 | 13.69 | 70.59 |
| (B, B, *) | 51.93 | 98.05 | 36.47 | 186.45 |
| (B, *, B) | 52.04 | 33.41 | 105.40 | 190.85 |
| (*, B, B) | 29.70 | 6.42 | 10.13 | 46.25 |
| (B, B, B) | 52.45 | 52.02 | 54.39 | 158.86 |
| |
Figure 5: Comparisons of times to perform parallel calculations when data is distributed over different directions. All distributions where parallelisation has occurred over the x-direction show dramatically decreased performance |
| Open with DEXTER | |
From these tests we see that distributing in the x direction performs very poorly either alone or when distributed along with others. It was also observed that speed up of codes in general is bad when data is distributed along this direction. This is probably related to the Fortran column major ordering of arrays (i.e. "first index changes fastest'') in memory which can lead to caching problems.
The y and z distributions perform well and it is seen that the distribution over both of these directions together performs the best overall. This is presumably because the decreased surface area of the boundaries between data distributed on the processors has lead to less communication. This is seen by comparing the y-derivative timing for the (*, B, *) distribution and the z-derivative timing for the (*, *, B) with the same for the (*, B, B) distribution in Table 1 in which both times are seen to decrease when data has been spread more evenly in different directions.
When incorporating shearing boundaries the results for distributing data along the y-direction is less efficient since gridpoints at one point on one side of the box in general need to communicate with points at a totally different location on the other side of the box as shown in the example of Fig. 6 where data has been distributed over 4 processors in the y-direction.
| |
Figure 6: Communication required for shearing boundaries when distribution occurs in the y-direction. In general, the points required across the x-boundary for one particular processor are not aligned on the same processor and are typically stored in two processors located at any position within the computer |
| Open with DEXTER | |
Here we see that due to the shearing, the calculations at one of the x-boundaries on processors 1 require communication to acquire data on processors 3 and 4. In general it could be any of the processors. This is obviously much more expensive and complex than simply communicating with points directly opposite the boundary. This in effect results in poorer performance when data is distributed in this direction because communication does not necessarily take place between neighbouring processors.
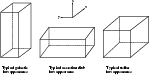 |
Figure 7: Different box dimensions for different applications of the code. Each performs better under different parallel distributions related to the grid dimensions. For example the galactic box performs more efficiently for distribution in the z-dimension due to the grid resolution being weighted in this direction |
| Open with DEXTER | |
From the above tests we see that the best performance of the parallel code can be achieved by distributing data along the y and zdirections.
We also need to take into account the different model dimensions that are likely to be used when determining which distribution method to use. We therefore perform a number of tests on the speed up of the code for different dimension models and different distributions.
We chose to determine the speed up of the code by comparing timings of the code when doubling the resolution and doubling the number of processors. In an ideally parallelised code the real time of communication should remain constant (however boundary conditions will effect results). We also use this method rather than keeping a fixed resolution and comparing timings when doubling the number of processors due to the limiting fact that the Cray T3E contains only 128Mb of RAM of local memory on each processor. This implies naturally that high resolution simulations can only be run on a large number of processors and hence trends in speed-up are impossible to test. The other alternative with this method is to use a low resolution simulation that will run on a small number of processors. However, this is an artificial test for two reasons: firstly the main aim is to run high resolution simulations and secondly when distributed over a large number of processors, communication time becomes artificially high since only a small number of gridpoints in a particular direction lie on a given processor. This test is designed to illustrate the essential reasons behind parallelising the code; namely that through parallelisation, high resolution simulations can be performed in appreciable times.
The test uses all parts of the code including magnetic terms, shearing and numerical diffusion. The test is not aimed at solving a physical problem but the data is initialised as it could be for a typical galactic run with a large scale azimuthal magnetic field. The code is then timed for performing 30 time-steps.
Three tests are displayed here showing the results for different distributions of data corresponding to different shapes of boxes that are commonly used in different astrophysical systems as shown in Fig. 7. For the galactic setup, distribution in the z-direction results in the best distribution of data amongst processors while for the accretion disk and stellar applications, yand y-z distributions are best. Hence grid resolutions and distributions of data are chosen to match each of these situations as closely as possibly. For all the tests performed we have roughly an equal number of gridpoints per processor making comparisons between distributions possible also.
For ideal parallelisation, the real time of calculation should remain constant when doubling the number of processors and doubling the grid resolution. We therefore measure performance on real time per grid-point. These are then scaled as a percentage of the time taken on two processors.
Table 2 shows the times for distributing the data in the vertical direction for a grid resolution that is biased towards the vertical. Figure 8 shows plots of the relative times and speed up of the code. Tables 3 and 4 along with Figs. 9 and 10 respectively show the results for the alternative types of box dimensions and data distributions.
| No. of | Grid | Real time | Relative |
| procs. | resolution | (s) | speed up |
| 2 |
|
742.61 | 2.00 |
| 4 |
|
764.51 | 3.95 |
| 8 |
|
711.29 | 8.62 |
| 16 |
|
708.45 | 17.40 |
| 32 |
|
738.99 | 33.56 |
| 64 |
|
734.29 | 68.26 |
| 128 |
|
732.26 | 136.99 |
| No. of | Grid | Real time | Relative |
| procs. | resolution | (s) | speed up |
| 2 |
|
879.23 | 2.00 |
| 4 |
|
905.84 | 3.94 |
| 8 |
|
808.41 | 8.97 |
| 16 |
|
802.86 | 18.18 |
| 32 |
|
862.69 | 34.01 |
| 64 |
|
870.33 | 68.03 |
| 128 |
|
898.92 | 131.58 |
| No. of | Grid | Real time | Relative |
| procs. | resolution | (s) | speed up |
| 2 |
|
811.98 | 2.00 |
| 4 |
|
824.25 | 3.96 |
| 8 |
|
827.86 | 7.96 |
| 16 |
|
772.57 | 17.24 |
| 32 |
|
778.36 | 34.30 |
| 64 |
|
796.55 | 68.5 |
| 128 |
|
792.46 | 136.02 |
| |
Figure 8:
Performance of the code starting from
|
| Open with DEXTER | |
| |
Figure 9:
Performance of the code starting from
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{H2618F10.eps}
\end{figure}](/articles/aa/full/2001/14/aah2618/Timg146.gif) |
Figure 10:
Performance of the code starting from
|
| Open with DEXTER | |
We see that out of the three tests, the times for the vertical distribution are the best. This is because the shearing boundaries are not affected by the parallelisation. Data that is required by one particular point on an x-boundary always lies on the same processor therefore expensive communication does not occur. We also note, that in general, as the number of processors increases (along with the grid resolution), the performance appears to improve which is seen from the graphs where the speed up is above optimal. This is due to the percentage of time taken up in calculating the boundary conditions diminishing as the overall size of the model increases. All the results show that the code has good speed up when doubling the resolution and doubling the number of processors with virtually linear speed up in all cases.
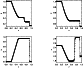 |
Figure 11:
Results for the weak Riemann shock-tube test where the
density on the left is initially set to |
| Open with DEXTER | |
The code has been tested against a number of standard hydrodynamical and magneto-hydrodynamical tests in 1D, 2D and 3D. These tests have been designed to test individual properties of the code as well as all components of the code working together. Some of these tests are "standard'' tests of fluid models and others have been incorporated to compare the results of our method against the existing analytical solutions and other numerical models.
Most of the hydrodynamical tests are designed to determine the
effectiveness of the numerical viscosities in stabilising the code,
removing unphysical features and capturing the essential physics of a
particular problem. They are also aimed at determining the ability of
the Cartesian grid to reproduce spherical features. For all tests we
use
![]() and
and
![]() for the coefficients of
the shock and hyperviscosities. The Prandtl number and magnetic
Prandtl numbers are equally set to unity.
for the coefficients of
the shock and hyperviscosities. The Prandtl number and magnetic
Prandtl numbers are equally set to unity.
Using the MHD test suite of Stone et al. (1992) and Stone & Norman (1992b) as a basis for the magneto-hydrodynamic tests, we perform a number of identical tests again using previously published results for comparison with our numerical method. These tests are designed to examine the stability of the fluid and magnetic field evolution and more specifically to check that the characteristics of the MHD flow are correct, specifically the propagation of MHD waves.
These tests have allowed us to determine the effectiveness of the algorithms used, as well as to show their weaknesses. All tests have been performed using resolutions comparable to those expected in "real'' simulations and hence act as a gauge on the accuracy one can expect from future calculations.
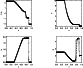 |
Figure 12:
Results for the strong Riemann shock-tube test where the
density on the left is initially set to |
| Open with DEXTER | |
The Riemann shock tube test (Sod 1978) has been used by many authors as a test of numerical algorithms. All components of the hydrodynamical code are used including numerical viscosities. This test determines the ability of the code to capture shocks, formed from discontinuities in the fluid properties, and therefore it particularly is a direct test of the shock viscosity employed.
Starting from an initial discontinuity in the density and energy, the fluid forms a shock front and a rarefraction wave. For this test an exact analytical solution can be found (e.g. Hawley et al. 1984), which provides an ideal situation for determining the accuracy of the code including the propagation speed of the waves, the jump conditions at the shock front, and the ability of the code in stabilising discontinuities within the fluid.
We perform two test cases; one using the standard setup described by Sod (1978) and another for which the shock is much stronger. This second test is included as a more accurate measure of the ability of the code to cope with more violent physical features, and as a more extreme test of the numerics.
Both tests are calculated in one dimension (we use the z-dimension
with closed boundaries) with a resolution of nz=255 with
![]() .
The gas has a ratio of specific heats of
.
The gas has a ratio of specific heats of
![]() with zero initial velocity. The density and energy, and therefore
pressure, are discontinuous at z=0.5. For the weak (standard) shock
tube test, we have on the left
with zero initial velocity. The density and energy, and therefore
pressure, are discontinuous at z=0.5. For the weak (standard) shock
tube test, we have on the left
![]() and with the strong shock
tube test this is
and with the strong shock
tube test this is
![]() .
All other variables are the same for
the two tests with
.
All other variables are the same for
the two tests with
![]() ,
,
![]() and
and
![]() .
.
Figure 11 shows the evolution of the variables for the weak shock at t=0.245 compared to the analytical solution, shown as a dashed line. Many features of the fluid properties have been captured well by the calculation. The position of the shock front, the contact discontinuity and the rarefraction wave are all correct and the magnitudes of the fluid properties in each region is correct. The main deviations from the analytical curve occur at the contact discontinuity and the shock front. At the shock front the shock is captured well within four gridpoints however a slight under-shoot occurs for the energy which is quickly corrected within three gridpoints. The model has not successfully reproduced the shape of the contact discontinuity for energy or density, with both variables being smoothed. This feature appears to be common amongst many different numerical schemes as shown in the figures by Sod (1978) and Stone & Norman (1992a). The discontinuities in the gradient of the rarefraction wave have been captured well by the scheme, although some smoothing is inevitable.
Figure 12 shows the equivalent variables at t=0.150 for the strong initial discontinuity, with density plotted as a natural logarithm. This, being a more rigorous test of the numerics, shows more unphysical features than the weak shock. However, the different regions of the flow are very clear and follow well from the true values - the main difference being the ability of the code to retain the strong shock features. The positions of the boundaries between the different regions all agree very well to the analytical solution, however it is noted that the shock front appears to have moved fractionally further. Small scale oscillations in the velocity are seen to be generated behind the shock, which is natural of a scheme of this type, however, the hyperdiffusion has minimised the magnitude of these. Again, the contact discontinuity is smeared by the simulation, and the plateau of maximum energy is not resolved, but does not deviate far from the true value. The shock front itself is still well resolved and retains the essential physical characteristics showing that the shock viscosity is implemented correctly. In this case, the under-shoot is smaller than for the weak shock. The rarefraction wave still clearly remains close to the analytical solution and the discontinuous gradients are well represented. Considering the strong initial conditions presented to the flow, we feel that the numerical solution presents a good fit to the analytical one.
![\begin{figure}
\par\includegraphics[width=6cm,clip]{H2618F19.eps}\hspace*{2cm}
\includegraphics[width=8.7cm,clip]{H2618F20.eps}
\end{figure}](/articles/aa/full/2001/14/aah2618/Timg158.gif) |
Figure 13: Lefthand panel shows spherically symmetric expansion of an adiabatic blast wave, showing grey-scale representation of logarithmic density at the horizontal mid-plane of a 3D simulation using 1273gridpoints at 22 Myrs. On the right we show the 1D profiles of density and velocity during the shock stage at 3 Myrs for the resolution 255 plotted on the analytical Sedov-Taylor solution |
| Open with DEXTER | |
| |
Figure 14: Position of the expanding remnants for different setups. The leftmost panel shows the expansion of adiabatic and radiative remnants in three dimensions. The panel on the right shows the expansion of adiabatic remnant in a uniform azimuthal magnetic field. The dashed line in both figures shows the Sedov-Taylor expansion law with the slope 0.4. For the magnetic case the expansion of the remnant in the azimuthal direction is shown with a solid line, while in the x-direction it is dot-dashed. The magneto-sonic wave moving in the x-direction is represented by the dotted line |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{H2618F23.eps}\hspace*{2.8cm}
\includegraphics[width=7.2cm,clip]{H2618F24.eps}
\end{figure}](/articles/aa/full/2001/14/aah2618/Timg160.gif) |
Figure 15: Interaction of blastwave with large-scale azimuthal magnetic field. The lefthand panel shows a 2D slice through the horizontal midplane with density shown in grey-scale with velocity field plotted on top with arrows. The righthand panel shows the voxel projection of the density with the perturbed magnetic field lines plotted on top. The expansion of the shock front is seen to be restricted to the azimuthal direction while the magneto-sonic wave perturbs the density in the poloidal directions |
| Open with DEXTER | |
The next set of tests is aimed at testing the capability of the code to model spherical features with a Cartesian grid. We perform three 3D tests of strong blast waves: adiabatic, radiative, and with a strong imposed magnetic field.
First we follow the evolution of an adiabatic shock created by an
instant injection of purely thermal energy, monitoring its shape,
radius and expansion velocity, and comparing it to the analytical
Sedov-Taylor solution (Taylor 1950; Sedov
1959). The explosion is initialised by adding 1051 ergs
of thermal energy, roughly corresponding to a realistic SN explosion
(e.g. Heiles 1987), in a single grid-point in the middle of
the computational volume sized 1 kpc3. The number of gridpoints
used in the test is 1273. The surrounding ISM has a uniform
density of 1.0 cm-3 and temperature 104 K without any magnetic
field. No heating or cooling terms are applied to the energy Eq. (4). According to the Sedov-Taylor solution, based on
similarity analysis, the shock front produced by a strong explosion in
a uniform medium (in a three-dimensional volume) moves through it so
that its radius as function of time is
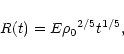 |
(34) |
The Sedov solution serves as a good approximation for a SN explosion
when the radiative losses are negligible, which is true roughly during
the first 105 years of its evolution (e.g. Shu 1992). When
the radiative losses become significant, they change the expansion
characteristics of the remnant, as discussed e.g. by Ostriker & McKee
(1988). We investigate a radiative remnant with the same setup as
used for the adiabatic case, but adopting a cooling function derived
by Dalgarno & McCray (1972) and Raymond et al.
(1976) that has been previously used in several ISM models
(e.g. Rosen & Bregman 1995; Vázquez-Semadeni et al. 1995), which is implemented as a sink term in the
energy Eq. (4) so that
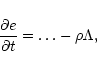 |
(35) |
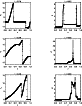 |
Figure 16: Results for the interacting blastwaves, taken in one-dimension. The points show the resolution of 511 gridpoints and the solid line is for 8191 gridpoints. Plots of velocity and density are shown at three different times (t=0.010, t=0.028 and t=0.038). The lower resolution case closely follows the evolution of the more accurate high resolution simulation however strong peaks are damped |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.3cm,clip]{H2618F31.eps}\hspace*{1cm}...
...\par\hspace*{3.5cm}\includegraphics[width=6.1cm,clip]{H2618F33.eps}
\end{figure}](/articles/aa/full/2001/14/aah2618/Timg167.gif) |
Figure 17: The two-dimensional evolution of interacting blastwaves generated from two equally strong point explosions (corresponding to a typical SNe of 1051 ergs) in a uniform medium with no magnetic field shown at three different times (t=5 Myrs, t=12 Myrs and t=34 Myrs). The collision occurred at t=1 Myr. Grey-scale and black contours shows logarithmic density with velocity field plotted with white arrows on top. The resolution is fixed at 127 gridpoints per kpc |
| Open with DEXTER | |
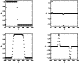 |
Figure 18: Advection of pulse of magnetic field in the zdirection. The upper two panels show the inital condition of the test with the left plot showing the radial magnetic field and on the right the azimuthal current density. The deviation from a square wave is due to the use of the magnetic potential. The final state is shown in the lower two panels The resolution is nz=255 and for a perfect initially square pulse, the edges would be located at z=255 and z=305 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{H2618F38.eps}\hspace*{1cm}...
....eps}\hspace*{1cm}
\includegraphics[width=6.9cm,clip]{H2618F41.eps}
\end{figure}](/articles/aa/full/2001/14/aah2618/Timg169.gif) |
Figure 19: Propagation of shear Alfvén wave in a fluid threaded by a vertical magnetic field. The upper panel is for an initially stationary fluid and the lower for a fluid with initial velocity of uz=1.5. For the stationary fluid, the wave is generated by a perturbation in velocity that was initially located between z=1 and z=2 whereas for the non-stationary case it is located between z=2and z=3. Both cases show that square pulses of magnetic field are generated, propagating perpendicular to the applied magnetic field at the correct velocity. The resolution is set to nz=255 |
| Open with DEXTER | |
| Ti [K] | ||
| 100 | 1.14 1015 | 2.000 |
| 2000 | 5.08 1016 | 1.500 |
| 8000 | 2.35 1011 | 2.867 |
| 105 | 9.03 1028 | -0.650 |
Finally, we investigate adiabatic blast waves in the presence of a
strong azimuthal magnetic field. The setup is identical to the
adiabatic case, but now we impose an azimuthal magnetic field of the
strength 5 ![]() G at each time-step, and follow the position of the
blast wave in the direction along the field lines (y-direction), and
perpendicular to them (x-direction), which curves are shown in
Fig. 14. The shape of the blast wave is shown as
density contours over-plotted with velocity field vectors at the
horizontal mid-plane in the left-hand panel of
Fig. 15. In the right-hand side of Fig. 15
we show a voxel projection of the 3D density field with perturbed
magnetic field lines. All these figures illustrate how the magnetic
field can severely affect the expansion. Along the magnetic field
lines the blast wave expands in a normal fashion and develops a strong
shock front. However due to magnetic tension of the field lines, this
does not occur along the x direction. We also see formation of a
magnetosonic wave, which propagates perpendicular to the field lines,
forming a weak spherical perturbation, slightly pinched at the
poles. The shape of the perturbation is similar to the one described
by Ferriére et al. (1991). In the x-direction the
expansion velocity of the blast wave is heavily damped, and most of
the expanding motion occurs in the y-direction, as seen e.g. in the
simulations of Tomisaka 1998). In
Fig. 14 the expansion in the y-direction is seen to
roughly follow the Sedov-Taylor law, but the x-direction strongly
deviates from it. The expansion of the magnetosonic wave is much
faster than the non-inhibited blast wave, since it is moving with the
Alfvén velocity 14 km s-1, which after approximately 4 Myrs
becomes faster than the blast wave itself. In three dimensions the
spherical blast wave is unrecognisable. Complex features have been
formed, where the magnetosonic wave has created a lemon-shaped weak
density perturbation within which the blast wave has produced a cavity
elongated in the y-direction.
G at each time-step, and follow the position of the
blast wave in the direction along the field lines (y-direction), and
perpendicular to them (x-direction), which curves are shown in
Fig. 14. The shape of the blast wave is shown as
density contours over-plotted with velocity field vectors at the
horizontal mid-plane in the left-hand panel of
Fig. 15. In the right-hand side of Fig. 15
we show a voxel projection of the 3D density field with perturbed
magnetic field lines. All these figures illustrate how the magnetic
field can severely affect the expansion. Along the magnetic field
lines the blast wave expands in a normal fashion and develops a strong
shock front. However due to magnetic tension of the field lines, this
does not occur along the x direction. We also see formation of a
magnetosonic wave, which propagates perpendicular to the field lines,
forming a weak spherical perturbation, slightly pinched at the
poles. The shape of the perturbation is similar to the one described
by Ferriére et al. (1991). In the x-direction the
expansion velocity of the blast wave is heavily damped, and most of
the expanding motion occurs in the y-direction, as seen e.g. in the
simulations of Tomisaka 1998). In
Fig. 14 the expansion in the y-direction is seen to
roughly follow the Sedov-Taylor law, but the x-direction strongly
deviates from it. The expansion of the magnetosonic wave is much
faster than the non-inhibited blast wave, since it is moving with the
Alfvén velocity 14 km s-1, which after approximately 4 Myrs
becomes faster than the blast wave itself. In three dimensions the
spherical blast wave is unrecognisable. Complex features have been
formed, where the magnetosonic wave has created a lemon-shaped weak
density perturbation within which the blast wave has produced a cavity
elongated in the y-direction.
We perform two tests, in one and two dimensions, to show the ability of the code to deal with interacting blast waves. The first follows the one-dimensional colliding blast wave test presented by Woodward & Colella (1984) who performed this test on various algorithms comparing a very high-resolution case to lower-resolution ones. We perform a similar test, comparing a high-resolution calculation to a moderate resolution case. One reason for this test is to compare the high-resolution case to the Woodward & Colella case as a check on shock velocities and density profiles, and a second reason is to see how the code adapts with different resolutions. If the code scales well (and in particular the numerical viscosities) between different resolutions then one would expect the shock positions and profiles to be in close agreement.
The test setup follows that of Woodward & Colella
(1984). The numerical domain is in the vertical
direction, again for reasons of boundary conditions, with ![]() and the ratio of specific heats set to be
and the ratio of specific heats set to be
![]() .
Velocity is
initially at zero with density everywhere set to be
.
Velocity is
initially at zero with density everywhere set to be ![]() .
Two
shock waves are generated by setting two discontinuities in the
pressure. For
.
Two
shock waves are generated by setting two discontinuities in the
pressure. For
![]() we set P=1000,
we set P=1000,
![]() P=0.01 and for
P=0.01 and for
![]() we have P=100, hence two blast
waves of different magnitudes are generated moving towards each other.
we have P=100, hence two blast
waves of different magnitudes are generated moving towards each other.
Since no exact analytical solution exists, we perform a very high-resolution test calculation to obtain profiles which can be considered to be highly accurate. For this we set nz=8191which allows the sharp density peak at the time of collision to be well resolved. For the moderate resolution, we set nz=511.
Figure 16 shows the evolution of the fluid at three different times, each of which can be compared to the figures shown by Woodward & Colella (1984). The very high-resolution calculation is shown as a dashed line with the moderate resolution plotted on top as diamonds. Evident from all the figures is that the shocks travel at identical speeds for both resolutions, an important factor when using the code at different resolutions. One also observes that the shapes of the curves are almost exactly the same. At t=0.028 we see a slight deviation in the velocity behind the shock front, but in all other aspects and at other times the different resolutions appear to be virtually identical. The lower resolution run obviously cannot resolve very small features, and this is evident at the time of collision when the density spike is smaller, but is in the correct position. At the final stage the density minima and maxima are again smoothed as a consequence of the lower resolution, but retain the same shape as the very high-resolution case. Overall, we feel that the lower resolution simulation compares very well to the high resolution case, and compared to the original Woodward and Colella figures of lower resolution calculations (which are however for 1200 grid zones) performs very well.
The second test we perform is a two-dimensional test on colliding spherical remnants produced by two equally strong explosions in a uniform medium, which is the configuration discussed e.g. by Courant & Friedrichs (1948), and studied also with numerical models e.g. by Yoshioka & Ikeuchi (1990) and Voinovich & Chernin (1995). We again initialise the two explosions as thermal energy releases in a single grid-point corresponding to a SN energy of 1051 ergs, located 0.4 kpc apart from each other. The remnants collide after 1 Myr, having equal expansion velocities, and instantly after the collision a reflected shock front is formed propagating back into the hot and sparse interiors, as seen in the top left panel of Fig. 17. At the location of collision, a tangential line forms, along which the radial flow stops persisting throughout the simulation, and thereby seen in all the panels of Fig. 17. Soon afterwards a new shock front, denoted as the Mach front by Courant & Friedrichs (1948) traveling along this line appears, with the velocity exceeding the expansion of the unperturbed remnants. This configuration seen in the simulation at this stage closely resembles the classical Courant-Friedrichs picture. The top right panel of Fig. 17 shows that after about 10 Myrs the Mach front has propagated outwards and increased its surface area, so that the whole systems starts becoming spherical on the outside, even more pronounced in the lower panel at 34 Myrs. At the same time the curved reflected shock fronts expand in the hot sparse interior having largest expansion velocities in the direction of the smallest density with vortical motions occurring leading to kidney-shaped structures. The appearance of the flow is in good agreement with other numerical simulations, such as the detailed calculation presented by Voinovich & Chernin (1995) and also with the results of Yoshioka & Ikeuchi (1990).
We now perform an advection test of a pulse of magnetic field. The test is initialised such that a pulse of magnetic field, which is as close as possible to a square wave, is advected at constant velocity in one direction. This is perhaps the least relevant test for the numerical scheme as it requires that most of the PDEs are disabled. In other words, the square pulse has no back-reaction on the fluid in any sense. The test is essentially used here to study the numerical diffusion of the wave (since numerical diffusion acts all the time and quite strongly where fluid properties vary rapidly between gridpoints) ensuring that numerical instabilities are quenched and that the evolution of the current that is generated at the leading and trailing edges of the pulse is correct.
The test is performed in one dimension along the vertical axis. The
use of the z-direction is different to Stone & Norman
(1992b) and arises from the fact that boundary conditions
in the vertical direction mean that setting up tests such as this (and
subsequent tests shown below) is simplified. Discontinuous values of
the magnetic vector potential in periodic directions result in
propagation of waves from the boundaries. This change in
direction also results in the use of Bx which in effect means that
the test should be otherwise identical. However, the use of the
magnetic vector potential causes a number of difficulties when
initialising the wave and obtaining a perfect square wave is
impossible since discontinuities in the magnetic vector potential lead
to ringing occurring at the corners of the wave. We therefore start
the test from a wave in which the edges of the pulse are spread over
three grid-zones rather than just one, which is already slightly
smoother than that of Stone & Norman. However we as closely as
possible follow their setup. The total width of the pulse is over 54
gridpoints, with the upper values covering 48. The initial shape of
the field and current is shown in the upper panels of
Fig. 18. The pulse is then advected over 250 gridpoints
for which
![]() with a velocity of uz=1.
with a velocity of uz=1.
The final state of the advected magnetic field and current is shown in lower two panels of Fig. 18. As expected from the use of the diffusive elements of the model, the edge of the pulse has now been smeared from the initial three grid-zones to approximately 10. The current density is therefore similarly smeared. As quoted by Stone & Norman, the use of the vector potential can lead to the production of non-monotonic currents. Indeed, it is seen that the trailing edges are non-monotonic. However, no sign reversal is seen and the deviations from monotonicity are very small in comparison to the maxima of the current.
The next test we perform is to propagate Alfvén waves initially generated from a shear flow. The test is again set up identically to that of Stone & Norman (1992b) except for the use of the z direction again for reasons stated above.
The test is intialised by threading the fluid with a vertical magnetic
field, Bz, and a small perturbation to uy is added to a small
region of the width one, the extent of the domain being 15. In terms
of dimensionless units, ![]() ,
Bz=1 and uy=0.001 in the
perturbed region. As with Stone & Norman, two tests are performed:
one for which uz=0 and the perturbed velocity is between the
regions of z=1 and z=2 and one for uz=1.5 with the perturbation
occurring between z=2 and z=3. The shearing motion then generates
square Alfvén waves propagating at an Alfvén velocity of
,
Bz=1 and uy=0.001 in the
perturbed region. As with Stone & Norman, two tests are performed:
one for which uz=0 and the perturbed velocity is between the
regions of z=1 and z=2 and one for uz=1.5 with the perturbation
occurring between z=2 and z=3. The shearing motion then generates
square Alfvén waves propagating at an Alfvén velocity of
![]() (with
(with ![]() ). For the first case of this test, these propagate
with and equal velocity in each direction (
). For the first case of this test, these propagate
with and equal velocity in each direction (![]() )
and for the
second case one has an overall velocity of
)
and for the
second case one has an overall velocity of
![]() and the
other
and the
other
![]() .
Both calculations have a resolution of
nz=255.
.
Both calculations have a resolution of
nz=255.
Figure 19 shows the final state of the azimuthal velocity, uy, and sheared magnetic field, By, for the two cases. For the first case the plots are shown after t=0.8. The waves have clearly traveled the correct distance of z=0.8corresponding to u=1 and have propagate evenly in both directions away from the initial sheared region. The second figure is shown after a time of t=1.0, when the two waves have traveled distances of z=2.5and z=0.5 corresponding to the right and left waves respectively. Again these correspond correctly to the overall velocities of u=2.5 and u=0.5. Also, the widths of the square pulses are almost identical to the initial width of the sheared region in both cases.
It can be seen that in the second case the diffusion has acted more strongly. This is due to the magnitude of the hyperdiffusion depending upon both Alfvén velocity and fluid velocity and hence being greater for the case in which uz=1.5.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{H2618F42.eps}\hspace*{2.2cm}
\includegraphics[width=6.9cm,clip]{H2618F43.eps}
\end{figure}](/articles/aa/full/2001/14/aah2618/Timg183.gif) |
Figure 20:
Results of the magnetically braked aligned rotator showing
the resulting azimuthal velocity and magnetic field at t=13. The fluid
is threaded by a vertical magnetic field and the fluid density remains
fixed with |
| Open with DEXTER | |
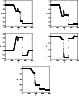 |
Figure 21: Results for MHD Riemann problem. The setup follows exactly that of the hydrodynamic counterpart with an additional discontinuous vertical magnetic field, aligned with the other fluid discontinuities. The subsequent evolution of various kinds of waves is shown at t=80 for density, pressure, vertical velocity, radial velocity and radial magnetic field. The grid resolution is set to 801 gridpoints |
| Open with DEXTER | |
The third test is the magnetic braking of an aligned rotator. This is virtually identical to the previous test in which the fluid is threaded by a magnetic field and a region of the fluid is then perturbed azimuthally. For this test however, there is a density contrast between the perturbed region and the steady region resulting in a setup which mimics a disk of high density surrounded by a low density medium. The perturbation generates Alfvén waves propagating away from the disk and also into the disk thus accelerating the fluid in the surrounding medium and decelerating the disk. Subsequent partial reflections from the surface of the disk further complicate the system, each being both transmitted as a lower amplitude waves into the medium and back into the disk. A more comprehensive discussion of the model is given by Stone & Norman (1992b).
Again, using identical parameters to Stone & Norman, the disk is of
density
![]() and the surrounding medium is of
and the surrounding medium is of
![]() .
The test again is in the z-direction with 300
grid-zones. The disk is located in the region z < 1 and the low
density medium extends from this point to z=15. The vertical
magnetic field has a strength of Bz=1. Setting uy=0.001 in the
region z<1 and zero elsewhere, we are able to make comparisons to
the analytical results of Mouschovias & Paleologou
(1980). The profiles of the resulting sheared magnetic
field, By, and azimuthal velocity, uy, are independent of the
initial velocity (varying only in magnitude).
.
The test again is in the z-direction with 300
grid-zones. The disk is located in the region z < 1 and the low
density medium extends from this point to z=15. The vertical
magnetic field has a strength of Bz=1. Setting uy=0.001 in the
region z<1 and zero elsewhere, we are able to make comparisons to
the analytical results of Mouschovias & Paleologou
(1980). The profiles of the resulting sheared magnetic
field, By, and azimuthal velocity, uy, are independent of the
initial velocity (varying only in magnitude).
Figure 20 shows the final state of the relevant quantities after t=13. The dashed line shows the analytical values for comparison. The waves, which are generated from the initial shear and subsequent reflections at the disk surface, closely match the profiles of the analytical values but are smoothed due to the inherent diffusion of the scheme. However, propagation speed and magnitudes are correct.
The next test is the MHD equivalent to the Riemann shock tube test (Sod 1978) . This has been discussed in detail for a number of numerical schemes by Brio & Wu (1988) and used as a subsequent test by Stone & Norman (1992b). This tests uses all elements of the code to evolve a fluid that is initiated with a discontinuous pressure and magnetic field at the midpoint with an additional component of the magnetic field along the direction of motion. Unlike the standard shock tube test, no known analytical solution exists for the subsequent evolution of the fluid and magnetic field. Hence we make comparisons to the previously published works mentioned above.
The hydrodynamical parts of the test are initialised exactly as in the
hydrodynamical counterpart. The domain size of the problem is however
larger (800 grid-zones with
![]() to match the published results
of Brio & Wu (1988) and Stone & Norman
(1992b). We again use the z direction due to the boundary
conditions and change the direction of the discontinuous magnetic
field accordingly. The discontinuity is at the centre of the
domain. Fluid to the left takes physical values of
to match the published results
of Brio & Wu (1988) and Stone & Norman
(1992b). We again use the z direction due to the boundary
conditions and change the direction of the discontinuous magnetic
field accordingly. The discontinuity is at the centre of the
domain. Fluid to the left takes physical values of
![]() ,
,
![]() and
and
![]() .
and to the right takes
.
and to the right takes
![]() ,
,
![]() and
and
![]() .
An additional magnetic field of Bz=0.75 is constant
throughout the domain. As in the previously published MHD Riemann
shock tube tests, we take
.
An additional magnetic field of Bz=0.75 is constant
throughout the domain. As in the previously published MHD Riemann
shock tube tests, we take ![]() .
As with the magnetic advection
test, the use of the magnetic vector potential produces problems when setting
up discontinuous magnetic fields. The initial
discontinuity is therefore spread over three grid-zones. However we feel
that, with the use of magnetic shock viscosities and hyperdiffusion,
this small initial difference has negligible effects on the resulting
evolution.
.
As with the magnetic advection
test, the use of the magnetic vector potential produces problems when setting
up discontinuous magnetic fields. The initial
discontinuity is therefore spread over three grid-zones. However we feel
that, with the use of magnetic shock viscosities and hyperdiffusion,
this small initial difference has negligible effects on the resulting
evolution.
Unlike the hydrodynamical case, the MHD shock tube test generates many kinds of waves as well as the shock and rarefraction wave. As quoted by Brio & Wu, the fluid can contain a compound wave which consists of a shock wave attached to a rarefraction wave of the same family. As seen by the results in Fig. 21, this complexity is clearly evident.
Figure 21 shows the final state of the fluid and magnetic field at t=80. All waves shown in the results of Brio & Wu are evident, including the left moving fast rarefraction wave, slow shock and rarefraction wave compound, right moving contact discontinuity, slow shock and fast rarefraction wave. Comparisons also show that they have moved with the correct velocities and magnitudes, and are in close agreement with the published results of Brio & Wu (1988) and Stone & Norman (1992b).
In this paper we have described a numerical model for simulating magnetised shear-flows in astrophysical systems such as galaxies or accretions disks. Starting from the basic non-ideal MHD equations describing the fluid, we have discussed their numerical implementation on the standard shearing box model. Using explicit finite-difference calculations, fluid properties are discretised onto a regular mesh in three dimensions. The fluid is advanced through time using a third order accurate predictor-corrector scheme, which has been shown to compare favourably to other advancing schemes.
An important feature of the model comes from the diffusion methods, which are implemented for two reasons, firstly to resolve and model discontinuities in the flow, and secondly to stabilize the numerics. The method works well as introducing diffusion only in the necessary regions leaving well resolved regions of the fluid unaffected.
An important aim of this work is to perform high resolution calculations and as a result the model has been designed to take advantage of parallel computers. We have therefore illustrated the methods we have invoked to parallelise the code and shown their performance. Similarly important feature of the model is to make it easily adaptable to incorporate new physics or numerical techniques. The parallelisation method adopted, namely HPF, has been chosen for its flexibility and the ease of data parallelisation on a finite-differences method. Certain features of the model, such as the vertical and shearing boundaries, add complexity to the parallelisation. However, having performed tests up to 128 processors, the code has been shown to parallelise well, enabling high resolution calculations within attainable times.
As well as giving the details of the methods we use, the other main aim of this paper has been to justify the use of this code in future simulations. We have performed several standard hydro- and magnetohydrodynamic tests in a number of dimensions illustrating the successes and limitation of the current method. We have shown that the shock-capturing technique has performed well in a number of cases, namely in modelling the Riemann shock tube problem and blast waves and their interactions. In all of these test cases the shocks have propagated at the correct speed and have shown profiles closely matching the true ones. In the cases of spherical blast waves we have also illustrated the capability of the method to produce spherical structures on a Cartesian grid. The performed set of magnetohydrodynamic tests have shown the capability of the code of propagating Alfvén waves at correct velocities and shapes. These tests have also shown the limitations of the use of magnetic vector potential rather than the magnetic field itself such as in modelling discontinuities in the field and maintaining the monotonicity of the current. However, deviations from the physical solution are minor, and considering the advantage of achieving solenoidal magnetic field, the use of the model is justified.
As a first task we plan to use this method to investigate various processes in the ISM, such as the nature of interstellar turbulence driven by stellar explosive events, the structures emerging in such a flow, leading to the investigation of dynamo processes in galaxies. Another application is to study accretion processes in accretion disks, in particular performing high-resolution calculations to study in more detail the stresses acting within them. This model, however, is far from complete, and additional physics can be added to it. These include self-gravity for modelling molecular cloud formation in the ISM, cooling functions and radiative transfer for accretion disks. However in its present state a number of physical setups can be investigated with this model, hopefully yielding interesting and reliable information.
Acknowledgements
We wish to thank Prof. Ilkka Tuominen for his support and the valuable comments during the work. We also acknowledge the Center for Scientific Computing (CSC) in Espoo, Finland, for the parallelisation assistance and computing time. Thanks also to Steve Brooks for his useful discussions on the features of HPF and also to Axel Brandenburg for his valuable comments regarding the numerics.
Centred, sixth order accurate, explicit finite difference operators are used for all the derivatives (first and second) of the pdes. Simple second order equivalents are used for the diffusive quantities. All values are co-located on each gridpoints. The derivatives take into account boundary conditions also which are also based on a centred template.
The centred scheme is identical for all three dimensions and presented below are the first and second derivatives of a variable f located at position i,j,k taken in the x-direction. Indices are changed accordingly for alternative directions.
The first derivative is calculated by:
| = | 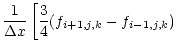 ![$\displaystyle \left. +\frac{1}{60} (f_{i+3,j,k} - f_{i-3,j,k})\right].$](/articles/aa/full/2001/14/aah2618/img194.gif) |
(A.1) |
The centred second derivative is as follows:
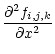 |
= | 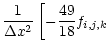 ![$\displaystyle \left. +\frac{1}{90} (f_{i+3,j,k} + f_{i-3,j,k})\right].$](/articles/aa/full/2001/14/aah2618/img199.gif) |
(A.2) |
The Adams-Bashforth-Moulton predictor-corrector scheme consists of a second order Adams-Bashforth predictor stage followed by the third order Adams-Moulton corrector. Both are adapted for use with a variable time-step.
The predictor stage is used to calculate the second order accurate
updated variable, fn+1*, at time
![]() .
From this predicted value a derivative of the function may be
obtained at the new time and used again to calculate the third-order
corrected value fn+1.
.
From this predicted value a derivative of the function may be
obtained at the new time and used again to calculate the third-order
corrected value fn+1.
The second-order Adams-Bashforth predictor uses the current function
value along with its calculated derivative and the derivative from the
previous time-step and is defined as
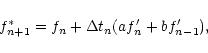 |
(B.1) |
After substitution of fn+1 and f'n-1 in expanded form,
| fn+1 | = | 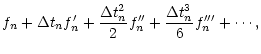 |
|
| f'n-1 | = | 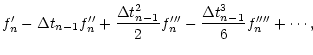 |
| a | = | ||
| b | = |
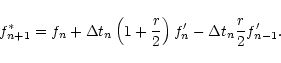 |
(B.2) |
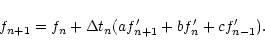 |
(B.3) |
| a | = | 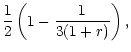 |
|
| b | = | 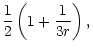 |
|
| c | = |
| fn+1=fn | + | 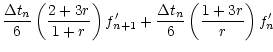 |
|
| - | (B.4) |
| f*n+1 | = | (B.5) | |
| fn+1 | = | (B.6) |