A&A 369, 574-588 (2001)
DOI: 10.1051/0004-6361:20010127

Mass-loss predictions for O and B stars as a function
of metallicity

Jorick S. Vink1 - A. de Koter2 - H. J. G. L. M. Lamers1,3


1 - Astronomical Institute, Utrecht University, PO Box 80000, 3508 TA Utrecht,
The Netherlands
2 - Astronomical Institute "Anton Pannekoek'', University of Amsterdam, Kruislaan 403, 1098 SJ Amsterdam,
The Netherlands
3 - SRON Laboratory for Space Research, Sorbonnelaan 2, 3584 CA Utrecht, The Netherlands

Received 24 July 2000 / Accepted 17 January 2001

Abstract
We have calculated a grid of massive star wind models and mass-loss rates for a wide range of metal abundances between $1/100 \le Z/\mbox{$Z_{\odot}$ }\le 10$. The calculation of this grid completes the Vink et al. (2000) mass-loss recipe with an additional parameter Z. We have found that the exponent of the power law dependence of mass loss vs. metallicity is constant in the range between 1/30 $\le$ $Z/\mbox{$Z_{\odot}$ }$ $\le$ 3. The mass-loss rate scales as $\dot{M} \propto Z^{0.85} \mbox{$v_{\infty}$ }^p$with p = -1.23 for stars with $\mbox{$T_{\rm eff}$ }\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\h... ...finterlineskip\halign{\hfil$\scriptscriptstyle ... K, and p = -1.60 for the B supergiants with $\mbox{$T_{\rm eff}$ }\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\h... ...finterlineskip\halign{\hfil$\scriptscriptstyle ... K. Taking also into account the metallicity dependence of $\mbox{$v_{\infty}$ }$, using the power law dependence $\mbox{$v_{\infty}$ }\propto Z^{0.13}$ from Leitherer et al. (1992), the overall result of mass loss as a function of metallicity can be represented by $\dot{M} \propto Z^{0.69}$ for stars with $\mbox{$T_{\rm eff}$ }\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\h... ...finterlineskip\halign{\hfil$\scriptscriptstyle ... K, and $\dot{M} \propto Z^{0.64}$ for B supergiants with $\mbox{$T_{\rm eff}$ }\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\h... ...finterlineskip\halign{\hfil$\scriptscriptstyle ... K. Although it is derived that the exponent of the mass loss vs. metallicity dependence is constant over a large range in Z, one should be aware of the presence of bi-stability jumps at specific temperatures. Here the character of the line driving changes drastically due to recombinations of dominant metal species resulting in jumps in the mass loss. We have investigated the physical origins of these jumps and have derived formulae that combine mass loss recipes for both sides of such jumps. As observations of different galaxies show that the ratio Fe/O varies with metallicity, we make a distinction between the metal abundance Z derived on the basis of iron or oxygen lines. Our mass-loss predictions are successful in explaining the observed mass-loss rates for Galactic and Small Magellanic Cloud O-type stars, as well as in predicting the observed Galactic bi-stability jump. Hence, we believe that our predictions are reliable and suggest that our mass-loss recipe be used in future evolutionary calculations of massive stars at different metal abundance. A computer routine to calculate mass loss is publicly available.

Key words: stars: early-type - stars: mass-loss - stars: supergiants - stars: winds - stars: evolution


   
1 Introduction

In this paper we predict the rate at which mass is lost due to stellar winds from massive O and B-type stars as a function of metal abundance: ${\dot{M} = f(Z)}$. The calculations are based on state-of-the-art modelling. The model description takes into account momentum transfer of radiation to gas in a way that photons are allowed to interact with ions in the wind more than just once. This method, which was pioneered by Abbott & Lucy (1985) and Schmutz et al. (1991), has been used in a previous study (Vink et al. 2000) where wind models including the effects of "multiple scattering'' were calculated for Galactic early-type stars. It was shown that our predictions agree with the observations for Galactic O stars, which resolved a persistent discrepancy between observed and theoretical mass-loss rates (Lamers & Leitherer 1993; Puls et al. 1996).

Metallicity is a key parameter that controls many aspects of the formation and the evolution of both stars and galaxies. For instance, the overall chemical enrichment of the interstellar medium (ISM) is a strong function of metallicity. Secondly, the relative importance of stellar winds compared to Supernova explosions depends on Z in the sense that stellar winds become more important with increasing metallicity (Leitherer et al. 1992). Since chemical elements are produced in stars with different masses, they enrich the ISM on different timescales. Massive stars mainly contribute to the enrichment of oxygen, other $\alpha $-elements and iron. Therefore, these elements are ejected on short timescales. Although carbon and nitrogen are also produced in massive stars, their main contribution comes from longer-lived intermediate mass stars. This implies that if the star formation history and the initial mass function are considered, metallicity is expected to cause a "differential'' chemical enrichment of the ISM in different galaxies.

Recent models of the chemical evolution versus redshift in the Universe predict that metallicity shows a stronger dependence on the local density (i.e. galaxy mass) than on redshift (Cen & Ostriker 1999). Hence, galaxies with high and low metal abundances are expected to be found at all cosmological distances. These models reasonably predict the range in metal abundance that has been observed. The metallicity reaches as high as 10 times the solar value $Z_{\odot}$ in central regions of active galactic nuclei and quasars (Artymowicz 1993; Hamann 1997), but is only about 1/50 $Z_{\odot}$ for the blue compact dwarf galaxy IZw18 (Sargent & Searle 1970; Izotov & Thuan 1999). Such low metallicity may imply that blue compact dwarf galaxies only experience their first episode of star formation. Based on the observed range in Z, we will study the mass loss properties of massive stars within the representative metallicity range of $1/100 \leq Z/Z_{\odot} \leq 10$. The driving mechanism of the winds of massive early-type stars is radiation pressure on numerous spectral lines (Castor et al. 1975, hereafter CAK; Abbott 1982; Pauldrach et al. 1986; Vink et al. 2000). It is important to know which lines are actually responsible for the acceleration of the winds. As hydrogen and helium only have very few lines in the relevant spectral range in which early-type stars emit most of their radiation, it is mainly lines of the metals that are responsible for the line driving. This thus implies that the stellar wind strengths are expected to depend on metal abundance.

Observational evidence for metallicity dependent stellar wind properties was found by Garmany & Conti (1985) and Prinja (1987). They found that the terminal flow velocity of the stellar wind in the Magellanic Cloud stars was lower than that of Galactic stars. The authors attributed this difference to an under-abundance of metals in the Magellanic Clouds compared to the Galaxy.

The quantitative dependence of $\dot{M}$ on Z was theoretically studied by CAK, Abbott (1982) and Kudritzki et al. (1987). These studies have shown that the $\mbox{$\dot{M}$ }(Z)$ relation is expected to behave as a power-law:

 \begin{displaymath}\mbox{$\dot{M}$ }\propto Z^{m} \end{displaymath} (1)

with predictions for the index m ranging between about 1/2 (Kudritzki et al. 1987) to 0.94 (Abbott 1982). Since these results were based on radiation-driven wind models that did not take into account the effect of "multiple scattering'', a new investigation of the $\dot{M}$ vs. Z relation, is appropriate. Especially since Eq. (1) is widely used in evolutionary calculations for massive stars, usually adopting m = 1/2 (e.g. Meynet et al. 1994).

We will use our ``Unified Monte Carlo'' method (Vink et al. 2000) to predict mass-loss rates of early-type stars over a wide range in metallicities and stellar parameters. In this approach, multiple scatterings are consistently taken into account and an artificial separation between the stellar photosphere and wind (core-halo) is avoided. The main question we will address is: "What is the dependence of stellar mass loss on metal abundance?''.

In Sects. 3 and 4, the method to calculate mass-loss rates and the adopted assumptions will be described. In Sect. 5, the resulting wind models and mass-loss rates will be presented. The relative importance of Fe and CNO elements to the line force will be discussed in Sect. 6. In Sects. 7 and 8 the dependence of the mass-loss rate on metallicity will be determined. This completes the Vink et al. (2000) mass-loss recipe to predict $\dot{M}$ as a function of stellar parameters with an additional Z dependence. It will be shown that over a large parameter space, the exponent of the $\dot{M}(Z)$ power law dependence is constant, but that at specific temperatures, one needs to take the presence of so-called bi-stability jumps into account. In Sect. 9 these mass-loss predictions will be compared with observed mass-loss rates for the Large Magellanic Cloud and the Small Magellanic Cloud. Finally, in Sect. 10, the study will be summarised.

   
2 Theoretical context

In this section we will discuss the basic physical processes that may play a role in determining the dependence of mass loss on metal abundance. We will describe the expected effects in terms of CAK theory. However, in our detailed predictions (Sect. 5), we will not use this formalism, but extend on it by including multiple scattering effects.

In CAK theory the line acceleration is conveniently expressed in units of the force multiplier M(t) and is given by (CAK, Abbott 1982):

 \begin{displaymath}M(t)~=~k~t^{- \alpha}\left(\frac{n_{\rm e}}{W}\right)^\delta \end{displaymath} (2)

where $n_{\rm e}$ is the electron density and W is the geometrical dilution factor. The parameters k, $\alpha $ and $\delta$ are the so-called force multiplier parameters. The first one, k, is a measure for the number of lines. The second parameter, $\alpha $, describes the ratio of the optically thick line acceleration over the total line acceleration (Gayley 1995; Puls et al. 2000) If only strong (weak) lines contribute to the force, then $\alpha = 1$ (0). The predicted value of $\alpha $ for O-type stars is typically 0.6 (Abbott 1982; Kudritzki et al. 1989). The parameter $\delta$ describes the ionization in the wind. Its value is usually $\delta \sim 0.1$. Finally, t is the optical depth parameter, given by:

 \begin{displaymath}t~=~ \sigma_{\rm e} v_{\rm th} \rho ({\rm d}r/{\rm d}v) \end{displaymath} (3)

where vth is the mean thermal velocity of the protons and $\sigma_{\rm e}$ is the electron scattering cross-section.

Abbott (1982) and Puls et al. (2000) have shown that the CAK force-multiplier parameter k is dependent on the metallicity in the following way:

 \begin{displaymath}k(Z)~\propto~Z^{1 - \alpha}. \end{displaymath} (4)

Kudritzki et al. (1989) have calculated analytical solutions for radiation-driven wind models that include the finite cone angle effect. The scaling relation for the mass-loss rate that was derived, is proportional to

 \begin{displaymath}\dot{M}~\propto~k^{1/\alpha_{\rm eff}} \end{displaymath} (5)

where

 \begin{displaymath}\alpha_{\rm eff} = \alpha - \delta. \end{displaymath} (6)

This implies that $\dot{M}$ is expected to depend on metallicity in the following way:

 \begin{displaymath}\dot{M}~\propto~Z^m~ \end{displaymath} (7)

with

 \begin{displaymath}m~=~\frac{1 - \alpha}{\alpha - \delta}\cdot \end{displaymath} (8)

Since a typical value for m is ( 1 - 0.6)/(0.6 - 0.1) = 0.8, one would expect a more linear ( $m \simeq 0.8$) dependence of $\dot{M}$ on Z, instead of the square-root (m = 1/2) dependence that was calculated by Kudritzki et al. (1987). However, as the force multiplier parameter $\alpha $ itself is dependent on metallicity, the terminal velocity $\mbox{$v_{\infty}$ }$ also becomes a function of Z: $\mbox{$v_{\infty}$ }\propto Z^q$. Note that Leitherer et al. (1992) indeed derived such a more linear ( $m \simeq 0.8$) dependence of $\dot{M}$ on Z, and additionally derived $\mbox{$v_{\infty}$ }\propto Z^{0.13}$. However, multi-line transfer was not taken into account in these calculations either.

We note that a pure power-law dependence of $\dot{M}$ on Z over the entire parameter space, is questionable. It may be expected that for a certain metallicity range Eq. (1) provides a useful representation of the mass loss vs. metallicity relation, but that at some minimum and maximum Z, deviations from a power-law may occur. For instance, deviations at high metallicity may occur when mass loss is so efficient that densities in the wind are so high that all relevant Fe lines become saturated. Hence, at some point, an increase in metallicity may no longer cause a substantial increase in mass loss and subsequently a flattening of the $\dot{M}(Z)$ relation is expected. Deviations at low metallicity, with subsequently low mass loss, may occur when only weak iron lines remain present. Other abundant ions, such as those of C, N, and O, which normally have far fewer effective driving lines than Fe, may start to dominate the driving because their main lines are still strong. Again a shallower slope of the $\mbox{$\dot{M}$ }(Z)$ relation is anticipated.

A second important item in the calculations of mass loss at different Z, is the possible presence of one or more "bi-stability'' jumps at different Z. For Galactic metallicities, at an effective temperature of $\sim$25000 K, the mass loss is predicted to increase dramatically by a factor of about five. The effect of this jump on terminal velocity has observationally been found by Lamers et al. (1995). The origin for this jump is related to a recombination from Fe  IV to III in the lower part of the wind (Vink et al. 1999). Since the ionization equilibrium does not only depend on temperature, but also on density, one may expect a shift in the position of this bi-stability jump as a function of Z. Moreover, at lower metallicity, other abundant ions, such as those of CNO, may start to dominate the wind driving, implying there could be additional bi-stability jumps at different Z due to recombinations of one of these elements.

In this paper we will therefore concentrate on three main issues: firstly, the global dependence of the mass-loss rate on Z; secondly, the presence and position of bi-stability jumps for different Z, and, thirdly, the relative importance of Fe and CNO elements at low metal abundance.

   
3 Method to calculate $\vec{\dot{M}}$

The mass-loss rates are calculated with a Monte Carlo (MC) method that follows the fate of a large number of photons from below the stellar photosphere through the wind and calculates the radiative acceleration of the wind material. The core of the approach is that the total loss of radiative energy is coupled to the momentum gain of the outflowing material. Since the absorptions and scatterings of photons in the wind depend on the density in the wind and hence on the mass-loss rate, it is possible to find a consistent model where the momentum of the wind material is exactly equal to the radiative momentum that has been transferred. The method is similar to the technique introduced by Abbott & Lucy (1985). The precise characteristics of our Unified MC approach have been described in Vink et al. (1999). The essential ingredients and the assumptions of our approach have extensively been discussed in Vink et al. (2000). The MC code uses a density and temperature structure that has been computed in a prior model atmosphere calculation ( ISA-WIND). The model atmospheres used for this study are calculated with the non-LTE unified Improved Sobolev Approximation code ( ISA-WIND) for stars with extended atmospheres. For details of the model atmosphere we refer the reader to de Koter et al. (1993, 1997). The chemical species that are explicitly calculated in non-LTE are H, He, C, N, O and Si. The iron-group elements, which are important for the radiative driving and consequently for $\dot{M}$, are treated in a generalised version of the "modified nebular approximation'' (Schmutz 1991).

The temperature structure of the ISA-WIND model atmosphere is based on the grey LTE approximation. This implies that radiative equilibrium is not strictly fulfilled, but that deviations at the one percent level may occur in ISA-WIND. In contrast, local radiative equilibrium is automatically enforced in MC-WIND. We mention that the total opacity that is treated in MC-WIND is larger than that treated in ISA-WIND. Regarding emissions, the frequency distribution of thermally emitted photons in MC-WIND is only based on the elements that were explicitly computed in the ISA-WIND atmosphere calculation. Regarding absorptions, the MC simulations include those due to metal ions (mostly iron), which are not accounted for in ISA-WIND. This inconsistency may introduce a small discrepancy in the frequency distribution between true emission and true absorption, causing an underestimate of thermal emissions relative to absorptions in spectral regions of high iron opacity, whereas in all other regions of the spectral energy distribution the situation is reversed. Nevertheless, because MC-WIND conserves total energy, we do not expect this effect to influence the predicted mass-loss rates significantly.

The line list that is used for these MC calculations consists of over 105 of the strongest transitions of the elements H - Zn extracted from the line list constructed by Kurucz (1988). Lines in the wavelength region between 50 and 7000 Å are included in the calculations with ionization stages up to stage VI. The wind was divided into about 50-60 concentric shells, with many narrow shells in the subsonic region and wider shells in supersonic layers. The division in shells is essentially made on the basis of the Rosseland optical depth scale, with typical changes in the logarithm of the optical depth of about 0.13. For each set of model parameters a certain number of photon packets is followed. For Galactic metallicities this number is typically about 2 105 (see Vink et al. 2000)

At lower Z, and consequently at lower mass-loss rates, however, the typical amount of photon packets has to be increased, to keep up good statistics, as one is shooting photons through a less dense wind. Consequently, photon packets experience smaller numbers of line interactions. We found that as long as there were typically $\sim$100 line scatterings in each supersonic shell, the derived mass loss was reasonably accurate, i.e. $\Delta$ log $\dot{M} \mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\display... ...offinterlineskip\halign{\hfil$\scriptscriptstyle ....

At extremely low metallicities ( $Z/\mbox{$Z_{\odot}$ }\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\h... ...offinterlineskip\halign{\hfil$\scriptscriptstyle ...) the line driving mechanism becomes very inefficient and accurate wind solutions can only be obtained for the highest stellar luminosities, i.e. log $L/\mbox{$L_{\odot}$ }\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\h... ...er{\offinterlineskip\halign{\hfil$\scriptscriptstyle ... 6. Hence, the lowest Z models ( $Z/\mbox{$Z_{\odot}$ }$ = 1/100) will only be calculated for $L/\mbox{$L_{\odot}$ }= 6$ (see Sect. 5).

   
4 The assumptions of the model grid

For every Z, the mass-loss rate was calculated for 12 values of $\mbox{$T_{\rm eff}$ }$ in the range between 12 500 and 50 000 K.

The abundances of the metallicity grid are given in Table 1. Z is the total metallicity content of all elements heavier than helium. Throughout the paper we will indicate the absolute value of the metals with Z and the value of metallicity relative to the Sun by $Z/\mbox{$Z_{\odot}$ }$, adopting $\mbox{$Z_{\odot}$ }= 0.019$ (Anders & Grevesse ). For every value of Z, the helium and hydrogen abundances, Y and X respectively, need be adjusted accordingly. X is simply given by

X = 1- Y- Z. (9)

For Y we adjust the abundances in the following way

 \begin{displaymath}Y~=~Y_{\rm p}~+\left(\frac{\Delta Y}{\Delta Z}\right) Z \end{displaymath} (10)

where $Y_{\rm p}$ is the primordial helium abundance and ( $\Delta Y/\Delta Z$) is an observed constant, discussed below.


 

 
Table 1: Adopted abundances of the wind models

( $Z/\mbox{$Z_{\odot}$ }$)		 X Y Z

1/30		 0.758 0.242 0.00063
1/10 0.752 0.246 0.0019
1/3 0.733 0.260 0.0063
1 0.68 0.30 0.019
3 0.52 0.42 0.057


We enumerate the assumptions in the model grid:

1.
Following Schaller et al. (1992) we adopt a primordial helium abundance of $Y_{\rm p}$ = 0.24 (Audouze 1987) and a ( $\Delta Y/\Delta Z$) ratio of 3 (Pagel 1992). The scaled solar metallicities were take from Allen (1973);

2.
All models have effective temperatures between 12 500 and 50 000 K with a stepsize of 2500 K in the range 12 500-30 000 K and a stepsize of 5000 K for the range between 30 000 and 50 000 K;

3.
To investigate whether the dependence of $\dot{M}$ on Z is universal for different luminosity and mass, it is calculated for three different values of the Eddington factor $\Gamma _{\rm e}$. This is the ratio between the gravitational and radiative acceleration due to electron scattering and is given by:

 \begin{displaymath} \Gamma_{\rm e}~=~\frac{L \sigma_{\rm e}}{4 \pi c G M}~=~7.66... ...ot}$ }}\right) \left(\frac{M}{\mbox{$M_{\odot}$ }}\right)^{-1} \end{displaymath} (11)

where $\sigma_{\rm e}$ is the electron scattering cross-section per unit mass (its dependence on $\mbox{$T_{\rm eff}$ }$ and composition is described in Lamers & Leitherer 1993). The other constants have their usual meaning. The values for $\Gamma _{\rm e}$ are given in Col. 1 of Table 2. The corresponding luminosities and masses are given in Cols. 2 and 3 of the same table;

4.
Also the dependence of $\mbox{$\dot{M}$ }$ on the adopted ratio of the terminal flow velocity over the escape velocity, $\mbox{$v_{\infty}$ /$v_{\rm esc}$ }$, was determined. Lamers et al. (1995) found that for Galactic supergiants the ratio $\mbox{$v_{\infty}$ /$v_{\rm esc}$ }\simeq 2.6$ for stars of types earlier than B1 and drops to $\mbox{$v_{\infty}$ /$v_{\rm esc}$ }\simeq 1.3$ for stars later than type B1. Therefore, we have calculated mass-loss rates for input ratios of $\mbox{$v_{\infty}$ /$v_{\rm esc}$ }$ of 1.3, 2.0 and 2.6 to investigate the mass loss for different values of this ratio.

We are aware that these ratios $\mbox{$v_{\infty}$ /$v_{\rm esc}$ }$ may vary for different metallicity. However, our goal here is to determine the dependence of mass loss on different stellar parameters, including $\mbox{$v_{\infty}$ /$v_{\rm esc}$ }$. If new observations with e.g. the Far Ultraviolet Spectroscopic Explorer show that the observed values of $\mbox{$v_{\infty}$ }$ at other Z are significantly different from Galactic values, the predicted mass-loss rates can easily be scaled to accommodate the new values of $\mbox{$v_{\infty}$ /$v_{\rm esc}$ }$;

5.
We have calculated $\dot{M}$ for wind models with a $\beta$-type velocity law for the accelerating part of the wind:

 \begin{displaymath} v(r)~=~\mbox{$v_{\infty}$ }~\left(1~-~\frac{R_*}{r}\right)^\beta\cdot \end{displaymath} (12)

Below the sonic point, a smooth transition from this velocity structure is made to a velocity that follows from the photospheric density structure. Vink et al. (2000) have shown that the predicted mass-loss rate is essentially insensitive to the adopted value of $\beta$. A value of $\beta=1$ was adopted for the supersonic velocity law.

 

 
Table 2: Adopted stellar and wind parameters for the set of unified models

$\Gamma _{\rm e}$		 log$\,L_*$ M* $T_{\rm eff}$ ( $Z/\mbox{$Z_{\odot}$ }$) $\left(\frac{\mbox{$v_{\infty}$ }}{\mbox{$v_{\rm esc}$ }}\right)$
  ( $\mbox{$L_{\odot}$ }$) ( $\mbox{$M_{\odot}$ }$) (kK) Range  
0.130 5.0 20 12.5-50.0 1/30-3 1.3-2.6
0.206 5.5 40 12.5-50.0 1/30-3 1.3-2.6
0.434 6.0 60 12.5-50.0 1/100-10 1.3-2.6


The total grid thus contains 540 models. Note that for each calculated point in the grid, several wind models had to be calculated to derive the mass-loss rate that is consistent with the radiative acceleration (see Lucy & Abbott 1993). This results in accurate and self-consistent values for $\mbox{$\dot{M}$ }$ (see Vink et al. 1999).

   
5 The predicted mass-loss rates and bi-stability jumps


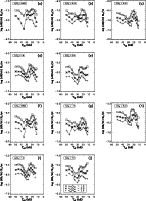  \begin{figure} \par {\psfig{file=mdotL5.ps, width = 16.85cm} } \par {\psfig{file=mdotL55.ps, width = 16.85cm} } \end{figure} Figure 1: The calculated mass-loss rates $\dot{M}$ as a function of $\mbox{$T_{\rm eff}$ }$ for five metallicities in the range $Z/\mbox{$Z_{\odot}$ }= 1/30 - 3$. The metal content is indicated in the legend at the upper part of each panel. Upper five panels a)-e) $\Gamma _{\rm e} = 0.130$ $(\log L/\mbox{$L_{\odot}$ }= 5.0)$. Lower five panels f)-j) $\Gamma _{\rm e} = 0.206$ $(\log L/\mbox{$L_{\odot}$ }= 5.5)$. The values for ( $\mbox{$v_{\infty}$ /$v_{\rm esc}$ }$) are indicated in the legend at the lower part of the last panel j)
Open with DEXTER


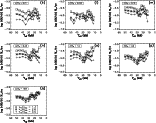  \begin{figure} \par {\psfig{file=mdotL6.ps, width = 18.0cm} } \end{figure} Figure 1: Continued. Series of $\dot{M}(Z)$ calculations with $\Gamma _{\rm e} = 0.434$ $(\log L/\mbox{$L_{\odot}$ }= 6.0)$. The calculated mass loss as a function of $\mbox{$T_{\rm eff}$ }$ for seven metallicities in the range $Z/\mbox{$Z_{\odot}$ }= 1/100 - 10$. The metal abundance is indicated in the legend at the upper part of each panel k-q). The values for ( $\mbox{$v_{\infty}$ /$v_{\rm esc}$ }$) are indicated in the legend of the last panel q)
Open with DEXTER

The calculated mass-loss rates are shown in the different panels of Fig. 1 and most results are also given in Table 3. They show bi-stability jumps superimposed on an overall behaviour where $\dot{M}$ decreases for decreasing $\mbox{$T_{\rm eff}$ }$. The reason for this $\dot{M}$ decrease is that the maximum of the flux distribution gradually shifts to longer wavelengths. Since there are significantly less lines at roughly $\lambda \mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\display... ...er{\offinterlineskip\halign{\hfil$\scriptscriptstyle ... 1800 Å than at shorter wavelength, the line acceleration becomes less effective at lower $T_{\rm eff}$, and thus the mass loss decreases.

However, most of the panels of Fig. 1 show bi-stability jumps, where the mass loss drastically increases. Before we can investigate the overall dependence of metallicity on mass loss, we need to describe the positions of these bi-stability jumps in $\mbox{$T_{\rm eff}$ }$.

 

 
Table 3: Predicted mass-loss rates for different metallicities

log $\dot{M}(\mbox{$M_{\odot} \,{\rm yr}^{-1}$ })$    

$\Gamma _{\rm e}$		 log$\,L_*$ M* $\mbox{$v_{\infty}$ /$v_{\rm esc}$ }$ $\mbox{$T_{\rm eff}$ }$ 1/100 1/30 1/10 1/3 1 3 10
  ( $\mbox{$L_{\odot}$ }$) ( $\mbox{$M_{\odot}$ }$)   (kK) $Z/\mbox{$Z_{\odot}$ }$ $Z/\mbox{$Z_{\odot}$ }$ $Z/\mbox{$Z_{\odot}$ }$ $Z/\mbox{$Z_{\odot}$ }$ $Z/\mbox{$Z_{\odot}$ }$ $Z/\mbox{$Z_{\odot}$ }$ $Z/\mbox{$Z_{\odot}$ }$

0.130		 5.0 20 2.6 50 - - -7.48 -7.03 -6.68 -6.23 -
        45 - - -7.56 -7.12 -6.63 -6.22 -
        40 - - -7.68 -7.18 -6.68 -6.29 -
        35 - - -7.56 -7.09 -6.76 -6.45 -
        30 - -7.98 -7.45 -7.19 -6.92 -6.60 -
      2.0 50 - -7.79 -7.25 -6.88 -6.46 -6.01 -
        45 - -7.93 -7.35 -6.91 -6.47 -5.97 -
        40 - -8.16 -7.47 -7.01 -6.48 -6.05 -
        35 - -8.45 -7.31 -6.93 -6.59 -6.29 -
        30 - -7.74 -7.31 -7.08 -6.76 -6.38 -
        27.5 - -7.71 -7.40 -7.12 -6.73 -6.26 -
        25 - -7.76 -7.42 -7.04 -6.48 -6.01 -
        22.5 - -7.75 -7.40 -6.84 -6.32 -5.99 -
        20 - -7.71 -7.24 -6.72 -6.41 -6.06 -
        17.5 - -7.66 -7.24 -6.88 -6.49 -6.12 -
        15 - -7.88 -7.42 -6.98 -6.62 -6.15 -
        12.5 - -8.10 -7.61 -7.27 -6.74 -6.13 -
      1.3 22.5 - -7.49 -6.96 -6.55 -6.15 -5.75 -
        20 - -7.43 -6.99 -6.53 -6.22 -5.83 -
        17.5 - -7.50 -7.06 -6.63 -6.28 -5.83 -
        15 - -7.53 -7.22 -6.85 -6.39 -5.79 -
        12.5 - -7.71 -7.41 -7.04 -6.32 -5.72 -

0.206		 5.5 40 2.6 50 - -7.30 -6.91 -6.36 -5.97 -5.53 -
        45 - -7.30 -7.12 -6.41 -5.95 -5.45 -
        40 - -7.45 -6.74 -6.47 -5.95 -5.53 -
        35 - -7.74 -6.92 -6.37 -6.06 -5.77 -
        30 - -7.10 -6.80 -6.58 -6.25 -5.90 -
      2.0 50 - -6.97 -6.56 -6.20 -5.76 -5.28 -
        45 - -7.02 -6.65 -6.22 -5.73 -5.24 -
        40 - -7.10 -6.73 -6.26 -5.75 -5.35 -
        35 - -7.33 -6.70 -6.27 -5.90 -5.60 -
        30 - -6.96 -6.70 -6.41 -6.10 -5.67 -
        27.5 - -7.04 -6.78 -6.48 -6.01 -5.56 -
        25 - -7.09 -6.79 -6.38 -5.75 -5.34 -
        22.5 - -7.07 -6.62 -6.12 -5.66 -5.33 -
        20 - -6.97 -6.52 -6.11 -5.75 -5.40 -
        17.5 - -6.88 -6.59 -6.17 -5.86 -5.43 -
        15 - -7.03 -6.78 -6.35 -5.93 -5.43 -
        12.5 - -7.35 -6.96 -6.70 -6.09 -5.31 -
      1.3 22.5 - -6.76 -6.27 -5.82 -5.44 -5.12 -
        20 - -6.61 -6.28 -5.88 -5.52 -5.18 -
        17.5 - -6.69 -6.40 -6.02 -5.59 -5.11 -
        15 - -6.82 -6.51 -6.13 -5.67 -5.03 -
        12.5 - -7.06 -6.78 -6.26 -5.65 -4.92 -
                       



 

 
Table 3: continued

log $\dot{M}(\mbox{$M_{\odot} \,{\rm yr}^{-1}$ })$    

$\Gamma _{\rm e}$		 logL* M* $\mbox{$v_{\infty}$ /$v_{\rm esc}$ }$ $\mbox{$T_{\rm eff}$ }$ 1/100 1/30 1/10 1/3 1 3 10
  ( $\mbox{$L_{\odot}$ }$) ( $\mbox{$M_{\odot}$ }$)   (kK) $Z/\mbox{$Z_{\odot}$ }$ $Z/\mbox{$Z_{\odot}$ }$ $Z/\mbox{$Z_{\odot}$ }$ $Z/\mbox{$Z_{\odot}$ }$ $Z/\mbox{$Z_{\odot}$ }$ $Z/\mbox{$Z_{\odot}$ }$ $Z/\mbox{$Z_{\odot}$ }$

0.434		 6.0 60 2.6 50 -6.81 -6.31 -5.84 -5.46 -5.07 -4.57 -4.31
        45 -6.80 -6.59 -5.87 -5.45 -4.99 -4.55 -4.31
        40 -6.86 -6.16 -5.95 -5.41 -4.97 -4.59 -4.42
        35 -7.16 -6.27 -5.95 -5.47 -5.05 -4.78 -4.60
        30 -6.78 -6.21 -5.90 -5.57 -5.29 -4.94 -4.52
      2.0 50 -6.42 -6.17 -5.67 -5.25 -4.86 -4.42 -4.23
        45 -6.47 -6.35 -5.69 -5.22 -4.76 -4.42 -4.24
        40 -6.58 -5.98 -5.73 -5.23 -4.76 -4.47 -4.32
        35 -6.78 -6.11 -5.74 -5.28 -4.88 -4.65 -4.47
        30 -6.47 -6.07 -5.80 -5.44 -5.14 -4.82 -4.38
        27.5 -6.50 -6.16 -5.99 -5.51 -5.19 -4.68 -4.23
        25 -6.60 -6.24 -5.92 -5.38 -4.95 -4.44 -4.11
        22.5 -6.52 -6.11 -5.63 -5.13 -4.78 -4.45 -4.17
        20 -6.33 -5.93 -5.59 -5.19 -4.83 -4.54 -4.26
        17.5 -6.36 -6.01 -5.74 -5.33 -4.90 -4.48 -4.11
        15 -6.54 -6.17 -5.90 -5.42 -4.85 -4.25 -3.94
        12.5 -6.71 -6.35 -5.99 -5.48 -4.51 -4.19 -3.99
      1.3 22.5 -6.24 -5.77 -5.36 -4.91 -4.55 -4.29 -4.10
        20 -6.06 -5.70 -5.37 -5.00 -4.63 -4.38 -4.12
        17.5 -6.09 -5.80 -5.52 -5.09 -4.59 -4.19 -3.97
        15 -6.29 -5.98 -5.65 -5.07 -4.28 -4.06 -3.91
        12.5 -6.49 -6.13 -5.75 -4.80 -4.30 -4.10 -3.95


5.1 The bi-stability jump at $\mathsfsl{T_{eff} \simeq 25~000}$ K

All panels show a bi-stability jump around $\mbox{$T_{\rm eff}$ }$ $\simeq$ 25 000 K. Here, Fe  IV recombines to Fe  III and as the latter ion is a more efficient line driver than the first, the acceleration in the lower part of the wind increases. This results in an upward jump in $\dot{M}$ of about a factor of five and subsequently a drop in $\mbox{$v_{\infty}$ }$ of about a factor 0.5 (Vink et al. 1999).

Since we know from both theory and observations that the Galactic ratio $\mbox{$v_{\infty}$ /$v_{\rm esc}$ }$ jumps from $\sim$2.6 at the hot side of the jump to $\sim$1.3 at the cool side of the jump, we can estimate the size of the jump in mass loss for the different metallicities by assuming a similar jump in the ratio $\mbox{$v_{\infty}$ /$v_{\rm esc}$ }$ of about a factor of two. The size of the jump is defined as the difference between the minimum $\dot{M}$ at the hot side of the jump (where $\mbox{$v_{\infty}$ /$v_{\rm esc}$ }$ = 2.6) and the maximum $\dot{M}$ at the cool side (where $\mbox{$v_{\infty}$ /$v_{\rm esc}$ }$ = 1.3). The size of the predicted jump in $\dot{M}$ (i.e. $\Delta$ log $\dot{M}$) is indicated in the last column of Table 4. For most models $\Delta\dot{M}$ is about a factor of five to seven. There is no clear trend with metallicity.

The position of the jump for different Z shifts somewhat in $\mbox{$T_{\rm eff}$ }$, since the ionization equilibrium does not only depend on temperature, but also on density and therefore on mass loss and thus on metallicity as well. To handle the influence of the metallicity on the position of the bi-stability jump in $\mbox{$T_{\rm eff}$ }$, we compare the characteristics of the wind models around the bi-stability jump. We will discuss this behaviour for the case of the highest wind densities ( $\Gamma _{\rm e}$ = 0.434), as for these models, the statistics in the Monte-Carlo code are the best (see Sect. 3). Nevertheless, the uniformity is checked for the other series of $\Gamma _{\rm e}$ also.

As in Vink et al. (2000), $\langle\rho\rangle$ is defined as the characteristic wind density at 50% of the terminal velocity of the wind. For a standard velocity law with $\beta=1$, this characteristic wind density is given by

 \begin{displaymath}\langle\rho\rangle~=~\frac{\dot{M}}{8 \pi R_*^2 \mbox{$v_{\infty}$ }}\cdot \end{displaymath} (13)

Figure 2 shows the behaviour of the characteristic density as a function of Z. This is done for both the minimum $\dot{M}$ (at the hot side of the jump) and the maximum $\dot{M}$ (at the cool side of the jump). The characteristic densities for the cool side of the jump are indicated with "diamond'' signs and with "plus'' signs for the hot side. The "filled circles'' represent the logarithmic average values of $\langle\rho\rangle$ for the "jump'' model for each metallicity. The "jump'' model is a hypothetical model between the two models where $\dot{M}$ is maximal and minimal. As expected, log $\langle\rho\rangle$ increases as the metallicity increases. Because the log of the average density at the jump shows a linear dependence on log ( $Z/\mbox{$Z_{\odot}$ }$), a linear fit is plotted. This is the solid line in Fig. 2. The relation is given by:
 
$\displaystyle {\rm log}< \rho >~$ = $\displaystyle ~- 13.636~(\pm~0.029)~$  
    $\displaystyle ~+~0.889~(\pm~0.026)~{\rm log} (Z/\mbox{$Z_{\odot}$ }).$ (14)

Figure 3 shows the effective temperature of the bi-stability jump as a function of $\langle\rho\rangle$. Again this is done for both the cool and hot side of the jump and for the average. The solid line indicates the best linear fit through these averages. The relation between the jump temperature (in kK) and log $\langle\rho\rangle$ is given by:

 \begin{displaymath}T_{\rm eff}^{\rm jump}~=~61.2~(\pm~4.0)~+~2.59~(\pm~0.28)~{\rm log} < \rho >\cdot \end{displaymath} (15)

It is now possible to estimate $\langle\rho\rangle$ for any Z using Eq. (14) and subsequently to predict the position of the jump in $\mbox{$T_{\rm eff}$ }$ using Eq. (15).
  \begin{figure} \par {\psfig{file=logZ.ps, width = 8.4 cm} } \end{figure} Figure 2: Characteristic density $\langle\rho\rangle$ at the bi-stability jump around 25 000 K as a function of Z. An explanation for the different symbols is given in the legend. The solid line indicates the best linear fit through the average jumps parameters for log $\langle\rho\rangle$
Open with DEXTER


  \begin{figure} \par {\psfig{file=jump.ps, width = 7.8 cm} } \end{figure} Figure 3: Characteristic density log $\langle\rho\rangle$ and $\mbox{$T_{\rm eff}$ }$ of the bi-stability jump around $\mbox{$T_{\rm eff}$ }$ = 25 000 K. An explanation for the different symbols is given in the legend. The solid line represents the best linear fit through the average jump parameters log $\langle\rho\rangle$ and $\mbox{$T_{\rm eff}$ }$
Open with DEXTER


 

 
Table 4: The size of the bi-stability jump around 25 000 K for different Z

$\Gamma _{\rm e}$		 logL* M* ( $Z/\mbox{$Z_{\odot}$ }$) $\Delta$ (log $\dot{M}$)
  ( $\mbox{$L_{\odot}$ }$) ( $\mbox{$M_{\odot}$ }$)    
0.130 5.0 20 1/30 -
      1/10 0.75
      1/3 0.77
      1 0.83
      3 0.86
0.206 5.5 40 1/30 0.66
      1/10 0.63
      1/3 0.81
      1 0.81
      3 0.81
0.434 6.0 60 1/100 0.72
      1/30 0.71
      1/10 0.74
      1/3 0.76
      1 0.76
      3 0.68
      10 0.43


5.2 Additional bi-stability jumps around 15 000 and 35 000 K

In many of the panels in Fig. 1 one can see more than just one bi-stability jump. In cases for high mass loss at relatively high Z, an additional jump is visible at $\mbox{$T_{\rm eff}$ }\simeq$ 15000 K (see e.g. panel (o) in Fig. 1). Leitherer et al. (1989) calculated atmospheric models for Luminous Blue Variables (LBVs) and found a recombination of iron group elements from doubly to singly ionised stages, which may explain mass-loss variability when LBVs change from minimum to maximum visual brightness phase (de Koter et al. 1996). Vink et al. (2000) also found this jump around 15000 K and attributed it to a recombination of Fe  III to Fe  II. Possibly this jump is related to the drop in the ratio $\mbox{$v_{\infty}$ /$v_{\rm esc}$ }$ from 1.3 to about 0.7 around spectral type A0 as identified by Lamers et al. (1995) on the basis of observed values for $\mbox{$v_{\infty}$ }$.

For the lower mass-loss rates at relatively low metallicity, at about $\mbox{$T_{\rm eff}$ }\simeq$ 35 000 K, another drastic increase in $\dot{M}$ occurs (e.g. panel (f) with $Z/\mbox{$Z_{\odot}$ }$ = 1/30 in Fig. 1). The origin of this 35 000 K jump, which appears only at low Z, will be discussed in Sect. 5.3.

In order to express the mass-loss behaviour as a function of metal content, it is obvious that all these jumps need to be accounted for. Since these additional jumps are only present in a few cases, the relationships can only be given as rough estimates. For the jump at $\mbox{$T_{\rm eff}$ }\simeq$ 15000 K:

 \begin{displaymath}T^{\rm jump}_{\sim15{\rm kK}}~=~43~+~1.9~{\rm log} < \rho > \cdot \end{displaymath} (16)

For the jump at $\mbox{$T_{\rm eff}$ }\simeq$ 35000 K:

 \begin{displaymath}T^{\rm jump}_{\sim35{\rm kK}}~=~192~+~10.4~{\rm log} < \rho > \cdot \end{displaymath} (17)

In both cases the jump temperature is in units of kK. It is again possible to estimate log $\langle\rho\rangle$ using Eq. (14) and then to roughly predict the positions of these additional bi-stability jumps in effective temperature using Eqs. (16) and (17). Later on these will be referred to when the complete mass-loss recipe is presented (Sect. 8).

   
5.3 The origin of the (low Z) jump at $\mathsfsl{T_{eff} \simeq}$ 35 000 K

Intuitively, one might attribute the jump at $\sim$35 000 K in models of low metal abundance (say $Z/\mbox{$Z_{\odot}$ }\le 1/30$) to the recombination of Fe  V to Fe  IV. This in analogue to the jump at $\sim$25000 K, due to the recombination of Fe  IV to Fe  III. However, in the next section we will show that this is not the case, since at lower Z the relative contribution of Fe vs. CNO in the line acceleration decreases (see also Puls et al. 2000).

Instead, the low Z jump at $\mbox{$T_{\rm eff}$ }\simeq 35~000$ K turns out to be caused by a recombination from carbon  IV to carbon  III (see Vink 2000). To summarise the physical origin of the jump: C  III has more lines in the crucial part of the spectrum than C  IV, therefore C  III is a more efficient driving ion causing the increase in mass loss at the bi-stability jump around 35 000 K at low Z. Whether this is also accompanied by a change in terminal velocity is an open question that may be answered if $\mbox{$v_{\infty}$ }$ determinations at very low Z become available.

   
6 The relative importance of Fe and CNO elements in the line acceleration at low $\vec Z$

6.1 The character of the line driving at different $\mathsfsl{Z}$


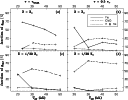  \begin{figure} \par {\psfig{file=Zrel.ps, width = 14.8 cm} } \end{figure} Figure 4: The relative contribution to the line acceleration for models with ( $\mbox{$v_{\infty}$ /$v_{\rm esc}$ }$) = 2.0, log $L_{*}/\mbox{$L_{\odot}$ }$ = 5.5 and $M_* = 40 ~\mbox{$M_{\odot}$ }$. The solid lines show the contribution of Fe lines. The dotted line is the contribution by C, N and O. The dashed line shows the contribution by H and He lines. a) and b) give the contribution for solar Z at resp. $v~=~v_{\rm sound}$ and at $v~=~0.5 \mbox{$v_{\infty}$ }$. c) and d) give the contribution for ( $Z/\mbox{$Z_{\odot}$ }$) = 1/30 at resp. $v~=~v_{\rm sound}$ and at $v~=~0.5 \mbox{$v_{\infty}$ }$
Open with DEXTER

Vink et al. (1999) have shown that for Galactic wind models around 25 000 K the elements C, N and O are important line drivers in the supersonic part of the wind, whereas the subsonic part of the wind is dominated by the line acceleration due to Fe. As the mass-loss rate is determined by the radiative acceleration below the sonic point, and the terminal velocity is determined by the acceleration in the supersonic part, these results imply that for Galactic wind models $\dot{M}$ is essentially set by Fe lines, whereas $\mbox{$v_{\infty}$ }$ is determined by the lighter elements, i.e. mainly by CNO.

To study the origin of the additional (low Z) jump around 35 000 K, it becomes necessary to investigate the relative importance of the species at low metallicity. To this end, additional Monte Carlo calculations were performed. One simulation was performed with a line list containing only Fe lines. A second calculation was done with a list of lines of CNO only, and finally a third simulation was performed with the lines of H and He. Figure 4 shows the relative importance for the line acceleration of these elements as a function of effective temperature for different parts of the wind, i.e. at $v~=~v_{\rm sound}$ and at $v~=~0.5 \mbox{$v_{\infty}$ }$. Panels (a) and (b) indicate the fractions in the acceleration at solar metallicity. Panels (c) and (d) present the same, but for the low metallicity models, i.e. $Z/\mbox{$Z_{\odot}$ }= 1/30$. Note that for the solar metallicity models in the supersonic region (panel b) the elements of Si, Cl, P and S are additional line drivers (see Vink et al. 1999).

Figure 4a shows that at solar Z, Fe dominates the line acceleration around the sonic point, where the mass-loss rate is fixed. However, this relative importance of iron decreases for increasing $\mbox{$T_{\rm eff}$ }$. Figure 4c shows that at the low metallicity, CNO already dominate the acceleration in the region around the sonic point. This implies that at low Z, CNO determine both the terminal velocity by dominating the supersonic line acceleration in Fig. 4d, as well as the mass loss by dominating the line acceleration around $v~=~v_{\rm sound}$. The only exception occurs at low effective temperature ( $\mbox{$T_{\rm eff}$ }=$ 20 000 K), where Fe still plays an important role in setting the mass loss.

These considerations thus explain why the high $\mbox{$T_{\rm eff}$ }$ jump at low Z is not caused by a recombination effect of iron, instead it turns out to be caused by a recombination of a CNO element, in this case C  IV to C  III (Vink 2000).

   
6.2 Observed abundance variations at different Z

Now we will make a distinction between the metal abundance Z derived on the basis of stellar iron and nebular oxygen lines. The reason for this distinction is that observations to study the chemical evolution of galaxies have shown that the ratio of Fe/O varies with metallicity.

Determinations of heavy-element abundances for metal poor blue compact galaxies (Izotov & Thuan 1999) as well as observations of Galactic halo stars (Pagel & Tautvaisiene 1995 and references therein) show a significant overabundance of O/Fe of about 0.4 dex with respect to the Sun.

These observed differential abundance variations between oxygen and iron could significantly alter our mass-loss predictions if $\dot{M}$ were set by Fe over the full range in Z. However, we have shown that at low Z, the mass loss is mainly determined by CNO instead of by Fe. Since the observed metallicity is mostly determined from nebular oxygen lines rather than from iron lines, this implies that our mass loss recipe will still yield the proper mass-loss rates. Only in those cases where the observed metallicity were determined from stellar iron lines instead of from nebular oxygen lines, one would need to transform the observed iron abundance ( $Z^{\rm obs}_{\rm Fe}$) to our adopted metallicity ( $Z^{\rm theory}$). This can easily be done according to the scaling relations given in Table 5. The first column of this table indicates the metallicity that has been adopted in the wind models. The second column shows for each Z which elements dominate the line driving around the sonic point, where the mass loss is set. The third column represents the observed abundance variation between oxygen and iron compared to the sun. For relatively high metallicity ( $Z/\mbox{$Z_{\odot}$ }\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\h... ...er{\offinterlineskip\halign{\hfil$\scriptscriptstyle ... 1/10), there is hardly any observed difference between the oxygen and iron abundances. As said, for very low metallicity ( $Z/\mbox{$Z_{\odot}$ }\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\h... ...er{\offinterlineskip\halign{\hfil$\scriptscriptstyle ... 1/30), this observed difference is about 0.4 dex. Because at low Z mass loss is mainly set by CNO, the observed oxygen abundances are the same as the adopted Z in the wind models (Col. 4), whereas in case iron lines were to be analysed, one should convert the iron abundance to our adopted $Z^{\rm theory}$, by comparing Cols. 5 and 1.


 

 
Table 5: Conversion table for the observed differential abundance variations between oxygen and iron

$Z^{\rm theory}$		 Dominant elements $\frac{[{\rm O/Fe}]}{[{\rm O/Fe}]_{\odot}}$ $Z^{\rm obs}_{\rm Oxygen}$ $Z^{\rm obs}_{\rm Fe}$

( $\mbox{$Z_{\odot}$ }$)		 that set $\dot{M}$   ( $\mbox{$Z_{\odot}$ }$) ( $\mbox{$Z_{\odot}$ }$)

1		 Fe 0 1 1
1/3 Fe 0 1 1
1/10 Fe 0 1 1

1/30		 CNO + 0.4 dex 1/30 1/75
1/100 CNO + 0.4 dex 1/100 1/250


   
7 The global metallicity dependence


  \begin{figure} \par {\psfig{file=zdepm20.ps, width = 8.5 cm} } \par {\psfig{file... ...s, width =8.5 cm} } \par {\psfig{file=zdepm60.ps, width = 8.5 cm} } \end{figure} Figure 5: The $\dot{M}(Z)$ dependence for three cases of $\Gamma _{\rm e}$. In all three panels, the dashed lines indicate the best linear fit through the models at different Z. Note that at $\Gamma _{\rm e} = 0.130$ the lowest Z model is not included in the fit, due to the presence of a bi-stability jump. All models have $\mbox{$T_{\rm eff}$ }$ = 50 000 K and constant ( $\mbox{$v_{\infty}$ /$v_{\rm esc}$ }$) = 2.0. The values of $\Gamma _{\rm e}$ are indicated in the legends
Open with DEXTER

Now we can determine the global $\dot{M}(Z)$ dependence over a wide range in metallicity. This $\dot{M}(Z)$ will be determined for the three $\Gamma _{\rm e}$ values separately. If the dependencies were identical for different $\Gamma _{\rm e}$, then we might simply add the metallicity dependence to the mass-loss recipe that was derived by Vink et al. (2000) for Galactic stars.

Figure 5 shows the $\dot{M}(Z)$ behaviour for the three cases of $\Gamma _{\rm e}$. To avoid complications due to the presence of the bi-stability jumps, we use models where $\mbox{$T_{\rm eff}$ }$ is above all of the identified jumps, i.e. at $\mbox{$T_{\rm eff}$ }$ = 50 000 K. In the case where $\Gamma _{\rm e}$ = 0.130, the linear fit is taken in the metallicity range $Z/\mbox{$Z_{\odot}$ }= 1/10 - 3$, because the model at $Z/\mbox{$Z_{\odot}$ }$ = 1/30 is influenced by the low Zbi-stability jump. This is why we have excluded this from the fit. The best linear fit is thus given by

 
$\displaystyle {\rm log}~\dot{M}$ = $\displaystyle ~-6.439~(\pm 0.024)$  
    $\displaystyle ~+~0.842~(\pm 0.039)~{\rm log}(Z/\mbox{$Z_{\odot}$ })$  
    $\displaystyle ~{\rm for}~\Gamma_{\rm e}~=~0.130.$ (18)

In case $\Gamma _{\rm e} = 0.206$, the models at $\mbox{$T_{\rm eff}$ }= 50\,000$K are not influenced by the low Z jump and a linear fit is taken over the full metallicity range of $Z/\mbox{$Z_{\odot}$ }= 1/30 - 3$. The best fit is given by
 
$\displaystyle {\rm log}~\dot{M}$ = $\displaystyle ~-5.732~(\pm 0.028)$  
    $\displaystyle ~+~0.851~(\pm 0.033)~{\rm log}(Z/\mbox{$Z_{\odot}$ })$  
    $\displaystyle ~{\rm for}~\Gamma_{\rm e}~=~0.206.$ (19)

Finally, in the case $\Gamma _{\rm e} = 0.434$, the $\dot{M}(Z)$ dependence is studied over an even wider metallicity range: $Z/\mbox{$Z_{\odot}$ }$ is 1/100 - 10. For this relatively high value of $\Gamma _{\rm e}$ it is computationally easier to calculate mass loss at the extremely low value $Z/\mbox{$Z_{\odot}$ }= 1/100$. The mass-loss rate at extremely high metallicity ( $Z/\mbox{$Z_{\odot}$ }= 10$) is determined for a somewhat different abundance ratio than the standard one that was used throughout the paper given by Eq. (10). The helium abundance is now kept constant (at Y = 0.42, see Table 1) increasing the metal fraction from three to ten times solar. It was checked whether the results are dependent on this choice of Y, but this turned out not to be the case.

One may expect the $\dot{M}(Z)$ relation to flatten at some high Z value due to saturation of iron lines (see Sect. 2). The lowest panel in Fig. 5 shows that this is indeed the case. However, this only happens above $Z/\mbox{$Z_{\odot}$ }= 3$. It implies that over the range from about $Z/\mbox{$Z_{\odot}$ }= 1/30 - 3$, the wind momentum behaves as a constant function of metallicity, i.e. mass loss vs. Z behaves as a power-law. The linear fit for the highest value of $\Gamma _{\rm e}$ is determined from the range $Z/\mbox{$Z_{\odot}$ }= 1/30 - 3$. The best fit is given by

 
$\displaystyle {\rm log}~\dot{M}$ = $\displaystyle ~-4.84~(\pm 0.020)$  
    $\displaystyle ~+~0.878~(\pm 0.023)~{\rm log}(Z/\mbox{$Z_{\odot}$ })$  
    $\displaystyle ~{\rm for}~\Gamma_{\rm e}~=~0.434.$ (20)

Combining Eqs. (18)-(20) for the three different values of $\Gamma _{\rm e}$, we find that over the metallicity range from $1/30 \le Z/\mbox{$Z_{\odot}$ }\le 3$ there is a constant power law for constant $\mbox{$v_{\infty}$ /$v_{\rm esc}$ }= 2.0$ and $\mbox{$T_{\rm eff}$ }$ = 50 000 K with $\dot{M} \propto Z^{0.86}$.

We have done similar analyses for the other effective temperatures in our model grid, some of these were affected by a bi-stability jump, but on average, these jumps cancelled out. The average power-law index factor m (Eq. (7)) was found to be m = 0.85 $\pm$ 0.10 for constant $\mbox{$v_{\infty}$ /$v_{\rm esc}$ }$. As was shown in Vink et al. (2000) $\dot{M}$ depends on $\mbox{$v_{\infty}$ /$v_{\rm esc}$ }$ as a power law: $\dot{M} \propto \mbox{$v_{\infty}$ }^p$, with $p = -1.226 \pm 0.037$ for stars with $\mbox{$T_{\rm eff}$ }\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\h... ...finterlineskip\halign{\hfil$\scriptscriptstyle ... K, and $p = -1.601 \pm 0.055$ for the B supergiants with $\mbox{$T_{\rm eff}$ }\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\h... ...finterlineskip\halign{\hfil$\scriptscriptstyle ... K. Therefore mass loss can be represented by

$\displaystyle \dot{M}~\propto~Z^m~\mbox{$v_{\infty}$ }^p$ $\textstyle \propto~$ $\displaystyle Z^{0.85}~\mbox{$v_{\infty}$ }^p$  
    $\displaystyle ~{\rm for}~1/30~\le~Z/\mbox{$Z_{\odot}$ }~\le~3.$ (21)

Because $\mbox{$v_{\infty}$ }$ also depends on the metal content Z, where Leitherer et al. (1992) have assumed $\mbox{$v_{\infty}$ }$ to behave as a power-law with $\mbox{$v_{\infty}$ }\propto Z^q$ and derived this value to be q = 0.13, the mass loss dependence on metallicity can also be represented by
 
$\displaystyle \dot{M}~\propto~Z^m Z^{pq}$ $\textstyle \propto~$ Z0.85 + pq  
    $\displaystyle ~{\rm for}~1/30~\le~Z/\mbox{$Z_{\odot}$ }~\le~3.$ (22)

The overall result of these effects results in a dependence of mass loss $\dot{M} \propto Z^{0.69}$ for the O stars and in $\dot{M} \propto Z^{0.64}$ for the B supergiants.

These power-law dependencies derived with our Monte Carlo approach yield a stronger metallicity dependence than the value of m = 1/2 that was derived by Kudritzki et al. (1987) and has since been used in many evolutionary calculations (e.g. Langer 1991; Maeder 1992; Schaller et al. 1992; Meynet et al. 1994; Vassiliadis & Wood 1994; Vanbeveren 1995; Iben et al. 1996; Deng et al. 1996).

   
8 Complete mass-loss recipe

In this section we present the "complete'' theoretical mass loss formula for OB stars over the range in $\mbox{$T_{\rm eff}$ }$ between 50 000 and 12 500 K and the range in Z between 1/30 and 3 times $\mbox{$Z_{\odot}$ }$. The mass-loss rate as a function of five basic parameters will be provided. These parameters are M*, L*, $\mbox{$T_{\rm eff}$ }$, $\mbox{$v_{\infty}$ /$v_{\rm esc}$ }$, and Z.

First, some relationships for the bi-stability jumps have to be connected. The position of this jump in $\mbox{$T_{\rm eff}$ }$ now depends both on the metallicity Z (this paper) and on the luminosity-to-mass ratio, i.e. $\Gamma _{\rm e}$ (Vink et al. 2000). The characteristic density $\langle\rho\rangle$ for the bi-stability jump around $\mbox{$T_{\rm eff}$ }\simeq$ 25 000 K can be determined by smoothly combining Eq. (14) from the present paper with Eq. (4) from Vink et al. (2000). The joint result is given by

 
$\displaystyle {\rm log}< \rho >$ = $\displaystyle - 14.94~(\pm 0.54)$  
    $\displaystyle ~+~0.85~(\pm 0.10)~{\rm log} (Z/\mbox{$Z_{\odot}$ })$  
    $\displaystyle ~+~3.2~(\pm 2.2)~\Gamma_{\rm e}.$ (23)

The positions (in $\mbox{$T_{\rm eff}$ }$) of the several bi-stability jumps can now be found using Eqs. (15)-(17) and (23).

We will divide our mass-loss recipe into two parts, taking into account only the bi-stability jump around 25 000 K, since this jump is present at all metallicities in all panels of Fig. 1.

If one wants a mass-loss rate for relatively high metallicity, say $Z/\mbox{$Z_{\odot}$ }\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\h... ...r{\offinterlineskip\halign{\hfil$\scriptscriptstyle ..., for low temperatures, $\mbox{$T_{\rm eff}$ }\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\h... ...er{\offinterlineskip\halign{\hfil$\scriptscriptstyle ... 15 000 K, one should take into account the presence of the Fe  III/ II jump, and follow the strategy that was described in Vink et al. (2000). One may simply use Eq. (25; below) below the Fe  III/ II jump, but one should increase the constant by a factor of five (or $\Delta$ log $\dot{M} = 0.70$) to a value of -5.99. The recipe can then be used until the point in the Hertzsprung-Russell Diagram (HRD) where line driven winds become inefficient (see Achmad & Lamers 1997). We suggest that below the Fe  III/ II jump $\mbox{$v_{\infty}$ /$v_{\rm esc}$ }= 0.7$ (Lamers et al. 1995) is adopted.

If one needs a mass-loss rate for low metallicity, say $Z/\mbox{$Z_{\odot}$ }\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\h... ...offinterlineskip\halign{\hfil$\scriptscriptstyle ..., at high temperatures $\mbox{$T_{\rm eff}$ }\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\h... ...er{\offinterlineskip\halign{\hfil$\scriptscriptstyle ... 35 000 K, one should be aware of the carbon jump and a similar strategy may be followed. Note that this jump is only present for cases where the wind density is weak, i.e. for stars with a relatively low luminosity. One can decrease the constant in Eq. (24; below) by a factor of five (or $\Delta$ log $\dot{M} = 0.70$) to a value of -7.40. In case one does not know the value for $\mbox{$v_{\infty}$ }$ such as is the case for evolutionary calculations, one would like to know the appropriate change in terminal velocity at the low Z jump. Leitherer et al. (1992) have calculated the dependence of $\mbox{$v_{\infty}$ }$ on Z and have found that $\mbox{$v_{\infty}$ }\propto Z^{0.13}$. Such a trend with metallicity has been confirmed by observations in the Magellanic Clouds, however, what happens to $\mbox{$v_{\infty}$ /$v_{\rm esc}$ }$ at extremely low Z is still an open question. We stress that if the observed values for $\mbox{$v_{\infty}$ }$ at very low Z turn out to be very different from the Galactic values, our mass-loss predictions can simply be scaled to accommodate the proper values of $\mbox{$v_{\infty}$ /$v_{\rm esc}$ }$ and our recipe will still yield the corresponding mass-loss rates.

Now we can present the complete mass-loss recipe including the metallicity dependence. This can be done by simply adding the constant Z dependence from Eq. (22) to the multiple linear regression relations from the Vink et al. (2000) recipe. We are indeed allowed to do so, as the $\dot{M}(Z)$ dependence was found to be independent of other investigated stellar parameters (see Sect. 7). For the hot side of the bi-stability jump $\sim$25 000 K, the complete recipe is given by:

 
$\displaystyle {\rm log}~\dot{M}$ = $\displaystyle ~-~6.697~(\pm 0.061)$  
    $\displaystyle ~+~2.194~(\pm 0.021)~{\rm log}(L_*/{10^5})$  
    $\displaystyle ~-~1.313~(\pm 0.046)~{\rm log}(M_*/30)$  
    $\displaystyle ~-~1.226~(\pm 0.037)~{\rm log}\left(\frac{\mbox{$v_{\infty}$ /$v_{\rm esc}$ }}{2.0}\right)$  
    $\displaystyle ~+~0.933~(\pm 0.064)~{\rm log}(\mbox{$T_{\rm eff}$ }/40\,000)$  
    $\displaystyle ~-~10.92~(\pm 0.90)~\{{\rm log}(\mbox{$T_{\rm eff}$ }/40\,000)\}^{2}$  
    $\displaystyle ~+~0.85~(\pm 0.10)~{\rm log} (Z/\mbox{$Z_{\odot}$ })$  
       
    $\displaystyle ~{\rm for}~27~500 < \mbox{$T_{\rm eff}$ }\le 50\,000~{\rm K}$ (24)

where $\dot{M}$ is in $\mbox{$M_{\odot}$ }$ ${\rm yr}^{-1}$, L* and M* are in solar units and $\mbox{$T_{\rm eff}$ }$ is in Kelvin. In this range the Galactic ratio of $\mbox{$v_{\infty}$ /$v_{\rm esc}$ }$ = 2.6. As was noted in Sect. 4, if the values for $\mbox{$v_{\infty}$ }$ at other Z are different from these Galactic values, then the mass-loss rates can easily be scaled accordingly. For the cool side of the bi-stability jump, the complete recipe is
 
$\displaystyle {\rm log}~\dot{M}$ = $\displaystyle ~-~6.688~(\pm 0.080)$  
    $\displaystyle ~+~2.210~(\pm 0.031)~{\rm log}(L_*/{10^5})$  
    $\displaystyle ~-~1.339~(\pm 0.068)~{\rm log}(M_*/30)$  
    $\displaystyle ~-~1.601~(\pm 0.055)~{\rm log}\left(\frac{\mbox{$v_{\infty}$ /$v_{\rm esc}$ }}{2.0}\right)$  
    $\displaystyle ~+~1.07~(\pm 0.10)~{\rm log}(\mbox{$T_{\rm eff}$ }/20\,000)$  
    $\displaystyle ~+~0.85~(\pm 0.10)~{\rm log} (Z/\mbox{$Z_{\odot}$ })$  
       
    $\displaystyle ~{\rm for}~12~500 \le \mbox{$T_{\rm eff}$ }\le 22\,500~{\rm K}$ (25)

where again $\dot{M}$ is in $\mbox{$M_{\odot}$ }$ ${\rm yr}^{-1}$, L* and M* are in solar units and $\mbox{$T_{\rm eff}$ }$ is in Kelvin. In this range the Galactic ratio of $\mbox{$v_{\infty}$ /$v_{\rm esc}$ }$ = 1.3. In the critical temperature range between 22 500 $\le \mbox{$T_{\rm eff}$ }\le$ 27 500 K, either Eq. (24) or Eq. (25) should be used depending on the position of the bi-stability jump given by Eq. (15). A computer routine to calculate mass loss as a function of stellar parameters is publicly available[*].

   
9 Comparison between theoretical $\vec{\dot{M}}$ and observations at subsolar $\vec Z$


  \begin{figure} \par {\psfig{file=lmclowz.ps, width = 8.8cm} } \par {\psfig{file=lmczsun.ps, width = 8.8cm} } \end{figure} Figure 6: Comparison between theoretical and observational $\dot{M}$ for O stars in the LMC. The upper panel is for an adopted $Z_{\rm LMC}~=~0.28~\mbox{$Z_{\odot}$ }$ and the lower panel is for an adopted metallicity $Z_{\rm LMC}~=~0.8~\mbox{$Z_{\odot}$ }$. The Puls et al. (1996) H$\alpha $ rates and de Koter rates are indicated with different symbols. The dashed lines are one-to-one relations, tools for convenient comparison between observations and theory
Open with DEXTER

Now we will compare our mass-loss predictions for different Z with the most reliable observational rates presently available. Unfortunately, there are only substantial samples available in the literature for the relatively nearby Large Magellanic Cloud (LMC) and the Small Magellanic Cloud (SMC). The metallicity of the LMC is only slightly smaller than the Galactic one and its absolute value is not accurately known. What complicates a meaningful comparison is that there are differences in the observed stellar and nebular abundances. Additionally, there are abundance gradients present in these galaxies, which makes a good comparison between our predicted $\dot{M}(Z)$ dependence and the observed mass-loss rates of the LMC sample rather difficult. As the metallicity difference between the Galaxy and the SMC is significantly larger, we should be able to test our predictions in a more meaningful way with the observed rates of the SMC sample.

Following Kudritzki et al. (1987), we did not adopt the individual abundance patterns quoted for the Clouds (e.g. Dufour 1984). Instead we simply scaled down all abundances by a constant factor adopting:

$\displaystyle Z_{\rm LMC}~=~0.28~\mbox{$Z_{\odot}$ }$      
$\displaystyle Z_{\rm SMC}~=~0.10~\mbox{$Z_{\odot}$ }.$     (26)

We are aware that the differential metal abundances in the Clouds could be different from the Galaxy due to a different stellar evolution at lower Z. However, we expect these effects to be of relatively minor importance, since the mass-loss rate at these metallicities ( $Z \mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\displaystyle ...) is still mainly determined by iron.

The upper panel of Fig. 6 shows the comparison between the observed LMC mass-loss rates and the theoretical values from our mass-loss recipe. The scatter between observations and theory can be attributed to errors in the stellar parameters and the mass-loss determinations, but may also be due to differential metal abundance patterns in the LMC. Note that there is a systematic difference between the two sets of mass-loss determinations themselves (Puls et al. 1996 vs. de Koter et al. 1997, 1998). The possible systematic differences between these two sets have been discussed in de Koter et al. (1998). Nevertheless, both samples show an offset with respect to our predictions. This could in principle be due to systematic errors in our predictions. However, since there is good agreement between observations and our predictions for a large sample of Galactic supergiants (Vink et al. 2000), we do not expect this to be the case. Perhaps the systematic offset is due to a too low assumed Z for the LMC. Haser et al. (1998) analysed individual O stars in the LMC and found metallicities significantly higher for these stars than usually derived from nebular abundance studies. Adopting the Haser et al. value of $Z = 0.8~\mbox{$Z_{\odot}$ }$ derived for the LMC O star SK-67$^{\rm o}$166, for the whole LMC sample, there is much better agreement between our predictions and the observed mass-loss rates (see the lower panel in Fig. 6). The scatter between observational and theoretical mass-loss rates decreases from 0.65 dex (1 $\sigma$) for the upper panel of Fig. 6 to only 0.36 dex for the lower panel of the figure.


  \begin{figure} \par {\psfig{file=smclowz.ps, width = 8.8cm} } % \end{figure} Figure 7: Comparison between theoretical and observational $\dot{M}$ for O stars in in the SMC with the adopted abundance of $Z_{\rm SMC}~=~0.10 ~\mbox{$Z_{\odot}$ }$. The dashed line is the one-to-one relation, a tool for convenient comparison between observations and theory
Open with DEXTER

Figure 7 shows the comparison between observed mass-loss rates and our predictions for the sample of the SMC stars. The figure shows a reasonable agreement between predictions and observations. We admit that there is quite a large scatter (0.55 dex) for which there may be several reasons. The important point at this stage is that the comparison with the SMC data yields good average agreement and thus yields support to the reliability of our mass loss recipe at metallicities other than solar.

For a test of our mass-loss recipe at extremely low Z, say $Z/\mbox{$Z_{\odot}$ }<$ 1/10, we will have to await new Hubble Space Telescope (HST) observations of some relatively nearby low metallicity galaxies.

   
10 Summary and conclusions

We have presented predictions of mass-loss rates for O and B stars over a wide range of metallicities. The calculations take the important effect of multiple line scattering into account in a consistent manner, using a "Unified Monte Carlo approach''. It is shown that there is a constant universal metallicity dependence over a wide range of metal abundance, which can be represented by $\dot{M} \propto Z^{0.85} \mbox{$v_{\infty}$ }^p$, but that one needs to take into account some specific positions in the HRD where recombinations of Fe or CNO ions may cause the mass loss to increase dramatically and produce "bi-stability'' jumps. It will be a challenge for the future to test our mass-loss recipe at extremely low Z in local starbursting galaxies, where the difference in mass-loss rate compared to the solar neighbourhood can be significant.

We can summarise the main results of the paper as follows:

1.
We have calculated a grid of wind models and mass-loss rates for a wide range of metallicities, covering $1/100 \le Z/\mbox{$Z_{\odot}$ }\le 10$;

2.
We have found that the mass loss vs. metallicity dependence behaves as a power-law with $\dot{M}~\propto Z^{0.69}$ for O stars and $\dot{M}~\propto Z^{0.64}$ for B supergiants. This is in contrast to an often applied square-root dependence of mass loss on Z;

3.
Although the $\dot{M}(Z)$ reaction is a constant function of Z, one should be aware of the presence of bi-stability jumps, where the character of the line driving changes drastically due to a change in the wind ionization resulting in jumps in mass loss. We have investigated the physical origins of these jumps and derived formulae that connect mass loss recipes at opposite sides of such bi-stability jumps. Additionally, we have made a distinction between the metal abundance derived from iron and from oxygen lines, since observations of different galaxies have shown that the [Fe/O] abundance ratio varies with metallicity;

4.
As our mass-loss predictions are successful in explaining the observed mass-loss rates for Galactic and Small Magellanic Cloud (Fig. 7) O-type stars, as well as in predicting the observed Galactic bi-stability jump, we believe that they are reliable and suggest that our mass-loss recipe be used in future evolutionary calculations, also at different Z. A computer routine to calculate mass loss is publicly available at the address astro.ic.ac.uk/$\sim$jvink/.

Acknowledgements
We thank the referee, Jon Bjorkman, for constructive comments that helped improve the paper. JV acknowledges financial support from the NWO Council for Physical Sciences. AdK acknowledges support from NWO Pionier grant 600-78-333 to L. B. F. M. Waters and from NWO Spinoza grant 08-0 to E. P. J. van den Heuvel.

References

 

Copyright ESO 2001