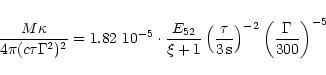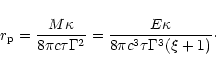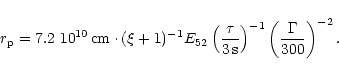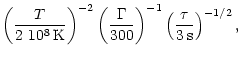A&A 369, 694-705 (2001)
DOI: 10.1051/0004-6361:20010131
Large scale magnetic fields and their dissipation in GRB fireballs
H. C. Spruit -
F. Daigne -
G. Drenkhahn
Max-Planck-Institut für Astrophysik, Postfach 1317, 85741
Garching bei München, Germany
Received 21 April 2000 / Accepted 17 January 2001
Abstract
We consider possible geometries of magnetic fields in GRB outflows,
and their evolution with distance from the source. For magnetically
driven outflows, with an assumed ratio of magnetic to kinetic energy
density of order unity, the field strengths are sufficient for
efficient production of  -rays by synchrotron emission in the
standard internal shock scenario, without the need for local
generation of small scale fields. In these conditions, the MHD
approximation is valid to large distances (
-rays by synchrotron emission in the
standard internal shock scenario, without the need for local
generation of small scale fields. In these conditions, the MHD
approximation is valid to large distances (
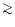 1019cm). In
outflows driven by nonaxisymmetric magnetic fields, changes of
direction of the field cause dissipation of magnetic energy by
reconnection. Much of this dissipation takes place outside the
photosphere of the outflow, and can convert a significant fraction
of the magnetic energy flux into radiation.
1019cm). In
outflows driven by nonaxisymmetric magnetic fields, changes of
direction of the field cause dissipation of magnetic energy by
reconnection. Much of this dissipation takes place outside the
photosphere of the outflow, and can convert a significant fraction
of the magnetic energy flux into radiation.
Key words: gamma-ray bursts - magnetic fields - radiation
mechanisms: nonthermal - shock waves
Several models for cosmic  -ray bursts (hereafter GRBs) make
use of rapidly rotating compact stellar-mass sources. Though many
details in each case are uncertain, the two more developed and popular
scenarios involve the coalescence of two compact objects (neutron star
+ neutron star or neutron star + black hole) and the collapse of a
massive star to a black hole (collapsar) (Mészáros & Rees
1992; Narayan et al. 1992; Woosley
1993; Paczynski 1998). Both lead to the
same system: a stellar mass black hole surrounded by a thick torus
made of stellar debris or of infalling stellar material partially
supported by centrifugal forces. An other interesting proposition
(Usov 1992; Kluzniak & Ruderman 1998; Spruit
1999) associates GRBs with highly magnetized millisecond
pulsars.
-ray bursts (hereafter GRBs) make
use of rapidly rotating compact stellar-mass sources. Though many
details in each case are uncertain, the two more developed and popular
scenarios involve the coalescence of two compact objects (neutron star
+ neutron star or neutron star + black hole) and the collapse of a
massive star to a black hole (collapsar) (Mészáros & Rees
1992; Narayan et al. 1992; Woosley
1993; Paczynski 1998). Both lead to the
same system: a stellar mass black hole surrounded by a thick torus
made of stellar debris or of infalling stellar material partially
supported by centrifugal forces. An other interesting proposition
(Usov 1992; Kluzniak & Ruderman 1998; Spruit
1999) associates GRBs with highly magnetized millisecond
pulsars.
The energy release by such a source can be fed from various
reservoirs. In the case of a thick disk + black hole system, the burst
can be powered by the accretion of disk material by the black hole or
by extracting directly the rotational energy of the black hole via the
Blandford-Znajek mechanism. In the case of a highly magnetised
millisecond pulsar the energy release comes from the rotational energy
of the neutron star.
Luminosities as high as those of GRBs cannot be radiated in the close
vicinity of the source. The energy released must first drive a wind
which rapidly becomes relativistic. Its kinetic energy is then
converted into  -rays (producing the prompt emission of the
GRB) at large radii via the formation of shocks, probably within the
wind itself (internal shock model) (Rees & Mészáros
1994; Daigne & Mochkovitch 1998). The wind is
finally decelerated by the external medium, which leads to a new shock
responsible for the afterglow emission observed in X-rays, optical
and radio bands (external shock model) (Katz 1994; Rhoads &
Paczynski 1993; Sari & Piran 1997; Wijers
et al. 1997).
-rays (producing the prompt emission of the
GRB) at large radii via the formation of shocks, probably within the
wind itself (internal shock model) (Rees & Mészáros
1994; Daigne & Mochkovitch 1998). The wind is
finally decelerated by the external medium, which leads to a new shock
responsible for the afterglow emission observed in X-rays, optical
and radio bands (external shock model) (Katz 1994; Rhoads &
Paczynski 1993; Sari & Piran 1997; Wijers
et al. 1997).
The Lorentz factor 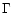 of the relativistic wind must reach high
values (
of the relativistic wind must reach high
values (
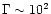 -103) both to produce
-103) both to produce  -rays
and to avoid photon-photon annihilation along the line of sight,
whose signature is not observed in the spectra of GRBs
(Goodman 1986, see also Baring 1995). This
limits the allowed amount of baryonic pollution in the flow to a very
low level and makes the production of the relativistic wind a
challenging problem. Only a few ideas have been proposed and none
appears to be fully conclusive at present.
-rays
and to avoid photon-photon annihilation along the line of sight,
whose signature is not observed in the spectra of GRBs
(Goodman 1986, see also Baring 1995). This
limits the allowed amount of baryonic pollution in the flow to a very
low level and makes the production of the relativistic wind a
challenging problem. Only a few ideas have been proposed and none
appears to be fully conclusive at present.
However it is suspected that large magnetic fields play an important
role. This is obvious in models using a highly magnetised millisecond
pulsar, but in the case of a thick disk + black hole system a magnetic
wind is also probably more efficient than the initial proposition
where the wind is powered by the annihilation of
neutrino-antineutrinos pairs along the rotational axis (Berezinskii
& Prilutskii 1987; Goodman et al. 1987;
Ruffert et al. 1997). The magnetic field in the disk
could be amplified by differential rotation to very large values (
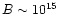 G) and a magnetically driven wind could then be emitted
from the disk (Thompson 1994; Mészáros & Rees
1997). under severe constraints on the field geometry
and the dissipation close to the disk, large values of the lorentz
factor can then be reached (Daigne & Mochkovitch
2000c,2000a).
G) and a magnetically driven wind could then be emitted
from the disk (Thompson 1994; Mészáros & Rees
1997). under severe constraints on the field geometry
and the dissipation close to the disk, large values of the lorentz
factor can then be reached (Daigne & Mochkovitch
2000c,2000a).
The emission of photons at large radii via the formation of shocks is
perhaps better understood than the central engine. It is believed that
a non-thermal population of accelerated electrons is produced behind
the shock waves and synchrotron and/or inverse Compton photons are
emitted. A magnetic field is then required. In the case of the
afterglow emission, the external shock is propagating in the
environment of the source, and the magnetic field has to be locally
generated by microscopic processes (Mészáros & Rees
1993; Wijers 1997; Thompson & Madau
2000). In the case of the prompt  -ray emission
which is probably due to internal shocks within the wind, such a
locally generated magnetic field is also usually invoked (Rees &
Mészáros 1994; Papathanassiou & Mészáros
1996; Sari & Piran 1997; Daigne &
Mochkovitch 1998). It has also been pointed out that a
large scale field originating from the source could play the same role
(Mészáros & Rees 1993,1997; Tavani
1996).
-ray emission
which is probably due to internal shocks within the wind, such a
locally generated magnetic field is also usually invoked (Rees &
Mészáros 1994; Papathanassiou & Mészáros
1996; Sari & Piran 1997; Daigne &
Mochkovitch 1998). It has also been pointed out that a
large scale field originating from the source could play the same role
(Mészáros & Rees 1993,1997; Tavani
1996).
The argumentation in this paper is organized as follows. In
Sect. 2 we show that for typical baryon loading, the
particle density in the outflow is so large that the MHD approximation
is appropriate out to distances of the order 1020cm. This will
turn out to be larger than the other relevant distances.
Due to the baryon loading, the GRB case is therefore different from
the essentially baryon-free pulsar wind case (e.g. Usov 1994),
where the MHD approximation breaks down much earlier, and plasma
theories of large amplitude electromagnetic waves (LAEMW) are applied.
The GRB case is actually simpler than the pulsar case in this respect.
The evolution of the magnetic field can therefore be dealt with in MHD
approximation. In Sect. 3 we discuss how the strength and
configuration of the field in the outflow depends on assumptions about
the central engine. This is done first without allowing for decay of
the field by internal MHD processes. In Sect. 4 we
show that the field strengths so obtained are sufficient to produce
synchrotron and/or inverse Compton emission in the standard internal
shock model, without the need for local generation of microscopic
magnetic fields. In Sect. 5 we then argue that internal
MHD processes are, in fact, likely to cause magnetic field energy
density to be released during the outflow. This may be a significant
contributor to the observed emission. The efficiency of conversion of
the primary energy of the central engine to observable  -rays
can also be much higher than in internal shock models. The arguments
are summarized again in Sect. 7.
-rays
can also be much higher than in internal shock models. The arguments
are summarized again in Sect. 7.
2 The validity of the MHD approximation
In this section, as well as throughout this paper, a prime denotes
quantities measured in the rest frame of the outflowing matter,
unprimed quantities are measured in the "laboratory'' frame (understood
here as a frame at rest relative to the central object of the burst).
In order to maintain the necessary current there must be enough plasma
available. As an example, consider the case of a magnetized outflow
with magnetic field of alternating direction, as happens in a
pulsar-like model (Sect. 3.4). We approximate this as a
plane sinusoidal wave with a wave number k and a angular frequency
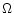 :
:
In a frame comoving with the fluid the field strength is
time-independent, hence the phase speed of the wave in the lab frame
is
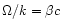 .
From the induction equation
.
From the induction equation
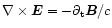 the relation between the electrical and
magnetic field amplitudes is
the relation between the electrical and
magnetic field amplitudes is
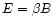 .
Ampère's equation gives
the current density,
.
Ampère's equation gives
the current density,
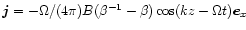 ,
or, with
,
or, with
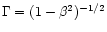 :
:
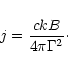 |
(3) |
(The same result is obtained if the current density is calculated in
MHD approximation in the comoving frame and then Lorentz transformed
back into the lab frame.) The current that can be maintained by the
outflowing medium is limited by the density of charged particles n.
The maximum current density (in the comoving frame) is
 ,
when the particles are given their maximum speed
c. In the lab frame this current density is (Melatos & Melrose 1996)
,
when the particles are given their maximum speed
c. In the lab frame this current density is (Melatos & Melrose 1996)
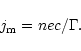 |
(4) |
If j gets larger than 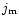 the simple ansatz of an
electromagnetic wave travelling with the same speed as the plasma
cannot hold any longer. Thus flux freezing is impossible and MHD is
not sufficient any more to describe the problem.
the simple ansatz of an
electromagnetic wave travelling with the same speed as the plasma
cannot hold any longer. Thus flux freezing is impossible and MHD is
not sufficient any more to describe the problem.
Plasma physical instabilities can set in at current densities much
lower than (4). They will produce an anomalous resistivity
in the plasma so that an electric field is present also in the rest
frame of the plasma. The electric field due to this resistivity is
small, however, compared to the magnetic field strength as long as the
charged particle density is larger than the minimum density. The MHD
approximation in this sense is then a good one on large scales, in
spite of the presence of small scale plasma processes.
If the outflow has a finite duration 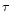 ,
and a constant speed
,
and a constant speed
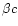 in this time interval, it moves as a shell of width
in this time interval, it moves as a shell of width
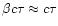 .
When the shell (assumed spherical) has expanded to
a radius r, the particle density measured in the lab frame is
.
When the shell (assumed spherical) has expanded to
a radius r, the particle density measured in the lab frame is
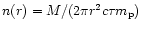 where M is the total mass ejected
and
where M is the total mass ejected
and  the proton mass.
With (3) and (4), the minimum particle density
the proton mass.
With (3) and (4), the minimum particle density
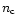 is
is
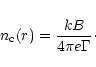 |
(5) |
If internal MHD processes can be neglected, the total electro-magnetic
energy
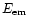 of the shell is conserved (see
Sect. 3). The field strength in the lab frame is then
of the shell is conserved (see
Sect. 3). The field strength in the lab frame is then
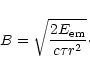 |
(6) |
With (5), and the known density n(r), we thus find that
the MHD approximation breaks down when the shell has reached the
critical radius
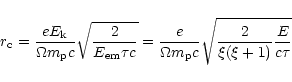 |
(7) |
where
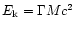 is the kinetic energy,
is the kinetic energy,
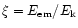 (in the lab frame) and
(in the lab frame) and
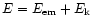 is the total energy.
Assuming
is the total energy.
Assuming 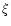 to be of the order unity we have
to be of the order unity we have
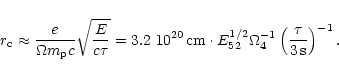 |
(8) |
The processes discussed in this paper happen well within time scales
smaller than
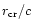 ,
and the MHD is justified.
,
and the MHD is justified.
In baryon-free cases, the expected values of 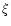 may be much higher
(Usov 1994), as in the typical pulsar-wind scenarios (Kennel
& Coroniti 1984; Begelman & Li 1992;
Blackman & Yi 1998), and the critical radius for MHD
condition correspondingly smaller. Such low baryon loading seems
rather unlikely, however, for the currently proposed scenarios for GRB
engines. Outflows from accretion disks, merging stars, and supernova
envelopes are all intrinsically highly baryon loaded environments, and
have some difficulties reaching baryon loadings as small as
may be much higher
(Usov 1994), as in the typical pulsar-wind scenarios (Kennel
& Coroniti 1984; Begelman & Li 1992;
Blackman & Yi 1998), and the critical radius for MHD
condition correspondingly smaller. Such low baryon loading seems
rather unlikely, however, for the currently proposed scenarios for GRB
engines. Outflows from accretion disks, merging stars, and supernova
envelopes are all intrinsically highly baryon loaded environments, and
have some difficulties reaching baryon loadings as small as
 .
Even in the rapidly magnetized msec neutron star
scenario (Spruit 1999), emergence of magnetic fields from
the star at the required short time scales is likely to imply that
some baryonic mass is lifted together with the magnetic fields.
.
Even in the rapidly magnetized msec neutron star
scenario (Spruit 1999), emergence of magnetic fields from
the star at the required short time scales is likely to imply that
some baryonic mass is lifted together with the magnetic fields.
3 Field geometries
![\begin{figure}
\hfill\includegraphics[width=0.17\hsize]{H2167F1.eps}\hfill
\in...
...fill
\includegraphics[width=0.50\hsize]{H2167F4.eps}\hfill\mbox{}
\end{figure}](/articles/aa/full/2001/14/aah2167/Timg39.gif) |
Figure 1:
Evolution of an initial dipole field by a radial outflow
(schematic). Top left: initial field configuration. Top right:
view on a larger scale, when the outflow, of finite duration
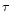 ,
now moves in a shell of width ,
now moves in a shell of width 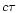 .
It has stretched
the field interior to the shell into a radial field. Lower left:
reconnection in the low-density interior region restores the
dipole field near the source. Lower right: as the shell moves out
its thickness becomes small compared the distance travelled, and
the further evolution depends on reconnection processes inside the
shell .
It has stretched
the field interior to the shell into a radial field. Lower left:
reconnection in the low-density interior region restores the
dipole field near the source. Lower right: as the shell moves out
its thickness becomes small compared the distance travelled, and
the further evolution depends on reconnection processes inside the
shell |
| Open with DEXTER |
A burst of duration 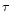 produces a shell of width
produces a shell of width 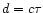 ,
travelling outward at a speed
,
travelling outward at a speed 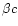 .
The observed radiation from
this shell is produced when it has expanded to a radius
.
The observed radiation from
this shell is produced when it has expanded to a radius 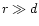 .
This
thin shell carries with it magnetic field lines from the source, which
we call "trapped field lines''. For the rest of this section, we assume
a relativistic outflow,
.
This
thin shell carries with it magnetic field lines from the source, which
we call "trapped field lines''. For the rest of this section, we assume
a relativistic outflow,
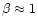 .
.
If reconnection processes inside the shell can be neglected, the field
lines are frozen in the expanding shell. If
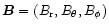 (in spherical coordinates), and the width of the shell is
constant, the components then vary with distance as
(in spherical coordinates), and the width of the shell is
constant, the components then vary with distance as
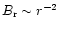 ,
,
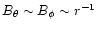 .
This is because the radial
component is divided over the surface of the spherical shell, while
the components parallel to the shell surface decrease with the
circumference. More formally, the induction equation
.
This is because the radial
component is divided over the surface of the spherical shell, while
the components parallel to the shell surface decrease with the
circumference. More formally, the induction equation
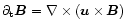 has the components
has the components
Assuming constant radial outflow
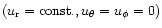 and spherical symmetry
and spherical symmetry
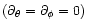 the time evolution in a comoving fluid element is
the time evolution in a comoving fluid element is
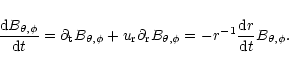 |
(11) |
Hence the tangential field
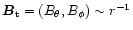 .
Since the expansion factor is very large between the
source and the radius from which the emitted radiation reaches us, the
radial component (varying as
.
Since the expansion factor is very large between the
source and the radius from which the emitted radiation reaches us, the
radial component (varying as 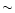 r-2) can be neglected and the
field is almost exactly parallel to the surface of the shell
(Fig. 1). If the width of the shell is constant, the magnetic
energy in the shell
r-2) can be neglected and the
field is almost exactly parallel to the surface of the shell
(Fig. 1). If the width of the shell is constant, the magnetic
energy in the shell
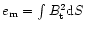 is constant. The magnetic field thus carries a constant
fraction of the kinetic energy of the outflow. Depending on how
large this fraction is, the trapped field can be sufficient to produce
the synchrotron emission proposed in internal shock models, without
the need for "in situ'' field generation mechanisms (Medvedev & Loeb
1999).
is constant. The magnetic field thus carries a constant
fraction of the kinetic energy of the outflow. Depending on how
large this fraction is, the trapped field can be sufficient to produce
the synchrotron emission proposed in internal shock models, without
the need for "in situ'' field generation mechanisms (Medvedev & Loeb
1999).
How many field lines are trapped in the outflow, and hence which
fraction of the outflow energy is magnetic, depends on conditions near
the source. We consider here the representative possibilities.
First consider a fireball expanding from the surface of a central
object (not specified further) of radius R and a dipolar magnetic
field of moment 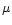 .
We assume that the magnetic field plays no role
in the driving of the outflow, but that it can confine plasma up to
its own energy density
.
We assume that the magnetic field plays no role
in the driving of the outflow, but that it can confine plasma up to
its own energy density 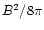 .
.
Assume first that the expansion is kinematic, i.e. that the magnetic
field is weak and its backreaction on the flow can be neglected. The
number of field lines trapped in the outflow is equal to the flux of
field lines outside crossing the dipole's equator outside the radius
R:
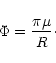 |
(12) |
This flux is a Lorentz invariant, so that the field strength of the
shell (as measured in the frame of the central engine) is of the order
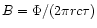 ,
or
,
or
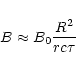 |
(13) |
where
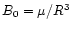 .
Whether this is a large field strength, compared
with the kinetic energy density
.
Whether this is a large field strength, compared
with the kinetic energy density
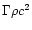 ,
depends on the
assumed dipole moment
,
depends on the
assumed dipole moment 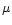 .
An upper limit to the dipole moment
follows from the requirement that the energy of the burst should be
able to open the field lines of the central object. Let the energy of
the burst be
.
An upper limit to the dipole moment
follows from the requirement that the energy of the burst should be
able to open the field lines of the central object. Let the energy of
the burst be
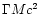 ,
where
,
where 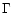 the asymptotic Lorentz
factor of the outflow and M the baryon load. If this energy was
initially confined in a region of size R (the size of the central
engine), the magnetic field strength B0 in the confining dipole
field of the source must satisfy
the asymptotic Lorentz
factor of the outflow and M the baryon load. If this energy was
initially confined in a region of size R (the size of the central
engine), the magnetic field strength B0 in the confining dipole
field of the source must satisfy
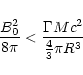 |
(14) |
in order for the field to be opened up by the fireball. With
(13), the magnetic energy density at distance r then
satisfies
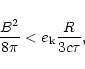 |
(15) |
where 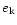 is the kinetic energy density in the shell:
is the kinetic energy density in the shell:
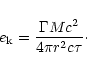 |
(16) |
For most central engine models considered, the duration of the burst
is long compared to the light travel time across the source,
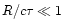 .
A "passive'' model, in which the magnetic field does
not play a role in driving the outflow, therefore can only yield field
strengths in the shell which are small compared with kinetic energy
density. Even at such a low field strength, however, the magnetic
field can become important for synchrotron emission in internal
shocks, as discussed below in Sect. 4.
.
A "passive'' model, in which the magnetic field does
not play a role in driving the outflow, therefore can only yield field
strengths in the shell which are small compared with kinetic energy
density. Even at such a low field strength, however, the magnetic
field can become important for synchrotron emission in internal
shocks, as discussed below in Sect. 4.
In magnetic models for GRB engines, the magnetic field serves to
extract rotation energy from a rapidly rotating relativistic object.
The details of such magnetic extraction (especially three-dimensional
ones) are still somewhat uncertain, but basic energetic considerations
are simple. Rotation of the mass-loaded field lines induces an
azimuthal field component 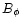 .
Let the distance from the rotating
object where this component is equal to the radial field be r0.
Except for cases with large baryon loading that are probably not
relevant for GRB engines, r0 is of the order of the Alfvén
radius, which can lie anywhere between the surface of the object Rand the light cylinder
.
Let the distance from the rotating
object where this component is equal to the radial field be r0.
Except for cases with large baryon loading that are probably not
relevant for GRB engines, r0 is of the order of the Alfvén
radius, which can lie anywhere between the surface of the object Rand the light cylinder
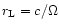 .
The energy output Ltransmitted by the azimuthal magnetic stress (
.
The energy output Ltransmitted by the azimuthal magnetic stress (
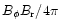 )
is
then of the order
)
is
then of the order
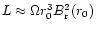 .
For a field
dominated by its dipole component
.
For a field
dominated by its dipole component 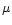 ,
this yields a luminosity
,
this yields a luminosity
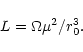 |
(17) |
For
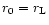 ,
this yields (by order of magnitude) the pulsar
spin-down formula for an inclined dipole rotating in vacuum, emitting
an electromagnetic wave from its light cylinder.
,
this yields (by order of magnitude) the pulsar
spin-down formula for an inclined dipole rotating in vacuum, emitting
an electromagnetic wave from its light cylinder.
![\begin{figure}
\parbox[c]{0.5\hsize}{
\includegraphics[width=\hsize]{H2167F5.e...
....eps}\\ [1ex]
\includegraphics[width=\hsize]{H2167F7.eps}
\par }
\end{figure}](/articles/aa/full/2001/14/aah2167/Timg78.gif) |
Figure 2:
Field configuration in quasi-spherical magnetic outflow
driven by a perpendicular rotator ("pulsar-like'' case)
(schematic). Left: view in the equatorial plane, with dots and
pluses indicating field lines into and out of the plane of the
drawing. Right: top view from the rotational pole. Bottom right:
same view on larger scale, at a later time 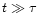 |
| Open with DEXTER |
The energy estimate (17) does not tell what the field
configuration in the outflow looks like. The possibilities for
dissipation of magnetic energy inside the outflow depend strongly on
this configuration, which in turn depends on the nature of the
magnetic field of the central engine. An important distinction is
whether the rotating magnetic field is axisymmetric or
nonaxisymmetric. In the nonaxisymmetric case, the outflow
contains magnetic fields varying on the rather small scale
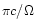 ,
the wavelength of the outgoing wave. In such a field,
internal dissipation turns out to be much more likely to be important
than in an axisymmetric field, where the length scale of the field is
of the order of the distance r. In the following, this is
illustrated with a few specific cases.
,
the wavelength of the outgoing wave. In such a field,
internal dissipation turns out to be much more likely to be important
than in an axisymmetric field, where the length scale of the field is
of the order of the distance r. In the following, this is
illustrated with a few specific cases.
Estimate (17) only gives the total luminosity. Which
fraction of it is in the form of kinetic energy and which in magnetic
energy depends on more physics. At one extreme is Michel's
(1969) model, in which the outflow consists of cold
(pressureless) matter accelerated exclusively by the magnetic field.
In this case, the ratio
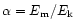 of
magnetic to kinetic luminosity is of the order
of
magnetic to kinetic luminosity is of the order
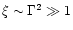 .
At large Lorentz factors, the energy is almost entirely in
electromagnetic form, in this model. This is probably a property of
the special geometry of the model, in which the flow is limited to the
equatorial plane. If outflow in other directions is considered, much
smaller values of
.
At large Lorentz factors, the energy is almost entirely in
electromagnetic form, in this model. This is probably a property of
the special geometry of the model, in which the flow is limited to the
equatorial plane. If outflow in other directions is considered, much
smaller values of 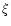 result (Begelman & Li 1994).
At the other extreme, consider a case in which most magnetic energy is
released inside the light cylinder, in the form of a dense pair plasma
(by some form of magnetic reconnection, for example). The result would
then be just like the hydrodynamic expansion of a simple (Goodman
1986; Paczynski 1986) pair plasma
fireball, and the resulting outflow would have
result (Begelman & Li 1994).
At the other extreme, consider a case in which most magnetic energy is
released inside the light cylinder, in the form of a dense pair plasma
(by some form of magnetic reconnection, for example). The result would
then be just like the hydrodynamic expansion of a simple (Goodman
1986; Paczynski 1986) pair plasma
fireball, and the resulting outflow would have 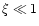 .
If some but
not all energy is dissipated close to the source, intermediate values
of
.
If some but
not all energy is dissipated close to the source, intermediate values
of 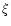 would result. Since these important questions have not been
resolved yet, we keep
would result. Since these important questions have not been
resolved yet, we keep 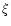 as a free parameter in the following.
Where necessary we assume that it typically has values or order unity.
as a free parameter in the following.
Where necessary we assume that it typically has values or order unity.
3.4 Nonaxisymmetric quasi-spherical outflow
Assume we have a perpendicular rotator, i.e. the rotating object has
its dipole axis orthogonal to the rotation axis. At the source surface
r0, the rotating field is then strongest at the equator, and one
expects the energy flux to be largest near the equatorial plane. With
each rotation, a "stripe'' consisting of a band of eastward and one of
westward azimuthal field moves outward (Fig. 2, see also
Coroniti 1990; Usov 1994). Assuming the
outflow to be relativistic, the width 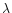 of such a stripe in
the rest frame of the central object is
of such a stripe in
the rest frame of the central object is
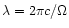 .
The
(absolute value of the) azimuthal flux
.
The
(absolute value of the) azimuthal flux 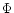 in each half-wavelength
is of the order of the poloidal flux outside the source surface r0,
in each half-wavelength
is of the order of the poloidal flux outside the source surface r0,
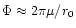 .
For spherical expansion of this amount of
azimuthal flux, the field strength at distance r is then
.
For spherical expansion of this amount of
azimuthal flux, the field strength at distance r is then
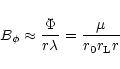 |
(18) |
while the the total (magnetic plus kinetic) energy density
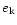 is
is
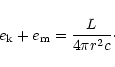 |
(19) |
Hence with (17) the ratio of magnetic energy density to
total energy density (in the lab frame) is of the order
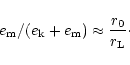 |
(20) |
3.5 Jet
Consider a collimated outflow along the axis of rotation
(Fig. 3). This might be achieved by magnetic models in which
the azimuthal field collimates the flow towards the axis by hoop
stress (Bisnovatyi-Kogan & Ruzmaikin 1976; Blandford
& Payne 1982; Sakurai 1985). In such a
model, one assumes an axisymmetric (about the rotation axis) poloidal
field, which is wound up into an azimuthal field wrapped around the
axis. Let the opening angle of the outflow be 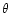 (assumed
constant), and
(assumed
constant), and 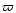 the cylindrical radius. At the source surface
the cylindrical radius. At the source surface
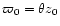 the poloidal and azimuthal field components
are equal, and in the absence of magnetic reconnection processes
the poloidal and azimuthal field components
are equal, and in the absence of magnetic reconnection processes
If the collimation angle is small, the field as seen in a frame
comoving with the jet is a slowly varying, nearly azimuthal field.
Such a field is known to be highly unstable to kink instabilities
(e.g. Bateman 1980). They operate on a time scale
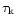 of the order of the Alfvén crossing time, i.e.
of the order of the Alfvén crossing time, i.e.
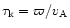 .
Though the details of this
process have not been worked out for jets (see however Lucek & Bell
1996,1997), it is likely that the release of magnetic
energy operates in two steps. In the first step, kink instability
transforms the axisymmetric configuration into a nonaxisymmetric,
helical, configuration. For an application to jets, see Königl &
Choudhuri (1985). This step is fast, operating on the
Alvén crossing time. At this stage, the field has already lost much
of its collimating ability, since the average azimuthal field strength
has decreased in favour of a less ordered field component. During the
instability, the so-called magnetic helicity is conserved, however, so
that only a fraction of the magnetic energy is released. The further
release of magnetic energy depends on reconnection processes. As
discussed in Sect. 5, this is also likely to proceed on
a time scale proportional to the Alfvén crossing time, though
somewhat slower than the kink process itself.
As in the quasi-spherical outflow case, we ignore this internal
dissipation of the magnetic energy for the moment, and return to it in
Sect. 5. For a jet expanding with fixed opening angle
.
Though the details of this
process have not been worked out for jets (see however Lucek & Bell
1996,1997), it is likely that the release of magnetic
energy operates in two steps. In the first step, kink instability
transforms the axisymmetric configuration into a nonaxisymmetric,
helical, configuration. For an application to jets, see Königl &
Choudhuri (1985). This step is fast, operating on the
Alvén crossing time. At this stage, the field has already lost much
of its collimating ability, since the average azimuthal field strength
has decreased in favour of a less ordered field component. During the
instability, the so-called magnetic helicity is conserved, however, so
that only a fraction of the magnetic energy is released. The further
release of magnetic energy depends on reconnection processes. As
discussed in Sect. 5, this is also likely to proceed on
a time scale proportional to the Alfvén crossing time, though
somewhat slower than the kink process itself.
As in the quasi-spherical outflow case, we ignore this internal
dissipation of the magnetic energy for the moment, and return to it in
Sect. 5. For a jet expanding with fixed opening angle
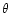 (see Fig. 3), the field strength then varies as
r-1 and the magnetic energy is constant with distance. Since only
a fraction of the magnetic energy is released in the kinking process,
the ratio of magnetic to kinetic energy density is still of the order
found in axisymmetric magnetic jet calculations (e.g. Camenzind
1987), i.e. of order unity:
(see Fig. 3), the field strength then varies as
r-1 and the magnetic energy is constant with distance. Since only
a fraction of the magnetic energy is released in the kinking process,
the ratio of magnetic to kinetic energy density is still of the order
found in axisymmetric magnetic jet calculations (e.g. Camenzind
1987), i.e. of order unity:
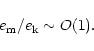 |
(23) |
![\begin{figure}
\includegraphics[height=6.5cm]{H2167F8.eps}\hfill
\includegraphics[height=6.5cm]{H2167F9.eps} \end{figure}](/articles/aa/full/2001/14/aah2167/Timg100.gif) |
Figure 3:
Jet-like outflow of finite duration, magnetically
driven by an axially symmetric rotator. Left: configuration near
the source, showing how the field in the outflow is wound into a
toroidal (azimuthal) field. Right: large scale view after a time
long compared to the duration 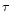 .
The field in the outflow is
now a "pancake'' of toroidal flux. Sketch ignores nonaxisymmetric
processes like kink instability and subsequent reconnection, which
can release energy from this configuration .
The field in the outflow is
now a "pancake'' of toroidal flux. Sketch ignores nonaxisymmetric
processes like kink instability and subsequent reconnection, which
can release energy from this configuration |
| Open with DEXTER |
4 The emission expected from internal shocks
The internal shock model assumes that the initial distribution of the
Lorentz factor in the shell is highly variable. Rapid layers catch up
with slower ones leading to internal shocks propagating within the
relativistic shell. The hot material behind the shock waves is
radiating efficiently and produces the observed prompt  -ray
emission of GRBs (Rees & Mészáros 1994; Kobayashi
et al. 1997; Daigne & Mochkovitch 1998;
Panaitescu & Mészáros 1999; Daigne &
Mochkovitch 2000b). We only summarize here the basic
assumptions of the model. For details see Daigne & Mochkovitch
(1998).
-ray
emission of GRBs (Rees & Mészáros 1994; Kobayashi
et al. 1997; Daigne & Mochkovitch 1998;
Panaitescu & Mészáros 1999; Daigne &
Mochkovitch 2000b). We only summarize here the basic
assumptions of the model. For details see Daigne & Mochkovitch
(1998).
Consider two layers of equal mass (for simplicity) and of Lorentz
factor 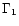 and
and 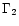 (
(
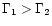 )
which are
emitted on a timescale
)
which are
emitted on a timescale
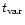 .
They will collide at a radius
.
They will collide at a radius
where 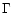 is as usual the mean Lorentz factor of the flow. The
average energy which is dissipated per proton in this shock is given
by
is as usual the mean Lorentz factor of the flow. The
average energy which is dissipated per proton in this shock is given
by
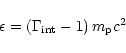 |
(26) |
with
![\begin{displaymath}\Gamma_{\rm int} =
\frac{1}{2}\left[\sqrt{\frac{\Gamma_1}{\Gamma_2}}
+\sqrt{\frac{\Gamma_2}{\Gamma_1}}\right].
\end{displaymath}](/articles/aa/full/2001/14/aah2167/img111.gif) |
(27) |
With
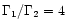 ,
which corresponds to a mildly
relativistic shock (
,
which corresponds to a mildly
relativistic shock (
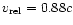 ), this gives
), this gives
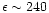 MeV.
MeV.
It is generally assumed (Rees & Mészáros 1994;
Papathanassiou & Mészáros 1996; Sari &
Piran 1997; Daigne & Mochkovitch 1998) that
behind the shock wave a fraction of the electrons come into (at least
partial) equipartition with the protons and become highly
relativistic. If a fraction
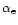 of the dissipated
energy goes into a fraction
of the dissipated
energy goes into a fraction 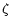 of the electrons, their
characteristic Lorentz factor (in the comoving frame) will be
of the electrons, their
characteristic Lorentz factor (in the comoving frame) will be
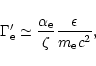 |
(28) |
which, for complete equipartition and
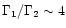 ,
yields
,
yields
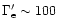 -200 if
-200 if
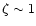 and
and
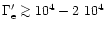 if only a small
fraction of the electrons are accelerated (
if only a small
fraction of the electrons are accelerated (
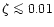 .
For some
theoretical arguments in favour of such an assumption, see e.g. Bykov
& Mészáros 1996). Such highly relativistic electrons
can emit
.
For some
theoretical arguments in favour of such an assumption, see e.g. Bykov
& Mészáros 1996). Such highly relativistic electrons
can emit  -rays by the synchrotron and/or the inverse Compton
process. A magnetic field is however required.
-rays by the synchrotron and/or the inverse Compton
process. A magnetic field is however required.
The magnetic field involved in the synchrotron radiation is usually
assumed to be generated locally by microscopic processes. Such a
process has been proposed by Medvedev & Loeb (1999).
(This is also assumed for the external shock propagating in the
interstellar medium and responsible for the afterglow; see however
Thompson & Madau 2000.) If this magnetic field is also
into equipartition with the protons and electrons, it will have
typical values of
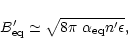 |
(29) |
where
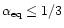 and n' is the comoving proton
number density, which can be estimated by
and n' is the comoving proton
number density, which can be estimated by
For typical radii
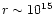 -1016cm and
-1016cm and
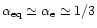 ,
this leads
to
,
this leads
to
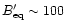 -1000G depending on the contrast
-1000G depending on the contrast
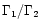 .
.
If the GRB is powered magnetically, however, the outflow is naturally
magetized. (One good reason for assuming magnetic powering is that
alternatives like
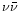 annihilation are energetically
inefficient.) As shown in Sect. 3, the magnetic energy
content of the outflow is constant as long as internal dissipation of
magnetic energy can be neglected. For the three cases considered, the
ratio
annihilation are energetically
inefficient.) As shown in Sect. 3, the magnetic energy
content of the outflow is constant as long as internal dissipation of
magnetic energy can be neglected. For the three cases considered, the
ratio
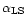 of the (large scale-) magnetic to kinetic
energy density is
of the (large scale-) magnetic to kinetic
energy density is
for a passively expanded source field, a magnetically driven
quasi-spherical outflow and a magnetically driven collimated jet
respectively (cf. Eqs. (15, 20, 23)).
For source sizes R = 106-107cm and durations
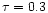 -30s the passively expanding field case has
-30s the passively expanding field case has
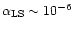 -10-3. The magnetically driven
quasi-spherical outflow would yield higher values,
-10-3. The magnetically driven
quasi-spherical outflow would yield higher values,
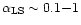 ,
assuming
,
assuming
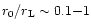 .
A magnetically driven jet would have a
.
A magnetically driven jet would have a
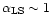 .
(These values hold as long as internal dissipation of magnetic energy
can be ignored (Sect. 5)).
.
(These values hold as long as internal dissipation of magnetic energy
can be ignored (Sect. 5)).
The corresponding comoving magnetic field in all cases is
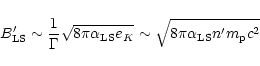 |
(35) |
which leads to (using the estimation of n' given by
Eq. (31)):
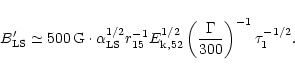 |
(36) |
We see that
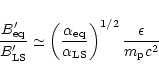 |
(37) |
and that, depending on the values of
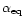 and
and
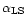 ,
the large scale magnetic field naturally has
strengths comparable with the equipartition fields usually invoked.
,
the large scale magnetic field naturally has
strengths comparable with the equipartition fields usually invoked.
Synchrotron emission by accelerated electrons in a magnetic field
occurs at a typical energy (observer frame)
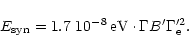 |
(38) |
Consider first the case where a large fraction of the electrons takes
part in the acceleration process,
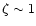 .
If the equipartition
is complete - equal amounts of energy in protons and electrons (and
magnetic fields if locally generated) - we then have
.
If the equipartition
is complete - equal amounts of energy in protons and electrons (and
magnetic fields if locally generated) - we then have
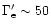 -500 so that for
-500 so that for
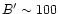 -1000G the synchrotron photon energy
-1000G the synchrotron photon energy
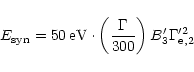 |
(39) |
is usually in the UV band (we don't consider here the high
contrasts
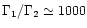 which could produce
synchrotron photons directly in the gamma-ray range even if
which could produce
synchrotron photons directly in the gamma-ray range even if
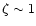 .
Such high contrasts are probably not realistic in
view of the difficulty to accelerate a wind to high Lorentz
factors).
.
Such high contrasts are probably not realistic in
view of the difficulty to accelerate a wind to high Lorentz
factors).  -rays can then be produced by inverse Compton
scattering on the synchrotron photons. We are in the Thomson limit
where
-rays can then be produced by inverse Compton
scattering on the synchrotron photons. We are in the Thomson limit
where
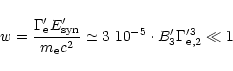 |
(40) |
so that
The fraction of the electron energy which is radiated in the
 -ray range has been computed by Daigne & Mochkovitch
(1998) and is given by
-ray range has been computed by Daigne & Mochkovitch
(1998) and is given by
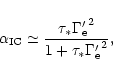 |
(43) |
where the optical 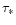 depth of the layer of relativistic
electrons is the solution of the equation
depth of the layer of relativistic
electrons is the solution of the equation
for an equipartition field and a large-scale magnetic field
respectively. Low values of the magnetic field increase the
efficiency
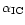 but B' cannot be too small because
(i)
but B' cannot be too small because
(i)
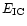 must stay in the
must stay in the  -ray range and (ii) the
typical time-scale of the radiative process
-ray range and (ii) the
typical time-scale of the radiative process
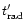 must be
shorter than the expansion time
must be
shorter than the expansion time
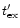 ,
otherwise the hot
layer is cooling adiabatically. These two time-scales are
,
otherwise the hot
layer is cooling adiabatically. These two time-scales are
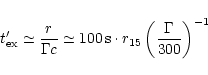 |
(46) |
and
The radiative efficiency (energy loss by radiation versus adiabatic
cooling) is then of the order
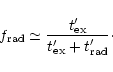 |
(49) |
We see that (i) for the equipartition magnetic field these two
conditions limit
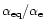 to the range
0.01-1 yielding low total efficiencies,
to the range
0.01-1 yielding low total efficiencies,
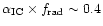 -0.1; (ii) for a passively expanded
source field (
-0.1; (ii) for a passively expanded
source field (
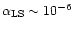 -10-3) it is
impossible to produce
-10-3) it is
impossible to produce  -rays for the lowest values of
-rays for the lowest values of
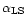 (both because
(both because
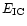 is too low and
is too low and
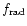 is very small). For
is very small). For
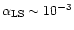 the magnetic field is still weak but for short bursts (n' is higher)
or high contrasts of Lorentz factors (
the magnetic field is still weak but for short bursts (n' is higher)
or high contrasts of Lorentz factors (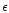 is higher) it is
possible to produce a
is higher) it is
possible to produce a  -ray burst with a total efficiency
-ray burst with a total efficiency
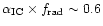 which is then
quite high; (iii) for a magnetically driven quasi-spherical outflow
(
which is then
quite high; (iii) for a magnetically driven quasi-spherical outflow
(
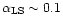 -1) the radiative efficiency is high
(
-1) the radiative efficiency is high
(
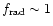 ), and there is no difficulty to produce
), and there is no difficulty to produce
 -rays via the inverse Compton emission.
However the efficiency of the IC process becomes very low if
-rays via the inverse Compton emission.
However the efficiency of the IC process becomes very low if
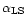 is to close to unity (
is to close to unity (
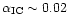 for
for
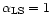 )
and is still low
(
)
and is still low
(
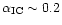 )
for
)
for
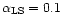 .
Values
of
.
Values
of 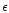 larger than 200MeV does not improve this efficiency
much. (iv) For a magnetically driven jet
the situation is very close to the
previous case with
larger than 200MeV does not improve this efficiency
much. (iv) For a magnetically driven jet
the situation is very close to the
previous case with
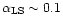 and the IC efficiency
is then very low.
and the IC efficiency
is then very low.
We consider now the other extreme case where only a small fraction of
the electrons are accelerated:
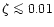 .
The Lorentz factor of
the electrons then reaches very high values of 5000-50000 and
.
The Lorentz factor of
the electrons then reaches very high values of 5000-50000 and
 -rays can be produced directly by synchrotron emission:
-rays can be produced directly by synchrotron emission:
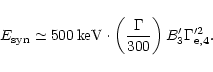 |
(50) |
We are in the Klein-Nishina limit where
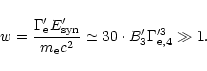 |
(51) |
The fraction of the energy which is directly radiated by synchrotron
photons is now given by
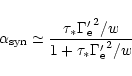 |
(52) |
and the optical depth is solution of a more complex equation (the
opacity has decreased compared to the Thomson regime by a factor
depending on w):
for the equipartition and large-scale magnetic field respectively. As
before we also need to check that the radiative time-scale
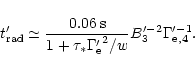 |
(55) |
is shorter than
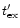 .
This is now always the case
(
.
This is now always the case
(
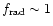 )
except for the lower values of
)
except for the lower values of
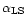 (10-6) or for the last internal shocks
occurring far from the source.
(10-6) or for the last internal shocks
occurring far from the source.
We then can conclude that (i) for an equipartition field
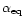 has to be of the same order as
has to be of the same order as
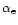 in order for the synchrotron process is to produce
in order for the synchrotron process is to produce
 -rays at high efficiency (
-rays at high efficiency (
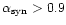 ). (ii)
For a passively expanded source field the case
). (ii)
For a passively expanded source field the case
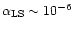 is again excluded because of an extremely low efficiency
and a typical energy which is more in the X-rays range. The case
is again excluded because of an extremely low efficiency
and a typical energy which is more in the X-rays range. The case
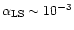 suffers the same limitations as
before, the efficiency is only
suffers the same limitations as
before, the efficiency is only
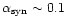 .
(iii)
For a magnetically driven quasi-spherical outflow and a magnetically
driven jet the situation is similar to the equipartition case: the
efficiency is very high (
.
(iii)
For a magnetically driven quasi-spherical outflow and a magnetically
driven jet the situation is similar to the equipartition case: the
efficiency is very high (
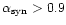 for a
quasi-spherical outflow and
for a
quasi-spherical outflow and
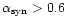 for a jet).
for a jet).
In conclusion for this section, a passive expanded source field is
probably too weak in most cases to produce a  -ray burst
without a locally generated magnetic field, but in the two other cases
described in this paper, a magnetically driven quasi-spherical outflow
and a magnetically driven collimated jet, there is no difficulty to
produce
-ray burst
without a locally generated magnetic field, but in the two other cases
described in this paper, a magnetically driven quasi-spherical outflow
and a magnetically driven collimated jet, there is no difficulty to
produce  -rays without any need of a supplementary field. The
efficiencies of the radiative process in these magnetically driven
cases are comparable to those already calculated for an equipartition
field. In particular, as was already pointed out in Daigne &
Mochkovitch (1998), this efficiency is expected to be
higher if the
-rays without any need of a supplementary field. The
efficiencies of the radiative process in these magnetically driven
cases are comparable to those already calculated for an equipartition
field. In particular, as was already pointed out in Daigne &
Mochkovitch (1998), this efficiency is expected to be
higher if the  -rays are directly produced by synchrotron
emission (which is possible if only a fraction of the electrons are
accelerated behind the shock waves).
-rays are directly produced by synchrotron
emission (which is possible if only a fraction of the electrons are
accelerated behind the shock waves).
5 Magnetic energy release in the outflow
Internal release of magnetic energy can be important for the
 -ray lightcurves if the time scale is sufficiently fast that
the release is significant before the outflow reaches the external
shock. It should not be too fast, however. If the release takes place
before the photospheric radius, i.e. in the optically thick part of
the outflow, the internal energy generated is not radiated away.
Instead, it is converted, through the radial expansion of the shell,
into kinetic energy.
-ray lightcurves if the time scale is sufficiently fast that
the release is significant before the outflow reaches the external
shock. It should not be too fast, however. If the release takes place
before the photospheric radius, i.e. in the optically thick part of
the outflow, the internal energy generated is not radiated away.
Instead, it is converted, through the radial expansion of the shell,
into kinetic energy.
Assume that the outflow is driven by the rotating magnetic field of
the central, compact object, i.e. that the field strength estimates
(20) or (23) apply. Depending on the field
configuration at the source, the field in the flow can be
nonaxisymmetric to a greater or lesser degree, and depending on the
nature of the acceleration process it can be quasi-spherical or more
collimated along the rotation axis. Consider again the two cases
discussed in Sect. 3.
In the perpendicular rotator case, the field consists of "stripes'' of
alternating polarity, in which the field energy can be released by
reconnection. In the axisymmetric jet case, the field is unstable to a
kinking process. The magnetic field in both cases is far from a
minimum energy configuration (a potential field). The free energy it
contains is available if it can be released on a sufficiently short
time scale.
The initial perturbations from which the MHD instabilities grow are
likely to be present at significant amplitude, from the start of the
outflow, except in the unlikely event that the field configuration of
the source is highly symmetric. Thus we may assume that the ordered
configurations of Figs. 2 and 3 significantly change
to more disordered ones within an MHD instability time scale. These
more disordered configurations then are subject to fast reconnection
processes.
Reconnection takes place on time scales governed by the Alfvén
speed. It depends on plasma resistivity as well, but in practical
reconnection configurations (as opposed to highly symmetric textbook
examples like tearing mode instability), the resistivity enters only
weakly. In the Sweet-Parker model for 2-D reconnection, for example
(e.g. Biskamp 1993), it enters through the logarithm of
the magnetic Reynolds number. In more realistic 3-D modes of
reconnection, the basic geometry of reconnection (a "chain link'' kind
of configuration) differs from the 2-D geometries. Also, the
reconnection tends to be distributed over many current sheets instead
of a few reconnection points (see Galsgaard & Nordlund
1996,1997, for recent numerical results).
The reconnection rate is still weakly dependent on the resistivity in
these 3-D configurations.
In the perpendicular rotator, the field in the outflow changes (in the
lab frame) on a length scale
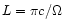 .
The time scale
.
The time scale
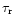 of magnetic energy release scales with the Alfvén
crossing time over this length scale. In a comoving frame
of magnetic energy release scales with the Alfvén
crossing time over this length scale. In a comoving frame
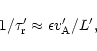 |
(56) |
where
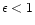 is a numerical factor of order unity measuring the
reconnection speed. In the lab frame, the energy release time scale is
is a numerical factor of order unity measuring the
reconnection speed. In the lab frame, the energy release time scale is
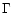 times longer, hence
times longer, hence
 |
(57) |
As the bulk Lorentz factor 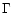 tends to infinity, the energy
release becomes arbitrarily slow. This is also understood by noting
that for
tends to infinity, the energy
release becomes arbitrarily slow. This is also understood by noting
that for
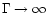 ,
the electromagnetic field of the
outflow in the observer frame becomes indistinguishable from a pure EM
wave in vacuum, whose energy content is conserved.
,
the electromagnetic field of the
outflow in the observer frame becomes indistinguishable from a pure EM
wave in vacuum, whose energy content is conserved.
The relativistic Alfvén speed is (e.g. Jackson
1999)
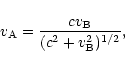 |
(58) |
where
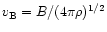 is the nonrelativistic Alfvén speed.
is the nonrelativistic Alfvén speed.
Let the ratio of magnetic energy flux (Poynting flux) to kinetic
energy flux be 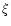 :
:
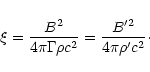 |
(59) |
Hence
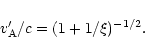 |
(60) |
For the models discussed above,
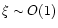 .
As long as the
magnetic energy density has not decayed by internal MHD processes, the
comoving Alfvén speed is thus of the order of the speed of light.
.
As long as the
magnetic energy density has not decayed by internal MHD processes, the
comoving Alfvén speed is thus of the order of the speed of light.
The magnetic dissipation radius, the distance 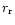 from the
source where magnetic energy release becomes important, is thus of the
order
from the
source where magnetic energy release becomes important, is thus of the
order
The length scale in the comoving frame, L', is equal to the
wavelength
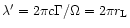 in the
perpendicular rotator case) or the lateral scale,
in the
perpendicular rotator case) or the lateral scale,
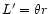 (in a
collimated outflow).
(in a
collimated outflow).
For the case of an axisymmetric outflow along the rotation axis, the
situation is a bit different. The length scale L of the magnetic
field is now the jet radius,
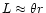 ,
where
,
where 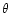 is the
opening angle of the jet. Since this is measured perpendicular to the
flow, it is the same in the lab and the comoving frame. In the
comoving frame, the time for an Alfvén wave to communicate over this
distance is
is the
opening angle of the jet. Since this is measured perpendicular to the
flow, it is the same in the lab and the comoving frame. In the
comoving frame, the time for an Alfvén wave to communicate over this
distance is
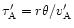 ,
in the lab
frame
,
in the lab
frame
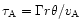 .
This is less
than the time for the flow to reach a distance r,
.
This is less
than the time for the flow to reach a distance r,
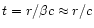 if
if
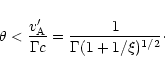 |
(63) |
If the jet is wider than this, parts of the flow moving at angles
separated by more than
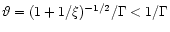 have no time to communicate by an Alfvén wave in the time elapsed
since the start of the flow, and behave as if they are causally
disconnected from each other. Kink instability will thus be limited to
an inner core of opening angle
have no time to communicate by an Alfvén wave in the time elapsed
since the start of the flow, and behave as if they are causally
disconnected from each other. Kink instability will thus be limited to
an inner core of opening angle
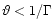 .
In directions
outside this angle, the instability is suppressed since it has to
communicate from one side to then other across the axis of the jet.
This reduces the fraction of the available magnetic energy that can be
tapped by MHD processes.
.
In directions
outside this angle, the instability is suppressed since it has to
communicate from one side to then other across the axis of the jet.
This reduces the fraction of the available magnetic energy that can be
tapped by MHD processes.
On the other hand, magnetic energy release in the inner core so
defined already starts very close to the source (where the length
scale
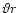 is small). Thus only a fraction of the dissipation
will happen in the optically thin, observable regions.
is small). Thus only a fraction of the dissipation
will happen in the optically thin, observable regions.
The conclusion from the above is that in the case of a perpendicular
rotator, there is a well defined "magnetic dissipation radius''
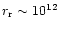 cm where most of the magnetic energy is
dissipated. For a purely axisymmetric outflow along the rotation axis,
on the other hand, only a fraction of the magnetic energy can be
released, unless the opening angle is less than
cm where most of the magnetic energy is
dissipated. For a purely axisymmetric outflow along the rotation axis,
on the other hand, only a fraction of the magnetic energy can be
released, unless the opening angle is less than 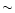
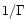 .
This
fraction probably dissipates close to the source, and not necessarily
in the optically thin region where it could contribute to the observed
emission. In intermediate cases, where both an axisymmetric and a
nonaxisymmetric component are present, the magnetic field in the
outflow changes direction on the length scale
.
This
fraction probably dissipates close to the source, and not necessarily
in the optically thin region where it could contribute to the observed
emission. In intermediate cases, where both an axisymmetric and a
nonaxisymmetric component are present, the magnetic field in the
outflow changes direction on the length scale
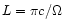 ,
without completely changing direction. In such cases, the amount of
the magnetic energy that can be released in directions outside the
central core
,
without completely changing direction. In such cases, the amount of
the magnetic energy that can be released in directions outside the
central core
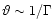 is of the order
is of the order
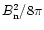 ,
where
,
where 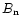 is the nonaxisymmetric
part of the field. This is a significant fraction of the total
magnetic energy unless the field is nearly axisymmetric. The
axisymmetric jet case, though attractive as a computable model, is
thus rather singular with respect to the question of magnetic
dissipation which we address in this paper.
is the nonaxisymmetric
part of the field. This is a significant fraction of the total
magnetic energy unless the field is nearly axisymmetric. The
axisymmetric jet case, though attractive as a computable model, is
thus rather singular with respect to the question of magnetic
dissipation which we address in this paper.
The reconnection radii derived above need to be compared with the
radius 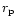 of photosphere in the outflow. If
of photosphere in the outflow. If 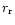 is larger than
is larger than 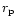 ,
the dissipation of magnetic energy
takes place mainly in the optically thin regime, and the dissipated
energy is radiated away locally. If on the other hand
,
the dissipation of magnetic energy
takes place mainly in the optically thin regime, and the dissipated
energy is radiated away locally. If on the other hand
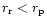 ,
the energy released from the initially ordered field
configuration increases the internal energy of the plasma. The radial
expansion of the flow converts this energy into kinetic energy of
outflow. Though this may be useful in obtaining large Lorentz factors,
it also implies that the magnetic energy left in the flow by the time
it passes through the photosphere is small if
,
the energy released from the initially ordered field
configuration increases the internal energy of the plasma. The radial
expansion of the flow converts this energy into kinetic energy of
outflow. Though this may be useful in obtaining large Lorentz factors,
it also implies that the magnetic energy left in the flow by the time
it passes through the photosphere is small if
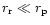 .
The net output of a magnetically driven fireball with
magnetic dissipation taking place mostly in the optically thick regime
would be essentially the same as a standard non-magnetic fireball,
with the attendant problem of a low efficiency of the production of
radiation by internal shocks.
.
The net output of a magnetically driven fireball with
magnetic dissipation taking place mostly in the optically thick regime
would be essentially the same as a standard non-magnetic fireball,
with the attendant problem of a low efficiency of the production of
radiation by internal shocks.
The photospheric radius in a steady relativistic outflow has been
derived by Abramowicz et al. (1991). Assume a total
amount of mass M is ejected with a constant Lorentz factor 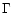 ,
at a rate
,
at a rate 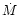 which is is constant in the time interval
which is is constant in the time interval
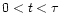 ,
(and zero outside this interval). The radius at which the
optical depth of the expanding shell reaches unity is then
,
(and zero outside this interval). The radius at which the
optical depth of the expanding shell reaches unity is then
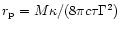 ,
where
,
where 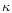 is the
opacity. This a factor
is the
opacity. This a factor 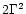 smaller than for photons
propagating through a non-moving shell. This is a consequence of the
expansion of the shell. The optical depth of a moving shell of
constant (in time) density is a Lorentz invariant, hence the same for
photons moving along the direction of the flow and those moving in the
opposite direction (assuming also that the opacity is
energy-independent). In a radial outflow, however, a photon sees a
different history of mass density depending on its direction.
smaller than for photons
propagating through a non-moving shell. This is a consequence of the
expansion of the shell. The optical depth of a moving shell of
constant (in time) density is a Lorentz invariant, hence the same for
photons moving along the direction of the flow and those moving in the
opposite direction (assuming also that the opacity is
energy-independent). In a radial outflow, however, a photon sees a
different history of mass density depending on its direction.
The result is widely used, e.g. Rees & Mészáros (1994)
and Beloborodov (2000), and is somewhat important for
the quantitative estimates below. Since its correctness is sometimes
questioned, we rederive it here in a different way from Abramowicz
et al. (1991), by working in the lab frame. Let a
photon be released at the inner edge 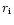 of the expanding
shell at time t=0. With the aid of a Minkowski diagram, one finds
that the photon exits at the outer edge of the shell at time
of the expanding
shell at time t=0. With the aid of a Minkowski diagram, one finds
that the photon exits at the outer edge of the shell at time
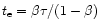 and radius
and radius
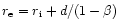 where
where
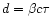 is the
shell thickness. To compute the optical depth traversed by the
photon, we note that by the assumption of a constant outflow rate the
density
is the
shell thickness. To compute the optical depth traversed by the
photon, we note that by the assumption of a constant outflow rate the
density 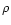 in the lab frame is only a function of r,
in the lab frame is only a function of r,
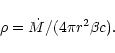 |
(64) |
If the shell were static, the optical depth per unit length would just
be
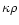 .
Since the scattering medium is flowing outward at
speed
.
Since the scattering medium is flowing outward at
speed 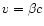 ,
the rate at which the photon overtakes its
scattering centers (per unit length or time in the lab frame) is
,
the rate at which the photon overtakes its
scattering centers (per unit length or time in the lab frame) is
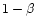 times the rate for a static shell (this is again easily seen
in a Minkowski diagram). Summing up, the optical depth traversed by
the photon is
times the rate for a static shell (this is again easily seen
in a Minkowski diagram). Summing up, the optical depth traversed by
the photon is
For very small duration 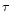 ,
this reduces to the optical depth
,
this reduces to the optical depth
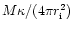 for a shell of mass M and fixed
radius
for a shell of mass M and fixed
radius 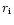 .
.
The optical depth is a decreasing function of time as the shell
expands and 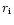 increases. Define now the photospheric
radius
increases. Define now the photospheric
radius 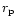 as the value of
as the value of 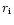 for which
for which
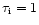 .
With
.
With
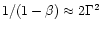 and solving
for
and solving
for 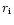 we get
we get
![\begin{displaymath}r_{\rm i} = c\tau\Gamma
\left[
\left(1+\frac{M\kappa}{4\pi (c\tau\Gamma^2)^2}\right)^{1/2}-1
\right],
\end{displaymath}](/articles/aa/full/2001/14/aah2167/img245.gif) |
(66) |
The parameter
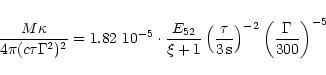 |
(67) |
is small for relevant GRB parameters. Thus we find the photospheric
radius to be
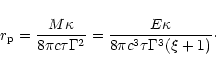 |
(68) |
Numerically,
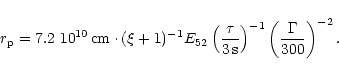 |
(69) |
As soon as the inner edge of the shell has expanded to this radius,
radiation can escape from the entire shell.
In addition to the baryons, pairs could also contribute to the
opacity. The photospheric radius (68) then does not apply,
because it includes only the constant opacity of scattering on the
electrons associated with the baryonic mass.
A general property of GRB fireball models is that the
photosphere lies well outside the region where pairs contribute to
the opacity. We summarize the argument here.
Assume a steady wind in which pairs dominate the kinetic energy flux
and the opacity, and in which the kinetic energy of the pairs is a
fraction 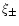 of the total luminosity
of the total luminosity 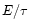 .
Let
.
Let
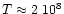 K be the temperature at the pair
photosphere (due to the steep dependence of the pair density on
temperature, this value does not depend much on conditions in the
outflow). Ignoring the opacity due to baryonic matter, the radius of
the pair photosphere
K be the temperature at the pair
photosphere (due to the steep dependence of the pair density on
temperature, this value does not depend much on conditions in the
outflow). Ignoring the opacity due to baryonic matter, the radius of
the pair photosphere 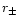 is (Usov 1994):
is (Usov 1994):
where
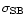 is the Stefan-Boltzmann constant and
is the Stefan-Boltzmann constant and
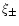 is the energy fraction in the pairs.
is the energy fraction in the pairs.
This value is much smaller than the photospheric radius (68).
Thus, for typical baryon-loaded GRB parameters pairs annihilate before
they reach the optically thin domain.
7 Discussion
Magnetic fields may well be the main agent tapping the
rotational/gravitational energy in the central engines of GRB (for
reviews see Mészáros 1999). Alternatives like the
production of pair plasma fireballs by neutrino annihilation have
turned out to have a rather small efficiency of conversion of
gravitational energy (Ruffert et al. 1997). A fireball
powered by magnetic fields ("magic hydrodynamics'') can in principle
produce  -rays in the same way as in field-free mechanisms,
namely by internal shocks in the optically thin part of the flow. A
well-known problem with the internal shock mechanism, however, is the
low efficiency of conversion to
-rays in the same way as in field-free mechanisms,
namely by internal shocks in the optically thin part of the flow. A
well-known problem with the internal shock mechanism, however, is the
low efficiency of conversion to  -rays Daigne & Mochkovitch
1998), of the order of a few percent. This is hard to
avoid, since efficient dissipation requires that a significant
fraction of the energy in the outflow is in relative motion between
parts moving at different velocities. The required large variations in
-rays Daigne & Mochkovitch
1998), of the order of a few percent. This is hard to
avoid, since efficient dissipation requires that a significant
fraction of the energy in the outflow is in relative motion between
parts moving at different velocities. The required large variations in
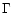 lead to dissipation close to the source, however, in the
optically thick regime. The dissipation taking place further out in
the optically thin regime is due to smaller velocity differences that
carry less energy. Ways to circumvent this limitation have been
invented (Kumar & Piran 2000; Beloborodov
2000; Lazzati et al. 1999). Even in
these schemes, however, it seems unrealistic to expect the
internal shocks to dissipate more than the external shock, hence the
conflict between observed gamma-ray fluences and actual estimations
of the energy dissipated by the external shock based on the
observations of a few afterglows remains.
lead to dissipation close to the source, however, in the
optically thick regime. The dissipation taking place further out in
the optically thin regime is due to smaller velocity differences that
carry less energy. Ways to circumvent this limitation have been
invented (Kumar & Piran 2000; Beloborodov
2000; Lazzati et al. 1999). Even in
these schemes, however, it seems unrealistic to expect the
internal shocks to dissipate more than the external shock, hence the
conflict between observed gamma-ray fluences and actual estimations
of the energy dissipated by the external shock based on the
observations of a few afterglows remains.
A magnetically powered outflow naturally carries a magnetic field with
it ("Poynting flux''). This raises the question whether dissipation of
this internal magnetic energy in the outflow can perhaps produce the
observed radiation with a better efficiency.
We have addressed this question by considering a few possible
scenarios for magnetic fields in GRB outflows. In the first, the
"passive scenario'', the magnetic field is assumed not to be
responsible at all for powering the outflow, but only advected
passively by an outflow produced by something else. We find that the
maximum field strengths possible in this case are small compared with
equipartition with the kinetic energy of the outflow, but still
potentially significant for the effective production of synchrotron
and/or inverse Compton emission in the internal shock model.
As magnetically-driven models we consider the case of a quasispherical
outflow produced by a rotating non-axisymmetric magnetic field, and
the case of a jet-like outflow along the axis of a rotating
axisymmetric field. The quasispherical case is like the models
produced for the Crab pulsar (Coroniti 1990; Gallant &
Arons 1994). It has been developed for a completely
baryon-free, pure pair-plasma outflow by Usov (1994). The
jet case is similar to magnetohydrodynamically driven wind models
(Blandford & Payne 1982; Sakurai 1985).
The magnetic field in all these cases is confined in an outward moving
shell of width  ,
where
,
where 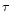 is the duration of the flow. If
internal dissipation is ignored in the outflow, the total magnetic
energy in the shell is constant, and the field strength B varies
with distance as r-1 (B and
is the duration of the flow. If
internal dissipation is ignored in the outflow, the total magnetic
energy in the shell is constant, and the field strength B varies
with distance as r-1 (B and 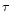 measured in the observer
frame). The configuration of the magnetic field in the shell is
different in each case (see Figs. 1-3). If the
central engine is time-dependent, for example in the form of a series
of sub-bursts, magnetic shells like this are produced by each
sub-burst, and the magnetic flux and energy in the shells is renewed
with each burst (i.e. not limited by the magnetic flux of the central
object).
measured in the observer
frame). The configuration of the magnetic field in the shell is
different in each case (see Figs. 1-3). If the
central engine is time-dependent, for example in the form of a series
of sub-bursts, magnetic shells like this are produced by each
sub-burst, and the magnetic flux and energy in the shells is renewed
with each burst (i.e. not limited by the magnetic flux of the central
object).
We find that the MHD approximation (in the sense that the electric
field in the fluid frame is small compared with the magnetic field) is
safe out to large distances from the source, of the order
1019cm or more. This is due to the relatively large amount of
baryons in the outflow compared with, say, a pulsar wind situation.
This simplifies the discussion of magnetic energy dissipation at least
conceptually, since the energy release can be studied without detailed
discussions of plasma processes (though they may enter again in the
discussion of what produces the radiation).
The field strength in a magnetically driven outflow depends on the
extent to which internal MHD processes have been able to dissipate
magnetic free energy in the flow. In the absence of such processes,
the magnetic energy density is typically of the same order as the
kinetic energy density in magnetically driven flows, and the field is
well-ordered (large scale). In the internal shock model, such fields
are sufficient to produce synchrotron and/or inverse Compton emission
in the  -ray range. The synchrotron case is favoured by a
higher efficiency during the whole course of the burst. There are now
some observational evidences that the magnetic field required for the
afterglow emission represents a small fraction of the equipartition
value whereas the prompt
-ray range. The synchrotron case is favoured by a
higher efficiency during the whole course of the burst. There are now
some observational evidences that the magnetic field required for the
afterglow emission represents a small fraction of the equipartition
value whereas the prompt  -ray emission via internal shocks is
possible only with more intense fields close to the equipartition
value (Galama et al. 1999). In the standard picture where
the afterglow is due to the forward shock propagating in the external
medium where no large scale field is present, it could mean that the
generation of a local magnetic field behind the shock wave is
inefficient. It is then possible that this locally generated field is
also very small behind internal shocks within the shell but we show
here that the large-scale field present in a magnetically driven
outflow has no difficulty in most cases to supply the strength
necessary for synchrotron and/or inverse Compton emission.
-ray emission via internal shocks is
possible only with more intense fields close to the equipartition
value (Galama et al. 1999). In the standard picture where
the afterglow is due to the forward shock propagating in the external
medium where no large scale field is present, it could mean that the
generation of a local magnetic field behind the shock wave is
inefficient. It is then possible that this locally generated field is
also very small behind internal shocks within the shell but we show
here that the large-scale field present in a magnetically driven
outflow has no difficulty in most cases to supply the strength
necessary for synchrotron and/or inverse Compton emission.
The rate of energy release through MHD processes like instabilities
and fast reconnection is governed by the Alfvén speed. In the rest
frame of the outflow, the Alfvén speed is of the order of the speed
of light if the kinetic and magnetic energy fluxes are similar. In
outflows produced by a perpendicular rotator, the magnetic field
changes sign on the small length scale 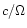 ,
and most of the
magnetic energy can be dissipated by reconnection. The typical radius
at which the energy release takes place in this case is
,
and most of the
magnetic energy can be dissipated by reconnection. The typical radius
at which the energy release takes place in this case is  1012cm for standard GRB parameters (1052erg, 3s,
1012cm for standard GRB parameters (1052erg, 3s,
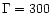 ). The photospheric radius, on the other hand, is small
(mostly because of the relativistic effect discussed by Abramowicz
et al. 1991),
). The photospheric radius, on the other hand, is small
(mostly because of the relativistic effect discussed by Abramowicz
et al. 1991),  1010cm. We can thus be
confident that dissipation of energy stored in the magnetic field of
the outflow occurs in the optically thin regime.
1010cm. We can thus be
confident that dissipation of energy stored in the magnetic field of
the outflow occurs in the optically thin regime.
In the case of an outflow produced by a purely axisymmetric rotating
magnetic object such changes of sign do not occur. Energy can still be
released by kink instabilities, but for causality reasons these are
not effective outside a narrow cone of angle  near the
rotation axis (Sect. 5). The expected amount of
magnetic dissipation in the optically thin regime is quite limited for
such an axisymmetric field. A purely axisymmetric configuration,
however, is a singular case, a priori unlikely for magnetic fields
produced in a transient object like the central engine of a GRB. In
the more likely case that a nonaxisymmetric field component is present
as well, the energy in this component can be released by reconnection
in nearly the same way as in the case of a perpendicular rotator.
near the
rotation axis (Sect. 5). The expected amount of
magnetic dissipation in the optically thin regime is quite limited for
such an axisymmetric field. A purely axisymmetric configuration,
however, is a singular case, a priori unlikely for magnetic fields
produced in a transient object like the central engine of a GRB. In
the more likely case that a nonaxisymmetric field component is present
as well, the energy in this component can be released by reconnection
in nearly the same way as in the case of a perpendicular rotator.
Magnetic energy dissipation in the optically thin regime is probably
not as simple as the shock dissipation in the internal shock model. In
particular, the way in which nonthermal electron distributions are
produced still needs to be investigated. It is likely that nonthermal
radiation is again produced, as in the internal shock model, but the
shape of the radiation spectrum may be more difficult to compute, as
well as the typical time scale of the radiative process, which should
be short compared to the expansion time scale (see (46):
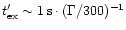 at
1013cm) to have a high radiative efficiency.
at
1013cm) to have a high radiative efficiency.
The main attraction of of GRB radiation produced by magnetic
dissipation in a magnetically driven outflow is the efficiency with
which the energy flux from the central engine can be converted into
observable radiation. This efficiency is limited only by the ratio of
Poynting flux to total energy flux in the flow. In the magnetically
driven cases considered, this ratio can be close to unity. In the
internal shock scenario, on the other hand, only a fraction
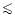 0.1
of the energy is dissipated in the optically thin region. Since the
bulk kinetic energy of the burst is dissipated in the afterglow, the
internal shock model predicts the afterglows to dominate the energy
output, which is probably inconsistent with current observations. In
magnetic dissipation models such as those discussed here, the energy
emitted in the afterglow can in principle be arbitrarily small
compared with the prompt emission. It is not yet clear, however, how
much of the magnetically dissipated energy can be in the form of
0.1
of the energy is dissipated in the optically thin region. Since the
bulk kinetic energy of the burst is dissipated in the afterglow, the
internal shock model predicts the afterglows to dominate the energy
output, which is probably inconsistent with current observations. In
magnetic dissipation models such as those discussed here, the energy
emitted in the afterglow can in principle be arbitrarily small
compared with the prompt emission. It is not yet clear, however, how
much of the magnetically dissipated energy can be in the form of
 -rays.
-rays.
-
Abramowicz, M. A., Novikov, I. D., & Paczynski, B. 1991,
ApJ, 369, 175
In the text
NASA ADS
-
Baring, M. G. 1995,
Ap&SS, 231, 169
In the text
NASA ADS
-
Bateman, G. 1980,
MHD Instabilities
(MIT Press, Cambridge) (Mass.), second edition
In the text
-
Begelman, M. C., & Li, Z.-Y. 1992,
ApJ, 397, 187
In the text
NASA ADS
-
Begelman, M. C., & Li, Z.-Y. 1994,
ApJ, 426, 269
In the text
NASA ADS
-
Beloborodov, A. M. 2000,
ApJL, 539, L25
In the text
NASA ADS
-
Berezinskii, V. S., & Prilutskii, O. F. 1987,
A&A, 175, 309
In the text
NASA ADS
- Biskamp, D. 1993, Nonlinear
magnetohydrodynamics, vol. 1 of Cambridge monographs on plasma
physics, CUP, Cambridge (Mass.)
In the text
-
Bisnovatyi-Kogan, G. S., & Ruzmaikin, A. A. 1976,
Ap&SS, 42, 401
In the text
NASA ADS
-
Blackman, E. G., & Yi, I. 1998,
ApJL, 498, L31
In the text
NASA ADS
-
Blandford, R. D., & Payne, D. G. 1982,
MNRAS, 199, 883
In the text
NASA ADS
-
Bykov, A. M., & Mészáros, P. 1996,
ApJL, 461, L37
In the text
NASA ADS
-
Camenzind, M. 1987,
A&A, 184, 341
In the text
NASA ADS
-
Coroniti, F. V. 1990,
ApJ, 349, 538
In the text
NASA ADS
-
Daigne, F., & Mochkovitch, R. 1998,
MNRAS, 296, 275
In the text
NASA ADS
-
Daigne, F., & Mochkovitch, R. 2000a,
in preparation
In the text
-
Daigne, F., & Mochkovitch, R. 2000b,
A&A, in press [astroph/0005193]
In the text
-
Daigne, F., & Mochkovitch, R. 2000c,
in 5th
Huntsville Symposium on gamma-ray bursts, ed. M. Kippen, R. Mallozzi, & G. Fishman, AIP
In the text
-
Galama, T. J., Briggs, M. S., Wijers, R. A. M., et al. 1999,
Nature, 398, 394
In the text
NASA ADS
-
Gallant, Y. A., & Arons, J. 1994,
ApJ, 435, 230
In the text
NASA ADS
-
Galsgaard, K., & Nordlund, Å. 1996,
JGR, 101, 13445
In the text
-
Galsgaard, K., & Nordlund, Å. 1997,
JGR, 102, 231
In the text
NASA ADS
-
Goodman, J. 1986,
ApJL, 308, L47
In the text
NASA ADS
-
Goodman, J., Dar, A., & Nussinov, S. 1987,
ApJL, 314, L7
In the text
NASA ADS
-
Jackson, J. D. 1999,
Classical electrodynmics
(Wiley, New York), third edition
In the text
-
Katz, J. I. 1994,
ApJL, 432, L107
In the text
NASA ADS
-
Kennel, C. F., & Coroniti, F. V. 1984,
ApJ, 283, 694
In the text
NASA ADS
-
Kluzniak, W., & Ruderman, M. 1998,
ApJL, 505, L113
In the text
NASA ADS
-
Kobayashi, S., Piran, T., & Sari, R. 1997,
ApJ, 490, 92
In the text
NASA ADS
-
Königl, A., & Choudhuri, A. R. 1985,
ApJ, 289, 173
(Erratum: ApJ, 305, 954)
In the text
NASA ADS
-
Kumar, P., & Piran, T. 2000
[astro-ph/9907096]
In the text
-
Lazzati, D., Ghisellini, G., & Celotti, A. 1999,
MNRAS, 309, L13
In the text
NASA ADS
-
Lucek, S. G., & Bell, A. R. 1996,
MNRAS, 281, 245
In the text
NASA ADS
-
Lucek, S. G., & Bell, A. R. 1997,
MNRAS, 290, 327
In the text
NASA ADS
-
Medvedev, M. V., & Loeb, A. 1999,
ApJ, 526, 697
In the text
NASA ADS
-
Melatos, A., & Melrose, D. B. 1996,
MNRAS, 279, 1168
In the text
NASA ADS
-
Mészáros, P. 1999
[astro-ph/9912546]
In the text
-
Mészáros, P., Laguna, P., & Rees, M. J. 1993,
ApJ, 415, 181
In the text
NASA ADS
-
Mészáros, P., & Rees, M. J. 1992,
MNRAS, 257, 29
In the text
-
Mészáros, P., & Rees, M. J. 1993,
ApJL, 418, L59
In the text
NASA ADS
-
Mészáros, P., & Rees, M. J. 1997,
ApJL, 482, L29
In the text
NASA ADS
-
Michel, F. C. 1969, ApJ, 158, 727
In the text
NASA ADS
-
Narayan, R., Paczynski, B., & Piran, T. 1992,
ApJL, 395, L83
In the text
NASA ADS
-
Paczynski, B. 1986,
ApJL, 308, L43
In the text
NASA ADS
-
Paczynski, B. 1998,
ApJL, 494, L45
In the text
NASA ADS
-
Panaitescu, A., & Mészáros, P. 1999,
ApJ, submitted
In the text
-
Papathanassiou, H., & Mészáros, P. 1996,
ApJL, 471, L91
In the text
NASA ADS
-
Rees, M. J., & Mészáros, P. 1994,
ApJL, 430, L93
In the text
NASA ADS
-
Rhoads, J. E., & Paczynski, B. 1993,
Am. Astron. Soci. Meeti., 183, 0417
In the text
NASA ADS
-
Ruffert, M., Janka, H.-T., Takahashi, K., & Schäfer, G. 1997,
A&A, 319, 122
In the text
NASA ADS
-
Sakurai, T. 1985,
A&A, 152, 121
In the text
NASA ADS
-
Sari, R., & Piran, T. 1997,
MNRAS, 287, 110
In the text
NASA ADS
-
Spruit, H. C. 1999,
A&A, 341, L1
In the text
NASA ADS
-
Tavani, M. 1996,
ApJ, 466, 768
In the text
NASA ADS
-
Thompson, C. A. 1994,
MNRAS, 270, 480
In the text
NASA ADS
-
Thompson, C. A., & Madau, P. 2000,
ApJ, in press [astro-ph/9909111]
In the text
-
Usov, V. V. 1992,
Nature, 357, 472
In the text
NASA ADS
-
Usov, V. V. 1994,
MNRAS, 267, 1035
In the text
NASA ADS
-
Wijers, R. A. M. J., Rees, M. J., & Mészáros, P. 1997,
MNRAS, 288, L51
In the text
NASA ADS
-
Woosley, S. E. 1993,
ApJ, 405, 273
In the text
NASA ADS
Copyright ESO 2001
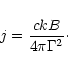
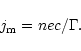
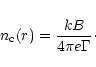
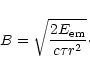
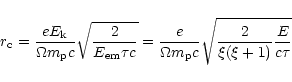
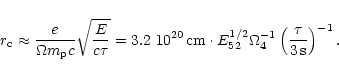
![\begin{figure}
\hfill\includegraphics[width=0.17\hsize]{H2167F1.eps}\hfill
\in...
...fill
\includegraphics[width=0.50\hsize]{H2167F4.eps}\hfill\mbox{}
\end{figure}](/articles/aa/full/2001/14/aah2167/Timg39.gif)
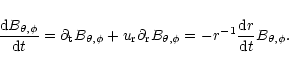
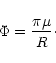
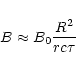
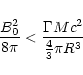
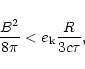
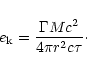
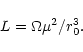
![\begin{figure}
\parbox[c]{0.5\hsize}{
\includegraphics[width=\hsize]{H2167F5.e...
....eps}\\ [1ex]
\includegraphics[width=\hsize]{H2167F7.eps}
\par }
\end{figure}](/articles/aa/full/2001/14/aah2167/Timg78.gif)
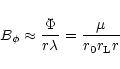
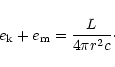
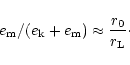
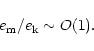
![\begin{figure}
\includegraphics[height=6.5cm]{H2167F8.eps}\hfill
\includegraphics[height=6.5cm]{H2167F9.eps} \end{figure}](/articles/aa/full/2001/14/aah2167/Timg100.gif)
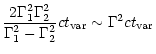
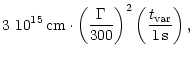
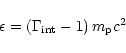
![\begin{displaymath}\Gamma_{\rm int} =
\frac{1}{2}\left[\sqrt{\frac{\Gamma_1}{\Gamma_2}}
+\sqrt{\frac{\Gamma_2}{\Gamma_1}}\right].
\end{displaymath}](/articles/aa/full/2001/14/aah2167/img111.gif)
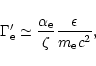
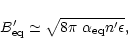
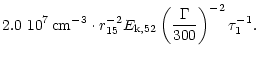
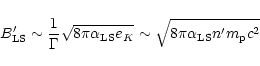
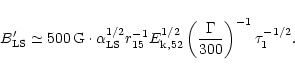
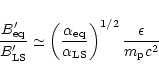
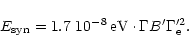
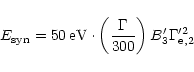
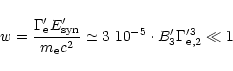
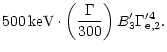
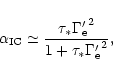
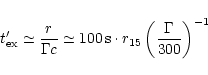
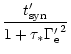
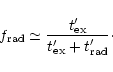
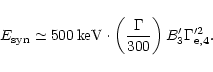
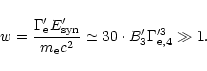
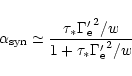
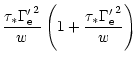
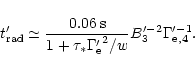
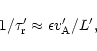

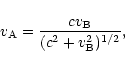
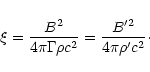
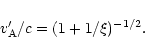
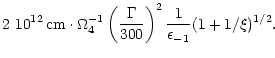
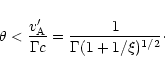
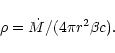
![\begin{displaymath}r_{\rm i} = c\tau\Gamma
\left[
\left(1+\frac{M\kappa}{4\pi (c\tau\Gamma^2)^2}\right)^{1/2}-1
\right],
\end{displaymath}](/articles/aa/full/2001/14/aah2167/img245.gif)