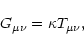A&A 369, 690-693 (2001)
DOI: 10.1051/0004-6361:20010089

Dyadosphere bending of light

V. A. De Lorenci1 - N. Figueiredo1 - H. H. Fliche2 - M. Novello3


1 - Instituto de Ciências, Escola Federal de Engenharia de Itajubá, Av. BPS 1303 Pinheirinho, 37500-903 Itajubá, MG, Brazil
2 - Université Aix-Marseille III, Laboratoire de Modélisation en Mécanique et Thermodynamique, UPRES EA 2596, Case 322, Avenue Escadrille Normandie-Niemen, 13397 Marseille Cedex 20, France
3 - Centro Brasileiro de Pesquisas Físicas, Rua Dr. Xavier Sigaud 150 Urca, 22290-180 Rio de Janeiro, RJ, Brazil

Received 4 November 1999 / Accepted 5 December 2000

Abstract
In the context of the static and spherically symmetric solution of a charged compact object, we present the expression for the bending of light in the region just outside the event horizon - the dyadosphere - where vacuum polarization effects are taken into account.

Key words: Black-hole physics - gravitational lensing - relativity


1 Introduction

The magnitude of the velocity of light described by effective nonlinear electromagnetic theories depends on the field dynamics. Such dependence implies an effective modification of the flat background metric into a curved one, which is accentuated when gravity processes are taken into account. The most famous examples of these aspects are the well known implications of QED in curved spacetimes. The weak field limit of the complete one loop QED is known as the Euler-Heisenberg Lagrangian (Heisenberg & Euler 1936; Schwinger 1951) which yields several important results such as, the phenomenon of birefringence (Birula & Birula 1970; Adler 1971; De Lorenci et al. 2000), which describes the distinct velocity of light propagation for each polarization direction. There are many works dealing with the applications of nonlinear electrodynamics, especially, concerning its coupling with a gravitational field. In this context, Drummond & Hathrell (1980) showed the possibility of superluminal velocities in certain spacetime configurations. Other interesting cases can be found in Novello et al. (1989); Daniels & Shore (1994), Latorre et al. (1995) and Shore (1996).

Recently, Ruffini (1998) and also Preparata et al. (1998) called our attention to a special region just outside the horizon of charged black holes where the electric field goes beyond its classical limit, implying a situation where effects of vacuum fluctuations should be considered. They called such region the dyadosphere. Assuming the existence of such a region, we could consider the possible consequences for the trajectories of light rays that cross it. In this work, we analyze the consequences for the phenomenon of light bending when vacuum fluctuation effects are taken into account. Under such conditions, the paths of light do not follow the usual geodesic of the gravitational field, so it is necessary to consider the effects of the modified QED vacuum (Drummond & Hathrell 1980; Dittrich & Gies 1998; De Lorenci et al. 2000; Novello et al. 2000).

In Sect. 2 we perform the coupling between nonlinear electrodynamics and gravity. We calculate the correction for the Reissner-Nordstron metric from the first contribution of the weak field limit of one loop QED. In Sect. 3 we present the light cone conditions for the case of wave propagation in the Reissner-Nordstron spacetime modified by QED vacuum polarization effects - the dyadosphere region. Finally, in Sect. 4, we derive the field equations for such a situation and evaluate its contribution to the bending of light. Some comments on lensing effects are presented in the Appendix.

   
2 The minimal coupling between gravitation and non-linear electrodynamics

The Einstein gravitational field equation is given by

 \begin{displaymath}G_{\mu\nu} = \kappa T_{\mu\nu}, \end{displaymath} (1)

where $\kappa$ is written in terms of the Newtonian constant G and light velocity c as $\kappa = 8 \pi G /c^4$.

Let us consider a class of theories defined by the general Lagrangian L = L(F), where $F = F^{\mu\nu}F_{\mu\nu}$. The corresponding energy momentum tensor has the form

 \begin{displaymath}T_{\mu\nu} = -Lg_{\mu\nu} + 4L_{F}F_{\mu\alpha}F_{\nu}\mbox{}^{\alpha} \end{displaymath} (2)

where LF denotes the derivative of L with respect to F. By considering minimal coupling of gravity to nonlinear electrodynamics, we obtain the following equations of motion, besides Einstein Eq. (1),
  
$\displaystyle {\left(L_F F^{\mu\nu}\right)_{\parallel\nu} = 0}$ (3)
$\displaystyle {\raisebox{.2ex}{$\stackrel{*}{F}$ }{}^{\mu\nu}{}_{\parallel\nu} = 0}$ (4)

where double bar ( ${\scriptstyle \parallel}$) represents the covariant derivative with respect to the curved background $g_{\mu\nu}$, and $\raisebox{.2ex}{$\stackrel{*}{F}$ }{}_{\mu\nu}$ is the dual electromagnetic tensor. For the static and spherically symmetric solution, the geometry is

 \begin{displaymath}{\rm d}s^2 = A(r){\rm d}t^2 - A(r)^{-1}{\rm d}r^2 -r^2{\rm d}\theta^2 - r^2\sin^2\theta {\rm d}\varphi^2 \end{displaymath} (5)

where A(r) is determined by the field equations. We set the only non zero component of the electromagnetic tensor to be F01 = f(r). Thus, the combined system of electromagnetism and gravity, Eqs. (1), (3) and (4), reduces to the set
  
$\displaystyle {r\frac{\partial A(r)}{\partial r} + A(r) = 1+\kappa\left[ r^2 L +4r^2 L_F f(r)^2\right]}$ (6)
$\displaystyle {L_F f(r) = - \frac{Q}{4r^2}\cdot}$ (7)

We are interested in the analysis of the weak field limit of the complete one-loop approximation of QED, given by the effective Lagrangian (Heisenberg & Euler 1936; Schwinger 1951)
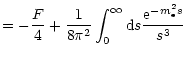
  $\textstyle {\cal L}$ $\displaystyle = -\frac{F}{4} + \frac{1}{8\pi^2}\int_{0}^{\infty} {\rm d}s \frac{{\rm e}^{-m_{\rm e}^2 s}}{s^3}$ $\displaystyle \left[\frac{e^2s^2G}{4} \frac{{\rm Re}\cosh\sqrt{2e^2s^2(F + i G)}} {{\rm Im}\cosh\sqrt{2e^2s^2(F + i G)}} - \frac{2e^2s^2F}{12} -1\right]$ (8)

where $G \doteq \raisebox{.2ex}{$\stackrel{*}{F}$ }{}_{\mu\nu}F^{\mu\nu}$. In the limit of low frequency $\nu \ll m_{\rm e}c^2/h$ one obtains the Euler-Heisenberg Lagrangian

 \begin{displaymath}L = -\frac{1}{4}F + \frac{\mu}{4}\left(F^2 + \frac{7}{4} G^2\right) \end{displaymath} (9)

with

 \begin{displaymath}\mu \doteq \frac{2\alpha^2}{45 m_{\rm e}^4}\cdot \end{displaymath} (10)

Since we only consider the electric component of $F_{\mu\nu}$there is no contribution due to the invariant G. Using Lagrangian (9), the integration of Eq. (6) is

 \begin{displaymath}A(r) = 1 - \frac{2m}{r} - \frac{\kappa}{r}\int^r {\rm d}r \left[\frac{r^2f(r)^2}{2} +3 \mu r^2 f(r)^4\right] \end{displaymath} (11)

where, in order to set the value of the first constant of integration, we have assumed the Schwarzschild solution in the limit of vanishing charge. Calculating the function f(r) from Eq. (7) in the appropriate order of approximation ${\cal O}(\mu)$, one gets

 \begin{displaymath}f(r) = \frac{Q}{r^2} -4\mu \frac{Q^3}{r^6}\cdot \end{displaymath} (12)

Introducing this result in Eq. (11) we finally obtain the expression for A(r):

 \begin{displaymath}A(r) = 1 - \frac{2m}{r} + \frac{\kappa Q^2}{2r^2} - \frac{\kappa \mu Q^4}{5 r^6}\cdot \end{displaymath} (13)

The Reissner-Nordstron case arises from this solution for the limit case $\mu = 0$. Equations (5) and (13) yield the correct form of the spacetime geometry taking into account the one-loop QED in the first order of approximation.

Since (13) is an approximation, it cannot be applied to the cases for which $1/r^6 \sim 1/r^2$. Thus the contribution of the last term in this equation is negligible for two reasons: $\mu$ is very small and $1/r^6 \ll 1/r^2$.

In the next sections, however, it is shown that, due to the non-linearity of the electrodynamics in the dyadosphere, there will be an additional correction which is comparable to the Reissner-Nordstron factor in terms of the radial variable.

One might want to investigate the effect of this metric on the gravitational lensing of light propagating in the vicinity of a charged compact object. In the Appendix we apply the formalism developed by Frittelli et al. (2000) to the background spacetime defined by Eq. (5).

   
3 Light cone condition

In the case of nonlinear electrodynamics, e.g., Euler-Heisenberg effective theory, the wave propagation will suffer a correction due to vacuum polarization effects. Such correction is usually presented in terms of a light cone condition, which in our case, is given by

 \begin{displaymath}k^\alpha k^\beta g_{\alpha\beta} = -4\frac{L_{FF}}{L_F}F^{\mu\alpha}F^{\nu} {}_{\alpha}k_{\mu}k_{\nu}. \end{displaymath} (14)

It is worth mentioning that there will be two different modes of propagation, one for each polarization direction (De Lorenci et al. 2000). Here we will deal only with the mode present in Eq. (14).

Condition (14) can be presented in a more appealing form as a slight modification of the background geometry

 \begin{displaymath}\left(g^{\mu\nu} + 4\frac{L_{FF}}{L_F}F^{\mu\alpha} F^{\nu}{}_{\alpha}\right) k_{\mu}k_{\nu} = 0. \end{displaymath} (15)

This property allows us to introduce the concept of an effective geometry (Novello et al. 2000) such that

 \begin{displaymath}\tilde{g}^{\mu\nu} = g^{\mu\nu} + 4\frac{L_{FF}}{L_F}F^{\mu\alpha} F^{\nu}{}_{\alpha} \end{displaymath} (16)

for which $k_{\mu}$ is a null vector. Hence, we can use the previous method to derive the bending of light in the presence of vacuum polarization effects due to nonlinear electrodynamics. Using such a definition, $k_{\mu}$ is a null vector in the effective geometry. It can be shown that the integral curves of the vector $k_\nu$ are geodesics. In order to accomplish this, an underlying Riemannian structure for the manifold associated with the effective geometry will be required. In other words, this implies a set of Levi-Civita connection coefficients $\tilde{\Gamma}^\alpha\mbox{}_{\mu\nu}= \tilde{\Gamma}^\alpha\mbox{}_{\nu\mu}$, by means of which there exists a covariant differential operator (the covariant derivative), which we denote by a semi-colon, such that

 \begin{displaymath} \tilde{g}^{\mu\nu}\mbox{}_{;\,\lambda} \equiv \tilde{g}^{\mu... ...lde{\Gamma}^\nu\mbox{}_{\sigma\lambda}\tilde{g}^{\sigma\mu}=0. \end{displaymath} (17)

From (17) it follows that the effective connection coefficients are completely determined from the effective geometry by the usual Christoffel formula.

Contraction of Eq. (17) with $k_\mu k_\nu$ results

 \begin{displaymath} k_\mu k_\nu \tilde{g}^{\mu\nu}\mbox{}_{,\,\lambda} = -2k_\mu... ...ilde{\Gamma}^\mu\mbox{}_{\sigma\lambda} \tilde{g}^{\sigma\nu}. \end{displaymath} (18)

Differentiating $\tilde{g}^{\mu\nu}k_\mu k_\nu = 0$, we have

 \begin{displaymath} 2k_{\mu,\,\lambda}k_\nu \tilde{g}^{\mu\nu} + k_\mu k_\nu \tilde{g}^{\mu\nu}\mbox{}_{,\,\lambda} = 0. \end{displaymath} (19)

From these expressions we obtain

 \begin{displaymath} \tilde{g}^{\mu\nu}k_{\mu;\,\lambda}k_\nu = 0. \end{displaymath} (20)

Since the propagation vector $k_\mu=\Sigma_{,\,\mu}$is a gradient, one can write $k_{\mu;\,\lambda}=k_{\lambda;\,\mu}$. Thus, Eq. (20) reads

 \begin{displaymath} \tilde{g}^{\mu\nu}k_{\lambda;\,\mu}k_\nu = 0 \end{displaymath} (21)

which states that $k_{\mu}$ is a geodesic vector. Since it is also a null vector in the effective geometry $\tilde{g}^{\mu\nu}$, it follows that its integral curves are therefore null geodesics.

   
4 The influence of QED on the trajectory of light

Taking the Lagrangian (9), and setting the only non-zero component of electromagnetic tensor to be F01 = f(r), it follows that

   
F = -2 f(r)2 (22)
$\displaystyle {L_F = -\frac{1}{4} - \mu f(r)^2}$ (23)
$\displaystyle {L_{FF} = \frac{\mu}{2}\cdot}$ (24)

Since we are analyzing the spherically symmetric and static solution of a charged compact object, we set the components of the background metric to be the same as the ones presented in Eq. (5). Thus, the non-vanishing components of the effective metric $\tilde{g}^{\mu\nu}$, up to terms quadratic on the constant $\mu$, are
    
$\displaystyle \tilde{g}^{00}$ = $\displaystyle A(r)^{-1}[1 + 8\mu f(r)^2]$ (25)
$\displaystyle \tilde{g}^{11}$ = $\displaystyle -A(r)[1 + 8\mu f(r)^2]$ (26)
$\displaystyle \tilde{g}^{22}$ = g22 (27)
$\displaystyle \tilde{g}^{33}$ = g33 (28)

where A(r) is given by (13). In what follows we will consider only the stronger term arising from quantum corrections. All other terms will be neglected. The function f(r) is calculated from the equations of the electromagnetic field, and its value is set by Eq. (12). Using these results we obtain the line element:
 
$\displaystyle {\rm d}\tilde{s}^2$=$\displaystyle \left[1-8\mu f(r)^2\right]\left[ A(r){\rm d}t^2 - A(r)^{-1}{\rm d}r^2\right]$$\displaystyle -r^2{\rm d}\theta^2 - r^2\sin^2\theta {\rm d}\varphi^2.$ (29)

From the variational principle, the following equations of motion are obtained:
   
$\displaystyle {\left[1-8\mu f(r)^2\right]A(r)\dot{t} = {\rm constant} \doteq h_0}$ (30)
$\displaystyle {r^2\dot{\varphi} = {\rm constant} \doteq l_0}$ (31)
$\displaystyle {\dot{r}^2 = \frac{h_0^2}{\left[1-8\mu f(r)^2\right]^2} - \frac{l_0^2A(r)}{r^2\left[1-8\mu f(r)^2\right]}\cdot}$ (32)

In these equations dots mean derivatives with respect to parameter $\tilde{s}$, and we have adjusted the initial conditions $\theta = \pi /2$ and $\dot{\theta} = 0$. Performing the change of variable r=1/v and expressing the derivatives with respect to the angular variable $\varphi$ we obtain from (30)-(32):

 \begin{displaymath}{v'}^2 = \frac{h_0^2}{l_0^2}\frac{1}{[1-8\mu f(r)^2]^2} - \frac{A(r)v^2}{1-8\mu f(r)^2} \end{displaymath} (33)

where $v'= {\rm d}v / {\rm d}\varphi$. In the required order of approximation, functions A(v) and f(v) are given by
  
f(v) = Q v2 (34)
A(v) = $\displaystyle 1 - 2mv + \frac{\kappa Q^2 v^2}{2} - \frac{\kappa \mu Q^4 v^6}{5}\cdot$ (35)

Thus, taking the derivative of Eq. (33) and using the above results, it follows that

 \begin{displaymath}v'' + v = 3mv^2 -\left(1 - 32 \frac{\mu h_0^2} {\kappa l_0^2}Q \right)\kappa Q^2 v^3 + {\cal O}(\mu^2,v^4). \end{displaymath} (36)

This shows that the contribution coming from QED is of the same order of magnitude as the classical Reissner-Nordstron charge term. One should notice that Eq. (36) could also be derived using the formalism developed by Virbhadra et al. (1998).

5 Conclusion

In this work we investigate the bending of light in the dyadosphere, a region just outside an event horizon of a non-rotating charged black hole, in which the electromagnetic field exceeds the critical value predicted by Heisenberg and Euler. In such region the propagation of light is affected not only by the gravitational field, but also by the modified QED vacuum. We show that by considering effects due to QED, the modified metric in the first order of approximation is given by Eq. (29).

We also show that the contribution from this effect appears in a significative order in terms of the radial variable. Indeed, it is of the same order of the charged term that arises from Reissner-Nordstron solution. Equation (36) shows that the correction term depends on both the ratio h0/l0 and the charge Q. Thus, for photons with the same frequency propagating in the dyadosphere, the effect will be stronger for those whose trajectory is closer to the center of attraction.

Since we obtained a contribution coming from QED of the same order of magnitude as the classical Reissner-Nordstrom charge term, an interesting extension of this work could be studying gravitational lensing effects for the metric presented in Eq. (29). It is also worth analysing the effects arising from the magnetic field due to the rotation of a charged compact object.

Acknowledgements
This work was partially supported by Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq), Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES) and Comité Français d'Évaluation de la Coopération Universitaire avec le Brésil (COFECUB).

   
Appendix A: Comments on lensing effect

Some interesting references about the lensing effect can be found in Virbhadra et al. (1998), Kling & Newman (1999), Frittelli et al. (2000) and Kling et al. (1999). Kling & Newman (1999), for instance, investigated aspects of light cones in the Schwarzschild geometry, making connections to gravitational lensing theory and to the so-called "null surface formulation''. Later Frittelli et al. (2000) proposed a definition of an exact lens equation without reference to a background spacetime and developed a formalism, which is then applied to the Schwarzschild solution.

Following this formalism, the exact gravitational lens equation in the framework of the metric (5) is given by


 
$\displaystyle \Theta(l,l_0,l_{\rm p})=\pm \left[\pi-2 \int_{l_0}^{l_{\rm p}}\frac{{\rm d}l}{\sqrt{l_{\rm p}^2 A(l_{\rm p})-l^2 A(l)}}\right.$$\displaystyle -\left. \int_{l}^{l_0}\frac{{\rm d}l'}{\sqrt{l_{\rm p}^2 A(l_{\rm p})-{l'}^2 A(l')}}\right].$ (A.1)

In the above equation, $\Theta(l,\,l_0,\,l_{\rm p})$ is the angular position of the source with respect to the direction defined by the observer and the lensing object (the optical axis) and $l = 1/\sqrt{2}r$ is the inverse radial distance. It follows that $l_0 = 1/\sqrt{2}r_0$ and $l_{\rm p} = 1/\sqrt{2}r_{\rm p}$, where r0 and $r_{\rm p}$ are, respectively, the position of the observer and the minimum distance between the light path and the lens. As usual, the origin of the coordinate system is the position of the lens.

A generic point in the light path is given in spherical coordinates by

 \begin{displaymath}\cos\theta=-\cos\theta_0\cos\Theta +\sin\theta_0\sin\Theta\cos\gamma \end{displaymath} (A.2)


 
$\displaystyle \tan\varphi=\frac{\sin\varphi_0 \sin\theta_0 - \tan\Theta(\cos\va... ...\tan\Theta(\sin\varphi_0\sin\gamma + \cos\varphi_0\cos\gamma\cos\theta_0)}\cdot$ (A.3)

The coordinate $\gamma$ is the azimuthal angle of the light path with respect to the optical axis and the observer is located at $(\varphi_0,\theta_0)$.

Applying Eq. (A.1) to the function A(r)derived in (13) it follows that there is no significant contribution from QED to the lensing effect for the same reasons discussed at the end of Sect. 2.

References

 

Copyright ESO 2001