F. Kemper¹ - L. B. F. M. Waters^1,2 - A. de Koter¹ - A. G. G. M. Tielens^3,4

1 - Astronomical Institute "Anton Pannekoek'', University of Amsterdam, Kruislaan 403, 1098 SJ Amsterdam, The Netherlands
2 - Instituut voor Sterrenkunde, Katholieke Universiteit Leuven, Celestijnenlaan 200B, 3001 Heverlee, Belgium
3 - SRON Laboratory for Space Research, PO Box 800, 9700 AV Groningen, The Netherlands
4 - Kapteijn Institute, University of Groningen, PO Box 800, 9700 AV Groningen, The Netherlands

Abstract
Infrared Space Observatory (ISO) observations have shown that O-rich Asymptotic Giant Branch (AGB) stars exhibit crystalline silicate features in their spectra only if their mass-loss rate is higher than a certain threshold value. Usually, this is interpreted as evidence that crystalline silicates are not present in the dust shells of low mass-loss rate objects. In this study, radiative transfer calculations have been performed to search for an alternative explanation to the lack of crystalline silicate features in the spectrum of low mass-loss rate AGB stars. It is shown that due to a temperature difference between amorphous and crystalline silicates it is possible to include up to 40% of crystalline silicate material in the circumstellar dust shell, without the spectra showing the characteristic spectral features. Since this implies that low mass-loss rate AGB stars might also form crystalline silicates and deposit them into the Interstellar Medium (ISM), the described observational selection effect may put the process of dust formation around AGB stars and the composition of the predominantly amorphous dust in the Interstellar Medium in a different light. Our model calculations result in a diagnostic tool to determine the crystallinity of an AGB star with a known mass-loss rate.

Key words: stars: AGB and post-AGB - circumstellar matter - dust, extinction - infrared: stars - radiative transfer

1 Introduction

Oxygen-rich Asymptotic Giant Branch (AGB) stars are M-type stars of intermediate mass ( $1~M_{\odot} < M < 8~M_{\odot}$ ) in the late stages of stellar evolution, which exhibit He- and H-shell burning (for a review on AGB stars, see Habing 1996, and references herein). These stars undergo an increasing mass loss while they evolve along the AGB; the stars with low mass-loss rates ( $\sim$ 10 $^{-8}-\sim$ 10^-6 $M_{\odot }$ yr^-1) are referred to as Miras, whereas the stars with high mass-loss rates ( $\sim$ 10 $^{-5}-\sim$ 10^-3 $M_{\odot }$ yr^-1) are the so-called OH/IR stars. In the cooling outflow dust formation occurs, which adds an infrared excess to the Spectral Energy Distribution (SED). In case of Miras, the dust shell is optically thin, and the underlying stellar spectrum is still visible, but the optically thick dust shell of OH/IR stars completely obscures the stellar spectrum, making these objects only detectable at infrared wavelengths (Bedijn 1987; van der Veen & Habing 1988).

Important reasons for studying the nature of dust in AGB stars can be found in the fact that these stars are the main contributors of dust into the interstellar medium. The properties of the dust in the ISM can thus be directly compared to the dust properties in shells around evolved stars. This will provide information on the processing of the dust in the ISM and will improve our insight into the life cycle of dust. Moreover, studying the condensation of dust in the outflows of AGB stars will provide useful diagnostics for the determination of the physical conditions in these outflows, thus increasing our understanding of this important stage of stellar evolution.

Most AGB stars exhibit an oxygen-rich chemistry, i.e. a number ratio C/O < 1, in their dust shells, which gives rise to the condensation of oxygen-rich dust species. Based on early infrared observations, the presence of silicate species has been proposed by several authors (e.g. Gilman 1969; Jones & Merrill 1976). Pre-ISO studies almost exclusively pointed toward the presence of amorphous Fe-bearing silicates; such dust shells are for example studied by Butchart & Whittet (1983); Pegourie & Papoular (1985) and Bedijn (1987). Infrared spectroscopy performed with the Infrared Space Observatory (Kessler et al. 1996) revealed the presence of crystalline silicates next to the amorphous silicate dust in the circumstellar dust shells of some evolved stars (Waters et al. 1996). In addition, the observed wavelengths of the emission bands of the crystalline silicates in evolved stars suggest that these grains contain little or no Fe, but are very Mg-rich (Molster et al. 1999). The data are consistent with no Fe in the grains. There seems to be a correlation between the peak of the SED, i.e. the optical depth toward the central star, and the presence of spectral features of crystalline olivine (forsterite, Mg₂SiO₄) and crystalline pyroxene (enstatite, MgSiO₃) (Waters et al. 1996; Cami et al. 1998; Sylvester et al. 1999), in the sense that this material is not seen in stars that are not obscured. This is usually interpreted as evidence that crystalline silicates are not present in the dust shells around low mass-loss rate AGB stars, which have an optically thin dust shell. Apparently, a threshold value for the mass-loss rate $\dot{M}$ is required to enable the condensation of crystalline silicate in the stellar outflows. This critical density would thus put constraints on the dust condensation sequence. Various explanations have been offered for this threshold density (Tielens et al. 1998; Gail & Sedlmayr 1999; Sogawa & Kozasa 1999). Yet, its existence is not well established.

In this study, we will evaluate the existence of the threshold value for the mass-loss rate below which crystalline silicates are not detected. Does the lack of crystalline silicate features in the SED of Miras really imply that the crystalline silicates are not present, or is some other effect at work suppressing the characteristic narrow features? We will study this issue by calculating a grid of detailed model spectra of circumstellar dust shells for a wide range of mass loss and degree of crystallinity.

In Sect. 2 the model for the circumstellar dust shell will be described, including the applied optical constants for the silicates. In Sect. 3 the results will be discussed for varying mass-loss rate and degree of crystallinity. Section 4 contains the physical explanation of the obtained results and highlights possible implications for the evolution of dust. A summary of this study is given in Sect. 5.

2 Modelling the circumstellar dust shell

The dust radiative transfer program MODUST (de Koter et al., in prep.) has been used to calculate detailed spectra of circumstellar dust shells. The code solves the transfer equations subject to the constraint of radiative equilibrium, fixing the temperature distribution of the dust grains. The solution technique focuses on the combined moment form of the transfer equation, such that the scattering term in the source function can be solved for explicitly, updating the Eddington factors throughout the lambda iteration by means of a ray-by-ray formal solution.

In the mode used in this paper, the dust is assumed to be distributed in a spherical shell with a radial density profile $\rho \propto r^{-2}$ , i.e. that of a time-independent stellar wind outflow at constant velocity

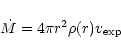
The models in this study cover a wide range in mass-loss rates and degree of crystallinity. The mass-loss rate is varied from 5 10^-8 to 10^-4 $M_{\odot }$ yr^-1. The crystallinity x, defined as

2.1 Dust optical constants

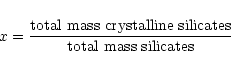
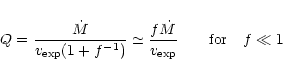
Previous studies of the SED of dust shells surrounding AGB stars (Bedijn 1987; Justtanont & Tielens 1992; Le Sidaner & Le Bertre 1993; Le Sidaner & Le Bertre 1996) used so-called astronomical or dirty silicates, of which the optical constants were observationally determined (Jones & Merrill 1976; Draine & Lee 1984). The chemical composition of astronomical silicate is not known, although likely the extra absorption is due to the presence of iron in the form of Fe²⁺ in the mineral (Schutte & Tielens 1989).

$\begin{figure*} \par\resizebox{10.8cm}{!}{\includegraphics{H2487F1.eps}} \hfill \parbox[b]{55mm}{ } \end{figure*}$

Figure 1: Fluxes calculated for a completely amorphous dust shell, i.e. x = 0, for a wide range of mass-loss rates, calculated for $v_{{\rm exp}} = 20$ kms^-1 and f = 0.01. In each panel, the mass-loss rate $\dot{M}$ ( $M_{\odot }$ yr^-1) is indicated. The spectra are normalised on the maximum value in the 2-100 $\mu$ m wavelength region. Around 10 and 20 $\mu$ m broad features due to amorphous silicates are present in the spectra, occurring either in emission or absorption, depending on $\dot{M}$ (see text). Note that in case of optically thin dust shells (low $\dot{M}$ ) the stellar spectrum with its characteristic molecular absorption bands is still visible at $\lambda < 8$ $\mu$ m, whereas for the optically thick case (high $\dot{M}$ ), the stellar flux at NIR wavelengths is completely absorbed by the dust

Open with DEXTER

In the last few years, accurate laboratory measurements of the optical constants of amorphous silicates (Dorschner et al. 1995) and crystalline silicates (Koike et al. 1993; Koike & Shibai 1998; Jäger et al. 1998) have become available. Together with the high spectral resolution of the ISO Short Wavelength Spectrometer (SWS) (de Graauw et al. 1996) and Long Wavelength Spectrometer (LWS) (Clegg et al. 1996) this opens the possibility to determine the dust composition in great detail, at least in principle. However, model calculations have shown that the SED can not be fitted using only the optical constants of amorphous and crystalline silicates. An additional source of opacity in the NIR appears to be missing (Kemper et al., in prep.). This is a well-known problem which dates back to Jones & Merrill (1976); Bedijn (1987) and Schutte & Tielens (1989). Although it is a fundamental issue, for the present study it suffices to use the optical constants of the amorphous silicates calculated from the observed spectra of AGB stars (Suh 1999). The thus obtained optical constants of the AGB silicate cannot provide information on the exact composition of the amorphous component of the dust shell, however for our studies of the appearance and strength of the crystalline silicate features, the use of the "Suh-silicate'' will not affect our results. As the peak position of the crystalline features in laboratory samples is strongly dependent on the Fe-content, ISO observations of AGB and post-AGB stars demonstrate that the dust shells only contain Mg-rich crystalline silicates (Molster et al. 1999; Sylvester et al. 1999). For these crystalline silicates, we used optical constants of two different types: forsterite (Mg₂SiO₄) and enstatite (MgSiO₃) (Jäger et al. 1998). It is important to realize that because of the low Fe-content, their absorptivity in the Near Infrared (NIR) is very low. Equal mass fractions of both crystalline species have been used, unless stated otherwise.

3 Model results

Here we present the model results for increasing mass-loss rates (Sect. 3.1) and increasing degree of crystallinity (Sect. 3.2). In Sect. 3.3 the observational constraints of ISO will be taken into account and applied to the model spectra.

3.1 Varying the mass-loss rate

$\begin{figure} \resizebox{10.8cm}{!}{\includegraphics{H2487F2.eps}} \hfill \parbox[b]{55mm}{ } \end{figure}$

Figure 2: Normalised fluxes calculated for a dust shell containing silicates with a degree of crystallinity x = 0.10, for the same mass-loss rates as in Fig. 1. The narrow features due to crystalline silicates start to appear in the 20-50 $\mu$ m range are only appearing for relatively high mass-loss rates. At $\dot{M} \approx 10^{-5}$ $M_{\odot }$ yr^-1 the crystalline silicates are also discernible as substructure in the 10 $\mu$ m feature (see also Fig. 11)

Open with DEXTER

$\begin{figure} \resizebox{10.8cm}{!}{\includegraphics{H2487F3.eps}} \hfill \parbox[b]{55mm}{ } \end{figure}$

Figure 3: Normalised fluxes calculated for a dust shell containing silicates with a degree of crystallinity x = 0.20, for the same mass-loss rates as in Fig. 1. The narrow features due to crystalline silicates in the 20 - 50 $\mu$ m range are only appearing for relatively high mass-loss rates. At $\dot{M} \approx 5 ~ 10^{-6}$ $M_{\odot }$ yr^-1 the crystalline silicates are also discernible as substructure in the 10 $\mu$ m feature (see also Fig. 11)

Open with DEXTER

In Figs. 1, 2 and 3 results of the model calculations are presented. Each figure shows the fluxes $F_{\nu} (\lambda[\mu \textrm{m}])$ for mass-loss rates varying from 10^-7 to 10^-4 $M_{\odot }$ yr^-1 for a constant degree of crystallinity. In Fig. 1 results for a dust shell consisting of completely amorphous dust are shown. Clearly visible are the bands due to Si-O stretching and O-Si-O-bending around 10 and 20 $\mu$ m respectively. The strength of these bands varies with increasing mass-loss rate; for low $\dot{M}$ the dust shell is optically thin and the amorphous silicate bands appear in emission. The strength of the emission bands increases with increasing mass-loss rate. When the radial optical depth of the peaks of the spectral features approaches unity, the features become self-absorbed. This occurs around $\dot{M} = 10^{-5}$ $M_{\odot }$ yr^-1 in case of the 10 $\mu$ m feature. For the 20 $\mu$ m feature this transition is less well defined, and occurs at a somewhat higher mass-loss rate. Figures 2 and 3 show the emerging spectra for a crystallinity of 10% and 20% respectively. The overall shape of these spectra resemble that of the amorphous silicate dust shell spectra in Fig. 1. However, while the degree of crystallinity remains constant, the narrow crystalline silicate features at 23.6, 27.6, 32.5, 36.1, 41.2 and 43.2 $\mu$ m become quite apparent at relatively high mass-loss rates.

In the models with low mass-loss rate, the narrow crystalline silicate features are not discernible. Let us first investigate the relative strength of the crystalline silicate features with respect to the amorphous dust continuum in some more detail. For this purpose the contrast is calculated by dividing the spectrum of a dust model of a given crystallinity by the spectrum of a model with equal properties and the same amorphous silicate dust mass, but which is lacking the mass component taken up by the crystalline silicates. Figure 4 shows the contrast for three different mass-loss rates, including 10% crystalline material. The narrow bands due to crystalline silicates at 27.6, 32.5, 36.1, 41.2 and 43.2 $\mu$ m show that the relative strength increases with mass-loss rate. Note that the continuum between the crystalline silicate features does not necessarily return to unity, as the "extra'' IR emission from crystalline silicates raises the temperature of the amorphous silicates slightly. For $\dot{M} = 10^{-7}$ $M_{\odot }$ yr^-1 the contrast between the crystalline silicate peaks and the surrounding continuum is less than 1% for all features; for $\dot{M} = 10^{-6}$ $M_{\odot }$ yr^-1 some peaks have a relative strength of $\sim 4$ % above continuum; whereas the strongest peaks of the $\dot{M} = 10^{-5}$ $M_{\odot }$ yr^-1 model show a contrast of $\sim$ 10% above continuum. The detection limit of ISO for broad spectral features in this wavelength region is - depending on the quality of the spectrum - around 5% of the continuum level, which implies that of the three curves plotted in Fig. 4 only the ISO spectrum of a star with an outflow of 10^-5 $M_{\odot }$ yr^-1 would result in a unambiguous detection of crystalline silicate features. A detection in the spectrum of an AGB star with $\dot{M} = 10^{-6}$ $M_{\odot }$ yr^-1 would be dubious. A typical Mira, with $\dot{M} = 10^{-7}$ $M_{\odot }$ yr^-1, with a crystallinity of 10% would not show the characteristic features. This result is consistent with the threshold mass-loss rate above which crystalline silicates are detected with ISO observations (Waters et al. 1996; Cami et al. 1998; Sylvester et al. 1999).

3.2 Varying the degree of crystallinity

$\begin{figure} \par\includegraphics[width=8.2cm,clip]{H2487F4.eps} \end{figure}$

Figure 4: Contrast plot of the 25-50 $\mu$ m region for different mass-loss rates at a constant degree of crystallinity x = 0.10. The $\dot{M}$ ( $M_{\odot }$ yr^-1) values are indicated for each curve. The contrast is obtained by dividing the model spectrum containing 10% crystalline dust by the model spectrum of a dust shell with an equal amount of amorphous dust, but lacking the crystalline dust component

Open with DEXTER

$\begin{figure} \par\includegraphics[width=8.1cm,clip]{H2487F5.eps} \end{figure}$

Figure 5: Contrast plot for $\lambda < 60$ $\mu$ m for different degrees of crystallinity x at a constant mass-loss rate of $\dot{M} = 10^{-7}$ $M_{\odot }$ yr^-1. The crystalline fraction x is indicated at each curve. The contrast is obtained by dividing the model spectrum of a dust shell with a certain degree of crystallinity by the model spectrum of a dust shell with exactly the same amount of amorphous dust, but which lacks the crystalline dust component. The ISO detection limit for emission features of 5% with respect to a continuum at $F_{\nu , {\rm cryst+amorph}}/F_{\nu , {\rm amorph}} = 1$ is indicated with a dashed line

Open with DEXTER

In order to determine the amount of crystalline silicates that should be present in a typical Mira dust shell such that the narrow features would be detected in an ISO spectrum, model spectra with different degrees of crystallinity have been calculated. For a typical Mira mass-loss of $\dot{M} = 10^{-7}$ $M_{\odot }$ yr^-1 the crystallinity has been varied from 5% to 50%. The spectra of the x=0.10 and x=0.20models, discussed in Sect. 3.1, are included in the overview. The contrast has been calculated in the same way as described above. The result is shown in Fig. 5, for models with $\dot{M} = 10^{-7}$ $M_{\odot }$ yr^-1. The dashed line indicates the 5% detection limit of ISO for solid state features, typical for $\lambda \sim$ 25-50 $\mu$ m, and thus gives an impression of which features will be discernible. As stated before, the relative flux of the crystalline silicate model in between the narrow crystalline silicate features is not necessarily equal to that of the amorphous model fluxes. The peak strength should therefore be compared to the local continuum, rather than to unity. For this purpose an additional base-line has to be subtracted. Following this method one easily sees that very high mass abundances of crystalline silicates are required for a marginal detection of crystalline silicate features in a typical Mira spectrum. For a crystallinity of x = 0.40 only the 43.2 $\mu$ m and 32.5 $\mu$ m features can be detected by ISO.

3.3 A trend in crystallinity?

From Sects. 3.1 and 3.2 it becomes clear that the comparison of the ISO detection limit with the contrast of the crystalline silicate features is essential for studying the correlation between mass-loss rate and crystallinity of AGB stars. From Fig. 5 the 43.2 $\mu$ m feature due to crystalline pyroxene (enstatite, MgSiO₃) has been selected for closer examination, which is a conservative choice. It shows the largest contrast with the local continuum, and would therefore be the first feature to be detected in the spectrum when mass loss or crystallinity increases, under the assumption that the mass fractions of crystalline pyroxene and forsterite are equal.

For a range of enstatite mass fractions and mass-loss rates the contrast spectra have been calculated. To determine the relative peak strength with respect to the local continuum, a first order polynomial base-line has been subtracted from the feature, such that the local continuum is equal to unity. Then the peak value of the 43.2 $\mu$ m feature was measured, and plotted in Fig. 6. Note that the enstatite mass fractions differ a factor 2 with the elsewhere used crystallinity x, because it was assumed in Sect. 2.1 that enstatite and forsterite are equally abundant. Figure 6 is a diagnostic tool to determine the crystalline pyroxene content of the silicates present in the dust shell around an AGB star. To do so, one has to determine the relative peak strength of the 43.2 $\mu$ m feature with respect to the local continuum, a quantity plotted on the vertical axis, and combine this with the mass-loss rate of the object. The data points of the sample of AGB stars previously analysed by Sylvester et al. (1999) are presented to illustrate the method. The relative strength is measured from ISO spectra with an accuracy of 2 percent of the continuum (Table 1). We adopted an accuracy of a factor 2 for the mass-loss rates. Using these data, one can estimate from Fig. 6 that the enstatite makes up around 3% $\pm$ 2% of the total silicate dust mass around WX Psc and OH 26.5+0.6, and around 6% $\pm$ 2% in OH 127.8+0.0 and OH 32.8-0.3. In CRL 2199 and OH 104.9+2.4 the enstatite mass fraction is well below 2-3%, whereas the upper limit obtained for o Cet (Mira itself) does not put interesting constraints on the enstatite content. The dust shell of o Cet could still easily contain a mass fraction of 20% of crystalline pyroxene. A constant enstatite mass fraction of $\sim$ 5% is consistent with the observed strength of the 43.2 $\mu$ m feature for a wide range of mass-loss rates.

Table 1: Relative fluxes and mass-loss rates of the sample stars from Sylvester et al. (1999)
Star rel. flux rel. flux $\dot{M}$ ref.

32.5 $\mu$ m 43.2 $\mu$ m $M_{\odot }$ yr^-1

o Cet < 0.05 < 0.05 1.0 10^-7 1

CRL 2199 < 0.05 < 0.05 1.5 10^-5 2, 3

WX Psc 0.115 0.090 1.9 10^-5 2, 4, 5, 6

OH 104.9+2.4 0.064 < 0.05 6.0 10^-5 6

OH 127.8+0.0 < 0.05 0.15 2.0 10^-4 3

OH 26.5+0.6 0.062 0.095 1.6 10^-4 3, 6, 7

AFGL 5379 0.077 0.093

OH 32.8-0.3 < 0.05 0.16 1.0 10^-4 3, 6, 8

1: Planesas et al. (1990), 2: Knapp & Morris (1985), 3: Justtanont & Tielens (1992),
4: Sopka et al. (1989), 5: Le Bertre & Winters (1998), 6: Schutte & Tielens (1989),
7: Justtanont et al. (1996), 8: Groenewegen (1994).

**Table 1:** Relative fluxes and mass-loss rates of the sample stars from Sylvester et al. (1999)
Star	rel. flux	rel. flux	$\dot{M}$	ref.
	32.5 $\mu$ m	43.2 $\mu$ m	$M_{\odot }$ yr^-1
o Cet	< 0.05	< 0.05	1.0 10^-7	1
CRL 2199	< 0.05	< 0.05	1.5 10^-5	2, 3
WX Psc	0.115	0.090	1.9 10^-5	2, 4, 5, 6
OH 104.9+2.4	0.064	< 0.05	6.0 10^-5	6
OH 127.8+0.0	< 0.05	0.15	2.0 10^-4	3
OH 26.5+0.6	0.062	0.095	1.6 10^-4	3, 6, 7
AFGL 5379	0.077	0.093
OH 32.8-0.3	< 0.05	0.16	1.0 10^-4	3, 6, 8

$\begin{figure} \par\includegraphics[width=8.4cm,clip]{H2487F6.eps}\end{figure}$

Figure 6: Relative strength of the 43.2 $\mu$ m feature with respect to the local continuum as determined by amorphous material as a function of $\dot{M}$ . The curves are calculated for enstatite mass fractions of 0.05; 0.10; 0.15 and 0.20; which are indicated in the plot. The dashed line represents the ISO detection limit at 43.2 $\mu$ m, which is $\sim$ 5%. For several AGB stars, $\dot{M}$ and $F_{\nu ,{\rm cryst}}/F_{\nu ,{\rm cont}}$ are indicated (see Table 1). For some stars, only an upper limit to the relative flux is given

Open with DEXTER

$\begin{figure} \par\includegraphics[width=8.4cm,clip]{H2487F7.eps} \end{figure}$

Figure 7: Relative strength of the 32.5 $\mu$ m forsterite feature with respect to the local continuum as a function of $\dot{M}$ . The curves are calculated for forsterite mass fractions of 0.05; 0.10; 0.15 and 0.20; which are indicated in the plot. The dashed line represents the ISO detection limit at 32.5 $\mu$ m, which is $\sim$ 5%. For a sample of AGB stars, $\dot{M}$ and $F_{\nu ,{\rm cryst}}/F_{\nu ,{\rm cont}}$ are indicated (see Table 1). For some stars, only an upper limit to the relative strength is available

Open with DEXTER

A similar analysis can be performed on the forsterite (Mg₂SiO₄, crystalline olivine) mass fraction, using the 32.5 $\mu$ m feature, which has the best contrast. For the same range of mass-loss rates the emerging dust spectrum has been calculated. The mass fraction of the crystalline olivine varied from 0% to 20%. All other input parameters had equal values as the parameters in the analysis of the crystalline pyroxene mass fraction. We calculated the relative peak value of the 32.5 $\mu$ m feature, by subtracting a first order polynomial from the forsterite contrast plots. Figure 7 shows the relative peak fluxes as a function of mass-loss rate, calculated for different mass fractions of forsterite. From this plot it is obvious that in low mass-loss rate AGB stars, the strength of the 32.5 $\mu$ m feature is less than 5% of the continuum, which makes it imperceptible for ISO, as is illustrated with the data for o Cet. For higher mass-loss rate AGB stars, the strength of the feature provides a reliable measure to determine the crystalline olivine mass fraction. The forsterite mass fraction of our sample of high mass-loss stars however, is at most 5% $\pm$ 2% for WX Psc. There is no evidence for an increasing forsterite mass fraction for higher mass-loss rates.

$\begin{figure} \par\includegraphics[width=8.4cm,clip]{H2487F8.eps} \end{figure}$

Figure 8: Relative peak strength of the 43.2 $\mu$ m feature as a function of mass-loss rate and fraction of mass taken by enstatite (MgSiO₃). The peak strength is determined with respect to the local continuum. A relative peak strength >5% is observable with ISO. The shaded area represents the values for $\dot{M}$ and enstatite mass fraction for which the strength of the 43 $\mu$ m feature is below the ISO detection limit. The mass fraction of enstatite is sampled at 0.00, 0.05, 0.10 and 0.20; and the mass-loss rate is sampled at $\dot{M}/10^6$ = 0.05, 0.1, 0.2, 0.5, 1, 2, 5, 10, 20, 50 and 100 $M_{\odot }$ yr^-1

Open with DEXTER

Figures 8 and 9 illustrate that an observational selection effect is present in the correlation between mass-loss rate and crystallinity reported in previous studies by Waters et al. (1996); Cami et al. (1998); Sylvester et al. (1999). The OH/IR stars with $$\dot{M} \mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\display... ...interlineskip\halign{\hfil$\scriptscriptstyle ...$ $M_{\odot }$ yr^-1 only have to contain a small mass fraction of crystalline pyroxene in their dust shells in order to exhibit the 43.2 $\mu$ m or 32.5 $\mu$ m feature. A few percent is already perceptible with ISO. However, the 43.2 and 32.5 $\mu$ m features in the spectra of Miras, with $$\dot{M} \mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\display... ...interlineskip\halign{\hfil$\scriptscriptstyle ...$ $M_{\odot }$ yr^-1, will only be detected for high crystallinity. For example, in the dust shell of o Cet, with $\dot{M} \approx 10^{-7}$ $M_{\odot }$ yr^-1, a dust mass fraction of 20% of enstatite could be present without showing the 43 $\mu$ m feature in its spectrum. The same goes for the 32.5 $\mu$ m forsterite feature. If we assume that equal amounts of crystalline pyroxene and olivine are present, the ISO detection limit only provides an upper-limit to the crystallinity of x = 0.40. If a constant crystallinity of x=0.10 (i.e. a mass fraction for both enstatite and forsterite of 5% of the total silicate mass) is assumed, while the star evolves along the AGB, the 32.5 $\mu$ m and 43.2 $\mu$ m features will appear in the spectrum when the mass loss is sufficiently high. The threshold value, defined by the ISO detection limit, is found at $\dot{M} \sim 10^{-6}$ $M_{\odot }$ yr^-1. This is consistent with observational studies that conclude that crystalline silicate features only appear to be present in high mass-loss rate objects.

$\begin{figure} \par\includegraphics[width=8.4cm,clip]{H2487F9.eps} \end{figure}$

Figure 9: Relative peak strength of the 32.5 $\mu$ m feature as a function of mass-loss rate and fraction of mass taken by forsterite (Mg₂SiO₄, crystalline olivine). The peak strength is determined with respect to the local continuum. A relative peak strength >5% is observable with ISO. The shaded area represents the values for $\dot{M}$ and forsterite mass fraction, for which the strength of the 32.5 $\mu$ m feature is below the ISO detection limit. The mass fraction of forsterite is sampled at 0.00, 0.05, 0.10, 0.15 and 0.20; and the mass-loss rate is sampled at $\dot{M}/10^6$ = 0.05, 0.1, 0.2, 0.5, 1, 2, 5, 10, 20, 50 and 100 $M_{\odot }$ yr^-1

Open with DEXTER

4 Physical explanation and discussion

The appearance of crystalline silicate features with increasing mass-loss rate for a constant degree of crystallinity may be caused by the difference in absorptivity in the NIR of crystalline and amorphous silicates. This difference is due to a difference in Fe-content of the amorphous and crystalline components. The crystalline silicates investigated do not contain any iron, whereas in the amorphous silicates the iron and magnesium contents are roughly equal. Previous laboratory studies (Koike et al. 1993; Jäger et al. 1998) have shown that the peak positions of crystalline silicate features strongly depend on the Fe-content of the silicate. At present, there have not been any detections of crystalline silicates containing iron around evolved stars, which justifies the use of laboratory data of pure Mg₂SiO₄ and MgSiO₃.

The absorptivity in the NIR and at shorter wavelengths increases with increasing Fe-content. The amorphous silicates thus absorb more radiation from the central star, which emits most of its flux at NIR wavelengths, than the crystalline silicates do, resulting in a large temperature difference between amorphous and crystalline material, the latter staying much cooler. In the mid and far infrared the absorptivity of both dust types are more or less equal. In an optically thick dust shell, where the stellar flux is absorbed and re-radiated several times by the dust, the grains in the outer regions are illuminated by a radiation field that typically peaks at mid infrared wavelengths. As in this wavelength regime only a small difference in absorptivity occurs, a large temperature difference between the amorphous and crystalline dust components will not develop. Summarising, at the inner radius of an optically thick dust shell the crystalline silicates are much colder than the amorphous silicate grains, but the temperature difference decreases at larger distances.

$\begin{figure} \par\includegraphics[angle=90,width=7.8cm,clip]{H2487F10.eps} \end{figure}$

Figure 10: ISO SWS spectrum of AFGL 2999. The spectrum of this star is typical for that of an object somewhere in between typical Miras and OH/IR stars. High resolution and high signal-to-noise observations may perhaps reveal crystalline silicate features as sub-structure in the broad amorphous 10 $\mu$ m feature. No crystalline silicates are seen at the 5 percent level in the 20-45 $\mu$ m range. The artefact at 28 $\mu$ m is due to calibration problems with band 3e of ISO SWS

Open with DEXTER

The implications for the strength of the crystalline silicate features due to this temperature difference are quite dramatic. In low mass-loss rate AGB stars (Miras), the dust shell is optically thin, implying the entire dust shell is visible and contributes to the SED. The relatively hot amorphous silicates at the inner radius then dominate the SED of a Mira, and the contrast of the crystalline silicates with respect to the amorphous silicate spectrum becomes very poor. In case of a high mass-loss rate AGB star, only the outer regions of the dust shell are visible, because the shell is optically thick at IR wavelengths. The temperature differences in the outer layers are small, as explained above, and therefore the crystalline and amorphous dust components both contribute in comparable amounts to the spectrum. This improved contrast of the crystalline silicates with respect to the amorphous dust emission enables the detection of the narrow crystalline features in the spectrum of OH/IR stars.

The ISO detection limit allows the presence of a significant fraction of crystalline silicates in the circumstellar shells of low mass-loss rate AGB stars. In fact, the ISO data are consistent with model calculations assuming that the crystallinity of the dust is constant with mass-loss. Until now, most theoretical studies (Tielens et al. 1998; Gail & Sedlmayr 1999; Sogawa & Kozasa 1999) assumed that crystalline silicates are only formed in high density outflows. The results presented in this study suggest that the possibility of the condensation of crystalline silicates in low mass-loss rate AGB stars should be considered in future studies.

4.1 How to search for crystalline silicates in Miras

To date, there are no significant detections of crystalline silicates in low mass-loss rate AGB stars reported. As shown above, this provides a relatively high upper limit to the mass fraction taken by crystalline silicates in the shells around these stars. In order to lower this upper limit and to investigate the presence of crystalline silicates in Miras, additional observations with a better detection limit than that of ISO, are required. Unfortunately, the most prominent and characteristic features of crystalline silicates appear in the 25-50 $\mu$ m region, and with the end of the ISO mission the opportunities to observe in this wavelength region are limited. An important future mission covering part of this wavelength region is SIRTF, which can perform intermediate resolution spectroscopy ( $R \sim 600$ ) up to $\lambda \approx 37$ $\mu$ m. The crystalline silicate feature with the largest contrast value within this wavelength range is the 32.5 $\mu$ m forsterite feature. In Fig. 9, the contrast of this feature with respect to the continuum is presented as a function of mass-loss rate and Mg₂SiO₄ mass fraction.

$\begin{figure} \par\includegraphics[width=8.2cm,clip]{H2487F11.eps} \end{figure}$

Figure 11: Predicted flux levels in the 7-13 $\mu$ m region for an AGB star with $\dot{M} = 5 ~ 10^{-6}$ $M_{\odot }$ yr^-1. Model spectra with three different crystallinities (x=0.0; x=0.10; x=0.20) are indicated. The broad emission feature is due to amorphous silicates. The substructure is due to crystalline silicate features that appear in absorption. The ISO SWS spectrum of AFGL 2999 is plotted for reference; in this spectrum it is not possible to detect crystalline silicate features, since the the substructure in the spectrum is mostly due to observational noise

Open with DEXTER

In addition, it is also possible to study the 10 and 20 $\mu$ m silicate features, which both can be observed from the ground. Since it is already known that the high mass-loss rate OH/IR stars contain crystalline silicates in their circumstellar dust shells, it is particularly interesting to study the 10 $\mu$ m feature of low and intermediate mass-loss rate objects, with $\dot{M} < 10^{-5}$ $M_{\odot }$ yr^-1. From Figs. 2 and 3 it one can conclude that the 10 $\mu$ m feature of intermediate mass-loss rate AGB stars ( $\dot{M} \approx 10^{-6}$ to 10^-5 $M_{\odot }$ yr^-1) would be the most likely to reveal the presence of crystalline silicates. The 10 $\mu$ m region has the intrinsically strongest resonance peaks of crystalline silicates. Superposed on the 10 $\mu$ m feature of amorphous silicates which is just optically thick ( $$\tau \mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\displaysty... ...r{\offinterlineskip\halign{\hfil$\scriptscriptstyle ...$ ) these strong resonances appear as absorption features in the spectrum. The intermediate mass-loss rate AGB stars can be easily recognised from the ratio between the strength of the 10 and 20 $\mu$ m features. For example AFGL 2999, of which the ISO SWS spectrum is shown in Fig. 10, can be identified as a $\dot{M} = 5 ~ 10^{-6}$ $M_{\odot }$ yr^-1 AGB star.

Figure 11 shows predicted 10 $\mu$ m features. The flux levels are calculated for models with $\dot{M} = 5 ~ 10^{-6}$ $M_{\odot }$ yr^-1 and x = 0.00, 0.10, 0.20. The broad amorphous silicate feature is partially optically thick and shows a flattened profile due to self-absorption. The additional opacity provided by the crystalline silicates appears as narrow absorption superposed on the broad amorphous silicate feature. The ISO spectrum of AFGL 2999 is plotted for reference, but the substructure in this spectrum is observational noise and it is therefore hard to disentangle the crystalline silicate mass fraction. However, it would certainly be possible reach a high S/N ratio and detect a crystallinity of 10% with the current ground-based spectrometers that cover the 10 $\mu$ m region, such as TIMMI2 mounted on the 3.6 m ESO telescope.

4.2 Implications for the dust formation and processing in the ISM

AGB stars are considered the main contributors of dust to the ISM, so one would expect a match between the dust composition in the ISM and in the shells of AGB stars. However, despite all evidence for crystalline silicates in AGB stars, there has as yet not been found any reliable evidence for crystalline silicates in the line of sight toward the Galactic Center (GC) (Lutz et al. 1996), or other lines of sight through the ISM (Demyk et al. 1999). In fact, the line of sight toward the GC is found to resemble closely the silicate feature of the evolved star $\mu$ Cep, and can be fitted with completely amorphous olivine (Vriend 1999; Bouwman et al. in prep.). Cesarsky et al. (2000) report a questionable detection of crystalline silicates in the Orion Bar.

On the other hand, it is doubtful that Miras contribute significantly to the dust population in the ISM. It is generally accepted that the Mira phase lasts $\sim$ 3 10⁵ yr, and the OH/IR phase $\sim$ 3000 yr (Habing 1996). The mass-loss rates for Miras and OH/IR stars ( $\dot{M}_{{\rm Mira}} \approx 10^{-7}$ $M_{\odot }$ yr^-1, and $\dot{M}_{{\rm OH/IR}} \approx 10^{-4}$ $M_{\odot }$ yr^-1) can be used to estimate the total mass lost in each of the two phases; for OH/IR stars this is $\sim$ 0.3 $M_{\odot }$ , for Miras $\sim$ 0.03 $M_{\odot }$ . Under the assumption that all Miras will eventually evolve into OH/IR stars, only a minor fraction ( $\sim$ 10%) of the interstellar dust population is formed in a Mira dust shell. So, the possibility that Miras contain a significant fraction of crystalline silicates in their dust shells does not heavily aggravate the discrepancy between the dust composition in the ISM and that in AGB dust shells, under the assumption that all Miras eventually evolve into OH/IR stars. However, if Mira stars indeed deposit dust with a high degree of crystallinity into the ISM, and a significant fraction of Miras does not evolve into OH/IR stars, it is more surprising that the interstellar silicate grains appear to have an amorphous lattice structure. Grain-grain collisions and ion bombardments might cause the required amorphitization. Due to the collision, the grain will partially melt and consequently solidify in an amorphous form on timescales shorter than the annealing timescales (Sylvester et al. 1999). In a future study (Kemper et al., in prep.) we will thoroughly examine the differences between silicates in the ISM and in circumstellar shells, and discuss possible mechanisms of grain processing.

5 Summary

In this work, three important aspects of crystalline silicates around AGB stars have been studied by modelling the dust shell. First, we have calculated spectra emerging from circumstellar dust shells for different mass-loss rates. Moreover, the effects of different degrees of crystallinity on the SED have been taken into account, as a function of optical depth toward the central star. Finally, we provide a useful and easy to use diagnostic tool to determine the degree of crystallinity for an AGB star with a known mass-loss rate. The dust shells of low mass-loss rate AGB stars can contain a significant fraction of crystalline silicates, while the characteristic sharp spectral peaks are indiscernible with ISO. This is caused by a large temperature difference in the inner parts of these optically thin dust shells, such that the relatively warm amorphous silicate emission dominates the SED. The temperature difference between the warm amorphous dust and the cold crystalline dust is caused by a difference in absorptivity at NIR and visible wavelengths, where the amorphous dust component more efficiently absorbs the stellar radiation. The low absorptivity of the crystalline component is due to the very low Fe-content of these dust species. In case of high mass-loss AGB stars, the radiation from the central star is absorbed by the dust and re-radiated several times, so that the dust in the outer parts receives a relatively red radiation field, which peaks in the mid-IR. In that region the absorptivity of crystalline and amorphous silicates are similar, leading to similar temperatures of both species. The dust shell is optically thick, so only the outer layers, where crystalline and amorphous silicates have similar temperatures, are visible, leading to a high contrast of the crystalline silicate features.

From these results one may conclude that crystallinity is not necessarily a function of mass-loss rate, as many observational and theoretical studies have suggested. The threshold value for the mass-loss rate above which crystalline silicates are observed is consistent with the ISO detection limit if a constant crystallinity of 10% is assumed. The strong observational selection effect undermines previously drawn conclusions regarding this threshold value. The meaning and the existence of the threshold mass-loss rate should be reconsidered. Future observations of the 10 $\mu$ m silicate feature of low mass-loss AGB stars at high spectral resolution can probably further constrain the upper limit for the crystalline silicate content in Miras. The low degree of crystallinity of grains in the interstellar medium with respect to grains in AGB shells, however, remains subject to further study.

Crystallinity versus mass-loss rate in asymptotic giant branch stars

1 Introduction

2 Modelling the circumstellar dust shell

2.1 Dust optical constants

3 Model results

3.1 Varying the mass-loss rate

3.2 Varying the degree of crystallinity

3.3 A trend in crystallinity?

4 Physical explanation and discussion

4.1 How to search for crystalline silicates in Miras

4.2 Implications for the dust formation and processing in the ISM

5 Summary

References