A&A 369, 87-98 (2001)
DOI: 10.1051/0004-6361:20010144
R. G. Gratton1 - P. Bonifacio2 - A. Bragaglia3 - E. Carretta1 - V. Castellani4 - M. Centurion2 - A. Chieffi5 - R. Claudi1 - G. Clementini3 - F. D'Antona6 - S. Desidera1,7 - P. François8 - F. Grundahl9 - S. Lucatello1,7 - P. Molaro2 - L. Pasquini8 - C. Sneden10 - F. Spite11 - O. Straniero12
1 -
Osservatorio Astronomico di Padova, Vicolo dell'Osservatorio 5, 35122
Padova, Italy
2 -
Osservatorio Astronomico di Trieste, Italy
3 -
Osservatorio Astronomico di Bologna, via Ranzani 1, 40127 Bologna, Italy
4 -
Dipartimento di Fisica, Università di Pisa, Italy
5 -
Istituto di Astrofisica Spaziale, CNR, Italy
6 -
Osservatorio Astronomico di Roma, Italy
7 -
Dipartimento di Astronomia, Università di Padova, Italy
8 -
European Southern Observatory
9 -
Department of Astronomy, University of Aarhus, Denmark
10 -
The University of Texas at Austin, USA
11 -
Observatoire de Meudon, France
12 -
Osservatorio Astronomico di Collurania, Italy
Received 18 December 2000 / Accepted 26 January 2001
Abstract
High dispersion spectra (
![]() )
for a quite large number of stars at
the main sequence turn-off and at the base of the giant branch in NGC 6397 and
NGC 6752 were obtained with the UVES on Kueyen (VLT UT2). The [Fe/H] values we
found are
)
for a quite large number of stars at
the main sequence turn-off and at the base of the giant branch in NGC 6397 and
NGC 6752 were obtained with the UVES on Kueyen (VLT UT2). The [Fe/H] values we
found are
![]() and
and
![]() for NGC 6397
and NGC 6752 respectively, where the first error bars refer to internal and the
second ones to systematic errors (within the abundance scale defined by our
analysis of 25 subdwarfs with good Hipparcos parallaxes). In both clusters
the [Fe/H]'s obtained for TO-stars agree perfectly (within a few percent) with
that obtained for stars at the base of the RGB. The
for NGC 6397
and NGC 6752 respectively, where the first error bars refer to internal and the
second ones to systematic errors (within the abundance scale defined by our
analysis of 25 subdwarfs with good Hipparcos parallaxes). In both clusters
the [Fe/H]'s obtained for TO-stars agree perfectly (within a few percent) with
that obtained for stars at the base of the RGB. The
![]() value we obtain for NGC 6397 is quite low, but it agrees with previous results
obtained for giants in this cluster. Moreover, the star-to-star scatter in
both O and Fe is very small, indicating that this small mass cluster is
chemically very homogenous. On the other hand, our results show clearly and
for the first time that the O-Na anticorrelation (up to now seen only for
stars on the red giant branches of globular clusters) is present among
unevolved stars in the globular cluster NGC 6752, a more massive cluster than
NGC 6397. A similar anticorrelation is present also for Mg and Al, and C and N.
It is very difficult to explain the observed Na-O, and Mg-Al anticorrelation
in NGC 6752 stars by a deep mixing scenario; we think it requires some non
internal mechanism.
value we obtain for NGC 6397 is quite low, but it agrees with previous results
obtained for giants in this cluster. Moreover, the star-to-star scatter in
both O and Fe is very small, indicating that this small mass cluster is
chemically very homogenous. On the other hand, our results show clearly and
for the first time that the O-Na anticorrelation (up to now seen only for
stars on the red giant branches of globular clusters) is present among
unevolved stars in the globular cluster NGC 6752, a more massive cluster than
NGC 6397. A similar anticorrelation is present also for Mg and Al, and C and N.
It is very difficult to explain the observed Na-O, and Mg-Al anticorrelation
in NGC 6752 stars by a deep mixing scenario; we think it requires some non
internal mechanism.
Key words: stars: abundances - stars: evolution - stars: population II - Galaxy: globular clusters
Globular clusters (GCs) are (with a few significant exceptions, most notably
the case of ![]() Cen) generally very homogenous as far as Fe-peak elements
are considered; on the other hand, abundances of the lighter elements (from C
to Al) show a complex, not yet adequately explained pattern. Rather wide
variations in the strength of the CH and CN bands among stars on the red giant
branch (RGB) were already noticed in the seventies (Osborn 1971, and many
other references; for reviews see Smith 1987; Kraft 1994), and found to be
correlated with other cluster properties (Norris 1987). More recently, a CN-CH
anticorrelation was found in Main Sequence (MS) stars of NGC 6752 (Suntzeff &
Smith 1991), 47 Tuc (Cannon et al. 1998), and M 71 (Cohen 1999a) from low
dispersion spectra. Even more striking is the Na-O anticorrelation among GC
red giants discovered by the Lick-Texas group (see e.g. Kraft et al. 1997).
Cen) generally very homogenous as far as Fe-peak elements
are considered; on the other hand, abundances of the lighter elements (from C
to Al) show a complex, not yet adequately explained pattern. Rather wide
variations in the strength of the CH and CN bands among stars on the red giant
branch (RGB) were already noticed in the seventies (Osborn 1971, and many
other references; for reviews see Smith 1987; Kraft 1994), and found to be
correlated with other cluster properties (Norris 1987). More recently, a CN-CH
anticorrelation was found in Main Sequence (MS) stars of NGC 6752 (Suntzeff &
Smith 1991), 47 Tuc (Cannon et al. 1998), and M 71 (Cohen 1999a) from low
dispersion spectra. Even more striking is the Na-O anticorrelation among GC
red giants discovered by the Lick-Texas group (see e.g. Kraft et al. 1997).
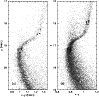 |
Figure 1: Positions of program stars (large symbols) on the Strömgren colour-magnitude diagram of NGC 6397 (panel a)) and NGC 6752 (panel b)). Photometry is from Grundahl et al. (1999). Note that photometry for NGC 6397 has not been calibrated yet, so that only instrumental magnitudes are given |
| Open with DEXTER | |
These features are indications of the presence of elements processed through the complete CNO-cycle in the atmospheres of some globular cluster stars; at temperatures where complete CNO cycle occurs, quite large amounts of Na may be produced by proton capture on 22Ne nuclei (Denissenkov & Denissenkova 1990; Langer & Hoffman 1995; Cavallo et al. 1996). Whatever the cause of these abundance anomalies, it appears to be related to the dense environment of GCs. In fact, field halo stars present surface abundances of Li, C, N, O, Na that are well explained by standard models, once a second mixing episode (only affecting Li, C and N abundances) after the RGB-bump is allowed (Gratton et al. 2000). Note that the RGB bump plays an important rôle, because there the molecular weight barrier created by the deepest inward penetration of the outer convective envelope (at the base of the RGB) is canceled by the outward shift of the H-burning shell. The absence of this barrier in the subsequent evolution allows deep mixing caused by e.g. meridional circulations (Sweigart & Mengel 1979; Charbonnel 1994; Denissenkov & Tout 2000). Hence, both the O-Na anticorrelation observed among giants, and the C and N anomalies observed in stars in different evolutionary phases, are peculiar to GCs.
The proposed explanations of the abundance anomalies in globular cluster stars have been oscillating for years between an "in situ'' mechanism (very deep mixing in RGB stars, possibly activated by a core rotation that might be larger in cluster than in field stars) and an external source of material (either primordial proto-cluster gas or processed material from a polluting companion). Since MS stars do not have a convective envelope able to enhance N while depleting C, these anomalies should be attributed mainly to a primordial origin and/or to pollution, while evolutionary mixing could possibly be responsible only for likely minor effects in RGB stars. However, rather surprisingly, an analysis of stars below the Turn-off (TO) of M 13 (Cohen 1999b) shows no variations in the strength of CN and CH molecular features, likely excluding primordial variation of C and N abundance in this cluster, which instead presents the clearest Na-O anticorrelation on the RGB (Kraft et al. 1997), and a range in the strength of CN and CH bands among giants (Suntzeff 1981). While the result of Cohen is very surprising, the published analysis is only qualitative. Very recently, Dr. J. Cohen kindly provided us with a copy of her new quantitative analysis of these spectra in advance of publication: this analysis shows that large variations in the abundances of C and N may indeed be accomodated within the observed upper limit for star-to-star variations in the CN and CH bands in M 13 main-sequence stars. However, in general, the relation between the Na-O and C-N anticorrelation is not yet well established. Observation of a Na-O anticorrelation among main sequence stars of globular clusters would be crucial, clearly ruling out the deep mixing scenario.
Earlier explorative studies of stars close to the TO and at the base of the
giant branch of a few clusters have been presented by King et al. (1998), Deliyannis et al. (1995) and Boesgaard et al. (1998) who used HIRES at Keck to gather spectra of three stars in M 92; and
Pasquini & Molaro (1996,1997) who exploited the presence of closer clusters
in the southern emisphere to obtain spectra of a few stars in NGC 6397 and 47
Tuc using EMMI at NTT (these stars are about a magnitude brighter than those of M 92). However, very low S/N observations of a handful of stars could be
obtained. Only UVES (D'Odorico et al. 2000) at the Kueyen (VLT UT2) Telescope
is able to provide abundances of O, Na, Mg, Al and other elements for
significant samples of well studied stars at the TO and at the base of RGB
(well below the RGB bump), crucial to clarify most of these issues. Here we
present a short description of the first results of the ESO Large Program
165.L-0263 devoted to the acquisition and analysis of high dispersion spectra
(
![]() )
of a fairly large sample of stars at the TO and at the base
of the RGB in NGC 6752, NGC 6397, and 47 Tuc. A more detailed presentation of
the analysis methods, and of related results for Li, will be given in
forthcoming papers, still in preparation.
)
of a fairly large sample of stars at the TO and at the base
of the RGB in NGC 6752, NGC 6397, and 47 Tuc. A more detailed presentation of
the analysis methods, and of related results for Li, will be given in
forthcoming papers, still in preparation.
Observations were carried out in two 6-nights runs (June and September 2000); due to poor weather conditions in the September run, we were not able to complete the acquisition of the spectra in 47 Tuc. Hence the present paper deals only with data for the two other clusters. In the same runs we also acquired data for 25 field stars with good parallaxes from the Hipparcos catalogue and metallicity similar to that of the GCs.
For each cluster, we selected two groups of stars: (i) dwarfs about 0.2 mag brighter than the turn-off (5 stars in NGC 6397 and 9 in NGC 6752); and (ii) stars at the base of the red giant branch (3 stars in NGC 6397 and 9 stars in NGC 6752), hereinafter called subgiants. Positions of the observed stars in the C-M diagrams of the two clusters (from Grundahl et al. 1999) are given in Fig. 1. A posteriori, radial velocities and chemical composition show that all stars are bona fide members of the clusters. Stars with likely strong and weak CN bands were selected from Strömgren photometry: the c1index seems in fact to be higher for CN-richer stars (see Grundahl et al. 1999). Given this choice, it should be clear that stars are not a random sample of stars in the different magnitude bins, but rather they were selected in order to include quite extreme cases of CN-poor and CN-rich stars. For comparison, we give in Fig. 2 also the location in a similar C-M diagram of the field stars we observed.
The observations were carried out using the dichroic beamsplitter #2. This
allowed us to observe simultaneously two spectral ranges with the two arms of the
spectrograph. Slightly different setups were used in the two runs: the blue
spectra cover the spectral range from about 3500 Å to about 4700 Å,
while the red spectra cover the range from 5700 Å to about 8700 Å. This
very broad spectral range allows observations of a large number of spectral
features. The resolution was set by the slit width: in most cases this was
1 arcsec (yielding a resolution of 43000 at order centers); however, this
value was sometimes changed according to the variable seeing conditions, from
0.7 arcsec in the best cases, down to 1.2 arcsec in the worst ones. The slit
length was always set at 8 arcsec, allowing accurate sky subtraction (necessary,
since observations were carried out in full moon). Most of the objects are
very faint (
![]() ), so that long exposures were required even with an 8 m
telescope like Kueyen, and a very efficient spectrograph like UVES. Typical
exposure times were
), so that long exposures were required even with an 8 m
telescope like Kueyen, and a very efficient spectrograph like UVES. Typical
exposure times were ![]() 1 hr for subgiants, and about 4 hr (split in 3
to 4 segments) for TO stars. The S/N (per pixel at 6700 Å; there are about 5
pixels per resolution element) of the resulting spectra is
1 hr for subgiants, and about 4 hr (split in 3
to 4 segments) for TO stars. The S/N (per pixel at 6700 Å; there are about 5
pixels per resolution element) of the resulting spectra is ![]() 100 in the
best cases, and down to about 20 in the worst ones. Relevant data are
presented in Tables 1-3.
100 in the
best cases, and down to about 20 in the worst ones. Relevant data are
presented in Tables 1-3.
| Star | Mv | B-V | b-y | [Fe/H] |
|
|
|
|
| HD/BD | H |
Best | Alonso et al. | |||||
| 10607 | 4.03 | 0.56 | 0.372 | -0.95 | 4.00 | 5780 | 5734 | |
| 29907 | 6.01 | 0.63 | 0.452 | -1.47 | 4.82 | 5636 | 5406 | |
| 31128 | 5.05 | 0.49 | 0.358 | -1.44 | 4.63 | 6279 | 5969 | |
| 108177 | 4.87 | 0.43 | 0.330 | -1.70 | 4.44 | 5884 | 6063 | 6067 |
| 116064 | 4.74 | 0.45 | 0.349 | -1.87 | 4.35 | 5770 | 5923 | |
| 120559 | 5.93 | 0.66 | 0.424 | -0.90 | 4.51 | 5207 | 5378 | |
| 121004 | 5.12 | 0.62 | 0.424 | -0.75 | 4.32 | 5401 | 5548 | |
| 126681 | 5.71 | 0.60 | 0.400 | -1.13 | 4.55 | 5444 | 5556 | 5541 |
| 132475 | 3.62 | 0.56 | 0.401 | -1.61 | 3.79 | 5596 | 5520 | 5788 |
| 134169 | 3.82 | 0.565 | 0.370 | -0.81 | 4.06 | 6106 | 5825 | 5874 |
| 134439 | 6.72 | 0.77 | 0.487 | -1.31 | 4.78 | 5151 | 5052 | 4974 |
| 134440 | 7.05 | 0.85 | 0.527 | -1.28 | 4.69 | 4777 | 4777 | 4746 |
| 140283 | 3.34 | 0.49 | 0.380 | -2.46 | 3.67 | 5560 | 5645 | 5691 |
| 145417 | 6.81 | 0.82 | 0.509 | -1.23 | 4.78 | 5096 | 4922 | |
| 159482 | 4.92 | 0.58 | 0.382 | -0.83 | 4.32 | 5546 | 5656 | |
| 166913 | 4.22 | 0.45 | 0.326 | -1.59 | 4.08 | 5921 | 6020 | |
| 181743 | 4.96 | 0.45 | 0.351 | -1.81 | 4.42 | 5749 | 5927 | |
| 188510 | 5.59 | 0.60 | 0.416 | -1.44 | 4.50 | 5412 | 5485 | 5564 |
| 189558 | 3.59 | 0.575 | 0.386 | -1.15 | 3.87 | 5829 | 5670 | 5663 |
| 193901 | 5.44 | 0.55 | 0.377 | -1.03 | 4.62 | 5848 | 5780 | 5750 |
| 194598 | 4.60 | 0.49 | 0.348 | -1.15 | 4.42 | 6064 | 5980 | 6017 |
| 204155 | 4.07 | 0.57 | 0.378 | -0.70 | 4.06 | 5907 | 5751 | |
| 205650 | 5.39 | 0.51 | 0.375 | -1.12 | 4.52 | 5628 | 5782 | |
| -35 0360 | 6.31 | 0.76 | 0.472 | -1.08 | 4.52 | 4957 | 5086 | 4980 |
| +05 3640 | 6.50 | 0.74 | 0.474 | -1.15 | 4.62 | 4987 | 5063 |
| Star | S/N | n. | [Fe/H] | rms | EW | [O/Fe] | [O/Fe] | EW | EW | [Na/Fe] | [Mg/Fe] | [Al/Fe] |
| lines | 7771 | LTE | nLTE | 8183 | 8194 | nLTE | nLTE | |||||
| Dwarfs | ||||||||||||
| 1543 | 91 | 23 | -2.02 | 0.12 | 14.7 | 0.32 | 0.16 | .. | 38.8 | 0.21 | 0.06 | 0.20 |
| 1622 | 82 | 21 | -2.02 | 0.10 | 13.3 | 0.27 | 0.11 | 28.5 | 40.7 | 0.28 | 0.10 | 0.26 |
| 1905 | 92 | 22 | -2.06 | 0.11 | 13.4 | 0.27 | 0.11 | 17.1 | 29.4 | 0.02 | 0.12 | 0.25 |
| 201432 | 97 | 22 | -2.00 | 0.11 | 12.8 | 0.25 | 0.08 | 17.0 | 35.6 | 0.08 | 0.06 | 0.10 |
| 202765 | 59 | 18 | -2.02 | 0.14 | 16.1 | 0.38 | 0.21 | 20.7 | 28.5 | 0.06 | -0.06 | 0.19 |
| Subgiants | ||||||||||||
| 669 | 91 | 27 | -2.01 | 0.11 | 6.0 | 0.34 | 0.26 | 62.9 | 86.8 | 0.48 | 0.23 | 0.46 |
| 793 | 105 | 31 | -2.04 | 0.12 | <6.0 | <0.34 | <0.26 | 39.9 | 72.1 | 0.21 | 0.28 | 0.31 |
| 206810 | 85 | 23 | -2.10 | 0.10 | 8.0 | 0.48 | 0.48 | 49.5 | 68.3 | 0.25 | 0.10 | 0.28 |
| Star | S/N | n. | [Fe/H] | rms | EW | [O/Fe] | [O/Fe] | EW | EW | [Na/Fe] | [Mg/Fe] | [Al/Fe] |
| lines | 7771 | LTE | nLTE | 8183 | 8194 | nLTE | nLTE | |||||
| Dwarfs | ||||||||||||
| 4428 | 49 | 22 | -1.52 | 0.14 | 35.7 | 0.35 | 0.24 | 24.4 | 57.1 | -0.35 | 0.04 | -0.48 (1) |
| 4383 | 49 | 23 | -1.42 | 0.19 | 46.0 | 0.60 | 0.49 | 33.6 | 61.5 | -0.23 | 0.01 | -0.11 (1) |
| 202316 | 44 | 21 | -1.56 | 0.20 | 28.7 | 0.31 | 0.20 | 42.6 | 69.0 | -0.09 | -0.06 | -0.45 (1) |
| 4341 | 42 | 23 | -1.57 | 0.26 | 21.6 | 0.30 | 0.21 | 63.4 | 83.7 | 0.18 | 0.06 | -0.76 (1) |
| 4458 | 33 | 17 | -1.52 | 0.27 | 19.4 | 0.04 | -0.06 | 71.9 | 82.6 | 0.24 | -0.09 | -0.63 (1) |
| 4661 | 21 | 16 | -1.24 | 0.17 | .. | .. | .. | 75.4 | 84.3 | 0.28 | 0.15 | -0.09 (1) |
| 5048 | 44 | 25 | -1.43 | 0.12 | 11.0 | -0.29 | -0.37 | 78.2 | 93.7 | 0.37 | -0.24 | 0.19 (1) |
| 4907 | 66 | 28 | -1.41 | 0.21 | 12.0 | -0.25 | -0.34 | 102.9 | 103.0 | 0.61 | -0.09 | 0.14 (1) |
| 200613 | 25 | 18 | -1.24 | 0.18 | .. | .. | .. | 103.5 | 110.1 | 0.64 | 0.06 | 0.60 (1) |
| Subgiants | ||||||||||||
| 1406 | 48 | 44 | -1.39 | 0.16 | 18.0 | 0.40 | 0.34 | 82.1 | 105.7 | 0.02 | 0.20 | 0.10 (2) |
| 1665 | 49 | 41 | -1.34 | 0.15 | .. | .. | .. | 86.7 | 116.6 | 0.10 | 0.10 | -0.13 (2) |
| 1445 | 35 | 33 | -1.53 | 0.13 | .. | .. | .. | 95.0 | .. | 0.19 | 0.06 | 0.33 (2) |
| 1563 | 44 | 38 | -1.42 | 0.17 | 17.4 | 0.38 | 0.33 | 97.0 | 131.0 | 0.25 | 0.11 | 0.17 (2) |
| 1400 | 70 | 41 | -1.44 | 0.14 | 15.3 | 0.33 | 0.28 | 103.4 | .. | 0.29 | 0.10 | 0.34 (2) |
| 1461 | 25 | 32 | -1.38 | 0.24 | .. | .. | .. | 94.9 | 144.4 | 0.29 | 0.10 | -0.06 (2) |
| 202063 | 29 | 38 | -1.49 | 0.27 | .. | .. | .. | 120.4 | 143.8 | 0.44 | 0.13 | 0.33 (2) |
| 1481 | 55 | 46 | -1.39 | 0.15 | .. | .. | .. | 122.5 | 166.2 | 0.54 | -0.07 | 0.69 (2) |
| 1460 | 38 | 32 | -1.37 | 0.15 | <14.0 | <0.25 | <0.19 | 137.4 | .. | 0.65 | -0.19 | 0.86 (2) |
 |
Figure 2: Colour-magnitude diagram for the field stars; MV is computed using Hipparcos parallaxes |
| Open with DEXTER | |
 |
Figure 3: Comparison between EWs measured on the spectra of two dwarfs in NGC 6397 (stars 1543 and 1622), and two dwarfs in NGC 6752 (stars 4907 and 4428). The rms obtained from these comparisons are 3.4 mÅ for the stars in NGC 6397, and 4.8 mÅ for the stars in NGC 6752 (assuming equal error for both stars) |
| Open with DEXTER | |
Equivalent widths (EWs) for a large number of lines were measured using an
authomatic procedure (similar to the one used in Bragaglia et al. 2001; full
details will be given elsewhere). Typical errors in the EWs (obtained by
comparing values measured on different, similar stars) are ![]() mÅ for
NGC 6397 stars, and
mÅ for
NGC 6397 stars, and ![]() mÅ for NGC 6752 stars, but they are as low as
mÅ for NGC 6752 stars, but they are as low as
![]() mÅ in the best cases (e.g. the Li lines at 6707 Å). As an
example, Fig. 3 compares EWs obtained for two TO-stars in NGC 6397
(stars 1543 and 1622) and two TO-stars in NGC 6752 (stars 4907 and 4428). From
this comparison, we obtain rms of 3.4 mÅ and 4.8 mÅ respectively for
typical EWs (assuming errors are the same for the two stars). These values are
comparable with results obtained for much brighter stars at other telescopes.
mÅ in the best cases (e.g. the Li lines at 6707 Å). As an
example, Fig. 3 compares EWs obtained for two TO-stars in NGC 6397
(stars 1543 and 1622) and two TO-stars in NGC 6752 (stars 4907 and 4428). From
this comparison, we obtain rms of 3.4 mÅ and 4.8 mÅ respectively for
typical EWs (assuming errors are the same for the two stars). These values are
comparable with results obtained for much brighter stars at other telescopes.
As discussed in Gratton et al. (1998), the single major
source of error in the derivation of distances to globular clusters is the
possible existence of systematic differences (of 0.015 mag) in the reddening
scales for nearby subdwarfs and the much farther globular clusters. One of the
aims of the present analysis was to derive accurate reddening estimates for
GCs by comparing the observed colours with (reddening free) effective
temperatures
![]() 's obtained from the spectra; for this reason our
temperatures are based on fitting of the wings of the H
's obtained from the spectra; for this reason our
temperatures are based on fitting of the wings of the H![]() profiles
with synthesized lines
profiles
with synthesized lines![]() and not on colours. We wish to emphasize that the
major concern here is the derivation of temperatures using a uniform procedure
for both field and cluster stars; this is also important to ensure that the
derived abundances may be directly comparable (again, a basic issue in the
derivation of accurate distances to clusters). This approach also allows a
proper discussion of systematic differences between the chemical compostion of
field and cluster stars. According to this approach, the systematic errors we
will report are the possible offsets of groups of stars (e.g. those belonging
to a cluster) with respect to the somewhat arbitrary scale defined by our
field stars, used uniformly throughout our analysis.
and not on colours. We wish to emphasize that the
major concern here is the derivation of temperatures using a uniform procedure
for both field and cluster stars; this is also important to ensure that the
derived abundances may be directly comparable (again, a basic issue in the
derivation of accurate distances to clusters). This approach also allows a
proper discussion of systematic differences between the chemical compostion of
field and cluster stars. According to this approach, the systematic errors we
will report are the possible offsets of groups of stars (e.g. those belonging
to a cluster) with respect to the somewhat arbitrary scale defined by our
field stars, used uniformly throughout our analysis.
The H![]() model lines were computed according to the precepts given in
Castelli et al. (1997); throughout this paper we used model
atmospheres extracted by interpolation within the grid by Kurucz with the
overshooting option switched off (Kurucz 1993). Within these models,
convection is considered using a mixing length approach, with a pressure scale
height value of
model lines were computed according to the precepts given in
Castelli et al. (1997); throughout this paper we used model
atmospheres extracted by interpolation within the grid by Kurucz with the
overshooting option switched off (Kurucz 1993). Within these models,
convection is considered using a mixing length approach, with a pressure scale
height value of
![]() .
It must be noted that it is not easy to derive
accurate H
.
It must be noted that it is not easy to derive
accurate H![]() profiles from Echelle spectra, owing to the quite short
free spectral range available for each order. We used the spectra extracted
by the UVES pipeline; our procedure consisted in two steps:
profiles from Echelle spectra, owing to the quite short
free spectral range available for each order. We used the spectra extracted
by the UVES pipeline; our procedure consisted in two steps:
Systematic errors in these temperatures might be not negligible, as shown by Barklem et al. (2000); however, as mentioned above, this is not our major concern, because, insofar temperatures are derived homogenously for cluster and field stars, such errors have very small impact on the present discussion, and on the derivation of distances and ages for globular clusters (discussed in a future paper). The adopted temperature scale is confirmed by analysis of line excitation: however, temperature from excitation have slightly larger error bars due to the limited range of excitation for lines measurable in warm, metal-poor dwarfs and subgiants.
For field stars, we compared these
![]() 's (Col. 7 of Table 1) with
those given by colours (B-V and b-y), using the calibration given by
Kurucz (1993); here we assumed that all these nearby (field) stars are unreddened.
Internal errors in
's (Col. 7 of Table 1) with
those given by colours (B-V and b-y), using the calibration given by
Kurucz (1993); here we assumed that all these nearby (field) stars are unreddened.
Internal errors in
![]() 's from colours are about 26 K. On average,
temperatures derived from H
's from colours are about 26 K. On average,
temperatures derived from H![]() are lower than those derived from colours
by
are lower than those derived from colours
by ![]() K, with a large r.m.s scatter of 188 K. For field stars, we
then corrected the temperatures from colours to those derived from H
K, with a large r.m.s scatter of 188 K. For field stars, we
then corrected the temperatures from colours to those derived from H![]() ,
and averaged the two values, giving a weight 4 to temperatures from colours,
and 1 to temperatures derived from
,
and averaged the two values, giving a weight 4 to temperatures from colours,
and 1 to temperatures derived from
![]() .
These are our "best
temperatures'' for the field stars (Col. 8 of Table 1).
.
These are our "best
temperatures'' for the field stars (Col. 8 of Table 1).
We may compare these "best temperatures'' with those obtained by Alonso et al. (1996) using the IR flux method (Col. 9 of
Table 1). Excluding the discrepant case of HD 132475, on average our best
![]() 's are lower than those given by Alonso et al. by
's are lower than those given by Alonso et al. by ![]() K
(rms
K
(rms
![]() K, 10 stars). Hence our
K, 10 stars). Hence our
![]() 's can be assumed to
be on the same scale of Alonso et al. Since temperatures from the IR flux
method are rather robust with respect to possible errors in model atmospheres
(although they are sensitive to uncertainties in the adopted reddening
values), this comparison shows that systematic errors in our temperature scale
from H
's can be assumed to
be on the same scale of Alonso et al. Since temperatures from the IR flux
method are rather robust with respect to possible errors in model atmospheres
(although they are sensitive to uncertainties in the adopted reddening
values), this comparison shows that systematic errors in our temperature scale
from H![]() profiles are likely not very large.
profiles are likely not very large.
When plotted one on top of the other (separately: dwarfs and subgiants, and
stars in different clusters), the H![]() profiles for cluster stars look
undistinguishable. Furthermore, we were unable to find any correlation
between colours and temperatures either from line excitation or H
profiles for cluster stars look
undistinguishable. Furthermore, we were unable to find any correlation
between colours and temperatures either from line excitation or H![]() profiles. We then concluded that the stars are intrinsically very similar,
and that the slightly different values of colours and temperatures we
derived for each star are due to random errors. In the following analysis, we
have then adopted for all stars in these groups the same average temperatures
(note however that this assumption is not critical in the present discussion).
profiles. We then concluded that the stars are intrinsically very similar,
and that the slightly different values of colours and temperatures we
derived for each star are due to random errors. In the following analysis, we
have then adopted for all stars in these groups the same average temperatures
(note however that this assumption is not critical in the present discussion).
Surface gravities ![]() were obtained from the location of the stars in
the colour magnitude diagram, assuming masses consistent with an age of 14 Gyr
(again, this assumption is not critical). As usual, microturbulent
velocities were obtained by eliminating trends of abundances derived from
individual Fe lines with expected line strength.
Star-to-star scatter in Fe abundances within each group (same cluster, same
evolutionary phase) were reduced by adopting for all stars the same
microturbulent velocity; these average values were then adopted in the final
analysis.
were obtained from the location of the stars in
the colour magnitude diagram, assuming masses consistent with an age of 14 Gyr
(again, this assumption is not critical). As usual, microturbulent
velocities were obtained by eliminating trends of abundances derived from
individual Fe lines with expected line strength.
Star-to-star scatter in Fe abundances within each group (same cluster, same
evolutionary phase) were reduced by adopting for all stars the same
microturbulent velocity; these average values were then adopted in the final
analysis.
The finally adopted atmospheric parameters (effective temperatures in
K/surface gravities/model metal abundances/microturbulent velocities in
km s-1) were as follows: NGC 6397 TO-stars (6476/4.10/-2.04/1.32);
NGC 6397 subgiants (5478/3.42/-2.04/1.32); NGC 6752 TO-stars
(6226/4.28/-1.43/0.70); NGC 6752 subgiants (5347/3.54/-1.43/1.10).
| Element |
|
|
|
| +100 K | +0.2 dex | +0.2 km s-1 | |
| TO-star | |||
| [Fe/H] | +0.096 | -0.054 | -0.050 |
| [O/Fe] | -0.161 | +0.123 | +0.048 |
| [Na/Fe] | -0.037 | +0.007 | +0.032 |
| [Mg/Fe] | -0.034 | +0.006 | +0.041 |
| [Al/Fe] | +0.001 | -0.012 | +0.007 |
| Subgiants | |||
| [Fe/H] | +0.108 | -0.023 | -0.049 |
| [O/Fe] | -0.200 | +0.098 | +0.044 |
| [Na/Fe] | -0.044 | -0.010 | +0.026 |
| [Mg/Fe] | -0.055 | +0.020 | +0.043 |
| [Al/Fe] | -0.080 | +0.021 | +0.038 |
Sensitivities of abundances to errors in the atmospheric parameters are given
in Table 4. Errors in final abundances are mostly due to possible errors in
the adopted
![]() 's. For our line list (dominated by low excitation
lines), Fe I abundances rise by 0.10 dex, [O/Fe] values by -0.20 dex, and
[Na/Fe] ones by -0.04 dex for a 100 K increase in the adopted
's. For our line list (dominated by low excitation
lines), Fe I abundances rise by 0.10 dex, [O/Fe] values by -0.20 dex, and
[Na/Fe] ones by -0.04 dex for a 100 K increase in the adopted
![]() .
Systematic errors in
.
Systematic errors in
![]() 's are dominated by uncertainties in the
fitting of the H
's are dominated by uncertainties in the
fitting of the H![]() profiles: they are about
profiles: they are about ![]() K for the dwarfs
and
K for the dwarfs
and ![]() K for the subgiants
K for the subgiants![]() , leading to errors in the [Fe/H] values of
, leading to errors in the [Fe/H] values of ![]() dex and
dex and
![]() dex respectively for TO-stars and subgiants. This value,
appropriate for cluster stars, is smaller than that given for field stars
simply because our
dex respectively for TO-stars and subgiants. This value,
appropriate for cluster stars, is smaller than that given for field stars
simply because our
![]() 's for cluster stars are actually the average
over the values obtained for several stars, and errors for individual stars
are given by uncertainties in the flat fielding procedure, that are only
weakly affected by S/N. Corresponding errors in [O/Fe]'s are
's for cluster stars are actually the average
over the values obtained for several stars, and errors for individual stars
are given by uncertainties in the flat fielding procedure, that are only
weakly affected by S/N. Corresponding errors in [O/Fe]'s are ![]() and
and
![]() dex; those in [Na/Fe] are
dex; those in [Na/Fe] are ![]() and
and ![]() dex. However,
in the context of the O-Na anticorrelation, errors in temperatures adopted for
individual stars are more important. In the case of NGC 6397, a quite realistic
estimate can be obtained by the star-to-star scatter in Fe abundances, that is
0.032 dex, corresponding to an rms spread of 33 K in the
dex. However,
in the context of the O-Na anticorrelation, errors in temperatures adopted for
individual stars are more important. In the case of NGC 6397, a quite realistic
estimate can be obtained by the star-to-star scatter in Fe abundances, that is
0.032 dex, corresponding to an rms spread of 33 K in the
![]() 's.
The adoption of a uniform temperature would then yield errors of
's.
The adoption of a uniform temperature would then yield errors of ![]() dex in [O/Fe]'s and
dex in [O/Fe]'s and ![]() dex in [Na/Fe]'s (to be compared with the
observed star-to-star scatter). In the case of NGC 6752, the star-to-star
scatter of 0.096 dex in [Fe/H]'s also includes an important contribution due
to noise in the EWs: in fact the rms reduces to 0.074 dex if only spectra
with S/N> 40 are considered. We conclude that errors in individual
dex in [Na/Fe]'s (to be compared with the
observed star-to-star scatter). In the case of NGC 6752, the star-to-star
scatter of 0.096 dex in [Fe/H]'s also includes an important contribution due
to noise in the EWs: in fact the rms reduces to 0.074 dex if only spectra
with S/N> 40 are considered. We conclude that errors in individual
![]() 's are
's are
![]() 73 K. Related errors in [O/Fe] and [Na/Fe] abundances are
73 K. Related errors in [O/Fe] and [Na/Fe] abundances are
![]() 0.15 and
0.15 and
![]() 0.03 dex. Again, these are the values to be compared
with the observed scatter.
0.03 dex. Again, these are the values to be compared
with the observed scatter.
Fe abundances were derived using a rather large number of lines, typically
![]() 20 and
20 and ![]() 30-40 for TO-stars and subgiants respectively. Full
details about the line list, including gf's, EWs and abundances from
individual lines, will be given in separate papers (in preparation).
30-40 for TO-stars and subgiants respectively. Full
details about the line list, including gf's, EWs and abundances from
individual lines, will be given in separate papers (in preparation).
The Fe abundance obtained for dwarfs in NGC 6397 (
![]() ,
where
this error bar is the internal error as given by the standard deviation of the
mean) is in good agreement with that determined from subgiants
(
,
where
this error bar is the internal error as given by the standard deviation of the
mean) is in good agreement with that determined from subgiants
(
![]() ). The average of the two groups is
). The average of the two groups is
![]() (this is the internal error of our analysis, obtained by combining
results for TO-stars and subgiants; systematic errors, within the abundance
scale defined by observations of the field stars, are mainly due to
uncertainties in the adopted temperature; again combining results for TO stars
and subgiants, that may be considered as independent each other, they are
(this is the internal error of our analysis, obtained by combining
results for TO-stars and subgiants; systematic errors, within the abundance
scale defined by observations of the field stars, are mainly due to
uncertainties in the adopted temperature; again combining results for TO stars
and subgiants, that may be considered as independent each other, they are ![]() dex). This value is less than that derived from giants in Carretta &
Gratton (1997):
dex). This value is less than that derived from giants in Carretta &
Gratton (1997):
![]() ), and Zinn & West (1984:
), and Zinn & West (1984:
![]() ). However it agrees very well with the value obtained by
Minniti et al. (1993:
). However it agrees very well with the value obtained by
Minniti et al. (1993:
![]() ), and the recent, comprehensive
analysis of giants and subgiants by Castilho et al. (2000:
), and the recent, comprehensive
analysis of giants and subgiants by Castilho et al. (2000:
![]() ).
).
The equilibrium of ionization is not well reproduced: abundances from neutral
Fe lines are 0.11 dex larger than those from singly ionized Fe lines. The same
result is obtained for NGC 6752 and our field stars. Note that a smaller
difference (0.07 dex) in the same sense is also present in our solar reference
analysis (in that case we obtained
![]() from Fe I lines,
and 7.45 from Fe II lines using the solar model atmosphere from Kurucz 1993,
with no overshooting). We then think most of the difference for the Sun is due
to either the adopted gf's values (these are laboratory values taken from
recent literature) or to the model atmospheres (models might underestimate the
temperature gradient in real atmospheres, perhaps due to an inappropriate
consideration of convection). The residual difference for the program stars
might be due to the adoption of slightly too high
from Fe I lines,
and 7.45 from Fe II lines using the solar model atmosphere from Kurucz 1993,
with no overshooting). We then think most of the difference for the Sun is due
to either the adopted gf's values (these are laboratory values taken from
recent literature) or to the model atmospheres (models might underestimate the
temperature gradient in real atmospheres, perhaps due to an inappropriate
consideration of convection). The residual difference for the program stars
might be due to the adoption of slightly too high
![]() 's
(
's
(![]() 40-50 K) or too low gravities (by
40-50 K) or too low gravities (by ![]() 0.1 dex). Note that it cannot be due
to departures from LTE, because the expected dominating effect
(overionization: Idiart & Thévenin 1999; Gratton et al. 1999) would lead to
larger abundances from Fe II lines than from Fe I ones (opposite to
observations).
0.1 dex). Note that it cannot be due
to departures from LTE, because the expected dominating effect
(overionization: Idiart & Thévenin 1999; Gratton et al. 1999) would lead to
larger abundances from Fe II lines than from Fe I ones (opposite to
observations).
The star-to-star scatter in [Fe/H] values is extremely small: the rms
scatter is only 0.04 dex (i.e. 10%) for NGC 6397. This seems a very
homogeneous cluster as far as Fe abundances are considered.
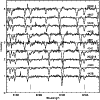 |
Figure 4: Spectral region including the 8183-94 Å Na I doublet in NGC 6752 TO-stars (stars are ordered according to decreasing Na abundances). The position of the Na lines is marked. Note that all these stars essentially have the same temperature, gravity, overall metal abundance and microturbulent velocity, so that observed variations in the line strengths can be directly interpreted as spread in the abundances |
| Open with DEXTER | |
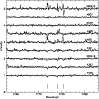 |
Figure 5: Same as Fig. 3, but for the region including the 7771-74 Å OI triplet in NGC 6752 TO-stars (stars are ordered according to decreasing Na abundances). The position of the O lines is marked |
| Open with DEXTER | |
On the other side, the [Fe/H] value for NGC 6752 (
![]() ,
internal error; systematic error is again
,
internal error; systematic error is again ![]() dex), obtained both from
TO and subgiant stars, which agree completely, coincides with that derived
from giants by Carretta & Gratton (1997:
dex), obtained both from
TO and subgiant stars, which agree completely, coincides with that derived
from giants by Carretta & Gratton (1997:
![]() ); it is
somewhat larger than the value quoted by Zinn & West (
); it is
somewhat larger than the value quoted by Zinn & West (
![]() )
and
Minniti et al. (1993:
)
and
Minniti et al. (1993:
![]() ). The spectra of NGC 6752 have a
S/N lower than those in NGC 6397, since we chose to observe more stars, even at
a lower S/N. The scatter of abundances for individual lines (from 0.12 to 0.27
dex) is larger than that obtained for stars in NGC 6397, roughly in agreement
with the lower S/N.
). The spectra of NGC 6752 have a
S/N lower than those in NGC 6397, since we chose to observe more stars, even at
a lower S/N. The scatter of abundances for individual lines (from 0.12 to 0.27
dex) is larger than that obtained for stars in NGC 6397, roughly in agreement
with the lower S/N.
For field stars we may compare the present Fe abundances with those derived by
Carretta et al. (2000). Limiting ourselves to only those stars for
which Carretta et al. considered high dispersion abundances, the present Fe
abundances are smaller on average by
![]() dex (11 stars,
dex (11 stars,
![]() dex). The slightly lower metal abundances are due to lower
dex). The slightly lower metal abundances are due to lower
![]() 's adopted in the present paper.
's adopted in the present paper.
In our analysis, oxygen abundances were derived from the permitted infrared
triplet (7771-74 Å): the forbidden lines are too weak in the program stars
to be reliably measured, and we did not observe the region of the OH band in
the near UV because the required exposure times would be prohibitive even for
an 8 meter telescope. Na abundances are based on the quite strong doublet at
8183-94 Å, clearly visible in all stars. We checked that telluric lines were
not blended with the stellar features. For both O and Na, our abundances
included non-LTE corrections, computed following the precepts of Gratton et al. (1999): however, these corrections are small and they do not affect any of
the conclusion reached in this paper. Mg abundances are based on a few high
excitation lines in the blue and yellow portion of the spectrum (typically
three to four lines were measured for each star). Finally, whenever possible
Al abundances were measured using the high excitation IR doublet at
8772.9/73.9 Å. However, this was possible only for subgiants in NGC 6752,
since in the other cases this doublet is too weak, and the only chance to
measure Al abundances is by using the resonance doublet at 3944/61 Å.
These lines, while stronger, are not ideal abundance indicators due to
saturation and the presence of large departures from LTE (see e.g. François
1986; Beyley & Cottrell 1987; and the discussion in Gratton & Sneden 1988).
An extensive discussion of departures from LTE for Al has been presented by
Baumüller & Gehren (1997): these authors found that rather large
(![]() 0.6 dex) non-LTE corrections are required for the resonance lines for model
atmosphere parameters appropriate for the program stars, in the sense that an
LTE analysis should grossly underestimate Al abundances. Application of such
corrections greatly improve the agreement between abundances from the
resonance lines and those derived from the 8772.9-73.9 Å doublet (for which
non-LTE corrections are small). Such corrections were then included in the
abundances listed in Tables 2 and 3. Although these large corrections might be
somewhat uncertain, analysis of these lines may still be useful to discuss the
Mg-Al anticorrelation insofar only stars with very similar atmospheric
parameters are considered, because in this case we expect that departures from
LTE should be essentially the same for all such stars.
0.6 dex) non-LTE corrections are required for the resonance lines for model
atmosphere parameters appropriate for the program stars, in the sense that an
LTE analysis should grossly underestimate Al abundances. Application of such
corrections greatly improve the agreement between abundances from the
resonance lines and those derived from the 8772.9-73.9 Å doublet (for which
non-LTE corrections are small). Such corrections were then included in the
abundances listed in Tables 2 and 3. Although these large corrections might be
somewhat uncertain, analysis of these lines may still be useful to discuss the
Mg-Al anticorrelation insofar only stars with very similar atmospheric
parameters are considered, because in this case we expect that departures from
LTE should be essentially the same for all such stars.
For NGC 6397, the O abundance is
![]() (internal error;
systematic errors are
(internal error;
systematic errors are ![]() 0.1 dex), and the average [Na/Fe] ratio is
0.1 dex), and the average [Na/Fe] ratio is
![]() .
This O excess is quite small in comparison to the
values usually found for metal-poor stars (see e.g. Gratton et al. 2000), but
it agrees very well with the mean values determined by Minniti et al. (1997):
.
This O excess is quite small in comparison to the
values usually found for metal-poor stars (see e.g. Gratton et al. 2000), but
it agrees very well with the mean values determined by Minniti et al. (1997):
![]() )
and Norris & Da Costa (1995: [O/Fe]
)
and Norris & Da Costa (1995: [O/Fe]![]() 0.1) from analysis of
the forbidden lines in red giant spectra. Also the Mg abundance we get is quite
low: this point will be discussed in a next paper. On the other side, the
[Na/Fe] value we found agrees well with that determined for a single red giant
by Carretta (1994:
0.1) from analysis of
the forbidden lines in red giant spectra. Also the Mg abundance we get is quite
low: this point will be discussed in a next paper. On the other side, the
[Na/Fe] value we found agrees well with that determined for a single red giant
by Carretta (1994:
![]() ), and for two more by Norris & Da Costa
(1995: [Na/Fe]
), and for two more by Norris & Da Costa
(1995: [Na/Fe]![]() 0.2), while it is somewhat larger than the value of
0.2), while it is somewhat larger than the value of
![]() found by Minniti et al. (1997). We wish to remark that none
of the program stars seem to be oxygen-poor and sodium-rich. The star-to-star
scatter in our determinations (0.15 and 0.14 dex, rms, respectively) is
larger than expected from errors in the EWs alone (we would expect rms
values of
found by Minniti et al. (1997). We wish to remark that none
of the program stars seem to be oxygen-poor and sodium-rich. The star-to-star
scatter in our determinations (0.15 and 0.14 dex, rms, respectively) is
larger than expected from errors in the EWs alone (we would expect rms
values of ![]() 0.10 dex): however it may be justified by some star-to-star
scatter in the atmospheric parameters (within the measuring errors), not
accounted for in our analysis (we are assuming that all dwarfs and subgiants
may be analyzed using the same model atmospheres), and by a small offset in
the results for dwarfs and subgiants (again, likely due to small errors in the
adopted set of atmospheric parameters, within our quoted uncertainties). Given
the small spread in Fe abundances, and the absence of a clear O-Na
anticorrelation, we conclude that NGC 6397 is indeed a very homogenous cluster.
On the whole, our results indicate that stars in this cluster conforms to the
paradigm set by field stars, confirming earlier findings by Bell & Dickens (1980).
0.10 dex): however it may be justified by some star-to-star
scatter in the atmospheric parameters (within the measuring errors), not
accounted for in our analysis (we are assuming that all dwarfs and subgiants
may be analyzed using the same model atmospheres), and by a small offset in
the results for dwarfs and subgiants (again, likely due to small errors in the
adopted set of atmospheric parameters, within our quoted uncertainties). Given
the small spread in Fe abundances, and the absence of a clear O-Na
anticorrelation, we conclude that NGC 6397 is indeed a very homogenous cluster.
On the whole, our results indicate that stars in this cluster conforms to the
paradigm set by field stars, confirming earlier findings by Bell & Dickens (1980).
 |
Figure 6: Run of the abundances of Na and of O for stars in NGC 6752. Filled squares are TO-stars, open squares are subgiants, and lines represent upper limits (for O) |
| Open with DEXTER | |
NGC 6752 presents a very different scenario (this is not too surprising, in view of the variations of the strength of CN and CH bands among stars on the MS already noticed by Suntzeff & Smith 1991). There is a clear anti-correlation between O and Na abundances even for stars at the TO. This is clearly illustrated by Figs. 4 and 5, where we plotted the spectral regions including the Na and O lines in these stars (stars are ordered according to decreasing Na abundances). Notice that all these stars have the same (or at least very similar) temperature, gravity, overall metal abundance and microturbulent velocity, so that observed variations in the line strengths may be directly interpreted as spread in the abundances: then, in spite of the fact that a few of the spectra are somewhat noisy, this result does not depend on details of the analysis, but rather is a solid purely observational evidence, largely independent of all the assumptions made. We found that Na abundances span a range of almost an order of magnitude. O abundances also change by a rather large factor; while not as extreme as in M 13, we found a rather extensive O-Na anticorrelation in NGC 6752 too. This anti-correlation is shown in Fig. 6. There is a small offset in the O-Na anticorrelation between TO-stars and subgiants, but we think this is an artefact of the analysis (slightly incorrect offsets in temperatures and gravities).
 |
Figure 7: Run of the c1 index from Strömgren photometry with the Na abundance for stars in NGC 6752. Filled squares are TO-stars, and open squares are subgiants |
| Open with DEXTER | |
There is some correlation between c1 and the O-Na trends (see Fig. 7). Note however that the scatter in this relation is quite large and the correlation is significant only for subgiants; this is not surprising, since our spectra shows that molecular bands are very weak in the spectra of TO-stars of NGC 6752, and their variations are not likely to affect significantly intermediate band colours like c1.
 |
Figure 8: Run of the abundances of Mg against that of Al for stars in NGC 6752. The upper panel shows results for TO-stars; the lower panel those for subgiants. Note that Al abundances for TO-stars were obtained using the resonance doublet, which is affected by large departures from LTE |
| Open with DEXTER | |
Figure 8 displays results for Mg and Al in NGC 6752. The
star-to-star variations in the Al abundances are large: ![]() 1 dex among
subgiants, and even more among TO-stars. These large variations cannot be
explained by observational errors, and (for TO-stars) by any plausible
differential non-LTE effect among stars with very similar atmospheric
parameters. On the other side, star-to-star variations in the Mg abundances
are much smaller (
1 dex among
subgiants, and even more among TO-stars. These large variations cannot be
explained by observational errors, and (for TO-stars) by any plausible
differential non-LTE effect among stars with very similar atmospheric
parameters. On the other side, star-to-star variations in the Mg abundances
are much smaller (
![]() 0.4 dex), and they may be seen clearly only among
subgiants; for TO-stars, the used Mg lines are quite weak and a larger
scatter in the abundances is due to errors in the EWs. Data for subgiants,
for which reliable Al abundances could be obtained from the high excitation Al
I doublet at 8772.9/73.9 Å, indicate that also for these elements there is a
clear anticorrelation between Mg and Al. Stars 1460 and 1481 (the two most
Na-rich subgiants) are clearly Mg-poor, Al-rich. We emphasize here that while
the Mg-Al anticorrelation is not obvious in panel a of Fig. 8, we
think that such an anticorrelation exists also for TO-stars because the Al
abundances show a very large star-to-star variation, correlated with Na
abundance variations; we think the anticorrelation is less obvious in this
case because we had to measure the resonance doublet of Al at 3944/61 Å, not
an ideal abundance indicator as we mentioned above, and moreover Mg abundances
have larger errors, comparable to the star-to-star variations seen among
subgiants.
0.4 dex), and they may be seen clearly only among
subgiants; for TO-stars, the used Mg lines are quite weak and a larger
scatter in the abundances is due to errors in the EWs. Data for subgiants,
for which reliable Al abundances could be obtained from the high excitation Al
I doublet at 8772.9/73.9 Å, indicate that also for these elements there is a
clear anticorrelation between Mg and Al. Stars 1460 and 1481 (the two most
Na-rich subgiants) are clearly Mg-poor, Al-rich. We emphasize here that while
the Mg-Al anticorrelation is not obvious in panel a of Fig. 8, we
think that such an anticorrelation exists also for TO-stars because the Al
abundances show a very large star-to-star variation, correlated with Na
abundance variations; we think the anticorrelation is less obvious in this
case because we had to measure the resonance doublet of Al at 3944/61 Å, not
an ideal abundance indicator as we mentioned above, and moreover Mg abundances
have larger errors, comparable to the star-to-star variations seen among
subgiants.
We are now preparing line lists to study CH and CN abundances. However, it seems clear that the strength of these bands is correlated with Na and O abundances. Also, there is a correlation with the Stromgren c1 index, albeit the scatter is quite large. Finally, in a forthcoming paper we will present a full discussion of the Li abundances in these stars. Here we anticipate that Li abundances in NGC 6752 stars seem also anticorrelated with the Na ones.
We have presented the first results of the ESO Large Program 165.L-0263: we
have used the UVES spectrograph on VLT2 to obtain high resolution (
![]() )
spectra for a quite large number of stars at the turn-off (14 stars
between the two GCs) and the base of the giant branch (12 stars) in the
globular clusters NGC 6397 and NGC 6752. Thanks to the efficiency and wide
spectral coverage of UVES we were able to obtain reliable EWs for a number
of lines of Fe, Li, O, Na, and other elements. The main results of this first
analysis are:
)
spectra for a quite large number of stars at the turn-off (14 stars
between the two GCs) and the base of the giant branch (12 stars) in the
globular clusters NGC 6397 and NGC 6752. Thanks to the efficiency and wide
spectral coverage of UVES we were able to obtain reliable EWs for a number
of lines of Fe, Li, O, Na, and other elements. The main results of this first
analysis are:
We are then forced to some primordial mechanism, like those proposed years ago
by Cottrell & Da Costa (1981) and D'Antona et al. (1983). In
both scenarios, the inhomogeneities are due to the mass lost by intermediate
mass stars (
![]() )
during the Asymptotic Giant Branch (AGB)
evolution and the planetary nebula expulsion: the two scenarios differ because
Cottrell & Da Costa think of a prolonged star formation, with most recently
formed stars having a different chemical composition from the first ones; while
D'Antona et al. consider pollution of the outer layers of already formed stars
by other objects in the cluster. Anyhow, in both scenarios the intracluster
gas is heavily nuclearly processed, due both to the occurrence of the third
dredge-up from the helium buffer (Iben 1975) and by Hot Bottom Burning (HBB)
at the basis of the convective envelopes of these massive AGB stars. Models
for these evolutionary phases (Sackmann & Boothroyd 1992; Ventura et al.
2000) successfully explain the occurrence and evolution of the lithium rich,
oxygen rich massive AGBs in the Magellanic Clouds (Smith et al. 1995).
Very recent models by Ventura et al. (2001) show that, in full stellar models
computed for these intermediate mass stars at the low metallicities of
Globular Clusters, the HBB temperature can reach values as large as 108 K.
At this temperature, the complete CNO cycle operates, depleting oxygen. At the
same time, p-captures on 24Mg and 20Ne produce Al (see also
Denissenkov et al. 1998) and Na. This model can then explain the
anticorrelations O-Na and Mg-Al. In this context it is very interesting to
note that no O-Na anticorrelation is seen in NGC 6397. Also, Li abundances in
this cluster follows the paradigma set by field metal-poor stars (Castilho et al. 2000). NGC 6397 is a quite small cluster (mass
)
during the Asymptotic Giant Branch (AGB)
evolution and the planetary nebula expulsion: the two scenarios differ because
Cottrell & Da Costa think of a prolonged star formation, with most recently
formed stars having a different chemical composition from the first ones; while
D'Antona et al. consider pollution of the outer layers of already formed stars
by other objects in the cluster. Anyhow, in both scenarios the intracluster
gas is heavily nuclearly processed, due both to the occurrence of the third
dredge-up from the helium buffer (Iben 1975) and by Hot Bottom Burning (HBB)
at the basis of the convective envelopes of these massive AGB stars. Models
for these evolutionary phases (Sackmann & Boothroyd 1992; Ventura et al.
2000) successfully explain the occurrence and evolution of the lithium rich,
oxygen rich massive AGBs in the Magellanic Clouds (Smith et al. 1995).
Very recent models by Ventura et al. (2001) show that, in full stellar models
computed for these intermediate mass stars at the low metallicities of
Globular Clusters, the HBB temperature can reach values as large as 108 K.
At this temperature, the complete CNO cycle operates, depleting oxygen. At the
same time, p-captures on 24Mg and 20Ne produce Al (see also
Denissenkov et al. 1998) and Na. This model can then explain the
anticorrelations O-Na and Mg-Al. In this context it is very interesting to
note that no O-Na anticorrelation is seen in NGC 6397. Also, Li abundances in
this cluster follows the paradigma set by field metal-poor stars (Castilho et al. 2000). NGC 6397 is a quite small cluster (mass
![]() ,
from
the integrated magnitude MV=-6.58, Harris 1996, and a mass-to-light ratio
of
,
from
the integrated magnitude MV=-6.58, Harris 1996, and a mass-to-light ratio
of ![]() 2, typical for a globular cluster). On the other side, the O-Na
anticorrelation is seen in the more massive cluster NGC 6752 (mass
2, typical for a globular cluster). On the other side, the O-Na
anticorrelation is seen in the more massive cluster NGC 6752 (mass ![]()
![]() ,
from the integrated magnitude MV=-7.68, Harris 1996, and
the same mass-to-light ratio used for NGC 6397). A (cluster) mass threshold
should be present in accretion scenarios (see e.g. Gratton 2001), and likely
also in the prolonged star formation models. We plan to address thoroughly
such problems in forthcoming papers.
,
from the integrated magnitude MV=-7.68, Harris 1996, and
the same mass-to-light ratio used for NGC 6397). A (cluster) mass threshold
should be present in accretion scenarios (see e.g. Gratton 2001), and likely
also in the prolonged star formation models. We plan to address thoroughly
such problems in forthcoming papers.
Acknowledgements
This research has made use of the SIMBAD data base, operated at CDS, Strasbourg, France. We wish to thank V. Hill for help during the observations, and P. Bertelli for useful comments. We thank our referee (J. Cohen) for having provided very useful suggestions and data in advance of publication