A&A 369, 222-238 (2001)
DOI: 10.1051/0004-6361:20010121
Multicomponent radiatively driven stellar winds
I. Nonisothermal three-component wind of hot B stars
J. Krticka1,2 -
J. Kubát2
1 - Katedra teoretické fyziky a astrofyziky PrF MU,
Kotlárská 2, 611 37 Brno, Czech Republic
2 -
Astronomický ústav, Akademie ved Ceské
republiky, 251 65 Ondrejov, Czech Republic
Received 12 September 2000 / Accepted 12 January 2001
Abstract
We computed models of a three-component nonisothermal radiatively driven
stellar wind for different spectral types of hot B stars.
We showed that friction heats mainly the outer parts of the wind and the
modified temperature stratification leads to a decrease of the outflow
velocity.
Contrary to the isothermal case, even the possibility of decoupling of
radiatively absorbing ions and (major) nonabsorbing component is
excluded for a realistic form of the driving force.
Regardless of the actual form of the driving force, we derived general
conditions under which decoupling of a stellar wind may occur.
We demonstrated that the possibility of decoupling is closely related to
the functional dependence of the driving force and to the ratio of
the densities of individual components.
We discuss several consequences of a multifluid phenomenon in hot star
winds, particularly metallicity effects and the implications of possible helium
decoupling on chemically peculiar stars.
We propose an explanation of the low terminal velocity of 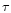 Sco based
on frictional heating.
Sco based
on frictional heating.
Key words: hydrodynamics -
stars: mass-loss -
stars: early-type -
stars: winds -
stars: individual: 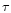 Sco
Sco
In fundamental papers, Lucy & Solomon (1970) and Castor et al.
(1975, hereafter CAK) showed that hot stars should have a
wind driven by radiation absorbed in spectral lines.
After some refinements of the theory of this wind (Abbott 1982;
Friend & Abbott 1986; Pauldrach et al. 1986) it was possible
to explain basic observed features of the radiatively driven stellar
wind.
Since the formulation of the basic theory it has been frequently assumed
that the wind was isothermal to make the problem as simple as possible.
Consequently, the thermal structure of the radiatively driven wind was
studied only occasionally.
Drew (1985) computed statistical, thermal, and ionization
equilibrium of P Cygni's wind and later extended the calculations for
many early-type stars (Drew 1989).
She showed that energy balance of a high density wind is dominated by
the equilibrium between photoionization heating and radiative cooling.
For low density winds, additional effects become important, such as the
so-called Doppler heating and cooling introduced by Gayley
& Owocki (1994).
This effect is a natural consequence of the dependence of the radiative
force on the velocity gradient (via the Doppler effect) and physically
it arises from the difference between absorption and emission frequency
in the moving medium.
The second mechanism is the frictional heating (Springmann & Pauldrach
1992) caused by inelastic collisions between different
particles.
The latter effect is also important for the overall structure of the
wind, because for low-density winds, friction may not be capable of driving
passive (non-absorbing) plasma.
Springmann & Pauldrach proposed that the so-called "ion runaway'' may
occur.
However, they did not solve the hydrodynamic equation itself; they
mainly intended to compute temperature structure of the wind affected by
frictional heating.
They explained the low terminal velocity of 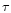 Sco as a consequence
of decoupling of absorbing ions.
Sco as a consequence
of decoupling of absorbing ions.
Babel (1995) computed a three-component model of the
radiatively driven wind and showed that for the case of a main-sequence
A star, friction may lead to decoupling of the passive plasma.
He explained the elemental separation in the atmosphere of chemically
peculiar stars on the basis of the multicomponent nature of the
wind.
These results stimulated many authors to study the possible effects of
decoupling, however, not by self-consistent solving of the appropriate
hydrodynamic equations.
Porter & Drew (1995) studied decoupling in the outflow from
B stars, Porter & Skouza (1999) using the theory of the
decoupled wind pointed out the possibility of the presence of pulsating
shells around stars with low-density radiatively driven wind, and Hunger
& Groote (1999) studied decoupling of helium in a stellar wind.
On the other hand, Krticka & Kubát (2000, hereafter KK)
showed on the basis of a simple theory (an isothermal two-component
wind) that for late B stars friction does not lead to decoupling of the
radiatively accelerated ions.
They uncovered a surprising fact that friction leads to an abrupt decrease
in the outflow velocity gradient.
However, they pointed out that for extremely low-density winds, ion
runaway may occur.
The basic shortfall of this model is the isothermicity of the wind and
neglecting of electrons.
In this paper, we intend to include both electrons and the possible
effect of the nonisothermal wind into our model.
We assume that the star has a stationary spherically symmetric
radiatively driven stellar wind consisting of three ideal gas
components, namely of a passive plasma (hydrogen ions with mass equal to
proton mass
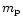 and charge equal to proton charge
and charge equal to proton charge
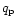 ), of
absorbing ions with mass
), of
absorbing ions with mass
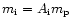 and charge
and charge
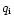 ,
and
of electrons with mass
,
and
of electrons with mass
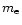 and charge
and charge
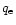 .
Finally, we assume that the temperature is the same for all three components
(
.
Finally, we assume that the temperature is the same for all three components
(
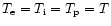 ).
).
Each component of the wind is adequately described by the continuity
equation
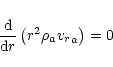 |
(1) |
and by the equation of motion (cf. Braginskij 1963)
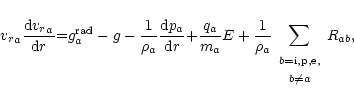 |
(2) |
where
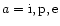 and subscripts
and subscripts
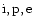 stand for
metallic ions, passive plasma, and electrons, respectively.
In these equations
vra and
stand for
metallic ions, passive plasma, and electrons, respectively.
In these equations
vra and 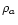 are radial velocity and
density of the corresponding particles,
are radial velocity and
density of the corresponding particles,
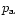 is partial pressure of
each component,
is partial pressure of
each component,
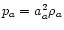 where isothermal sound speed is
aa2=kT/ma,
g is gravitational acceleration,
where isothermal sound speed is
aa2=kT/ma,
g is gravitational acceleration,
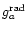 is
radiative acceleration acting on absorbing ions and electrons (we assume
no radiative force acting on passive plasma), E is the charge separation
electric field and Rab is the frictional force
exerted by component b on component a.
Gravitational acceleration acting on each component of the fluid has the
form
is
radiative acceleration acting on absorbing ions and electrons (we assume
no radiative force acting on passive plasma), E is the charge separation
electric field and Rab is the frictional force
exerted by component b on component a.
Gravitational acceleration acting on each component of the fluid has the
form
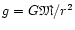 ,
where
,
where
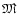 is the stellar mass and G is
the gravitational constant.
The radiative acceleration acting on an electron is given by the absorption
on the free electrons and has the form
is the stellar mass and G is
the gravitational constant.
The radiative acceleration acting on an electron is given by the absorption
on the free electrons and has the form
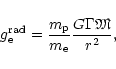 |
(3) |
where
is the ratio of the acting radiative force caused by absorption of
radiation by free electrons and gravitational force (L is the stellar
luminosity).
We take the radiative acceleration acting on absorbing ions in the form
(see Castor et al. 1975)
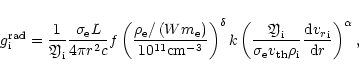 |
(4) |
with force multipliers k, 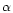 ,
,
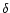 after Abbott
(1982).
Here,
after Abbott
(1982).
Here,
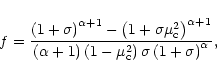 |
(5) |
is the finite disk correction factor (Friend & Abbott 1986;
Pauldrach et al. 1986),
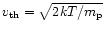 is the thermal speed,
and
is the thermal speed,
and
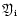 is the ratio of the metallic ion density to passive
plasma density
(we used the same value as in KK,
is the ratio of the metallic ion density to passive
plasma density
(we used the same value as in KK,
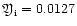 ).
We introduced the latter ratio to enable calculation of the radiative
force not from the whole plasma density (as is usually adopted in the
standard CAK theory) but from the absorbing ion density.
).
We introduced the latter ratio to enable calculation of the radiative
force not from the whole plasma density (as is usually adopted in the
standard CAK theory) but from the absorbing ion density.
There is an apparent contradiction in using the hydrogen thermal
speed instead of the ion thermal speed.
Use of the ion thermal speed seems natural, since only ions
are accelerated by radiation.
As was found by Abbott (1982), the acceleration from a
single line in the isothermal wind
is independent of the thermal speed.
Therefore the choice of the formula for
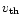 is completely
arbitrary, and he decided to choose the hydrogen thermal speed for the
calculation of the wind parameters k,
is completely
arbitrary, and he decided to choose the hydrogen thermal speed for the
calculation of the wind parameters k, 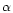 ,
and
,
and 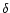 .
Since we are using his parameters for the calculation of the line force,
it is necessary to use the same thermal speed for the calculation
of the line force as Abbott (1982) did, namely the hydrogen
thermal speed.
.
Since we are using his parameters for the calculation of the line force,
it is necessary to use the same thermal speed for the calculation
of the line force as Abbott (1982) did, namely the hydrogen
thermal speed.
Frictional force (per unit volume)
Rab acting between both
components has the form (Springmann & Pauldrach 1992):
The friction coefficient
kab is given by
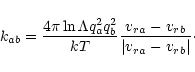 |
(7) |
The Coulomb logarithm is of the form (cf. Lang 1974)
![\begin{displaymath}\ln\Lambda =
\ln\left[\frac{24\pi}{\sqrt{n}}\left(\frac{kT}{4\pi e^{2}}\right)^{3/2}\right],
\end{displaymath}](/articles/aa/full/2001/13/aa10271/img37.gif) |
(8) |
where n is the particle density (
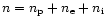 ), e is the
elementary charge, G(x) is so the called Chandrasekhar function, which
is defined in terms of the error function
), e is the
elementary charge, G(x) is so the called Chandrasekhar function, which
is defined in terms of the error function 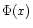 (see Dreicer
1959)
(see Dreicer
1959)
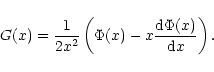 |
(9) |
The Chandrasekhar function has the following behavior.
For 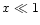 is
is
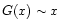 ,
for
,
for
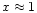 reaches its maximum value
and for
reaches its maximum value
and for 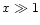 is
is
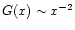 .
The argument of the Chandrasekhar function in Eq. (6) is
.
The argument of the Chandrasekhar function in Eq. (6) is
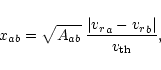 |
(10) |
where
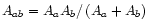 is the reduced atomic mass.
is the reduced atomic mass.
The term
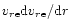 in the electron momentum equation can be
neglected compared to the electron pressure term and consequently the electron
momentum equation can be used to determine charge separation electric
field E
in the electron momentum equation can be
neglected compared to the electron pressure term and consequently the electron
momentum equation can be used to determine charge separation electric
field E
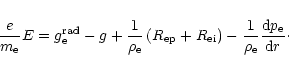 |
(11) |
Electron velocity and density are calculated from the condition of
quasi-neutrality and from the zero current condition
We assume a nonisothermal wind, so the system of continuity and momentum
equations should be supplemented by the energy (heat transfer) equation
which in the case of equal temperature of all components takes the form
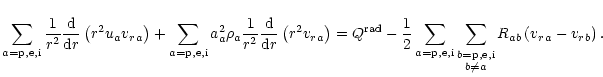 |
|
|
(14) |
The internal energy is chosen to be
ua=3/2 na kT.
Apparently, using continuity Eq. (1) the heat transfer
equation can be rewritten in a more simple form
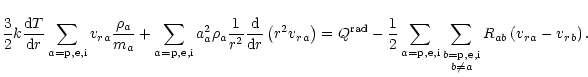 |
|
|
(15) |
Two terms on the left-hand side describe advection and adiabatic
cooling, respectively.
The right-hand side terms stand for radiative heating/cooling and for
frictional heating, respectively.
For consistent determination of radiative heating and cooling it would
be necessary to include all bound-free and free-free transitions for all
species considered and also inelastic collisions, and to solve a
complete set of equations of statistical equilibrium as well as the
radiative transfer equation.
It would be computationally very costly.
The main sources of radiative heating and cooling in the atmospheres of hot
stars are the hydrogen Lyman bound-free and free-free transitions.
According to NLTE
hydrogen-helium
model atmosphere calculations (Kubát 2001) the contribution
of inelastic collisions to heating/cooling is much smaller
in the outermost parts of the atmosphere
(at least by a factor of 100).
Note that radiative bound-bound transitions do not contribute to the
radiative heating/cooling term
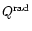 ,
since they transfer
energy between radiation and internal energy of atoms and
the amount of energy transferred directly to the ionic motion is
negligible.
Thus, we decided to estimate the radiative heating/cooling term
,
since they transfer
energy between radiation and internal energy of atoms and
the amount of energy transferred directly to the ionic motion is
negligible.
Thus, we decided to estimate the radiative heating/cooling term
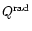 using the former two mechanisms only (hydrogen Lyman
bound-free and free-free transitions).
The detailed form of heating and cooling in the above-mentioned
transitions is (see Kubát et al. 1999)
using the former two mechanisms only (hydrogen Lyman
bound-free and free-free transitions).
The detailed form of heating and cooling in the above-mentioned
transitions is (see Kubát et al. 1999)
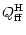 |
= |
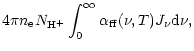 |
(16a) |
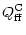 |
= |
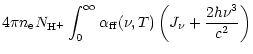 |
|
| |
|
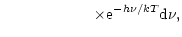 |
(16b) |
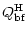 |
= |
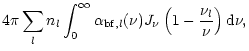 |
(16c) |
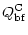 |
= |
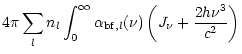 |
|
| |
|
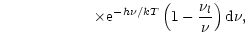 |
(16d) |
and the total energy transfered via radiation is
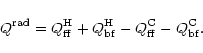 |
(17) |
Free-free and photoionization cross-sections are taken from Mihalas
(1978),  is considered to be constant throughout the wind
and it is taken as emergent radiation from a spherically symmetric
static hydrogen model atmosphere for a corresponding stellar type
(Kubát 2001).
is considered to be constant throughout the wind
and it is taken as emergent radiation from a spherically symmetric
static hydrogen model atmosphere for a corresponding stellar type
(Kubát 2001).
Generally, critical points are points where derivatives of individual
variables cannot be determined directly from equations.
A three-component stellar wind generally should have three critical
points.
However, neglecting the term containing the derivative of the electron
velocity in the electron equation of motion simplifies the problem, leaving
only two critical points.
Below we write the equations of motion and energy in a simplified
form.
We include all terms without derivatives into the terms Fi(i=a for the equations of motion, i=3 for the energy equation).
The equations of motion then
read
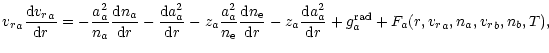 |
|
|
(18) |
where za=qa/e.
Similarly, the energy equation can be rewritten as
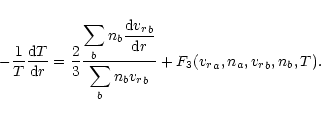 |
(19) |
Expressing derivatives of temperature, densities of each component and
electron velocity with the help of derivatives of passive plasma and
the velocity of absorbing ions, we arrive at a matrix form of the
equations, namely
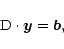 |
(20) |
where 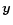 is the column vector, defined as
is the column vector, defined as
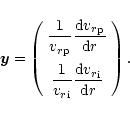 |
(21) |
The column vector 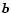 does not depend on any of the derivatives
and includes the terms Fi from Eqs. (18) and
(19).
Diagonal elements the of matrix D are
does not depend on any of the derivatives
and includes the terms Fi from Eqs. (18) and
(19).
Diagonal elements the of matrix D are
![$\displaystyle D_{aa}={v_r}_{a}^{2}-
{v_r}_{a}\frac{\partial g_{a}^{{\rm rad}}}{...
...laystyle
\sum_{{b}\neq{\rm e}}\left(1+z_{b}\right)n_{b}{v_r}_{b}}\right)\right]$](/articles/aa/full/2001/13/aa10271/img75.gif) |
|
|
(22) |
where a stands for i or p, and off-diagonal elements read
![\begin{displaymath}D_{ac}=-a_{a}^{2}\frac{n_{c}}{{n}_{{\rm e}}}
\left[z_{c}z_{a...
...um_{{b}\neq{\rm e}}\left(1+z_{b}\right)n_{b}{v_r}_{b}}\right],
\end{displaymath}](/articles/aa/full/2001/13/aa10271/img76.gif) |
(23) |
where a,c stands for i or p.
In these equations we accounted for quasineutrality and zero-current
conditions (Eqs. (12), (13)).
At singular points, the determinant of matrix D equals zero.
General calculation of singular points for arbitrary values of number
densities would be rather complicated.
One should look for two roots of an equation
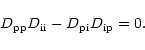 |
(24) |
Thus, we confine our discussion to a realistic case, when the ionic
number density is
much lower than the passive plasma number density.
In this case, the off-diagonal terms
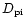 can be neglected,
and Eq. (24) can be split into two equations
that determine the critical points, namely
can be neglected,
and Eq. (24) can be split into two equations
that determine the critical points, namely
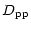 |
= |
0 |
(25a) |
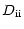 |
= |
0. |
(25b) |
Note that such separation of two critical points is possible not only in
the standard case
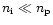 ,
but also in the nonrealistic case,
,
but also in the nonrealistic case,
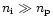 .
.
However, when the wind is not decoupled (i.e.
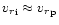 ),
the second
condition (25b) is not met anywhere in the wind,
because the non-zero term containing the derivative of the radiative force is
substantially higher than the other terms (see also KK).
Therefore, different condition must be used to fix the mass-loss rate.
),
the second
condition (25b) is not met anywhere in the wind,
because the non-zero term containing the derivative of the radiative force is
substantially higher than the other terms (see also KK).
Therefore, different condition must be used to fix the mass-loss rate.
Such condition can be derived from momentum equations (2) by
multiplying the equations for absorbing ions and passive plasma by
the corresponding density and summing them
(again, only terms including derivatives of variables are explicitly
written, the rest is included in the term Fi), namely
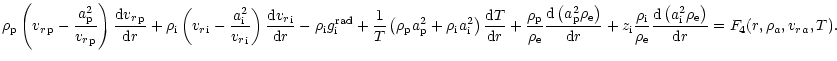 |
|
|
(26) |
Using the quasineutrality Eq. (12) and recalling
Eq. (19), we obtain
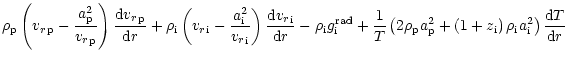 |
|
|
|
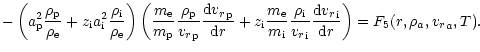 |
|
|
(27) |
Finally, if the condition
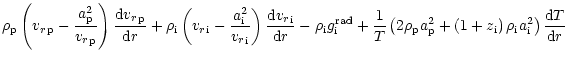 |
|
|
|
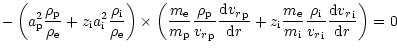 |
|
|
(28) |
holds, then the total equation of motion (26) does not depend
on the derivatives of any variables.
This condition is used to fix the mass-loss rate (see Sect. 2.6).
The fact that the ionic critical point is not met anywhere in the wind
is very interesting, particularly in connection with the so-called
Abbott waves (Abbott 1980).
At first glance, one can conclude that such purely ionic Abbott
waves can disseminate from any point in the wind upstream of the flow.
However, our preliminary simple linear stability analysis of the
two-component case indicates that such purely ionic Abbott waves are
heavily damped
when the corresponding Chandrasekhar function does not reach its maximum
value.
Thus, similar to the one-component case, the last point in the wind
from which upstream waves can propagate is that defined by
Eq. (28).
The detailed stability analysis will be presented in our next paper.
2.5 Boundary conditions
We assume that at the inner boundary, radiative equilibrium holds,
therefore the boundary condition for temperature is
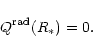 |
(29) |
2.5.2 Boundary condition for velocity
To avoid problems concerning two critical points, we start to calculate
our models at the passive plasma critical point; consequently, the boundary
condition for passive plasma velocity is (see Eq. (22), (25a))
![$\displaystyle {{v_r}}_{{\rm p}}^2(R_{*})=
{a}_{{\rm p}}^2\left[1+\frac{{n}_{{\r...
...aystyle
\sum_{{b}\neq{\rm e}}\left(1+z_{b}\right)n_{b}{v_r}_{b}}\right)\right].$](/articles/aa/full/2001/13/aa10271/img89.gif) |
|
|
(30) |
The boundary condition for absorbing ions can be derived from the passive
plasma equation of motion (2), which at the passive plasma
critical point may be rewritten as
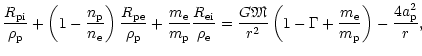 |
|
|
(31) |
where we used the boundary condition for temperature
(29) and neglected frictional heating.
For stars with solar abundances, we may further neglect the number
density of absorbing ions, (
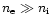 ),
and taking into account that the electron and passive plasma number
densities are nearly equal (
),
and taking into account that the electron and passive plasma number
densities are nearly equal (
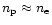 )
we write the boundary
condition for absorbing ions in a simpler form,
)
we write the boundary
condition for absorbing ions in a simpler form,
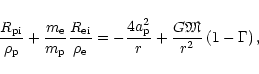 |
(32) |
which was used in our models.
Further simplification of the boundary condition for ion velocity may be
obtained by taking into account the fact that the individual components
are fully coupled at the base of the wind, as is the case in our models.
The boundary condition then takes the much simpler form
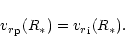 |
(33) |
Thus, our results do not change significantly if we suppose that
velocities of all components are equal at the base of the wind.
We incorporated the possibility of different boundary velocities
only for the sake of physical consistence of our models.
Providing that at some point deep in the atmosphere (with radius
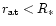 ), both passive plasma and absorbing ion
velocities are nearly equal, then
), both passive plasma and absorbing ion
velocities are nearly equal, then
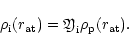 |
(34) |
Finally, using the continuity Eq. (1), the boundary
condition for the passive plasma density may be written in the form
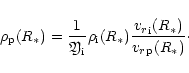 |
(35) |
The boundary value of ionic density is chosen in order to obtain
the three-component
CAK solution (see Sect. 2.6).
The charge conservation Eq. (12) and zero current condition
(13) can be used directly as boundary conditions for electron
density and electron velocity, respectively.
2.6 Numerical method
There exist several numerical methods that may be suitable for this
problem.
As an example, methods based on numerical simulations are frequently
applied.
The system is simply allowed to develop until it reaches a stationary state.
Such a method was used for the investigation of stellar wind structure,
particularly in 2D, e.g. by Owocki et al. (1994) and Petrenz &
Puls (2000).
Another method (integral method) was developed by Beutler (1979)
and was applied to a solar wind problem by Bürgi (1992).
The Henyey method (Henyey et al. 1964) was used to solve equations
of the radiatively driven stellar wind by Nobili & Turolla
(1988).
This method a modified Newton-Raphson method.
The hydrodynamic equations are linearized and also the CAK condition is
included into the set of linearized equations.
The latter method was selected by us.
Equations, which we solve (i.e. Eqs. (1), (2),
(12), (13), (15))
together with the appropriate boundary conditions (Eqs. (12),
(13), (29), (32), (35))
may formally be written as
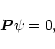 |
(36) |
where 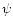 is a column vector of variables
(
is a column vector of variables
(
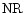 is the number of grid points),
is the number of grid points),
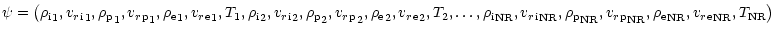 |
|
|
(37) |
and 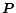 is a non-linear operator.
The Newton-Raphson method adopted here employs the iterative scheme
is a non-linear operator.
The Newton-Raphson method adopted here employs the iterative scheme
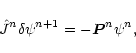 |
(38) |
where 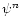 is solution in the nth iteration and
is solution in the nth iteration and
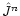 is the Jacobian in the nth iteration,
is the Jacobian in the nth iteration,
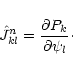 |
(39) |
To solve the system of Eqs. (38) for
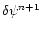 we used the numerical package LAPACK, developed at the University of
Tennessee.
we used the numerical package LAPACK, developed at the University of
Tennessee.
Although the original Henyey method handles critical points well (Nobili
& Turolla 1988), due to some numerical problems
we
decided to modify
the method as described in KK.
Here we only briefly summarize our approach.
For each model we search for the boundary density
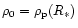 that enables us to pass smoothly through the
point similar to the CAK point defined by the Eq. (28).
In each step we fix the value of
that enables us to pass smoothly through the
point similar to the CAK point defined by the Eq. (28).
In each step we fix the value of 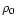 ,
perform several
Newton-Raphson iterations (described above) and after inspection of
the obtained results we modify its value
in the following manner.
If condition (28) is not met, we increase the value of
,
perform several
Newton-Raphson iterations (described above) and after inspection of
the obtained results we modify its value
in the following manner.
If condition (28) is not met, we increase the value of
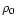 ,
whereas in the opposite case (or even if the model does not
converge) we decrease the value of
,
whereas in the opposite case (or even if the model does not
converge) we decrease the value of 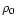 .
The steps are repeated until a satisfactory value of
.
The steps are repeated until a satisfactory value of 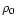 is
obtained (i.e. the error of our estimate of
is
obtained (i.e. the error of our estimate of 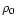 is
is 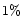 ).
Note that this a bit complicated procedure affects only the resulting
mass-loss rate and does not
change the overall picture of the downstream flow.
).
Note that this a bit complicated procedure affects only the resulting
mass-loss rate and does not
change the overall picture of the downstream flow.
For comparison purposes, we also calculated one-component models of a
stellar wind.
They are described by continuity Eq. (1), equation of
motion (2), and energy Eq. (15), where 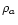 and vra are replaced by density and velocity of the whole fluid
and vra are replaced by density and velocity of the whole fluid
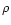 ,
vr, respectively. Friction terms and electric
charge separation electric field are not accounted for.
The one-component equations are
,
vr, respectively. Friction terms and electric
charge separation electric field are not accounted for.
The one-component equations are
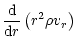 |
= |
0 |
(40a) |
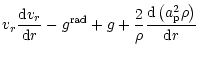 |
= |
0 |
(40b) |
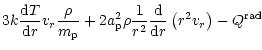 |
= |
0, |
(40c) |
where the radiative force is
(compared to three-component notation)
Inserting derivatives of density (from continuity Eq. (40a) and temperature (from energy Eq. (40c)) into the equation of motion (40b) we obtain the critical point
of the above system of equations (the well known CAK critical point) in the form
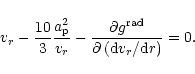 |
(41) |
To solve this set of equations,
we used the same method as described in Sect. 2.6, however, with
essentially lower number of variables and equations.
 |
Figure 1:
Upper panel: one-component (dotted line) and three-component
(radiatively accelerated ions - dashed line, passive plasma
and electrons
- full
line) radiatively driven stellar wind model of a B0 star.
Notice that both curves coincide.
In addition, the location of the CAK critical point for both wind
models is almost the same and it is given by condition
(32).
Lower panel: comparison of temperature stratification of
one-component (dotted line) and three-component
(solid line)
radiatively driven
stellar wind models of a B0 star |
| Open with DEXTER |
 |
Figure 3:
The same as Fig. 1 for a B3 star.
Notice the differences both in velocities and in temperature structure
caused by frictional heating (see the text) |
| Open with DEXTER |
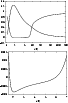 |
Figure 4:
Radiative heating or cooling (dashed line) and
frictional heating (solid line) relative to the
adiabatic cooling in the model of a B3 star wind.
Note that in the range
2 R*- 6 R* the wind is slightly radiatively cooled (see the
lower panel for detailed plot of radiative cooling
in this region) |
| Open with DEXTER |
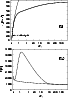 |
Figure 5:
The same as Fig. 1 for a B4 star. Heating is even greater than for
a B3 star - cf. Fig. 3 |
| Open with DEXTER |
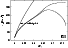 |
Figure 7:
The dependence of velocities on radius for a B5 star. The meaning of
particular lines is same as in Fig. 1 |
| Open with DEXTER |
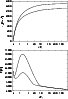 |
Figure 8:
Comparison of three-component models with (dashed line) and without
(solid line) Doppler heating/cooling.
Only ionic velocity is shown for both models |
| Open with DEXTER |
Parameters of model stars are given in Table 1.
Main sequence stellar parameters are taken from Harmanec (1988)
and force multipliers are adopted from Abbott (1982).
3.1 Stellar winds with no significant effect of friction
For stars with high density winds where the drift velocity between
components is low compared to the thermal speed, no significant
differences between one-component and three-component winds occur.
This behavior is shown in Figs. 1 and 2 for the
case of B0 and B2 stars, respectively.
The temperature profile of such wind is controlled mainly by equilibrium
between radiative heating and radiative cooling.
Similar models have been previously described by other authors
(Springmann & Pauldrach 1992, model of 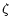 Pup therein,
KK, model of
Pup therein,
KK, model of 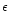 Ori therein), however, using simpler assumptions.
Ori therein), however, using simpler assumptions.
3.2 Decrease of the outflow velocity due to frictional heating
For stars with lower density, friction begins to play an important role
(see Figs. 3 and 5 for the case of B3 and B4 stars,
respectively).
To maintain the common flow, a sufficient amount of momentum must be
transferred to the passive component.
Near the stellar photosphere, the wind is relatively dense.
From inspection of the frictional force (Eq. (6)), it follows that
the drift velocity between absorbing ions and passive plasma can be low
compared to the thermal speed of hydrogen.
Consequently,
frictional heating can be neglected in this region and the temperature
structure is set mainly by the radiative processes and adiabatic cooling
(see Drew 1989 for more detailed calculations).
Hence, the three-component temperature is equal to its one-component
value at the base of the wind.
However, this is not valid throughout the wind.
At the outer parts of the wind the density decreases.
Since the frictional force depends on the product of densities, the
drift velocity should increase to accelerate the passive plasma
(cf. Fig. 6 for the quantity
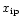 ).
Consequently, frictional heating increases,
but it also depends on the product of the densities of
the interacting particles.
Since the density of particles decreases, frictional heating reaches
its maximum value and also decreases in the outermost parts of the wind.
Therefore, at the outer parts of the wind the temperature is given by the
balance between radiative heating and cooling and the three-component
temperature is again equal to its one-component value.
Finally, note that because
).
Consequently, frictional heating increases,
but it also depends on the product of the densities of
the interacting particles.
Since the density of particles decreases, frictional heating reaches
its maximum value and also decreases in the outermost parts of the wind.
Therefore, at the outer parts of the wind the temperature is given by the
balance between radiative heating and cooling and the three-component
temperature is again equal to its one-component value.
Finally, note that because
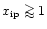 ,
the maximum of the
Chandrasekhar function is not met anywhere in the wind.
Thus, decoupling of radiatively accelerated ions and major passive
component is excluded in such models.
The behavior of individual heating or cooling terms is shown in
Fig. 4.
Note that in a particular case of a B3 star, radiative heating of a wind
changes to radiative cooling in the domain of the wind where frictional
heating is important.
The most important component in frictional heating is caused by
encounters of non-absorbing and absorbing ions.
Encounters of electrons and absorbing ions supply about two magnitudes less to
frictional heating.
Finally, frictional heating originating from encounters of non-absorbing
ions and electrons is negligible due to the low drift velocity between these
species.
,
the maximum of the
Chandrasekhar function is not met anywhere in the wind.
Thus, decoupling of radiatively accelerated ions and major passive
component is excluded in such models.
The behavior of individual heating or cooling terms is shown in
Fig. 4.
Note that in a particular case of a B3 star, radiative heating of a wind
changes to radiative cooling in the domain of the wind where frictional
heating is important.
The most important component in frictional heating is caused by
encounters of non-absorbing and absorbing ions.
Encounters of electrons and absorbing ions supply about two magnitudes less to
frictional heating.
Finally, frictional heating originating from encounters of non-absorbing
ions and electrons is negligible due to the low drift velocity between these
species.
Because the charge separation electric field is not a dominant term in
momentum equations of both passive and active components, the electron
component is only important in the temperature equation.
Thus, the only effect of the electron component is a slight increase of
temperature in the region where frictional heating is important.
In most of our models, the electron velocity is very similar to the
passive plasma velocity.
The velocity profile is affected by changes in the temperature
structure through the dependence of radiative acceleration on the
thermal speed (see Eq. (4)).
The higher the temperature, the greater the thermal speed and the lower
the radiative acceleration.
Consequently, the wind terminal velocity decreases.
Similarly Vink et al. (1999) concluded that lowering the
radiative acceleration in the supersonic region leads to the lowering of
the outflow velocity.
To our knowledge, the effect of lowering of the outflow
velocity by frictional heating is not mentioned anywhere in the
literature.
At the lowest densities, the ionic component of the wind is unable to
drag the passive plasma component out of the atmosphere, as displayed in
Fig. 7.
We see that the ionic and passive plasma decouple well below the
point where the escape velocity is reached and the passive plasma
falls back onto the stellar surface.
However, this reaccretion should be studied using time-dependent
calculations (cf. Porter & Skouza 1999).
Moreover, for such low densities, a different type of solution is valid.
As was shown by Babel (1996), the hydrostatic solution for
passive plasma and the wind solution for absorbing ions exist
simultaneously.
This type of solution was also studied for the case of a two-component
wind (KK, model of B5 star with
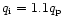 ).
).
Only in this case does the resulting mass-loss rate of the three-component
model differ significantly from its one-component value.
Near the CAK point, temperature is higher almost by a factor of two than
in the one-component case.
As will be discussed in Sect. 4.3, a higher temperature below
the CAK point lowers the mass-loss rate.
In our particular case, the mass-loss rate computed in the
three-component case is
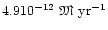 ,
contrary to its one-component value
,
contrary to its one-component value
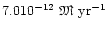 .
Moreover, a lower temperature below the CAK point lowers the flow velocity
and for this case the dependence of velocity on radius in one-component
and three-component models differ significantly even below the
critical point.
This effect was enabled by including the variations in temperature and
it is completely missing for isothermal winds in a two-component model
(see KK and model of B5 star with
.
Moreover, a lower temperature below the CAK point lowers the flow velocity
and for this case the dependence of velocity on radius in one-component
and three-component models differ significantly even below the
critical point.
This effect was enabled by including the variations in temperature and
it is completely missing for isothermal winds in a two-component model
(see KK and model of B5 star with
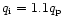 therein).
therein).
However, there is another mechanism that is able to affect the thermal
equilibrium of the wind, namely the Doppler heating (and cooling).
This mechanism was studied in detail by Gayley & Owocki (1994).
Doppler heating/cooling transfers energy directly from radiation to the
motion of the atoms with the help of a difference between the
absorption and emission frequency in a moving medium with a velocity
gradient within the same line.
Inclusion of this effect requires a detailed knowledge of the line
list (and, consequently, a huge amount of computer time), so we calculated
only approximate values of the Doppler heating/cooling based on
estimates from Gayley & Owocki (1994) in order to
qualitatively estimate its effect.
We added the Doppler heating/cooling term
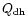 into the
radiative heating/cooling term
into the
radiative heating/cooling term
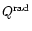 .
For
.
For
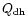 we used the formula
we used the formula
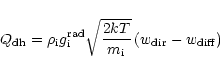 |
(42) |
given by Gayley & Owocki (1994, Eq. (26) therein),
where
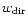 is a heating component of direct radiation and
is a heating component of direct radiation and
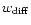 is a heating component of diffuse radiation
Note that their heating/cooling term
is a heating component of diffuse radiation
Note that their heating/cooling term
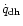 is
defined per unit mass whereas
is
defined per unit mass whereas
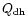 is defined per unit
volume, so we inserted the term
is defined per unit
volume, so we inserted the term
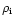 .
For the difference
.
For the difference
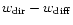 we used
the rough estimate suggested by the same authors
we used
the rough estimate suggested by the same authors
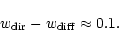 |
(43) |
We computed a B3 star model with inclusion of Doppler heating/cooling
(see Fig. 8).
The effect of Doppler heating/cooling is comparable to the effect of
frictional heating and the total effect
approximately
doubles our temperature maximum.
However, the qualitative picture of our results does not change.
Detailed inclusion of Doppler heating/cooling as well as improved
treatment of the line list will be dealt within our next paper(s).
From the dependence of the radiative force in the multicomponent
approach (Eq. (4)) on the metallic density we can directly
derive the dependence of the force-multipliers k, 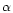 on the
metallicity.
If the metallicity changes, then the actual metallic density is modified as
on the
metallicity.
If the metallicity changes, then the actual metallic density is modified as
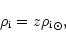 |
(44) |
where
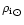 is the corresponding solar value of the ion
density and z is the actual abundance relative to its solar value.
Consequently, the radiative acceleration acting on absorbing ions varies
according to (see Eq. (4))
is the corresponding solar value of the ion
density and z is the actual abundance relative to its solar value.
Consequently, the radiative acceleration acting on absorbing ions varies
according to (see Eq. (4))
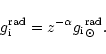 |
(45) |
Since the radiative force acting on the fluid in the one-component
approximation is given by
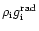 ,
metallicity
effect can be described by the dependence of the force-multiplier k on the
metallicity as
,
metallicity
effect can be described by the dependence of the force-multiplier k on the
metallicity as
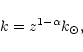 |
(46) |
which is the same result as obtained by Puls et al. (2000),
who used the line statistics approach.
This scaling law was also discussed by Abbott (1982).
Consider a situation in which the flow consists of two species, one of which
is active and receives momentum (say, via radiative acceleration) and the
second one is passive and is dragged via friction.
Let us change the density in the wind (e.g. changing the boundary
condition).
For high densities, the frictional force is able to transfer
sufficient amount of momentum from the active to the passive component.
If the density is lower, then, because the velocity law is nearly the
same, the frictional acceleration should be the same too.
However, the corresponding density of the active component is now lower;
therefore, to maintain the same frictional acceleration, the drift
velocity between both components should be higher
(see Eqs. (6), (7)).
Apparently, this picture has its limitations.
If the maximum of the Chandrasekhar function is reached, the frictional
acceleration is not able to maintain the two-component flow. The
behavior of the velocity law out of this point depends generally on the
densities of both components and on the force acting on active
component.
This will be discussed for two basic different cases below.
If the density of the active component is significantly higher than the
density of the passive component, then decoupling of the passive
component from the major flow is possible.
This can be seen easily from the equation of motion of the active
component (Eq. (2)).
The friction term can be neglected because the passive plasma density is
substantially lower than the active plasma density and therefore the
passive component does not influence the active component.
Contrary, lowering of the frictional term in the equation of motion of a
passive component should be balanced by lowering of the passive plasma
velocity gradient, i.e. decoupling is possible.
Clearly, if the passive component reaches the escape velocity, then it
leaves the star separately; if its velocity is lower than the actual
escape velocity then the passive component falls back onto the star.
Interestingly, the point where the minor component decouples from the
main flow does not depend on its density.
This can be seen easily from the equation of motion (2) of the
minor component.
The only term which depends on the minor component density is the gas
pressure term, which can be neglected.
Thus, if the wind is not significantly heated during decoupling, the
point where the minor component decouples does not depend on its
density.
The location of this point depends on the mass and charge of
both components and on the major component density.
However, in this case, we completely neglected the effect of frictional
heating.
Therefore, the situation described may be generally more complicated,
especially if the force acting on the major component depends on temperature
(as the line-force actually does).
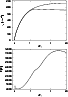 |
Figure 9:
Wind model with major active component
(dashed line) allowing for decoupling of the
passive component (solid line) |
| Open with DEXTER |
To manifest such theoretical results we computed a wind model of a B3
star (using parameters listed in the Table 1) with an artificially
enhanced ion-to-hydrogen ratio of
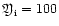 .
The numerical model obtained in Fig. 9 supports
preceding theoretical considerations.
Both components decouple.
Moreover, the wind is significantly heated, attaining a maximum temperature
of about
.
The numerical model obtained in Fig. 9 supports
preceding theoretical considerations.
Both components decouple.
Moreover, the wind is significantly heated, attaining a maximum temperature
of about
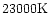 .
.
4.2.2 The minor active component
The situation is completely different in the case when the component
receiving the major amount of momentum is a minor element relative to
the passive plasma.
This is the common case in the radiatively driven stellar wind.
At the point where the Chandrasekhar function reaches its
maximum, frictional acceleration is not capable of transfering sufficient
amount of momentum to the passive plasma.
Quantitatively, the frictional force is lower by 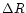 compared to
the case when it is capable of maintaining the common flow of both
components.
Therefore, the velocity gradient of the passive component p should
drop by
compared to
the case when it is capable of maintaining the common flow of both
components.
Therefore, the velocity gradient of the passive component p should
drop by
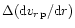 .
The equation of motion yields
.
The equation of motion yields
where the continuity equation was used.
This decrease of the frictional force also affects the active component.
For the change in the velocity gradient of active plasma
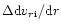 we can write (from the equation of motion of the
active plasma)
we can write (from the equation of motion of the
active plasma)
where
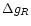 is the change of force that drives active plasma.
Such a picture is valid for both isothermal and nonisothermal wind.
However, especially in the latter case, it should be justified by
numerical calculations.
Generally, there are two possible cases of downstream flow,
based on whether the driving force depends on the velocity
gradient or not.
is the change of force that drives active plasma.
Such a picture is valid for both isothermal and nonisothermal wind.
However, especially in the latter case, it should be justified by
numerical calculations.
Generally, there are two possible cases of downstream flow,
based on whether the driving force depends on the velocity
gradient or not.
First, we assume that the driving force gR does not depend on the
velocity gradient
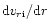 .
Then the velocity gradient should change substantially,
given that in this region
.
Then the velocity gradient should change substantially,
given that in this region
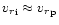 and the change of the active component velocity gradient reads
and the change of the active component velocity gradient reads
In this case, decoupling is possible.
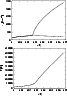 |
Figure 10:
Model of a B3 star wind with constant driving acceleration for
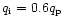 (see the text).
The notation is the same as in Fig. 1
(see the text).
The notation is the same as in Fig. 1 |
| Open with DEXTER |
To prove this conclusion, we computed
nonisothermal
models with constant acceleration
(i.e. acceleration which does not depend on the velocity gradient).
We selected a model of a B3 star and as the driving acceleration we chose the
radiative force in the CAK approximation computed for the beta-velocity
law with
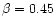 and
and
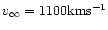 .
This computed force we held fixed during Newton-Raphson iterative steps.
For high values of
.
This computed force we held fixed during Newton-Raphson iterative steps.
For high values of
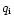 for which the Chandrasekhar function does not
reach its maximum, no decoupling occurs.
On the other hand, for low values of ionic charge
for which the Chandrasekhar function does not
reach its maximum, no decoupling occurs.
On the other hand, for low values of ionic charge
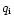 for which
friction is not capable of driving the passive plasma flow, runaway of
ions occurs, enabled by steep increase in the ionic velocity
gradient, as was already discussed
(see Fig. 10).
Finally, the friction heats the flow, increasing the wind temperature by of
orders of magnitude.
This offers a plausible model of how wind temperatures sufficient to produce
X-rays can be attained.
for which
friction is not capable of driving the passive plasma flow, runaway of
ions occurs, enabled by steep increase in the ionic velocity
gradient, as was already discussed
(see Fig. 10).
Finally, the friction heats the flow, increasing the wind temperature by of
orders of magnitude.
This offers a plausible model of how wind temperatures sufficient to produce
X-rays can be attained.
On the other hand, if the driving force is an increasing function of the
velocity gradient, then an abrupt increase of the velocity gradient of
the active component (contrary to the previous case) enhances the
driving force and further disrupts the momentum balance.
Therefore, in this case, the momentum balance would not be achieved by
an increase of the velocity gradient, but rather by a decrease.
The velocity gradient should drop according to
If the first two left-hand side terms can be neglected (as in the case
of the radiative force in the Sobolev approximation, see KK), the above
equation can be rewritten
In the case of the Sobolev approximation this means that the active
component velocity gradient drops and decoupling is not possible.
Thus, in the supersonic flow, the possibility of ion runaway
crucially depends on the driving force.
However, this conclusion cannot be proved in the nonisothermal case, due
to the dependence of radiative acceleration on temperature.
When the velocity difference between active and passive components
rises, the wind is significantly heated by friction and the radiative
acceleration is lower.
This decreases the outflow velocity and increases wind density such
that the Chandrasekhar function does not reach its maximum
value and thus even the possibility of decoupling is excluded
(see Sect. 3.2).
The most complicated situation occurs when the densities of both active
and passive components are nearly equal.
In this case, the above-mentioned equations cannot be used in such a simple
form because the possibility of decoupling crucially depends on the
functional dependence of the driving force, i.e. dependence on the
velocity gradient, temperature etc.
The question of whether decoupling is possible or not should thus be solved
only using careful numerical computations.
However, the latter case probably has limited astrophysical relevance,
because hydrogen is the most abundant element in the majority of stars.
On the other hand, there exists an interesting class of hydrogen-deficient
stars where the case of nearly equal densities may occur.
However, such analysis, although interesting, goes far beyond the scope
of this paper.
4.3 Mass-loss rate
Since condition (28), used to fix the mass-loss rate in the
case when both components are coupled (i.e.
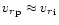 and
and
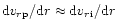 )
is
nearly the same as the CAK condition (41), the three-component
mass loss rate and the one-component mass loss rate
(showed in the Table 2)
in this limit are
nearly the same.
Moreover, a condition (28) leads to a maximum mass-loss rate,
for which a stable solution exists, similar to the one-component case
(see Poe et al. 1990).
)
is
nearly the same as the CAK condition (41), the three-component
mass loss rate and the one-component mass loss rate
(showed in the Table 2)
in this limit are
nearly the same.
Moreover, a condition (28) leads to a maximum mass-loss rate,
for which a stable solution exists, similar to the one-component case
(see Poe et al. 1990).
Table 2:
Mass-loss rates of one-component (1C) and three-component (3C) models.
All values are
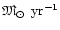
| Star |
B0 |
B1 |
B2 |
B3 |
B4 |
B5 |
 Sco
Sco |
| 1C |
3 10-8 |
1 10-8 |
4 10-9 |
4 10-10 |
6 10-11 |
7 10-12 |
1 10-8 |
| 3C |
3 10-8 |
1 10-8 |
4 10-9 |
4 10-10 |
6 10-11 |
5 10-12 |
1 10-8 |
This is not true in the case when the gas is significantly heated by
friction near the CAK point.
Higher temperature increases thermal speed and therefore decreases
radiative acceleration in the Sobolev approximation Eq. (4).
As was discussed by Vink et al. (1999), as the line acceleration
in the subsonic region decreases, mass-loss rate decreases.
It is interesting
to discuss the influence of heating on the observed mass-loss rates.
Recent detailed theoretical study of mass-loss rates of Vink et al.
(2000) showed that there is a
quite
good agreement between theoretical mass-loss rates for O stars and
mass-loss rates deduced from radio emission and H profile.
On the other hand, theoretical mass-loss rates for B stars are in
good agreement with mass-loss rates calculated from radio emission
(Scuderi et al. 1998)
but not with mass-loss rates deduced from H
profile.
On the other hand, theoretical mass-loss rates for B stars are in
good agreement with mass-loss rates calculated from radio emission
(Scuderi et al. 1998)
but not with mass-loss rates deduced from H profiles
(Kudritzki et al. 1999).
Since the radio emission
originates
at several hundred stellar radii
(Lamers & Leitherer 1993) where the radiative equilibrium holds
(see Fig. 5), the "radio mass-loss rates'' are not affected by
frictional heating.
However, the H
profiles
(Kudritzki et al. 1999).
Since the radio emission
originates
at several hundred stellar radii
(Lamers & Leitherer 1993) where the radiative equilibrium holds
(see Fig. 5), the "radio mass-loss rates'' are not affected by
frictional heating.
However, the H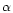 line
originates from layers closer to the star and therefore can be affected
by frictional heating.
Thus, proper inclusion of
the frictional (and possibly Doppler) heating can help
understanding of the discrepancy between mass-loss determined
by various methods for B stars.
line
originates from layers closer to the star and therefore can be affected
by frictional heating.
Thus, proper inclusion of
the frictional (and possibly Doppler) heating can help
understanding of the discrepancy between mass-loss determined
by various methods for B stars.
5.1 Decoupling of helium
 |
Figure 11:
Decoupling of helium (dotted line) from common hydrogen (solid
line) and absorbing ion (dashed line) flow in the model of a B3 star
four-component wind.
In the outermost parts of the wind the electron velocity
(dashed-dotted line) differs slightly from the hydrogen velocity |
| Open with DEXTER |
The interesting paper of Hunger & Groote (1999) motivated us to
test whether we are also able to predict decoupling of helium on the basis of
our multicomponent model.
Therefore we introduced two new variables to describe the helium flow,
namely helium density
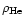 and helium radial velocity
and helium radial velocity
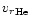 .
We assumed helium atoms to have mass
.
We assumed helium atoms to have mass
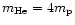 and charge
and charge
 .
The helium velocity and density are obtained from continuity
Eq. (1) and equation of motion Eq. (2).
We added appropriate helium terms into the energy Eq. (15)
and into the critical point condition Eq. (28).
We assumed a solar abundance of helium at the base of the wind and equal
base velocities of helium and hydrogen.
The ion velocity is determined as described in Sect. 2.5.2.
We stress that these models are not fully self-consistent because we did
not include the helium critical point.
This is completely beyond the scope of the present article; we aim only to
show that helium decoupling from the main absorbing ions -
hydrogen flow is possible.
Detailed calculations of a four-component model including helium will be
published elsewhere.
.
The helium velocity and density are obtained from continuity
Eq. (1) and equation of motion Eq. (2).
We added appropriate helium terms into the energy Eq. (15)
and into the critical point condition Eq. (28).
We assumed a solar abundance of helium at the base of the wind and equal
base velocities of helium and hydrogen.
The ion velocity is determined as described in Sect. 2.5.2.
We stress that these models are not fully self-consistent because we did
not include the helium critical point.
This is completely beyond the scope of the present article; we aim only to
show that helium decoupling from the main absorbing ions -
hydrogen flow is possible.
Detailed calculations of a four-component model including helium will be
published elsewhere.
The model of the four-component flow in a B3 star is given in
Fig. 11 for
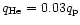 .
At a point where the common flow of hydrogen and absorbing ions is
not able to support helium flow, the latter decouples from the other
components and its velocity decreases.
Because the helium velocity is lower than the escape velocity,
helium can reaccrete to the star, creating possible surface helium
overabundance if magnetic fields are present (Hunger & Groote
1999) or possible He shells (Porter & Skouza 1999).
Note that such stationary models cannot be extended to an arbitrary radius.
During deceleration the helium critical point is again reached, and
further operation of the gravitational force reverses the
direction of the helium flow and causes its backfalling to the stellar
surface.
Such a situation cannot be correctly described by our model.
.
At a point where the common flow of hydrogen and absorbing ions is
not able to support helium flow, the latter decouples from the other
components and its velocity decreases.
Because the helium velocity is lower than the escape velocity,
helium can reaccrete to the star, creating possible surface helium
overabundance if magnetic fields are present (Hunger & Groote
1999) or possible He shells (Porter & Skouza 1999).
Note that such stationary models cannot be extended to an arbitrary radius.
During deceleration the helium critical point is again reached, and
further operation of the gravitational force reverses the
direction of the helium flow and causes its backfalling to the stellar
surface.
Such a situation cannot be correctly described by our model.
The wind is significantly heated by friction between helium and
other components beyond the point where helium decouples from the
main flow.
Higher temperatures would lower the argument
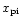 of the
Chandrasekhar function (see Eq. (10)) and therefore lower the
frictional force between hydrogen and metallic components.
Thus, to maintain a common flow of hydrogen and absorbing ions, the drift
velocity should increase.
of the
Chandrasekhar function (see Eq. (10)) and therefore lower the
frictional force between hydrogen and metallic components.
Thus, to maintain a common flow of hydrogen and absorbing ions, the drift
velocity should increase.
Helium decoupling is sensitive to the helium charge and therefore
to the temperature.
For such low temperatures, which are commonly attained
in the stellar wind of B stars, decoupling would be possible.
However, if the helium charge would rise (due to higher wind temperature)
e.g. to
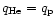 no helium decoupling would occur.
Thus, the detailed picture of helium decoupling is much more
complicated and needs further study.
no helium decoupling would occur.
Thus, the detailed picture of helium decoupling is much more
complicated and needs further study.
If the present picture of helium decoupling is correct, then Bp and Ap
stars with winds could be X-ray sources.
Recently this was justified by Dachs & Hummel
(1996) for the case of the young open cluster NGC 2516.
Unfortunately, it is not clear if the source of the X-rays are Bp stars
themselves or their possible cool companions with hot coronae.
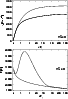 |
Figure 12:
Three-component wind model of 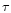 Sco.
The notation is the same as in Fig. 1. Note that inclusion of
frictional heating lowers the outflow velocity towards observed
values
Sco.
The notation is the same as in Fig. 1. Note that inclusion of
frictional heating lowers the outflow velocity towards observed
values |
| Open with DEXTER |
This well-studied star is a puzzling object.
Although it became a benchmark star for theoretical and observational
studies, its nature is not yet well known.
The observed terminal velocity estimate - about
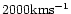 (Abbott 1978;
Lamers & Rogerson 1978) contradicts the value
(Abbott 1978;
Lamers & Rogerson 1978) contradicts the value
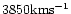 obtained from a detailed theoretical
study by Pauldrach (1987).
Springmann & Pauldrach (1992) were able to reduce the
theoretical value using the two-component model of the stellar wind,
however, using a lower value of a mass-loss rate.
obtained from a detailed theoretical
study by Pauldrach (1987).
Springmann & Pauldrach (1992) were able to reduce the
theoretical value using the two-component model of the stellar wind,
however, using a lower value of a mass-loss rate.
Our one-component model with much simpler atomic physics than Pauldrach
(1987) predicts a terminal velocity
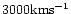 ,
well above the experimental
result.
Therefore, we computed a three-component model of this star to find out if
our models are able to explain the low terminal velocity of this star.
According to Kilian (1994), we reduced the metallicity to the value
z=0.6.
Unfortunately, even such a three-component model yielded nearly the same
value for terminal velocity as the one-component model.
Therefore, we assumed slightly reduced metallicity contrary to Kilian,
z=0.3, to allow for greater frictional heating.
This artificial change of the metallicity does not indicate our mistrust
of observed metallicity values.
Rather it indicates that our model assumptions (e.g. the representative
nature of our ions) do not correspond to the reality of
,
well above the experimental
result.
Therefore, we computed a three-component model of this star to find out if
our models are able to explain the low terminal velocity of this star.
According to Kilian (1994), we reduced the metallicity to the value
z=0.6.
Unfortunately, even such a three-component model yielded nearly the same
value for terminal velocity as the one-component model.
Therefore, we assumed slightly reduced metallicity contrary to Kilian,
z=0.3, to allow for greater frictional heating.
This artificial change of the metallicity does not indicate our mistrust
of observed metallicity values.
Rather it indicates that our model assumptions (e.g. the representative
nature of our ions) do not correspond to the reality of  Sco.
We believe more detailed models in the future can explain the low terminal velocity of
Sco.
We believe more detailed models in the future can explain the low terminal velocity of  Sco more precisely.
Nevertheless, based on these assumptions, we showed that frictional
heating may play an
important role in the model of
Sco more precisely.
Nevertheless, based on these assumptions, we showed that frictional
heating may play an
important role in the model of  Sco wind because it reduces its
terminal velocity to
Sco wind because it reduces its
terminal velocity to
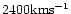 ,
closer to
the observed values.
Moreover, the computed velocity profile (see Fig. 12) is very similar
to that derived from a detailed UV-line fit by Hamann (1981).
,
closer to
the observed values.
Moreover, the computed velocity profile (see Fig. 12) is very similar
to that derived from a detailed UV-line fit by Hamann (1981).
We would like to emphasize that our computed low value for the terminal
velocity was not obtained due to the reduced value of metallicity,
because our wind model with z=0.3 without frictional heating yields
nearly the same terminal velocity as the one-component model with
z=1.0.
The low value of terminal velocity was obtained due
to the inclusion of frictional heating into our models.
Although Springmann & Pauldrach (1992) also explained the low terminal
velocity of 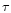 Sco on the basis of multicomponent flow, our
approach is substantially different,
their explanation being on ion runaway.
Another problem arising for other low-density wind stars is
the determination of the mass-loss rate.
Our obtained value,
Sco on the basis of multicomponent flow, our
approach is substantially different,
their explanation being on ion runaway.
Another problem arising for other low-density wind stars is
the determination of the mass-loss rate.
Our obtained value,
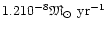 ,
is
about a factor of
3 lower than that obtained from the usual CAK approximation (see e.g. Cohen
et al. 1997, who used the "cooking formula'' of Kudritzki et al. 1989),
due to the reduced metallicity in our models.
This value is slightly higher than a new upper-limit of the mass-loss rate,
,
is
about a factor of
3 lower than that obtained from the usual CAK approximation (see e.g. Cohen
et al. 1997, who used the "cooking formula'' of Kudritzki et al. 1989),
due to the reduced metallicity in our models.
This value is slightly higher than a new upper-limit of the mass-loss rate,
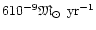 ,
constrained by Zaal et
al. (1999) from infrared emission; however, this result is
sensitive to a star's effective temperature.
,
constrained by Zaal et
al. (1999) from infrared emission; however, this result is
sensitive to a star's effective temperature.
Finally, Waters et al. (1993) reported the presence of hydrogen
emission lines in the infrared spectrum of 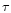 Sco and concluded that
Sco and concluded that
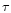 Sco is a pole-on Be star. However, Murdoch et al.
(1994) suggested that infrared hydrogen emission is caused by
the presence of NLTE effects (see also Zaal et al. 1999).
Our NLTE spherically-symmetric static model of the photosphere
of
Sco is a pole-on Be star. However, Murdoch et al.
(1994) suggested that infrared hydrogen emission is caused by
the presence of NLTE effects (see also Zaal et al. 1999).
Our NLTE spherically-symmetric static model of the photosphere
of 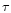 Sco predicts infrared emission both in hydrogen and helium
lines.
Sco predicts infrared emission both in hydrogen and helium
lines.
We computed three-component models of a radiatively driven wind of hot B
stars.
We showed that friction has a negligible effect in high density winds,
i.e. in stars with a relatively high mass-loss rate.
For these stars, three-component calculations yield the same results as
the common one-component ones.
For low density winds the inclusion of friction leads to heating of the
flow.
We showed that in self-consistent hydrodynamic models, friction can heat
the gas to temperatures up to two times the effective temperature.
This heating leads to lowering of the radiative force and, consequently,
to the lowering of the outflow velocity.
Lower outflow velocity leads to higher density and this means, together
with higher thermal speed, that the drift velocity of both components
is too low to allow decoupling of passive and absorbing components.
Finally, stars where absorbing plasma is not able to drag the passive
plasma out from the atmosphere have a purely metallic wind, as has
already been shown by Babel (1995,1996).
We derived general conditions for decoupling of a multicomponent flow.
We showed that if the density of the accelerated component is higher
than the density of the passive component, then decoupling is possible,
regardless of the actual form of driving force.
On the other hand, if the density of the accelerated component is lower
than the density of the passive component, then the possibility of
decoupling is given by the functional dependence of the driving force.
If the driving force does not change substantially in the region where
decoupling is possible, then decoupling of individual components is
again possible.
If the driving force scales with velocity gradient (as in the
Sobolev approximation), then decoupling of individual components is not
possible.
Our calculations indicate that friction is able to heat the wind to the
temperatures of the order of
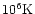 (see
Fig. 10).
Such a hot medium is able to emit X-ray radiation.
However, quantitative estimates of X-ray luminosity are beyond the scope
of this paper.
(see
Fig. 10).
Such a hot medium is able to emit X-ray radiation.
However, quantitative estimates of X-ray luminosity are beyond the scope
of this paper.
There are many applications of the multifluid model of stellar wind.
Considering helium as a fourth component, one can
apply the model of a multicomponent wind to the
study of chemically peculiar stars.
We are also able to fit the outflow velocity of the star 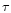 Sco
closer to the observed value.
Sco
closer to the observed value.
Unfortunately, our approach of handling the problem is still not
satisfactory.
Mainly, the approximation of one-type absorbing ions with parameters
which are not rigidly given may lead to some misunderstanding.
The approximation
of constant ionic charge is not self-consistent because the degree of
ionization changes with temperature and density.
Moreover, allowing for a macroscopic electric field may lead to some
observable effects (Porter 1999, private communication).
Such studies with the inclusion of inspection of stability of multicomponent
flow will be the subject of future papers.
However, we are now able to describe the general picture of multifluid
flow, which will likely not be strongly affected by future refinements.
Acknowledgements
The authors would like to thank Dr. John Porter for his comments on the
manuscript.
This research made use of NASA's Astrophysics Data System Abstract
Service (Kurtz et al. 2000; Eichhorn et al. 2000; Accomazzi et al. 2000; Grant et al. 2000).
This work was supported by projects K1-003-601/4 and K1-043-601.
The non-linear operator
P has following form:
- for i=1
| P1 |
= |
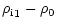 |
(A.1a) |
| P2 |
= |
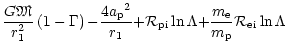 |
(A.1b) |
| P3 |
= |
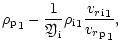 |
(A.1c) |
| P4 |
= |
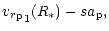 |
(A.1d) |
| P5 |
= |
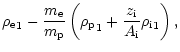 |
(A.1e) |
| P6 |
= |
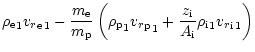 |
(A.1f) |
| P7 |
= |
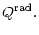 |
(A.1g) |
- for
|
P7i-6 |
= |
![$\displaystyle {\left[\frac{{\rm d} \left(r^2 {\rho}_{{\rm i}}{{v_r}}_{{\rm i}} \right)} {{\rm d}r}\right]}_i$](/articles/aa/full/2001/13/aa10271/img191.gif) |
(A.2a) |
| P7i-5 |
= |
![$\displaystyle {{v_r}}_{{\rm i},i}{\left[\frac{{\rm d} {{v_r}}_{{\rm i}} } {{\rm...
...rac{{\rm d} {a}_i^2} {{\rm d}r}\right]}_i-
\frac{{q}_{{\rm i}}}{{m}_{{\rm i}}}E$](/articles/aa/full/2001/13/aa10271/img192.gif) |
|
| |
- |
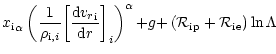 |
(A.2b) |
| P7i-4 |
= |
![$\displaystyle {\left[\frac{{\rm d} \left(r^2 {\rho}_{{\rm p}}{{v_r}}_{{\rm p}} \right)} {{\rm d}r}\right]}_i$](/articles/aa/full/2001/13/aa10271/img194.gif) |
(A.2c) |
| P7i-3 |
= |
![$\displaystyle {{v_r}}_{{\rm p},i}{\left[\frac{{\rm d} {{v_r}}_{{\rm p}} } {{\rm...
... d} {a}_{{\rm p}}^2} {{\rm d}r}\right]}_i
-\frac{{q}_{{\rm p}}}{{m}_{{\rm p}}}E$](/articles/aa/full/2001/13/aa10271/img195.gif) |
|
| |
+ |
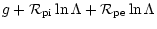 |
(A.2d) |
| P7i-2 |
= |
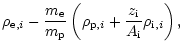 |
(A.2e) |
| P7i-1 |
= |
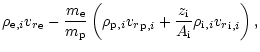 |
(A.2f) |
| P7i |
= |
![$\displaystyle \frac{3}{2} k {\left[\frac{{\rm d} T} {{\rm d}r}\right]}_i
\sum_{a={\rm p,e,i}}{{v_r}}_{{a},i}
\frac{\rho_{{a},i}}{m_{a}}$](/articles/aa/full/2001/13/aa10271/img199.gif) |
|
| |
+ |
![$\displaystyle \sum_{a={\rm p,e,i}}a_{a}^2\rho_{{a},i}
\frac{1}{{r}_i^2}{\left[\frac{{\rm d} \left(r^2 {{v_r}}_{a}\right)} {{\rm d}r}\right]}_i-Q^{{\rm rad}}$](/articles/aa/full/2001/13/aa10271/img200.gif) |
|
| |
- |
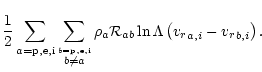 |
(A.2g) |
- for
| P7i-6 |
= |
![$\displaystyle {\left[\frac{{\rm d} \left(r^2 {\rho}_{{\rm i}}{{v_r}}_{{\rm i}} \right)} {{\rm d}r}\right]}_i$](/articles/aa/full/2001/13/aa10271/img191.gif) |
(A.3a) |
| P7i-5 |
= |
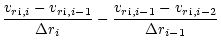 |
(A.3b) |
| P7i-4 |
= |
![$\displaystyle {\left[\frac{{\rm d} \left(r^2 {\rho}_{{\rm p}}{{v_r}}_{{\rm p}} \right)} {{\rm d}r}\right]}_i$](/articles/aa/full/2001/13/aa10271/img194.gif) |
(A.3c) |
| P7i-3 |
= |
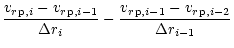 |
(A.3d) |
| P7i-2 |
= |
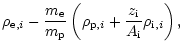 |
(A.3e) |
| P7i-1 |
= |
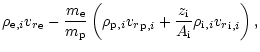 |
(A.3f) |
| P7i |
= |
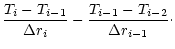 |
(A.3g) |
We used following abbreviations:
![$\displaystyle {\left[\frac{{\rm d} X} {{\rm d}r}\right]}_i$](/articles/aa/full/2001/13/aa10271/img206.gif) |
= |
 |
(A.4a) |
| |
|
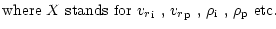 |
|
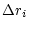 |
= |
ri-ri-1, |
(A.4b) |
| yi |
= |
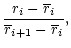 |
(A.4c) |
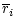 |
= |
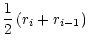 |
(A.4d) |
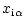 |
= |
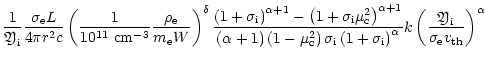 |
(A.4e) |
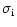 |
= |
![$\displaystyle \frac{{r}_i}{{{v_r}}_{{\rm i}} }{\left[\frac{{\rm d} {{v_r}}_{{\rm i}} } {{\rm d}r}\right]}_i-1$](/articles/aa/full/2001/13/aa10271/img216.gif) |
(A.4f) |
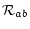 |
= |
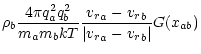 |
(A.4g) |
| |
|
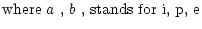 |
|
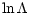 |
= |
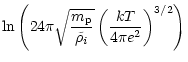 |
(A.4h) |
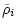 |
= |
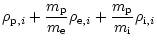 |
(A.4i) |
| E |
= |
![$\displaystyle \frac{{m}_{{\rm e}}}{e}\left(
{g}_{{\rm e}}^{{\rm rad}}-g
-{\left...
...ht]}_i
-{{\cal R}}_{\rm ep} \ln\lambda -
{{\cal R}}_{\rm ei} \ln\lambda \right)$](/articles/aa/full/2001/13/aa10271/img224.gif) |
(A.4j) |
where i denotes ith point of the grid. In some circumstances (when the argument of the Chandrasekhar function is
comparable with the thermal speed) it is convenient to introduce the new
independent variable
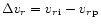 and use this variable in the
linearization and computation of the Chandrasekhar function.
and use this variable in the
linearization and computation of the Chandrasekhar function.
For a calculation of the model below the critical point we typically use
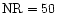 grid points, whereas for the model above the critical point we
use
grid points, whereas for the model above the critical point we
use
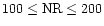 grid points.
In both cases, the grid points are spaced logarithmically (although this
leads to nearly linear placement of grid points in the former case).
grid points.
In both cases, the grid points are spaced logarithmically (although this
leads to nearly linear placement of grid points in the former case).
- Abbott, D. C. 1978, ApJ, 225, 893
In the text
NASA ADS
- Abbott, D. C. 1980, ApJ, 242, 1183
In the text
NASA ADS
- Abbott, D. C. 1982, ApJ, 259, 282
In the text
NASA ADS
- Accomazzi, A., Eichhorn, G.,
Kurtz, M. J., Grant, C. S., & Murray, S. S. 2000, A&AS, 143, 85
In the text
NASA ADS
- Babel, J. 1995, A&A, 301, 823
In the text
NASA ADS
- Babel, J. 1996, A&A, 309, 867
In the text
NASA ADS
- Beutler, G. 1979, Numerische Integration von
gewöhnlichen Differentialgleichungen, Mitt.
Satell.-Beobachtungsstn. Zimmerwald, 4, Astron. Inst.,
Univ. of Bern, Bern, Switzerland
In the text
- Braginskij, S. I. 1963, in Voprosy teorii plazmy,
vol. 1, ed. M. A. Leontovich, Gosatomizdat, Moskva, 183
In the text
- Bürgi, A. 1992, J. Geophys. Res., 97, 3137
In the text
NASA ADS
- Castor, J. I., Abbott, D. C., & Klein, R. I. 1975,
ApJ, 195, 157 (CAK)
In the text
NASA ADS
- Cohen, D. H., Cassinelli, J. P., & Waldron, W. L.
1997, ApJ, 488, 397
In the text
NASA ADS
- Dachs, J., & Hummel, W. 1996, A&A, 312, 818
In the text
NASA ADS
- Dreicer, H. 1959, Phys. Rev., 115, 238
In the text
- Drew, J. E. 1985, MNRAS, 217, 867
In the text
NASA ADS
- Drew, J. E. 1989, ApJS, 71, 267
In the text
NASA ADS
- Eichhorn, G., Kurtz, M. J.,
Accomazzi, A., Grant, C. S., & Murray, S. S. 2000, A&AS, 143,
61
In the text
NASA ADS
- Friend, D. B., & Abbott, D. C. 1986, ApJ, 311, 701
In the text
NASA ADS
- Grant, C. S., Accomazzi, A., Eichhorn,
G., Kurtz, M. J., & Murray, S. S. 2000, A&AS, 143, 111
In the text
NASA ADS
- Gayley, K. G., & Owocki, S. P. 1994, ApJ, 434, 684
In the text
NASA ADS
- Hamann, W.-R. 1981, A&A, 100, 169
In the text
NASA ADS
- Harmanec, P. 1988, Bull. Astron. Inst. Czechosl.,
39, 329
In the text
NASA ADS
- Henyey, L. G., Forbes, J. E., & Gould, N. L. 1964,
ApJ, 139, 306
In the text
NASA ADS
- Hunger, K., & Groote, D. 1999, A&A, 351, 554
In the text
NASA ADS
- Kilian, J. 1994, A&A, 282, 867
In the text
NASA ADS
- Krticka, J., & Kubát, J. 2000, A&A, 359, 983
(KK)
In the text
NASA ADS
- Kubát, J. 2001, A&A, 366, 210
In the text
NASA ADS
- Kubát, J., Puls, J., & Pauldrach, A. W. A. 1999,
A&A, 341, 587
In the text
NASA ADS
- Kudritzki, R. P., Pauldrach, A. W. A., Puls, J.,
& Abbott, D. C. 1989, A&A, 219, 205
In the text
NASA ADS
- Kudritzki, R. P., Puls, J., Lennon, D. J., et al.
1999, A&A, 350, 970
In the text
NASA ADS
- Kurtz, M. J., Eichhorn, G., Accomazzi,
A., et al. 2000, A&AS, 143, 41
In the text
NASA ADS
- Lamers, H. J. G. L. M., & Leitherer, C. 1993, ApJ, 412, 771
In the text
NASA ADS
- Lamers, H. J. G. L. M., & Rogerson, J. B. 1978, A&A,
66, 417
In the text
NASA ADS
- Lang, K. R. 1974, Astrophysical Formulae
(Springer-Verlag, Berlin)
In the text
- Lucy, L. B., & Solomon, P. M. 1970, ApJ, 159, 879
In the text
NASA ADS
- Mihalas, D. 1978, Stellar Atmospheres. 2nd ed.
(W. H. Freeman Comp., San Francisco)
In the text
- Murdoch, K. A., Drew, J. E., & Anderson, L. S. 1994,
A&A, 284, L27
In the text
NASA ADS
- Nobili, L., & Turola, R. 1988, ApJ, 333, 248
In the text
NASA ADS
- Owocki, S. P., Cranmer, S. R., & Blondin, J. M. 1994,
ApJ, 424, 887
In the text
NASA ADS
- Pauldrach, A. W. A. 1987, A&A, 183, 295
In the text
NASA ADS
- Pauldrach, A., Puls, J., & Kudritzki, R. P. 1986, A&A,
164, 86
In the text
NASA ADS
- Petrenz, P., & Puls, J. 2000, A&A, 358, 956
In the text
NASA ADS
- Poe, C. H., Owocki, S. P., & Castor, J. I. 1990, ApJ,
358, 199
In the text
NASA ADS
- Porter, J. M., & Drew, J. E. 1995, A&A, 296, 761
In the text
NASA ADS
- Porter, J. M., & Skouza, B. A. 1999, A&A, 344, 205
In the text
NASA ADS
- Puls, J., Springmann, U., & Lennon, M. 2000,
A&AS, 141, 23
In the text
NASA ADS
- Scuderi, S., Panagia, N., Stanghellini, C.,
Trigilio, C., & Umana, G. 1998, A&A, 332, 251
In the text
NASA ADS
- Springmann, U. W. E., & Pauldrach, A. W. A. 1992,
A&A, 262, 515
In the text
NASA ADS
- Vink, J. S., De Koter, A., & Lamers, H. J. G. L. M.
1999, A&A, 350, 181
In the text
NASA ADS
- Vink, J. S., De Koter, A., & Lamers, H. J. G. L. M.
2000, A&A, 362, 295
In the text
NASA ADS
- Waters, L. B. F. M., Marlborough, J. M., Geballe,
T. R., Oosterbroek, T., & Zaal, P. 1993, A&A, 272, L9
In the text
NASA ADS
- Zaal, P. A., de Koter, A., Waters, L. B. F. M.,
et al. 1999, A&A, 349, 573
In the text
NASA ADS
Copyright ESO 2001
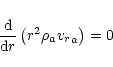
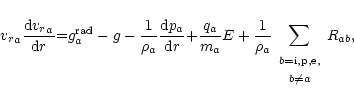
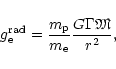
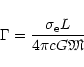
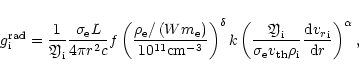
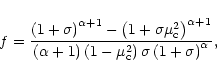
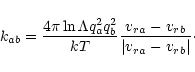
![\begin{displaymath}\ln\Lambda =
\ln\left[\frac{24\pi}{\sqrt{n}}\left(\frac{kT}{4\pi e^{2}}\right)^{3/2}\right],
\end{displaymath}](/articles/aa/full/2001/13/aa10271/img37.gif)
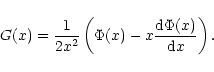
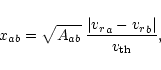
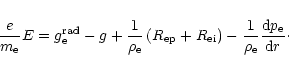
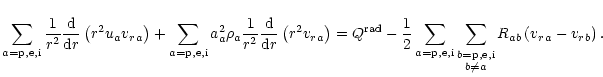
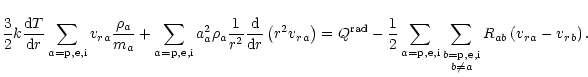
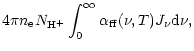
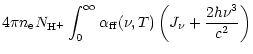
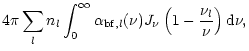
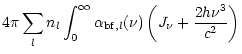
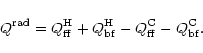
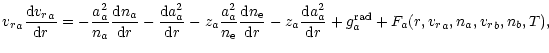
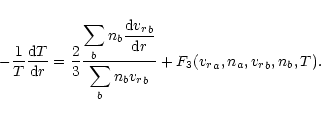
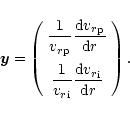
![$\displaystyle D_{aa}={v_r}_{a}^{2}-
{v_r}_{a}\frac{\partial g_{a}^{{\rm rad}}}{...
...laystyle
\sum_{{b}\neq{\rm e}}\left(1+z_{b}\right)n_{b}{v_r}_{b}}\right)\right]$](/articles/aa/full/2001/13/aa10271/img75.gif)
![\begin{displaymath}D_{ac}=-a_{a}^{2}\frac{n_{c}}{{n}_{{\rm e}}}
\left[z_{c}z_{a...
...um_{{b}\neq{\rm e}}\left(1+z_{b}\right)n_{b}{v_r}_{b}}\right],
\end{displaymath}](/articles/aa/full/2001/13/aa10271/img76.gif)
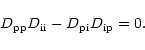
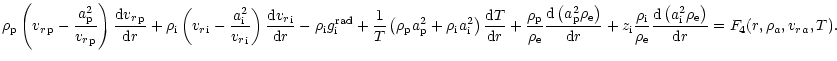
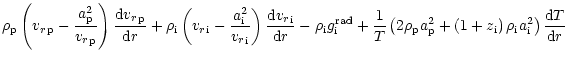
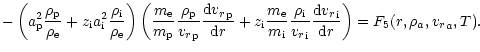
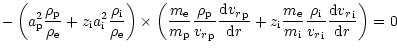
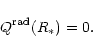
![$\displaystyle {{v_r}}_{{\rm p}}^2(R_{*})=
{a}_{{\rm p}}^2\left[1+\frac{{n}_{{\r...
...aystyle
\sum_{{b}\neq{\rm e}}\left(1+z_{b}\right)n_{b}{v_r}_{b}}\right)\right].$](/articles/aa/full/2001/13/aa10271/img89.gif)
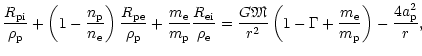
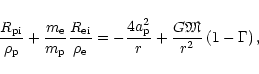
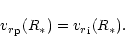
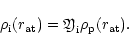
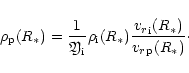
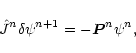
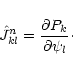
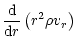
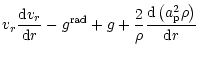
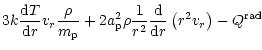
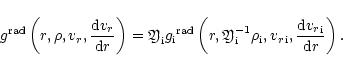
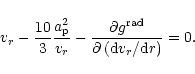





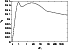

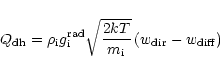
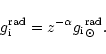
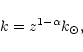

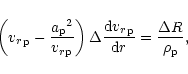
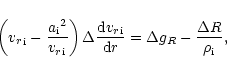
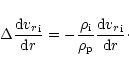

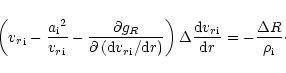
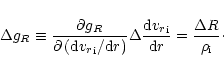


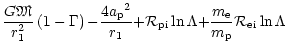
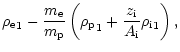
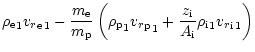
![$\displaystyle {\left[\frac{{\rm d} \left(r^2 {\rho}_{{\rm i}}{{v_r}}_{{\rm i}} \right)} {{\rm d}r}\right]}_i$](/articles/aa/full/2001/13/aa10271/img191.gif)
![$\displaystyle {{v_r}}_{{\rm i},i}{\left[\frac{{\rm d} {{v_r}}_{{\rm i}} } {{\rm...
...rac{{\rm d} {a}_i^2} {{\rm d}r}\right]}_i-
\frac{{q}_{{\rm i}}}{{m}_{{\rm i}}}E$](/articles/aa/full/2001/13/aa10271/img192.gif)
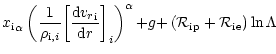
![$\displaystyle {\left[\frac{{\rm d} \left(r^2 {\rho}_{{\rm p}}{{v_r}}_{{\rm p}} \right)} {{\rm d}r}\right]}_i$](/articles/aa/full/2001/13/aa10271/img194.gif)
![$\displaystyle {{v_r}}_{{\rm p},i}{\left[\frac{{\rm d} {{v_r}}_{{\rm p}} } {{\rm...
... d} {a}_{{\rm p}}^2} {{\rm d}r}\right]}_i
-\frac{{q}_{{\rm p}}}{{m}_{{\rm p}}}E$](/articles/aa/full/2001/13/aa10271/img195.gif)
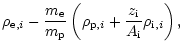
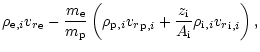
![$\displaystyle \frac{3}{2} k {\left[\frac{{\rm d} T} {{\rm d}r}\right]}_i
\sum_{a={\rm p,e,i}}{{v_r}}_{{a},i}
\frac{\rho_{{a},i}}{m_{a}}$](/articles/aa/full/2001/13/aa10271/img199.gif)
![$\displaystyle \sum_{a={\rm p,e,i}}a_{a}^2\rho_{{a},i}
\frac{1}{{r}_i^2}{\left[\frac{{\rm d} \left(r^2 {{v_r}}_{a}\right)} {{\rm d}r}\right]}_i-Q^{{\rm rad}}$](/articles/aa/full/2001/13/aa10271/img200.gif)
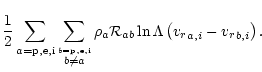
![$\displaystyle {\left[\frac{{\rm d} X} {{\rm d}r}\right]}_i$](/articles/aa/full/2001/13/aa10271/img206.gif)
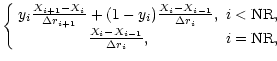
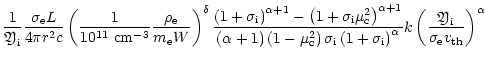
![$\displaystyle \frac{{r}_i}{{{v_r}}_{{\rm i}} }{\left[\frac{{\rm d} {{v_r}}_{{\rm i}} } {{\rm d}r}\right]}_i-1$](/articles/aa/full/2001/13/aa10271/img216.gif)
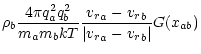
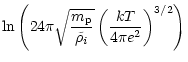
![$\displaystyle \frac{{m}_{{\rm e}}}{e}\left(
{g}_{{\rm e}}^{{\rm rad}}-g
-{\left...
...ht]}_i
-{{\cal R}}_{\rm ep} \ln\lambda -
{{\cal R}}_{\rm ei} \ln\lambda \right)$](/articles/aa/full/2001/13/aa10271/img224.gif)
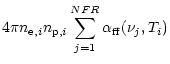
![$\displaystyle \left[J_{j}-\left(J_{j}+\frac{2h\nu_j^3}{c^2}\right){\rm e}^{-h\nu_j/k{T}_i} \right]
\Delta\nu_j$](/articles/aa/full/2001/13/aa10271/img228.gif)
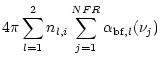
![$\displaystyle \left[J_{j}-\left(J_{j}+\frac{2h\nu_j^3}{c^2}\right){\rm e}^{-h\nu_j/k{T}_i} \right]$](/articles/aa/full/2001/13/aa10271/img230.gif)
![$\displaystyle \left[1-\frac{\nu_{l}}{\nu_j}\right]\Delta\nu_j$](/articles/aa/full/2001/13/aa10271/img231.gif)
![$\displaystyle {1+\frac{{n}_{{\rm p}}}{{n}_{{\rm e}}}
\left[{z}_{{\rm p}}^2+\fra...
...{\displaystyle
\sum_{{b}\neq{\rm e}}\left(1+z_{b}\right)n_{b}{v_r}_{b}}\right]}$](/articles/aa/full/2001/13/aa10271/img232.gif)