A&A 369, 308-322 (2001)
DOI: 10.1051/0004-6361:20010108

Magnetically driven superluminal motion from rotating black holes

Solution of the magnetic wind equation in Kerr metric

C. Fendt - J. Greiner

Astrophysikalisches Institut Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany

Received 21 August 2000 / Accepted 19 January 2001

Abstract
We have investigated magnetically driven superluminal jets originating from rotating black holes. The stationary, general relativistic, magnetohydrodynamic wind equation along collimating magnetic flux surfaces has been solved numerically. Our jet solutions are calculated on a global scale of a spatial range from several to several 1000 gravitational radii. Different magnetic field geometries were investigated, parameterized by the shape of the magnetic flux surface and the magnetic flux distribution. For a given magnetic flux surface we obtain the complete set of physical parameters for the jet flow. In particular, we apply our results to the Galactic superluminal sources GRS1915+105 and GRO1655-40. Motivated by the huge size indicated for the Galactic superluminal knots of about 109 Schwarzschild radii, we point out the possibility that the jet collimation process in these sources may be less efficient and therefore intrinsically different to the AGN. Our results show that the observed speed of more than 0.9c can be achieved in general by magnetohydrodynamic acceleration. The velocity distribution along the magnetic field has a saturating profile. The asymptotic jet velocity depends either on the plasma magnetization (for a fixed field structure) or on the magnetic flux distribution (for fixed magnetization). The distance where the asymptotic velocity is reached, is below the observational resolution for GRS1915+105 by several orders of magnitude. Further, we find that highly relativistic speeds can be reached also for jets not emerging from a region close to the black hole, if the flow magnetization is sufficiently large. The plasma temperature rapidly decreases from about 1010 K at the foot point of the jet to about 106 K at a distance of 5000 gravitational radii from the source. Temperature and the mass density follow a power law distribution with the radius. The jet magnetic field is dominated by the toroidal component, whereas the velocity field is dominated by the poloidal component.

Key words: accretion, accretion disks-Black hole physics - MHD - stars: mass loss - ISM: jets and outflows - galaxies: jets


1 Introduction

1.1 Relativistic jets and galactic superluminal motion

Apparent superluminal jet motion originating in the close environment of a rotating black hole is observationally indicated for two classes of sources concerning mass and energy output. One class is the family of radio loud active galactic nuclei (hereafter AGN). In the AGN standard model highly relativistic jet motion is explained by magnetohydrodynamic processes in a black hole - accretion disk environment (for a review see Blandford 1990). Jets are magnetically accelerated and possibly also collimated by magnetic forces. However, the detailed interaction process of the magnetized black hole - accretion disk system which is believed to lead to the ejection of high velocity blobs is not yet fully understood.

The other class are galactic binary systems for which radio observations have also detected superluminal motion (see reviews of Fender 2000 or Greiner 2000). The two most prominent examples are the high energy sources GRS1915+105 (Mirabel & Rodriguez 1994) and GRO1655-40 (Hjellming & Rupen 1995; Tingay et al. 1995). The de-projected jet speed of both sources is $\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\displaystyle ...0.9c and surprisingly similar, although for GRS1915+105 also a higher velocity component has been observed recently (Fender et al. 1999). GRO1655-40 is a binary consisting of a $7.02 \pm 0.22\,M_{\odot}$ black hole and a $2.3\,M_{\odot}$ F-subgiant (Orosz & Bailyn 1997) at a distance of 3 kpc. GRS 1915+105 is at 10-12 kpc distance (Fender et al. 1999), but the component masses of the presumed binary are not known. Order of magnitude estimates based on X-ray variability and QPO properties range from 10-80 $M_{\odot}$ (Morgan et al. 1997; Greiner et al. 1998). As for the AGN jet sources, observational evidence for a black hole - accretion disk system is found also for the Galactic superluminal sources. Observations have also indicated that accretion disk instabilities may be related to jet ejection (Greiner et al. 1996; Belloni et al. 1997; Mirabel et al. 1998). Therefore, the jet formation process for extragalactic jets and their Galactic counterparts may be the same, although the mechanism that accelerates and collimates the GRS1915+105 ejecta is yet unclear (Rodriguez & Mirabel 1999).

Optical polarization measurements have been obtained for the microquasar GRO J1655-40 (Scaltriti et al. 1997; Gliozzi et al. 1998). The polarization angle is approximately parallel to the accretion disk plane. The amount of polarization has been found to vary smoothly with the orbital phase, being smallest at binary phase 0.7-0.8. It has been noted that the occasionally observed X-ray dips occur at the same phase interval (Ueda et al. 1998; Kuulkers et al. 1998) suggesting that it may be related to either a thickening of the disk rim at the impact site of the accretion stream from the companion or the overflow of this stream above/below the disk. The orbital polarization modulation rules out a synchrotron origin in the jet, and implies the presence of electron scattering plasma above the accretion disk which is asymmetrically distributed or asymmetrically illuminated. The existence of such scattering plasma is consistent with the interpretation of the iron features as observed with ASCA as absorption lines and edges in a thick, cool torus of column $N_{\rm H} > 10^{23}~{\rm cm}^{-2}$ (Ueda et al. 1998).

The relativistic speed observed for the Galactic superluminal sources ($\sim$0.9-0.98c de-projected) corresponds to a bulk Lorentz factor of $\gamma = 2$-5 although this number is not very accurate (e.g. Fender et al. 1999). Therefore, for any theoretical investigation of these objects at least special relativity has to be taken into account. If the superluminal motion originates close to a black hole, also general relativistic effects may become important.

The ejection of matter itself is not a stationary process. In GRS1915+105 also repeated emission of knots is observed (Rodriguez & Mirabel 1999). X-ray and radio observations suggest that a wide range of ejected mass and ejection frequency is possible.

Though the galactic jet sources are nearby, they are not better resolved spatially because the distance ratio between AGN and microquasars is smaller than their mass ratios. Nevertheless, an important implication may also come from the observed size of the superluminal knots which are observationally resolved. In the case of GRS1915+105 the characteristic dimension of the "jet'' is 35mas, equivalent to 7   1015cm at a distance of 12.5kpc (Rodriguez & Mirabel 1999). We emphasize that such a knot size corresponds to $\sim$109Schwarzschild radii for $R_{\rm S} = 1.5 ~ 10^6\,(M/5\,M_{\odot}){\rm cm}$! This is a huge factor and may be in distinctive difference to the AGN jets. Similarly, the VLBA data show the core as a collimated jet down to a distance of 10AU from the central source with an opening angle of <10$^\circ$ (see Mirabel & Rodriguez 1999) corresponding to $10^7\,(M/5~M_{\odot})$ Schwarzschild radii. The length of the radio jet is about 100AU.

However, when interpreting the observed emission region, one has to keep in mind that this region may not represent the jet flow itself, but some part of another, larger, structure. For example, in some extragalactic jet sources there is indication that the knots travel along helical trajectories, believed to be prescribed by a large-scale helical magnetic field of an almost cylindrically collimated jet (Zensus et al. 1995; Camenzind & Krockenberger 1992).

In GRO1655-40 the motion of the radio knots is complicated and requires (at least) precession between different ejections (Hjellming & Rupen 1995). The knot structures in GRS1915+105 remained fixed implying that the whole knot moves with the same speed without spatial diffusion and with an axial velocity profile more or less constant.

Based on minimum energy arguments and only relativistic electrons responsible for the synchrotron radiation in the knots of GRS1915+105, Rodriguez & Mirabel (1999) derive a magnetic field strength of about 50mG to 7mG, the decrease resulting from the expansion of the knot. They also estimate the rest mass of a knot of $\ge$1023g, and together with (steady) photon luminosity of $\simeq$ $3 ~ 10^{38}\,{\rm erg\,s^{-1}}$, exclude radiation as driving mechanism for the knots.

1.2 Theory of magnetic jets

From the introductory remarks it is clear that a quantitative analysis of superluminal motion must take into account both magnetohydrodynamics (hereafter MHD) and (general) relativity.

The first theoretical formulation of the electromagnetic force-equilibrium in Kerr space-time around rotating black holes was given by Blandford & Znajek (1977) and Znajek (1977), who discovered the possibility of extracting rotational energy and angular momentum from the black hole electromagnetically.

Camenzind (1986, 1987) formulated a fully relativistic stationary description of MHD flows, basically applicable to any field geometry. The structure of such collimating jet magnetospheres in the case of Kerr space time was presented by Fendt (1997). Solutions of the so-called wind equation in Kerr geometry (see below) considering the stationary plasma motion along the magnetic field were obtained by Takahashi et al. (1990), however, mainly discussing the accretion flow onto the black hole.

While the asymptotic structure of the propagating jets becomes more and more understood with the help of time-dependent magnetohydrodynamical, also relativistic, simulations (e.g. Nishikawa et al. 1997; Mioduszewski et al. 1997; Hardee et al. 1998), the process of jet formation itself and the collimation of the outflow region is a task still too complex for numerical simulations. The involved length scales and gradients require a high resolution in grid size and time stepping. Koide et al. (1998) were first to perform general relativistic MHD simulations of jet formation close to the black hole. In their model, the interaction of an initially cylindrical magnetic field with a Keplerian accretion disk results first in an inflow of matter towards the black hole. This accretion stream interacts with the hydrostatic corona around the black hole giving rise to a relativistic gas pressure driven jet. At larger radii a magnetically driven wind is initiated from the accretion disk. The simulations were performed for less than two rotations of the inner disk (corresponding to less than 0.02 rotations of the disk at the outer edge of the grid). Although these results of the first fully general relativistic MHD simulations look indeed very exciting, some objections can be raised about the underlying model. The initial condition applied is that of a hydrostatic corona around a black hole, an assumption which is not compatible with the boundary of a black hole horizon. Such a configuration is not stable and will immediately collapse. Recently, the authors extended their work applying an initial coronal structure in steady infall surrounding a non-rotating black hole (Koide et al. 1999). They find a two-layered jet consisting of a magnetically driven jet around a gas-pressure driven jet. In addition, Koide et al. (2000) considered the quasi-steady infall of the corona around a Kerr black hole. They find that jet formation seems to differ for co-rotating and counter-rotating disks. The jet ejection tends to be easier in the latter case with a jet origin much closer to the hole. Also, a new feature of another magnetically driven (though sub-relativistic) jet appears within the gas-pressure driven jet. The computations were lasting over a few inner disk orbits. Therefore, the observed events of mass ejection could still be a relict of the initial condition and may not be present in the long-term evolution. Clearly, it would be interesting to perform the Koide et al. simulations for a longer time and look whether the mass ejection continues over many disk orbits, whether the simulation evolves into a final stationary state (as e.g. in Ouyed & Pudritz 1997; Fendt & Elstner 2000), or whether the jet formation retains its unsteady behavior which could explain the emission of superluminal knots observed in the relativistic jets.

1.3 Aim of the present study

In this paper, a stationary magnetic jet flow along a given magnetic flux surface is investigated in the context of general relativity. Due to the stationary approach, we cannot treat any time-dependent phenomena. Our emphasis is to trace the large scale behavior of the flow from it's origin close to the black hole to large distances. This is an essential point in particular for the Galactic superluminal sources because of the possible huge spatial extension of the jets compared to the central black hole. The stationary model allows for a global treatment of the jet flow, i.e. an investigation over a large range of magnitudes for density and magnetic field strength. This is not yet feasible with time-dependent MHD codes presently available. In particular, we address the following topics.

The structure of this paper is as follows. In Sect.2, basic equations for relativistic magnetospheres are reviewed in the context of Kerr metrics. In Sect.3, the model underlying our numerical calculations is discussed. We present our numerical results in Sect.4 and discuss solutions with different geometry and jet parameters. We summarize our paper in Sect.5.

2 Description of a MHD flow in Kerr metric

Under the assumptions of axisymmetry, stationarity and infinite conductivity, the MHD equations reduce to a set of two basic equations describing the local force-balance across the field and along the field (for references, see, e.g., Blandford & Znajek 1977; Thorne et al. 1986; Camenzind 1986, 1987; Okamoto 1992; Beskin & Pariev 1993; Beskin 1997).

The trans-field or Grad-Shafranov equation determines the field structure, whereas the wind equation describes the flow dynamics along the field. Due to the stationarity assumption, certain conservation laws apply. The total energy density, the total angular momentum density, the mass flow rate per flux surface and the iso-rotation parameter are conserved quantities along the surfaces of constant magnetic flux (Camenzind 1986).

In this paper the motion of a magnetized plasma is calculated from the wind equation. The plasma moves along a prescribed axisymmetric magnetic flux surface which originates in a region close to a rotating black hole.

2.1 Space-time around rotating black holes

The space-time around a rotating black hole with a mass M and angular momentum per unit mass a is described using Boyer-Lindquist coordinates with the line element

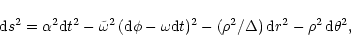\begin{displaymath}{\rm d}s^2 = \alpha^2{\rm d}t^2 - \tilde{\omega}^2\,({\rm d}\... ...d}t)^2 -(\rho^2/\Delta)\,{\rm d}r^2 - \rho^2\,{\rm d}\theta^2, \end{displaymath} (1)

where t denotes the global time, $\phi$ the angle around the axis of symmetry, $r,\theta$ similar to there flat space counterpart spherical coordinates, and where geometrical units c=G=1 have been applied (see Appendix A for further definitions). The horizon of the Kerr black hole is located at $r_{\rm H}= M + \sqrt{M^2 - a^2}$. We will normalize all radii to gravitational radii $r_{\rm g}= r_{\rm H}(a=M) = M$. The angular velocity of an observer moving with zero angular momentum (ZAMO) is $\omega = ({\rm d}\phi/{\rm d}t)_{\rm ZAMO}$, corresponding to the angular velocity of the differentially rotating space. The lapse function is $\alpha= ({\rm d}\tau/{\rm d}t)_{\rm ZAMO}$ describing the lapse of the proper time $\tau$ in the ZAMO system to the global time t.

2.2 Description of the electromagnetic field

In the 3+1 split of Kerr space time (Thorne et al. 1986) the electromagnetic field $\vec{B}, \vec{E}$, the current density $\vec{j}$, and the electric charge density $\rho_{\rm c}$ can be described very similar to the usual expressions, if measured by the ZAMO's according to the locally flat Minkowski space. These local experiments then have to be put together by a global observer for a certain global time using the lapse and shift function for the transformation from the local to the global frame.

With the assumption of axisymmetry a magnetic flux surface can be defined measuring the magnetic flux through a loop of the Killing vector 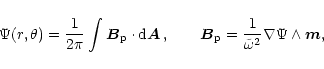$\vec{m} = \tilde{\omega}^2\nabla\phi$,

\begin{displaymath}\Psi (r,\theta) = \frac {1}{2 \pi} \int {\vec {B}}_{\rm p} \c... ...m p} = \frac{1}{\tilde{\omega}^2}\nabla \Psi \wedge {\vec{m}}, \end{displaymath} (2)

corresponding to the magnetic flux through an area $\pi (r\,\sin\theta)^2$ around the symmetry axis (in the limit of Minkowski space).

With the assumption of a degenerated magnetosphere, $ \vert\,\vert\vec{B}\vert^2 - \vert\vec{E}\vert^2 \vert >> \vert \vec{E} \cdot \vec{B} \vert \simeq 0 $an "angular velocity of field lines'' can be derived from the derivative of the time component of the vector potential $\Omega_{\rm F}= \Omega_{\rm F}(\Psi) = -2 \pi c ({\rm d}A_0/{\rm d}\Psi) $. We will denote this quantity with the term "iso-rotation parameter''.

2.3 The wind equation

It has been shown that a stationary, polytropic, general relativistic MHD flow along an axisymmetric flux surface $\Psi(r,\theta)$ can be described by the following wind equation for the poloidal velocity $u_{\rm p}\equiv \gamma v_{\rm p}/c$,

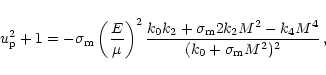\begin{displaymath}u_{\rm p}^2 + 1 = -\sigma_{\rm m}\left(\frac{E}{\mu}\right)^2... ...ma_{\rm m}2 k_2 M^2 - k_4 M^4}{(k_0 + \sigma_{\rm m}M^2)^2}\,, \end{displaymath} (3)

where
k0 = $\displaystyle g_{33} \Omega_{\rm F}^2 + 2 g_{03} \Omega_{\rm F}+ g_{00},$  
k2 = $\displaystyle 1 - \Omega_{\rm F}\frac{L}{E},$  
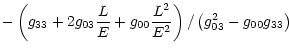k4 = $\displaystyle - \left(g_{33} + 2 g_{03} \frac{L}{E} + g_{00} \frac{L^2}{E^2} \right) / \left( g_{03}^2 - g_{00} g_{33} \right)$  

(Camenzind 1986; Takahashi et al. 1990). The Alfvén Mach number M is defined as $M^2 = 4 \mu n u_{\rm p}^2 / \tilde{B}_{\rm p}^2 $, with the proper particle density n, the specific enthalpy $\mu$, and a poloidal magnetic field $\tilde{B}_{\rm p}= B_{\rm p}/ (g_{00)}+g_{03}\Omega_{\rm F}) $, rescaled for mathematical convenience. The quantity $\sigma_{\rm m}$ stands for the sign of the metric (we have chosen $\sigma_{\rm m}= -1$, see Appendix A). For a polytropic gas law with the index $\Gamma \equiv n/m$, the wind Eq. (3) can be converted into a polynomial equation,

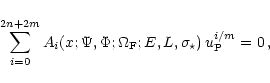\begin{displaymath}\sum\limits_{i=0}^{2n+2m} A_i (x;\Psi,\Phi;\Omega_{\rm F};E,L,\sigma_{\star})\, u_{\rm P}^{i/m} = 0 \,, \end{displaymath} (4)

(Camenzind 1987; Englmaier 1993; Jensen 1997), where the coefficients Ai are now defined as functions of the normalized cylindrical radius $x=R/r_{\rm g}$ (see Appendix B). The shape of the axisymmetric magnetic flux surface $\Psi $ is prescribed as function $z(x;\Psi)$. The flux function $\Phi = \sqrt{-g}\tilde{B}_{\rm p}$ describes the opening of the flux tube. The faster $\Phi$ decreases the faster magnetic energy is converted into kinetic energy. We define the dimensionless magnetization parameter[*] at the "injection'' point $x_{\star }$ following Takahashi et al. (1990),

\begin{displaymath}\sigma_{\star} = \frac{\Phi^2_{\star}}{4\pi m_{\rm p} I_{{\rm p}\star}}, \end{displaymath} (5)

measuring the Poynting flux in terms of particle flux $I_{\rm p} \equiv \sqrt{-g}\,nu_{\rm p}$, where $m_{\rm p}$ is the particle mass (here the proton mass). The magnetization determines the maximum energy available for plasma acceleration and thus determines also the asymptotic poloidal velocity. The other wind parameters are total energy density E, total angular momentum L, and the iso-rotation parameter $\Omega _{\rm F}$. The non relativistic limit of Eq.(4) has been solved numerically by Kudoh & Shibata (1995, 1997).

We choose the polytropic index $\Gamma = 5/3$for a hot relativistic proton-electron plasma (a hot electron-positron plasma would imply $\Gamma = 4/3$). Then, at each radius x the polynomial Eq. (4) has 2n+2m = 16 solutions. Some of these mathematical solutions have no physical meaning, e.g. because $u_{\rm p}^2$ is negative. The remaining physical solutions form a bunch of different curves in the $u_{\rm p}(x)$-diagram representing different solution branches (see our solution S1 in Appendix C, Fig. C.1). The unique branch of the "wind'' solution starts at a small radius with small velocity continuing outwards with increasing velocity. For an other parameter choice also "accretion'' branches can be found, starting from a large radius with small velocity and continuing inwards with increasing velocity (not shown in Fig. C.1).

However, not for all parameters $E,L,\sigma$ there exist physical solutions which are continuous functions of x and therefore defined along the whole flux surface. It is well known that at the magnetosonic points the wind Eq. (3) becomes singular (see Camenzind 1986; Takahashi et al. 1990). Regularity of the solution requires a flow velocity equal to the speed of the MHD waves in order to obtain a smooth (self-consistent) transition at the magnetosonic points. In order to match astrophysical boundary conditions we fix the following parameters,

The critical wind solution for a given flux surface can then be found by varying the flow parameters in Eq.(4). Due to numerical convenience, we vary In turn, the condition of a regular flow at the magnetosonic points fixes the sound speed and magnetization and, thus, jet mass flow rate and temperature.

3 The model assumptions

3.1 The model in general

Observationally the jet phenomenon of AGN, young stellar objects and microquasars is always connected to the signatures of an accretion disk. We therefore assume a similar disk-jet scenario for the jet formation in Galactic superluminal jet sources. In general our model geometry follows the standard model for jet formation in AGN (cf. Blandford 1990).

Two typical length scales enter the problem. (i) The gravitational radius $r_{\rm g}$ measures the influence of gravity on the metric. (ii) The asymptotic light cylinder $R_{\rm L}$ describes the influence of rotation on the electrodynamics.


  \begin{figure} \par\includegraphics[width=5.5cm,clip]{ms10209f1.eps} \end{figure} Figure 1: Model geometry applied for our numerical calculations. The poloidal field structure is prescribed as magnetic flux surfaces with different opening angle. The flux surfaces have different foot point radii along the accretion disk (not visible). The central source is a black hole implying that general relativistic effects have to be taken into account. The toroidal field follows from the solution of the wind equation
Open with DEXTER

3.2 The central black hole

The black hole mass and angular momentum determine the geometry of space. Since we use dimensionless equations normalized to the gravitational radius, our results scale with the mass of the black hole. For parameter estimates we assume a black hole mass of $5\,M_{\odot}$ which is about the value inferred for the galactic superluminal sources. The angular momentum a as the other black hole parameter is not known for any of the relativistic jet sources. Interpretation of the high effective temperatures of the accretion disk as well as the stable QPO frequency (as Thirring-Lense effect) suggests that $a \mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\displaystyle ... for GRS1915+105 and GRO1655-40 (Zhang et al. 1997). Theoretically, one may expect a rapidly rotating black hole because of angular momentum conservation during the collapse and also accretion of angular momentum from the accretion disk (King & Kolb 2000). Here, we choose a = 0.8, a value which is not extreme, but clearly different to Schwarzschild metric. The rotation rate of the black hole is defined as $\Omega_{\rm H}\equiv \omega(r_{\rm H}) = a/(2Mr_{\rm H})$. The Kerr parameter a does not influence the solution of the wind equation directly. However, for rotating black holes the marginally stable orbit $r_{\rm ms}$ is closer to the horizon, $r_{\rm ms}=6r_{\rm g}$ for a=0 and $r_{\rm ms}\simeq r_{\rm g}$ for $a\simeq 1$(This is the case for a co-rotating disk. For a retrograde disk rotation $r_{\rm ms}\simeq 9r_{\rm g}$ for $a\simeq 1$). Therefore, assuming that the jet magnetic field is anchored just at the marginally stable orbit, for a rapidly rotating black hole the maximum angular velocity of the jet foot points increases by a factor of 63/2/2=7.4. Correspondingly, the light cylinder radius of the jet moves inward by the same factor.

In addition to the well-known special relativistic light cylinder, the differential rotation of the space $\omega$ leads to the formation of a second light surface. At this position the "rotational velocity'' of the field lines relative to the ZAMO equals the speed of light (see Blandford & Znajek 1977). The position of the two light surfaces $\tilde{\omega}_{\rm L}$ is defined by $\tilde{\omega}_{\rm L}^2 = (\pm \alpha \,c / (\Omega_{\rm F}- \omega))^2$, where the + (-) sign holds for the outer (inner) light surface with $\Omega_{\rm F}> \omega$ ( $\Omega_{\rm F}< \omega$). However, these light surfaces have no direct implication for the MHD flow. In the limit of a strong magnetization, the MHD Alfvén surfaces (for inflow and outflow) approach the corresponding light surfaces.

3.3 The accretion disk

X-ray observations of GRS1915+105 detected strong intensity variations indicating major instabilities of an accretion disk (Greiner et al. 1996). Belloni et al. (1997) find that the highly variable X-ray spectra could be explained if the inner disk is alternatively removed and replenished due to a thermal-viscous instability. Simultaneous X-ray and infrared observations of GRS1915+105 revealed evidence for a disk-jet interrelation (Eikenberry et al. 1998; Mirabel et al. 1998). The observed flares in the X-ray and IR bands have a consistent offset delay of $\sim$30min indicating an origin from the same event.

The accretion rate in GRS 1915+105 and GRO J1655-40 can be determined from the observed X-ray luminosities (e.g. Greiner et al. 1998). Depending on the chosen efficiency (5% in non-rotating versus 42% in maximally rotating black holes) the accretion rate ranges between 1- $9 ~ 10^{-7} ~M_{\odot}~ {\rm yr}^{-1}$ (GRS 1915+105) and 0.8- $7 ~ 10^{-8} ~M_{\odot}~ {\rm yr}^{-1}$ (GRO J1655-40), respectively.

From the theoretical point of view an accretion disk surrounding the black hole is the essential component concerning magnetic jet formation. It is considered to be responsible for the following necessary ingredients for jet formation, propagation, and collimation.

3.4 Model parameters for the wind motion

3.4.1 The magnetization parameter

The leading parameter for the wind solution along a fixed poloidal field is the magnetization parameter (5). Re-normalization to astrophysical units gives

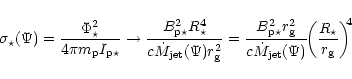\begin{displaymath}\sigma_{\star}(\Psi) = \frac{\Phi_{\star}^2}{4\pi m_{\rm p} I... ...Psi)} \!\!\left(\frac{R_{\rm\star}}{r_{\rm g}}\right)^{\!\!4} \end{displaymath} (6)

where $\dot{M}_{\rm jet}(\Psi) \simeq 4\pi m_{\rm p} n_{\rm\star}c u_{\rm p\star}R_{\rm\star}^2$is the jet mass flux enclosed by an area of radius $R_{\rm\star}$. A first order estimate of the magnetization can be derived from the disk equipartition field strength. Then, with a reasonable assumption on the jet mass flow rate related to the disk accretion rate, this gives the jet magnetization. Although the equipartition field strength is model-dependent, the different models (e.g. either advection dominated disk or standard disk, either Kramer's opacity or Thomson scattering) give rather similar results. A self-similar advection dominated disk model with the accretion rate $\dot{M}_{\rm acc}$ gives

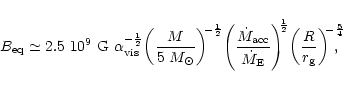\begin{displaymath}B_{\rm eq} \simeq 2.5 ~ 10^9 ~ {\rm G}\,\,\alpha_{\rm vis}^{-... ...\left(\frac{R}{r_{\rm g}}\right)^{\!\!-\frac{5}{4}}\!\!\!\!\!, \end{displaymath} (7)

where $\dot{M}_{\rm E} = 1.1 ~ 10^{-7}(M/5 ~ M_{\odot})\,M_{\odot}\, {\rm yr^{-1}}$is the Eddington luminosity and $\alpha_{\rm vis}$ is the viscosity parameter (see e.g. Narayan et al. 1998). In comparison, an optically thin standard accretion disk with Thomson opacity gives $ B_{\rm eq} \simeq \sqrt{8\pi P} = \sqrt{8\pi a T^4/3} \simeq 1.8 ~ 10^8\ {\rm G}\,\alpha_{\rm vis}^{-1/2}(M/5 ~ M_{\odot})^{-1/2} (R/r_{\rm g})^{-3/4} $(see Blandford 1990). Note that these estimates are only valid within certain limits of the accretion rate and the disk radius. Using the advection dominated disk model equipartition field strength, we obtain the following estimate for the magnetization at the injection radius,

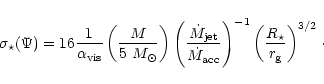\begin{displaymath}\sigma_{\star}(\Psi) = 16 \frac{1}{\alpha_{\rm vis}} \left(... ...\frac{R_{\rm\star}}{r_{\rm g}}\right)^{3/2}\cdot \nonumber \\ \end{displaymath}  

A comparison with the original Michel magnetization parameter $\sigma_{\rm M}$must take into account a factor $(r_{\rm g}/R_{\rm L})^2$. The magnetization parameter derived from the field distribution in a standard accretion disk model (see above) will give a similar result. We emphasize that we do not "apply'' a certain disk model (e.g. the ADAF model) in our computations. However, a comparison in the context of accretion disk theory just puts our wind parameters on a safer ground. Note, that neither the ADAF model nor the standard disk model takes into account the influence of magnetic fields. Moreover, the ADAF estimates as cited in Eq.(7) rely on the self-similar assumption. Compared to the standard disk, by definition, the matter in the ADAF disk would be rapidly advected possibly influencing also the wind ejection. However, such a detailed treatment is beyond the scope of this paper and may only be considered in numerical simulations investigating the disk-jet interaction itself (Koide et al. 1998, 1999, 2000)


  \begin{figure} \par\includegraphics[width=8.5cm,clip]{ms10209f2.ps} \end{figure} Figure 2: Projected magnetic flux surface. Shape of the poloidal field line/flux surface as function z(x) for the solutions S4 (and S4b, S3, S1) and S9 (and S3c2)
Open with DEXTER


 

 
Table 1: Comparison of leading parameters for the wind solution. Magnetic flux distribution $\tilde{\Phi}/{\tilde{\Phi}}_{\star}$, shape of the poloidal field line z(x), iso-rotation parameter $\Omega _{\rm F}$, sound speed at the injection radius $c_{\rm s\star }$, magnetization at the injection radius $\sigma _{\star }$, cylindrical Alfvén radius $x_{\rm A}$, cylindrical injection radius $x_{\star }$, total energy E, normalized to $m_{\rm p} c^2$normalized total angular momentum $\tilde{L} = L/E$, asymptotic velocity $u_{{\rm p}\infty }$, and angular momentum parameter of the black hole a. Other Parameters are: $\Gamma = 5/3$, $u_{\rm p\star }=0.006$ (S3-S9), $u_{\rm p\star }= 0.17$ (S3q, S3u2), $u_{\rm p\star }= 0.21$ (S3u3)
  prescribed   calculated                
  $\tilde{\Phi}/{\tilde{\Phi}}_{\star}$ z(x) $\Omega _{\rm F}$ $c_{\rm s\star }$ $\sigma _{\star }$ $x_{\rm A}$ $x_{\star }$ E $\tilde{L}$ $u_{{\rm p}\infty }$ a
S3 $\sim$1 0.1(x-x0)6/5 0.035 0.05165 979.4 22.931 8.3 2.7887 20.04 2.531 0.8
S3c2 $\sim$1 0.1(x-x0)3/2 0.035 0.0529 1356 22.931 8.3 2.764 19.95 2.58 0.8
S4 $\sim$x-1/2 0.1(x-x0)6/5 0.035 0.049 2380 22.931 8.3 2.7879 20.04 2.60 0.8
S4b $\sim$x-1/2 0.1(x-x0)6/5 0.014 0.0390 14 680 57.0 15.3 2.6730 47.07 2.48 0.8
S9 $\sim$x-1/2 0.1(x-x0)3/2 0.035 0.05165 2777 22.92 8.3 2.7572 19.93 2.57 0.8
S3q $\sim$1 0.1(x-x0)6/5 0.14 0.31 480 5.83 3.3 8.917 6.616 8.48 0.8
S3u $\sim$1 0.1(x-x0)6/5 0.14 0.27 100 5.33 3.3 3.16 5.69 2.96 0.8
S3u2 $\sim$1 0.1(x-x0)6/5 0.14 0.27 82.5 5.33 3.3 4.66 6.35 4.55 10-8
S3u3 $\sim$1 0.1(x-x0)6/5 0.14 0.27 205.7 5.33 3.3 4.65 6.35 4.48 10-8


3.4.2 The magnetic field distribution

The normalized magnetic field distribution is prescribed by

We apply different functions for z(x) and $\tilde{\Phi}(x)$ in order to investigate the influence of collimation, rotation and magnetic flux distribution on the acceleration of matter. One example is z(x)=0.1 (x-x0)6/5 describing an almost conical surface with only a slight collimation (see Fig. 2). Here, x0 defines the intersection of the field line with the equatorial plane, with x0 somewhat smaller than $x_{\star }$. The idea behind this choice is that the matter is expected to couple to the jet magnetic field above the accretion disk (with $z(x_{\star}) > 0$). An example for the magnetic flux distribution is $\tilde{\Phi}(x)= (x/x_{\star})^{-1/2}$, resulting in magnetic flux function $\Phi(x)$ decreasing with radius faster than a monopole where $\Phi(x)=1$.

Prescribing both the flux distribution and the shape of the flux surface does not over-determine the problem. The magnetic flux function $\Phi$ describes the opening of the magnetic flux tubes. With z(x), the shape of the flux surface chosen, the choice of the flux function just defines the position of the "other'' flux surfaces. In a fully self-consistent approach, the field structure is determined by the solution of the Grad-Shafranov equation. Such solutions are not yet available.

3.4.3 The plasma temperature

The temperature distribution along the field line follows a polytropic gas law, $T = T_{\star} \left(n/n_{\star}\right)^{\Gamma-1}$. In our approach the temperature at the injection radius $x_{\star }$ is determined by choosing the sound speed at this point, $c_{\rm s\star }$,

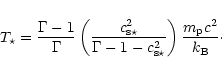\begin{displaymath}T_{\star} = \frac{\Gamma -1 }{\Gamma} \left(\frac{c_{\rm s\st... ...- c_{\rm s\star}^2}\right) \frac{m_{\rm p}c^2}{k_{\rm B}}\cdot \end{displaymath} (8)

For typical parameters applied in our calculations, $c_{\rm s\star}= 0.05$, $\Gamma = 5/3$ this gives a gas temperature of the disk corona of about 1.5   1010 K at a jet injection radius $x_{\star }= 8.3$. This temperature is in rough agreement with the disk temperature of the advection dominated accretion disk models at small radii (Narayan et al. 1998). A smaller $x_{\star }$ requires a higher sound speed parameter implying a higher temperature $T_{\star}$.

3.4.4 The iso-rotation parameter $\Omega_{\mathsf F}$

The iso-rotation parameter $\Omega_{\rm F}(\Psi)$ of the field line is determined from the position of the injection radius $x_{\star }$. This choice corresponds to the interpretation often applied for $\Omega _{\rm F}$as the "angular rotation of the field lines''. Here, we assume that the field lines are anchored in a Keplerian disk, $\Omega_{\rm F}\simeq \Omega_{\rm Disk} \simeq \Omega_{\rm K}(x_{\star})$. The angular velocity of the last stable circular orbit around a Kerr black hole is $\Omega_{\rm F}(x_{\star}) \sim \pm (x_{\star}^{3/2}\pm a)^{-1}$ (the $\pm$ stands for co-rotation or retrograde rotation, respectively). For a radial position not too close to the black hole, the angular velocity in the accretion disk follows its Newtonian value. Close to a black hole $\Omega _{\rm F}$ is limited due to the "rotation of space'' $\omega$. An injection radius $x_{\star }= 8.3$ gives $\Omega_{\rm F}=0.04$ which is about $0.1\,\Omega_{\rm H}$for a=0.8.


  \begin{figure} \par\includegraphics[width=7.6cm,clip]{ms10209f3a.ps}\par\include... ...ms10209f3b.ps}\par\includegraphics[width=7.6cm,clip]{ms10209f3c.ps} \end{figure} Figure 3: Solution S3. Properties of the critical wind solution along a given flux surface (see parameters in Table 1). The small window shows the solution branches around the slow magnetosonic point enlarged. The wind branch is the one with increasing velocity. The critical (magnetosonic) points are located at the intersections of the two solution branches (see Appendix C for details). Top: poloidal velocity $\alpha u_{\rm p}$ (in c). The asymptotic jet velocity of $u_{\rm p}= 2.5 $ is reached after about x = 108. Middle: normalized proper particle density n ( thick line) and temperature T in K ( thin line). Below: normalized poloidal ( thick line) and toroidal ( thin lines) field strength, $B_{\rm p}, B_{\phi }$. Note that the injection radius is $x_{\star }= 8.3$
Open with DEXTER

4 Results and discussion

We now discuss our numerical solutions of the general relativistic magnetic wind equation for different field geometries and input parameters. With the prescribed poloidal field our solution is uniquely defined by the conditions along the jet foot point and the condition of regularity across the magnetosonic points. Due to the stationarity assumption and the prescription of the field distribution, the spatial range of the computation is in principle not limited in radius. This is essential if one considers the huge size of Galactic superluminal jets in terms of the size of the central object.

In general, we show that the acceleration of plasma from regions close to a black hole to the speed of $0.92\,c$ observed for Galactic superluminal motion is possible to achieve. Depending on the poloidal magnetic field distribution, the asymptotic speed of the jet is reached at a radius of about 100 gravitational radii.

For comparison the leading parameters for our astrophysical solutions are summarized in Table 1. For illustration, we show the example solution S1 demonstrating the typical features of the wind solution branches in the case of super- or sub-critical parameters (Fig. C.1, Appendix C). The meaning of our figures is explained in detail in Appendix C.

4.1 The wind solution - a collimating relativistic jet

The time scale for the superluminal GRS1915+105 jet is at least one month until the blobs become invisible in radio light. Mirabel & Rodriguez (1994) estimated that the ejection event for a blob lasts about 3 days. This time period would correspond to a value of $\Omega_{\rm F}= 0.016$(for $M=5~M_{\odot}$) and an injection radius of about $x_{\star}\simeq 15$. The orbital period of the foot points rotating at the marginally stable orbit (for a=0.8) is an order of magnitude less. The time scale derived for the intervals between the emission of jet knots is much larger as the period of the marginally stable orbit. The true location of the jet origin not yet known. Therefore, we suggest that the jet foot point should be located outside the marginally stable orbit in order to maintain a jet flow for some time. For the first set of solutions we chose a foot point radius of $x_{\star }= 8.3$or $x_{\star}= 15.3$.

The fact that the kinematic time scale of the blobs is at least 10 times larger than the time scale for the generation of the blobs supports the assumption of stationarity in our calculations. Clearly, on the long-term time evolution the presence of the blobs them self tells us that the jet flow is time-dependent.

Compared to the other solutions in this sample with $x_{\star }= 8.3$, solution S3 is weakly magnetized (Fig. 3). The initial opening angle of the magnetic flux surface is large (Fig. 2). The magnetic flux function $\tilde{\Phi}(x)$ is constant along the field line. The asymptotic poloidal velocity of $u_{\rm p}= 2.5 $ is reached beyond a radius $x \simeq 10^8$ (corresponding to a distance from the black hole of $z(x) \simeq 4 ~ 10^8$).

Figure 3 also shows the distribution of other dynamical variables. The poloidal field strength $B_{\rm p}$ decreases with the opening of the magnetic flux surfaces. While the poloidal field distribution is prescribed in our approach, the toroidal magnetic field profile is a result of computation and therefore determined by the critical wind solution. At the injection point the toroidal field strength is about two times smaller than the poloidal component. Outside the Alfvén radius the toroidal field becomes much larger than the poloidal component. For large radii the magnetic field helix is dominated by the toroidal component. In this region we find the toroidal field component following a power law distribution d $(\log B_{\phi}) \simeq {\rm d}(\log x)$. Therefore, in the asymptotic part the poloidal electric current is almost constant $I \sim xB_{\phi} \sim {\rm const.}$In relativistic MHD electric -fields cannot be neglected. The electric field orientation is perpendicular to the magnetic flux surfaces and the field strength is $\vert\vec{E}_{\perp}\vert = (R/R_{\rm L}) B_{\rm P}$. Therefore, the electric field is dominating the poloidal magnetic field outside the light cylinder.

Density and temperature are interrelated by the polytropic gas law. At the injection point the gas temperature $T\simeq 10^{10}$ K (Fig. 3). The proper particle density at the injection point $n_{\rm\star}$ depends from the choice of the mass flux (in units of the magnetic flux). Therefore, the calculated density profile n(x) may be applied to different mass flow rates (as long as the magnetization $\sigma _{\star }$ is the same). Density and temperature decrease rapidly along the field line following the polytropic expansion. For $x \mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\displaystyle ... the proper particle density follows a power law $n/n_{\rm\star}= 4 ~ 10^{-5} x^{-1.8}$. At $x\simeq 1000$ the gas temperature is about 106 K. Therefore we can estimate the size of a X-ray emitting region of about several $1000\,r_{\rm g}$ in diameter. For the example of GRS1915+105 this corresponds to 3.5   10-9 arcsec. It would be interesting to calculate the X-ray spectra of such an relativistically expanding high temperature gas distribution.

Solution S3c2 has the same distribution of the magnetic flux function $\Phi$ as solution S3. The magnetic flux surfaces, however, are collimating more rapidly. The derived critical wind solution has a higher magnetization, although the terminal speed and the total energy density $E(\Psi)$ of the S3c2 solution is similar to S3. Because of the higher magnetization type S3c2 jet solutions have a correspondingly lower mass flow rate. The asymptotic speed is reached already at about x=1000equivalent to a distance from the central black hole of about z=3200.

Solution S9 relies on the same magnetic flux surface as S3c2. As a difference to S3c2, the magnetic flux function decreases with radius implying a (spatially) faster magnetic field decay. As a consequence, the jet reaches its asymptotic velocity of $u_{\rm p}= 2.57$ even at about x=100. The derived flow magnetization is higher compared to S3c2 and S3 balancing the fast decay of the magnetic field distribution and we obtain the same asymptotic speed. This is interesting because it proves that not only the magnetization, but also the distribution of the magnetic flux along the field line determines the asymptotic speed.

Note that solution S9 reaches the same asymptotic speed as S3c2 only because of its higher magnetization. Indeed, a solution similar to S9, but having the same magnetization $\sigma_{\star}= 1356$ as for S3c2, only reaches an asymptotic speed of $u_{\rm p}= 1.81$ (not shown). Also, such a solution would be only very weakly magnetized in the asymptotic regime as the normalized flow magnetization changes as $\sigma \sim 1/\sqrt{x}$ for the $\Phi \sim 1$ solutions or $\sigma \sim 1/x$ for the $\Phi \sim 1\sqrt{x}$ solutions[*], respectively. Similarly, in comparison, the asymptotical toroidal magnetic field is weaker by some orders of magnitude (a factor ten at x=1000). In all the solutions presented in this paper the asymptotic jet is dominated by the kinetic energy. For the solutions with the large injection radius $x_{\star }= 8.3$, the magnetic energy is being converted into kinetic energy almost completely already at a radius of about several 100 gravitational radii.

Solution S4 has the same magnetic flux distribution as S9, however, the field line is only weakly collimating. The asymptotic jet speed and the magnetization parameter is about the same. Only, the initial acceleration is weaker because the magneto-centrifugal mechanism works less efficient in the field with a smaller opening angle.

Solution S4b has essentially the same field distribution as S4, but the injection radius is chosen larger. Therefore, the iso-rotation parameter $\Omega _{\rm F}$ is decreased by a factor of (8.3/15.3)3/2. As a result, a critical wind solution with a comparable asymptotic speed could be obtained only for a very high plasma magnetization. This proves that highly relativistic jets can be expected even if the jet is not emerging from a region close to the black hole. Such a solution is feasible if the mass flow rate in the jet decreases with radius faster than the field strength (or flux distribution). The question remains whether such field strengths can be found at this position.

We summarize the results of this section. The asymptotic speed is determined by the plasma magnetization and the distribution of the magnetic flux along the field line. The shape of the magnetic flux surface determines the velocity profile along the field, thus, the position where the asymptotic velocity is reached. Highly relativistic outflows can be obtained even if the jet foot point is not very close to the black hole. However, in this case a high plasma magnetization is necessary. But this seems to be in contradiction to the accretion disk theory (see below).


  \begin{figure} \par\includegraphics[width=7.5cm,clip]{ms10209f4a.ps}\hspace*{0.5... ...s}\hspace*{0.5mm} \includegraphics[width=7.5cm,clip]{ms10209f4d.ps} \end{figure} Figure 4: Wind solutions S9 ( upper left), S3c2 ( lower left), S4 ( upper right), S4b ( lower right). Branches of poloidal velocity $\alpha u_{\rm p}$ along the field line in units of the speed of light. For the solution parameters see Table 1. See caption of Fig. 3 for further explanation
Open with DEXTER

4.2 The role of the magnetization

The magnetic acceleration of jets and winds can be understood either as a consequence of converting Poynting flux (magnetic energy) to kinetic energy or due to Lorentz forces along the poloidal field line. In general, the higher the plasma magnetization the more energy can be transformed into kinetic energy of the wind. It has been shown theoretically for a cold wind that the relation between magnetization and asymptotic velocity is that of a power law, $u_{{\rm P}\infty} \sim {\sigma_{\rm M}}^{1/3}$, for conical outflows (Michel 1969) and for collimating flows (Fendt & Camenzind 1996), if the flux distribution is the same, respectively. However, both papers do not consider gravity (and no general relativistic effects). The new solutions presented in this paper are in general agreement with those results in the sense that a higher magnetization leads to a higher velocity. However, we are dealing with the hot wind equation and cannot derive a power law distribution from Table 1, since the other wind parameters may vary between the different solutions. In difference to the cold wind solutions the magnetization is not a free parameter. Instead, it is fixed by the regularity condition at the magnetosonic points.

The wind magnetization is determined by the disk properties at the jet injection points along the disk surface. For a standard thin disk model that the ratio of the mass flow rate in the jet to the disk accretion rate is about 1% (Ferreira 1997). The observational data for various jet-disk systems are consistent with this theoretical value. The accretion disk magnetic flux can be estimated assuming equipartition between magnetic field pressure (energy) and gas pressure (thermal energy) in the disk (see Sect.3.4.1). From Eq.(7) we find an equipartition field strength of about $ B_{\rm eq} \simeq 5 ~ 10^8$ G, if $\alpha_{\rm vis} \simeq 0.1$ and $R_{\rm\star}= 10r_{\rm g}$. Equation (8) then defines an upper limit for the plasma magnetization at the injection radius, $\sigma_{\star}= 5 ~ 10^4 $, for $\dot{M}_{\rm jet}\simeq 0.1\ \dot{M}_{\rm acc}$. Such a value is in general agreement with our solutions (Table 1). The maximum equipartition field strength estimated with the above given formulae can be much larger for Galactic black hole jet sources as for AGN (see Eq.(7)). For a low black hole mass (with a smaller horizon) the disk comes closer to the singularity and therefore becomes hotter.

Again, we note that our estimate for the magnetization comes from comparison of different disk models (Sect.3.4.1). However, this does not mean that we apply a certain disk model for our computations.

Finally, we come back to the wind solutions S4 and S4b. As already mentioned, these solutions demonstrate that the jet origin must not be necessarily close to the black hole. One may think that a strong magnetization at larger disk radii would do the job. On the other hand, the equipartition field strength in the disk decreases with radius implying that the highest magnetization and, thus, jet velocities must be expected from the inner part of the disk. Only, if the mass transfer rate from the disk into the jet decreases more rapidly with radius than the field strength, the magnetization increases.

4.3 The influence of the rotating black hole

As the main issue of our paper is the search for MHD wind solutions in Kerr metric, it is necessary to clarify the role of general relativity for the jet acceleration itself. Clearly, at an injection radius of $R_{\rm\star}= 8.3$ general relativistic effects are not very dominant.

For comparison we have calculated wind solutions for a smaller injection radius $x_{\star }= 3.3$ (solution S3q, S3u, Figs. D.1, D.2). The main effect is a much higher asymptotic velocity resulting from the rapid rotation, $\Omega _{\rm F}$, at the smaller radius $x_{\star }$. With our choice $\Omega _{\rm F}= 0.14$ the asymptotic velocity drastically increases from $u_{\rm p}=2.503$ (S3) to $u_{\rm p}= 8.4792$ (S3q). In order to obtain the critical solution for the higher rotation rate, the wind parameters have to be changed accordingly. $\sigma _{\star }$ is decreased by a factor of two, while $c_{\rm s\star }$ and $u_{\rm p\star}$must be increased substantially. The large sound speed is in agreement with the smaller injection radius, since a higher disk temperature and pressure is expected close to the hole. The Alfvén radius is decreased by a factor of four, however, its location relative to the outer light cylinder remains the same.

The limiting case of Minkowski metric can be achieved by setting M=0 and a=0 in the Boyer-Lindquist parameters (see Appendix A). For such a wind solution (S3u2) the magnetization is lower, although the asymptotic wind speed is the same as in the Schwarzschild case (see Fig. D.2). This becomes clear if we take into account that for S3u2 the wind flow does not have to overcome the gravitational potential. Thus, less magnetic energy is needed to obtain the same asymptotic speed by magnetic acceleration. Further, we find from solutions for different angular momentum parameters a that in general the wind flow originating from a black hole with a smaller a is faster. As an extreme example we show the solution S3u3 calculated with $a\simeq0$ but otherwise the same parameter set (see Fig. D.2). This solution is magnetized stronger compared to the case of a=0.8, thus, resulting in a higher asymptotic wind velocity. We believe that the reason for such a behavior is the fact that the effective potential of a black hole weakens (at this location) for increasing values of a. Therefore, less magnetic energy is necessary to overcome the effective potential.

In the end, the results of this section are not surprising. They demonstrate that the wind/jet is basically magnetically driven. As a consequence, the acceleration takes place predominantly across the Alfvén point as expected from MHD theory. Therefore, the scenario is similar to the case of classical pulsar theory in Minkowski metric. For relativistic jets with a high magnetization the Alfvén point is always very close to the light surface, which is defined by the angular velocity of the field line foot point. Usually, the Alfvén point is located at a radius large compared to the gravitational radius. Thus, the influence of the general relativistic metric is marginal. Only, if the Alfvén radius comes close to the hole, the choice of the metric will determine the jet acceleration.

4.4 The question of collimation

The huge size observed for the knots of the Galactic superluminal sources leaves the possibility that the jet is basically un-collimated.

Our numerical solutions have shown that the asymptotic speed of the jet does not depend very much on the degree of collimation in the flow. That speed is reached within a distance of about $ 10^8r_{\rm g}$. However, the observed upper limit for the knot size is still a factor 10 larger. Therefore, from our solutions, the observed knots are consistent with both a collimated and an un-collimated jet flow. In particular, solution S9 which is more collimated, has the same asymptotic speed as solution S4.

In the case of extragalactic jets a high degree of collimation is indicated. The "lighthouse model'' by Camenzind & Krockenberger (1992) gives opening angles of only 0 $.\!\!^\circ$1 for the quasar 2C 273 or 0 $.\!\!^\circ$05 for typical BLLac objects. The question arises whether there could be an intrinsic difference between the jets of AGN and Galactic high energy sources. Why should Galactic superluminal jets be un-collimated? A difference in the jet magnetization seems to be unlikely since the jet velocities are comparable. We hypothesize that if the jets of these sources are systematically different, this should rather be caused by the conditions in the jet environment. If the jets are collimated by external pressure, a different external/internal pressure ratio will affect the degree of jet collimation. Extragalactic jets are believed to be confined by an external medium (see Fabian & Rees 1995; Ferrari et al. 1996). It is likely that Galactic superluminal sources provide an example where the jet pressure exceeds the pressure of the ambient medium. While AGN jets bore a funnel through the galactic bulge, Galactic superluminal jets freely expand into the empty space. Such a picture seems to be supported by the fact that the Galactic superluminal jet knots move with constant velocity over a long distance.

5 Summary

We have investigated magnetically driven superluminal jets originating from a region close to a rotating black hole. The stationary, general relativistic, magnetohydrodynamic wind equation along collimating magnetic flux surfaces was solved numerically. The wind solutions were normalized to parameters typical for Galactic superluminal sources.

The assumption of stationarity allows us to calculate the jet velocity on a global scale over a huge radial range in terms of radius of the central source. The wind is launched close to the rotating black hole at several gravitational radii. The calculation was performed up to a radius of 104 gravitational radii, but is in general not limited in radius. In some cases the asymptotic speed may be reached only at a distance of several 108 gravitational radii. Different magnetic field geometries were investigated. The model allows for a choice of the shape of the magnetic flux surface and the flux distribution of that field.

The physical wind solution is defined by the regularity condition at the magnetosonic points. As the poloidal field is prescribed, the choice of the following input parameters determines the wind solution completely, (i) the injection radius of the matter into the jet, (ii) the injection velocity and (iii) the plasma magnetization (the ratio of magnetic flux to mass flux). The results of our numerical computation are the following.

In summary, our numerical calculations have shown that the highly relativistic speed observed for galactic superluminal sources can be achieved by magnetic acceleration. For a given magnetic flux surface we obtain the complete set of physical parameters for the jet flow. The calculated temperature, density and velocity profile along the jet would provide a interesting set of input parameters for computing the spectral energy distribution.

Acknowledgements
C. F. thanks Mikael Jensen at Lund Observatory for discussions and the analytical proof of the equations in Appendix B. We acknowledge fruitful comments by the referee Dr. Koide helping to improve the presentation of this paper, especially Sect.4.3.

Appendix A: Parameters of Kerr metric

For the reason of completeness, here we list the parameters applied in the equations of Kerr geometry. In Boyer-Lindquist coordinates with the parameters

$\displaystyle \rho^2$ $\textstyle \equiv$ $\displaystyle r^2 + a^2\,\cos^2\theta, \quad\quad\quad\quad\quad\quad \Delta \equiv r^2 + a^2 - 2M\,r,$  
$\displaystyle \Sigma^2$ $\textstyle \equiv$ $\displaystyle (r^2 + a^2)^2 -a^2\Delta\sin^2\theta, \quad\quad \tilde{\omega}\equiv (\Sigma/\rho)\,\sin\theta,$  
$\displaystyle \omega$ $\textstyle \equiv$ $\displaystyle 2\,a\,M\,r / c\,\Sigma^2, \quad\quad\quad\quad\quad\quad \ \ \alpha \equiv \rho\,{\sqrt{\Delta}} / \Sigma,$  

the components of the metric tensor are defined as
g00 = $\displaystyle \sigma_{\rm m}( 2 r/\rho(r,\theta)^2 - 1 )$  
g03 = $\displaystyle - \sigma_{\rm m}2 r a \sin(\theta)^2 / \rho(r,\theta)^2$  
g11 = $\displaystyle \sigma_{\rm m}\rho(r,\theta)^2 / \Delta(r,\theta)$  
g22 = $\displaystyle \sigma_{\rm m}\rho(r,\theta)^2$  
g33 = $\displaystyle \sigma_{\rm m}\Sigma(r,\theta)^2\sin(\theta)^2 / \rho(r,\theta)^2$  
g $\textstyle \equiv$ $\displaystyle {\rm Det(g_{\mu \nu})} = - g_{11} g_{22} ( g_{30}^2 - g_{00}g_{33}).$  

In our paper we have chosen a negative sign of the metric, $\sigma_{\rm m}= -1$.

Appendix B: Wind polynomial

Here we provide the polynomial coefficients of the general relativistic magnetohydrodynamic wind Eq.(4). For a derivation, see Camenzind (1986), Takahashi et al. (1990), or Jensen (1997). The specific angular momentum, properly normalized, is

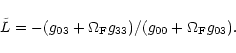\begin{displaymath}\tilde{L}= - (g_{03} + \Omega_{\rm F}g_{33}) / (g_{00} + \Omega_{\rm F}g_{03}). \end{displaymath} (B.1)

For convenience we define the following parameters,
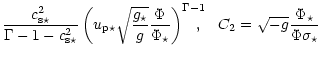C1 = $\displaystyle \frac{c_{\rm s\star}^2}{\Gamma-1-c_{\rm s\star}^2} \left(u_{\rm p... ...a-1} \!\!\!\!\!, \quad C_2 = \sqrt{-g} \frac{\Phi_{\star}}{\Phi \sigma_{\star}}$  
D1 = $\displaystyle g_{00}+2 \Omega_{\rm F}g_{03}+\Omega_{\rm F}^2 g_{33}, \quad D_2 = (1 - \Omega_{\rm F}\tilde{L})^2$  
D3 = $\displaystyle -(g_{33} +2 \tilde{L}g_{03} +\tilde{L}^2 g_{00})/(g_{03}^2-g_{00} g_{33}).$  

With the corresponding values at the injection radius $x_{\star }$the total specific energy density of the flow E is defined as

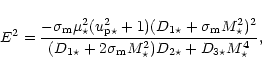\begin{displaymath}E^2 = \frac{-\sigma_{\rm m}\mu_{\star}^2 (u_{\rm p\star}^2+1)... ...gma_{\rm m}M_{\star}^2) D_{2\star} + D_{3\star} M_{\star}^4} , \end{displaymath} (B.2)

where $M_{\star}$ denotes the Alfvén Mach number at the injection radius. The polynomial coefficients of the wind Eq. (4) are
$\displaystyle \tilde{a}_{1,2n+2m}$ = C22  
$\displaystyle \tilde{a}_{2,2n+m}$ = $\displaystyle 2 \sigma_{\rm m}C_2 D_1$  
$\displaystyle \tilde{a}_{3,2n}$ = $\displaystyle D_1^2+C_2^2+\sigma_{\rm m}E^2 C_2^2 D_3$  
$\displaystyle \tilde{a}_{4,2n-m}$ = $\displaystyle 2 \sigma_{\rm m}C_2 D_1+2 E^2 C_2 D_2$  
$\displaystyle \tilde{a}_{5,2n-2m}$ = $\displaystyle D_1^2+\sigma_{\rm m}E^2 D_1 D_2$  
$\displaystyle \tilde{a}_{6,n+3m}$ = 4 C1 C22  
$\displaystyle \tilde{a}_{7,n+2m}$ = $\displaystyle 6 \sigma_{\rm m}C_1 C_2 D_1$  
$\displaystyle \tilde{a}_{8,n+m}$ = $\displaystyle 2 C_1 D_1^2+4 C_1 C_2^2+\sigma_{\rm m}2 E^2 C_1 C_2^2 D_3$  
$\displaystyle \tilde{a}_{9,n}$ = $\displaystyle \sigma_{\rm m}6 C_1 C_2 D_1+2 E^2 C_1 C_2 D_2$  
$\displaystyle \tilde{a}_{10,n-m}$ = 2 C1 D12  
$\displaystyle \tilde{a}_{11,4m}$ = 6 C12 C22  
$\displaystyle \tilde{a}_{12,3m}$ = $\displaystyle 6 \sigma_{\rm m}C_1^2 C_2 D_1$  
$\displaystyle \tilde{a}_{13,2m}$ = $\displaystyle C_1^2 D_1^2+6 C_1^2 C_2^2+\sigma_{\rm m}E^2 C_1^2 C_2^2 D_3$  
$\displaystyle \tilde{a}_{14,m}$ = $\displaystyle 6 \sigma_{\rm m}C_1^2 C_2 D_1$  
$\displaystyle \tilde{a}_{15,0}$ = C12 D12  
$\displaystyle \tilde{a}_{16,5m-n}$ = 4 C13 C22  
$\displaystyle \tilde{a}_{17,4m-n}$ = $\displaystyle 2\sigma_{\rm m}C_1^3 C_2 D_1$  
$\displaystyle \tilde{a}_{18,3m-n}$ = 4 C13 C22  
$\displaystyle \tilde{a}_{19,2m-n}$ = $\displaystyle 2\sigma_{\rm m}C_1^3 C_2 D_1$  
$\displaystyle \tilde{a}_{20,6m-2n}$ = C14 C22  
$\displaystyle \tilde{a}_{21,4m-2n}$ = C14 C22.  

All coefficients with the same second index have to be summed up, $A_i = \sum_{j} \tilde{a}_{j,i}$. The polytropic indices n=5, m=3 give a polynomial of 16th order.

Appendix C: Example wind solution in Kerr metric

Here we show an example solution of the wind Eq. (4). The parameters are chosen such that a variation of $\sigma _{\star }$ and $c_{\rm s\star }$ clearly demonstrates the criticality of the wind solution. They do not necessarily match astrophysical constraints. However, the asymptotic poloidal velocity is comparable to the speed of the Galactic superluminal sources. The solution (solution S1) considers a highly magnetized plasma flow with $\sigma_{\star}\simeq 5\,10^4 $. The flux geometry is that of a slightly collimating cone with an opening angle decreasing with distance from the source.

Figure C.1 shows the solution branches with a positive $u_{\rm p}^2$. An overlay of solutions for three parameter sets is displayed in order to show the typical behavior of wind solution.

  \begin{figure} \par\includegraphics[width=7.6cm,clip]{ms10209fc1.ps} \end{figure} Figure C.1: Example solution S1. Overlay of solutions $u_{\rm p}(x)$ for three different parameter sets. $\sigma _{\star }= 49830$, $ c_{\rm s\star }= 0.4585$ gives the critical solution which is regular across the magnetosonic points. The critical wind solution is the continuous branch starting with low velocity and accelerating to high speed. The magnetization $\sigma _{\star }$ is the critical parameter for the FM point, whereas $c_{\rm s\star }$ is the critical parameter for the SM point. Sub- or super-critical solutions are obtained by variation of the parameters $\sigma _{\star }$, $c_{\rm s\star }$. The choice of $\sigma _{\star }= 51\,830$, $ c_{\rm s\star }= 0.4485$ results in gaps in $x(u_{\rm p})$, the choice of $\sigma _{\star }= 48\,830$, $ c_{\rm s\star }= 0.4685$ in gaps in $u_{\rm p}(x)$. The other parameters are $x_{\rm A}= 31.2$, $u_{\rm p\star }= 0.01$, $x_{\star }= 3.0$, $\Omega _{\rm F}= 0.1\ \Omega _{\rm H}= 0.025$, a = 0.8

There is only one unique solution, the critical solution, with one branch continuing from small to large radii without any gaps in $u_{\rm p}$ or x. The magnetosonic points are located at the intersections of the solution branches of the critical solution. The critical wind solution is regular at all three magnetosonic points. It is defined by a unique set of the parameters E,L and $\sigma$ (for $\Omega _{\rm F}$ prescribed). In the critical solution the slow magnetosonic point is passed close to the foot point of the jet. The Alfvén point is located at x = 31 and the fast magnetosonic point not far beyond. The asymptotic speed of the flow is $u_{\rm p}= 2.28$, equivalent to $v_{\rm p}\simeq = 0.9\,c$ (not shown in the figure).

Sub- or super-critical wind parameters lead to solution branches which are not defined for all radii or all velocities. Even for a slight variation of these parameters the solution will be not continuous anymore, implying "jumps'' or "shocks'' across the gaps in the solution branches. At these locations the stationary character of the solution most probably breaks down. Such solution branches are inconsistent with the assumptions and are therefore referred to as unphysical.

Appendix D: The wind solution for a small injection radius

For comparison, we show solutions of the wind equation with a small injection radius $x_{\star }= 3.3$ as well as solutions in the limit of Minkowski and Schwarzschild metric (for a discussion see Sect.4.3). Solution S3q corresponds to solution S3, however, with a magnetization smaller by a factor of two. The asymptotic speed is $u_{\rm p}= 8.48$and much larger than for S3. Also solutions S3u, S3u2, S3u3 correspond to S3 and S3q. However, in this case the Alfvén radius and the derived magnetization parameter are lower resulting in a lower asymptotic speed. Solution S3u is the Kerr solution for a=0.8, S3u3 the Schwarzschild solution (a=10-8), and S3u2 the Minkowski solution where we set a=10-8 and M=0 in the Boyer-Lindquist parameters (see Appendix A). For a comparison of all solutions see Table 1.


  \begin{figure} \par\includegraphics[width=7.5cm,clip]{10209f1.eps} \end{figure} Figure D.1: Example solutions with a small injection radius $x_{\star }= 3.3$. Rotation rate $\Omega _{\rm F}= 0.14$. Solution S3q with a=0.8, $x_{\rm A}= 5.83$, $\sigma _{\star }= 480$has a high asymptotic velocity $u_{\rm p}= 8.48$


  \begin{figure} \par\includegraphics[width=7.5cm,clip]{ms10209fd2a.ps}\par\includ... ...10209fd2b.ps}\par\includegraphics[width=7.5cm,clip]{ms10209fd2c.ps} \end{figure} Figure D.2: Example solutions with a small injection radius $x_{\star }= 3.3$. Rotation rate $\Omega _{\rm F}= 0.14$. Top: solution S3u with a=0.8, $x_{\rm A}= 5.33$, and a smaller $\sigma _{\star }= 100$ and a lower asymptotic velocity $u_{\rm p}= 2.96$. Middle: solution S3u3 in Schwarzschild metric, a=10-8, $x_{\rm A}= 5.33$. The asymptotic speed is $u_{\rm p}= 4.48$ with $\sigma _{\star }= 205.7$. Bottom: solution S3u2 in Minkowski metric, a=10-8, M=0. The asymptotic speed is $u_{\rm p}= 4.55$ while $\sigma _{\star }= 82.5$

References

 

Copyright ESO 2001