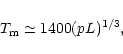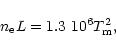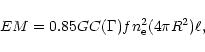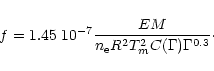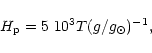A&A 368, 888-900 (2001)
DOI: 10.1051/0004-6361:20010026
CHANDRA-LETGS X-ray observations of Capella
Temperature, density and abundance diagnostics
R. Mewe1 - A. J. J. Raassen1,2 - J. J. Drake3 - J. S. Kaastra1 - R. L. J. van der Meer1 - D. Porquet4
1 - Space Research Organization Netherlands (SRON),
Sorbonnelaan 2, 3584 CA Utrecht, The Netherlands
2 -
Astronomical Institute "Anton Pannekoek'', Kruislaan 403,
1098 SJ Amsterdam, The Netherlands
3 -
Smithsonian Astrophysical Observatory, 60 Garden Street,
Cambridge, MA 02138, USA
4 -
CEA/DSM/DAPNIA, Service d'Astrophysique, CEA Saclay, 91191 Gif-sur-Yvette Cedex, France
Received 12 October 2000 / Accepted 15 December 2000
Abstract
We report an analysis of the X-ray spectrum of Capella from 6 to 175
Å obtained with the Low Energy Transmission Grating Spectrometer (LETGS) on board
of the X-ray space observatory CHANDRA. Many emission line features
appear that can be resolved much better as compared to former
instruments (EUVE and ASCA). Coronal electron densities (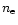 )
and
temperatures (T) of brightly emitting regions are constrained by an
analysis of ratios of density- and temperature-sensitive lines of
helium-like ions and highly ionized iron atoms. Lines emitted by
e.g., O VII & VIII, Mg X-XII, Si XII-XIV, Fe IX, X & XV-XXIII are
used to derive T. Line ratios in the helium-like triplets of C V, N VI,
O VII, Mg XI, and Si XIII yield T in the range 0.5-10 MK, and
)
and
temperatures (T) of brightly emitting regions are constrained by an
analysis of ratios of density- and temperature-sensitive lines of
helium-like ions and highly ionized iron atoms. Lines emitted by
e.g., O VII & VIII, Mg X-XII, Si XII-XIV, Fe IX, X & XV-XXIII are
used to derive T. Line ratios in the helium-like triplets of C V, N VI,
O VII, Mg XI, and Si XIII yield T in the range 0.5-10 MK, and
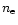 in the range 109-1013 cm-3. The Fe IX/X ratio
yields
in the range 109-1013 cm-3. The Fe IX/X ratio
yields 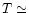 0.9 MK, while lines from Fe XVIII to XXII give
0.9 MK, while lines from Fe XVIII to XXII give 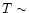 6-10 MK. Flux ratios of Fe XX-XXII lines indicate for the
electron densities an upper limit in the range
6-10 MK. Flux ratios of Fe XX-XXII lines indicate for the
electron densities an upper limit in the range
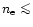 (2-5) 1012 cm-3.
From line ratios of Fe XVII and Fe XVIII we derive constraints on the
optical depth
(2-5) 1012 cm-3.
From line ratios of Fe XVII and Fe XVIII we derive constraints on the
optical depth 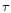 of
of 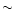 1-1.5.
An emission measure distribution is derived from Fe line intensities.
Results for element abundances (relative to Fe) from a 4-T model are:
O and Ne/Fe about solar, N, Mg and Si/Fe
1-1.5.
An emission measure distribution is derived from Fe line intensities.
Results for element abundances (relative to Fe) from a 4-T model are:
O and Ne/Fe about solar, N, Mg and Si/Fe  2
2 solar.
The results for Tand
solar.
The results for Tand 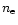 are described in terms of quasi-static coronal loop models
and it is shown that the X-ray emission originates from compact
structures much smaller than the stellar radii.
are described in terms of quasi-static coronal loop models
and it is shown that the X-ray emission originates from compact
structures much smaller than the stellar radii.
Key words: stars: individual: Capella - stars: coronae - stars: late-type - stars: activity -
X-rays: stars -
atomic processes vspace-1mm
The G1 III + G8/K0 III binary Capella with a 104.0233-day orbit at
a distance of 13 pc (Strassmeier et al. 1993) is one of the brightest
non-degenerate stellar X-ray sources. Observations by Linsky et al. (1998) with the GHRS spectrometer on the Hubble Space Telescope
(HST) on Sept. 1995 and on April 1996 indicate that the optically
brightest (by
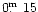 )
and more fastly rotating (v sin i=36 kms-1) G1
component (mass 2.6
)
and more fastly rotating (v sin i=36 kms-1) G1
component (mass 2.6 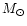 ,
radius 9.2
,
radius 9.2 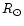 )
is about 3-10
times brighter in the chromospheric and transition-region UV lines
than the slowly rotating (v sin i=3 kms-1) G8/K0 star
(2.7
)
is about 3-10
times brighter in the chromospheric and transition-region UV lines
than the slowly rotating (v sin i=3 kms-1) G8/K0 star
(2.7 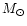 ,
12.2
,
12.2 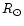 ). The Sept. 1995 observations showed that
the coronae around the G1 and G8 stars were equally bright in the hot
(107 K) coronal Fe XXI 1354 Å line, but recent observations with
the HST STIS by Johnson et al. (2001) on October 1999 indicate that the
G8 corona was at least 5 times fainter than the G1 corona in the Fe XXI
line, the latter having changed relative to the Sept. 1995 observations
by only 50% or less. These results suggest that the hot corona of
the G8 star is quite strongly variable whereas that of the G1 is not.
). The Sept. 1995 observations showed that
the coronae around the G1 and G8 stars were equally bright in the hot
(107 K) coronal Fe XXI 1354 Å line, but recent observations with
the HST STIS by Johnson et al. (2001) on October 1999 indicate that the
G8 corona was at least 5 times fainter than the G1 corona in the Fe XXI
line, the latter having changed relative to the Sept. 1995 observations
by only 50% or less. These results suggest that the hot corona of
the G8 star is quite strongly variable whereas that of the G1 is not.
Due to the coronal structure of Capella
its spectrum is rich in
emission lines in the soft X-ray region and has been well studied by many
earlier instruments with lower spectral resolution
(for references see, e.g., Brinkman et al. 2000).
The spectra of Capella obtained with the LETGS are of high
quality and agree with the pre-flight calculated instrumental spectral
resolution (cf. Brinkman et al. 2000).
The wavelength region of the LETGS between 6-42 Å contains a number of
helium-like line "triplets'' from Si XIII to C V which provide density
as well as temperature diagnostics for plasmas with temperatures in
the range 1-10 MK and densities in the range
108-1013 cm-3. The long-wavelength region between
90-140 Å contains a series of lines from 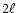 -
-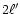 transitions in Fe XVIII-Fe XXIII which provide density and
temperature diagnostics for relatively hot (
transitions in Fe XVIII-Fe XXIII which provide density and
temperature diagnostics for relatively hot (
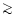 5 MK) and dense
(
5 MK) and dense
(
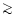 1012 cm-3) plasmas (e.g., Mewe et al. 1985, 1991;
Brickhouse et al. 1995).
From EUVE spectra of Capella, Dupree et al. (1993), Schrijver et al. (1995), and Brickhouse (1996) have derived electron densities
1012 cm-3) plasmas (e.g., Mewe et al. 1985, 1991;
Brickhouse et al. 1995).
From EUVE spectra of Capella, Dupree et al. (1993), Schrijver et al. (1995), and Brickhouse (1996) have derived electron densities 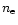 in
the range 1012-1013 cm-3 at a temperature
in
the range 1012-1013 cm-3 at a temperature 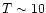 MK. More recently, Brickhouse et al. (2000) have analyzed
the coronal temperature and abundance structure of the coronae of
Capella based on EUVE and ASCA observations covering a broad wavelength
range. Our work presented here
covers the ASCA region and part of the EUVE region,
though in more detail due to the higher spectral resolution
(
MK. More recently, Brickhouse et al. (2000) have analyzed
the coronal temperature and abundance structure of the coronae of
Capella based on EUVE and ASCA observations covering a broad wavelength
range. Our work presented here
covers the ASCA region and part of the EUVE region,
though in more detail due to the higher spectral resolution
(
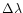
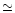 0.06 Å) of the LETG spectrometer. In the present
paper, the long-wavelength iron lines have been studied for the
purposes of providing further insights into the coronal
temperature structure as well as for density diagnostics.
Section 2 discusses the observations, the data reduction, the counting
rate/photon flux conversion, and the correction for interstellar
absorption. Section 3 discusses branching ratios for
0.06 Å) of the LETG spectrometer. In the present
paper, the long-wavelength iron lines have been studied for the
purposes of providing further insights into the coronal
temperature structure as well as for density diagnostics.
Section 2 discusses the observations, the data reduction, the counting
rate/photon flux conversion, and the correction for interstellar
absorption. Section 3 discusses branching ratios for 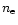 -independent
lines decaying from the same upper level or within the same ion in
relation to theoretical values and the consequences for optical depth
and source size. In Sect. 4 the analysis of the temperature
diagnostic for helium-like triplets and iron lines is presented and
Sect. 5 discusses briefly the determination of the electron density
from the iron lines and the helium-like triplets.
Section 6 describes the emission measure distribution and
Sect. 7 discusses the results in terms of quasi-static loop models.
-independent
lines decaying from the same upper level or within the same ion in
relation to theoretical values and the consequences for optical depth
and source size. In Sect. 4 the analysis of the temperature
diagnostic for helium-like triplets and iron lines is presented and
Sect. 5 discusses briefly the determination of the electron density
from the iron lines and the helium-like triplets.
Section 6 describes the emission measure distribution and
Sect. 7 discusses the results in terms of quasi-static loop models.
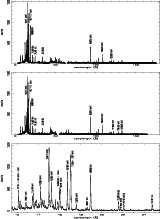 |
Figure 1:
CHANDRA-LETGS spectrum of Capella observed on 9 Nov. 1999 in +1 order
(top), in -1 order (middle), and detail of -1 order spectrum between 12-25 Å (bottom). Spectra are
corrected for background. Several prominent lines are labelled with the emitting ions |
| Open with DEXTER |
Notes to Tables
1 and
2
- a observed wavelength in Å.
- b measured counting rate in 10-4 c/s.
- c line photon flux in 10-4 phot/cm2/s, averaged over +1 & -1 order and corrected for interstellar absorption.
- d predicted wavelength in Å and line identification (ID); see Phillips et al. (1999) (solar and
laboratory measurements between 5 and 20 Å), Mason et al. (1984) (solar observations between 90 and 175 Å), and Mewe et al. (1985, 1995a) (full wavelength range in MEKAL code)
- e only total intensity is given because Fe XVIII and O VIII lines are blended
Spectra of Capella were obtained in the calibration phase during
6-12 September 1999 (cf. Brinkman et al. 2000)
and subsequently on 9 November 1999, using the High Resolution
Camera (HRC-S) and the Low Energy Transmission Grating (LETG) on board
the X-ray observatory CHANDRA.
In the present paper we study the second spectrum
(exposure time 85.4 ksec).
The HRC-S is equipped with three microchannel plate detectors (10 cm each) in
one row. The 0th order diffraction signal is aimed at the central detector,
such, that for the +1 and -1 diffraction orders, the wavelength regions that
fall in the gaps between the detector plates do not overlap (see
Fig. 1).
This way the
central plate covers nominally the range of -50 (-1 order) to +60 (+1 order) Å, the outer
plates -55 to -165 Å and +65 to +175 Å. The dispersion is 1.15 Å/mm.
Figure 1 shows the LETGS spectra of Capella in the
+1 & -1 order with the gaps between 62-65 Å and 52-56 Å (+1 and -1 order, respectively)
and a detail of the -1 order spectrum between 12-25 Å.
The spectra were rebinned to intervals of 0.02 Å and corrected for
the background.
Around the dispersion axis a source box is defined. The edge of the box is a
function of the wavelength, small at short wavelengths and wide at long
wavelengths, like a bowtie. The background box is defined as the area from 10
to 39.5 arcsec above and under the dispersion axis. The ratio of the source to
background area ranges from 1:25 at the short wavelengths to 1:6 at the edge of
the detector.
For each bin the number of counts is integrated in the cross dispersion
direction inside the boxes. The net number of source counts is calculated as
follows:
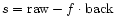 ,
,
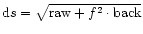 ,
,
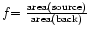 ,
where
,
where
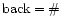 counts in background box,
counts in background box,
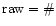 counts in source box, and
counts in source box, and
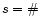 net source counts in source box with error ds.
net source counts in source box with error ds.
By visual inspection we selected the prominent lines and fitted them with
Gaussian profiles. This has yielded values for the
wavelength, FWHM, and the number of photon counts (including
uncertainties) for each line. By comparing wavelengths and line counts with expected values
we have identified all lines given in Tables 1 and 2.
To represent the background due to continuum radiation we introduce a constant shift.
The intensities of the emission line features in the
spectrum are based on integration over the line profile to obtain
the total counts. For isolated lines
the Gaussian line width turns out to be consistent with the average
theoretical instrumental width, which implies that Doppler broadening
can be neglected compared to the instrumental width.
The measured FWHM of the instrumental profile is about 0.068 Å for wavelengths
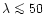 Å (and increasing with
Å (and increasing with 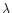 at long wavelengths). This
is in good agreement with the results of the pre-flight ground calibration.
Blended lines were fitted by multiple Gauss profiles with the proper instrumental width.
The LETGS instrumental profile is
actually closer to a Lorentzian function than to a Gaussian; we have
investigated the effect of using Lorentzian
profiles in the analysis but usually found no significant differences in
derived line parameters.
at long wavelengths). This
is in good agreement with the results of the pre-flight ground calibration.
Blended lines were fitted by multiple Gauss profiles with the proper instrumental width.
The LETGS instrumental profile is
actually closer to a Lorentzian function than to a Gaussian; we have
investigated the effect of using Lorentzian
profiles in the analysis but usually found no significant differences in
derived line parameters.
Counting rates I and 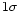 uncertainties are given in Tables 1 and 2.
The observed counting rates I (10-4 c/s) have been converted to photon fluxes F (10-4 phot/cm2/s) using the
preliminaryin-flight effective area model for the spectrometer (for details of the calibration, see van der Meer
et al. 2001).
The observed flux at Earth was further corrected for interstellar absorption, assuming an interstellar column density
uncertainties are given in Tables 1 and 2.
The observed counting rates I (10-4 c/s) have been converted to photon fluxes F (10-4 phot/cm2/s) using the
preliminaryin-flight effective area model for the spectrometer (for details of the calibration, see van der Meer
et al. 2001).
The observed flux at Earth was further corrected for interstellar absorption, assuming an interstellar column density
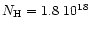 cm-2 (see Schrijver et al. 1995), using the cross sections of Morrison & McCammon (1983).
In Tables 1 and 2 we give the photon flux F averaged over the +1 & -1 order and corrected for interstellar absorption.
cm-2 (see Schrijver et al. 1995), using the cross sections of Morrison & McCammon (1983).
In Tables 1 and 2 we give the photon flux F averaged over the +1 & -1 order and corrected for interstellar absorption.
In the overlapping wavelength regions (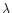 <35 Å) the obtained fluxes are in agreement with values obtained with the CHANDRA-HETGS by
Canizares et al. (2000) and with data from the RGS on board XMM-Newton (see Audard et al. 2001; cf. their Table 1 for a comparison of fluxes).
For the long-wavelength region (
<35 Å) the obtained fluxes are in agreement with values obtained with the CHANDRA-HETGS by
Canizares et al. (2000) and with data from the RGS on board XMM-Newton (see Audard et al. 2001; cf. their Table 1 for a comparison of fluxes).
For the long-wavelength region (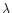 >90 Å) we have compared the LETGS fluxes with the EUVE fluxes obtained by Brickhouse et al. (2000).
The LETGS/EUVE flux ratio was in the range
>90 Å) we have compared the LETGS fluxes with the EUVE fluxes obtained by Brickhouse et al. (2000).
The LETGS/EUVE flux ratio was in the range 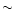 0.5 to 0.8 which is explained by a different activity level of Capella (see e.g.,
comparison by Linsky et al. 1998).
0.5 to 0.8 which is explained by a different activity level of Capella (see e.g.,
comparison by Linsky et al. 1998).
This section presents a comparison of observations with model
predictions. First, we consider branching ratios for lines decaying
from the same upper level and some optical depth effects. Second, we
consider some lines decaying from different upper levels.
The branching ratio is defined as the ratio of the photon
fluxes of two lines decaying from the same upper level. The
uncertainty of the branching ratio is given by the uncertainty of the radiative
transition probabilities A of the lines which is typically about
25% each (see below). The comparison of the measured and theoretical
branching ratios provides a good figure of merit for the quality of the flux
measurements as well as a check on the assumption of the optically
thin model, i.e., optical line depth
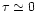 .
.
In Table 3, photon flux ratios of two lines decaying from the same
upper level are compared to the theoretical branching ratios. The
theoretical values are from the NIST compilation, from MEKAL (Mewe et al. 1985, 1995a) as implemented in the SPEX code (Kaastra et al. 1996),
from recent calculations at SRON using the Cowan code programs, and
from work by Brickhouse et al. (1995). From this table we notice that
the theoretical ratios from MEKAL for the Fe XVIII pair and three
of the Fe XIX pairs are somewhat lower than those from the three other
theories, which are in good agreement with each other. For all except
one the theoretical line ratios in Table 3 are within the experimental
statistical errors of the Capella line ratios. For some of
the ratios the statistical error is also very large, e.g., the ratio
102.22/97.88 for which the deviation between
the +1 and -1 order is apparently large, though the flux for
97.88 Å should only be treated as an upper limit.
The only disagreement concerns the
ratio 101.55/109.97. However, taking into account an uncertainty of 25% for
the theoretical values as indicated by the NIST database
(classification "C'') all ratios agree with the theoretical values.
Brickhouse et al. (1995) observed a deviation for the ratio
101.55/111.7. She suggests a blend for the line at
101.55 Å. Although in our case the ratios related to the 101.55 Å line are about 25% larger than the theoretical value (which is in
agreement with some blending) they are all within the combined statistical and
NIST error bars.
Schrijver et al. (1995) and Mewe et al. (1995b) have investigated the
possibility that strong resonance photons are scattered out of the
line of sight in late-type stellar coronae. Branching ratios can be
used to check the assumption of the optical thin model because effects
of resonance scattering would affect the measured branching ratio.
From the fact that the intensities of, e.g., the strong resonance
lines Fe XVIII 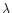 93.92 and Fe XIX
93.92 and Fe XIX 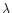 108.37 are in good
agreement with the intensities of other lines sharing the same upper
levels, we can derive a constraint on the optical depth taking into
account the systematic uncertainties of the theoretical transition
probabilities A (typical 25% for each A, hence 35% for the branching ratio)
which dominate over the statistical errors (typically 10%). If we
rule out a reduction in the resonance line intensity larger than
about 30%, then on the basis of a simple "escape-factor'' model
(escape factor
108.37 are in good
agreement with the intensities of other lines sharing the same upper
levels, we can derive a constraint on the optical depth taking into
account the systematic uncertainties of the theoretical transition
probabilities A (typical 25% for each A, hence 35% for the branching ratio)
which dominate over the statistical errors (typically 10%). If we
rule out a reduction in the resonance line intensity larger than
about 30%, then on the basis of a simple "escape-factor'' model
(escape factor
![$P(\tau) \simeq [1 + 0.43 \tau]^{-1}$](/articles/aa/full/2001/12/aah2499/img46.gif) for a homogeneous
mixture of emitters and absorbers in a slab geometry (e.g., Kaastra
& Mewe 1995)) we can put a constraint on the optical depth:
for a homogeneous
mixture of emitters and absorbers in a slab geometry (e.g., Kaastra
& Mewe 1995)) we can put a constraint on the optical depth:
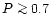 yields
yields
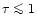 for the Fe XVIII
for the Fe XVIII 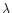 93.92 line.
93.92 line.
Line transitions of Ne-like Fe XVII yield the strongest emission lines
seen in the LETGS spectrum in the range 15-17 Å (cf. Fig. 1 and Table 2).
For the very strong Fe XVII 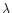 15.014 resonance line we can also
derive a constraint on the optical depth as follows.
15.014 resonance line we can also
derive a constraint on the optical depth as follows.
In principle, the ratio
of the strong Fe XVII 15.014 Å resonance line (with a large oscillator strength
f=2.66) to a presumably optically thin Fe XVII line with a relatively small oscillator strength
(e.g., 16.780 Å, f=0.101, or 15.265 Å, f=0.593)
yields the optical depth 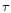 in the 15.014 Å line, applying the escape-factor model.
Solar physicists have used this technique
to derive the density in active regions on the Sun from the optical depth and the estimated
plasma dimension
in the 15.014 Å line, applying the escape-factor model.
Solar physicists have used this technique
to derive the density in active regions on the Sun from the optical depth and the estimated
plasma dimension 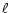 (e.g., Saba et al. 1999).
Though the 16.780 Å line has the smallest f-value we prefer to use the 15.265 Å line
because the 16.780 Å
(e.g., Saba et al. 1999).
Though the 16.780 Å line has the smallest f-value we prefer to use the 15.265 Å line
because the 16.780 Å
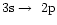 line can be affected by radiative cascades.
line can be affected by radiative cascades.
From the measured Fe XVII 15.014/15.265 photon flux ratio of 2.85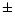 0.14 we derive for a plasma of
7 MK (as derived from the Fe XVII 15.265/Fe XVIII 16.078 ratio, see Sect. 4.1) an upper limit to the optical depth
0.14 we derive for a plasma of
7 MK (as derived from the Fe XVII 15.265/Fe XVIII 16.078 ratio, see Sect. 4.1) an upper limit to the optical depth 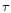 of the Fe XVII 15.014 Å line by comparing to the corresponding line ratios
given by experiment (2.8-3.2) (Livermore Electron Beam Ion Trap (EBIT)) or theory (3.3-4.7) (cf. Brown
et al. 1998; Bhatia & Doschek 1992).
Taking the EBIT ratio we obtain from the condition
of the Fe XVII 15.014 Å line by comparing to the corresponding line ratios
given by experiment (2.8-3.2) (Livermore Electron Beam Ion Trap (EBIT)) or theory (3.3-4.7) (cf. Brown
et al. 1998; Bhatia & Doschek 1992).
Taking the EBIT ratio we obtain from the condition
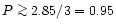 an upper limit of
an upper limit of
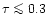 ,
whereas the theoretical
ratio would give a more conservative upper limit of
,
whereas the theoretical
ratio would give a more conservative upper limit of
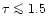 from
from
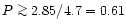 .
.
The constraints on 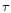 imply a
constraint on the extent of the emitting plasma though the averaging over the stellar surface makes a straightforward
interpretation difficult.
The optical depth
imply a
constraint on the extent of the emitting plasma though the averaging over the stellar surface makes a straightforward
interpretation difficult.
The optical depth 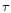 for a Doppler-broadened resonance line can be written
as (Mewe et al. 1995b):
for a Doppler-broadened resonance line can be written
as (Mewe et al. 1995b):
where
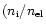 )
is the ion fraction (from Arnaud & Raymond 1992),
)
is the ion fraction (from Arnaud & Raymond 1992),
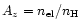 the elemental abundance
relative to hydrogen with
the elemental abundance
relative to hydrogen with
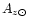 the corresponding value for the
solar photosphere as given by Anders & Grevesse (1989),
the corresponding value for the
solar photosphere as given by Anders & Grevesse (1989),
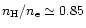 the ratio of hydrogen to electron density
(in cm-3),
the ratio of hydrogen to electron density
(in cm-3), 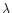 the wavelength in Å, f the absorption oscillator
strength, M the atomic weight, T the temperature (in K or T6in MK), and
the wavelength in Å, f the absorption oscillator
strength, M the atomic weight, T the temperature (in K or T6in MK), and
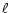 a characteristic plasma dimension (in cm), and
a characteristic plasma dimension (in cm), and
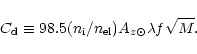 |
(2) |
For Fe XVII 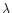 15.014, Fe XVIII
15.014, Fe XVIII 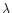 93.92, and Fe XIX
93.92, and Fe XIX
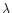 108.37 we obtain from Eq. (2)
108.37 we obtain from Eq. (2)
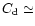 0.25, 0.05, and
0.04, respectively for a temperature
0.25, 0.05, and
0.04, respectively for a temperature
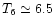 (see
Sect. 4). Assuming solar abundances (
(see
Sect. 4). Assuming solar abundances (
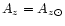 = 4.68
10-5 for Fe), the constraints on
= 4.68
10-5 for Fe), the constraints on 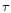 yield corresponding upper
limits for
yield corresponding upper
limits for
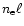 of about 2 1020, 5 1020, and
6 1020 cm-2 for these three cases. With a density of
typically
of about 2 1020, 5 1020, and
6 1020 cm-2 for these three cases. With a density of
typically
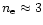 1012 cm-3 (see Sect. 5.1) we
derive upper limits to the typical size
1012 cm-3 (see Sect. 5.1) we
derive upper limits to the typical size 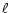 of the emitting region
in the range (1-2) 108 cm, i.e. much smaller than the stellar
radii (
of the emitting region
in the range (1-2) 108 cm, i.e. much smaller than the stellar
radii (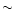
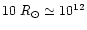 cm), but slightly above the
typical loop size as derived from the electron density in a comparable
temperature region (cf. Table 9, Fe XX-XXI). For the Sun loop sizes
typically range from 3 109 cm for compact active region loops to
2 1010 cm for large-scale quiet region loops (see e.g., Mewe
1991, Table 1).
cm), but slightly above the
typical loop size as derived from the electron density in a comparable
temperature region (cf. Table 9, Fe XX-XXI). For the Sun loop sizes
typically range from 3 109 cm for compact active region loops to
2 1010 cm for large-scale quiet region loops (see e.g., Mewe
1991, Table 1).
The above analysis, however, is strictly valid only
if all flux is concentrated
in one single loop. If one observes a collection of loops distributed more or less homogeneously
over the stellar surface, the effects of optical depth tend to average out.
There may be significant resonance scattering
of photons into the line of sight. In this situation it is
possible that there is indeed significant optical depth in certain
structures, but that this is compensated for by the azimuthal average
over the stellar disk whereby some lines of sight pick up photons
that are scattered and others lose photons to scattering (e.g., Wood & Raymond 2000).
Nevertheless, the above analysis still serves to demonstrate the
usefulness of investigating optical depths to provide further clues on
the emitting geometry.
Table 4:
Line ratios based on different upper levels
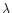 (Å)
(Å) |
+1a |
-1a |
av.b |
Mc |
Bd |
| Fe XVI |
|
|
|
|
|
| 54.14/54.728 |
0.70 |
gap |
0.67(.15) |
0.56 |
-- |
| Fe XIX |
|
|
|
|
|
| 91.02/101.55 |
0.49 |
0.56 |
0.42(.07) |
0.156 |
0.241 |
| 91.02/108.37 |
0.16 |
0.16 |
0.130(.014) |
0.057 |
0.082 |
| 91.02/109.97 |
1.1 |
1.7 |
1.09(.19) |
0.287 |
0.476 |
| 108.37/109.97 |
7.0 |
10.4 |
8.4(1.4) |
5.00 |
5.48 |
| 108.37/111.70 |
10.0 |
13.6 |
11.4(2.6) |
6.34 |
6.95 |
| Fe XX |
|
|
|
|
|
| 118.66/121.83 |
0.48 |
0.68 |
0.55(.07) |
0.517 |
0.517 |
| 118.66/132.85 |
0.47 |
0.44 |
0.28(.03) |
0.355 |
0.386 |
| 121.83/132.85 |
0.97 |
0.65 |
0.55(.06) |
0.679 |
0.754 |
| Fe XXII |
|
|
|
|
|
| 117.17/135.78 |
2.1 |
1.8 |
1.17(.2) |
0.853 |
0.991 |
- a measured counting rate ratio in +1 and -1 order of spectrum.
- b line photon flux ratio averaged over +1 and -1 order and corrected for
interstellar absorption (in parentheses the mean statistical 1
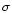 error).
error).
- c calculated with SPEX/MEKAL code (Mewe et al. 1985, 1995a; Kaastra et al. 1996).
- d Brickhouse et al. (1995).
In Table 4 ratios are given for lines that belong to the same Fe ion,
but that do not decay from the same upper level. In this case they cannot
be compared to the ratios of the transition probabilities, the
branching ratio as given by NIST and COWAN. However, comparison with
MEKAL and Brickhouse et al. (1995) is still possible, as they take
into account the populations of the levels due to collisional
excitations and radiative decays. Only
density-independent lines are used.
In Table 4 all ratios in Fe XIX that
include the line at 91.02 Å are far too high. This implies
blending by an unknown feature
or a theoretical flux value far too low for that line.
There is some indication for this, given the
considerable difference between the MEKAL and Brickhouse values,
suggesting some uncertainties in the calculation of the proper flux
value. This situation renders
this line at 91.02 Å problematic for density and temperature
diagnostics. The ratios including the Fe XX line at 132.85 Å also
deviate from the theoretical values.
However, 132.85 Å is well known to be blended with a line
of Fe XXIII; the relative contributions of Fe XX and Fe XXIII
depend on the temperature regime and for Capella are expected to be
dominated by Fe XX. The
deviant behaviour of the lines at 91.02 Å and 132.85 Å appears again
in Sects. 4 and 5 where we discuss the temperature and density
diagnostics. For completeness, these lines were included in the tables though the results
based on their ratios should be considered as less reliable.
![\begin{figure}
\par\includegraphics[angle=-90, width=8.2cm, clip]{h2499fig2a.ps}...
...ps}\par\includegraphics[angle=-90, width=8.2cm, clip]{h2499fig2c.ps}\end{figure}](/articles/aa/full/2001/12/aah2499/Timg70.gif) |
Figure 2:
Temperature dependence of photon flux ratios between Fe XVIII to Fe XXI
lines.
The observed ratios are indicated |
| Open with DEXTER |
In Fig. 3 and Table 5 theoretical ratios of temperature-sensitive lines of
higher charge state ions
of iron are shown and compared
with the observations (Brickhouse et al. 1995).
The line ratios from the lower charge state Fe ions Fe IX and Fe X
indicate that these ions are formed in a plasma with a temperature of
about 1 MK. For the higher Fe ions Fe XVIII, Fe XIX, and Fe XX
temperatures of 6 MK or more are observed, but for ions higher than
Fe XX the temperature increases to 8 or 10 MK. These results are consistent with those obtained by Brickhouse et al. (2000) on the basis of EUVE observations.
We notice some deviations including the Fe XIX lines at 108 and 120
Å and those at 101, 109, and 111 Å. The first two both decay from
the same upper level (922.908 cm-1), while the three others all
decay from the level at 984.760 cm-1. In the ratio between the Fe XIX/Fe XX this results in a lower temperature when the two lines at
108 and 120 Å are involved and a somewhat higher temperature when
the three other lines are used. Errors induced in the computed
populations of the levels in the theoretical model resulting from
inaccurate collisional excitation rates are likely
to be the underlying reason. We notice from Table 5 a fairly regular
increase of the temperature from 6 MK up to 10 MK going from Fe XVIII
to Fe XXII. This favours a multi-temperature model; this comes as
no surprise based on the earlier analyses using EUVE and ASCA
observations that arrived at similar conclusions (e.g., Dupree et al. 1993; Brickhouse et al. 2000).
The wide dynamic wavelength range of the LETGS allows to study
simultaneously the
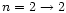 and
and
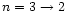 iron line transitions
in the L-shell and to compare the derived temperatures. In
the short wavelength range, around 16 Å the observed features
correspond to
iron line transitions
in the L-shell and to compare the derived temperatures. In
the short wavelength range, around 16 Å the observed features
correspond to
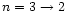 transitions,
while in the wavelength range above 80 Å the
lines originate from
transitions,
while in the wavelength range above 80 Å the
lines originate from
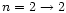 transitions.
From the measured photon flux ratio Fe XVII 15.265Å/Fe XVIII
transitions.
From the measured photon flux ratio Fe XVII 15.265Å/Fe XVIII
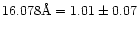 we derive a temperature of 7.0
we derive a temperature of 7.0 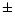 0.2 MK using
MEKAL, but after correcting (enhancing) the Fe XVIII flux by a factor 2.14
as indicated by the results from a benchmark study of the MEKAL code
with solar flare spectra by Phillips et al. (1999; their Table A8).
The two Fe XVII/Fe XVIII
0.2 MK using
MEKAL, but after correcting (enhancing) the Fe XVIII flux by a factor 2.14
as indicated by the results from a benchmark study of the MEKAL code
with solar flare spectra by Phillips et al. (1999; their Table A8).
The two Fe XVII/Fe XVIII
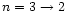 ratios result in higher temperatures than the
ratios based on
ratios result in higher temperatures than the
ratios based on
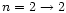 transitions. As a test case the ratio Fe
XVIII/Fe XVIII between an
transitions. As a test case the ratio Fe
XVIII/Fe XVIII between an
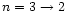 and an
and an
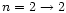 transition was calculated. It results in an even higher temperature
of 10 MK. However, this ratio covers a large wavelength range and is
more sensitive to flux calibration errors.
transition was calculated. It results in an even higher temperature
of 10 MK. However, this ratio covers a large wavelength range and is
more sensitive to flux calibration errors.
Higher temperature regions (T = 10 MK) are present in the coronae of
Capella (e.g., Brickhouse et al. 2000), though with emission measures
more than an order of magnitude below those of the dominant temperature of
several MK. Lines of higher Fe ionization stages (e.g., Fe XXIV)
that could constrain higher temperatures are outside the range in
which the LETGS has either insufficient spectral resolution or
sensitivity to yield accurate measurents of their fluxes.
The LETGS spectra of Capella contain a number of interesting emission
line features in the short wavelength region between 6 and 45 Å that
originate from the He-like ions Si XIII, Mg XI, Ne IX, O VII, N VI, and C V.
It concerns the resonance line 1s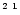 S0 - 1s2p 1P1(r),
the intercombination line 1s
S0 - 1s2p 1P1(r),
the intercombination line 1s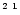 S0 - 1s2p 3P1,2(i)and the forbidden line 1s
S0 - 1s2p 3P1,2(i)and the forbidden line 1s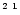 S0 - 1s2s 3S1(f). There
are combinations of these
three transitions that are strongly temperature- and density-sensitive. The
resonance line intensity is comparable to the sum of the intensities
of the two other lines and increases at higher temperatures, while for
high density the intercombination line becomes intense compared to the
forbidden line. Of the six ions mentioned above,
the Ne IX triplet could not be used because of severe blending
of the r and i lines by Fe XIX lines and partly blending of the f line by an Fe XVII line.
For C V the i and f lines are rather weak, but for N VI and O VII three clearly separated components
were measured. For Mg XI and Si XIII the intercombination line was
blended by the resonance line, but a
double Gaussian fit enabled us to deconvolve these lines, resulting in
measured wavelengths in very good agreement (within about 0.005-0.01
Å) with the
theoretical values. In the case of Si, the measurement
should be considered less certain due to the lower spectral resolution
at these wavelengths.
S0 - 1s2s 3S1(f). There
are combinations of these
three transitions that are strongly temperature- and density-sensitive. The
resonance line intensity is comparable to the sum of the intensities
of the two other lines and increases at higher temperatures, while for
high density the intercombination line becomes intense compared to the
forbidden line. Of the six ions mentioned above,
the Ne IX triplet could not be used because of severe blending
of the r and i lines by Fe XIX lines and partly blending of the f line by an Fe XVII line.
For C V the i and f lines are rather weak, but for N VI and O VII three clearly separated components
were measured. For Mg XI and Si XIII the intercombination line was
blended by the resonance line, but a
double Gaussian fit enabled us to deconvolve these lines, resulting in
measured wavelengths in very good agreement (within about 0.005-0.01
Å) with the
theoretical values. In the case of Si, the measurement
should be considered less certain due to the lower spectral resolution
at these wavelengths.
From the ratio
G = (i + f)/r the
temperature is determined for each He-like ion and is given in
Table 6. We observe a wide
range of temperatures from about 0.5 MK for N VI up to 5 MK for the
higher stages of ionization (Si XIII). However, the N VI temperature
appears somewhat discrepant in comparison to those derived for C and
O and we suspect it might be affected by line blending. The
temperatures were all derived using an updated version of the plasma
radiative loss
and line fitting program SPEX developed at SRON and from recent
calculations by Porquet & Dubau (2000) and by Mewe et al. (2001)
including all recombinations. Another possibility for obtaining the coronal
temperature from He-like ions is to use the ratio between the
resonance lines of these ions and the resonance lines of the one
higher ionized stages, the H-like ions, of the same element. These
ratios and the derived temperatures are collected also in Table 6. The
single He-like ion ratios result in a lower temperature than the
ratios from He-like versus H-like ions. The conclusion is that the
H-like ions are formed in another (hotter) area than the He-like
ions. Therefore the obtained temperature is a mixture and
average of the two areas.
- a measured counting rate ratio in +1 and -1 order of spectrum.
- b line photon flux ratio averaged over +1 and -1 order and corrected for
interstellar absorption (in parentheses the mean statistical 1
 error).
error).
- c
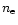 (in cm-3) derived from Brickhouse et al. (1995).
(in cm-3) derived from Brickhouse et al. (1995).
- d line intensity too high compared to theoretical values (see Table 4 and paragraph 3.2); results less reliable.
From a number of density-sensitive iron lines at wavelengths above 90
Å (e.g., Fe XX to Fe XXII) the electron density can be investigated for
plasmas with relatively high temperatures (
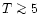 MK). For the
determination of the electron density in the coronal plasma of Capella
ratios of density-dependent lines of Fe XX, Fe XXI, and Fe XXII were
used. The data used and density values obtained are listed in Table 7. The
theoretical density dependence for these lines is taken from the work
by Brickhouse et al. (1995). The theoretical flux ratio-
MK). For the
determination of the electron density in the coronal plasma of Capella
ratios of density-dependent lines of Fe XX, Fe XXI, and Fe XXII were
used. The data used and density values obtained are listed in Table 7. The
theoretical density dependence for these lines is taken from the work
by Brickhouse et al. (1995). The theoretical flux ratio-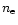 curves
are very flat for low densities and start to deviate from the
low-density plasma situation only for values of
curves
are very flat for low densities and start to deviate from the
low-density plasma situation only for values of
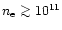 cm-3.
This makes the method insensitive for the lower limit.
The
cm-3.
This makes the method insensitive for the lower limit.
The 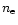 values obtained
for the ions Fe XX to Fe XXII, however, are consistently around
values obtained
for the ions Fe XX to Fe XXII, however, are consistently around  1012 cm-3and all with an upper limit of
1012 cm-3and all with an upper limit of
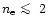 -
-
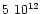 cm-3.
cm-3.
Two of the three transitions of the He-like ions described above are
also strongly density-dependent (e.g., Gabriel & Jordan 1969),
namely the ratio of the intercombination line (i) and the
forbidden line (f). Line ratios (i/f) were derived from measured
values and the corresponding plasma densities
were derived; the results are listed in Table 8. The
uncertainty of the counting rate of the O VII intercombination line
justifies an upper limit only. As for the temperature diagnostics,
the obtained values are from SPEX and from Porquet & Dubau (2000)
and Mewe et al. (2001).
If we compare the results for i/f and 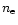 with those obtained by
Ness et al. (2001) in the case of C, N, and O, we note that the values
are slightly different but in agreement within the error bars. Ness
et al. (2001) find for O VII a somewhat different value for i/f(
with those obtained by
Ness et al. (2001) in the case of C, N, and O, we note that the values
are slightly different but in agreement within the error bars. Ness
et al. (2001) find for O VII a somewhat different value for i/f(
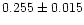 )
based on a method in which the total
spectrum is fitted with a model for the continuum plus background,
whereas we fit the background-subtracted spectrum. Because below
about 109 cm-3 the dependence of i/f on
)
based on a method in which the total
spectrum is fitted with a model for the continuum plus background,
whereas we fit the background-subtracted spectrum. Because below
about 109 cm-3 the dependence of i/f on 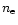 becomes very
flat (Fig. 5 of Ness et al.) this gives a much lower upper limit for
becomes very
flat (Fig. 5 of Ness et al.) this gives a much lower upper limit for
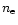 (only 5 108 cm-3) than we find but the difference is
still acceptable within the statistical uncertainties.
(only 5 108 cm-3) than we find but the difference is
still acceptable within the statistical uncertainties.
From the observations of Capella with the High-Energy Transmission
Grating on CHANDRA Canizares et al. (2000) obtain a slightly larger
i/f ratio for O VII (
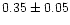 ,
but consistent with our ratio
of
,
but consistent with our ratio
of
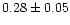 )
implying a higher electron density within the
range (8-20) 109 cm-3. Again the difference in i/f may be
due to a different treatment of the continuum plus background.
)
implying a higher electron density within the
range (8-20) 109 cm-3. Again the difference in i/f may be
due to a different treatment of the continuum plus background.
For the lower ions C V, N VI, and O VII we obtain densities typically in the
range 109-1010 cm-3 for temperatures between about 0.5
and 2 MK. Such densities are typical of those for active coronal
regions on the Sun. In the case of Capella, similar densities for the
lower temperature (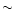 1-2 MK) plasma were suggested by Schrijver et al. (1995)
and by Brickhouse (1996) in analyses of EUVE spectra.
The higher ions Mg XI and Si XIII associated with higher temperatures (
1-2 MK) plasma were suggested by Schrijver et al. (1995)
and by Brickhouse (1996) in analyses of EUVE spectra.
The higher ions Mg XI and Si XIII associated with higher temperatures (
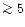 MK)
suggest much higher densities, i.e. 1012-1013 cm-3, that
are consistent with the results obtained for the highly ionized Fe
ions. Such high densities have been observed on the Sun only during
flares, but were derived earlier from EUVE spectra of Capella (cf. Sect. 1).
We note, however, that the density obtained for Si XIII is significantly higher
than the upper limit found from Mg XI.
For the same line complex observed with the CHANDRA HETG (albeit at a different
time), Canizares et al. (2000) obtained a ratio i/f of
MK)
suggest much higher densities, i.e. 1012-1013 cm-3, that
are consistent with the results obtained for the highly ionized Fe
ions. Such high densities have been observed on the Sun only during
flares, but were derived earlier from EUVE spectra of Capella (cf. Sect. 1).
We note, however, that the density obtained for Si XIII is significantly higher
than the upper limit found from Mg XI.
For the same line complex observed with the CHANDRA HETG (albeit at a different
time), Canizares et al. (2000) obtained a ratio i/f of
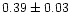 ,
which is to be compared with our value of
,
which is to be compared with our value of
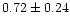 .
It is clear from the recent analysis of HST STIS spectra by
Johnson et al. (2001) that the hot 10 MK component of the Capella coronae
can be highly variable, and so it is therefore
possible that the higher density we derived based on observations made
at a different time is real. However, since the spectral resolution
of the LETGS is fairly low at the wavelength of the Si He-like
complex, rendering line deconvolution more difficult, this
density should perhaps be treated with caution at this time.
.
It is clear from the recent analysis of HST STIS spectra by
Johnson et al. (2001) that the hot 10 MK component of the Capella coronae
can be highly variable, and so it is therefore
possible that the higher density we derived based on observations made
at a different time is real. However, since the spectral resolution
of the LETGS is fairly low at the wavelength of the Si He-like
complex, rendering line deconvolution more difficult, this
density should perhaps be treated with caution at this time.
We performed an emission measure (EM) analysis of the Capella LETGS
data by comparing measured line fluxes with the theoretical fluxes as
calculated by MEKAL for a given emission measure and formation
temperature for a particular line, assuming solar abundances (Anders & Grevesse 1989).
Figure 4 (top) presents the results of
the EM distribution based on the analysis of the iron lines. For all
Fe-ions used the error bars are given. These error bars contain two
components. When having many lines (and values) for one particular
ion, the error is dominated by the statistical error of these
values. In case of one single transition or two closely lying values
for an ion, the error is dominated by the uncertainty in the flux as
given in Tables 1 and 2. The larger error bar for Fe XVI is probably due
to the fact that all lines used are near the gap between the detectors
where the efficiency declines rapidly and the calibration is
uncertain.
![\begin{figure}
\par\includegraphics[angle=-90, width=8cm, clip]{h2499fig3a.ps}\v...
...2mm}
\includegraphics[angle=-90, width=8cm, clip]{h2499fig3b.ps} %\end{figure}](/articles/aa/full/2001/12/aah2499/Timg138.gif) |
Figure 3:
EM distribution derived from Fe IX to Fe XXII line intensities for the
Capella CHANDRA-LETGS observations (top) compared to the results from a 4-T fitting with SPEX and
from observations with EUVE (Brickhouse et al. 2000)
and EXOSAT (Lemen et al. 1989) (bottom) |
| Open with DEXTER |
For comparison we give in the bottom panel of Fig. 3 the results from two other instruments:
EXOSAT (Lemen et al. 1989) and EUVE (Brickhouse et al. 2000). These distributions are comparable
to our results given the fact that the results are obtained at different times and with
different instruments.
Using the SPEX code (Kaastra et al. 1996)
we have fitted the Chandra Capella spectrum with a 4-temperature model with variable
abundances. The result scaled to the solar abundance of iron
is shown in the bottom panel of Fig. 3 and agrees satisfactorily with the emission measure
distribution given on top.
The derived ratios of and Ne to Fe are
close to solar or mildly subsolar, while the N, Mg, and Si ratios
are about a factor of 2 larger than compared to that taken from Anders & Grevesse (1989).
For Mg and Si these results agree with those from
Brickhouse et al. (2000) based on an analysis of EUVE and
ASCA spectra, but our Ne/Fe ratio is a factor of 3 larger.
Because the two binary components both contribute to the observed X-ray emission (see Sect. 1), any
interpretation of the composite spectrum can only be given in terms of average stellar properties.
We derive from our observations global properties of the X-ray emitting
coronal structures using a standard model of a quasi-static, semi-circular,
magnetic loop with constant cross section as developed by Rosner et al. (1978; hereafter RTV).
In the RTV loop model
the basic loop parameters are related through
a simple scaling law:
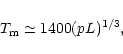 |
(3) |
where the apex temperature 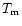 in K, the loop semilength L in cm, and the pressure p in dyne cm-2.
Or with
in K, the loop semilength L in cm, and the pressure p in dyne cm-2.
Or with
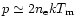 we write:
we write:
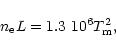 |
(4) |
where 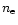 is the apex electron density in cm-3.
is the apex electron density in cm-3.
Generalizations of the basic RTV model have been developed by Vesecky et al. (1979; hereafter
VAU), including cross sections that increase with height in a way representing loop field structures by a
magnetic line dipole below the chromosphere. The scaling law is only slightly modified by the VAU results which
can be conveniently approximated by introducing into the rhs of Eqs. (3 or 4) an additional multiplication factor
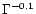 or
or
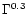 ,
respectively. Here
,
respectively. Here 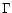 is the ratio of the loop cross section at the apex to that at the
loop footpoint, the expansion factor.
It turns out that a large variety of solar loops ranging from small bright points to active-region loops and
large-scale structures can be modeled by these scaling laws (e.g., discussion by Mewe 1991).
is the ratio of the loop cross section at the apex to that at the
loop footpoint, the expansion factor.
It turns out that a large variety of solar loops ranging from small bright points to active-region loops and
large-scale structures can be modeled by these scaling laws (e.g., discussion by Mewe 1991).
Applying Eq. (4) for the derived densities (Sect. 5) we obtain estimates for the loop
semilengths L (Table 9), taking
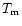 equal to the temperature of maximum line formation (from MEKAL).
equal to the temperature of maximum line formation (from MEKAL).
For a given density the emission measure places an additional constraint on the emitting volume (i.e. the "filling factor'').
From the measured line fluxes and the known emissivities at temperature of maximum line formation we derive the emission measure
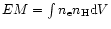 ,
where V is the volume contributing to the emission (for cosmic abundances the hydrogen density
,
where V is the volume contributing to the emission (for cosmic abundances the hydrogen density
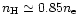 ). In Table 9 we give EM for various lines.
). In Table 9 we give EM for various lines.
Assuming for simplicity that the X-ray corona consists of one class of
N identical loops with parameters
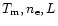 ,
we derive for the emission measure
,
we derive for the emission measure
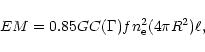 |
(5) |
where R is the stellar radius
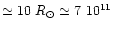 cm (Strassmeier et al. 1993) averaged for
the two components of Capella.
The factor G corrects for the fraction of the corona occulted by the
stellar disk: G=0.5 for compact loops which we consider here.
cm (Strassmeier et al. 1993) averaged for
the two components of Capella.
The factor G corrects for the fraction of the corona occulted by the
stellar disk: G=0.5 for compact loops which we consider here.
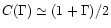 is an empirical correction for
is an empirical correction for 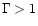 to the RTV loop volume derived from the
VAU model.
The fractional coverage of the stellar surface with footpoints of N identical X-ray emitting
loops with cross section S at the base, the socalled
to the RTV loop volume derived from the
VAU model.
The fractional coverage of the stellar surface with footpoints of N identical X-ray emitting
loops with cross section S at the base, the socalled
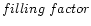 ,
equals
,
equals
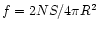 .
Finally,
.
Finally, 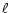 is the emission scale length, which is
limited either by the loop size (
is the emission scale length, which is
limited either by the loop size (
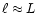 for
for
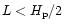 )
(case 1) or
by the pressure scale height (
)
(case 1) or
by the pressure scale height (
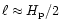 for
for
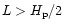 )
(case 2). For case 1 (as
)
(case 2). For case 1 (as
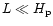 )
we derive from Eq. (6) and using Eq. (4) (with the factor
)
we derive from Eq. (6) and using Eq. (4) (with the factor
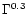 )
for the filling factor
)
for the filling factor
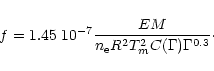 |
(6) |
Using the measured fluxes for various helium-like lines and some iron lines we present in
Table 9 the filling factors calculated with Eq. (7) for two loop geometries: 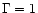 (RTV loop) and
(RTV loop) and 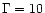 ,
respectively. The filling factors for the low-temperature regions are about 30% or more for the case
,
respectively. The filling factors for the low-temperature regions are about 30% or more for the case 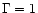 ,
i.e., comparable
to those for active RS CVn systems, but much higher than for active regions on the Sun (few %, cf. Mewe 1991).
However, loops with large expansion (
,
i.e., comparable
to those for active RS CVn systems, but much higher than for active regions on the Sun (few %, cf. Mewe 1991).
However, loops with large expansion (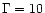 )
should have a filling factor that is closer to that of active regions on the Sun.
The hot, compact loops have probably a very small filling factor.
)
should have a filling factor that is closer to that of active regions on the Sun.
The hot, compact loops have probably a very small filling factor.
The results appear to show the existence of two main classes of loop structures
in the coronae of the binary system Capella. On the one hand, the analysis of
the lower ions N VI and O VII indicates temperatures, densities, and
loop lengths that are more or less representative of active coronal regions
on the Sun (with relatively large filling factors).
On the other hand, the higher He-like ions
Mg XI and Si XIII and the highly ionized Fe ions (Fe XX-XXII) indicate
the presence of a class of much more compact and dense, hot loops (with very
small filling factors). On the Sun temperatures and densities this high - as observed in non-flaring active regions in the
coronae of Capella -
are seen only during flares. For both classes of loop systems
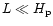 and R,
where the pressure scale height
and R,
where the pressure scale height 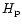 (in cm) is given by
(in cm) is given by
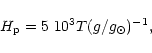 |
(7) |
where
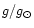 is the surface gravity expressed in solar units (for
is the surface gravity expressed in solar units (for
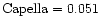 )
and T in K.
)
and T in K.
In all cases the loop sizes are much smaller than the stellar radius so that
it is clear that the X-ray emission originates from compact regions
that must be
supported by strong magnetic fields (e.g., of the order of several
hundred Gauss as was suggested by Dupree et al. 1993). Similar
conclusions were drawn for other active binaries based on a review of
EUVE observations by Drake (1996).
Echo the salient features of earlier EUVE analyses, we have
established different temperature regimes in the Capella coronal
plasmas: from
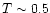 -2 MK for Fe IX & X, N VI, and O VII,
-2 MK for Fe IX & X, N VI, and O VII,
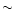 5-6. MK for Fe XVIII-XX up to
5-6. MK for Fe XVIII-XX up to 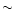 9 MK for Fe XXI and
Fe XXII. The upper limit to the densities obtained from Fe XX-XXII
lines is about 3 1012 cm-3. The density of the plasma
obtained from density sensitive lines of He-like triplets N VI and O
VII is in the range 109-1010 cm-3 for
9 MK for Fe XXI and
Fe XXII. The upper limit to the densities obtained from Fe XX-XXII
lines is about 3 1012 cm-3. The density of the plasma
obtained from density sensitive lines of He-like triplets N VI and O
VII is in the range 109-1010 cm-3 for 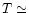 0.5-2 MK and from Mg XI and Si XIII in the range
1012-1013 cm-3 for
0.5-2 MK and from Mg XI and Si XIII in the range
1012-1013 cm-3 for 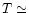 5-9 MK.
5-9 MK.
Abundances derived for various elements are about solar (O, Ne) or twice
solar (N, Mg, Si).
The results for the densities and emission measures are interpreted in
terms of quasi-static loop models. They appear to show the existence
of two main classes of loop structures in the coronae of Capella. The
analysis of the lower ions N VI and O VII indicates temperatures,
densities, and loop lengths that are more or less representative for
active coronal regions on the Sun (with relatively large filling
factors). On the other hand, the higher He-like ions Mg XI and Si
XIII and the highly ionized Fe ions (Fe XX-XXII) indicate the
presence of a class of much more compact and dense, hot loops (with
very small filling factors). On the Sun temperatures and densities
this high are seen only during flares. For both classes of loops the
size is much smaller than the pressure scale height and the stellar
radius.
Comparisons between ratios of lines decaying from the same upper level and branching ratios give confidence in
the in-flight total area calibration and the detector sensitivity as well as the reliability of the calculated
transition probabilities.
Based on photon fluxes of lines, sensitive to resonance scattering, we have derived conservative upper limits to
the optical depth of the lines Fe XVIII 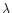 93.92 and Fe XVII
93.92 and Fe XVII 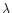 15.014 of 1 and 1.5, respectively.
15.014 of 1 and 1.5, respectively.
Acknowledgements
The Space Research Organization Netherlands (SRON) is supported
financially by NWO. We thank Nancy Brickhouse for her contribution to
the effort to
obtain for Capella a long observation time with the LETGS during the
initial in-flight calibration of the CHANDRA transmission gratings in
the context of the "Emission Line Project'' headed by her and Jeremy
Drake. JJD was supported by NASA contract NAS8-39073 to the Chandra
X-ray Center during the course of this research. Finally, we wish to thank the referee
for helpful comments that allowed us to improve the paper.
- Anders, E., & Grevesse, N. 1989, Geochimica et Cosmochimica Acta, 53, 197
In the text
NASA ADS
- Arnaud, M., & Raymond, J. 1992, ApJ, 398, 394
In the text
NASA ADS
- Audard, M., Behar, E., Güdel, M., et al. 2001, A&A, in press
In the text
- Bhatia, A. K., & Doschek, G. A. 1992,
At. Data Nucl. Data Tables, 52, 1
In the text
NASA ADS
- Brickhouse, N. S. 1996, in Proc. IAU Coll. 152, Astrophysics in the Extreme Ultraviolet, ed. S. Bowyer, & R. F. Malina (Dordrecht, Kluwer), 105
In the text
- Brickhouse, N. S., Raymond, J. C., & Smith, B. W. 1995, ApJS, 97, 551
In the text
NASA ADS
- Brickhouse, N. S., Dupree, A. K., Edgar, R. J., et al. 2000, ApJ, 530, 387
In the text
NASA ADS
- Brinkman, A. C., Gunsing, C. J. T., Kaastra, J. S., et al. 2000, ApJL, 530, L111
In the text
NASA ADS
- Brown, G. V., Beiersdorfer, P., Liedahl, D. A., et al. 1998, ApJ, 502, 1015
In the text
NASA ADS
- Canizares, C. R., Huenemoerder, D. P., Davis, D. S., et al. 2000, ApJL, 539, L41
In the text
NASA ADS
- Cowan, R. D. 1981, The Theory of Atomic Structure and Spectra (Berkeley, CA, Univ. of California Press)
In the text
- Drake, J. J. 1996, in Cool Stars, Stellar Systems
and the Sun, Ninth Cambridge Workshop, ed. R. Pallavicini, & A. Dupree, ASP Conf. Ser., 109, 203
In the text
- Dupree, A. K., Brickhouse, N. S., Doschek, G. A., Green, J. C., & Raymond, J. C. 1993, ApJ, 418, L41
In the text
NASA ADS
- Gabriel, A. H., & Jordan, C. 1969, MNRAS, 145, 241
In the text
NASA ADS
- Johnson, O., Drake, J. J., Kashyap, V., et al. 2001, submitted to ApJL
In the text
- Kaastra, J. S., & Mewe, R. 1995, A&AL, 302, L13
In the text
- Kaastra, J. S., Mewe, R., & Nieuwenhuijzen, H. 1996, in UV and X-ray Spectroscopy of Astrophysical and Laboratory Plasmas, ed. K. Yamashita, & T. Watanabe (Universal Academy Press, Inc., Tokyo), 411 (SPEX)
In the text
- Lemen, J. R., Mewe, R., & Schrijver, C. J. 1989, ApJ, 341, 474
In the text
NASA ADS
- Linsky, J. L., Wood, B. E., Brown, A., & Osten, R. A. 1998, ApJ, 492, 767
In the text
NASA ADS
- Mason, H. E., Bhatia, A. K., Kastner, S. O., Neupert, W. M., & Swartz, M. 1984, Solar Phys., 92, 199
In the text
NASA ADS
- Mewe, R. 1991, Adv. Space Sci. Rev., 11, (1) 127
In the text
- Mewe, R., Gronenschild, E. H. B. M., & van den Oord, G. H. J. 1985, A&ASS, 62, 197
In the text
- Mewe, R., Kaastra, J. S., & Liedahl, D. A. 1995a, Legacy, 6, 16 (MEKAL)
In the text
- Mewe, R., Kaastra, J. S., Schrijver, C. J., van den Oord, G. H. J., & Alkemade, F. J. M. 1995b, A&A, 296, 477
In the text
NASA ADS
- Mewe, R., Lemen, J. R., & Schrijver, C. J. 1991, Astrophys. Space Sci., 182, 35
In the text
NASA ADS
- Mewe, R., Porquet, D., Raassen, A. J. J., & Dubau, J. 2001, in preparation
In the text
- Morrison, R., & McCammon, D. 1983, ApJ, 270, 119
In the text
NASA ADS
- Ness, J.-U., Mewe, R., Schmitt, J. H. M. M., et al. 2001, A&A, in press
In the text
- Phillips, K. J. H., Mewe, R., Harra-Murnion, L. K., et al. 1999, A&ASS, 138, 381
In the text
- Porquet, D., & Dubau, J. 2000, A&ASS, 143, 495
In the text
- Rosner, R., Tucker, W. M., & Vaiana, G. S. 1978, ApJ, 220, 643 (RTV) In the text
NASA ADS
- Saba, J. L. R., Schmelz, J. T., Bhatia, A. K., & Strong, K. T. 1999, ApJ, 510, 1064 In the text
NASA ADS
- Schrijver, C. J., Mewe, R., van den Oord, G. H. J., & Kaastra, J. S. 1995, A&A, 302, 438
In the text
NASA ADS
- Strassmeier, K. G., Hall, D. S., Fekel, F. C., & Scheck, M. 1993, A&ASS, 100, 173
In the text
- van der Meer, R. L. J., et al. 2001, in preparation (calibration paper)
In the text
- Vesecky, J. F., Antiochos, J. H., & Underwood, J. H. 1979, ApJ, 233, 987 (VAU) In the text
NASA ADS
- Wood, K., & Raymond, J. 2000, ApJ, 540, 563
In the text
NASA ADS
Copyright ESO 2001

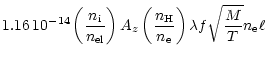
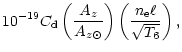
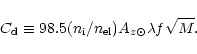
![\begin{figure}
\par\includegraphics[angle=-90, width=8.2cm, clip]{h2499fig2a.ps}...
...ps}\par\includegraphics[angle=-90, width=8.2cm, clip]{h2499fig2c.ps}\end{figure}](/articles/aa/full/2001/12/aah2499/Timg70.gif)
![\begin{figure}
\par\includegraphics[angle=-90, width=8cm, clip]{h2499fig3a.ps}\v...
...2mm}
\includegraphics[angle=-90, width=8cm, clip]{h2499fig3b.ps} %\end{figure}](/articles/aa/full/2001/12/aah2499/Timg138.gif)