A&A 368, 994-1005 (2001)
DOI: 10.1051/0004-6361:20010068
R. Aznar Cuadrado - C. S. Jeffery
Armagh Observatory, College Hill, Armagh BT61 9DG, N. Ireland
Received 21 July 2000 / Accepted 4 January 2001
Abstract
The atmospheric parameters of 34 hot subdwarf B stars have been obtained
using a combination of 61 short and long-wave IUE spectra, together with
new and existing optical and infrared photometric data. Using a grid of
high-gravity helium-deficient model atmospheres and a ![]() -minimization
procedure, 15 single sdB stars and 19 composite systems, containing a hot
subdwarf B star and a cool main-sequence companion, were analyzed. From the
(
-minimization
procedure, 15 single sdB stars and 19 composite systems, containing a hot
subdwarf B star and a cool main-sequence companion, were analyzed. From the
(
![]() -
-
![]() )
diagram of our results, we conclude
that the majority of the cool companions to our sample of binary sdB
stars are main sequence stars, in the range of 4000
)
diagram of our results, we conclude
that the majority of the cool companions to our sample of binary sdB
stars are main sequence stars, in the range of 4000
![]() 6000 and mass 0.8 < M/
6000 and mass 0.8 < M/
![]() .
The lower limit on detectability
of cool stars in composite sdB of our sample is
.
The lower limit on detectability
of cool stars in composite sdB of our sample is ![]() 3600 K,
corresponding to a spectral type of M1 or later (Lang 1992).
3600 K,
corresponding to a spectral type of M1 or later (Lang 1992).
Key words:
stars: formation, early-type, subdwarfs, fundamental parameters
(luminosities, temperatures) -
binaries: spectroscopic
Subdwarf B (sdB) stars are considered to be core helium burning stars of mass
![]() 0.5
0.5 ![]() with a very thin hydrogen-rich envelope
(
with a very thin hydrogen-rich envelope
(
![]() 0.01
0.01 ![]() ,
Heber 1986). However, their evolutionary status it is
still unclear. It is very difficult to account for the very small hydrogen
envelope mass within single-star evolution theory (Sweigart 1997). The
hypothesis of close binary evolution was firstly suggested by Mengel et al.
(1976) to explain the formation of sdB stars, and latterly corroborated by
Saffer et al. (1998) with the discovery of short-period systems of white
dwarfs and sdB stars. Hence, it is important to investigate whether binary
star interactions can explain the removal of surface hydrogen.
,
Heber 1986). However, their evolutionary status it is
still unclear. It is very difficult to account for the very small hydrogen
envelope mass within single-star evolution theory (Sweigart 1997). The
hypothesis of close binary evolution was firstly suggested by Mengel et al.
(1976) to explain the formation of sdB stars, and latterly corroborated by
Saffer et al. (1998) with the discovery of short-period systems of white
dwarfs and sdB stars. Hence, it is important to investigate whether binary
star interactions can explain the removal of surface hydrogen.
Excess infrared flux from the direction of a hot subdwarf star can be interpreted in several ways. It can be due to a late type companion, hot dust surrounding the star, or free-free emission from a stellar wind. In each case the data can be analysed to yield information on the hot subdwarf and its evolution.
Previous studies have indicated that many sdB stars are members of binary systems with cool companions (e.g. Allard et al. 1994), fractions of between 50% and 100% have been claimed (Bixler et al. 1991). The point in studying companions to hot subdwarfs is that we can learn things about the hot subdwarfs that are not easy to observe directly due to the problems of modelling hot atmospheres and the relatively large distances to these stars that, currently, preclude astrometric analysis for the majority.
Another interest lies in the classification of the secondary stars, as this information can be used to set limits on how the hot subdwarfs formed. Deconvolving the energy distribution of the detectable binary sdB stars of our sample, would permit an estimate of the position of the secondaries within the HR diagram, a question of persistent interest for stellar evolution studies.
In this work, we make an attempt to determine the atmospheric parameters of
a sample of 34 hot subdwarf B stars. UV, optical and infrared fluxes are
interpreted with the aid of high-gravity hydrogen-rich model atmospheres and
a ![]() -minimization procedure. In Sect. 2 the observations and data
calibration are described. In Sect. 3 existing ultraviolet spectra and optical
and infrared data are presented, together with new Strömgren uvby and
near-infrared Johnson RI photometry of a small sample of hot subdwarf B
stars. In Sect. 4 the procedure used to fit the observations and determine the
atmospheric parameters is described. Section 5 presents the resulting
atmospheric parameters of our sample of 34 sdB stars, along with an internal
error analysis. The results presented are compared in Sect. 6 with those in
the literature, including previous determinations of the atmospheric
parameters. In Sect. 7 the Hertzsprung-Russell diagram of the sample is
discussed. A discussion and conclusions are presented in Sects. 8 and 9,
respectively.
-minimization procedure. In Sect. 2 the observations and data
calibration are described. In Sect. 3 existing ultraviolet spectra and optical
and infrared data are presented, together with new Strömgren uvby and
near-infrared Johnson RI photometry of a small sample of hot subdwarf B
stars. In Sect. 4 the procedure used to fit the observations and determine the
atmospheric parameters is described. Section 5 presents the resulting
atmospheric parameters of our sample of 34 sdB stars, along with an internal
error analysis. The results presented are compared in Sect. 6 with those in
the literature, including previous determinations of the atmospheric
parameters. In Sect. 7 the Hertzsprung-Russell diagram of the sample is
discussed. A discussion and conclusions are presented in Sects. 8 and 9,
respectively.
Strömgren uvby and Johnson RI photometry was obtained in two
different observing runs during the nights of 1999, June 1, 2, 3, and in 2000,
May 10, with the 1.0 m Jacobus Kapteyn Telescope (JKT), at the Isaac
Newton
Group of Telescopes, La Palma. The detectors used in those runs were the
![]() TEK4 and the
TEK4 and the
![]() SITe2 CCD, respectively. Standard aperture
photometry was performed on a sample of 13 hot subdwarfs.
SITe2 CCD, respectively. Standard aperture
photometry was performed on a sample of 13 hot subdwarfs.
Secondary Strömgren standards from Stetson (1991) observed in uvb and y filters and Johnson standards from Landolt (1992) observed in R and I filters were used to derive the instrumental colour transformations and extinction coefficients. Standards were observed close to the zenith during evening and morning twilight, and at regular intervals throughout each night. Bias exposures were taken each afternoon and sky flat-field frames were obtained in each twilight. Several observations of each sdB star were made in each filter in order to improve photometric accuracy.
For a determination of the instrumental colour transformation of the
standard system, extinction coefficients and zero points, initial CCD
reduction was carried out using the standard data reduction package
IRAF/CCDRED (Massey 1992). This included the trimming of the
data section, bias and flat-field corrections. Instrumental magnitudes for
the standard stars were determined using aperture photometry techniques
within the IRAF package DAOPHOT (Massey & Davies
1992). An aperture of radius 14
![]() was chosen in order to be consistent
when calibrating the instrumental magnitudes of our standard stars with
results obtained by Landolt (1991) and Stetson (1992).
was chosen in order to be consistent
when calibrating the instrumental magnitudes of our standard stars with
results obtained by Landolt (1991) and Stetson (1992).
Colour-dependent transformations were applied to determine standard magnitudes from our instrumental magnitudes. The transformation equations were solved using tasks within the IRAF package PHOTCAL (Massey & Davies 1992).
From the sample of stars observed during these two observing runs, 13 sdB stars, the fraction which is contaminated by unrelated background/foreground stars is small (15%), where the nearest stars in the field is found within 10 arcsec from our target (Thejll et al. 1994). A faint star has been observed close to PG 1230+052 and PG 1452+198.
| Object | LW Image | exp(s) | SW Image | exp(s) |
| 1 PG 0004+133 | LWP18429 | 1080 | SWP39286 | 960 |
| 2 PG 0105+276 | SWP56271 | 1500 | ||
| 3 PG 0110+262 | SWP55828 | 600 | ||
| 4 PG 0229+064 | SWP48617R | 22320 | ||
| 5 PG 0232+095 | LWP18430 | 420 | SWP39287 | 360 |
| SWP39288 | 720 | |||
| 6 PG 0240+046 | LWP18452 | 2700 | SWP39307 | 2100 |
| 7 PG 0314+146 | SWP51740 | 600 | ||
| 8 PG 0342+026 | LWP07462 | 160 | SWP27466R | 9600 |
| 9 PG 0749+658 | LWP31669 | 180 | SWP56166 | 300 |
| 10 PG 0839+399 | LWP09826 | 1800 | SWP29995 | 1800 |
| 11 PG 0856+121 | LWP03484 | 1200 | SWP23159 | 900 |
| 12 PG 0900+400 | LWP30587 | 1200 | SWP54558 | 1200 |
| 13 PG 0934+186 | LWP07463 | 2100 | SWP27468 | 1500 |
| LWP08298 | 1080 | SWP28393 | 1200 | |
| 14 PG 1040+234 | SWP56384 | 1200 | ||
| 15 PG 1047+003 | LWP08242 | 1200 | SWP28350 | 900 |
| 16 PG 1049+013 | SWP57007 | 3600 | ||
| 17 PG 1104+243 | LWP06222 | 240 | SWP27465R | 12600 |
| 18 PG 1230+052 | LWP08243 | 1260 | SWP26176 | 600 |
| 19 PG 1233+426 | LWP02149 | 330 | SWP21373R | 18000 |
| 20 PG 1336 -018 | LWP06224 | 840 | SWP26175 | 1080 |
| 21 PG 1432+004 | LWP03501 | 840 | SWP23176 | 600 |
| 22 PG 1433+239 | LWR03302 | 840 | SWP03722 | 780 |
| 23 PG 1449+653 | LWR14118 | 21840 | SWP34298 | 900 |
| 24 PG 1452+198 | LWP03503 | 480 | SWP23178 | 360 |
| 25 PG 1629+081 | LWP13481 | 540 | SWP33790 | 420 |
| 26 PG 1701+359 | LWP21097 | 1200 | SWP42337 | 1500 |
| 27 PG 1718+519 | LWP20308 | 1200 | SWP41571 | 450 |
| 28 BD+29 |
LWR16266 | 215 | SWP20344 | 140 |
| 29 PG 2110+127 | SWP41573 | 300 | ||
| 30 PG 2135+045 | SWP57331 | 3600 | ||
| 31 PG 2148+095 | SWP56148 | 600 | ||
| 32 PG 2214+184 | SWP44816 | 1200 | ||
| 33 PG 2226+094 | SWP56149 | 1200 | ||
| 34 PG 2259+134 | LWP23244 | 1320 | SWP44821 | 2460 |
| SWP56182 | 1500 |
In order to complement our Strömgren uvby and Johnson RI photometry of a sample of hot subdwarf stars, and to be able to perform our energy distribution analysis, we have compiled published optical and infrared data, as well as ultraviolet data from the IUE (International Ultraviolet Explorer) satellite.
| star | R |
|
I |
|
J |
|
H |
|
K |
|
| 1 PG 0004+133 | 13.062b | 0.008 | 13.099b | 0.023 | 13.301h | 0.031 | 13.313h | 0.033 | 13.343h | 0.044 |
| 2 PG 0105+276 | 14.362b | 0.006 | 14.349b | 0.020 | 14.347h | 0.043 | 13.821h | 0.043 | 13.712h | 0.054 |
| 3 PG 0110+262 | 12.892b | 0.010 | 12.744b | 0.012 | 12.442h | 0.032 | 12.222h | 0.036 | 12.181h | 0.029 |
| 4 PG 0229+064 | 11.999b | 0.025 | 12.105b | 0.026 | 12.290f | 0.180 | 12.320f | 0.150 | 12.350f | 0.130 |
| 5 PG 0232+095 | ----- | ----- | ----- | ----- | 11.090f | 0.130 | 10.770f | 0.070 | 10.620f | 0.110 |
| 8 PG 0342+026 | 11.022b | 0.015 | 11.092b | 0.019 | 11.670e | 0.080 | 11.890e | 0.130 | 11.860e | 0.200 |
| 9 PG 0749+658 | 12.100b | 0.000 | 12.028b | 0.000 | ----- | ----- | ----- | ----- | ----- | ----- |
| 10 PG 0839+399 | 14.442g | 0.005 | 14.635g | 0.012 | 14.850h | 0.035 | 15.096h | 0.068 | 15.006h | 0.108 |
| 11 PG 0856+121 | 13.933g | 0.055 | 13.073g | 0.082 | 13.931h | 0.038 | 14.034h | 0.050 | 14.137h | 0.076 |
| 12 PG 0900+400 | 12.570c | 0.000 | 12.290d | 0.000 | 11.922h | 0.034 | 11.616h | 0.051 | 11.484h | 0.036 |
| 13 PG 0934+186 | 13.267g | 0.009 | 13.516g | 0.020 | 13.751h | 0.029 | 13.947h | 0.043 | 13.875h | 0.044 |
| 14 PG 1040+234 | 13.283b | 0.024 | 13.107b | 0.024 | 12.758h | 0.029 | 12.503h | 0.032 | 12.448h | 0.034 |
| 15 PG 1047+003 | 13.489a | 0.145 | 13.643a | 0.151 | 14.114h | 0.030 | 14.210h | 0.040 | 14.300h | 0.077 |
| 16 PG 1049+013 | 14.351b | 0.000 | 14.185b | 0.000 | ----- | ----- | ----- | ----- | ----- | ----- |
| 17 PG 1104+243 | 11.161b | 0.018 | 11.001b | 0.019 | 10.732h | 0.031 | 10.523h | 0.031 | 10.451h | 0.024 |
| 18 PG 1230+052 | 13.355a | 0.076 | 13.538a | 0.074 | ----- | ----- | ----- | ----- | ----- | ----- |
| 19 PG 1233+426 | 12.142g | 0.002 | 12.342g | 0.003 | 12.630h | 0.034 | 12.716h | 0.032 | 12.837h | 0.040 |
| 20 PG 1336 -018 | 13.370a | 0.194 | 13.483a | 0.204 | ----- | ----- | ----- | ----- | ----- | ----- |
| 21 PG 1432+004 | 12.817a | 0.086 | 12.965a | 0.084 | ----- | ----- | ----- | ----- | ----- | ----- |
| 22 PG 1433+239 | 12.654a | 0.062 | 12.834a | 0.061 | ----- | ----- | ----- | ----- | ----- | ----- |
| 23 PG 1449+653 | 13.538b | 0.000 | 13.527b | 0.000 | ----- | ----- | ----- | ----- | ----- | ----- |
| 24 PG 1452+198 | 12.644g | 0.001 | 12.848g | 0.003 | 13.058h | 0.032 | 13.178h | 0.031 | 13.273h | 0.040 |
| 25 PG 1629+081 | 12.774b | 0.049 | 12.771b | 0.051 | ----- | ----- | ----- | ----- | ----- | ----- |
| 26 PG 1701+359 | 13.244b | 0.053 | 13.249b | 0.053 | 13.140h | 0.032 | 12.938h | 0.032 | 12.882h | 0.035 |
| 27 PG 1718+519 | 13.577b | 0.024 | 13.395b | 0.029 | 13.008h | 0.026 | 12.716h | 0.032 | 12.664h | 0.033 |
| 28 BD+29 |
10.014a | 0.035 | 9.979a | 0.035 | 9.740e | 0.010 | 9.550e | 0.010 | 9.540e | 0.030 |
| 29 PG 2110+127 | 12.758b | 0.008 | 12.577b | 0.011 | 12.260e | 0.070 | 12.070e | 0.050 | 12.120e | 0.080 |
| 30 PG 2135+045 | 14.627b | 0.022 | 14.597b | 0.059 | ----- | ----- | ----- | ----- | ----- | ----- |
| 31 PG 2148+095 | 12.961b | 0.015 | 12.865b | 0.017 | 12.180e | 0.110 | 12.340e | 0.170 | 12.060e | 0.400 |
| 32 PG 2214+184 | 14.205a | 0.037 | 14.423a | 0.037 | ----- | ----- | ----- | ----- | ----- | ----- |
| 33 PG 2226+094 | 13.903b | 0.012 | 13.666b | 0.032 | ----- | ----- | ----- | ----- | ----- | ----- |
| 34 PG 2259+134 | 14.570a | 0.041 | 14.808a | 0.041 | 14.910h | 0.042 | 14.857h | 0.063 | 14.897h | 0.140 |
61 low-resolution observations of 34 sdB stars made with the large aperture (LAP) of the International Ultraviolet Explorer (IUE) have been collected from the IUE Final Archive, as "IUE Newly Extracted Spectra'' (INES, Nichols & Linsky 1996), and are shown in Table 1. Column 1 shows the name and an identification number of each star, Cols. 2 and 4 give the sequential image numbers from the Long Wavelength Prime and Redundant (LWP and LWR) and Short Wavelength Prime (SWP) cameras. Columns 3 and 5 show the effective exposure times of each image. An "R" after SWP image number indicates a high resolution spectrum, which has been rebinned onto the low resolution wavelength scale.
Published optical Johnson-Morgan UBV and Strömgren uvby
data, and infrared Johnson RIJHK photometry have been collected
as follows.
Strömgren uvby photometry has been adopted from Wesemael
et al. (1992) for all sdB stars used in this work, with the exception of
BD+29![]() 3070 for which we have used our observations with the
JKT (J99):
3070 for which we have used our observations with the
JKT (J99):
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Broad band photometry
has been adopted for PG 0900+400: U=12.140, B=13.100, V=12.870
(Ferguson et al. 1984), and PG 1433+239: U=11.330, B=12.340,
V=12.540 (Iriarte 1959).
Table 2 shows the infrared Johnson RIJHK
photometric data used in this work, together with their sources.
.
Broad band photometry
has been adopted for PG 0900+400: U=12.140, B=13.100, V=12.870
(Ferguson et al. 1984), and PG 1433+239: U=11.330, B=12.340,
V=12.540 (Iriarte 1959).
Table 2 shows the infrared Johnson RIJHK
photometric data used in this work, together with their sources.
The photometric magnitudes used in our energy distribution analysis were
converted into fluxes using
![]() ,
where the scale factors
,
where the scale factors
![]() are adopted from Heber et al. (1984) for
the Strömgren uvby filters, and from Johnson (1966) for the infrared
RIJHK filters.
are adopted from Heber et al. (1984) for
the Strömgren uvby filters, and from Johnson (1966) for the infrared
RIJHK filters.
In order to make a reliable measurement of the atmospheric parameters of sdB stars, it is necessary to deconvolve the hot star flux from that of any cool companion which may be present.
Supposing that binary sdB stars are composed of a hot B-type star and a cool main-sequence or sub-giant star, theoretical flux distributions of both components of the system with a given temperature and gravity can be calculated using appropriate model atmospheres.
In the case of a single sdB star, this model was computed for a given
effective temperature
![]() ,
surface gravity
,
surface gravity ![]() ,
and angular
diameter
,
and angular
diameter ![]() .
In the case of a binary system the model was characterized
by the effective temperatures, surface gravities and angular diameters of
both individual components of the binary system, (
.
In the case of a binary system the model was characterized
by the effective temperatures, surface gravities and angular diameters of
both individual components of the binary system, (
![]() ,
,
![]() ,
,
![]() ,
,
![]() and
and
![]() ,
,
![]() ), together with a given chemical
composition, metallicity and interstellar extinction
), together with a given chemical
composition, metallicity and interstellar extinction
![]() .
The
latter was characterized by the coefficient EB-V together with
the galactic reddening laws of Seaton (1979) and Howarth (1983).
.
The
latter was characterized by the coefficient EB-V together with
the galactic reddening laws of Seaton (1979) and Howarth (1983).
A grid of high-gravity helium-deficient model atmospheres (O'Donoghue
et al. 1997) was used to represent the spectrum of the sdB star. This
grid of line-blanketed LTE-model atmospheres accounts for the known helium
depletion in the atmospheres of B subdwarfs while maintaining solar
metallicity. NLTE effects can be neglected for effective temperatures below
35000K (Kudritzki 1979). This grid of synthetic spectra covers the
effective temperature range 20000 to 40000K (with a spacing of
2000 K), surface gravities range 5.0 to 7.0 dex (with a spacing of 0.5 dex in log g), and 0.0 to 0.3 in He abundance (with a spacing of 0.1 in
![]() ).
).
LTE line-blanketed plane-parallel Kurucz (1993) model atmospheres were used to represent the cool companion on the binary system. This grid of models was selected with surface gravities log g = 4.5 and effective temperatures from 3500 to 18000K (with a spacing of 250 K), having the same metallicity as the hot subdwarf flux distributions.
Model fits were performed for each of the values of composition and surface gravity for which models were available, and the best result adopted, i.e., no interpolation in these parameters was attempted.
The physical parameters of the sdB in our sample were obtained by fitting
the observed fluxes
![]() with a theoretical flux distribution
of the form:
with a theoretical flux distribution
of the form:
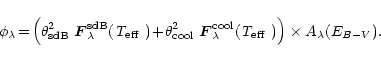 |
(2) |
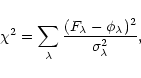 |
(3) |
To locate the minimum in the ![]() surface we used a version of
AMOEBA, which performs a multidimensional minimization, by the
"downhill simplex" method of Nelder & Mead (1965). The implementation
of the method is an extension to binary stars of that described by Jeffery
et al. (2000) in a study of the UV flux variability of hydrogen-deficient
stars.
surface we used a version of
AMOEBA, which performs a multidimensional minimization, by the
"downhill simplex" method of Nelder & Mead (1965). The implementation
of the method is an extension to binary stars of that described by Jeffery
et al. (2000) in a study of the UV flux variability of hydrogen-deficient
stars.
| Star | log g | E(B-V) |
|
|
T
|
|
| (ergs cm-2 s-1) | (K) | (rad) | ||||
|
|
|
|||||
| 1 PG 0004+133 | 5.0 | 0.20 | 0.0 |
|
|
|
| 4 PG 0229+064 | 6.0 | 0.11 | 0.0 |
|
|
|
| 6 PG 0240+046 | 5.5 | 0.06 | 0.3 |
|
|
|
| 7 PG 0314+146 | 6.0 | 0.00 | 0.0 |
|
|
|
| 8 PG 0342+026 | 6.0 | 0.15 | 0.0 |
|
|
|
| 10 PG 0839+399 | 6.0 | 0.02 | 0.0 |
|
|
|
| 13 PG 0934+186 | 6.0 | 0.00 | 0.0 |
|
|
|
| 15 PG 1047+003 | 6.0 | 0.02 | 0.2 |
|
|
|
| 18 PG 1230+052 | 6.0 | 0.02 | 0.0 |
|
|
|
| 19 PG 1233+426 | 5.0 | 0.03 | 0.0 |
|
|
|
| 20 PG 1336 -018 | 6.0 | 0.02 | 0.1 |
|
|
|
| 21 PG 1432+004 | 5.5 | 0.07 | 0.0 |
|
|
|
| 22 PG 1433+239 | 6.0 | 0.05 | 0.0 |
|
|
|
| 24 PG 1452+198 | 6.0 | 0.02 | 0.0 |
|
|
|
| 34 PG 2259+134 | 5.5 | 0.10 | 0.2 |
|
|
|
Together with the grids of hot and cool model atmospheres, the
![]() -minimization needs initial estimates of
-minimization needs initial estimates of
![]() and
EB-V. In very particular cases, the nature of the
and
EB-V. In very particular cases, the nature of the ![]() surface makes
extremely important the definition of those initial parameters, since
AMOEBA can get stuck in a false minimum. We also define the maximum
step that AMOEBA can take, and whether a single parameter can vary or
remain fixed during the search.
surface makes
extremely important the definition of those initial parameters, since
AMOEBA can get stuck in a false minimum. We also define the maximum
step that AMOEBA can take, and whether a single parameter can vary or
remain fixed during the search.
It is well known that the effective temperature dependence of emergent monochromatic fluxes varies as a function of wavelength (Blackwell & Shallis 1977). Specifically, in determining the angular diameter of a star it is essential to minimise the error in this quantity, which can be directly attributable to an uncertain effective temperature; preferably, that means normalising using an infrared flux which is well down the Rayleigh-Jeans tail and not too close to the 2200 Å feature. For hot stars, where the maximum of the Planck function is close to 1000Å, the V-band flux is an acceptable choice. Hence, the normalization of observed and model fluxes has been performed at the V-band (5500Å) by assigning a high weight to the photometric data at this wavelength.
| Star |
|
E(B-V) |
|
|
|
|
|
|
| (ergs cm-2 s-1) | (K) | (K) | (rad) | (rad) | ||||
|
|
|
|
||||||
| 2 PG 0105+276 | 6.0 | 0.01 | 0.0 |
|
|
|
|
|
| 3 PG 0110+262 | 6.0 | 0.00 | 0.0 |
|
|
|
|
|
| 5 PG 0232+095 | 6.0 | 0.10 | 0.0 |
|
|
|
|
|
| 9 PG 0749+658 | 6.0 | 0.00 | 0.0 |
|
|
|
|
|
| 11 PG 0856+121 | 5.5 | 0.02 | 0.0 |
|
|
|
|
|
| 12 PG 0900+400 | 5.0 | 0.00 | 0.0 |
|
|
|
|
|
| 14 PG 1040+234 | 6.0 | 0.02 | 0.0 |
|
|
|
|
|
| 16 PG 1049+013 | 5.0 | 0.00 | 0.1 |
|
|
|
|
|
| 17 PG 1104+243 | 5.0 | 0.00 | 0.0 |
|
|
|
|
|
| 23 PG 1449+653 | 5.5 | 0.02 | 0.0 |
|
|
|
|
|
| 25 PG 1629+081 | 5.5 | 0.00 | 0.0 |
|
|
|
|
|
| 26 PG 1701+359 | 6.0 | 0.00 | 0.1 |
|
|
|
|
|
| 27 PG 1718+519 | 6.0 | 0.01 | 0.0 |
|
|
|
|
|
| 28 BD+29 |
6.0 | 0.00 | 0.0 |
|
|
|
|
|
| 29 PG 2110+127 | 7.0 | 0.03 | 0.0 |
|
|
|
|
|
| 30 PG 2135+045 | 5.5 | 0.03 | 0.0 |
|
|
|
|
|
| 31 PG 2148+095 | 6.0 | 0.00 | 0.0 |
|
|
|
|
|
| 32 PG 2214+184 | 5.0 | 0.00 | 0.2 |
|
|
|
|
|
| 33 PG 2226+094 | 6.0 | 0.00 | 0.0 |
|
|
|
|
|
![\begin{figure}
\par\includegraphics[width=8cm,clip]{h2345F1a.ps}\hspace*{4mm}
\includegraphics[width=8cm,clip]{h2345F1b.ps}\end{figure}](/articles/aa/full/2001/12/aah2345/Timg201.gif) |
Figure 1: Best fits of UV-optical-infrared observations to theoretical models representing a single subdwarf B star (left) and a composite system (right) are shown. The light shading represents the IUE spectrum of the star with the data plotted as error bars (the IUE spectrum is composed by a SW spectrum, 1150-1980Å, and a LW spectrum, 1850-3350Å), and the standard deviation of the flux in each photometric band (Strömgren uvby and infrared Johnson RIJHK). The theoretical model atmospheres from the best fit with the observational data is represented by a solid line spectrum. Labels refer to the identification number in Table 1 |
| Open with DEXTER | |
The fitting procedures outlined in the previous section were applied to all 34 stars in our sample, assuming first that the star was single and second that it was binary. For a single star both single and binary solutions should give the same result for the sdB star while the binary solution will give a nonsense result for the hypothetical cool star. On the other hand, a binary star will yield quite different single and binary star solutions and the single star solution will not match the observed fluxes at all wavelengths.
On the basis of these comparisons, the initial sample was divided into two groups comprising 15 single sdB stars and 19 binaries containing an sdB star and a cool companion.
Table 3 shows the results of the best fits in the case
that the sdB stars energy distribution represents a single star. Columns 1
and 2 give the star identifiers, Cols. 3, 4 and 5 give the
adopted surface gravity, interstellar extinction and atmospheric helium
abundances, respectively. Column 6 gives the integrated IUE flux,
![]() ,
and its standard
deviation,
,
and its standard
deviation,
![]() .
Column 7 gives the effective temperature and standard error, and Col. 8
gives the angular radius for each spectrum.
Table 4 presents the results of the best fits in the
case that the energy distribution of the observed sdB star represents a binary
system containing a hot subdwarf and a cool companion.
.
Column 7 gives the effective temperature and standard error, and Col. 8
gives the angular radius for each spectrum.
Table 4 presents the results of the best fits in the
case that the energy distribution of the observed sdB star represents a binary
system containing a hot subdwarf and a cool companion.
Figure 1 presents the best fits of our UV-optical-infrared observations to theoretical models representing a single subdwarf B star (left panel) and a composite system (right panel), containing a hot subdwarf and a cool companion.
In Fig. 2 we show the detailed fit of the composite sdB PG 0749+658, where the theoretical model characterizing the system (solid line) is the combination of a model representing a hot star (dash-dotted line) and a model representing a cool star (dashed line). It is easy to see that the presence of a cool companion in the system produces a flattened continuum in the redder wavelengths range due to the introduced infrared excess. In this way, the slope of the theoretical model atmospheres representing a composite system is flatter than the slope of a model representing a single star. In the case of the sdB PG 0856+121 (No. 11), the slope of the theoretical model atmospheres representing the system is higher compared with the rest of the composite systems of the sample. The contribution of the cool component in PG 0856+121 is smaller than in the other cases, explained by the fact that its cool companion has the lowest effective temperature of the sample.
The IUE spectra were rebinned at the sampling resolution of the model
atmospheres. Error bars are asymmetric because of the logarithmic scale. In
cases where
![]() ,
the lower error is set to
,
the lower error is set to
![]() .
This is the case around Lyman
.
This is the case around Lyman ![]() in stars such
as PG 0229+064 (No. 4), PG 2214+184 (No. 32) and
PG 2226+096 (No. 33), and in LWR/P spectra such as PG 0232+095
(No. 5) and PG 2259+134 (No. 34).
in stars such
as PG 0229+064 (No. 4), PG 2214+184 (No. 32) and
PG 2226+096 (No. 33), and in LWR/P spectra such as PG 0232+095
(No. 5) and PG 2259+134 (No. 34).
The absence of any photometric data at wavelengths longer than 5500 Å precludes a stringent limit in the determination of atmospheric parameters and the detection of a possible cool companion to some sdBs. This is the case for PG 0240+046 (No. 6) and PG 0314+146 (No. 7).
In the case of a single subdwarf B star, the observed energy distribution is
a function of several parameters, i.e.,
![]() .
For a composite system, the flux distribution depends on the
parameters of the hot subdwarf and the cool component:
.
For a composite system, the flux distribution depends on the
parameters of the hot subdwarf and the cool component:
![]() .
.
In our multi-dimensional fitting procedure, the solution of the system will be more or less sensitive to the initial estimates of some particular atmospheric parameter.
The internal errors associated with the best set of atmospheric parameters,
provided by the ![]() -minimization procedure, are given by the diagonal
elements
-minimization procedure, are given by the diagonal
elements
![]() of the inverse of the covariance matrix
of the inverse of the covariance matrix
![]() .
.
During our ![]() -minimization procedure some parameters are not allowed to
vary, i.e., log g,
-minimization procedure some parameters are not allowed to
vary, i.e., log g,
![]() and, in some cases, EB-V. For those parameters
we make some assumptions for their standard errors. We assume to be 0.2 dex
the standard error of the surface gravity, 0.01 is assumed for the
interstellar extinction and 0.01 for the helium abundance. The effective
temperature is a variable parameter inside the procedure, i.e., its result will
depend on the initial estimates of the fixed parameters, so its standard error
must be calculated. On the other hand, the angular radius of the star is a
parameter directly linked to the effective temperature and the total flux of
the spectrum,
and, in some cases, EB-V. For those parameters
we make some assumptions for their standard errors. We assume to be 0.2 dex
the standard error of the surface gravity, 0.01 is assumed for the
interstellar extinction and 0.01 for the helium abundance. The effective
temperature is a variable parameter inside the procedure, i.e., its result will
depend on the initial estimates of the fixed parameters, so its standard error
must be calculated. On the other hand, the angular radius of the star is a
parameter directly linked to the effective temperature and the total flux of
the spectrum,
![]() ,
and its standard error can be
considered the one obtained from the
,
and its standard error can be
considered the one obtained from the ![]() -minimization procedure.
-minimization procedure.
Model fits for values of
![]() either side of the optimum value were
also performed and the difference in the T
either side of the optimum value were
also performed and the difference in the T
![]() value derived were used to
calculate the additional uncertainty in T
value derived were used to
calculate the additional uncertainty in T
![]() due to an assumed error of
due to an assumed error of
![]() 0.2 dex in g. The same procedure was followed for EB-V for an
assumed error of
0.2 dex in g. The same procedure was followed for EB-V for an
assumed error of ![]() 0.01 and
0.01 and
![]() for an assumed error of
for an assumed error of ![]() 0.1. The
total uncertainty given in Tables 3 and
4 is the square root of the sum of the squares of
these additional uncertainties plus the formal error from the
0.1. The
total uncertainty given in Tables 3 and
4 is the square root of the sum of the squares of
these additional uncertainties plus the formal error from the ![]() fitting, i.e.,
fitting, i.e.,
| |
Figure 2: Detailed fit of the composite system PG 0749+658. The light shading represents the IUE spectrum (1150-3350Å) with the data plotted as error bars, and the standard deviation of the flux in the Strömgren uvby and near-infrared Johnson RI photometric bands. The theoretical model characterizing the system (solid line) is the combination of a model representing a hot star (dash-dotted line) and a model representing a cool star (dashed line) |
| Open with DEXTER | |
Several other attempts have been made to determine the atmospheric parameters of sdB stars, many in a similar way to that described here.
For example, T![]() is estimated either from an analysis of the ultraviolet
energy distribution and from intermediate or narrow band photometry
(Lamontagne et al. 1987), or by using reddening free colour indices (Theissen
et al. 1993). A Balmer line profile then provides the surface gravity.
Finally, the equivalent width of a strong helium line gives an estimate of the
helium abundance (Möehler et al. 1990; Saffer et al. 1994). The flux-ratio
diagram (hereafter FRD) method (Wade 1982) has been used to derive approximate
T
is estimated either from an analysis of the ultraviolet
energy distribution and from intermediate or narrow band photometry
(Lamontagne et al. 1987), or by using reddening free colour indices (Theissen
et al. 1993). A Balmer line profile then provides the surface gravity.
Finally, the equivalent width of a strong helium line gives an estimate of the
helium abundance (Möehler et al. 1990; Saffer et al. 1994). The flux-ratio
diagram (hereafter FRD) method (Wade 1982) has been used to derive approximate
T![]() and spectral types of the components of binary sdB stars (Allard et al.
1994). By fitting line-blanketed Kurucz model spectra and ultraviolet, optical
and IR fluxes Ulla & Thejll (1998) were able to determine estimates of T
and spectral types of the components of binary sdB stars (Allard et al.
1994). By fitting line-blanketed Kurucz model spectra and ultraviolet, optical
and IR fluxes Ulla & Thejll (1998) were able to determine estimates of T![]() and relative radii of the two components of composite sdB stars.
and relative radii of the two components of composite sdB stars.
The atmospheric parameters of sdB stars overlapping our sample have been
gathered from the literature in Table 5.
A comparative analysis has been performed between the results obtained with
our ![]() -minimization procedure and those obtained in previous works.
Note that in some occasions
several estimations of T
-minimization procedure and those obtained in previous works.
Note that in some occasions
several estimations of T![]() have been performed by different authors.
In Table 5, the last column showing the reference
for each cited measurement has an asterisk whenever these values have been
used in our comparative analysis.
have been performed by different authors.
In Table 5, the last column showing the reference
for each cited measurement has an asterisk whenever these values have been
used in our comparative analysis.
| Object | Previous measurements | Ref | ||||
|
|
|
|
|
EB-V | ||
| (K) | (K) | (c.g.s) | ||||
| 1 PG 0004+133 |
|
|
0.028 | 0.110 | M90 |
|
| 2 PG 0105+276 |
|
|
A94 |
|||
| 3 PG 0110+262 |
|
|
A94 | |||
|
|
|
|
0.000 | U98 |
||
| 4 PG 0229+064 |
|
|
0.137 | S94 |
||
| 5 PG 0232+095 |
|
|
|
0.000 | U98 |
|
| 6 PG 0240+046 |
|
|
0.550 | 0.000 | Tj94 |
|
| 8 PG 0342+026 |
|
|
0.100 | L87 | ||
|
|
|
0.003 | 0.080 | M90 | ||
|
|
|
0.004 | S94 |
|||
| 25000 |
5.25 |
0.000 | 0.104 | Th95 | ||
| 9 PG 0749+658 |
|
|
A94 |
|||
|
|
|
0.004 | S94 | |||
| 10 PG 0839+399 |
|
|
0.002 | S94 |
||
| 11 PG 0856+121 |
|
|
0.020 | M90 | ||
|
|
|
0.001 | S94 |
|||
| 12 PG 0900+400 |
|
|
F84 |
|||
| 14 PG 1040+234 |
|
|
A94 |
|||
| 15 PG 1047+003 |
|
|
0.010 | H99 |
||
|
|
|
0.000 | 0.050 | O98 | ||
| 16 PG 1049+013 |
|
|
A94 |
|||
| 17 PG 1104+243 |
|
|
F84 |
|||
|
|
|
0.030 | L87 | |||
|
|
|
A94 | ||||
| 18 PG 1230+052 |
|
|
0.001 | S94 |
||
| 19 PG 1233+426 |
|
|
L85 | |||
|
|
|
0.005 | S94 |
|||
| 20 PG 1336 -018 |
|
3750 | W93 | |||
|
|
3000 |
|
0.050 | K98 |
||
| 21 PG 1432+004 |
|
|
0.005 | 0.030 | M90 | |
|
|
|
0.000 | 0.015 | Th95 |
||
| 22 PG 1433+239 |
|
|
0.000 | S94 | ||
|
|
|
O98 |
||||
| 23 PG 1449+653 |
|
|
A94 |
|||
| 24 PG 1452+198 |
|
|
0.014 | 0.000 | M90 |
|
| 25 PG 1629+081 |
|
A94 |
||||
| 26 PG 1701+359 |
|
|
0.010 | Th93 | ||
|
|
|
A94 |
||||
|
|
|
0.000 | 0.015 | Th95 | ||
| 27 PG 1718+519 |
|
|
0.010 | Th93 | ||
|
|
|
A94 | ||||
|
|
|
|
0.000 | 0.015 | Th95 |
|
| 28 BD+29 |
|
|
|
U98 |
||
| 29 PG 2110+127 |
|
|
0.060 | Th93 | ||
|
|
|
A94 |
||||
|
|
|
0.004 | S94 | |||
|
|
|
|
0.000 | 0.050 | Th95 | |
|
|
5750 |
|
0.100 | U98 | ||
| 30 PG 2135+045 |
|
|
A94 |
|||
|
|
|
0.016 | S94 | |||
| 31 PG 2148+095 |
|
|
A94 | |||
|
|
|
|
U98 |
|||
| 32 PG 2214+184 |
|
|
0.023 | S94 |
||
| 34 PG 2259+134 |
|
|
0.022 | 0.030 | Th93 |
|
|
|
|
0.000 | 0.015 | Th95 | ||
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{h2345F3.ps}\end{figure}](/articles/aa/full/2001/12/aah2345/Timg313.gif) |
Figure 3:
Comparison between effective temperatures obtained in previous works
and with our method, in the case of single sdB stars (filled triangles) and
hot components of composite systems (filled circles). The diagonal solid line
represents perfect agreement between T
|
| Open with DEXTER | |
Figure 3 shows the effective temperatures of sdB stars
obtained by previous authors compared with those obtained with our
![]() -minimization procedure. Each point of the plot represents the
measurements of T
-minimization procedure. Each point of the plot represents the
measurements of T![]() for a single sdB star (filled triangles) or for the hot
component of a composite sdB stars (filled circles). The vertical error bars
correspond to the standard error of the measurements obtained from previous
work, while the horizontal error bars show the uncertainty in the calculation
of the T
for a single sdB star (filled triangles) or for the hot
component of a composite sdB stars (filled circles). The vertical error bars
correspond to the standard error of the measurements obtained from previous
work, while the horizontal error bars show the uncertainty in the calculation
of the T![]() using our procedure. In a perfect agreement between results
obtained with our method and previous works, all the points within its error
bars should stand over the diagonal solid line. The agreement with previous
T
using our procedure. In a perfect agreement between results
obtained with our method and previous works, all the points within its error
bars should stand over the diagonal solid line. The agreement with previous
T![]() measurements is shown to be satisfactory for most of the targets. Stars
with the worst agreement between T
measurements is shown to be satisfactory for most of the targets. Stars
with the worst agreement between T![]() measurements have been labeled in the
plot with their identification number. All our single sdB stars lie within the
temperature range 20000
measurements have been labeled in the
plot with their identification number. All our single sdB stars lie within the
temperature range 20000
![]() 36000, while the hot
components of binary sdB stars appear to have temperatures within the interval
15000
36000, while the hot
components of binary sdB stars appear to have temperatures within the interval
15000
![]() 36000.
36000.
Figure 4 shows the effective temperatures of the cool
companions in binary sdB stars obtained by previous authors compared with
those obtained with our ![]() -minimization procedure. The majority of the
cool components of our sample of binary sdB stars have temperatures in the
range 3800
-minimization procedure. The majority of the
cool components of our sample of binary sdB stars have temperatures in the
range 3800
![]() 6000, with the exception of
PG 1701+359 (No. 26) and BD+29
6000, with the exception of
PG 1701+359 (No. 26) and BD+29![]() 3070 (No. 28), having
approx. 6500K and 8000K, respectively. Our measurements of
T
3070 (No. 28), having
approx. 6500K and 8000K, respectively. Our measurements of
T![]() of cool companions are mostly higher than those obtained by other
authors. Stars with the poorest agreement are labelled in the plot with their
identification numbers. We believe that, in general, our use of photometry
from the UV to the near-infrared provides a more reliable measure of T
of cool companions are mostly higher than those obtained by other
authors. Stars with the poorest agreement are labelled in the plot with their
identification numbers. We believe that, in general, our use of photometry
from the UV to the near-infrared provides a more reliable measure of T![]() for both components than, for example, those obtained using the FRD method.
for both components than, for example, those obtained using the FRD method.
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{h2345F4.ps}\end{figure}](/articles/aa/full/2001/12/aah2345/Timg315.gif) |
Figure 4: As Fig. 3 but for the case of cool components in composite sdB stars |
| Open with DEXTER | |
We briefly comment on those cases in which the largest discrepancies are
found between our T![]() measurements and those of other authors.
measurements and those of other authors.
PG 0240+046 (No. 6): This single star was classified as a helium-rich
subdwarf O star (Thejll et al. 1994), with
![]() .
Our results agree with
this, although the model atmospheres used in our calculations had
.
Our results agree with
this, although the model atmospheres used in our calculations had
![]() .
Models with higher helium abundances would be needed for a better analysis
of this system.
.
Models with higher helium abundances would be needed for a better analysis
of this system.
PG 0342+026 (No. 8), PG 1701+359 (No. 26), PG 1718+519
(No. 27), PG 2110+127 (No. 29) and PG 2259+134 (No. 34): These
single and composite systems are another case of interest, for which several
authors have measured T![]() obtaining quite different values (see
Table 5). In the cases of the single PG 0342+026 and
PG 2259+134 our results are in better agreement with those from
Theissen et al. (1993). In the cases of composite PG 1701+359 and
PG 1718+519, our measurements of T
obtaining quite different values (see
Table 5). In the cases of the single PG 0342+026 and
PG 2259+134 our results are in better agreement with those from
Theissen et al. (1993). In the cases of composite PG 1701+359 and
PG 1718+519, our measurements of T![]() agree better with the results by
Theissen et al. (1995). However, for PG 2110+127 our T
agree better with the results by
Theissen et al. (1995). However, for PG 2110+127 our T![]() is in good
agreement with those obtained by Allard et al. (1994) and Theissen
et al. (1993).
is in good
agreement with those obtained by Allard et al. (1994) and Theissen
et al. (1993).
BD+29![]() 3070 (No. 28): For this particular star a very big
disagreement exists between measurements of T
3070 (No. 28): For this particular star a very big
disagreement exists between measurements of T![]() reported by Ulla & Thejll
(1998) and those coming from our analysis. The enhancement of the energy
distribution above 4500Å of the theoretical model atmosphere
representing this system demonstrates the presence of a cool companion of high
T
reported by Ulla & Thejll
(1998) and those coming from our analysis. The enhancement of the energy
distribution above 4500Å of the theoretical model atmosphere
representing this system demonstrates the presence of a cool companion of high
T![]() .
A reddening of
.
A reddening of
![]() was assigned by those authors,
which is comparable with our estimate
EB-V=0.00, so the big difference
found in T
was assigned by those authors,
which is comparable with our estimate
EB-V=0.00, so the big difference
found in T![]() can not be associated with this factor. This particular star
has to be verified. The high effective temperature of the cool component
obtained with our method would imply an early spectral type (A6) main-sequence
star (Lang 1982).
can not be associated with this factor. This particular star
has to be verified. The high effective temperature of the cool component
obtained with our method would imply an early spectral type (A6) main-sequence
star (Lang 1982).
PG 1049+013 (No. 16): A big discrepancy also occurs with the
T![]() measurements of the hot component of this composite sdB star. Allard
et al. (1994) found
measurements of the hot component of this composite sdB star. Allard
et al. (1994) found
![]() K while
our measurement gives a much lower temperature
(18600
K while
our measurement gives a much lower temperature
(18600![]() 700K). The value of u magnitudes used by those
authors in their work leads to a very high T
700K). The value of u magnitudes used by those
authors in their work leads to a very high T![]() for the hot subdwarf.
However, in our analysis the trend of the IUE spectrum of PG 1049+013
implies the presence of a much cooler sdB component.
for the hot subdwarf.
However, in our analysis the trend of the IUE spectrum of PG 1049+013
implies the presence of a much cooler sdB component.
PG 0900+400 (No. 12) and PG 1104+243 (No. 17): The large
uncertainties in the measurement of T![]() by Ferguson et al. (1984) on the
hot components of these systems (
by Ferguson et al. (1984) on the
hot components of these systems (![]() 5000K) makes our measurements
consistent with those of those authors. The FRD method
has been used by those authors for obtaining the spectral types of the cool
companions of these systems. Thus, such large errors in the determination
of T
5000K) makes our measurements
consistent with those of those authors. The FRD method
has been used by those authors for obtaining the spectral types of the cool
companions of these systems. Thus, such large errors in the determination
of T![]() on these two hot subdwarfs will lead to large uncertainties in the
determination of T
on these two hot subdwarfs will lead to large uncertainties in the
determination of T![]() on their cool companions (
on their cool companions (![]() 1000K has
been adopted).
1000K has
been adopted).
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{h2345F5.ps} .\end{figure}](/articles/aa/full/2001/12/aah2345/Timg322.gif) |
Figure 5:
Positions of the cool stars in composite sdB stars in the
(
|
| Open with DEXTER | |
The determination of effective temperatures and surface gravities of sdB stars is of special interest for understanding the evolution of hot subdwarf stars. In view of our results obtained for the physical parameters of sdB stars, it is worthwhile to check the interpretation of the evolutionary status of both components of the binary systems of our sample.
A modified Hertzsprung-Russell (Luminosity-Effective temperature) diagram can be built up to locate the approximate positions of the cool components of our binary systems, with the parameters derived from our method.
Figure 5 shows the location of the cool stars in composite
sdB of our sample within the Hertzsprung-Russell
(
![]() -
-
![]() )
diagram. The
surface luminosity ratio used in this plot has been calculated with the
parameters derived from our method as follow:
)
diagram. The
surface luminosity ratio used in this plot has been calculated with the
parameters derived from our method as follow:
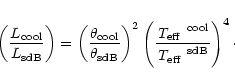 |
(5) |
The majority of the cool companions lie close to the main sequence with
luminosities within 0.5 dex of the assumed ZAMS. Four stars,
PG 0900+400 (No. 12), PG 1049+013 (No. 16),
PG 1629+081 (No. 25) and PG 2148+095 (No. 31), lie between 0.5
and 1.0 dex above the assumed ZAMS; these are also consistent with
main-sequence luminosities given the anticipated error in
![]() .
Two stars, PG 0232+095 (No. 5) and PG 2226+094 (No. 33), have
luminosities >1 dex above the ZAMS and appear to have evolved away from
the main sequence. Furthermore, one star, PG 1701+359 (No. 26),
appears to be subluminous, being 0.5 dex below the assumed ZAMS.
.
Two stars, PG 0232+095 (No. 5) and PG 2226+094 (No. 33), have
luminosities >1 dex above the ZAMS and appear to have evolved away from
the main sequence. Furthermore, one star, PG 1701+359 (No. 26),
appears to be subluminous, being 0.5 dex below the assumed ZAMS.
Due to the uncertainty in our assumption of the surface luminosity of sdB
stars, the effective temperature is the major parameter of constraint in
our HR diagram. The large majority of the cool stars in composite sdB are
in the range of T
![]() 4000
4000
![]() 6000.
According to these effective temperatures, they are consistent with
main-sequence stars of masses between 0.8
6000.
According to these effective temperatures, they are consistent with
main-sequence stars of masses between 0.8
![]() 1.3,
with the exception of BD+29
1.3,
with the exception of BD+29![]() 3070 (No. 28) (about 1.8
3070 (No. 28) (about 1.8 ![]() ),
and the very low-mass stars PG 0856+121 (No. 11) and PG 1629+081
(No. 25), about 0.4
),
and the very low-mass stars PG 0856+121 (No. 11) and PG 1629+081
(No. 25), about 0.4 ![]() and 0.65
and 0.65 ![]() ,
respectively.
,
respectively.
With our results and assumption on subdwarf B surface luminosity, we can conclude that the majority of the cool components of our sample of binary sdB stars are main-sequence stars.
The fact that there is no spectrophotometric evidence for a cool companion in an observed sdB star does not mean that a cool companion is not present but, perhaps, only that is not detectable with a particular method. Thus, it is important to estimate lower limits on detectability of companions of possible binary systems.
In order to determine the coolest main sequence stars detectable with our
method, we constructed a series of test spectra for composite systems having
relative radii comparable to those of sdB and MS stars, and with a range of
T
![]() for both stars. We found that for all sdB temperatures
for both stars. We found that for all sdB temperatures
![]() ,
all MS companions with
,
all MS companions with
![]() were
recovered if the hot star parameters were fixed in the fit. Relaxing this
condition, we always recovered MS stars with
were
recovered if the hot star parameters were fixed in the fit. Relaxing this
condition, we always recovered MS stars with
![]() .
For cooler
test companions, we consistently recovered
.
For cooler
test companions, we consistently recovered
![]() ,
but the
angular radii were always reduced in such a way that total flux was conserved.
Consequently, for the coolest companions
,
but the
angular radii were always reduced in such a way that total flux was conserved.
Consequently, for the coolest companions
![]() ,
there is
a systematic tendency to overestimate T
,
there is
a systematic tendency to overestimate T
![]() but not
but not
![]() .
This affects those stars in our sample which are
already furthest from the main-sequence (Fig. 5). It does not
affect our conclusion that the majority of companions in our sample are main
sequence stars, nor does it affect the luminosity function
(Fig. 6).
.
This affects those stars in our sample which are
already furthest from the main-sequence (Fig. 5). It does not
affect our conclusion that the majority of companions in our sample are main
sequence stars, nor does it affect the luminosity function
(Fig. 6).
If the sample of sdB stars were truly representative and the distribution of sdB companions representative of low-mass stars in the field, the fraction of binary sdB stars might then be estimated from a suitable luminosity function (e.g. Lang 1980).
Our sample of 19 cool companions of composite sdB stars are in the range of
absolute visual magnitudes
![]() ,
11 of these being
main-sequence stars between the interval
,
11 of these being
main-sequence stars between the interval
![]() .
.
With these absolute visual magnitudes an histogram has been built
(Fig. 6) where the number of objects, in bins of
![]() ,
are represented. Thus, assuming that the luminosity
function of the secondary stars of our composite sdB can be represented by
that of single stars of luminosity class V, the main-sequence luminosity
function by Lang (1980) (hereafter LF80) has been normalized to the interval
,
are represented. Thus, assuming that the luminosity
function of the secondary stars of our composite sdB can be represented by
that of single stars of luminosity class V, the main-sequence luminosity
function by Lang (1980) (hereafter LF80) has been normalized to the interval
![]() ,
and integrated over all the range of
,
and integrated over all the range of ![]() within which
binary systems are detectable with our method. In Fig. 6 filled
circles represent this luminosity function binned with the same resolution as
our histogram. Poisson statistics have been used to estimate the standard
errors of the luminosity function per interval of
within which
binary systems are detectable with our method. In Fig. 6 filled
circles represent this luminosity function binned with the same resolution as
our histogram. Poisson statistics have been used to estimate the standard
errors of the luminosity function per interval of ![]() .
.
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{h2345F6.ps}\end{figure}](/articles/aa/full/2001/12/aah2345/Timg336.gif) |
Figure 6:
Histogram representing the number of cool companions in
composite sdB stars used in this work, per magnitude, at different absolute
visual magnitudes, |
| Open with DEXTER | |
The fact that only five composite sdB stars have been observed beyond
![]() means that, either there are no M dwarf companions among sdB stars,
or that strong selection effects are present in our sample. Extending LF80
to the range
means that, either there are no M dwarf companions among sdB stars,
or that strong selection effects are present in our sample. Extending LF80
to the range
![]() ,
we would expect to observe
,
we would expect to observe ![]() 8 cool
companions in the interval
8 cool
companions in the interval
![]() ,
,
![]() 11 secondary components
of composite sdB within
11 secondary components
of composite sdB within
![]() and
and ![]() 19 within
19 within
![]() .
Although a larger sample of composite sdB stars is
required, there already appears to be a shortfall of cool sdB companions with
.
Although a larger sample of composite sdB stars is
required, there already appears to be a shortfall of cool sdB companions with
![]() .
Indeed, if sdB stars follow the main-sequence luminosity
function, given the shape of the LF for
.
Indeed, if sdB stars follow the main-sequence luminosity
function, given the shape of the LF for
![]() (Gould et al. 1997),
then all of our sample should be binaries with cool unseen companions!
(Gould et al. 1997),
then all of our sample should be binaries with cool unseen companions!
However, the selection criterion for our sample is that the target was
observed with IUE. This implies a complicated mix of selection effects imposed
by the original observing programmes - bright, single, composite, peculiar,
etc. The principal problem is the absence of companions with
![]() ,
since the detection at
,
since the detection at
![]() may be spurious.
The deficit is
may be spurious.
The deficit is ![]() 2 mag-1 detected versus
2 mag-1 detected versus ![]() 8 mag-1 predicted
from the LF.
8 mag-1 predicted
from the LF.
Thus, we can only place limits on the sdB binary fraction of between
![]() 56%, based on the shortfall of sdB companions with
56%, based on the shortfall of sdB companions with
![]() ,
actually detected, and 100
,
actually detected, and 100![]() assuming a standard LF for main-sequence stars.
We cannot yet establish that this binary fraction is fundamentally
different to that for the supposed progenitor stars. The fraction of F/G main
sequence stars which have companions is
assuming a standard LF for main-sequence stars.
We cannot yet establish that this binary fraction is fundamentally
different to that for the supposed progenitor stars. The fraction of F/G main
sequence stars which have companions is ![]() 67% (Duquennoy & Mayor 1991).
67% (Duquennoy & Mayor 1991).
In general, the effective temperatures of the cool companions of composite
sdB stars obtained with our method are systematically higher than those
measured by other authors. If T
![]() of the cool star is reduced, its radius
must increase in order to conserve the flux due to the cool star in the
composite spectrum. Thus, if previous studies are correct, cool companions
would have to be more evolved than they appear to be here. Thus, we
believe that our measurements of T
of the cool star is reduced, its radius
must increase in order to conserve the flux due to the cool star in the
composite spectrum. Thus, if previous studies are correct, cool companions
would have to be more evolved than they appear to be here. Thus, we
believe that our measurements of T
![]() are consistent with the majority of
cool companions of our sample being main sequence stars. The assumption of
log g = 4.5 used in our analysis does not affect the T
are consistent with the majority of
cool companions of our sample being main sequence stars. The assumption of
log g = 4.5 used in our analysis does not affect the T
![]() of the companions.
of the companions.
The fact that our T
![]() measurements of cool companions are higher than those
measured by other authors (Ferguson et al. 1984; Allard et al. 1994; Thejll
et al. 1995; Ulla & Thejll 1998), makes their absolute visual magnitudes
fainter than our own (see Table 6), being
measurements of cool companions are higher than those
measured by other authors (Ferguson et al. 1984; Allard et al. 1994; Thejll
et al. 1995; Ulla & Thejll 1998), makes their absolute visual magnitudes
fainter than our own (see Table 6), being ![]() 2 mag brighter
than those of Allard et al. (1994). In these studies, the absolute visual
magnitudes were deduced from T
2 mag brighter
than those of Allard et al. (1994). In these studies, the absolute visual
magnitudes were deduced from T
![]() or spectral types assuming the cool
components lie on the Population I main sequence tabulated by Allen (1973).
or spectral types assuming the cool
components lie on the Population I main sequence tabulated by Allen (1973).
As suggested in Sect. 6.1, the FRD method may mislead
the determination of T
![]() .
Typical errors in the classification of a star
with this method of the order of
.
Typical errors in the classification of a star
with this method of the order of ![]() 2 subclasses imply a difference of
2 subclasses imply a difference of
![]() 1 mag in the calculation of the absolute visual magnitude,
1 mag in the calculation of the absolute visual magnitude, ![]() .
.
| Object | T
|
Previous measurements | ||||
| (K) | (mag) |
|
|
|
|
|
| 2 PG0105+276 |
|
5.79 | -- | 8.20 | -- | -- |
| 3 PG0110+262 |
|
4.36 | -- | 6.60 | 5.10 | 6.23 |
| 5 PG0232+095 | 3.79 | -- | -- | 6.30 | 6.17 | |
| 9 PG0749+658 |
|
5.19 | -- | 7.50 | -- | -- |
| 12 PG0900+400 |
|
4.09 | 6.70 | -- | -- | - |
| 16 PG1049+013 |
|
5.24 | -- | 8.70 | -- | -- |
| 17 PG1104+243 | 4.46 | 6.60 | 6.90 | -- | -- | |
| 23 PG1449+653 |
|
6.05 | -- | 7.00 | -- | -- |
| 25 PG1629+081 |
|
8.19 | -- | 8.20 | -- | -- |
| 26 PG1701+359 |
|
5.48 | -- | 7.80 | -- | -- |
| 27 PG1718+519 | 3.90 | -- | 6.90 | -- | -- | |
| 28 BD+29 |
|
2.59 | -- | -- | -- | 5.45 |
| 29 PG2110+127 |
|
4.49 | -- | 6.60 | -- | 4.78 |
| 30 PG2135+045 |
|
6.38 | -- | 6.70 | -- | -- |
| 31 PG2148+095 |
|
5.64 | -- | 6.90 | -- | 5.77 |
On the basis of the available optical and infrared photometry,
we can conclude that the energy distribution of 15 sdB stars of our sample
are consistent with those of a single sdB star, and 19 sdB stars of the
sample show evidences of the presence of a cool companion in the system. In
the case of single hot subdwarf stars their effective temperatures range
between
![]() .
However, hot
components of composite sdB stars of our sample have effective temperatures
ranging
.
However, hot
components of composite sdB stars of our sample have effective temperatures
ranging
![]() .
The majority of the
cool stars of composite sdBs in our sample are believed to be main-sequence
stars with effective temperatures between 3800 K and 6000 K,
although two of them, PG 0232+095 and PG 2226+094, seem to be
more evolved. Based on their effective temperatures, the majority of the
cool stars of our sample have masses in the range
.
The majority of the
cool stars of composite sdBs in our sample are believed to be main-sequence
stars with effective temperatures between 3800 K and 6000 K,
although two of them, PG 0232+095 and PG 2226+094, seem to be
more evolved. Based on their effective temperatures, the majority of the
cool stars of our sample have masses in the range
![]() .
.
Our sample of 19 cool companions are in the range of absolute visual
magnitudes
![]() ,
11 of these being main-sequence
stars in the interval
,
11 of these being main-sequence
stars in the interval
![]() .
.
The results of this work show that the majority of the cool companions to our sample of sdB stars are main-sequence stars, in contrast to previous results based on data over a shorter wavelength range and obtained using different techniques (Allard et al. 1994; Theissen et al. 1995).
It is not clear whether the cool companions have influenced the evolution of the sdB star or otherwise caused their peculiar properties. However, some of the binaries identified in this work will be close binaries which have interacted, some will be non-interacting pairs and some will be unrelated optical doubles, i.e. background/foreground stars (Sect. 2), which may explain why some cool companions appear under/over-luminous (see Fig. 5).
Acknowledgements
This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation.
The authors would like to thank Tony Lynas-Gray for providing the high-gravity helium-deficient model atmospheres used in this work. We thank Ulrich Heber and Sabine Möehler for good comments and useful suggestions in improving this paper. Thanks go also to the anonymous referee for valuable advice.
This research is supported by a grant to the Armagh Observatory from the Northern Ireland Department of Culture, Arts and Leisure.