A&A 368, 866-872 (2001)
DOI: 10.1051/0004-6361:20010084
V. V. Makarov - C. Fabricius
Copenhagen University Observatory, Juliane Maries Vej 30, 2100 Copenhagen Ø, Denmark
Received 28 June 2000 / Accepted 5 January 2001
Abstract
Thirty one probable kinematic members of the nearby TW Hya association of
young stars are selected from the RASSBSC/Tycho-2 sample of stars luminous
in X-rays, detected by ROSAT. Eight of them have been listed already as members
of the association, and 23 are new candidates. The association occupies
a volume of some 106 pc3, the nearest member being at a distance
of only 17.5 pc from the Sun. The lower bound internal velocity
dispersion is estimated
at 0.8 km s-1, which is considerably larger than is expected in a gravitationally
bound open cluster. The total mass of the group is estimated at 31solar masses. The centre of mass lies at 73 pc from us in the direction
close to the position of the prototype star TW Hya. A realistic
kinematical model fitting both the observed trigonometric parallaxes
and radial velocities involves a linear expansion of the group with the
rate 0.12 km s-1 pc-1, which defines a dynamical age of 8.3 Myr,
in good agreement with previous age estimations for T Tauri members.
Likewise the nearby Carina-Vela moving group of X-ray
stars, the TW Hya association appears to be an outpost of the Gould Belt
structure rather than an isolated open cluster.
Key words: open clusters and associations: individual: TW Hya - Stars: kinematics - X-rays: stars
The present census of the TWA includes at least 13 star systems (Webb et al. 1999; Sterzik et al. 1999; Webb & Zuckerman 2000), all exhibiting enhanced X-ray luminosities and spectra typical of T Tauri stars. Their common origin is further confirmed by similar kinematics, i.e. radial velocities and proper motions.
The new data used in this paper are accurate proper motions from the Tycho-2 catalogue (Høg et al. 2000a) for bright X-ray stars observed by ROSAT. The original sample of ROSAT sources identified with Tycho-2 stars is described in Sect. 2. Inspired by the young moving group in Carina-Vela (Makarov & Urban 2000), which seems to stretch over 100 pc in the radial direction and across the sky, we extend the search area and select 23 new kinematic members of the association in addition to 8 previously known. The selection is described in Sect. 4. The extended list of candidate members permits us to construct a kinematic model of the group, which is a development of the classical convergent point method, as described in Sect. 3. Finally, Sect. 5 (Conclusions) concerns some implications of the kinematic model and the issue of a possible relation between the TWA and the Gould Belt.
The Tycho-2 Catalogue contains accurate positions, proper motions and
two-colour photometry for 2.5 million stars. Magnitudes in two passbands
![]() and
and ![]() are given for all
the stars in the catalogue, and accurate proper motions for 96%
of them. The errors of
are given for all
the stars in the catalogue, and accurate proper motions for 96%
of them. The errors of ![]() magnitudes are within 0.05 mag at
magnitudes are within 0.05 mag at
![]() mag
and within 0.16 mag at 11.5 mag.
The median standard error of proper motions is
2.5 mas/yr at
mag
and within 0.16 mag at 11.5 mag.
The median standard error of proper motions is
2.5 mas/yr at
![]() mag and 1.5 mas/yr at magnitude 9.5. It is presently
the most accurate reference catalogue among those statistically complete
down to V=11.5 mag.
mag and 1.5 mas/yr at magnitude 9.5. It is presently
the most accurate reference catalogue among those statistically complete
down to V=11.5 mag.
The proper motions in Tycho-2 were computed by combining the Tycho-2 positions at epoch about 1991.5 with those from the Astrographic Catalogue at epoch about 1905 and 143 other transit circle and photographic catalogues, generally at intermediate epochs. Systematically, the proper motions reproduce the Hipparcos reference system extremely well (Urban et al. 2000). With regard to accidental errors, they are quite similar in quality to Hipparcos proper motions, but they are more accurate in case of binary stars, being less perturbed by orbital motions with periods much below 100 yr (Makarov et al. 2000).
Another major source of information in this paper is the RASS Bright Source
Catalogue, based on the observations in the 0.1-2.4 keV energy band obtained
with the PSPC instrument of the ROSAT satellite (Voges et al. 1999).
It includes ![]() sources down to a limiting PSPC count rate of
0.05 cts s-1. These data represent the most complete
and sensitive X-ray sky survey ever published.
sources down to a limiting PSPC count rate of
0.05 cts s-1. These data represent the most complete
and sensitive X-ray sky survey ever published.
The RASSBSC/Tycho-2 sample was obtained by positional cross-identification
of sources in the RASS BSC and Tycho-2 catalogues.
Two objects were reckoned matching in position if the angular distance
between them was smaller than
![]() ,
where
,
where
![]() is the RASS BSC positional error, which is generally a few tens of
arcsec. The Tycho-2 Catalogue contains double
stars resolved down to separation 0.8 arcsec. Some of the X-ray sources
were therefore matched to 2 or even 3 Tycho-2 stars. Since there is no
way to reasonably tell which of the optical counterparts is responsible
for the X-ray emission, all such double identifications, constituting
about 10% of the total, were retained.
The sample contains 7096 Tycho-2 stars matched to 6594 RASS BSC sources.
is the RASS BSC positional error, which is generally a few tens of
arcsec. The Tycho-2 Catalogue contains double
stars resolved down to separation 0.8 arcsec. Some of the X-ray sources
were therefore matched to 2 or even 3 Tycho-2 stars. Since there is no
way to reasonably tell which of the optical counterparts is responsible
for the X-ray emission, all such double identifications, constituting
about 10% of the total, were retained.
The sample contains 7096 Tycho-2 stars matched to 6594 RASS BSC sources.
Following A. Heck (1978), two closely related methods to infer distances of members of a cluster are distinguished, the convergent point method and the moving cluster method. For a comprehensive historical overview of the methods the reader is referred to Dravins et al. (1999). The methods arise, conceptually, from the same principle. If a group of stars of a sizeable angular extent share the same motion in space, with respect to the observer, then, upon the geometrical projection onto the celestial sphere, the angular extent will change with time, and the cluster will contract, in infinity, to a single point. Translated into observed proper motions, the geometrical projection effect results in a measurable gradient of proper motion components across the cluster (the moving cluster method), or into a common convergent point, in which all the proper motion vectors intersect when extended around the sphere (the convergent point method). Rather arbitrarily, these two methods may be distinguished by whether the convergent point coordinates are explicitly estimated from the directions of proper motion vectors. Since coordinates of the convergent point are explicitly determined in this paper, the method in use is a variant of the convergent point method.
The general recipe of the method is:
1) Determine coordinates of the convergent point from the available proper motion directions;
2a) Determine the centroid velocity vector from the convergent point, proper motion magnitudes and available radial velocities, or
2b) Determine the centroid velocity vector from the convergent point, proper motion magnitudes and available trigonometric parallaxes;
3) Determine kinematic parallax and radial velocity for each star.
Traditionally, the option 2a) was used by many authors, because trigonometric parallaxes were too scarce and imprecise in comparison with radial velocities. The advance of the Hipparcos Catalogue in 1997 changed the situation, and now radial velocity data often lag in quality and number. Lindegren et al. (2000), in their all-round maximum-likelihood approach use Hipparcos parallaxes as the original data to derive astrometric radial velocities. We do the same in this paper. We demonstrate, furthermore, that a comparison of astrometric radial velocities with observed radial velocities can reveal the presence of internal expansion or contraction in a cluster, and we develop the classical convergent point method to accomodate an isotropic uniform expansion.
Following the designations in (Makarov et al. 2000), the basic parameters involved in the computation are
The next step is estimating the total bulk velocity of the group
![]() .
At this point, we know the angular distance
.
At this point, we know the angular distance ![]() between each star
and the convergent point. Using available trigonometric parallaxes, the
centroid velocity is derived from
between each star
and the convergent point. Using available trigonometric parallaxes, the
centroid velocity is derived from
| (3) |
| (4) |
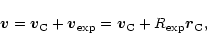 |
(5) |
The centre of mass is determined in the following way. For each star, we
convert the observed Tycho-2 colour
![]() into Johnson B-V, and
into Johnson B-V, and ![]() magnitude into V, using the approximate relations given in Vol. 1 of ESA 1997.
Absolute magnitudes MV are computed from the estimated kinematic distances.
Using the formula in Reid (1992) for main sequence stars, the mass is estimated
from the absolute magnitude and colour. Finally, the masses, positions and
kinematic distances are used to determine the centre of mass location.
In the basic kinematic Model I, this procedure is straightforward, because
the kinematic distances are independent of the centre of mass location. In
the second model, with non-zero expansion rate, the process becomes iterative,
since the model velocity for each star, and hence the kinematic distance,
depends on the centre of mass location.
magnitude into V, using the approximate relations given in Vol. 1 of ESA 1997.
Absolute magnitudes MV are computed from the estimated kinematic distances.
Using the formula in Reid (1992) for main sequence stars, the mass is estimated
from the absolute magnitude and colour. Finally, the masses, positions and
kinematic distances are used to determine the centre of mass location.
In the basic kinematic Model I, this procedure is straightforward, because
the kinematic distances are independent of the centre of mass location. In
the second model, with non-zero expansion rate, the process becomes iterative,
since the model velocity for each star, and hence the kinematic distance,
depends on the centre of mass location.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{H2292.f1.ps}
\end{figure}](/articles/aa/full/2001/12/aah2292/Timg37.gif) |
Figure 1: Positions and proper motions of the 31 selected kinematic members of the TWHya association |
| Open with DEXTER | |
We inspect all RASSBSC/Tycho-2 stars with measured proper motions in a large
area of the sky of above ![]() deg2 depicted in Fig. 1. The
stars are selected with proper motions greater than 30 mas/yr, crossing a
circle of radius
deg2 depicted in Fig. 1. The
stars are selected with proper motions greater than 30 mas/yr, crossing a
circle of radius
![]() centred on
centred on
![]() which is the
convergent point of the "classical'' members, determined by a non-linear
which is the
convergent point of the "classical'' members, determined by a non-linear ![]() adjustment of Model I. The cut on
adjustment of Model I. The cut on ![]() is meant to clean the sample
of more distant kinematic
interlopers, but it may in fact leave out real distant members of TWA. The
limit of
is meant to clean the sample
of more distant kinematic
interlopers, but it may in fact leave out real distant members of TWA. The
limit of
![]() may seem restrictive, because two previously known members
of the association, TWA 6 and 11, deviate by more than this angle from the
assumed convergent point. They would not have been included by our criteria,
meaning that probably more loosely associated members could be found in the
area, and that the internal velocity dispersion of 0.8 km s-1
derived in the next section might be an underestimation.
may seem restrictive, because two previously known members
of the association, TWA 6 and 11, deviate by more than this angle from the
assumed convergent point. They would not have been included by our criteria,
meaning that probably more loosely associated members could be found in the
area, and that the internal velocity dispersion of 0.8 km s-1
derived in the next section might be an underestimation.
| star | TWA | RA | Dec |
|
|
|
vr |
|
|
|
|||
|
| mas/yr | mag | mag | pc | pc | kms-1 | kms-1 | deg | |||||
| 53911 | 1 | 11 01 51.9 | -34 42 17.2 | 75.4 | 11.34 | 0.75 | 56.4 | 57.1 | 12.7 | 13.5 | 0.6 | 0.22 | -3.37 |
| 7201-0027-1 | 2 | 11 09 13.8 | -30 01 39.8 | 92.6 | 11.36 | 2.21 | 47.1 | 10.6 | 2.9 | 0.88 | -4.17 | ||
| 55505 | 4 | 11 22 5.3 | -24 46 39.5 | 96.8 | 9.24 | 1.40 | 46.7 | 45.7 | 9.1 | -0.3 | -0.14 | -4.29 | |
| 7223-0275-1 | 5 | 11 31 55.3 | -34 36 27.5 | 86.7 | 11.72 | 1.69 | 50.9 | 10.0 | -1.8 | -0.66 | -3.33 | ||
| 7183-1477-1 | 6 | 10 18 28.7 | -31 50 02.8 | 60.6 | 12.00 | 1.89 | 67.4 | 16.2 | -10.8 | -2.91 | -4.05 | ||
| 7190-2111-1 | 7 | 10 42 30.1 | -33 40 16.6 | 125.7 | 11.06 | 1.54 | 33.6 | 11.0 | -1.6 | -0.61 | -3.32 | ||
| 57589 | 9 | 11 48 24.2 | -37 28 49.2 | 58.1 | 11.32 | 1.64 | 50.3 | 76.3 | 12.6 | 1.9 | 0.63 | -3.45 | |
| 61498 | 11 | 12 36 1.0 | -39 52 10.2 | 57.4 | 5.77 | 0.02 | 67.1 | 78.1 | 10.5 | 4.6 | 1.93 | -5.17 | |
| 46535 | 09 29 28.6 | -44 31 56.5 | 93.5 | 7.03 | 0.54 | 39.7 | 39.5 | 16.0 | 22.1: | 3.8 | 1.39 | -3.98 | |
| 47039 | 09 35 11.8 | -35 49 25.5 | 73.9 | 6.52 | 0.46 | 63.4 | 50.5 | 16.9 | 12.71 | -0.3 | 0.10 | -5.40 | |
| 48273 | 09 50 30.1 | +04 20 37.1 | 157.9 | 6.29 | 0.49 | 45.9 | 26.6 | 10.7 | 17.4: | 4.5 | 1.91 | -5.17 | |
| 0829-0845-1 | 09 58 27.2 | +08 50 43.7 | 38.4 | 10.11 | 0.81 | 111.7 | 20.4 | 3.2 | 0.82 | -3.62 | |||
| 6604-0118-1 | 09 59 8.4 | -22 39 34.6 | 63.7 | 10.09 | 1.26 | 62.8 | 16.5 | -5.26 | -1.63 | -3.78 | |||
| 49530 | 10 06 47.4 | +05 36 41.4 | 37.0 | 6.29 | 1.08 | 105.9 | 116.4 | 20.7 | 16.7: | -2.4 | -0.99 | -4.63 | |
| 6625-1087-1 | 10 08 3.5 | -26 36 38.6 | 36.7 | 11.11 | 1.02 | 110.1 | 21.3 | -2.8 | -0.55 | -2.97 | |||
| 7178-1493-1 | 10 10 46.7 | -34 47 53.1 | 75.2 | 11.61 | 0.86 | 53.4 | 15.2 | -5.7 | -1.61 | -2.54 | |||
| 7183-1879-1 | 10 16 45.4 | -31 08 44.2 | 45.1 | 11.58 | 1.12 | 90.3 | 18.9 | 1.9 | 0.41 | -2.91 | |||
| 7188-0575-1 | 10 22 4.5 | -32 33 27.0 | 123.3 | 10.26 | 1.31 | 33.2 | 12.2 | -2.2 | -0.87 | -3.06 | |||
| 50796 | 10 22 18.0 | -10 32 15.5 | 79.1 | 11.14 | 1.34 | 34.0 | 53.8 | 13.1 | -0.5 | -0.18 | -2.61 | ||
| 7710-2231-1 | 10 32 10.2 | -39 05 46.5 | 32.7 | 9.27 | 1.25 | 126.4 | 22.5 | 0.1 | 0.04 | -3.82 | |||
| 52462 | 10 43 28.3 | -29 03 51.4 | 218.3 | 7.81 | 1.02 | 21.6 | 19.4 | 9.0 | 0.4 | 0.16 | -3.98 | ||
| 52787 | 10 47 31.2 | -22 20 52.9 | 126.5 | 8.44 | 0.96 | 34.9 | 34.1 | 9.9 | 3.5 | 1.51 | -3.86 | ||
| 53486 | 10 56 30.8 | +07 23 18.5 | 268.1 | 7.47 | 1.09 | 17.6 | 16.7 | 3.7 | 3.9 | 1.79 | -4.55 | ||
| 55899 | 11 27 29.4 | -39 52 35.4 | 31.2 | 7.33 | 0.08 | 142.5 | 140.3 | 21.8 | 0.9 | 0.28 | -4.56 | ||
| 57129 | 11 42 48.1 | -35 48 57.5 | 57.0 | 9.37 | 0.64 | 105.2 | 77.7 | 12.9 | 29.1: | -4.0 | -1.56 | -3.48 | |
| 57269 | 11 44 38.5 | -49 25 02.7 | 135.9 | 9.12 | 1.02 | 48.6 | 32.2 | 8.5 | -1.2 | -0.53 | -2.84 | ||
| 57524 | 11 47 24.5 | -49 53 03.0 | 34.9 | 9.14 | 0.70 | 104.0 | 125.5 | 20.0 | 2.4 | 0.87 | -3.52 | ||
| 59315 | 12 10 6.5 | -49 10 50.7 | 160.3 | 8.24 | 0.78 | 37.8 | 27.7 | 6.6 | 0.0 | 0.01 | -4.17 | ||
| 7760-0835-1 | 12 13 7.0 | -40 56 31.6 | 32.7 | 9.86 | 0.60 | 136.5 | 19.4 | 3.3 | 0.99 | -3.55 | |||
| 8238-1462-1 | 12 21 55.7 | -49 46 12.5 | 40.0 | 10.10 | 0.90 | 111.1 | 16.8 | 2.8 | 1.00 | -3.85 | |||
| 8234-2856-1 | 12 22 4.3 | -48 41 25.0 | 32.4 | 10.59 | 0.95 | 137.6 | 20.1 | 1.8 | 0.48 | -3.31 |
This selection yields 31 stars, including 8 previously known members adopted
from the literature. They are listed in Table 1. Using X-ray fluxes
measured by ROSAT, the ![]() and
and ![]() magnitudes from the Tycho-2
Catalogue, and tabulated bolometric corrections for
main sequence stars from Johnson (1966), the ratio of X-ray to
bolometric luminosities are computed
(last column in Table 1). The Tycho magnitudes and colours are transformed
into the Johnson system by the approximate relations for main sequence
stars given in (ESA 1997, Vol. 1). It is noted that our
magnitudes from the Tycho-2
Catalogue, and tabulated bolometric corrections for
main sequence stars from Johnson (1966), the ratio of X-ray to
bolometric luminosities are computed
(last column in Table 1). The Tycho magnitudes and colours are transformed
into the Johnson system by the approximate relations for main sequence
stars given in (ESA 1997, Vol. 1). It is noted that our
![]() values are systematically smaller than those given
by Webb et al. (1999). The reason for this discrepancy is difficult to
find out, because Webb et al. do not describe explicitly which bolometric
correction they have used. Our
estimates vary from -5.4 for HIP 47039 and -5.2 for HIP 48273 to -2.5for TYC 7178-1493-1. The X-ray performance of the former two would be modest
even by the 600 Myr old Hyades standards (Stern et al. 1995), although such faint
sources are indeed observed sometimes in the much younger Pleiades (Micela et al. 1999)
and
values are systematically smaller than those given
by Webb et al. (1999). The reason for this discrepancy is difficult to
find out, because Webb et al. do not describe explicitly which bolometric
correction they have used. Our
estimates vary from -5.4 for HIP 47039 and -5.2 for HIP 48273 to -2.5for TYC 7178-1493-1. The X-ray performance of the former two would be modest
even by the 600 Myr old Hyades standards (Stern et al. 1995), although such faint
sources are indeed observed sometimes in the much younger Pleiades (Micela et al. 1999)
and ![]() Per (Randish et al. 1996) clusters. The star HIP 47039 has a measured
radial velocity of
Per (Randish et al. 1996) clusters. The star HIP 47039 has a measured
radial velocity of
![]() ,
not too different from the predicted
+16.9 (Table 1). The star HIP 48273 = HD 85217 is a spectroscopic binary,
and therefore its observed radial velocity of +17.4 may be disturbed,
against the predicted +10.7. But a short-period orbital motion could hardly
hamper so much the Tycho-2 proper motions. It seems more likely that the
velocity of this star is about 42 km s-1 instead of the 25 kms-1 as estimated for the association. Summarizing, these two stars
are quite likely statistical interlopers in our sample.
,
not too different from the predicted
+16.9 (Table 1). The star HIP 48273 = HD 85217 is a spectroscopic binary,
and therefore its observed radial velocity of +17.4 may be disturbed,
against the predicted +10.7. But a short-period orbital motion could hardly
hamper so much the Tycho-2 proper motions. It seems more likely that the
velocity of this star is about 42 km s-1 instead of the 25 kms-1 as estimated for the association. Summarizing, these two stars
are quite likely statistical interlopers in our sample.
Another relatively moderate X-ray emitter in the sample is HIP 53486 = HD
94765. It is potentially the nearest member of the association.
Spectroscopic observations are needed to establish its age and to determine
its radial velocity. The predicted radial velocity in the kinematic model II
is low (+3.7), because it is dumped by the counter expansion velocity
component (see next section). Whether the true
![]() is so low
should provide a check on our assumption of a linear expansion out to
distances above 50 pc from the centre.
is so low
should provide a check on our assumption of a linear expansion out to
distances above 50 pc from the centre.
The HIP 46535 = HD 82241 is related by Eggen (1995) to pre-main-sequence stars in the Pleiades supercluster. The known radial velocity of it (+22.1 in the Simbad data base) is not in a good agreement with the predicted +16.0. That this star is an interloper can not be precluded.
Observational evidence of young age have been collected and published for some
of the new additions to the TWA list, apart from the high X-ray activity.
The HIP 59315 (G5V) is known to be chromospherically active. The TYC
6604-0118-1 = SAO 178272 (K2V) has a lithium 6707.8 Å equivalent
width of 0.143 Å and rotation velocity
![]() kms-1(Favata et al. 1995), as expected of a young dwarf.
kms-1(Favata et al. 1995), as expected of a young dwarf.
The star HIP 49530 = HR 3973, one of the most distant in the group, is
remarkable by its quoted spectral type K1III. Some K giants, prominent on the
X-ray sky, are indeed embedded in the Gould Belt. A young age of this star
can not be precluded, although its X-ray luminosity might be ascribed to
the binary component. Importantly, two other distant stars, HIP 55899 (A0V)
and HIP 57524 (G3/G5p) are related by de Zeeuw et al (1999) to the Lower
Centaurus Crux (LCC) OB association, which overlaps with the lower left
corner of the area in Fig. 1. Obviously, de Zeeuw et al. would have included some more
of the stars in our sample as members of LCC, should they not impose a lower
limit on distance to its stars. Reversely, we could find more stars belonging
kinematically to LCC by loosing our limit on ![]() mas/yr. This might mean
that the TWA on the large scale is not separated clearly from the background
LCC association and the Gould Belt as a whole.
mas/yr. This might mean
that the TWA on the large scale is not separated clearly from the background
LCC association and the Gould Belt as a whole.
The companion star fraction (CSF) for main sequence stars, describing the
frequency of binary and triple
stars, is known to correlate well with the age of a
stellar aggregate (e.g., Patience et al. 1998). Over the binary separation range 5 to
50 AU, the CSF drops from about 0.40 for T Tauri stars (several million years
old) through 0.30 in the Hyades (600 Myr) to 0.14 for nearby field G dwarfs.
We should expect therefore a high frequency of binaries in our sample.
Two stars among the 8 original members, TWA 5 and 6, are suspected to be
spectroscopic binaries (Webb et al. 1999). HIP 57129 = HD 101799 is a well-known
contact binary. The number of known visual binaries includes TWA 2 (separation
27 AU), TWA 5 (97 AU), TWA 9 (302 AU) and TWA 11 (513 AU). To this number,
we add from the new members HIP 49530, resolved by speckle interferometry
(14 AU) (McAlister et al. 1987) and HIP 57269, resolved by Hipparcos at
![]() arcsec (21 AU).
arcsec (21 AU).
Attempting to detect more visual binaries, we used the original Tycho-2 observations and the extant double star reduction software (Høg et al. 2000b) for non-Hipparcos members. Normally, due to the poor photon statistics and broad slit response function of the Tycho instrument, resolutions of stars at separations below about 0.6 arcsec and with component magnitudes fainter than 11.5would be reckoned ambiguous. Fortunately, some of the stars in the present selection happen to be close to the so-called nodes of the scanning law of the satellite, and thus received a number of observations much above the average (120) and well-distributed in position angle. Still, the results given below for three stars should be taken with caution, because the conditions are really challenging the Tycho instrument capabilities.
The star TYC 7190-2111-1 = TWA 7, with 188 Tycho observations, is resolved
into two components at angular separation 1.78 arcsec (60 AU)
and position angle
![]() .
The estimated magnitudes are
.
The estimated magnitudes are
![]() ,
,
![]() for the primary, and
for the primary, and
![]() ,
,
![]() for the secondary.
for the secondary.
The star TYC 7760-0835-1, with 249 Tycho observations, is resolved
at angular separation 0.32 arcsec (44 AU) and position angle
![]() .
The estimated magnitudes are
.
The estimated magnitudes are
![]() ,
,
![]() for the
primary, and
for the
primary, and
![]() ,
,
![]() for the secondary.
for the secondary.
The star TYC 8234-2856-1, with 273 Tycho observations, is resolved
at angular separation 0.42 arcsec (58 AU) and position angle
![]() .
The estimated magnitudes are
.
The estimated magnitudes are
![]() ,
,
![]() for the
primary, and
for the
primary, and
![]() ,
,
![]() for the secondary.
for the secondary.
Taking into account all separations, the estimated CSF for the group is 0.42, in good agreement with the assumed youth, and, quite likely, more double stars are to be resolved.
For the 31 stars listed
in Table 1, Model I yields a convergent point at
![]() .
In a few iterations, we found a
.
In a few iterations, we found a
![]() km
s-1, which together with the above mentioned convergent point, provides
only 10 deviants with
km
s-1, which together with the above mentioned convergent point, provides
only 10 deviants with
![]() among the 31 stars. This
matches the expected number of deviants for a normal distribution of errors.
among the 31 stars. This
matches the expected number of deviants for a normal distribution of errors.
Using the Hipparcos trigonometric parallaxes for the 17 HIP stars in the
sample, we calibrate ![]() .
The formal precision of the Hipparcos
distances is typically 10 to 15 percent, while the formal precision
of kinematic distances (from
.
The formal precision of the Hipparcos
distances is typically 10 to 15 percent, while the formal precision
of kinematic distances (from
![]() km s-1) is about 4 percent. The result is a total velocity of
22 kms-1.
km s-1) is about 4 percent. The result is a total velocity of
22 kms-1.
The inadequacy of this basic model (Model I) emerges when one
starts to compare the predicted radial velocities
![]() with the observed ones. Webb & Zuckerman (2000) determined a common
radial velocity of
with the observed ones. Webb & Zuckerman (2000) determined a common
radial velocity of ![]() km s-1 for several very young stars
around TW Hya. Sterzik et al. (1999) found a little larger +13.5 for
TW Hya. These measures are obviously in disagreement with velocities
in the interval +3.2 to +5.8 predicted from Model I for the original
members TWA 1, 2, 4 and 5. We could not reconcile the observed radial velocities
with the Tycho-2 proper motions even when only a few originally known
members were involved. In order to reproduce much higher radial velocities,
the true convergent point ought to be considerably closer to the TWA location
than the spot where the proper motions do cross. It is concluded, that
the observed motions of the TWA stars are somewhat diverted from the true
direction of the centroid motion, most likely by a superimposed expansion
component. Another option would be an outward velocity
component independent of the distance, but in such a model the stars would
not be co-eval.
km s-1 for several very young stars
around TW Hya. Sterzik et al. (1999) found a little larger +13.5 for
TW Hya. These measures are obviously in disagreement with velocities
in the interval +3.2 to +5.8 predicted from Model I for the original
members TWA 1, 2, 4 and 5. We could not reconcile the observed radial velocities
with the Tycho-2 proper motions even when only a few originally known
members were involved. In order to reproduce much higher radial velocities,
the true convergent point ought to be considerably closer to the TWA location
than the spot where the proper motions do cross. It is concluded, that
the observed motions of the TWA stars are somewhat diverted from the true
direction of the centroid motion, most likely by a superimposed expansion
component. Another option would be an outward velocity
component independent of the distance, but in such a model the stars would
not be co-eval.
The parameters of the centroid in the second, more viable model are: distance
![]() pc, position
pc, position
![]() .
Thus, the centroid is at 16 pc
from the historically first member
TW Hya. The total mass of the 31 stars is
.
Thus, the centroid is at 16 pc
from the historically first member
TW Hya. The total mass of the 31 stars is
![]() .
The estimated
velocity dispersion
.
The estimated
velocity dispersion
![]() km s-1 and the expansion rate
km s-1 and the expansion rate
![]() kms-1 pc-1. The centroid velocity
vector in the galactic coordinates
kms-1 pc-1. The centroid velocity
vector in the galactic coordinates![]() is
(U,V,W)=(-12.7,-20.6,-6.2) kms-1.
The peculiar motion of TWA is
(-2.7,-15.3,+1.0)kms-1, assuming a peculiar velocity of the Sun of
(10.0,5.3,7.2)
kms-1 (Dehnen & Binney 1998). This implies that the group moves at 16 km
s-1 almost directly
away from the Sun with respect
to the local standard of rest, and that it lags behind the local
Galactic rotation. Such an outward motion is characteristic of the nearby Sco-Cen
OB associations in the 4th Galactic quadrant.
is
(U,V,W)=(-12.7,-20.6,-6.2) kms-1.
The peculiar motion of TWA is
(-2.7,-15.3,+1.0)kms-1, assuming a peculiar velocity of the Sun of
(10.0,5.3,7.2)
kms-1 (Dehnen & Binney 1998). This implies that the group moves at 16 km
s-1 almost directly
away from the Sun with respect
to the local standard of rest, and that it lags behind the local
Galactic rotation. Such an outward motion is characteristic of the nearby Sco-Cen
OB associations in the 4th Galactic quadrant.
The estimated velocity dispersion of 0.8 kms-1 in one component
puts the TWA in between gravitationally bound open clusters like the
Hyades with
![]() to 0.4 kms-1 (Gunn et al. 1988; Perryman et al. 1998;
Makarov et al. 2000) and the Pleiades with
to 0.4 kms-1 (Gunn et al. 1988; Perryman et al. 1998;
Makarov et al. 2000) and the Pleiades with
![]() to 0.6 kms-1
(Jones 1970; Geffert et al. 1995), and gravitationally unbound OB associations
like Scorpius OB2 with
to 0.6 kms-1
(Jones 1970; Geffert et al. 1995), and gravitationally unbound OB associations
like Scorpius OB2 with
![]() to 1.5 kms-1 (de Bruijne 1999).
However, there is a possibility of bias in our estimation, coming from the
limit of
to 1.5 kms-1 (de Bruijne 1999).
However, there is a possibility of bias in our estimation, coming from the
limit of
![]() in the selection of proper motion candidates (Sect. 4.1).
In order to evaluate the size of the bias, we conducted a simple simulation,
introducing various
in the selection of proper motion candidates (Sect. 4.1).
In order to evaluate the size of the bias, we conducted a simple simulation,
introducing various ![]() into Model I for the given sample of
stars. Of the 31 stars, none are expected to miss the
into Model I for the given sample of
stars. Of the 31 stars, none are expected to miss the
![]() circle at
circle at
![]() kms-1, only 4 at 1.5, 16 at 1.8 and all at 2.0.
The true dispersion is therefore unlikely to be in the interval 0.9 to
1.5 kms-1, where our sample appears to be complete. But if the true
dispersion is in 1.5 to 2.0 kms-1, a severe underestimation may
occure. If the true dispersion is greater or equal than 2.0 kms-1our selection is meaningless.
kms-1, only 4 at 1.5, 16 at 1.8 and all at 2.0.
The true dispersion is therefore unlikely to be in the interval 0.9 to
1.5 kms-1, where our sample appears to be complete. But if the true
dispersion is in 1.5 to 2.0 kms-1, a severe underestimation may
occure. If the true dispersion is greater or equal than 2.0 kms-1our selection is meaningless.
The expansion rate of 0.12 km s-1 pc-1 defines a dynamic age of 8.3 Myr. This agrees remarkably well with the previous estimations for 11 T Tauri members in (Webb et al. 1999). Nine of their 11 members are located between the 106 and 107 yr isochrones (Fig. 3 loc cit), and only two systems appear to be older (TWA 6 and 9). A spread of ages of several Myr can not be precluded.
The discovery that very young X-ray active late type stars in the Solar
vicinity are associated with the Gould Belt (Guillout et al. 1998) changed our
conception of this largely mysterious formation. It becomes clear now
that the Belt is rather well filled with dim late type stars of young age,
so a Gould Disk or Plane would be a better name. The near edge (if there is
any) of the Sco-Cen OB associations in the 4th Galactic quadrant appears
to be clumpy, comprising open clusters like IC 2391 and IC 2602 and loose
moving groups like the Carina-Vela (Makarov & Urban 2000). It was proposed that the
Carina-Vela group is a swirl or an extension of the nearby Lower Centaurus
Crux association, reaching very close to the Sun. The TWA may be a similar
extension of the LCC, situated to the north of the Carina-Vela group. In
our sample of probable kinematic members of TWA, we do not see any clear
separation from the LCC in distances. However, the space velocity of LCC
is approximately
(U,V,W)=(-12,-13,-7) km s-1 (de Zeeuw et al. 1999), i.e., deviates
from our estimate by ![]() 8 kms-1 in the V component, that is mostly
in the line-of-sight direction. The reason for this difference might be that
our uniform expansion kinematic model does not extrapolate to the more distant
LCC. Our model predicts a radial velocity of
8 kms-1 in the V component, that is mostly
in the line-of-sight direction. The reason for this difference might be that
our uniform expansion kinematic model does not extrapolate to the more distant
LCC. Our model predicts a radial velocity of ![]() for the LCC,
while the observed value is around +12.
If uniform expansion is common for young stellar associations in the
Gould Belt, its rate may vary among different groups in accordance with
their age. The recent determination of the K term of the systematic
velocity field, representing uniform isotropic expansion, resulted in a value
of
for the LCC,
while the observed value is around +12.
If uniform expansion is common for young stellar associations in the
Gould Belt, its rate may vary among different groups in accordance with
their age. The recent determination of the K term of the systematic
velocity field, representing uniform isotropic expansion, resulted in a value
of
![]() kms-1 kpc-1 for Gould Belt stars younger than
30 Myr at distances 100 to 600 pc (Torra et al. 2000). This clearly shows that
the Gould Belt is not expanding from a single point, but was rather born
as a large structure. Different parts of the structure may therefore have
varying kinematics and age. Interestingly, Torra et al.'s Fig. 14 suggests,
that the Gould Belt expansion rate continues to grow rapidly with decreasing
distance from the Sun, but, unfortunately, no sufficient data is available
yet for the close vicinity within 100 pc. If this trend proves to be real,
the difference of 8 kms-1 in outwards motion between the LCC and TWA
may be a part of the general pattern, rather than a peculiarity.
kms-1 kpc-1 for Gould Belt stars younger than
30 Myr at distances 100 to 600 pc (Torra et al. 2000). This clearly shows that
the Gould Belt is not expanding from a single point, but was rather born
as a large structure. Different parts of the structure may therefore have
varying kinematics and age. Interestingly, Torra et al.'s Fig. 14 suggests,
that the Gould Belt expansion rate continues to grow rapidly with decreasing
distance from the Sun, but, unfortunately, no sufficient data is available
yet for the close vicinity within 100 pc. If this trend proves to be real,
the difference of 8 kms-1 in outwards motion between the LCC and TWA
may be a part of the general pattern, rather than a peculiarity.
A small group of young stars like the TWA, could conceivably be born in a small compact cloud generally associated with the much larger Gould Belt structure. At the star formation burst, the cloud exploded, or started to expand internally, so that the new-born stars acquired a spread of outwards motions with respect to the centre of mass. The remaining diffused matter was also involved in the expansion, and it has become so thin by now that it is very difficult to detect. It would be very important to find out if internal expansion is also present in other nearby pre-main-sequence and OB associations.
A scrutiny of radial velocities of the 31 selected stars should help to weed out remaining interlopers in the sample and to test our assumption of an isotropic uniform expansion. If the rate of expansion turns out to be rather distance-independent, the more distant stars from the centre should be systematically older than the T Tauri members in the close vicinity of TW Hya.
Acknowledgements
This work was supported by the Danish Space Board. We have made use of the Simbad data base operated at the Centre de Données Astronomiques de Strasbourg.