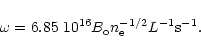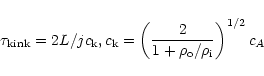A&A 368, 1095-1107 (2001)
DOI: 10.1051/0004-6361:20010073
Active region oscillations
E. O'Shea 1 - D. Banerjee 2 - J. G. Doyle 3 - B. Fleck 4 - F. Murtagh 5
1 - ESA Space Science Department, ESTEC Solar System Division,
Keplerlaan 1, 2201 AZ, Noordwijk,
The Netherlands
2 -
Centre for Plasma Astrophysics, K.U. Leuven, Celestijnenlaan 200 B, 3001,
Heverlee, Belgium
3 -
Armagh Observatory, College Hill, Armagh BT61 9DG, N. Ireland
4 -
ESA Space Science Department, NASA/GSFC, Mailcode 682.3, Greenbelt,
MD 20771, USA
5 -
School of Computer Science, The Queen's University of Belfast,
Belfast BT7 1NN, N. Ireland
Received 21 February 2000 / Accepted 4 January 2001
Abstract
We report here on an investigation of high
frequency oscillations in active regions, carried out using high cadence
observations of O V 629 Å, Mg IX 368 Å and Fe XVI
335 Å with the Coronal Diagnostic Spectrometer ( CDS) on SOHO.
Using the techniques of wavelet analysis on various temporal series
datasets, we find that certain oscillation frequencies are favoured for each
line.
We find furthermore that a  5 min oscillation signature is commonly
present in all lines, suggesting a coupling of the photospheric driver with
the transition region and coronal loop modes.
We report on the tendency for higher
frequency oscillations to be present at lower intensity values, suggesting
that higher frequency oscillations occur in interloop regions or at loop
boundaries, possibly as a result of some resonant absorption process. In
addition, we find that the coronal lines of Fe XVI
and Mg IX show more significant oscillations in the velocity than in
the intensity, which suggests that in the velocity we measure additional
non-compressive wave modes not visible in the intensity. As this effect is
not seen in the transition region line of O V it would seem that these
additional non-compressive modes are produced in and limited to the corona.
We suggest that there are two main mechanisms responsible for the observed
oscillations; either resonant Alfvén and/or fast kink waves or
propagating slow magnetoacoustic waves, both present in coronal loops.
5 min oscillation signature is commonly
present in all lines, suggesting a coupling of the photospheric driver with
the transition region and coronal loop modes.
We report on the tendency for higher
frequency oscillations to be present at lower intensity values, suggesting
that higher frequency oscillations occur in interloop regions or at loop
boundaries, possibly as a result of some resonant absorption process. In
addition, we find that the coronal lines of Fe XVI
and Mg IX show more significant oscillations in the velocity than in
the intensity, which suggests that in the velocity we measure additional
non-compressive wave modes not visible in the intensity. As this effect is
not seen in the transition region line of O V it would seem that these
additional non-compressive modes are produced in and limited to the corona.
We suggest that there are two main mechanisms responsible for the observed
oscillations; either resonant Alfvén and/or fast kink waves or
propagating slow magnetoacoustic waves, both present in coronal loops.
Key words: Sun: UV radiation: Sun: oscillations: Sun: waves: Sun: corona
It is known from observations that the solar atmosphere is threaded with
strong magnetic fields in the form of flux tubes, which form coronal loops,
the
transverse dimensions of which are much shorter than the longitudinal ones.
The study of oscillations from these loops can provide clues to the
understanding of coronal heating. In the literature, different theoretical
mechanisms have been
suggested as possible candidates for coronal heating (see
reviews by e.g. Hollweg 1990; Narain & Ulmschneider 1996). Observations of
coronal oscillations can provide a useful diagnostic tool to test the
validity of these theoretical predictions. The oscillations are observed as
either the intensity oscillations of a spectral line or of the continuum or
as the velocity oscillations in the Doppler profiles, each providing separate
but distinct clues to the heating from different parts of the corona.
In this paper we will concentrate on those oscillations found in coronal
active region datasets.
A large number of attempts have been made to detect oscillations in the
corona. However, despite the existence of a large body of literature, the
results are not conclusive. Koutchmy et al. (1983) reported Doppler velocity
oscillations
with periods near 300, 80 and 43 s, but found no prominent intensity
oscillations from the measurement of the green coronal line at 5303 Å.
McKenzie & Mullan (1997) reported loop oscillations in
YOHKOH/SXT images, revealing marginal oscillations in brightness with
amplitudes of  1% and periods of 10-62 s. Ireland et al. (1999)
presented an analysis of active region oscillations for several
transition region and coronal lines as observed by CDS on SOHO.
Cowsik et al. (1999) reported on high frequency, low-amplitude continuum
intensity oscillations in the solar corona during the total solar eclipse of
26 February 1998. Recently, Aschwanden et al. (1999) detected spatial
oscillations of coronal loops with TRACE. These loops having periods
ranging from 258 to 320 s were interpreted as kink mode
magnetohydrodynamic standing waves. They also compiled a very useful
summary of previous temporal
observations, methods and theoretical interpretations in a tabular
format (see their Table 1). Using TRACE, Nakariakov et al. (1999)
observed a decaying transversal oscillation of a long, thin, bright
coronal loop in the Fe XI 171 Å emission line. These oscillations
were excited by a solar flare in an adjacent active region. The decay time
of the oscillation was 14.5
1% and periods of 10-62 s. Ireland et al. (1999)
presented an analysis of active region oscillations for several
transition region and coronal lines as observed by CDS on SOHO.
Cowsik et al. (1999) reported on high frequency, low-amplitude continuum
intensity oscillations in the solar corona during the total solar eclipse of
26 February 1998. Recently, Aschwanden et al. (1999) detected spatial
oscillations of coronal loops with TRACE. These loops having periods
ranging from 258 to 320 s were interpreted as kink mode
magnetohydrodynamic standing waves. They also compiled a very useful
summary of previous temporal
observations, methods and theoretical interpretations in a tabular
format (see their Table 1). Using TRACE, Nakariakov et al. (1999)
observed a decaying transversal oscillation of a long, thin, bright
coronal loop in the Fe XI 171 Å emission line. These oscillations
were excited by a solar flare in an adjacent active region. The decay time
of the oscillation was 14.5 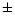 2.7 min for an
oscillation with a frequency of 3.9
2.7 min for an
oscillation with a frequency of 3.9 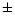 0.13 mHz.
0.13 mHz.
In this paper we present time series observations of O V
629 Å, Mg IX 368 Å and Fe XVI 335 Å lines in active
regions, as observed by the Coronal Diagnostic Spectrometer ( CDS)
onboard SOHO. With these observations and the methods of wavelet
analysis we examine intensity and velocity oscillations
for evidence of different wave modes.
The results of our analysis are then discussed and compared to different
theoretical models available in the literature.
Table 1:
Details of the temporal series observations
| Dates |
Datasets |
Pointing |
Start |
End |
| |
|
X, Y |
UT |
UT |
| 24 July 1997 |
s8486r00 |
279, 358 |
19:17 |
19:51 |
| |
s8486r01 |
301, 358 |
19:51 |
20:25 |
| |
s8486r02 |
249, 357 |
20:25 |
20:59 |
| 25 July 1997 |
s8490r00 |
439, 371 |
11:30 |
12:04 |
| |
s8490r02 |
387, 377 |
12:37 |
13:11 |
| |
s8490r03 |
367, 375 |
13:11 |
13:45 |
| 13 April 1998 |
s10850r03 |
-311, 353 |
07:53 |
08:15 |
| |
s10850r04 |
-311, 353 |
08:15 |
08:37 |
| |
s10850r05 |
-311, 353 |
08:37 |
09:00 |
| 15 July 1999 |
s16831r00 |
438, 296 |
13:03 |
13:37 |
| |
s16831r01 |
438, 296 |
13:37 |
14:10 |
| 15 July 1999 |
s16833r00 |
488, 208 |
14:25 |
14:58 |
| |
s16833r01 |
488, 208 |
14:58 |
15:32 |
| 16 July 1999 |
s16844r00 |
661, 320 |
21:15 |
21:48 |
| |
s16844r01 |
661, 320 |
21:48 |
22:22 |
| 16 July 1999 |
s16846r00 |
711, 225 |
22:36 |
23:10 |
| |
s16846r01 |
711, 225 |
23:10 |
23:43 |
2 Observations and data reduction
To obtain these observations we used the Coronal Diagnostic Spectrometer
( CDS) onboard the SOHO satellite and, in particular, the
Normal Incidence Spectrometer ( NIS). The data discussed
here were obtained from three observing periods in 1997, 1998 and 1999.
Further details of these observations are summarised in Table 1.
The 1997 and 1999 data were obtained using the observing sequence
CHROM_ N4, with a slit size of 4  119 arcsec2 and a
cadence of
119 arcsec2 and a
cadence of  10 s, while the 1998 data was obtained using the
CHROM_ HI observing sequence, with a slit size of 4
10 s, while the 1998 data was obtained using the
CHROM_ HI observing sequence, with a slit size of 4  89
arcsec2 and a cadence of
89
arcsec2 and a cadence of  7 s. These sequences recorded data
for three spectral lines, namely O V 629 Å
(log
7 s. These sequences recorded data
for three spectral lines, namely O V 629 Å
(log
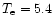 K), Mg IX 368 Å (log
K), Mg IX 368 Å (log
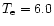 K) and Fe XVI 335 Å (log
K) and Fe XVI 335 Å (log
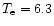 K). All datasets from each of
the three years contained 200 time frames. The eight datasets from
15-16 July 1999 were obtained after the recovery of SOHO and so the
lines show the characteristic broadened wings. This broadening has the
effect of blending the Mg IX 368 Å line with that of the
nearby Mg VII 367 Å line. We were able to fit the Mg IX
component of this blend satisfactorily by using a double Gaussian, and by
fixing the position of the Mg VII line.
In all other cases fitting was done using a single Gaussian as the lines
were found to be generally symmetric.
The fitting was done using the updated CFIT software available in
the CDS software tree.
K). All datasets from each of
the three years contained 200 time frames. The eight datasets from
15-16 July 1999 were obtained after the recovery of SOHO and so the
lines show the characteristic broadened wings. This broadening has the
effect of blending the Mg IX 368 Å line with that of the
nearby Mg VII 367 Å line. We were able to fit the Mg IX
component of this blend satisfactorily by using a double Gaussian, and by
fixing the position of the Mg VII line.
In all other cases fitting was done using a single Gaussian as the lines
were found to be generally symmetric.
The fitting was done using the updated CFIT software available in
the CDS software tree.
Rotational compensation was not used for any of the temporal series and the
data was thus obtained in a sit-and-stare mode.
Due to the relatively large width of the slit (4 arcsec), and following the
discussion of Doyle et al. (1998) for Fourier power spectra, we estimate that
the effect of the sit-and-stare mode on the resulting (wavelet) power would
be to spread the power over a frequency range of at most
 1 mHz, depending on the size of the source and location of the active
region.
1 mHz, depending on the size of the source and location of the active
region.
Using the standard CDS software procedure VDS_ CALIB we
de-biased and flat fielded the data. The resulting data after running this
procedure were in units of photon-events/pixel/sec. Multiplying by the
exposure time yielded units of photon-events/pixel. The data was cleaned of
cosmic ray hits by using the CDS software procedure CDS_ CLEAN.
Slant and tilt corrections were applied to the data using another CDS
software procedure, NIS _ROTATE. To improve the signal-to-noise, the
data was binned by three pixels along the slit, in effect creating new pixels
of  5
5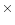 4 arcsec2.
4 arcsec2.
We subsequently obtained the total number of photon-events in a line by
integrating under the fitted line profile. Note that in
Sect. 3 these photon-events are referred to as "counts''. The
velocity values presented in this paper are relative velocities, that is,
they are calculated relative to an averaged profile summed over all pixels
along the slit and all time frames. This averaged profile was fitted by a
Gaussian and its "rest'' wavelength determined. All other profiles were then
measured relative to this "rest'' wavelength.
No absolute calibration exists for the velocity scale, so that the derived
velocities are therefore merely indicative of the presence of line shifts.
![\begin{figure}
\par\includegraphics[width=17.2cm,height=7.4cm,clip]{h2037_fig1.ps}
\end{figure}](/articles/aa/full/2001/12/aah2037/Timg7.gif) |
Figure 1:
a) The intensity time series, the corresponding wavelet power spectrum and
its global wavelet spectrum for the O V 629 Å line at pixel position 3 in
dataset s8486r02. b) The corresponding plots for the O V 629 Å
velocity values |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=17.2cm,height=7.4cm,clip]{h2037_fig2.ps}
\end{figure}](/articles/aa/full/2001/12/aah2037/Timg8.gif) |
Figure 2:
a) The intensity time series, the corresponding wavelet power spectrum and
its global wavelet spectrum for the Mg IX 368 Å line at pixel position 22 in
dataset s8490r03. b) The corresponding plots for the Mg IX 368 Å
velocity values |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=17.2cm,height=7.4cm,clip]{h2037_fig3.ps}
\end{figure}](/articles/aa/full/2001/12/aah2037/Timg9.gif) |
Figure 3:
a) The intensity time series, the corresponding wavelet power spectrum and
its global wavelet spectrum for the Fe XVI 335 Å line at pixel position
11 in dataset s16844r00. b) The corresponding plots for the Fe XVI
335 Å velocity values |
| Open with DEXTER |
The localised (in time)
nature of wavelet transforms allows the study of the duration of any
statistically significant oscillations as well as their frequency/period. We
use the software provided by Torrence & Compo (1998),
and we refer the reader to this paper for further details on the techniques
of wavelet analysis involved. This wavelet software utilises
the Morlet wavelet.
It should be noted that the wavelet transform suffers from edge effects at
both ends of the time series. The region in which these effects are
important is defined by the "cone of influence'' ( COI). We use the
definition of COI given by Torrence & Compo (1998) but see also
Meyers et al. (1993) for an alternative discussion.
To remove high frequency noise present in the data wavelet-based noise
filtering was used. The CDS data used contains Poisson (detector) and
Gaussian (fitting) noise components. This was modelled as Gaussian overall,
on the
grounds that (i) asymptotically Poisson noise becomes Gaussian, and
(ii) the addition of Gaussians remains Gaussian. The principle of this is
wavelet filtering is similar to filtering in Fourier space. First the signal
is decomposed into wavelet space, the data is then filtered at each of the
wavelet resolution levels (or scales), and then the signal is recomposed.
This filtering was done using a noise estimation method similar to that
discussed in Starck & Murtagh (1998). That is, the standard deviation was
estimated at each wavelet scale and hard thresholding was carried out in
wavelet space, using a 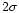 detection (
detection ( 95%) level.
The particular wavelet transform used for this is a redundant transform known
as the B3 spline à trous wavelet transform. The wavelet
mother function is rather like a Mexican hat, with a high central
bump, negative side lobes, and is point symmetric.
Further details and a background on many applications of this transform can
be found in Starck et al. (1998). The associated MR/1 package was used in
this work.
95%) level.
The particular wavelet transform used for this is a redundant transform known
as the B3 spline à trous wavelet transform. The wavelet
mother function is rather like a Mexican hat, with a high central
bump, negative side lobes, and is point symmetric.
Further details and a background on many applications of this transform can
be found in Starck et al. (1998). The associated MR/1 package was used in
this work.
The statistical significance of the resulting filtered data was estimated by
using a Monte Carlo or randomisation method. The advantage of using the
randomisation method is that it is distribution free or non-parametric, i.e.
it is not limited or constrained by any specific noise model, such as
Poisson, Gaussian, etc. We follow the method of Fisher randomisation as
outlined by Nemec & Nemec (1985) and implemented in the UK Starlink
software package, PERIOD (Dhillon & Privett 1997).
We shall briefly discuss the method used in more detail below. The
randomisation test is based on the assumption that, if there is no periodic
signal in the time series data, then the measured values (intensity,
velocity, etc.) are independent of their observation times. For example, the
intensities I1, I2,... In, observed at
times t1, t2,... tn, are just as likely to have occurred in
any other order Ir(1), Ir(2),... Ir(n), where n is the
total number of observations and r(1), r(2),... r(n) is a random
permutation of the subscripts 1, 2,... n. By using the maximum power peak in
the global wavelet spectrum, which is just the average of the wavelet power
over time and similar to a smoothed Fourier power
spectrum (Torrence & Compo 1998), at the "test statistic'' (see Dhillon & Privett 1997) it was possible to test
the hypothesis that there was no periodicity in our data. Ideally this would
have been done by evaluating the peak power from the original ordering of
the time series data and then comparing it to the peak powers evaluated from
the n! equally likely permutations of the time series data. The proportion
of permutations that gave a value greater or equal to the peak power of the
original time series would then provide an estimate of p, the probability
that no periodic component is present in the data, i.e. a large value
of p suggests that there is little or no real periodicity in the data
whereas a small value of p suggests that the measured periodicity is
likely to be real. In practise n! is usually so large that it is not
possible to do this, due to computational and time constraints, and so the
peak powers are generally calculated for only a random sample of m
permutations. By carrying out this approximation, for a random sample of 150
permutations, we were able to obtain a reliable estimate of p. For
a sample of 150 random permutations the standard errors of the p values
are no greater than 0.04 (Nemec & Nemec 1985). Of course, the larger the
number of permutations chosen, m, the lower the standard error of the p
value.
The probability levels for this work are written as the values
of
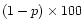 ,
i.e. the percentage probability that periodic
components are present in the data. We arbitrarily choose a value
of 95% as the lowest acceptable probability level. That is, only global
wavelet spectra that show a power peak with a probability greater
than 95% are deemed to be due to "real'' oscillations in the time series
sequences.
Occasionally the estimated p value can have a value of zero, i.e.
there being an almost zero chance that the observed time series oscillations
could have occurred by chance. In this case, and following
Nemec & Nemec (1985), the 95% confidence interval can be obtained using
the binomial distribution, and is given by 0.0 < p < 0.01, that is,
the probability (
,
i.e. the percentage probability that periodic
components are present in the data. We arbitrarily choose a value
of 95% as the lowest acceptable probability level. That is, only global
wavelet spectra that show a power peak with a probability greater
than 95% are deemed to be due to "real'' oscillations in the time series
sequences.
Occasionally the estimated p value can have a value of zero, i.e.
there being an almost zero chance that the observed time series oscillations
could have occurred by chance. In this case, and following
Nemec & Nemec (1985), the 95% confidence interval can be obtained using
the binomial distribution, and is given by 0.0 < p < 0.01, that is,
the probability (
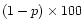 )
in this case is between 99-100%.
)
in this case is between 99-100%.
3 Results
In this section we present the results
of a wavelet analysis carried out on the different active region datasets.
In Sect. 3.1, specific examples for selected regions are discussed
while in Sect. 3.2 a detailed statistical analysis of all observed
intensity and velocity oscillations is presented.
3.1 Examples of wavelet analysis
In Fig. 1 we plot the intensity and velocity time series, wavelet
spectra and the global wavelet spectra for the O V line, at pixel
position 3 in dataset s8486r02. In the time series of the intensity and
velocity the (wavelet) filtered time series are shown as the bold
line, while the unfiltered original is shown as the dotted grey line.
In the intensity time
series in Fig. 1a we can see a strong 5-7 min period
oscillating group. The frequencies corresponding to these oscillations are
clearly shown in the wavelet spectrum plot underneath, where the darker
colours indicate higher powers (the colour bar is inverted). Note that we do
not consider frequencies lower than 2 mHz, as they are located in the
COI and are therefore potentially affected by edge effects. From the
wavelet spectrum plot we can see that the oscillation changes from being
a  3.0 mHz (
3.0 mHz ( 5 min) oscillation for the first 15 min to a
longer 2.0-2.3 mHz (
5 min) oscillation for the first 15 min to a
longer 2.0-2.3 mHz ( 7 min) oscillation for the last 15 min. In
the global wavelet spectrum, which is the average of the wavelet spectrum
over time (see Torrence & Compo 1998), the main
oscillation frequency, corresponding to the maximum power, is measured as
2.3 mHz, or a period of 7 min. The second peak in the global wavelet
spectrum, however, indicates that there is another weaker oscillation
frequency present in this dataset at a frequency of 4.1 mHz or
7 min) oscillation for the last 15 min. In
the global wavelet spectrum, which is the average of the wavelet spectrum
over time (see Torrence & Compo 1998), the main
oscillation frequency, corresponding to the maximum power, is measured as
2.3 mHz, or a period of 7 min. The second peak in the global wavelet
spectrum, however, indicates that there is another weaker oscillation
frequency present in this dataset at a frequency of 4.1 mHz or  4 min. Both these oscillations give probabilities of 99-100% using the
randomisation method and therefore both of them are considered statistically
significant (i.e. they are both
4 min. Both these oscillations give probabilities of 99-100% using the
randomisation method and therefore both of them are considered statistically
significant (i.e. they are both 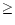 95%). In Fig. 1b, the
time series plot of the velocity clearly shows
oscillations at a much higher frequency. This is confirmed in the wavelet
spectrum where the dark contours indicate oscillations present between 3.0
and 20 mHz (
95%). In Fig. 1b, the
time series plot of the velocity clearly shows
oscillations at a much higher frequency. This is confirmed in the wavelet
spectrum where the dark contours indicate oscillations present between 3.0
and 20 mHz ( 5 min to 50 s periods). From the global wavelet
spectrum at
the right the main frequency of oscillation is measured from the maximum
power peak to be 4.1 mHz, with a second weaker oscillation peak at 14.4 mHz.
Note that in this case the randomisation test gives a probability of 95%
for the 4.1 mHz oscillation, but only 60% for the 14.4 mHz oscillation. As
such only the 4.1 mHz oscillation is considered as being statistically
significant here.
5 min to 50 s periods). From the global wavelet
spectrum at
the right the main frequency of oscillation is measured from the maximum
power peak to be 4.1 mHz, with a second weaker oscillation peak at 14.4 mHz.
Note that in this case the randomisation test gives a probability of 95%
for the 4.1 mHz oscillation, but only 60% for the 14.4 mHz oscillation. As
such only the 4.1 mHz oscillation is considered as being statistically
significant here.
In Fig. 2 we carry out the same analysis for the Mg IX line
at pixel position 22 in dataset s8490r03. Again in the plots of the
intensity and
velocity time series the filtered results are plotted as the bold line, while
the unfiltered results are shown as a grey dotted line. In the intensity
time series plot and below
it in the wavelet spectrum plot it is possible to see that the main
oscillations are occurring at frequencies of between 7.0 and  20 mHz.
From the global wavelet spectrum the main frequency of
oscillation for this line, measured from the peak power, is at 15.7 mHz
(
20 mHz.
From the global wavelet spectrum the main frequency of
oscillation for this line, measured from the peak power, is at 15.7 mHz
( 1.1 min), with a
secondary oscillation at 7.5 mHz (
1.1 min), with a
secondary oscillation at 7.5 mHz ( 2.2 min). These frequencies are
considerably larger than those found in the O V line. However, from
the randomisation test the 15.7 mHz oscillation only has a probability of
81% and so is not considered statistically significant. The secondary
oscillation of 7.5 mHz, on the other hand, has a probability of 96% and so
is considered statistically significant.
2.2 min). These frequencies are
considerably larger than those found in the O V line. However, from
the randomisation test the 15.7 mHz oscillation only has a probability of
81% and so is not considered statistically significant. The secondary
oscillation of 7.5 mHz, on the other hand, has a probability of 96% and so
is considered statistically significant.
If we look at the time series plot of the velocity, in
Fig. 2b, we can see that it too has
a high frequency of oscillation. The main oscillation frequency can be seen
from the wavelet spectrum plot to be between 10 and 20 mHz. Note that
these high frequency oscillations occur in short bursts lasting no more
than  5 min. From the global wavelet spectrum the main frequency of
oscillation, measured from the main peak is at 13.8 mHz (
5 min. From the global wavelet spectrum the main frequency of
oscillation, measured from the main peak is at 13.8 mHz ( 1.2 min),
with a probability of 97% from the randomisation test. The secondary
oscillation frequency is however much lower,
at a value of 2.1 mHz (
1.2 min),
with a probability of 97% from the randomisation test. The secondary
oscillation frequency is however much lower,
at a value of 2.1 mHz ( 8 min), with a probability of 99-100%.
8 min), with a probability of 99-100%.
In Fig. 3 we carry out a similar analysis for the Fe XVI
line at
pixel position 11 in dataset s16844r00. In the plot of the time series for
the intensity shown in Fig. 3a, a rapidly oscillating group can
be seen for the first 5 min. This is picked up in the wavelet spectrum
plot as the dark contour at a little under 20 mHz. Another high frequency
event is recorded at 25 min, again lasting for only a few minutes. In
the global wavelet plot the average of these frequencies turns out to be at
15.0 mHz, with a probability of 97%.
However, the main oscillation frequency in this time series, as measured by
the global wavelet spectrum, is at a lower
frequency of 4.5 mHz (or a period of  3.7 min). Interestingly this
lower frequency oscillation occurs between the times of the higher frequency
oscillations, i.e. between a time of 5 and 25 min, as can be seen from
the wavelet spectrum plot in Fig. 3a. However, this lower
frequency of 4.5 mHz is found not to be statistically significant having a
probability of only 87%.
3.7 min). Interestingly this
lower frequency oscillation occurs between the times of the higher frequency
oscillations, i.e. between a time of 5 and 25 min, as can be seen from
the wavelet spectrum plot in Fig. 3a. However, this lower
frequency of 4.5 mHz is found not to be statistically significant having a
probability of only 87%.
In Fig. 3b
we carry out the same analysis for the corresponding Fe XVI velocity.
From the wavelet spectrum plot we can see that the velocity time series shows
little high frequency oscillations until a time of  15 min, when a
strong oscillation at
15 min, when a
strong oscillation at  9 mHz begins, that then last for
9 mHz begins, that then last for  5 min.
Slightly higher oscillations are then present for the rest of the observation
time. The main frequency of oscillation is at 9.7 mHz (
5 min.
Slightly higher oscillations are then present for the rest of the observation
time. The main frequency of oscillation is at 9.7 mHz ( 1.7 min),
with a probability of 95%,
as measured from the strongest peak in the global wavelet spectrum, with the
secondary frequency of oscillation at 2.2 mHz (
1.7 min),
with a probability of 95%,
as measured from the strongest peak in the global wavelet spectrum, with the
secondary frequency of oscillation at 2.2 mHz ( 7.5 min), with a
probability of 99-100%.
7.5 min), with a
probability of 99-100%.
It will be noticed from these few examples that the same
frequencies are generally not present in the intensity and the velocity
oscillations of each region. This is perhaps an indication of different wave
modes being separately responsible for the intensity and velocity
oscillations.
![\begin{figure}
\par\includegraphics[width=16.5cm,height=7.4cm,clip]{h2037_fig4.ps}
\end{figure}](/articles/aa/full/2001/12/aah2037/Timg13.gif) |
Figure 4:
The summed counts over time of the intensity time series versus
the primary frequencies of oscillation found in
these time series for Fe XVI 335 Å (left panel), Mg IX
368 Å (middle panel), O V 629 Å (right panel). Note that the
x-axis of the O V plot is only plotted up to 10 mHz |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=16.5cm,height=7.4cm,clip]{h2037_fig5.ps}
\end{figure}](/articles/aa/full/2001/12/aah2037/Timg14.gif) |
Figure 5:
The summed counts over time of the intensity time series versus
the secondary frequencies of oscillation found in the these time series
for Fe XVI 335 Å (left panel), Mg IX
368 Å (middle panel), O V 629 Å (right panel). Note that the
x-axis of the O V plot is only plotted up to 10 mHz |
| Open with DEXTER |
3.2 Statistical analysis
The data used in this analysis was obtained over three years and in three
different active regions, at the coordinates shown in
Table 1. In total, 17 datasets were examined, 6 from 1997, 3 from
1998 and 8 from 1999. In this work we collect together the results from
these three observing periods to provide a larger statistical sample. We do
this in the hope of evaluating the most commonly occurring oscillations in
active regions.
By using the global wavelet spectrum and the randomisation method
(see Sect. 2) we investigated the main intensity and
velocity oscillation frequencies at each slit position in each dataset. At
each slit position the frequencies corresponding to the primary and
the secondary peaks in the global wavelet spectrum were recorded, as was the
value of the summed counts over time in the intensity time series being
investigated. The primary and secondary oscillation frequencies were only
accepted, as being due to "real'' oscillations, and therefore recorded, if
the probability value from the randomisation method was greater than 95% in
each case.
In this way we were
able to build-up a list of all statistically significant intensity and
velocity oscillation frequencies in the three lines for each dataset,
together with an indication of the total intensity of the line where the
oscillations were occurring. A frequency of 2.0 mHz was chosen as
the lower cut-off as frequencies below this value were judged to be in the
COI and therefore potentially affected by edge effects. As the cadence
in the 1997 and 1999 datasets is slightly different from that of the 1998
datasets, we rounded off all measured frequencies to the nearest 0.5 mHz, thus
enabling the results for all datasets to be combined for a statistical study.
![\begin{figure}
\par\includegraphics[width=16.5cm,height=7.4cm,clip]{h2037_fig6.ps}
\end{figure}](/articles/aa/full/2001/12/aah2037/Timg15.gif) |
Figure 6:
The summed counts over time of the velocity time series versus
the primary frequencies of oscillation found in
these time series for Fe XVI 335 Å (left panel), Mg IX
368 Å (middle panel), O V 629 Å (right panel). Note that the
x-axis of the O V plot is only plotted up to 10 mHz |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=16.5cm,height=7.4cm,clip]{h2037_fig7.ps}
\end{figure}](/articles/aa/full/2001/12/aah2037/Timg16.gif) |
Figure 7:
The summed counts over time of the velocity time series versus
the secondary frequencies of oscillation found in the these time series
for Fe XVI 335 Å (left panel), Mg IX
368 Å (middle panel), O V 629 Å (right panel). Note that the
x-axis of the O V plot is only plotted up to 10 mHz |
| Open with DEXTER |
In Fig. 4 we plot the total intensity measured at each slit
position versus the main frequency of oscillation in the intensity, measured
from the primary peak in the global wavelet spectrum. Similarly, in
Fig. 5 we plot the total intensity versus the secondary
oscillation frequency found in the global wavelet spectra, i.e. frequencies
corresponding to the second strongest peak in the global wavelet spectrum.
(The oscillations measured from the primary and secondary peaks in the
global wavelet spectra will subsequently only be referred to as the primary
and secondary oscillations.)
In Figs. 6 and 7 we plot the corresponding results for
the velocity oscillations.
By examining these plots it will be noticeable that the higher intensity
values show a tendency to correspond to the lower frequency values. This is
particularly clear by looking at the plots for the Mg IX
and Fe XVI lines in these figures. This suggests that the higher
oscillation frequencies preferentially occur in the less bright parts of
the active regions, such as the interloop regions.
Also noticeable is the fact that all lines show a slight change in the
distribution of frequency in the primary and secondary oscillations. For
example, while the Fe XVI and Mg IX lines show similar
distributions in both Figs. 4 and 5, there are however
slightly more of the secondary oscillations at higher frequencies and less
at the lower frequencies. The distribution of the O V oscillation
frequencies shows a bigger change. For example, in Fig. 5 the
secondary oscillation frequencies of O V lie at values of
between 3.0-6.0 mHz, in comparison with the primary oscillations plotted
in Fig. 4 which lie at lower frequencies between 2.0-4.0 mHz. A
similar effect is also seen in the frequencies measured from the velocity
oscillations which are plotted in Figs. 6 and 7. Here
again we can see that the distribution of O V frequencies changes and
increases in value as we pass from the primary oscillations to the secondary
oscillations.
To examine the overall distribution of frequencies in the intensity
oscillations more carefully we plot, in Fig. 8, histograms of the
frequencies obtained from the primary and secondary peaks in the global
wavelet spectrum. The histograms of the primary oscillations are plotted in
bold lines. From these primary oscillation histograms it can be seen that
the most common frequencies found in each line lie between 2.0-5.0 mHz. In
fact the histograms peak at 3.0 mHz ( 5 min) in the case of
the Fe XVI and O V lines. Both the Mg IX
and Fe XVI lines also show separate peaks at 4.5 mHz. These results
indicates that low frequency 2.0-5.0 mHz (
5 min) in the case of
the Fe XVI and O V lines. Both the Mg IX
and Fe XVI lines also show separate peaks at 4.5 mHz. These results
indicates that low frequency 2.0-5.0 mHz ( 3.3-8.3 min)
oscillations, typically centred at around 3.0 mHz (or
3.3-8.3 min)
oscillations, typically centred at around 3.0 mHz (or  5 min) are
commonly present in lines from the transition region as well as the corona.
It may be that what we are seeing in these high temperature transition
region and coronal lines is the influence of the photospheric five minute
oscillations, which appear to be imprinting their characteristic periods
of oscillation on to the upper atmospheric layers.
From the histograms of primary oscillation frequencies it can be seen that
the Mg IX and Fe XVI lines also show some primary oscillations
at higher frequencies between about 5.0 and 10.0 mHz. On the other hand, the
transition region O V line shows very few, if any, oscillations at
frequencies higher than 5 mHz.
5 min) are
commonly present in lines from the transition region as well as the corona.
It may be that what we are seeing in these high temperature transition
region and coronal lines is the influence of the photospheric five minute
oscillations, which appear to be imprinting their characteristic periods
of oscillation on to the upper atmospheric layers.
From the histograms of primary oscillation frequencies it can be seen that
the Mg IX and Fe XVI lines also show some primary oscillations
at higher frequencies between about 5.0 and 10.0 mHz. On the other hand, the
transition region O V line shows very few, if any, oscillations at
frequencies higher than 5 mHz.
If we now look at the histograms of the
secondary oscillations (plotted as the thin lines in the same figure) we
can see a different picture. There are now many more
oscillations present at higher frequencies in each line.
Examining the secondary oscillation histograms of the Fe XVI line we
can see that there are now many more high frequency oscillations present,
particularly in the range 5.0-10.0 mHz. The increase in the number of
oscillations in the 8.0-10.0 mHz range is particularly marked. Note,
however, that there is still a sizeable peak in the histogram at 3.0 mHz. We
see the same result in the Mg IX line where there is an increase in
the number of oscillations with frequencies between 5.0-10.0 mHz.
The results from the O V line show the appearance of a new
distribution of frequencies from  2.0-8.0 mHz, with peaks present in
the histogram at 3.5 and 5.5 mHz.
It is probable that the reason we do not see as many of these higher
frequencies in the primary oscillations (e.g. Fig. 4) is that the
strength of the primary oscillation generally has the effect of masking the
presence of these weaker higher frequency oscillations.
As the strength of the low frequency
oscillations seem to have the effect of obscuring the
weaker higher frequency oscillations, one way of seeing a more correct
distribution of all measured oscillation frequencies would be to plot both
the primary and secondary oscillations in a combined histogram plot.
2.0-8.0 mHz, with peaks present in
the histogram at 3.5 and 5.5 mHz.
It is probable that the reason we do not see as many of these higher
frequencies in the primary oscillations (e.g. Fig. 4) is that the
strength of the primary oscillation generally has the effect of masking the
presence of these weaker higher frequency oscillations.
As the strength of the low frequency
oscillations seem to have the effect of obscuring the
weaker higher frequency oscillations, one way of seeing a more correct
distribution of all measured oscillation frequencies would be to plot both
the primary and secondary oscillations in a combined histogram plot.
![\begin{figure}
\par\includegraphics[width=16.5cm,height=7.4cm,clip]{h2037_fig8.ps}
\end{figure}](/articles/aa/full/2001/12/aah2037/Timg17.gif) |
Figure 8:
Histograms of primary oscillation frequencies (bold line) and secondary oscillation frequencies (thin line), obtained from the intensity time series of Fe XVI 335 Å (left panel), Mg IX 368 Å (middle panel) and O V 629 Å (right panel) |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=16.5cm,height=7.4cm,clip]{h2037_fig9.ps}
\end{figure}](/articles/aa/full/2001/12/aah2037/Timg18.gif) |
Figure 9:
Histograms of the combined oscillation frequencies, from the primary and secondary oscillations, obtained from the intensity time series of
Fe XVI 335 Å (left panel), Mg IX 368 Å (middle panel) and
O V 629 Å (right panel) |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=16.5cm,height=7.4cm,clip]{h2037_fig10.ps}
\end{figure}](/articles/aa/full/2001/12/aah2037/Timg19.gif) |
Figure 10:
Histograms of primary oscillation frequencies (bold line) and secondary oscillation frequencies (thin line), obtained from the velocity time series of Fe XVI 335 Å (left panel), Mg IX 368 Å (middle panel) and O V 629 Å (right panel) |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=16.5cm,height=7.4cm,clip]{h2037_fig11.ps}
\end{figure}](/articles/aa/full/2001/12/aah2037/Timg20.gif) |
Figure 11:
Histograms of the combined oscillation frequencies, from the primary and secondary oscillations, obtained from the velocity time series of
Fe XVI 335 Å (left panel), Mg IX 368 Å (middle panel) and
O V 629 Å (right panel) |
| Open with DEXTER |
We do this in Fig. 9. In this figure the histogram of
the Fe XVI line shows there to be a large number of frequencies
between 2.0-5.0 mHz, peaking at 3.0 mHz. It also shows numerous higher
frequencies present all the way up to 19.0 mHz.
From the same figure it can be seen that the Mg IX line also has a
large number of oscillations with frequencies in the 2.0-5.0 mHz range,
with the majority occurring at 2.0 mHz. Higher frequency oscillations are
present up to 18 mHz, similar to the result found in the Fe XVI line.
The histogram of the O V line shows that the majority of its
oscillations occur at 3.0 mHz, together with a smaller number at 5.5 mHz, as
evidenced by the peaks at these values. It is noticeable that the O V
line does not show any oscillations with frequencies greater than
8.5 mHz.
In Fig. 10 we plot the histograms of the primary and secondary
oscillations measured in the velocity. It can be seen for the primary
oscillations of Fe XVI, plotted as the bold line histogram, that the
most commonly measured frequency is at 2.5 mHz, with numerous 4.0 mHz
oscillations also being present. At higher frequencies the oscillations are
mainly concentrated between 6.0-11.0 mHz but there are frequencies present
all the way up to 14.5 mHz. In the histogram for the secondary oscillations,
plotted here as the thin line, there is still a peak at 2.5 mHz, but now
also a stronger peak present at 6.5 mHz. In the case of these secondary
oscillations it can be easily seen that there are now many more oscillations
located at the higher frequencies, e.g. in addition to the strong 6.5 mHz
peak, there are now more oscillations present in the 10.0-20.0 mHz range.
The primary oscillation histogram of the Mg IX velocity measurements
shows that the most commonly occurring frequency of oscillation is at
2.5 mHz. The strong peak in the histogram at 4.0 mHz indicates that
oscillations at this frequency are also common. At higher
frequencies (>5.0 mHz) there are oscillations present at all frequencies
up to 15.0 mHz, with a slight increase in the number of oscillations
at  10.0/10.5 mHz, where there is a small peak in the histogram. In
the secondary oscillation histogram the main frequencies of oscillation are
located typically at higher frequencies, with the largest number being
present between 6.0-15.0 mHz. There are also numerous oscillations present
with frequencies up to 20.0 mHz. Note however that there are also still a
sizeable number of frequencies present at 3.0 and 4.0 mHz, as indicated by
the peaks in the histograms.
10.0/10.5 mHz, where there is a small peak in the histogram. In
the secondary oscillation histogram the main frequencies of oscillation are
located typically at higher frequencies, with the largest number being
present between 6.0-15.0 mHz. There are also numerous oscillations present
with frequencies up to 20.0 mHz. Note however that there are also still a
sizeable number of frequencies present at 3.0 and 4.0 mHz, as indicated by
the peaks in the histograms.
In the O V histogram it is clear that the most commonly occurring
frequency is at 2.5 mHz, with a short tail of frequencies being present up
to 8.5 mHz. In the secondary oscillations, on the other hand, there is a
broad band of frequencies present from 2.0 to 16.5 mHz, with local peaks
at 4.0 and 6.0 mHz. As in the intensity oscillations it is clear that the
secondary oscillations for this line are present at higher frequencies with
respect to the primary oscillations. Again this probably indicates that the
strong primary oscillations of O V have the effect of blocking out
these weaker higher frequency oscillations.
Note that we can again see in these velocity oscillations that the main
frequencies of oscillation lie between 2.0-5.0 mHz, for all the lines. Thus
it appears that the velocity measurements are also being affected by some
process that causes most of the oscillations to occur with periods around
five minutes, i.e. between 2.0-5.0 mHz (200-500 s).
By combining and plotting the primary and
secondary oscillation frequencies in one histogram, as we did with the
intensity oscillations, we are able to produce the plot shown in
Fig. 11. For Fe XVI we can see that the majority of
oscillations are present at the lower frequencies, concentrated at 2.5
and 4.0 mHz, with a decreasing number of higher frequencies present all
the way up to 20.0 mHz.The localised peaks at 2.5, 4.0 and 6.5 mHz etc.
possibly indicates that these are favoured frequencies of oscillation
for this line.
For the Mg IX line it can be seen from the plot that the majority
of oscillations are also present at low frequencies, with concentrations
at 2.5 and 4.0 mHz. In addition, there are a sizeable number of oscillations
present all the way up to 20 mHz, but concentrated mainly between 6.0-15.0 mHz. In the O V line the majority of oscillation are present at 2.5
and 6.0 mHz. There are, however, also oscillations present at higher
frequencies all the way up to 16.5 mHz.
There is a noticeable increase in the number of frequencies present in the
velocity histograms of the Mg IX and Fe XVI lines in
Fig. 11 in comparison with the intensity histograms in
Fig. 9. The numbers in the O V histograms however remain
more or less the same. We suggest that this may be due to a change in the
nature of the wave mode as we pass from the transition region line
of O V to the coronal lines of Mg IX and Fe XVI.
This and the other results that we obtained here will be discussed
further in the next section.
From the detailed analysis of the previous section we found a number of
distinct results which we shall discuss in more detail here.
Firstly, we have found from these results that there is a tendency for the
higher frequency oscillations, in both the intensity and velocity
oscillations, to occur in locations where the total intensity is least. This
suggests that the higher frequency oscillations are occurring in the darker
regions of the active regions, possibly in the interloop/loop boundary
regions and further that some mechanism is acting on the loop boundaries.
We tentatively note that resonant absorption is likely to occur where
inhomogeneities are most pronounced, such as the boundaries of isolated flux
tubes.
Secondly, we have seen, by combining the primary and secondary oscillations
of intensity and velocity (e.g. Figs. 9 and 11), that
the majority of the oscillations in all lines are present in the range
of 2-5 mHz (200-500 s). In fact, typically the largest number of
oscillations are found around periods of  5 min, i.e. 2.5-3.0 mHz.
The presence of such a large number of low frequency oscillations, with
periods around 5 min, in the transition region and the corona strongly
suggests the influence, in some manner, of the photospheric five minute
oscillations on the upper solar atmosphere. We note that a coupling between
the photospheric driver and the coronal loop mode would explain the
prevalence of the
5 min, i.e. 2.5-3.0 mHz.
The presence of such a large number of low frequency oscillations, with
periods around 5 min, in the transition region and the corona strongly
suggests the influence, in some manner, of the photospheric five minute
oscillations on the upper solar atmosphere. We note that a coupling between
the photospheric driver and the coronal loop mode would explain the
prevalence of the  5 min or
5 min or  3 mHz peak in all the frequency
histograms. Aschwanden et al. (1999) found that a fraction (up to 15%) of
the loops are in resonance with the 5 min driver.
3 mHz peak in all the frequency
histograms. Aschwanden et al. (1999) found that a fraction (up to 15%) of
the loops are in resonance with the 5 min driver.
Thirdly, while all lines were found to have a majority of their frequencies
in the 2.0-5.0 mHz range, it was noticeable that the Mg IX
and Fe XVI lines shared many common characteristics at higher
frequencies (>5.0 mHz) in both the intensity and velocity. For
example, from the combined histograms of the intensity and velocity
oscillations (see Figs. 9 and 11), both Fe XVI
and Mg IX can be seen to have most of their higher
frequency (>5.0 mHz) oscillations concentrated roughly in
the 5.0-10.0 mHz range, with a continuous range of frequencies present
all the way out to  20 mHz. Local maxima in the frequency histograms,
however, suggest that some higher frequencies may be more favoured than
others, e.g. at 6.5 mHz in the Fe XVI velocity histogram. The
similarity between the intensity and velocity frequencies of the O V
is also clear from the combined histograms in Figs. 9
and 11. For example, both have most of their oscillations
at 2.5-3.0 mHz, with a smaller amount weaker at 5.5-6.0 mHz. The only
slight difference being that in the velocity O V has more
oscillations at higher frequencies, up to 16.5 mHz.
While overall we find roughly the same frequencies in the intensity and the
velocity oscillations it should be noted that the same values of frequency
rarely occur simultaneously in both the intensity and velocity measurements
of a single region. This was discussed briefly in Sect. 3.1
where we suggested it might be due to the influence of two different wave
modes (compressive and non-compressive), each being separately responsible
for either the intensity or velocity oscillations.
20 mHz. Local maxima in the frequency histograms,
however, suggest that some higher frequencies may be more favoured than
others, e.g. at 6.5 mHz in the Fe XVI velocity histogram. The
similarity between the intensity and velocity frequencies of the O V
is also clear from the combined histograms in Figs. 9
and 11. For example, both have most of their oscillations
at 2.5-3.0 mHz, with a smaller amount weaker at 5.5-6.0 mHz. The only
slight difference being that in the velocity O V has more
oscillations at higher frequencies, up to 16.5 mHz.
While overall we find roughly the same frequencies in the intensity and the
velocity oscillations it should be noted that the same values of frequency
rarely occur simultaneously in both the intensity and velocity measurements
of a single region. This was discussed briefly in Sect. 3.1
where we suggested it might be due to the influence of two different wave
modes (compressive and non-compressive), each being separately responsible
for either the intensity or velocity oscillations.
Fourthly and finally, it is noticeable that Fe XVI and Mg IX
show more significant oscillations in the velocity than in the intensity.
This can be confirmed by comparing Figs. 9 and 11.
This larger number of oscillations in the velocity with respect to the
intensity for the coronal lines may be indicative of the fact that in the
velocity oscillations we are measuring additional wave modes that are not
visible in the intensity. This would suggest that this additional wave mode
is of a non-compressive type, such as an Alfvén wave, that would not be
easily measured in the intensity oscillations. However the fact that there
are some oscillations in the intensity in the coronal lines suggests that
there are also compressive wave types present, possibly magnetoacoustic in
nature. For the O V line there is not an appreciable difference in
the numbers of oscillations measured in the intensity and the velocity. This
can again be confirmed by comparing Figs. 9 and 11. It
may be that the waves causing the intensity and velocity oscillations in
the O V line are generally compressive in nature, and therefore are
measurable equally in both intensity and velocity measurements. This, of
course, then suggests that there is some mechanism at play that is creating
additional non-compressive waves in the coronal lines but not in the
transition region line of O V. We do not speculate further here on
the nature of this proposed mechanism except to point out that resonant absorption in the coronal loops would be expected to produce kinetic Alfvén waves (Ionson 1978).
Before we briefly discuss the above results in terms of possible theoretical
mechanisms, we compare our results to similar findings by other authors
(see also Table 2).
Koutchmy et al. (1983) found periods of 43, 80 and 300 s in Doppler
velocities measured using the Fe XVI green coronal line at 5303 Å.
These were discussed by them in terms of resonant Alfvén oscillations of a
coronal arch. Using estimated values for the coronal density, magnetic field
and loop length they found periods of 84.5 s and 43 s for
the first and second modes which closely match their observations.
McKenzie & Mullan (1997) found periods of 10-62 s for coronal loops
measured with the YOHKOH soft X-ray telescope. They suggested that these
oscillations were due to the loop oscillating in its global mode.
Ruderman et al. (1997) proposed that if a resonant torsional Alfvén wave
with a single frequency heats a whole coronal loop, the driving frequency
corresponding to this resonance is given by
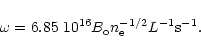 |
(1) |
Using
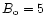 G,
G,
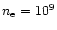 cm-3 and
cm-3 and
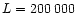 km one
obtains
km one
obtains
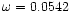 corresponding to a period of 116 s. Decreasing
the loop
length results in a linear decrease in the calculated period.
corresponding to a period of 116 s. Decreasing
the loop
length results in a linear decrease in the calculated period.
Roberts et al. (1984) suggested that the observations found by Koutchmy et al. (1983) could also be interpreted as standing fast kink waves in
coronal loops. For the fast kink mode (standing fast magneto-acoustic
waves), which would correspond to lateral displacements of the loop, the
periods are given by,
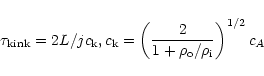 |
(2) |
where cA is the Alfvén speed inside the loop, ck is the speed of
propagation of the kink mode,
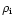 and
and
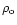 are the plasma
densities inside and outside the loop respectively, and j determines the
number (j-1) of nodes in the oscillation along the loop, with j=1 when
the apex of the loop is disturbed whereas for j=2 the apex is undisturbed.
The modes j=1,2 are the most easy to excite. Using the values as reported
by Nakariakov et al. (1999) of
are the plasma
densities inside and outside the loop respectively, and j determines the
number (j-1) of nodes in the oscillation along the loop, with j=1 when
the apex of the loop is disturbed whereas for j=2 the apex is undisturbed.
The modes j=1,2 are the most easy to excite. Using the values as reported
by Nakariakov et al. (1999) of
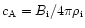 = 800 km s-1
and assuming an order of magnitude density enhancement for a typical coronal
loop, i.e
= 800 km s-1
and assuming an order of magnitude density enhancement for a typical coronal
loop, i.e
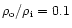 ,
and the length of the loop as
,
and the length of the loop as
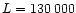 km, periods of 240 and 120 s are obtained for j=1, 2
respectively. Clearly for a smaller loop length, one will have shorter
periods and consequently higher frequency oscillations in the entire
loop, e.g. the compact SXR-bright flare loops have
lengths
km, periods of 240 and 120 s are obtained for j=1, 2
respectively. Clearly for a smaller loop length, one will have shorter
periods and consequently higher frequency oscillations in the entire
loop, e.g. the compact SXR-bright flare loops have
lengths
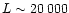 km (Aschwanden et al. 1999).
km (Aschwanden et al. 1999).
From TRACE observations, Nakariakov et al. (1999) interpreted their
in-phase displacement in a coronal loop as being caused by the global
kink mode. This is the normal mode of the loop in which all parts of the
loop oscillate transversely and in phase. They also observed a decay in
the loop oscillations which could be attributed to dissipation of the resonant
global mode due to viscosity and resistivity. The waves can be dissipated in
a narrow dissipation layer inside the loop (estimated to be
 15 km), which leads to heating of coronal loops. The
effect of viscous dissipation on the resonant absorption of the global
mode has been investigated by Ofman et al. (1994).
15 km), which leads to heating of coronal loops. The
effect of viscous dissipation on the resonant absorption of the global
mode has been investigated by Ofman et al. (1994).
Aschwanden et al. (1999) found periods of approx. 280 s for spatial
oscillations of coronal loops measured using the Fe IX 171 Å line
of TRACE. Due to the high
spatial resolution of TRACE the oscillations were detectable as
transverse (lateral) displacements of spatial loop positions. After
investigating various MHD modes of coronal loops, they concluded
that the observed periods of the asymmetric, sinusoidal displacements are
most consistent with the fast kink mode. They also found little phase shift
along the loops, implying a standing wave mode with fixed nodes.
From eclipse observations, Singh et al. (1997) and Cowsik et al. (1999)
reported intensity oscillations with periods  5-100 s. These
were interpreted as compressional magneto-acoustic waves. Furthermore, they
showed that the fast mode oscillations in active regions can provide
sufficient energy flux for heating of the solar corona, as was concluded
earlier by Porter et al. (1994).
5-100 s. These
were interpreted as compressional magneto-acoustic waves. Furthermore, they
showed that the fast mode oscillations in active regions can provide
sufficient energy flux for heating of the solar corona, as was concluded
earlier by Porter et al. (1994).
Ireland et al. (1999), using Fe XVI 335 Å and Mg IX 368 Å
lines from CDS, found periods of 60-70 s for the Fe XVI
line, but no significant periods for the Mg IX line. In addition, they
found large numbers of oscillations around 160-200 s for
the O V 629 Å line.
Moortel et al. (2000) using the TRACE Fe IX line found propagating
variations in the intensity of a coronal loop footpoint. They measured
these intensity variations to have periods of 180-240 s. From the
propagation speed of these intensity variations ( 150 kms-1) they
consider the oscillations to be good candidates for being propagating slow
magneto-acoustic waves travelling into the corona. They further point out
that, unlike the observations of Aschwanden et al. (1999), no flare
occurred near the time of their observations.
150 kms-1) they
consider the oscillations to be good candidates for being propagating slow
magneto-acoustic waves travelling into the corona. They further point out
that, unlike the observations of Aschwanden et al. (1999), no flare
occurred near the time of their observations.
Table 2:
Summary of previous results
| Authors |
Lines |
Main Periods |
| |
|
(sec) |
| Koutchmy et al. (1983) |
Fe XVI 5303 Å |
43, 80, 300 |
| McKenzie and Mullan (1997) |
Soft X-rays |
10-62 |
| Ireland et al. (1999) |
Fe XVI 335 Å |
60-70 |
| |
Mg IX 368 Å |
no periods |
| |
O V 629 Å |
160-200 |
| |
( CDS) |
|
| Aschwanden et al. (1999) |
Fe IX ( TRACE) |
280 |
| Cowsik et al. (1999) |
Continuum |
90, 25, 7 |
Recently, Nightingale et al. (1999) studied the time variability of
EUV brightenings in coronal loops with TRACE. The brightenings
were interpreted as being produced by compressional waves that travel
with the sound speed in coronal loops. They found an electron density
compression by a factor of 1.3-2.0 with respect to the ambient plasma, but
did not find any signature of heating. These authors concluded that the
brightenings were related to some physical process distinctly
different from the flare-like process, where a density increase correlates
with a temperature increase. Transient EUV brightenings
propagating with speeds of 75-200 km s-1 along coronal loops have also
been reported by Berghmans & Clette (1999) from EIT observations. It is
interesting to note that Pérez & Doyle (2000) reported transition region
electron density enhancements in the range 1.5-2.0 (based on a O IV
electron density sensitive line pair), which they suggested to be related to
ultraviolet explosive events.
We will now compare our observed values with the values discussed above,
some of which are also shown in Table 2. In Sect. 3.2
we saw that oscillations at frequencies between 2-5 mHz, that is, period
of 200-500 s are common in all the lines. In addition, we found that
the Fe XVI and Mg IX lines shared roughly the same frequency
bands in both the intensity and the velocity. Unfortunately due to
the wavelet filtering applied by us, higher frequencies (>20 mHz) could
not be distinguished from noise, and so the lowest periods that could be
found by us are at  50 s. It is impossible therefore to compare
with the lowest periods found in the literature, for
example, the 43 s period found by Koutchmy et al. (1983) or the values
of 25 and 7 s found by Cowsik et al. (1999). However, the few
frequencies larger than 10 mHz (<100 s periods), found in the
high frequency tails of the Mg IX and Fe XVI histograms
in Figs. 9 and 11 are close in value to the upper
range of periods found by McKenzie & Mullan (1997), the value of
80 s found by Koutchmy et al., the value of 90 s found by
Cowsik et al. and the values of 60-70 s found by Ireland et al.
for the Fe XVI line. The period of 280 s measured by
Aschwanden et al. (1999), the 300 s period measured by Koutchmy et al.,
the 180-240 s periods found by Moortel et al. (2000) and
the 160-200 s period found by Ireland et al., for their O V
line measurements, all easily fall into the range of the ubiquitous low
frequency 2-5 mHz (200-500 s) oscillations measured in our analysis.
50 s. It is impossible therefore to compare
with the lowest periods found in the literature, for
example, the 43 s period found by Koutchmy et al. (1983) or the values
of 25 and 7 s found by Cowsik et al. (1999). However, the few
frequencies larger than 10 mHz (<100 s periods), found in the
high frequency tails of the Mg IX and Fe XVI histograms
in Figs. 9 and 11 are close in value to the upper
range of periods found by McKenzie & Mullan (1997), the value of
80 s found by Koutchmy et al., the value of 90 s found by
Cowsik et al. and the values of 60-70 s found by Ireland et al.
for the Fe XVI line. The period of 280 s measured by
Aschwanden et al. (1999), the 300 s period measured by Koutchmy et al.,
the 180-240 s periods found by Moortel et al. (2000) and
the 160-200 s period found by Ireland et al., for their O V
line measurements, all easily fall into the range of the ubiquitous low
frequency 2-5 mHz (200-500 s) oscillations measured in our analysis.
It is difficult from the results presented here to know which mechanism is
responsible for the observed oscillations, and, indeed, the different
frequencies found by us may be indicative of more than one wave mode or
mechanism being responsible for the observed oscillations.
From our results we find that higher frequency oscillations tend to occur
preferentially in the interloop/loop boundary regions, possibly as the
result of some resonant absorption process. In the high temperature
coronal lines, we find more significant oscillations in the velocity than in
the intensity, which suggests that in the velocity we measure additional
non-compressive wave modes not visible in the intensity. As this effect is
not seen in the transition region line of O V it suggests that these
additional non-compressive modes are produced in and limited to the corona.
In addition, we find that a  5 min oscillation signature is commonly
present in all lines, strongly suggesting a coupling of the photospheric
driver with the transition region and coronal loop modes.
We conclude from our results and from the above discussion, that there are
two main mechanisms responsible for the observed oscillations; either
resonant Alfvén and/or fast kink waves or propagating slow magnetoacoustic
waves (Moortel et al. 2000), both present in coronal loops.
5 min oscillation signature is commonly
present in all lines, strongly suggesting a coupling of the photospheric
driver with the transition region and coronal loop modes.
We conclude from our results and from the above discussion, that there are
two main mechanisms responsible for the observed oscillations; either
resonant Alfvén and/or fast kink waves or propagating slow magnetoacoustic
waves (Moortel et al. 2000), both present in coronal loops.
Acknowledgements
Research at Armagh Observatory is grant-aided by the Dept. of Education for
N. Ireland while partial support for software and hardware is provided by the
STARLINK project which is funded by the UK PPARC. Information on
the wavelet filtering program, MR/1, may be found
at www.multiresolution.com.
Wavelet software was provided by C. Torrence and G. Compo, and is available
at URL: http://paos.colorado.edu/research/wavelets/. This work was
supported by PPARC grant GR/K43315 plus a short-term fellowship
to DB from Armagh Observatory.
EOS and BF are members of the European Solar Magnetometry
Network (www.astro.su.se/ dorch/esmn/). We would
like to thank the CDS team at Goddard Space Flight Center for their
help in obtaining the present data.
CDS is part of SOHO, the Solar and Heliospheric Observatory,
which is a mission of international cooperation between ESA
and NASA.
- Aschwanden, M. J., Fletcher, L., Schrijver, C. J., & Alexander, D. 1999, ApJ, 520, 880
In the text
NASA ADS
- Berghmans, D., & Clette, F. 1999, Solar Phys., 186, 207
In the text
NASA ADS
- Cowsik, R., Singh, J., Saxena, A. K., Srinivasan, R., & Raveendran,
A. V. 1999, Solar Phys., 188, 89
In the text
NASA ADS
- Dhillon, V. S., & Privett, G. J. 1997, Starlink User Note, 167.5
In the text
- Doyle, J. G., van den Oord, G. H. J., O'Shea, E., & Banerjee, D. 1998, Solar Phys., 181, 51
In the text
NASA ADS
- Doyle, J. G., van den Oord, G. H. J., O'Shea, E., & Banerjee, D. 1999, A&A, 347, 335
NASA ADS
- Harrison, R. A. 1997, Solar Phys., 175, 467
NASA ADS
- Hollweg, J. V. 1990, Computer Science Reports, 12, 205
In the text
- Ionson, J. 1978, ApJ, 226, 650
In the text
NASA ADS
- Ireland, J., Walsh, R. W., Harrison, R. A., & Priest, E. R. 1999, A&A, 347, 355
In the text
NASA ADS
- Koutchmy, S., Zugzda, Y. D., & Locans, L. 1983, A&A, 120, 185
In the text
NASA ADS
- Meyers, S. D., Kelley, B. G., & O'Brien, J. J. 1993, Mon. Wea. Rev., 121, 2858
In the text
- De Moortel, I., Ireland, J., & Walsh, R. W. 2000, A&A, 355, L23
In the text
NASA ADS
- McKenzie, D. E., & Mullan, D. J. 1997, Solar Phys., 176, 127
In the text
NASA ADS
- Nakariakov, V. M., Ofman, L., DeLuca, E. E., Roberts, B., & Davila, J. M., Science, 285, 862
- Narain, U., & Ulmschneider, P. 1996, Space Sci. Rev., 75, 453
In the text
NASA ADS
- Nemec, A. F., & Nemec, J. M. 1985, AJ, 90, 2317
In the text
NASA ADS
- Nightingale, R. W., Aschwanden, M. J., & Hurlburt, N. E. 1999, Solar Phys, 190, 249
In the text
NASA ADS
- Ofman, L., Davila, J. M., & Steinolfson, R. S. 1994, ApJ, 421, 360
In the text
NASA ADS
- Pérez, M. E., & Doyle, J. G. 2000, A&A, 360, 331
In the text
NASA ADS
- Porter, L. J., & Klimchuk, J. A., & Sturrock, P. A. 1994, ApJ, 435, 482
In the text
NASA ADS
- Roberts, B., Edwin, P. M., & Benz, A. O. 1984, ApJ, 279, 857
In the text
NASA ADS
- Ruderman, M. S., Berghmans, D., Goossens, M., & Poedts, S. 1997, A&A, 320, 305
In the text
NASA ADS
- Singh, J., Jagdev, C. R., Raveendran, A. V., et al. 1997,
Solar Phys., 170, 235
In the text
NASA ADS
- Starck, J. L., & Murtagh, F. 1998, PASP, 110, 193
In the text
NASA ADS
- Starck, J. L., Murtagh, & F., Bijaoui 1998, Image and Data Analysis: The Multiscale Approach (Cambridge University Press)
- Torrence, C., & Compo, G. P. 1998, Bull. Amer. Meteor. Soc., 79, 61
In the text
Copyright ESO 2001
![\begin{figure}
\par\includegraphics[width=17.2cm,height=7.4cm,clip]{h2037_fig1.ps}
\end{figure}](/articles/aa/full/2001/12/aah2037/Timg7.gif)
![\begin{figure}
\par\includegraphics[width=17.2cm,height=7.4cm,clip]{h2037_fig2.ps}
\end{figure}](/articles/aa/full/2001/12/aah2037/Timg8.gif)
![\begin{figure}
\par\includegraphics[width=17.2cm,height=7.4cm,clip]{h2037_fig3.ps}
\end{figure}](/articles/aa/full/2001/12/aah2037/Timg9.gif)
![\begin{figure}
\par\includegraphics[width=16.5cm,height=7.4cm,clip]{h2037_fig4.ps}
\end{figure}](/articles/aa/full/2001/12/aah2037/Timg13.gif)
![\begin{figure}
\par\includegraphics[width=16.5cm,height=7.4cm,clip]{h2037_fig5.ps}
\end{figure}](/articles/aa/full/2001/12/aah2037/Timg14.gif)
![\begin{figure}
\par\includegraphics[width=16.5cm,height=7.4cm,clip]{h2037_fig6.ps}
\end{figure}](/articles/aa/full/2001/12/aah2037/Timg15.gif)
![\begin{figure}
\par\includegraphics[width=16.5cm,height=7.4cm,clip]{h2037_fig7.ps}
\end{figure}](/articles/aa/full/2001/12/aah2037/Timg16.gif)
![\begin{figure}
\par\includegraphics[width=16.5cm,height=7.4cm,clip]{h2037_fig8.ps}
\end{figure}](/articles/aa/full/2001/12/aah2037/Timg17.gif)
![\begin{figure}
\par\includegraphics[width=16.5cm,height=7.4cm,clip]{h2037_fig9.ps}
\end{figure}](/articles/aa/full/2001/12/aah2037/Timg18.gif)
![\begin{figure}
\par\includegraphics[width=16.5cm,height=7.4cm,clip]{h2037_fig10.ps}
\end{figure}](/articles/aa/full/2001/12/aah2037/Timg19.gif)
![\begin{figure}
\par\includegraphics[width=16.5cm,height=7.4cm,clip]{h2037_fig11.ps}
\end{figure}](/articles/aa/full/2001/12/aah2037/Timg20.gif)