3 Analysis and results

The absorption profiles of the DLA system at $z_{\rm abs} = 3.025$ are characterized by two dominating components (2 and 3) separated by about 20 km s^-1 with the red one slightly stronger than the blue as it can be seen from the non-saturated metal lines in Fig. 1. The strong and saturated metal lines reveal that additional material in smaller amount is present redwards the two main features (components 4, 5, 6 and 7). The region on the blue side of the main absorption components is sharp and relatively free from material with only one weak component (component 1) at about -30 kms^-1. In total seven components are needed to fit the metal lines absorption profiles, with two main components containing about 80% of the total column density per transition.

Figure 2: Damped Ly$\beta$ absorption profile. The vertical lines mark the positions of the three major hydrogen components (see text for details). The solid thin curve represents the best fit solution and the dotted thin curves delimit the range of uncertainty of the hydrogen column density

Figure 3: Ly$\epsilon$, Ly8, Ly10 and Ly12 profiles plotted against velocity. The vertical scale goes from 0 to 1 for each plotted transition. The zero velocity is fixed at z = 3.024856. The vertical lines mark the positions of the three hydrogen components. The solid thin curve represents the best fit solution

The DLA system at $z_{\rm abs} = 3.025$ is a very good candidate for the deuterium analysis since it shows a relatively simple velocity structure dominated by two strong components, a low metallicity of [Zn/H] $\approx -1.25$, indicating that the measured D/H will be representative of primordial D/H and the hydrogen Lyman series lines can be followed down to Ly12.

We used a $\chi^2$ minimization routine fitlyman (Fontana & Ballester 1995) in MIDAS to fit Voigt profiles to the observed absorption profiles, and obtain for each fitted absorption component the wavelength, the column density N, the Doppler parameter b and the corresponding errors.

In the case of high hydrogen column densities like in DLA systems, we expect the neutral and low ionization metal lines to trace the H, therefore we model the Lyman series (Ly$\beta$ to Ly12) absorption profiles with three features corresponding to the two main components (2 and 3) and the reddest component (7) as determined from the metal lines (Fig. 1). The contribution of the weaker component 7 is required only to better constrain the fit on the red edge of the Lyman lines. The relative intensities of these three major hydrogen components were scaled with the metal lines assuming they have approximatively the same abundance ratios from component to component.

Figure 4: Same as Fig. 3. The fit in this case is performed by considering the two main components for D and the three components for H (see text for details)

Starting from this basis we obtained the final H I column densities and b-values (free parameters) by fitting simultaneously the lines of the Lyman series and by assuming the same redshift for the three H components as for the metal lines. The Ly$\beta$ absorption profile provides a very good constraint to the total H I column density and the Ly8, Ly9, Ly10 and Ly12 profiles (which are the ones free from strong contamination) to the b-values. From the best fit (Figs. 2 and 3, Table 1) we derived a total H I column density of $\log N$(H I) $= 20.63\pm 0.09$ in close agreement with the Pettini et al. (1994) value of $20.7\pm 0.1$.

Adding other components to the hydrogen fit with low column densities as the ones observed in the stronger metal lines, component 1 at -30 km s^-1 and components 4, 5 and 6 at slightly higher redshifts than the two main components, does not change significantly neither the total H I column density of the two main components nor the fit on the blue and red wings of the Lyman lines. Figure 3 however clearly shows that the fit with three hydrogen components systematically fails to reproduce the edge of the blue wing in the higher members of the hydrogen Lyman series, Ly$\epsilon$, Ly8, Ly10 and Ly12, at about -82 kms^-1 from the two H main components (2 and 3) which is the expected displacement of the corresponding D lines.

We then add to the model the deuterium by assuming its contribution only to the two main components (2 and 3). In the fitting procedure we assumed the same redshift for the two fitted components as for H and we left the column densities and the broadening parameters b as free parameters.

The best fit performed over D I Ly8 and Ly10 improves the $\chi^2$ of the hydrogen fit by a factor of 3. It reproduces nicely the blue wing of the Ly8, Ly10 and Ly12 absorption profiles and is consistent with Ly$\epsilon$ (see Fig. 4). It gives a deuterium abundance of

$$\frac{\rm D}{\rm H} = (2.24\pm 0.67)~10^{-5} .$$

The error follows from the H and D fits and it includes the uncertainties in placing the continuum level and the errors on the b-values. The D I column densities and the b-values of the two fitted components are given in Table 1.

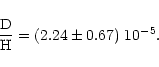
To check the stability of our result when the assumption that H and D mimic the metal structure is relaxed, we made a fit of the Ly$\beta$, Ly$\epsilon$, Ly8, Ly10 and Ly12 lines with three H and D components by keeping both their redshifts and column densities as free parameters. We obtained a satisfactory fit with shifts of the components with respect to the values given in Table 1 of less than 4 kms^-1. The derived D/H ratio was comprised within our D/H error range. A fit with only one strong H component and the corresponding D component gave also a D/H ratio within our D/H error range.