A&A 368, 912-931 (2001)
DOI: 10.1051/0004-6361:20000577
1 - Central Astronomical Observatory of the Russian
Academy of Sciences at Pulkovo, 196140 Saint-Petersburg, Russia
2 - Isaac Newton Institute of Chile, St.-Petersburg Branch, Chile
Received 9 December 1999 / Accepted 22 December 2000
Abstract
We present the results of statistical analyses of a sample
of 627 Be stars. The parameters of intrinsic polarization
![]() ,
projected rotational velocity
,
projected rotational velocity
![]() ,
and near IR excesses have been investigated.
The values of
,
and near IR excesses have been investigated.
The values of ![]() have been estimated for
a much larger and more representative sample of Be stars
(
have been estimated for
a much larger and more representative sample of Be stars
(![]() 490 objects) than previously.
We have confirmed that most Be stars of early spectral
type have statistically larger values of polarization and IR
excesses in comparison with the late spectral type stars.
It is found that the distributions of
490 objects) than previously.
We have confirmed that most Be stars of early spectral
type have statistically larger values of polarization and IR
excesses in comparison with the late spectral type stars.
It is found that the distributions of
![]() diverge
considerably for the different spectral subgroups. In contrast to
late spectral types (B5-B9.5), the distribution of
diverge
considerably for the different spectral subgroups. In contrast to
late spectral types (B5-B9.5), the distribution of
![]() for B0-B2 stars does not peak at the value
for B0-B2 stars does not peak at the value
![]() %.
Statistically significant differences in the mean projected rotational
velocities (
%.
Statistically significant differences in the mean projected rotational
velocities (
![]() )
are found for different spectral
subgroups of Be stars in the sense that late spectral type stars
(V luminosity class) generally rotate faster than early types,
in agreement with previously published results.
This behaviour is, however, not obvious for the III-IV luminosity
class stars. Nevertheless, the calculated values of the ratio
)
are found for different spectral
subgroups of Be stars in the sense that late spectral type stars
(V luminosity class) generally rotate faster than early types,
in agreement with previously published results.
This behaviour is, however, not obvious for the III-IV luminosity
class stars. Nevertheless, the calculated values of the ratio
![]() of the true rotational velocity,
of the true rotational velocity, ![]() ,
to the critical
velocity for break-up,
,
to the critical
velocity for break-up, ![]() ,
is larger for late spectral
type stars of all luminosity classes. Thus, late spectral type stars
appear to rotate closer to their break-up rotational velocity.
The distribution of near IR excesses for early spectral subgroups
is bi-modal, the position of the second peak displaying
a maximum value
,
is larger for late spectral
type stars of all luminosity classes. Thus, late spectral type stars
appear to rotate closer to their break-up rotational velocity.
The distribution of near IR excesses for early spectral subgroups
is bi-modal, the position of the second peak displaying
a maximum value
![]() for O-B1.5 stars, decreasing to
for O-B1.5 stars, decreasing to
![]() for intermediate spectral types (B3-B5).
It is shown that bi-modality disappears for late spectral types (B6-B9.5).
No correlations were found between
for intermediate spectral types (B3-B5).
It is shown that bi-modality disappears for late spectral types (B6-B9.5).
No correlations were found between ![]() and near IR excesses
and between E(V-L) and
and near IR excesses
and between E(V-L) and ![]() for the different subgroups of
Be stars. In contrast to near IR excesses, a relation between
for the different subgroups of
Be stars. In contrast to near IR excesses, a relation between ![]() and far IR excesses at 12
and far IR excesses at 12 ![]() m is clearly seen.
A clear relation between
m is clearly seen.
A clear relation between ![]() and
and ![]() (as well as between
(as well as between ![]() and
and
![]() )
is found by
the fact that plots of these parameters are bounded by a "triangular"
distribution of
)
is found by
the fact that plots of these parameters are bounded by a "triangular"
distribution of ![]() :
:![]() ,
with a decrease of
,
with a decrease of ![]() towards very small and very large
towards very small and very large ![]() (and
(and
![]() )
values. The latter behaviour can be understood in the context of a larger
oblateness of circumstellar disks for the stars with a rapid rotation.
From the analysis of correlations between different observational
parameters we conclude that circumstellar envelopes for the majority of
Be stars are optically thin disks with the range of the half-opening angle
of
)
values. The latter behaviour can be understood in the context of a larger
oblateness of circumstellar disks for the stars with a rapid rotation.
From the analysis of correlations between different observational
parameters we conclude that circumstellar envelopes for the majority of
Be stars are optically thin disks with the range of the half-opening angle
of
![]() .
.
Key words: classical Be stars: polarization - projected rotational velocities - near IR excesses - far IR excesses
One of the challenging questions in Be stars investigations is the
geometrical form of their circumstellar (CS) envelopes. There is still active debate
as to the average value of the opening angle of CS disks around classical
Be stars and on the application of the wind-compressed disk model (WCD). The
ideas on this matter at present are rather controversial. Most authors
have considered geometrically thin CS disks with half-opening angles
![]() as follows from the WCD theory of Bjorkman & Cassinelli
(1993) and Owocki et al. (1994) (see for example Wood et al. 1997;
Quirrenbach et al. 1997 etc.). However,
acceptance of such a narrow disks faces several problems in the
interpretation of spectroscopic characteristics (Moujtahid et al.
1999; Rivinius et al. 1999) and the observed IR excesses
in Be stars (Porter 1997).
Moreover, the observed phase transitions -
Be
as follows from the WCD theory of Bjorkman & Cassinelli
(1993) and Owocki et al. (1994) (see for example Wood et al. 1997;
Quirrenbach et al. 1997 etc.). However,
acceptance of such a narrow disks faces several problems in the
interpretation of spectroscopic characteristics (Moujtahid et al.
1999; Rivinius et al. 1999) and the observed IR excesses
in Be stars (Porter 1997).
Moreover, the observed phase transitions -
Be
![]() Be-shell
Be-shell
![]() normal B - cannot be
explained in the framework of a geometrically thin disk model
(Moujtahid et al. 1999). Others used disk models with larger
values of
normal B - cannot be
explained in the framework of a geometrically thin disk model
(Moujtahid et al. 1999). Others used disk models with larger
values of
![]() (Porter 1996) or
(Porter 1996) or
![]() (Hanuschik 1996; Waters et al.
1987) removing some of the difficulties. Finally, some authors
recently returned to the model of flattened ellipsoids or spheroidal
envelopes (Moujtahid et al. 1999) similar to those proposed
earlier by Doazan & Thomas (1982). Although a low level of
intrinsic polarization of Be stars is considered as an indication that
the envelope must be strongly flattened, other geometries can produce
the same level of polarization (see Wood et al. 1996a,
1996b). The IR excesses and spectroscopic characteristics,
considered separately, also do not provide unique interpretation
on CS geometries. Nevertheless, it is well established
that the observed IR excess and polarization of radiation for classical Be
stars both have a common origin. The excess is due to free-free and
free-bound emission from the dense ionized CS gas, with the polarization
being engendered by scattering within clouds of free electrons around the
star. Moreover, classical Be stars are very fast rotators and at least a few
of them rotate close to their break-up velocities. This rapid rotation is
considered as a trigger mechanism for CS envelope formation. To obtain some
conclusions on the geometry of CS envelopes around classical Be stars,
analysis of correlations between different observational parameters seems
strongly desirable (see, for example, Coté & Waters 1987). For
the same reason, it is very important to investigate each of the observed
parameters statistically for as large a representative sample as possible.
During the last 20 years there have been several attempts to carry out such
kinds of investigation for large samples of classical Be stars (from 50 up
to 200 objects). However, such sample sizes are still sometimes insufficiently
large to provide irrefutable conclusions and some authors indicate this fact
themselves (see, for example, Quirrenbach et al. 1997 or Ghosh et al.
1999). By taking a relatively large sample of 90 objects,
by adding the "new'' data from Ghosh et al. (1999) and
McDavid (1999, 2000) to the "old'' data from McLean & Brown
(1978) and Poeckert et al. (1979), Yudin (2000)
came to quite different conclusions on the dependence between
(Hanuschik 1996; Waters et al.
1987) removing some of the difficulties. Finally, some authors
recently returned to the model of flattened ellipsoids or spheroidal
envelopes (Moujtahid et al. 1999) similar to those proposed
earlier by Doazan & Thomas (1982). Although a low level of
intrinsic polarization of Be stars is considered as an indication that
the envelope must be strongly flattened, other geometries can produce
the same level of polarization (see Wood et al. 1996a,
1996b). The IR excesses and spectroscopic characteristics,
considered separately, also do not provide unique interpretation
on CS geometries. Nevertheless, it is well established
that the observed IR excess and polarization of radiation for classical Be
stars both have a common origin. The excess is due to free-free and
free-bound emission from the dense ionized CS gas, with the polarization
being engendered by scattering within clouds of free electrons around the
star. Moreover, classical Be stars are very fast rotators and at least a few
of them rotate close to their break-up velocities. This rapid rotation is
considered as a trigger mechanism for CS envelope formation. To obtain some
conclusions on the geometry of CS envelopes around classical Be stars,
analysis of correlations between different observational parameters seems
strongly desirable (see, for example, Coté & Waters 1987). For
the same reason, it is very important to investigate each of the observed
parameters statistically for as large a representative sample as possible.
During the last 20 years there have been several attempts to carry out such
kinds of investigation for large samples of classical Be stars (from 50 up
to 200 objects). However, such sample sizes are still sometimes insufficiently
large to provide irrefutable conclusions and some authors indicate this fact
themselves (see, for example, Quirrenbach et al. 1997 or Ghosh et al.
1999). By taking a relatively large sample of 90 objects,
by adding the "new'' data from Ghosh et al. (1999) and
McDavid (1999, 2000) to the "old'' data from McLean & Brown
(1978) and Poeckert et al. (1979), Yudin (2000)
came to quite different conclusions on the dependence between
![]() and
and
![]() than those of McLean & Brown (1978)
who used only 67 stars.
than those of McLean & Brown (1978)
who used only 67 stars.
The general aim of the proposed exercises here is to investigate statistically
the data of
![]() and
and
![]() for the largest possible sample of
classical Be stars, to compare the behaviour with near and far IR excesses
and to search for possible correlations between the parameters. Another aim
is to investigate possible differences between spectral subgroups
from the general assembly of classical Be stars. These analyses may give
new insight on the configuration of CS envelopes.
for the largest possible sample of
classical Be stars, to compare the behaviour with near and far IR excesses
and to search for possible correlations between the parameters. Another aim
is to investigate possible differences between spectral subgroups
from the general assembly of classical Be stars. These analyses may give
new insight on the configuration of CS envelopes.
For the statistical analysis here, data for 627 Be stars have been
compiled from different sources, taking into account an overlap of
the list of emission line stars from the SIMBAD database and the
catalogue of Be stars of Jaschek & Egret (1982). All Be
stars which have been considered in the past as young Herbig Be
stars have been excluded; a few Be stars from recent papers (see,
for example, Steele et al. 1999) have been added.
Of course it is impossible to be sure that all the collected objects
are definitely of classical type, but the fraction of "doubtful"
objects cannot be large (as follows from further discussion, see Sect. 6
and Fig. 2). Thus we can say that the compilation represents the largest
ever, more or less homogeneous, sample of classical Be stars.
Note that for selection, we collected only stars of III, IV and V
luminosity class and the sample does not include any supergiants.
Emission line stars of the spectral type A and later are also excluded.
No limitation has been made on the level of observed polarization
(
![]() )
of the sample stars. Thus we have in hand for
statistical study:
)
of the sample stars. Thus we have in hand for
statistical study:
Because the main aim of the present investigation is a statistical study of different observed parameters and correlations between them, it is important to minimize any uncertainties and all kind of statistical biases. Since a principal characteristic of Be stars is their temporal variability, it is best to use the mean values of investigated parameters for each star. The averaging was done by the weighting procedure according to the standard errors of individual measurements (see, for example, Smart 1958).
For the discussion of the various parameters, it is useful to construct the
relative distributions of observed values in the form of histograms. For
this reason it is very important to choose the best binwidths for the
distributions. As will be shown below, the chosen binwidths of 0.3%,
![]() and 50 kms-1 for polarization, colour and rotational velocity
respectively are typically larger than the error associated with the
individual measurements and even larger than the range of variability
associated with any of the stars. Consider now the reduction of each of
the recorded parameters.
and 50 kms-1 for polarization, colour and rotational velocity
respectively are typically larger than the error associated with the
individual measurements and even larger than the range of variability
associated with any of the stars. Consider now the reduction of each of
the recorded parameters.
At present, most Be star investigations have used the data of
![]() mainly from Slettebak (1982) (164 classical Be
stars). Other old data are also available and these are supplemented
by numerous more recent collections. The only problem in compiling
mainly from Slettebak (1982) (164 classical Be
stars). Other old data are also available and these are supplemented
by numerous more recent collections. The only problem in compiling
![]() values from different sources is that they have different
scales and accurate calibrations between the compiled data are required to
avoid systematic errors. It is well known that there is a difference between
the "new'' and "old'' Slettebak's scales (Slettebak et al. 1975).
First of all we compared the
values from different sources is that they have different
scales and accurate calibrations between the compiled data are required to
avoid systematic errors. It is well known that there is a difference between
the "new'' and "old'' Slettebak's scales (Slettebak et al. 1975).
First of all we compared the ![]() data of Slettebak (1975)
with those determined or compiled by others for the same stars and
calculated least-squares fits to the data. Following this calibration
process, we transformed individual values of
data of Slettebak (1975)
with those determined or compiled by others for the same stars and
calculated least-squares fits to the data. Following this calibration
process, we transformed individual values of
![]() from different
sources into the common "new'' scale of Slettebak et al. (1975).
Stars which after transformation provided strong disparities in their values
according to the source catalogue were excluded. Average weighted
values of
from different
sources into the common "new'' scale of Slettebak et al. (1975).
Stars which after transformation provided strong disparities in their values
according to the source catalogue were excluded. Average weighted
values of
![]() and associated standard errors were obtained
for each star using the weighting procedure already mentioned above
(see Smart 1958). For the case of single measurements, we used
the value of a standard error indicated in the reference or adopted a
value for the error equal to 10% of the measured value.
This procedure allows exclusion of most systematic and incidental errors
and helped to obtain a new expanded homogeneous data set. The determined values
of
and associated standard errors were obtained
for each star using the weighting procedure already mentioned above
(see Smart 1958). For the case of single measurements, we used
the value of a standard error indicated in the reference or adopted a
value for the error equal to 10% of the measured value.
This procedure allows exclusion of most systematic and incidental errors
and helped to obtain a new expanded homogeneous data set. The determined values
of
![]() for each star with the standard error are presented in
Appendix I. It can be seen that for more than 95% program stars, the standard
error is less than
for each star with the standard error are presented in
Appendix I. It can be seen that for more than 95% program stars, the standard
error is less than ![]() kms-1.
kms-1.
The values of near IR excesses E(V-L) were calculated by a classical
approach using the measurements of observed and normal colour indices and
interstellar reddening in the respective photometric bands, this being
summarized as:
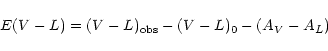 |
(1) |
Currently, the intrinsic polarization components have been estimated for
only about 90 classical Be stars.
![\begin{figure}
\par\includegraphics[width=8cm,height=6.3cm,clip]{9470f1a.ps}\par\vspace*{5mm}
\includegraphics[width=7.8cm,height=6cm,clip]{9470f1b.ps}\end{figure}](/articles/aa/full/2001/12/aa9470/Timg54.gif) |
Figure 1:
Dependence between the interstellar polarization and the distance
in the
|
| Open with DEXTER | |
Two typical examples of the reduction scheme are presented in Fig. 1.
Note that, in some cases, ![]() may not display monotonic growth
due to the line of sight passing through interstellar dust clouds
with complex structure and different orientation of dust grains.
For the cases where the distance to an object could not be determined
from the Hipparcos data or the parallax errors were too large,
we estimated the distance to a star either from reddening or from an
absolute magnitude-spectral type/luminosity calibration. In a few cases
an interstellar component has been estimated by the investigation of the
uniformity of polarization vectors in the vicinity of the star. The
parameters of
may not display monotonic growth
due to the line of sight passing through interstellar dust clouds
with complex structure and different orientation of dust grains.
For the cases where the distance to an object could not be determined
from the Hipparcos data or the parallax errors were too large,
we estimated the distance to a star either from reddening or from an
absolute magnitude-spectral type/luminosity calibration. In a few cases
an interstellar component has been estimated by the investigation of the
uniformity of polarization vectors in the vicinity of the star. The
parameters of
![]() ,
,
![]() and
and ![]() for the program
stars are presented in Appendix II. It is seen that except for a few stars,
most values of
for the program
stars are presented in Appendix II. It is seen that except for a few stars,
most values of
![]() and thus less than the chosen
histogram binwidth.
and thus less than the chosen
histogram binwidth.
An independent by-product of this study is the new set of estimates of interstellar polarization components, this being useful for other future investigations.
In Fig. 2a the values of the excess E(V-L) are plotted against spectral
type for the entire sample. The following features are immediately obvious.
Firstly, there is a clear upper limit for a given spectral type with the
maximum value of about
![]() for B0-B2 stars and with the decrease
of near IR excesses toward later than B2 spectral types. A similar result
was obtained by Dougherty et al. (1991) who found that most of
late type stars show little or no near IR excess colour but for a
significantly smaller statistical sample. However, in contrast to previous
studies, we conclude that the decrease of the upper limit of E(V-L)towards late spectral
types is well fitted by a function in the form of an exponential decay
rather than the linear decay. For the spectral interval from B1 to B9.5
the best fit is described as follows:
for B0-B2 stars and with the decrease
of near IR excesses toward later than B2 spectral types. A similar result
was obtained by Dougherty et al. (1991) who found that most of
late type stars show little or no near IR excess colour but for a
significantly smaller statistical sample. However, in contrast to previous
studies, we conclude that the decrease of the upper limit of E(V-L)towards late spectral
types is well fitted by a function in the form of an exponential decay
rather than the linear decay. For the spectral interval from B1 to B9.5
the best fit is described as follows:
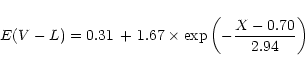 |
(2) |
![\begin{figure}
\par\includegraphics[width=8cm,height=6cm,clip]{9470f2a.ps}\par\v...
...pace*{2.5mm}
\includegraphics[width=7cm,height=6cm,clip]{9470f2c.ps}\end{figure}](/articles/aa/full/2001/12/aa9470/Timg66.gif) |
Figure 2:
Near IR excess E(V-L), intrinsic polarization, and |
| Open with DEXTER | |
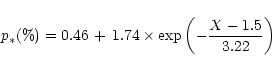 |
(3) |
In Fig. 2c the values of
![]() are plotted against spectral type for
the entire sample. First impressions suggest that there are no significant
differences in
are plotted against spectral type for
the entire sample. First impressions suggest that there are no significant
differences in
![]() for the subtypes of Be stars. However, there
is a possible trend in the average values in the sense that later spectral
type stars rotate faster than early ones. The best linear fit for this
trend is:
for the subtypes of Be stars. However, there
is a possible trend in the average values in the sense that later spectral
type stars rotate faster than early ones. The best linear fit for this
trend is:
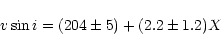 |
(4) |
The value of projected rotational velocity shows a large scatter for all
Be star subspectral types but with a clear concentration around the values between
200 to 250 kms-1. All Be stars exhibit a projected rotational velocities
which are less than a critical rotational velocity for the given spectral
type. We will investigate the distribution of
![]() in more
detail in the next section.
in more
detail in the next section.
Two well-known investigations of projected rotational velocities of Be stars
were completed 18 years ago (Slettebak 1982 - for a sample of 164
objects; Fukuda 1982 - for a sample of 239 objects). Slettebak
noted that there are no strong differences in the rotational characteristics
of Be stars of different spectral types or luminosity classes. To the
contrary, Fukuda arrived at a different conclusion showing that the middle
and later types rotate faster on average than early Be stars, but
the influence of luminosity class was not studied. Since then, several
attempts to carry out similar kinds of investigation for different samples of
classical Be stars have been made with somewhat different conclusions (see,
for example, Zorec et al. 1990; Balona 1990; Zorec &
Briot 1997; Grady et al. 1989; Steele 1999
etc.). It is now possible to reassess the situation using the numerous and
homogeneous
![]() data collected and reduced in the present study.
We investigate here the distributions of projected rotational velocities of
the program stars for four different spectral subgroups (O-B1.5, B2-B2.5,
B3-B5.5 and B6-B9.5) and different luminosity classes.
data collected and reduced in the present study.
We investigate here the distributions of projected rotational velocities of
the program stars for four different spectral subgroups (O-B1.5, B2-B2.5,
B3-B5.5 and B6-B9.5) and different luminosity classes.
Investigation of a distribution such as
![]() is a classical
problem of mathematical statistics. In the first place, we corrected the
constructed histograms from the influence of errors (
is a classical
problem of mathematical statistics. In the first place, we corrected the
constructed histograms from the influence of errors (
![]() )
using Eddington's algorithm (see Smart 1958). One of the
distributions (viz: for the entire sample of Be stars) is presented
in Fig. 3. To compare the distributions, the following parameters should be
calculated and analyzed: the mean (
)
using Eddington's algorithm (see Smart 1958). One of the
distributions (viz: for the entire sample of Be stars) is presented
in Fig. 3. To compare the distributions, the following parameters should be
calculated and analyzed: the mean (
![]() )
and the root
mean square deviation (
)
and the root
mean square deviation (![]() ). To calculate these parameters for a
given distribution we used the weighting procedure according to the standard
error associated with each contributing measurement (see, for example,
Brooks et al. 1994). However, in order to make meaningful comments
on the similarity or differences between the distributions, in the first
place their distribution functions should be analyzed. As a first step we
should try to investigate their "Normality''. If the distribution is
demonstrably non-Normal, other types of function might then be considered
and applied. To test for Normality, we calculated the
coefficients of skewness (g1) and the coefficients of kurtosis
(g2) for each of the distributions. A detailed description of
this procedure has been given recently by Brooks et al. (1994)
together with the analytical expressions for
). To calculate these parameters for a
given distribution we used the weighting procedure according to the standard
error associated with each contributing measurement (see, for example,
Brooks et al. 1994). However, in order to make meaningful comments
on the similarity or differences between the distributions, in the first
place their distribution functions should be analyzed. As a first step we
should try to investigate their "Normality''. If the distribution is
demonstrably non-Normal, other types of function might then be considered
and applied. To test for Normality, we calculated the
coefficients of skewness (g1) and the coefficients of kurtosis
(g2) for each of the distributions. A detailed description of
this procedure has been given recently by Brooks et al. (1994)
together with the analytical expressions for ![]() and
and ![]() .
We calculated unbiased estimators of these coefficients with the associated
variances (see Table 1) and compared the values with those tabulated in the
above mentioned paper for the 95% and 99% confidence levels. This analysis
indicates immediately that all of the distributions may be considered
as Normal at the 99% confidence level and thus we don't need to invoke
other types of distribution functions. At this stage, we cannot say whether
the high arithmetical significance of the statistics for Normality carries
real physical significance in the sense that it is an expected intrinsic
characteristic of the
.
We calculated unbiased estimators of these coefficients with the associated
variances (see Table 1) and compared the values with those tabulated in the
above mentioned paper for the 95% and 99% confidence levels. This analysis
indicates immediately that all of the distributions may be considered
as Normal at the 99% confidence level and thus we don't need to invoke
other types of distribution functions. At this stage, we cannot say whether
the high arithmetical significance of the statistics for Normality carries
real physical significance in the sense that it is an expected intrinsic
characteristic of the ![]() distributions of Be stars.
Such kind investigations might be the matter of future studies.
distributions of Be stars.
Such kind investigations might be the matter of future studies.
![\begin{figure}
\par\includegraphics[width=7cm,height=7cm,clip]{9470f3.ps}\end{figure}](/articles/aa/full/2001/12/aa9470/Timg81.gif) |
Figure 3:
Observed distribution of |
| Open with DEXTER | |
The calculated parameters for each of the distributions are given in
Table 1.
| III, III-IV classes luminosity | |||||
| spectral range: | O-B1.5 | B2-B2.5 | B3-B5.5 | B6-B9.5 | O-B9.5 |
| N stars: | 37 | 30 | 28 | 40 | 135 |
|
|
|||||
| g1 |
|
|
|
|
|
| g2 |
|
|
|
|
|
|
|
456 | 408 | 383 | 320 | 385 |
|
|
0.45 | 0.52 | 0.50 | 0.65 | 0.52 |
|
|
259 | 269 | 245 | 264 | 259 |
|
|
0.57 | 0.66 | 0.64 | 0.83 | 0.67 |
| IV-V, V classes luminosity | |||||
| spectral range: | O-B1.5 | B2-B2.5 | B3-B5.5 | B6-B9.5 | O-B9.5 |
| N stars: | 66 | 78 | 78 | 61 | 283 |
|
|
|||||
| g1 |
|
|
|
|
|
| g2 |
|
|
|
|
|
|
|
527 | 479 | 448 | 398 | 464 |
|
|
0.38 | 0.43 | 0.53 | 0.61 | 0.49 |
|
|
257 | 264 | 300 | 309 | 292 |
|
|
0.49 | 0.55 | 0.67 | 0.78 | 0.63 |
| all classes luminosity (CL) including the stars with undefenite CL | |||||
| spectral range: | O-B1.5 | B2-B2.5 | B3-B5.5 | B6-B9.5 | O-B9.5 |
| N stars: | 106 | 116 | 121 | 120 | 463 |
|
|
|||||
| g1 |
|
|
|
|
|
| g2 |
|
|
|
|
|
|
|
502 | 458 | 429 | 362 | 436 |
|
|
0.40 | 0.45 | 0.56 | 0.62 | 0.50 |
|
|
256 | 261 | 307 | 288 | 280 |
|
|
0.51 | 0.57 | 0.72 | 0.80 | 0.64 |
| the data from Slettebak 1982 | |||||
| spectral range: | B0-B1.5 | B2-B2.5 | B3-B5.5 | B6-B9.5 | |
| N stars: | 25 | 35 | 51 | 54 | |
|
|
236 | 193 | 221 | 228 | |
| the transformed data from Fukuda 1982 | |||||
| spectral range: | B0-B1.5 | B2-B2.5 | B3-B5.5 | B6-B9.5 | O-B9.5 |
| N stars: | 69 | 63 | 50 | 57 | 239 |
|
|
189 | 196 | 239 | 244 | 214 |
| the data from Zorec & Briot 1997 | |||||
| spectral range: | B0-B1.5 | B2-B3 | B4-B7 | B8-B9.5 | |
|
|
230 | 190 | 220 | 130 | |
|
|
240 | 250 | 250 | 280 | |
| the data from Grady et al. 1989 | |||||
| spectral range: | B6-B9.5 | ||||
| N stars: | 40 | ||||
|
|
226 | ||||
| Spectral type: | O8 | O9 | B0 | B0.5 | B1 | B1.5 | B2 | B2.5 | B3 | B4 | B5 | B6 | B7 | B8 | B9 |
| 500 | 460 | 430 | 412 | 395 | 383 | 365 | 355 | 340 | 325 | 310 | 295 | 284 | 275 | 270 | |
| 600 | 560 | 520 | 502 | 483 | 465 | 445 | 435 | 420 | 400 | 386 | 374 | 362 | 352 | 344 | |
| 626 | 596 | 565 | 540 | 520 | 500 | 483 | 470 | 460 | 442 | 425 | 410 | 400 | 396 | 391 |
To test the differences between the dispersions, we can use Fisher's
criterion (F-test). Simple calculations indicate that for the III-IV
luminosity classes, the differences between the dispersion for the
distributions are statistically insignificant at the 95% confidence level
(except late type stars). For the V class, it was found that the difference
in ![]() is significant at 95% confidence level between O-B2.5 and B3-B9
spectral subgroups.
is significant at 95% confidence level between O-B2.5 and B3-B9
spectral subgroups.
As the next step, we may compare the mean values of
![]() and
the ratio of
and
the ratio of
![]() for selected subgroups. It is well
known that the mean true velocities and critical velocities are very
different, depending on the luminosity class and spectral class (see for
example Zorec et al. 1990). For our purposes we
interpolated/extrapolated the values of
for selected subgroups. It is well
known that the mean true velocities and critical velocities are very
different, depending on the luminosity class and spectral class (see for
example Zorec et al. 1990). For our purposes we
interpolated/extrapolated the values of
![]() from Moujtahid et al.
(1999) and Zorec (2000) and present them in Table 2. The
values of
from Moujtahid et al.
(1999) and Zorec (2000) and present them in Table 2. The
values of
![]() for given spectral subgroups (presented in
Table 1) have been calculated taking into account the specific population
of stars of different spectral subtypes and luminosity classes in a
subgroup. Simple calculations indicate that the differences between the mean
values of
for given spectral subgroups (presented in
Table 1) have been calculated taking into account the specific population
of stars of different spectral subtypes and luminosity classes in a
subgroup. Simple calculations indicate that the differences between the mean
values of
![]() (or
(or
![]() )
for all spectral
subgroups of III-IV luminosity classes are insignificant. There is, however,
a pronounced trend in the ratio
)
for all spectral
subgroups of III-IV luminosity classes are insignificant. There is, however,
a pronounced trend in the ratio
![]() for these stars.
For the V class, no differences were found between the O-B1.5 and B2-B2.5
subgroups, as well as between subgroups B3-B5.5 and B6-B9.5. Nevertheless,
for the subgroups O-B2.5 and B3-B9.5, there is strong statistically
significant difference at the 99% confidence level in agreement with the
result of Fukuda (1982) who found a clear distinction in
for these stars.
For the V class, no differences were found between the O-B1.5 and B2-B2.5
subgroups, as well as between subgroups B3-B5.5 and B6-B9.5. Nevertheless,
for the subgroups O-B2.5 and B3-B9.5, there is strong statistically
significant difference at the 99% confidence level in agreement with the
result of Fukuda (1982) who found a clear distinction in ![]() between B2 and B3 stars. For reference, we present in Table 1 the
between B2 and B3 stars. For reference, we present in Table 1 the
![]() data from other sources. The data of Fukuda
(1982) (from his Table 5) were transformed into the "new''
Slettebak's scale. As follows from Table 1, most early determined values are
in agreement (in general) with our data (obtained with 2 to 3 times better
statistical quality).
data from other sources. The data of Fukuda
(1982) (from his Table 5) were transformed into the "new''
Slettebak's scale. As follows from Table 1, most early determined values are
in agreement (in general) with our data (obtained with 2 to 3 times better
statistical quality).
We confirm that late type Be stars rotate faster on average than early types
and the trend in the ratio
![]() (see Table 1) is
also real. We conclude that late type Be stars of all luminosity classes
rotate closer to their critical break-up velocity. Whether these differences
have affect on the physical characteristics of CS envelopes, or not, will be
considered in Sect. 8.
(see Table 1) is
also real. We conclude that late type Be stars of all luminosity classes
rotate closer to their critical break-up velocity. Whether these differences
have affect on the physical characteristics of CS envelopes, or not, will be
considered in Sect. 8.
Finally, it was found that the ratio
![]() (or
(or
![]() )
increases from dwarfs to sub-giants/giants for
early spectral type stars (O-B1.5 and B2) though not obvious for middle and
late spectral types (see Table 1). This clearly contradicts the results
of Steele (1999) who investigated a small sample of Be stars
separated into three subgroups according to the luminosity class
(III, IV, V-13, 8 and 34 objects respectively). Although our
statistical study for sub-giants and giants is also not based on a large
sample (135 objects), the behaviour is clearer for the sequence of
)
increases from dwarfs to sub-giants/giants for
early spectral type stars (O-B1.5 and B2) though not obvious for middle and
late spectral types (see Table 1). This clearly contradicts the results
of Steele (1999) who investigated a small sample of Be stars
separated into three subgroups according to the luminosity class
(III, IV, V-13, 8 and 34 objects respectively). Although our
statistical study for sub-giants and giants is also not based on a large
sample (135 objects), the behaviour is clearer for the sequence of
![]() luminosity classes
(see Table 3). This phenomenon can be easily explained in terms of a
more rapid evolution of high-mass stars and the acceleration of their
rotation. The main sequence lifetime is significantly shorter for B0 stars
than for B9 stars (see, for example, Bisnovatyi-Kogan 1989). It
may be supposed that most of O-B1.5 and B2 stars of III and IV luminosity
classes are possibly in the secondary contraction phase but, on average,
the late spectral type stars are not.
luminosity classes
(see Table 3). This phenomenon can be easily explained in terms of a
more rapid evolution of high-mass stars and the acceleration of their
rotation. The main sequence lifetime is significantly shorter for B0 stars
than for B9 stars (see, for example, Bisnovatyi-Kogan 1989). It
may be supposed that most of O-B1.5 and B2 stars of III and IV luminosity
classes are possibly in the secondary contraction phase but, on average,
the late spectral type stars are not.
| Spectral type: | O-B1.5 | B2-B2.5 | B3-B5 | B6-B9 |
|
|
0.38 | 0.43 | 0.53 | 0.61 |
|
|
0.43 | 0.49 | 0.50 | 0.64 |
|
|
0.46 | 0.56 | 0.51 | 0.65 |
As already mentioned, a detailed study of near IR excesses of classical
Be stars was undertaken by Dougherty et al. (1994). They used
near IR excesses for a sample of 144 Be stars (115 stars with E(V-L) data)
for statistical analysis. One of the conclusions was that the excess
increases with wavelength and 60% of Be stars exhibit a significant excess
in the L band. They also found a bi-modal distribution of the excesses for
the wavelengths greater than 2.2 ![]() m but they did not study this behaviour
in detail. For this reason, we investigate here the distributions of E(V-L)colour excesses. We have collected the data of V and L photometry for
m but they did not study this behaviour
in detail. For this reason, we investigate here the distributions of E(V-L)colour excesses. We have collected the data of V and L photometry for
![]() 200 stars and, for an additional 40 stars, the values of E(V-L)were estimated by an extrapolation of JHK data. Thus, by essentially
doubling the size of the data base over Dougherty et al. (1994),
we are able to compare the E(V-L) distributions for different subgroups of
Be stars.
200 stars and, for an additional 40 stars, the values of E(V-L)were estimated by an extrapolation of JHK data. Thus, by essentially
doubling the size of the data base over Dougherty et al. (1994),
we are able to compare the E(V-L) distributions for different subgroups of
Be stars.
![\begin{figure}
\par\includegraphics[width=7.8cm,height=4.5cm,clip]{9470f4a.ps}\p...
...ce*{2mm}
\includegraphics[width=7.8cm,height=4.5cm,clip]{9470f4d.ps}\end{figure}](/articles/aa/full/2001/12/aa9470/Timg152.gif) |
Figure 4: Observed distributions of E(V-L) (corrected for errors) for different subgroups of Be stars. The short-dashed and long-dashed vertical lines indicate the positions of two peaks for a bi-modal Gaussian distribution |
| Open with DEXTER | |
The distribution of E(V-L) for the entire sample shows the same bi-modal
shape behaviour as described by Dougherty et al. (1994) but in a
more pronounced form. We performed the same procedure for error correction
of the histograms as in the previous section.
| Subgroup: | O-B1 | B2 | B3-B5 | B6-B9 |
| N stars: | 57 | 59 | 58 | 67 |
|
|
0.93 | 0.72 | 0.41 | 0.17 |
| N stars: | 29 | 38 | 38 | 40 |
|
|
1.90 | 1.59 | 1.39 | 0.72 |
| Parameters of bi-modal Gaussian fits for E(V-L) | ||||
| Peak 1:
|
|
|
|
|
| Peak 1:
|
|
|
|
|
| Peak 2:
|
|
|
|
|
| Peak 2:
|
|
|
|
|
| Parameters of bi-modal Gaussian fits for E(V-12) | ||||
| Peak 1:
|
0.75 ? |
|
? |
|
| Peak 1:
|
|
|
||
| Peak 2:
|
|
|
|
|
| Peak 2:
|
|
|
|
|
Firstly, late spectral type stars exhibit smaller values of E(V-L) on
average (see Table 4), this already mentioned in Sect. 4 and noted earlier
by Dougherty et al. (1991, 1994), possibly due to a
lower electron density in their CS environment. It is obvious from Fig. 4
and in Table 4, that a bi-modal form is present for the first three spectral
subgroups of Be stars (O-B1.5, B2-B2.5 and B3-B5.5). For these subgroups,
the mean values of E(V-L) corresponding to the first peak are approximately
the same, within the length of the sampling step, with
![]() .
Statistical
analyses, similar to those made in previous section, indicate that all the
distributions may be well approximated by a bi-modal Gaussian form.
This bi-modality for O-B1.5, B2-B2.5 and B3-B5.5 spectral subgroups is
confirmed to a 99% level of confidence. We performed a more detailed study
of the B3-B5.5 spectral subgroup and found that a bi-modal distribution
is present for B3 type stars with two peaks centered at
.
Statistical
analyses, similar to those made in previous section, indicate that all the
distributions may be well approximated by a bi-modal Gaussian form.
This bi-modality for O-B1.5, B2-B2.5 and B3-B5.5 spectral subgroups is
confirmed to a 99% level of confidence. We performed a more detailed study
of the B3-B5.5 spectral subgroup and found that a bi-modal distribution
is present for B3 type stars with two peaks centered at
![]() and
and
![]() ), but bi-modality
is not present for B4-B5 stars. For B6-B9.5 stars, the distribution also
does not exhibit bi-modality and the mean value of E(V-L) for the best
simple Gaussian fit is the same as the first peaks for other subgroups.
), but bi-modality
is not present for B4-B5 stars. For B6-B9.5 stars, the distribution also
does not exhibit bi-modality and the mean value of E(V-L) for the best
simple Gaussian fit is the same as the first peaks for other subgroups.
![\begin{figure}
\par\includegraphics[width=8cm,height=7cm,clip]{9470f5.ps}\end{figure}](/articles/aa/full/2001/12/aa9470/Timg195.gif) |
Figure 5: Observed distributions of E(V-12) (corrected from errors) for the entire sample of Be stars. The short-dashed and long-dashed lines indicate the position of two peaks for a bi-modal Gaussian distribution |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.8cm,height=4.5cm,clip]{9470f6a.ps}\p...
...ce*{2mm}
\includegraphics[width=7.8cm,height=4.5cm,clip]{9470f6d.ps}\end{figure}](/articles/aa/full/2001/12/aa9470/Timg196.gif) |
Figure 6: Observed distributions of E(V-12) (corrected from errors) for different subgroups of Be stars. The short-dashed and long-dashed lines indicate the positions of the two peaks for a bi-modal Gaussian distribution |
| Open with DEXTER | |
The important difference between the various bi-modal distributions is that
the second peak has its maximum at different values of E(V-L). The behaviour
is that for early spectral types, the second peak appears at larger values of
E(V-L). This difference is clearly obvious in a numerical form in Table 4
where the parameters of these distributions are given. Using a t-test and
T-test, it is easy to demonstrate that the differences between the positions
of the second peaks are statistically significant at the 99% confidence
level. Note that, for the optically thin case, the excess emission in the
near IR is proportional to the emission measure which is a function of the
mean electron density in formation regions and the ionizing stellar fluxes.
It is easy to show from our data that the changes in
![]() may be well described by a linear function of
may be well described by a linear function of
![]() in
the form:
in
the form:
![]() .
The predicted
.
The predicted
![]() values correspond well to the observed
values.
values correspond well to the observed
values.
![\begin{figure}
\par\includegraphics[width=7.8cm,height=7.2cm,clip]{9470f7.ps}\end{figure}](/articles/aa/full/2001/12/aa9470/Timg200.gif) |
Figure 7:
E(V-12) colour excess versus spectral type for the entire
sample of Be stars. The upper limit is indicated by the solid line. The
long-dashed line indicates the value of |
| Open with DEXTER | |
It is of interest to compare the behavior of E(V-L) with that for
far IR excesses at ![]() m. Dougherty et al. (1994),
with the reference to a private communication of Waters, mentioned
the presence of bi-modality of the E(V-12) distribution for Be
stars. To check this suggestion we constructed the similar diagrams
for E(V-12). Although bi-modality is clearly seen for the entire
sample of Be stars (Fig. 5), it reflects rather the different
contributions of early and late type stars. Our sample is
insufficiently large to provide any conclusion on bi-modality for
different spectral subgroups. Slight evidence of two peaks in the
E(V-12) distribution exists only for B2 stars (see Fig. 6). An
important point, however, is that the average value of
m. Dougherty et al. (1994),
with the reference to a private communication of Waters, mentioned
the presence of bi-modality of the E(V-12) distribution for Be
stars. To check this suggestion we constructed the similar diagrams
for E(V-12). Although bi-modality is clearly seen for the entire
sample of Be stars (Fig. 5), it reflects rather the different
contributions of early and late type stars. Our sample is
insufficiently large to provide any conclusion on bi-modality for
different spectral subgroups. Slight evidence of two peaks in the
E(V-12) distribution exists only for B2 stars (see Fig. 6). An
important point, however, is that the average value of
![]() and the position of the maximum peak in the
distributions is not significantly different between the first
three subgroups (see Table 4). Coté & Waters (1987)
considered the far IR data for a sample of 101 Be stars and found
the constant upper limit in E(V-12) for stars earlier than B3.
The same conclusion follows from the analysis of our data for 150
objects (see Fig. 7). This indicates that the characteristics of
the outer parts of CS envelopes are similar for early and middle
spectral type stars. For the majority of Be stars, with the excess
emission increasing with wavelength, the CS envelopes must become
optically thick from at least
and the position of the maximum peak in the
distributions is not significantly different between the first
three subgroups (see Table 4). Coté & Waters (1987)
considered the far IR data for a sample of 101 Be stars and found
the constant upper limit in E(V-12) for stars earlier than B3.
The same conclusion follows from the analysis of our data for 150
objects (see Fig. 7). This indicates that the characteristics of
the outer parts of CS envelopes are similar for early and middle
spectral type stars. For the majority of Be stars, with the excess
emission increasing with wavelength, the CS envelopes must become
optically thick from at least
![]() m (Gehrz et al.
1974). With this assumption, for any kind of geometry for
the CS environment, the excess E(V-12) is proportional to the
effective surface area of the emitting region. It is easy to show
that the relation between the upper limit of the excess E(V-12)and
m (Gehrz et al.
1974). With this assumption, for any kind of geometry for
the CS environment, the excess E(V-12) is proportional to the
effective surface area of the emitting region. It is easy to show
that the relation between the upper limit of the excess E(V-12)and ![]() will be fairly linear for B3-B9 stars in contrast
to the E(V-L):
will be fairly linear for B3-B9 stars in contrast
to the E(V-L): ![]() relation. But the behaviour in
early type stars is more complicated.
relation. But the behaviour in
early type stars is more complicated.
An unresolved point is the nature of the peak 1 in the E(V-L) distributions
for early and intermediate spectral type stars. There are several
possibilities to explain the value of
![]() for some objects:
for some objects:
a)
there are many Be stars surrounded by small CS
envelopes indicated by low emission in H![]() ;
;
b)
the photometric data of V and L used for calculation
of the E(V-L) excesses were obtained mainly non-simultaneously;
c)
spectral classification of some early type stars can be dubious.
For case (a), we would expect a lower
![]() values for the stars
which are concentrated under peak 1. Although the analysis of our data
shows some decrease in the polarization level for such stars in comparison
with peak 2, the difference in
values for the stars
which are concentrated under peak 1. Although the analysis of our data
shows some decrease in the polarization level for such stars in comparison
with peak 2, the difference in
![]() for the two peaks is
small and insignificant (see Table 5).
for the two peaks is
small and insignificant (see Table 5).
| Subgroup: | O-B1 | B2 | B3-B5 | |||
| peak 1 | peak 2 | peak 1 | peak 2 | peak 1 | peak 2 | |
|
|
|
|
|
|
|
|
| N stars: | 26 | 26 | 16 | 38 | 26 | 20 |
|
|
0.57 | 0.85 | 0.52 | 0.63 | 0.42 | 0.52 |
For the cases (b) and (c), we would expect a more single-peaked
distribution with more extended tails rather than a bi-modal
distribution. Finally, it should be remembered that each Be star
can show at any time one of the phases -
normal B
![]() Be
Be
![]() Be-shell. These phases are
characterized by different spectral behaviours (a normal absorption-line
spectrum or emission/shell spectrum) due to changes of electron density
and/or of geometry of the CS envelopes (Doazan et al. 1988). There
is no doubt that during the normal B phase, the electron density is too
small to produce any considerable IR excess. According to Dougherty et al.
(1994), for the IR excess in the L-band to be detectable, the
density of the CS plasma has to be
Be-shell. These phases are
characterized by different spectral behaviours (a normal absorption-line
spectrum or emission/shell spectrum) due to changes of electron density
and/or of geometry of the CS envelopes (Doazan et al. 1988). There
is no doubt that during the normal B phase, the electron density is too
small to produce any considerable IR excess. According to Dougherty et al.
(1994), for the IR excess in the L-band to be detectable, the
density of the CS plasma has to be ![]()
![]() .
To
account for the maximum level of
.
To
account for the maximum level of
![]() observed
for the stars under peak 1 (with the above value of density and typical sizes
of CS environment
observed
for the stars under peak 1 (with the above value of density and typical sizes
of CS environment ![]()
![]() ), in the framework of the
disk model, the half-opening angle of the disk cannot be smaller than
10
), in the framework of the
disk model, the half-opening angle of the disk cannot be smaller than
10![]() to 15
to 15![]() .
The important point is that in order to explain a
bi-modal character of the distributions, one can suggest that the transition
time between the normal B and Be/Be-shell phases is much shorter than the
duration of the phases themselves. In this case, we can observe an object
either at the normal B phase (with
.
The important point is that in order to explain a
bi-modal character of the distributions, one can suggest that the transition
time between the normal B and Be/Be-shell phases is much shorter than the
duration of the phases themselves. In this case, we can observe an object
either at the normal B phase (with
![]() )
or at the Be/Be-shell
phase with E(V-L) values from the distribution under peak 2. In principle,
our suggestion is supported by the data of Doazan et al. (1986),
who found significant spectral variations in
)
or at the Be/Be-shell
phase with E(V-L) values from the distribution under peak 2. In principle,
our suggestion is supported by the data of Doazan et al. (1986),
who found significant spectral variations in ![]() CrB on a time scale of
3 months when the star changed its phase from shell to normal. At the same
time, the duration of the phases in Be stars (or an envelope lifetime) is
typically of the order of decades (Cramer et al. 1995;
Fox 1991). Our suggestion is consistent also with the hypothesis
that the formation of CS envelopes in Be stars is due to short lasting
huge mass ejections (Hubert & Floquet 1998; Moujtahid et al.
1999; Zorec et al. 2000a, 2000b). All the above
may be also valid to explain bi-modality in E(V-12) distributions (if it
exists). Hubert-Delplace et al. (1981) and Mennickent et al.
(1994) noted that the time scale of phase transitions is shorter
in early-type Be stars than in late spectral types. Thus we would expect less
pronounced bi-modality in late types too, this not being obvious in our data.
The apparent absence of bi-modality for late spectral types (B4-B5 and
B6-B9.5) can be explained by the notion that the second peak would be placed
toward smaller values of E(V-L). Its possible location is perhaps masked
by a combination of the chosen binwidth in association with the small
statistical sample.
CrB on a time scale of
3 months when the star changed its phase from shell to normal. At the same
time, the duration of the phases in Be stars (or an envelope lifetime) is
typically of the order of decades (Cramer et al. 1995;
Fox 1991). Our suggestion is consistent also with the hypothesis
that the formation of CS envelopes in Be stars is due to short lasting
huge mass ejections (Hubert & Floquet 1998; Moujtahid et al.
1999; Zorec et al. 2000a, 2000b). All the above
may be also valid to explain bi-modality in E(V-12) distributions (if it
exists). Hubert-Delplace et al. (1981) and Mennickent et al.
(1994) noted that the time scale of phase transitions is shorter
in early-type Be stars than in late spectral types. Thus we would expect less
pronounced bi-modality in late types too, this not being obvious in our data.
The apparent absence of bi-modality for late spectral types (B4-B5 and
B6-B9.5) can be explained by the notion that the second peak would be placed
toward smaller values of E(V-L). Its possible location is perhaps masked
by a combination of the chosen binwidth in association with the small
statistical sample.
As was noted before, (see Sect. 4.1 and Fig. 2b), Be stars of earlier
spectral type tend to exhibit larger values of intrinsic polarization.
Thanks to the large bank of calculated values of ![]() (
(![]() 500
objects), it is possible to investigate the above mentioned behaviour in
detail.
500
objects), it is possible to investigate the above mentioned behaviour in
detail.
| Spectral type: | O-B0 | B1 | B2 | B3 | B4 | B5 | B6 | B7 | B8 | B9 | |
| No. of stars: | 47 | 118 | 146 | 58 | 22 | 25 | 20 | 23 | 23 | 11 | |
|
|
0.83 | 0.85 | 0.75 | 0.59 | 0.52 | 0.48 | 0.47 | 0.45 | 0.29 | 0.22 | |
|
|
1.25 | 1.28 | 1.13 | 0.88 | 0.78 | 0.72 | 0.70 | 0.67 | 0.43 | 0.33 | |
| Spectral range | O-B1.5 | B2-B2.5 | B3-B5.5 | B6-B9.5 | O-B9.5 | ||||||
| No. of stars: | 166 | 146 | 105 | 77 | 495 | ||||||
|
|
0.84 0.48 | 0.75 0.48 | 0.55 0.48 | 0.37 0.28 | 0.68 0.48 | ||||||
|
|
1.27 | 1.13 | 0.82 | 0.56 | 1.02 | ||||||
Analysis of the intrinsic polarization distribution for classical Be
stars was first performed by McLean & Brown (1978) for a sample
of 67 objects. They noted a rapid rise of the distribution toward
smaller values of
![]() .
The distribution established here (corrected
for errors) for a sample of 495 objects (see Fig. 8) is similar to that
obtained by McLean & Brown (1978). However, with the chosen
binwidth (0.3%), our distribution peaks at
.
The distribution established here (corrected
for errors) for a sample of 495 objects (see Fig. 8) is similar to that
obtained by McLean & Brown (1978). However, with the chosen
binwidth (0.3%), our distribution peaks at
![]() with the
average weighted value
with the
average weighted value
![]() and
and
![]() .
Our large sample allows us also to study for the first time the distributions
of
.
Our large sample allows us also to study for the first time the distributions
of
![]() for the representative samples of Be stars of different
spectral subgroups. These distributions, also error corrected, are shown in
Figs. 9a-c. For O-B1.5 stars we used a slightly larger binwidth (0.35%)
because of the possibly larger uncertainties in determination of interstellar
components. It is clearly seen that the histograms are significantly
different for each spectral subgroup. In contrast to late type stars, the
distributions for early spectral types (O-B1.5 and B2-B2.5) do not peak at
the value
for the representative samples of Be stars of different
spectral subgroups. These distributions, also error corrected, are shown in
Figs. 9a-c. For O-B1.5 stars we used a slightly larger binwidth (0.35%)
because of the possibly larger uncertainties in determination of interstellar
components. It is clearly seen that the histograms are significantly
different for each spectral subgroup. In contrast to late type stars, the
distributions for early spectral types (O-B1.5 and B2-B2.5) do not peak at
the value
![]() .
This result is significant in spite of the
relatively large standard deviations (see Table 6). Similar to the analysis
for E(V-L) distributions, we performed a more detailed study of the
B3-B5 spectral subgroup and found again that such behaviour is present
with just B3 stars, but it disappears for B4-B5 stars.
.
This result is significant in spite of the
relatively large standard deviations (see Table 6). Similar to the analysis
for E(V-L) distributions, we performed a more detailed study of the
B3-B5 spectral subgroup and found again that such behaviour is present
with just B3 stars, but it disappears for B4-B5 stars.
![\begin{figure}
\par\includegraphics[width=7cm,height=7cm,clip]{9470f8.ps}\end{figure}](/articles/aa/full/2001/12/aa9470/Timg223.gif) |
Figure 8: Distribution of intrinsic polarization (corrected for errors) for the entire sample of Be stars. The vertical dashed line indicates the mean value of polarization |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.1cm,height=4cm,clip]{9470f9a.ps}\par...
...pace*{2mm}
\includegraphics[width=7.1cm,height=4cm,clip]{9470f9d.ps}\end{figure}](/articles/aa/full/2001/12/aa9470/Timg224.gif) |
Figure 9: Distributions of intrinsic polarization (corrected for errors) for different spectral subgroups of Be stars. The vertical dashed line indicates the mean value of polarization |
| Open with DEXTER | |
The next point to consider is the possible differences in polarization
of Be and Be-shell stars. This comparison is quite important as there is
active debate on the change in the structure of CS envelopes of Be and
Be-shell stars (Marborough et al. 1993; Hanuschik 1996;
van Kerkwijk et al. 1995). It was found earlier that for some
objects, the level of polarization increases when a star goes through a
shell phase (Arsenijevic et al. 1987). Using a small statistical
sample, Fox (1993b) noted a little higher level of polarization of
Be-shell stars (12 objects,
![]() )
in comparison with non-shell
stars (21 objects,
)
in comparison with non-shell
stars (21 objects,
![]() )
(note, however, the magnitudes of the
errors). On the other hand, Ghosh et al. (1999) found no distinction
in polarization level between 24 Be and 5 Be-shell stars. Using the data of
Hanuschik (1996) we are able to identify 46 Be-shell stars which have
shown shell characteristics at some point in their observed history and
compare their behaviour with others. The average values of the parameters
for non-shell stars have been calculated using the data from Tables 4 and 6
for the same specific population of stars of different spectral subtypes as
in the shell subgroup. As follows from Table 7, no differences (in
polarization and IR excesses) exist between Be non-shell and Be-shell stars.
A compilation of polarimetric data for Pleione (see WUPPOL 1999)
for different phases (Be and Be-shell) also shows the absence of a
significant changes in the polarization level. This suggests that the phase
transition Be
)
(note, however, the magnitudes of the
errors). On the other hand, Ghosh et al. (1999) found no distinction
in polarization level between 24 Be and 5 Be-shell stars. Using the data of
Hanuschik (1996) we are able to identify 46 Be-shell stars which have
shown shell characteristics at some point in their observed history and
compare their behaviour with others. The average values of the parameters
for non-shell stars have been calculated using the data from Tables 4 and 6
for the same specific population of stars of different spectral subtypes as
in the shell subgroup. As follows from Table 7, no differences (in
polarization and IR excesses) exist between Be non-shell and Be-shell stars.
A compilation of polarimetric data for Pleione (see WUPPOL 1999)
for different phases (Be and Be-shell) also shows the absence of a
significant changes in the polarization level. This suggests that the phase
transition Be
![]() Be-shell has no strong affect on the
parameters describing the inner parts of the disks. Note, however, that all
Be-shell stars show significant variability in photometry and polarimetry
and the averaging over a long period is not a correct procedure. For this
reason, the above discussion can be considered as only a preliminary
suggestion. A statistical analysis of the rotational characteristics of
Be-shell stars is much more informative as their
Be-shell has no strong affect on the
parameters describing the inner parts of the disks. Note, however, that all
Be-shell stars show significant variability in photometry and polarimetry
and the averaging over a long period is not a correct procedure. For this
reason, the above discussion can be considered as only a preliminary
suggestion. A statistical analysis of the rotational characteristics of
Be-shell stars is much more informative as their ![]() values do not
depend on the phase changes. In this context it is interesting to investigate
an inclination aspect of Be and Be-shell stars as discussed earlier by
Moujtahid et al. (1999). Although the errors are large, the mean
viewing angle ("i'') of Be-shell stars derived from the ratio
values do not
depend on the phase changes. In this context it is interesting to investigate
an inclination aspect of Be and Be-shell stars as discussed earlier by
Moujtahid et al. (1999). Although the errors are large, the mean
viewing angle ("i'') of Be-shell stars derived from the ratio
![]() is larger on average than that for other
Be stars (
is larger on average than that for other
Be stars (
![]() and
and
![]() respectively). Thus,
Be-shell stars are viewed closer to the CS disk plane and none of them are
observed at the angle less than
respectively). Thus,
Be-shell stars are viewed closer to the CS disk plane and none of them are
observed at the angle less than
![]() .
.
| E(V-L) | E(V-12) | ||
| Be-shell (N stars) | 0.61 |
|
|
| non-shell (N stars) | 0.57 |
|
|
The last point for consideration is a deviation of the distribution peaks
from
![]() for early type stars. Although the problems in detection
of the peak in a distribution with very small values of p are discussed by
McLean & Brown (1978), the differences detected here are probably
real. The first possibility to explain the behaviour is that most early type
stars in our sample are more distant objects. The estimates of interstellar
components for them are not so precise, so that the displacement from 0%
can be attributed to inaccuracy of its removal. On the other hand, the
behaviour can be explained if the suggestion on the randomly oriented
rotation axes of envelopes is not true. This point will be discussed in a
separate paper. Finally, it may be due to more complicated geometries
associated with the CS environments of early-type stars.
for early type stars. Although the problems in detection
of the peak in a distribution with very small values of p are discussed by
McLean & Brown (1978), the differences detected here are probably
real. The first possibility to explain the behaviour is that most early type
stars in our sample are more distant objects. The estimates of interstellar
components for them are not so precise, so that the displacement from 0%
can be attributed to inaccuracy of its removal. On the other hand, the
behaviour can be explained if the suggestion on the randomly oriented
rotation axes of envelopes is not true. This point will be discussed in a
separate paper. Finally, it may be due to more complicated geometries
associated with the CS environments of early-type stars.
An excellent discussion on the problems of analysis of the polarization distribution of classical Be stars has been presented by McLean & Brown (1978), and a detailed discussion of near and far IR characteristics was made by Coté & Waters (1987) and Dougherty et al. (1991, 1994). Such kind of theoretical work is beyond the purpose of our paper and we will discuss some of our results only briefly. Our very large statistical sample allows us to explore possible correlations between the parameters discussed here and to make some suggestions on CS envelope geometries.
First, no clear correlations exist between the intrinsic polarization and
near IR excesses neither for a sample of 209 stars (see Fig. 10a) nor for
different spectral subgroups.
![\begin{figure}
\par\includegraphics[width=7.2cm,height=6.8cm,clip]{9470f10a.ps}\...
...e*{2mm}
\includegraphics[width=7.2cm,height=6.8cm,clip]{9470f10b.ps}\end{figure}](/articles/aa/full/2001/12/aa9470/Timg251.gif) |
Figure 10: Correlation between near a) and far b) IR excesses and intrinsic polarization for the entire sample of Be stars |
| Open with DEXTER | |
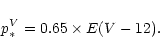 |
(5) |
Note that although the correlation between near and far IR excesses clearly
exists (with a correlation coefficient of
![]() ), there is a
significant scattering of the data points (see Fig. 11).
), there is a
significant scattering of the data points (see Fig. 11).
![\begin{figure}
\par\includegraphics[width=7.2cm,height=6.8cm,clip]{9470f11.ps}\end{figure}](/articles/aa/full/2001/12/aa9470/Timg257.gif) |
Figure 11:
Correlation between near and far IR excesses for the entire sample of
Be stars. The dashed lines represent a possible non-linear fit for the
observational data for E(V-L):
|
| Open with DEXTER | |
On the one hand, the behaviour can be due to the fact that CS envelopes are
optically thin at 3.5 ![]() m but optically thick at
m but optically thick at
![]() m
(Gehrz et al. 1974). This may lead to the behaviour indicated
for E(V-L):
m
(Gehrz et al. 1974). This may lead to the behaviour indicated
for E(V-L):
![]() )
dependencies. The theoretical
interpretation of these dependencies is beyond the purpose of our paper
note, however, that a similar behaviour was discussed theoretically by
Dougherty et al. (1994). The regions of large E(V-L) and
E(V-12) values in Fig. 11 are occupied mainly by early type stars
(see Fig. 2a and Coté & Waters 1987). These hotter stars can
ionize larger volumes of CS matter, leading to the increase in E(V-L)excesses). Poeckert & Marborough (1982) noted that the dramatic
change in ionization structure of CS envelopes is obvious around
)
dependencies. The theoretical
interpretation of these dependencies is beyond the purpose of our paper
note, however, that a similar behaviour was discussed theoretically by
Dougherty et al. (1994). The regions of large E(V-L) and
E(V-12) values in Fig. 11 are occupied mainly by early type stars
(see Fig. 2a and Coté & Waters 1987). These hotter stars can
ionize larger volumes of CS matter, leading to the increase in E(V-L)excesses). Poeckert & Marborough (1982) noted that the dramatic
change in ionization structure of CS envelopes is obvious around
![]() K corresponding to spectral types
B4-B6. At the same time the effective surface area of the emitting regions
which are responsible for the excess E(V-12) for B0-B5 stars does not
change strongly (see previous section). On the other hand, it is possible to
suggest the presence of an additional component to CS envelopes for early
spectral type objects close to the star which may be responsible for an
increase of near IR excesses. The absence of this second component in late
type stars leads to the increase of correlation coefficients for
E(V-L): E(V-12) dependence from B2 to B9 stars.
K corresponding to spectral types
B4-B6. At the same time the effective surface area of the emitting regions
which are responsible for the excess E(V-12) for B0-B5 stars does not
change strongly (see previous section). On the other hand, it is possible to
suggest the presence of an additional component to CS envelopes for early
spectral type objects close to the star which may be responsible for an
increase of near IR excesses. The absence of this second component in late
type stars leads to the increase of correlation coefficients for
E(V-L): E(V-12) dependence from B2 to B9 stars.
![\begin{figure}
\par\includegraphics[width=7.1cm,height=6.7cm,clip]{9470f12a.ps}\...
...e*{2mm}
\includegraphics[width=7.1cm,height=6.7cm,clip]{9470f12b.ps}\end{figure}](/articles/aa/full/2001/12/aa9470/Timg265.gif) |
Figure 12:
Correlation between near a) and far b) IR excesses with |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.2cm,height=6.6cm,clip]{9470f13a.ps}\...
...e*{2mm}
\includegraphics[width=7.2cm,height=6.6cm,clip]{9470f13b.ps}\end{figure}](/articles/aa/full/2001/12/aa9470/Timg266.gif) |
Figure 13:
Correlation between near a) and far b) IR excesses with the ratio of
|
| Open with DEXTER | |
Another important negative result is the absence of any correlation between
near-far IR excesses and
![]() for 220 and 118 Be stars
respectively (see Figs. 12a,b) (and for any spectral subgroup considered
separately). This behaviour may result from the small optical depth of CS
environment for the majority of Be stars in the near IR. Another possibility
to account for this behaviour is a suggestion of either a more spherical
geometry for the CS environment where the near IR emission arises or the
presence of two independent regions - a disk component and a spherical
component or polar lobes, both responsible for the near IR emission. The
suggestion on two distinct regions in CS environment in classical Be stars
(a diffuse polar stellar wind and a dense equatorial disk) is discussed
currently in literature (see, for example, Porter, 1998 and
references therein). Moreover, in context of polarization modeling, Fox
(1991) supposed that for some Be stars the polar region can be the
dominant source of free electrons. To minimize the uncertainties due to
mixing in a same diagram involving stars with different masses and
luminosity classes, we re-construct Fig. 12 using the ratio
for 220 and 118 Be stars
respectively (see Figs. 12a,b) (and for any spectral subgroup considered
separately). This behaviour may result from the small optical depth of CS
environment for the majority of Be stars in the near IR. Another possibility
to account for this behaviour is a suggestion of either a more spherical
geometry for the CS environment where the near IR emission arises or the
presence of two independent regions - a disk component and a spherical
component or polar lobes, both responsible for the near IR emission. The
suggestion on two distinct regions in CS environment in classical Be stars
(a diffuse polar stellar wind and a dense equatorial disk) is discussed
currently in literature (see, for example, Porter, 1998 and
references therein). Moreover, in context of polarization modeling, Fox
(1991) supposed that for some Be stars the polar region can be the
dominant source of free electrons. To minimize the uncertainties due to
mixing in a same diagram involving stars with different masses and
luminosity classes, we re-construct Fig. 12 using the ratio
![]() instead of the values of
instead of the values of ![]() .
However, as follows
from Fig. 13, no correlations appear even with this adjustment. As was noted
above, however, CS envelopes are optically thick at 12
.
However, as follows
from Fig. 13, no correlations appear even with this adjustment. As was noted
above, however, CS envelopes are optically thick at 12 ![]() m. In the
framework of this assumption, strongly flattened disks would produce high
colour excesses for the case of pole-on orientation and significantly lower
excesses at high inclinations (edge-on). For the geometrically thick disks
(with
m. In the
framework of this assumption, strongly flattened disks would produce high
colour excesses for the case of pole-on orientation and significantly lower
excesses at high inclinations (edge-on). For the geometrically thick disks
(with
![]() )
we would expect an opposite behaviour, namely high
excesses at
)
we would expect an opposite behaviour, namely high
excesses at
![]() and lower excesses at
and lower excesses at
![]() .
The absence of
correlations between E(V-12) and
.
The absence of
correlations between E(V-12) and ![]() indicates that the effective
surface area of emitting regions is approximately equal for pole-on
(
indicates that the effective
surface area of emitting regions is approximately equal for pole-on
(
![]() )
and edge-on
(
)
and edge-on
(
![]() )
cases, where R is the radius
of the disk and
)
cases, where R is the radius
of the disk and ![]() is its half-opening angle. Regarding the disk-like
structure, from simple geometrical considerations, this is realized for disks
with a half-opening angle
is its half-opening angle. Regarding the disk-like
structure, from simple geometrical considerations, this is realized for disks
with a half-opening angle
![]() .
Such behaviour can never be
obtained for ellipsoidal envelopes as the effective surface area (and thus
E(V-12)) would be always larger for a pole-on orientation! In addition,
note that according to Fox (1991, 1994) optically thin
ellipsoidal envelopes are unable to produce polarizations in excess of 1.2%.
Thus, the implication of this configuration of CS envelopes is at least
questionable. Assuming
.
Such behaviour can never be
obtained for ellipsoidal envelopes as the effective surface area (and thus
E(V-12)) would be always larger for a pole-on orientation! In addition,
note that according to Fox (1991, 1994) optically thin
ellipsoidal envelopes are unable to produce polarizations in excess of 1.2%.
Thus, the implication of this configuration of CS envelopes is at least
questionable. Assuming
![]() ,
for the difference
in E(V-12) not to be detectable at 3
,
for the difference
in E(V-12) not to be detectable at 3![]() level, the ratio of
the effective surface areas for pole-on and edge-on disks cannot exceed 0.6.
With this ratio the range of the half-opening angle of CS disks is
level, the ratio of
the effective surface areas for pole-on and edge-on disks cannot exceed 0.6.
With this ratio the range of the half-opening angle of CS disks is
![]() .
Waters (1986) showed that for a disk with
.
Waters (1986) showed that for a disk with
![]() ,
the effect of inclination on the excess flux cannot be
negligible for
,
the effect of inclination on the excess flux cannot be
negligible for
![]() .
Our estimate of
.
Our estimate of ![]() is in agreement with
that of Waters (1986) and Hanuschik (1996) but it clearly
contradicts theoretical predictions for WCD models of Bjorkman & Cassinelli
(1993) and Owocki et al. (1994). De Araújo et al.
(1994) have determined the angle of a CS envelope where the density
has decreased by a factor of 1/e with respect to the equatorial value as
about
is in agreement with
that of Waters (1986) and Hanuschik (1996) but it clearly
contradicts theoretical predictions for WCD models of Bjorkman & Cassinelli
(1993) and Owocki et al. (1994). De Araújo et al.
(1994) have determined the angle of a CS envelope where the density
has decreased by a factor of 1/e with respect to the equatorial value as
about
![]() which is also in agreement with our data. Our large
statistical sample allows us to suggest that any uncertainties due to
non-simultaneous observations and/or variability of observed parameters
should not affect the results significantly and the lack of any strong
correlations is a real outcome.
which is also in agreement with our data. Our large
statistical sample allows us to suggest that any uncertainties due to
non-simultaneous observations and/or variability of observed parameters
should not affect the results significantly and the lack of any strong
correlations is a real outcome.
However, if all Be stars are surrounded by CS disks, correlations might be
expected between the intrinsic polarization and projected rotational
velocities. This dependence was first investigated by McLean & Brown
(1978) and recently for a larger sample of stars by Yudin
(2000). In both cases, the relation between ![]() and
and
![]() shows a triangular distribution but with very different
boundaries. According to McLean & Brown (1978), the polarization
exhibits a maximum scatter for the largest values of
shows a triangular distribution but with very different
boundaries. According to McLean & Brown (1978), the polarization
exhibits a maximum scatter for the largest values of ![]() .
In contrast,
Yudin (2000) found that
.
In contrast,
Yudin (2000) found that
![]() reaches maximum values for
stars with projected rotational velocities in the intermediate range of
150 kms-1
reaches maximum values for
stars with projected rotational velocities in the intermediate range of
150 kms-1
![]() kms-1 (Feature 1) and there are none (with
a few exceptions) with large polarization among the stars with relatively low
kms-1 (Feature 1) and there are none (with
a few exceptions) with large polarization among the stars with relatively low
![]() (<100 kms-1), (Feature 2) and very high
(<100 kms-1), (Feature 2) and very high
![]() (>300 kms-1), (Feature 3). Note that Yudin (2000)
used the data of intrinsic polarization for about 90 objects and his result
is well confirmed in the present study for the largest list of intrinsic
polarization of classical Be stars currently available (337 objects, see
Fig. 14). The distribution constructed here has a peak at the value
(>300 kms-1), (Feature 3). Note that Yudin (2000)
used the data of intrinsic polarization for about 90 objects and his result
is well confirmed in the present study for the largest list of intrinsic
polarization of classical Be stars currently available (337 objects, see
Fig. 14). The distribution constructed here has a peak at the value
![]() kms-1 and the boundary lines are described by:
kms-1 and the boundary lines are described by:
![]() for
for
![]() kms-1and
kms-1and
![]() for
for
![]() and
and
Finally, note that less than 3% of Be stars are located outside of the triangular distribution.
Let us consider now a few hypothesis in context to Feature 3. First,
to account for this behaviour, it must be remembered that a rapidly rotating
Be star (with the value of
![]() -400 kms-1) is at the
stability limit and has a large coefficient of non-sphericity.
-400 kms-1) is at the
stability limit and has a large coefficient of non-sphericity.
![\begin{figure}
\par\includegraphics[width=7.2cm,height=6.6cm,clip]{9470f14.ps}\end{figure}](/articles/aa/full/2001/12/aa9470/Timg293.gif) |
Figure 14:
Correlation between |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.2cm,height=6.6cm,clip]{9470f15.ps}\end{figure}](/articles/aa/full/2001/12/aa9470/Timg294.gif) |
Figure 15:
Correlation between |
| Open with DEXTER | |
The second possibility to account for the above mentioned behaviour is that
the triangular shaped distribution might be the result of a combination of
two facts established above namely: larger mean projected rotational
velocities and smaller absolute values of polarization for late spectral
type stars. In this case, most late spectral type stars will be located at
the lower right side of the diagram that tending to the decrease of
polarization toward larger values of ![]() for the sample of Be stars.
However, a similar diagram constructed with just B6-B9.5 stars again shows
the same behaviour with a triangular distribution - as well as for the other
spectral subgroups of Be stars treated separately. Therefore, the common
behaviour is attributed to rapid rotation independently on spectral subtypes.
for the sample of Be stars.
However, a similar diagram constructed with just B6-B9.5 stars again shows
the same behaviour with a triangular distribution - as well as for the other
spectral subgroups of Be stars treated separately. Therefore, the common
behaviour is attributed to rapid rotation independently on spectral subtypes.
An alternative suggestion is that the stars with a rapid rotation may form
narrower CS gaseous disks. Because the generated polarization is proportional
to the ratio of thickness to length of the disk (or to an opening angle, see,
for example, Dolginov et al. 1995), such narrower disks produce a
significantly lower level of polarization due to increased dilution by
unpolarized starlight. Inasmuch as we exclude from consideration multiple
scattering, ellipsoidal envelopes, geometrically thick and strongly flattened
disks, let us discuss now the optically thin CS disks with
![]() .
For disk-like envelopes the maximum degree of
polarization (
.
For disk-like envelopes the maximum degree of
polarization (
![]() -
-![]() for the optical depth
for the optical depth
![]() )
occurs at
)
occurs at
![]() (Waters & Malborough 1992;
Fox 1993a, - for single-scattering, plus attenuation) that is
similar to the above derived upper limit of
(Waters & Malborough 1992;
Fox 1993a, - for single-scattering, plus attenuation) that is
similar to the above derived upper limit of ![]() .
As follows from the
theoretical calculations of Fox (1993b, 1994) and Waters &
Malborough (1992), a decrease of
.
As follows from the
theoretical calculations of Fox (1993b, 1994) and Waters &
Malborough (1992), a decrease of ![]() from
from
![]() to
to
![]() leads to the decreasing in polarization from 1.5-2% to 0.5-0.7%.
In addition, the above mentioned authors showed that polarization reaches
a maximum at the inclination angle
leads to the decreasing in polarization from 1.5-2% to 0.5-0.7%.
In addition, the above mentioned authors showed that polarization reaches
a maximum at the inclination angle
![]() rather than at
rather than at
![]() .
Thus, for exactly edge-on orientation of CS envelopes the
observed polarization is reduced by about 0.3-0.5%. Taking into account the
star's non-sphericity, a combination of these three effects can reduce the
intrinsic polarization to zero for stars with rapid rotation, viewed edge-on.
Although the models of disk formation around early-type stars currently
discussed in the literature (rotation induced bi-stability and wind
compressed disks) cannot explain the existence of CS disks with
.
Thus, for exactly edge-on orientation of CS envelopes the
observed polarization is reduced by about 0.3-0.5%. Taking into account the
star's non-sphericity, a combination of these three effects can reduce the
intrinsic polarization to zero for stars with rapid rotation, viewed edge-on.
Although the models of disk formation around early-type stars currently
discussed in the literature (rotation induced bi-stability and wind
compressed disks) cannot explain the existence of CS disks with
![]() ,
in both models the opening angle of a disk decreases with
the increase of the ratio
,
in both models the opening angle of a disk decreases with
the increase of the ratio
![]() .
.
An interesting point is that the peak in the distribution
![]() :
:
![]() is different for our spectral subgroups
(see Table 8). In the framework of the above suggestion, the compression of
CS disks which affects the depolarization, sets in for lower values of
is different for our spectral subgroups
(see Table 8). In the framework of the above suggestion, the compression of
CS disks which affects the depolarization, sets in for lower values of
![]() for early type stars. However, this hypothesis
requires a more detailed theoretical study.
for early type stars. However, this hypothesis
requires a more detailed theoretical study.
| O-B1 | B2 | B3-B5 | B6-B9 | O-B9 | |
|
|
0.33 | 0.41 | 0.47 | 0.56 | 0.41 |
|
|
0.40 | 0.45 | 0.56 | 0.62 | 0.50 |
|
|
0.42 | 0.52 | 0.60 | 0.71 | 0.52 |
|
|
0.51 | 0.57 | 0.72 | 0.80 | 0.64 |
Finally, note that our study is essentially just one of statistical analysis only of some of the observational characteristics of Be stars and most physical explanations are only a simple sketch. To construct a self-consistent model of Be phenomena, a detailed theoretical interpretation of the new results presented here and earlier results well confirmed in the present study now needs to be undertaken.
Acknowledgements
I wish to express my sincere thanks to Dr. D. Clarke (Glasgow University) for useful discussions and for the help in the improving of the text. I also thank the referee (Dr. J. Zorec) for his helpful comments. We acknowledge the use of the SIMBAD database and this research has made use of the VizieR Service at Centre de Données Astronomiques de Strasbourg. The research described in this paper was made possible in part by the 99-02-16336 grant of RFBR.
| HD | HR | MWC | Sp | E(V-L) |
|
|
E(V-12) | other name | remarks |
| 144 | 7 | 2 | B9IIIe | 0.05 | 0.30 | 10 Cas | |||
| 4180 | 193 | 8 | B2Ve | 0.87 | 0.23 | 1.48 | 22 Cas,o Cas | ||
| 5394 | 264 | 9 | B0IVe+sh | 1.76 | 0.43 | 2.13 | |||
| 6811 | 335 | 420 | B6.5IIIe | 0.15 | 0.14 | 0.44 | |||
| 7636 | 12 | B2IIIne | 0.51 | 1.86 | V764 Cas | ||||
| 9709 | 426 | B8V | |||||||
| 10144 | 472 | B3Vep | 0.20 | 0 | -0.05 | ||||
| 10516 | 496 | 16 | B0.5IVe+sh | 1.80 | 2.17 | 2.36 | |||
| 11415 | 542 | B3V | 0.12 | 0.28 |
|
||||
| 12302 | 23 | B1Vep | 0.55 | 0.80 | V780 Cas | ||||
| 12856 | 25 | B0pe | 0.91 | ||||||
| 13051 | 27 | B1IVe | 1.72 | 0.92 | V351 Per | ||||
| 13429 | 439 | B3V | |||||||
| 13661 | 29 | B2Ve | 0.5 | V594 Per | |||||
| 13669 | 707 | B2Vne | |||||||
| 13758 | B1V | 1.48 | |||||||
| 13867 | 442 | B5Ve | |||||||
| 13890 | 443 | B1IIIe | 0.95 | ||||||
| 14422 | 37 | B1Vpe | 0.16 | 0.47 | V424 Per | ||||
| 14605 | 44 | B1IVpe | 0.70 | 0.47 | V361 Per | ||||
| 14850 | B7III/IVe | ||||||||
| 15238 | 47 | B3V | V529 Cas | ||||||
| 15450 | 48 | B1IIIe | 0.97 | V555 Per | |||||
| 18552 | 894 | 455 | B8Vne | 0.38 | |||||
| 18877 | 721 | B9Ve | 0.45 | ||||||
| 19243 | B1Ve | 0.78 | 1.91 | ||||||
| 20017 | B7Ve | 0.62 | |||||||
| 20134 | 64 | B2.5Vep | 0.90 | ||||||
| 20336 | 985 | 65 | B2.5Ven | 0.80 | 0.65 | 0.86 | BK Cam | ||
| 20340 | 723 | B3Ve | |||||||
| 20418 | 989 | B5V | 0.13 | 31 Per | |||||
| 20899 | 725 | B9e | |||||||
| 21212 | 67 | B1e | 1.82 | 2 | 1.89 | ||||
| 21362 | 1037 | B6Vn | 0.1 | ||||||
| 21455 | 1047 | B7V | 0.10 | 1.02 | |||||
| 21551 | 1051 | B7V | 0 | 0.85 | |||||
| 21641 | 727 | B8.5Ve | 0.26 | ||||||
| 21650 | 68 | B6Ve | 0.6 | ||||||
| 22192 | 1087 | 69 | B4.5Ve+sh | 0.58 | 1.7 | 1.84 | |||
| 22298 | 70 | B2Vne | 1.12 | 1.25 | CT Cam | ||||
| 22780 | 1113 | 463 | B7Vne | 0.38 | 0.47 | ||||
| 23016 | 1126 | B8.5Vne | 0.04 | 0.55 | 13 Tau | ||||
| 23302 | 1142 | 72 | B6IIIe | 0.13 | 0.09 | 1.25 | 17 Tau | ||
| 23478 | B3IVe: | 1.3 | |||||||
| 23480 | 1156 | 73 | B6.5IVe | 0.55 | 0.18 | 0.57 | 23 Tau,V971 Tau | ||
| 23552 | 1160 | 464 | B8Vne | 0.16 | 0.73 | ||||
| 23630 | 1165 | 74 | B7IIIe | 0.19 | 0.12 | 0.60 | |||
| 23800 | B1.5IVe | 1.26 | |||||||
| 23862 | 1180 | 75 | B8Vpe+sh | 0.58 | 0.38 | 1.02 | 28 Tau | ||
| 23982 | 76 | B4e | 1.83 | ||||||
| 24479 | 1204 | 77 | B9.5Ve | 0.21 | -0.04 | ||||
| 24534 | 1209 | O9.5Vep | 0.50 | 0.48 | 0.89 | X Per | |||
| 25348 | 80 | B1Vpnne | 1.16 | DE Cam | |||||
| 25799 | B3V | 0.45 | V490 Per | ||||||
| 25940 | 1273 | 81 | B4Ve | 0.57 | 0.17 | 1.53 | 48 Per,MX Per | ||
| 26356 | 1289 | B5Ve | 0.06 | 1.07 | |||||
| 26398 | 468 | B7III | 1.57 | ||||||
| 26420 | 82 | B3Ve | 0.66 | ||||||
| 26670 | 1305 | B6V | |||||||
| 26906 | 83 | B2Ve | 1.22 | V586 Per | |||||
| 27846 | B1.5V | ||||||||
| 28497 | 1423 | 86 | B1Ve | 1.21 | 1.02 | 2.26 | DU Eri | Vega-type? | |
| 29441 | 733 | B2.5Vne | V1150 Tau | ||||||
| 29866 | 1500 | 88 | B7.5IVne | 0.28 | 1.19 | 0.80 | |||
| 30076 | 1508 | 89 | B2Ve | 0.84 | 0.17 | 1.04 | DX Eri,56 Eri | ||
| 30123 | 736 | B8IIIe | |||||||
| 32190 | B1Ve | 0.08 | V1153 Tau | ||||||
| 32343 | 1622 | 96 | B3Ve | 0.99 | 0.12 | 2.06 | 11 Cam,BV Cam | ||
| 32990 | 1659 | B2Ve | 0.50 | 0.69 | 103 Tau | ||||
| 32991 | 1660 | 98 | B3Ve | 0.80 | 0.40 | 1.88 | 105 Tau,V1155 Tau | ||
| 33152 | 99 | B1Ve | 0.75 | V412 Aur | |||||
| 33232 | 100 | B2Vne | 0.75 | 0.92 | |||||
| 33328 | 1679 | B2IVne | 0.26 | 0.24 | |||||
| 33461 | 101 | B2Vnne | 1.85 | 0.64 | 1.93 | V415 Aur | |||
| 33599 | B5pe | 0.7 | |||||||
| 33604 | 103 | B2Ve | 0.44 | ||||||
| 33988 | 104 | B0Ve | 0.22 | 12 Aur | |||||
| 34257 | 489 | B5/8e | |||||||
| 34921 | 107 | B0IVpe | 1.52 | 2 | 1.94 | ||||
| 34959 | 1761 | B5Vpn | 0.7 | V1369 Ori | |||||
| 35165 | 1772 | B5IVe+sh | 0.12 | 0.7 | |||||
| 35345 | 109 | B1.5Vpe | 0.65 | ||||||
| 35347 | 494 | B1Ve | 1.11 |
||||||
| 35411 | 1788 | B1V+B2V | 0.15 | 0.20 | 0.15 | ||||
| 35439 | 1789 | 110 | B1Vpe | 0.47 | 0.46 | 2.06 | 25 Ori, V1086 Ori | ||
| 36012 | 757 | B4Ve | 0.10 | V1372 Ori | |||||
| 36376 | 760 | B3/8e | V1374 Ori | ||||||
| 36408 | 1847 | B7IIIe | 0.54 | ||||||
| 36576 | 1858 | 111 | B1.5IVe | 0.58 | 1.17 | 2.00 | 120 Tau | ||
| 36665 | 501 | B0/8e | |||||||
| 37115 | 114 | B6Ve | 0.86 | 0.37 | Vega-type? | ||||
| 37202 | 1910 | 115 | B1IVe+sh | 0.96 | 1.13 | 1.83 | 123 Tau, |
||
| 37330 | 116 | B6V | 0.26 | ||||||
| 37490 | 1934 | 117 | B3IIIe | 1.02 | 0.27 | 1.07 | |||
| 37541 | 769 | B5e | |||||||
| 37657 | 118 | B3Ve | 1.32 | V434 Aur | |||||
| 37795 | 1956 | 119 | B7.5Ve | 0.28 | 0.15 | 0.86 | |||
| 37967 | 1961 | B2.5Ve | 1.1 | 1.76 | V731 Tau | ||||
| 38010 | 124 | B1Vpe | 0.33 | 2.21 | V1165 Tau | ||||
| 38087 | B5Ve | 0.49 | 2.5 | 3.79 | |||||
| 38191 | 125 | B1Vne | 0.5 | ||||||
| 38708 | B3Ve | 1.06 | V438 Aur | ||||||
| 39018 | 779 | B9e | |||||||
| 39340 | B3Ve | 0.13 | |||||||
| 39478 | 129 | B2Ve | 2 |
| HD | HR | MWC | Sp | E(V-L) |
|
|
E(V-12) | other name | remarks |
| 40193 | B8Vne | 0.4 | |||||||
| 40978 | 131 | B3Ve | 0.58 | V447 Aur | |||||
| 41335 | 2142 | 133 | B2Vne | 1.57 | 0.60 | 2.23 | V696 Mon | ||
| 42054 | 2170 | 134 | B4IVnne | 0 | 1.72 | Vega-type? | |||
| 42529 | 794 | B9e | |||||||
| 42545 | 2198 | B5Vne | 0.1 | 69 Ori | |||||
| 43285 | 2231 | 136 | B5.5Ve | 0 | 0.08 | ||||
| 43544 | 2249 | B2.5Ven | 0.13 | 0.05 | |||||
| 43703 | 799 | B1IVe | 1.3 | ||||||
| 44458 | 2284 | 138 | B1Ve+sh | 1.40 | 0.72 | 2.24 | FR CMa | ||
| 44506 | 2288 | B3Ve+sh | 0.39 | ||||||
| 44637 | 139 | B2Vpe | 0.6 | ||||||
| 44996 | 2309 | 526 | B2.5Ve | 0.12 | |||||
| 45314 | 140 | B0IVpe | 0.63 | 0.2 | |||||
| 45542 | 2343 | 141 | B6IIIe+sh | 0.07 | 0.10 | 0.54 | 18 Gem, |
||
| 45626 | B7pe | 0.5 | 1.25 | ||||||
| 45725 | 2356 | 143 | B3Ve+sh | 1.04 | 0.24 | 2.25 | |||
| 45726 | 2357 | B3Vpe | 0.13 | ||||||
| 45871 | 2364 | B5Ve | |||||||
| 45910 | 145 | B2IIIpe+sh | 1.85 | 0.70 | 2.23 | AX Mon | |||
| 45995 | 2370 | 146 | B2Vne | 1.20 | 0.91 | 2.28 | |||
| 46380 | 530 | B1Ve | 1.28 | V728 Mon | |||||
| 46680 | B9IV | ||||||||
| 47054 | 2418 | 150 | B8Ve | 0.34 | 0.83 | ||||
| 47359 | B0.5Vp | 0.7 | |||||||
| 47761 | 531 | B1Ve | 0.6 | V733 Mon | |||||
| 48282 | B3III | 1.0 | |||||||
| 48917 | 2492 | 152 | B2Ve | 0.95 | 0.51 | 1.80 | 10 CMa,FT CMa | Vega-type? | |
| 49131 | 2501 | B2IIIe | 2.09 | HP CMa | Vega-type? | ||||
| 49330 | 821 | B0pnne | 1.14 | V739 Mon | |||||
| 49336 | 2510 | B4Vne | 1.65 | V339 Pup | Vega-type? | ||||
| 49787 | 153 | B2Ve | 0.7 | ||||||
| 49888 | 534 | B3Ve | 0.50 | ||||||
| 49977 | 154 | B2Ve | 1.95 | KU CMa | |||||
| 50013 | 2538 | 155 | B1.5IVne | 1.84 | 0.3 | 2.71 | |||
| 50083 | 156 | B2Ve | 1.25 | 2.27 | V742 Mon | ||||
| 50123 | 2545 | 157 | B6IVe | 1.42 | 1.84 | Vega-type? | |||
| 50658 | 2568 | 537 | B8IIIe | 0.19 | 0.6 | 19 Aur | |||
| 50696 | B1Vnne | 0.6 | |||||||
| 50820 | 2577 | 827 | B3IVe | 1.52 | 1.41 | ||||
| 50938 | 540 | B3Ve | LL CMa | ||||||
| 51354 | 160 | B3Ve | 1.0 | ||||||
| 51480 | 161 | B8e | 1.53 | 0.55 | 1.97 | V644 Mon | young? | ||
| 52244 | 163 | B2IIIpne | 1.33 | LP CMa | |||||
| 52356 | B4Ve | LQ CMa | |||||||
| 52437 | 2628 | B2Vne | 0.12 | FU CMa | |||||
| 52721 | B2Ve | 0.71 | 1.4 | 2.79 | GU CMa | ||||
| 52812 | B3V | 1.05 | |||||||
| 52918 | 2648 | B1Ve | 0.35 | 0.4 | 1.42 | 19 Mon | |||
| 53257 | 2659 | B9IV | 44 Gem | ||||||
| 53367 | 166 | B0IVe | 1.25 | 0.75 | 2.53 | V750 Mon | |||
| 53416 | B8e | ||||||||
| 54309 | 2690 | 167 | B1.5IVe | 1.14 | 0.55 | 1.76 | FV CMa | ||
| 54464 | 836 | B2.5Ve | 0 | ||||||
| 54475 | 2691 | B2V | |||||||
| 54786 | B0pe | 1 | |||||||
| 55135 | 168 | B4Vne | 0.30 | ||||||
| 55538 | B2Ve | 0.65 | HI CMa | ||||||
| 55606 | B1Vpnne | 0.55 | |||||||
| 56014 | 2745 | 170 | B3IIIp+sh | 0.33 | 0.25 | 1.11 | 27 CMa,EW CMa | ||
| 56139 | 2749 | 171 | B2.5Ve | 0.92 | 0.14 | 1.15 | |||
| 56806 | B1.5Vpnne | 0.3 | |||||||
| 57150 | 2787 | 173 | B2Ve | 1.04 | 0.77 | 1.98 | NV Pup | Vega-type? | |
| 57219 | 2790 | B2Vne | 0.10 | 0.03 | 0.26 | NW Pup | |||
| 57386 | 174 | B2Ve | 0.18 | ||||||
| 57393 | 556 | B2Vnne | 0.6 | ||||||
| 57539 | B5III | 0.5 | |||||||
| 58011 | B1Vnep | 0.1 | |||||||
| 58050 | 2817 | 176 | B2Ve | 0.69 | 1.12 | OT Gem | |||
| 58127 | B6e | ||||||||
| 58155 | 2819 | B3V | |||||||
| 58343 | 2825 | 177 | B3Ve | 0.86 | 0.40 | 1.64 | FW CMa | ||
| 58715 | 2845 | 178 | B8Ve | 0.24 | 0.14 | 0.60 | |||
| 58978 | 2855 | 179 | B0.5IVne+sh | 1.10 | 0.85 | 1.88 | FY CMa | ||
| 59094 | 561 | B1Ve | 1.18 | 0.18 | V370 Pup | ||||
| 59498 | B2Vne | 0.12 | |||||||
| 60307 | B3.5IIIe | ||||||||
| 60606 | 2911 | 183 | B3Vne | 1.21 | 2.17 | OW Pup,Z Pup | |||
| 60757 | 848 | B5e | V763 Mon | ||||||
| 60848 | 184 | O8Vpe | 1.20 | 0.22 | BN Gem | ||||
| 60855 | 2921 | 565 | B2Ve | 0.14 | 0.31 | 1.03 | |||
| 61224 | 2932 | B9IIIe | |||||||
| 61355 | B3Vep | 0.8 | |||||||
| 61925 | 2968 | B5IV | |||||||
| 62367 | 567 | B8e | |||||||
| 62532 | B1Vpnne | 0.55 | |||||||
| 62654 | B3Vne | 0.7 | |||||||
| 62729 | 572 | B3Ve | |||||||
| 62753 | 185 | B2.5Vne | 0.65 | V387 Pup | |||||
| 62780 | 573 | B2IIIne | 1.90 | ||||||
| 63150 | B0.5IVnep | 1.5 | |||||||
| 63359 | B1Vpe | 0.9 | |||||||
| 63462 | 3034 | 186 | B1IVe | 1.21 | 0.2 | 1.71 | o Pup | ||
| 64109 | 187 | B8e | |||||||
| 64298 | B2IVnne | 0.68 | |||||||
| 65663 | B8V | ||||||||
| 65719 | B2.5IIIe | 0.15 | V408 Pup | ||||||
| 65875 | 3135 | 190 | B2.5Ve | 1.08 | 0.15 | 1.82 | V695 Mon | ||
| 66194 | 3147 | B2.5Ve | 0.24 | 0.32 | 0.67 | V374 Car | Vega-type? | ||
| 68468 | 577 | B4e | |||||||
| 68980 | 3237 | 192 | B1.5Ve | 0.79 | 1.97 | r Pup,MX Pup | |||
| 69168 | B3V | 0.16 | |||||||
| 69404 | 193 | B2Vne | 0.4 | ||||||
| 69425 | B1Vne | 1.11 | |||||||
| 71072 | 857 | B3.5IVe |
| HD | HR | MWC | Sp | E(V-L) |
|
|
E(V-12) | other name | remarks |
| 71510 | 3330 | B2Ve | 0.06 | ||||||
| 71934 | B2IVne | 0.46 | |||||||
| 72014 | B1Vnne | 0.65 | |||||||
| 72063 | 858 | B2Vne | 0.9 | ||||||
| 72067 | 3356 | B2Ven | 0.2 | 1.54 | |||||
| 74401 | B1.5IIIne | 1.3 | |||||||
| 75081 | 3488 | B9Ve | |||||||
| 75311 | 3498 | 195 | B3Vne | 0.18 | 0.65 | V344 Car | |||
| 75658 | B1IVe | 0.45 | |||||||
| 76534 | B2V | 0.29 | 0.53 | OU Vel | |||||
| 77032 | B2Vne | 1.14 | |||||||
| 77320 | 3593 | B2.5Ve | 0.83 | 1.24 | IU Vel | ||||
| 78764 | 3642 | 196 | B2IVe | 0.08 | V345 Car | ||||
| 79351 | 3659 | B2.5V | a Car | ||||||
| 79621 | 3670 | B9V | |||||||
| 79778 | B2IVne | 0.2 | |||||||
| 80834 | B5Vnne | 0.73 | |||||||
| 81357 | 859 | B8.5e | binary | ||||||
| 81654 | B2Ve | 0.69 | |||||||
| 81753 | 3745 | B5Ve | Vega-type? | ||||||
| 82830 | B1IIIne | 2.0 | |||||||
| 83043 | B2Vpne | 0.92 | |||||||
| 83060 | B2Vnep | 0.50 | |||||||
| 83597 | B1.5Ve | 1.78 | |||||||
| 83953 | 3858 | 197 | B6Ve | 0.46 | 0.32 | 1.78 | I Hya | Vega-type? | |
| 84523 | B3Ve | 0.25 | |||||||
| 84567 | 3878 | B0.5IIIne | 0.25 | ||||||
| 86272 | B2Vne | 0.5 | |||||||
| 86612 | 3946 | 581 | B4Ve | 0.82 | 0.01 | OY Hya | |||
| 86689 | B2Vne | 0.71 | |||||||
| 87380 | B1IVn | 0.20 | |||||||
| 87543 | 3971 | B7IVne | 0.20 | 1.44 | |||||
| 87901 | 3982 | B7V | 0.12 | 0.1 | 0.11 | ||||
| 88661 | 4009 | 199 | B2IVpne | 0.97 | 1.89 | QY Car | |||
| 89080 | 4037 | B8IIIe+sh | 0.34 | 0.45 | 0.71 | ||||
| 89884 | 582 | B5IIIe | |||||||
| 89890 | 4074 | 201 | B3IIIe | 0.27 | |||||
| 90187 | B1IIIne | 0.45 | |||||||
| 90563 | B2Ve | 0.9 | |||||||
| 91120 | 4123 | 205 | B9Vne+sh | 0.13 | 0.23 | Z Crv,5 Crv | |||
| 91188 | B4IIIe | 1.25 | |||||||
| 91465 | 4140 | 208 | B4Ve+sh | 0.98 | 1.16 | 1.64 | P Car | ||
| 92027 | B2.5Vne | 0.71 | |||||||
| 92061 | B1.5IIIe | 0.05 | |||||||
| 92714 | B2Ve | 1.1 | |||||||
| 92938 | 4196 | B4V | 0.24 | V518 Car | |||||
| 93030 | 4199 | B0Vp | 0.3 | 0.02 | |||||
| 93237 | 4206 | B5IV | 0.25 | DR Cha | |||||
| 93561 | B1IIInne | 1.0 | |||||||
| 93563 | 4221 | B8.5IIIe+sh | 0.91 | ||||||
| 93683 | B1IVnep | 1.8 | |||||||
| 94648 | B2Ve | 0.3 | FK Car | ||||||
| 96357 | B1.5Vne | 1.3 | |||||||
| 96864 | B1.5IVnep | 1.4 | |||||||
| 98624 | B1Vne | 1.1 | |||||||
| 98927 | B1IIInne | 0.8 | |||||||
| 99354 | B1IIIne | 0.84 | |||||||
| 100199 | B1III | 0.5 | |||||||
| 100324 | B2Vne | 2 | KP Mus | ||||||
| 100673 | 4460 | B9Ve | 0.12 | ||||||
| 100856 | B2IVpe | V843 Cen | |||||||
| 100889 | 4468 | B9.5V | 0.04 | 0.05 | |||||
| 102742 | B3Ve | 0.15 | |||||||
| 102776 | 4537 | B3Vne | 0.13 | ||||||
| 105382 | 4618 | B6IIIe | 0 | -0.02 | V863 Cen | ||||
| 105435 | 4621 | 219 | B2IVne | 0.97 | 0.33 | 1.91 | |||
| 105521 | 4625 | B3IVe | 0.38 | V817 Cen | |||||
| 105675 | B2IVne | 1.55 | |||||||
| 105753 | B2IVne | 0.7 | |||||||
| 107348 | 4696 | 221 | B8Vne | 0.27 | 0.04 | ||||
| 109387 | 4787 | 222 | B6IIIpe+sh | 0.63 | 0.24 | 1.73 | |||
| 109857 | B8Ve | 0.96 | Vega-type? | ||||||
| 110335 | 4823 | 223 | B6IVe+sh | 1.05 | 1.44 | 39 Cru,CH Cru | |||
| 110432 | 4830 | 224 | B2Vpe | 1.29 | 1.3 | 2.13 | BZ Cru | ||
| 110863 | B2IIInep | 1.94 | DQ Cru | ||||||
| 112078 | 4897 | B4Vne | 0.07 | -0.11 | |||||
| 112091 | 4899 | 225 | B5Vne | 0.62 | 0.12 | 1.57 | |||
| 112999 | B6IIIn | 0.9 | |||||||
| 113120 | 4930 | 226 | B1.5IIIne | 0.93 | 0.4 | 1.82 | |||
| 113605 | B2Vpe | 0.7 | |||||||
| 113902 | 4951 | B8V | 0.04 | ||||||
| 114200 | B1IIIne | 0.4 | |||||||
| 114800 | B2IVne | 1.7 | V955 Cen | ||||||
| 114981 | B4Vne | 0.02 | V958 Cen | Vega-type? | |||||
| 116781 | B0IIIne | 0.8 | |||||||
| 117111 | B2Vne | 0.6 | |||||||
| 117357 | B0.5IIIne | 0.8 | |||||||
| 118246 | B3Ve | 0.05 | GP Vir | ||||||
| 120324 | 5193 | 229 | B2IV-Ve | 0.97 | 0 | 0.10 | Vega-type? | ||
| 120991 | 5223 | 230 | B2IIIep | 1.22 | 0.09 | V767 Cen | |||
| 121556 | B2IVnep | 1.73 | |||||||
| 121847 | 5250 | B8Ve+sh | -0.12 | 0.04 | -0.11 | 47 Hya | |||
| 122450 | B2IIIe | 0.66 | |||||||
| 122669 | B0.5Ve | 1.1 | 0.48 | ||||||
| 122691 | B1Vnne | 1.3 | 1.2 | ||||||
| 124367 | 5316 | 231 | B4Vne | 0.82 | 0.35 | 2.07 | V795 Cen | ||
| 124771 | 5336 | B3V | 0.37 | 0.61 | Vega-type? | ||||
| 125159 | B2Ve | 0.3 | |||||||
| 127489 | B2Ve | 0.46 | V1010 Cen | ||||||
| 127617 | B7III/IVe | ||||||||
| 127972 | 5440 | 232 | B1.5Vne+sh | 0.19 | 0.47 | 0.83 | Vega-type? | ||
| 129954 | 5500 | B2.5Ve | 0.67 | CO Cir | |||||
| 131492 | 5551 | B3Ve | 0.68 | 0.5 | 0.49 | ||||
| 133738 | B1.5Ve | 0.81 | |||||||
| 134401 | B2Vne | 1.2 | |||||||
| HD | HR | MWC | Sp | E(V-L) |
|
|
E(V-12) | other name | remarks |
| 134481 | 5646 | B9Ve | 0.05 | 0.29 |
|
||||
| 135160 | 5661 | 234 | B0.5Ve | 0.27 | 0.4 | ||||
| 135734 | 5683 | B8Ve | 0.62 | ||||||
| 136415 | 5704 | B5IVe+F8 | 0.36 | ||||||
| 136556 | B1Vne | 1.45 | |||||||
| 137387 | 5730 | 235 | B3IVpe+sh | 1.02 | 0.45 | 1.43 |
|
||
| 137432 | 5736 | B4Ve | 0.08 | ||||||
| 137518 | B1IIInep | 1.0 | |||||||
| 138749 | 5778 | 237 | B6Vnne | 0.17 | 0.15 | -0.05 | 4 CrB, |
||
| 138769 | 5781 | B3IV | 0.05 | KT Lup | |||||
| 139431 | B2Ve | ||||||||
| 139790 | B3IIIne | 1.8 | |||||||
| 140336 | B1IIIne | 0.6 | |||||||
| 140784 | 5860 | B8Vn | 0.1 | ||||||
| 140926 | B2IVne | 0.42 | |||||||
| 140946 | B2IVne | 0.5 | |||||||
| 141637 | 5885 | B1.5Vn | 0.62 | 1 Sco | |||||
| 141926 | B2IIInne | 1.05 | 2.81 | ||||||
| 142184 | 5907 | B2Vne | 0.20 | 0.17 | 0.76 | ||||
| 142237 | B3IVne | 0.65 | |||||||
| 142926 | 5938 | 584 | B9pe+sh | 0.29 | 0.16 | 4 Her,V839 Her | |||
| 142983 | 5941 | 239 | B3IVe+sh | 0.62 | 0.73 | 1.64 | FX Lib,48 Lib | ||
| 144320 | B1Vne | 0.85 | V364 Nor | ||||||
| 144708 | 6002 | B9V | |||||||
| 144965 | B3Ve | ||||||||
| 144970 | B0Ve | 1.0 | |||||||
| 145846 | B1.5Vne | 0.85 | |||||||
| 146444 | B4Ve | 1.25 | |||||||
| 146463 | B2IVnep | 1.5 | |||||||
| 147274 | B7IVe | 0.65 | |||||||
| 147302 | B3Vne | 0.35 | |||||||
| 147756 | B1.5Vne | 0.1 | |||||||
| 148184 | 6118 | 241 | B1.5Vpe | 1.10 | 0.41 | 2.18 | 7 Oph, |
Vega-type? | |
| 148259 | B2Ve | 0.3 | OZ Nor | ||||||
| 148877 | B7Vep | 0.25 | |||||||
| 149298 | B1Ve | 1.3 | |||||||
| 149313 | B2IVne | 0.39 | |||||||
| 149671 | 6172 | B7IVe | 0.16 | ||||||
| 149729 | B2Vn | 0.38 | |||||||
| 149757 | 6175 | O9Ve | 0.50 | 0.82 | 13 Oph, |
||||
| 152060 | B2IVe | 1.2 | |||||||
| 152478 | 6274 | B3Vep+sh | 0.78 | 0.97 | 2.18 | ||||
| 152541 | B7Ve | 0.35 | |||||||
| 152979 | B2IVe | 0.1 | |||||||
| 153261 | 6304 | 245 | B2IVe | 0.95 | 0.99 | 1.83 | V828 Ara | Vega-type? | |
| 153295 | 588 | B2IIIe | 1 | ||||||
| 153879 | 246 | B1.5Vne | 0.8 | ||||||
| 154040 | 868 | B2Ve | 1.4 | ||||||
| 154111 | B5Vne | 0.4 | |||||||
| 154154 | B2IVnne | 0.80 | 1.7 | ||||||
| 154243 | 250 | B3Vnne | 2.0 | ||||||
| 154450 | 251 | B0.5IVnne | 1.7 | V956 Sco | |||||
| 154911 | 871 | B0.5IVne | 0.35 | ||||||
| 155438 | B6IVn | 0.6 | |||||||
| 155806 | 6397 | 252 | O8Ve | 1.75 | 0.30 | young? | |||
| 155851 | 253 | B1IIInne | 1.0 | ||||||
| 156325 | 6422 | 254 | B5Vne | 0.06 | 1.6 | V1077 Sco | |||
| 156468 | 255 | B1Ve | 0.65 | V1078 Sco | |||||
| 157042 | 6451 | 258 | B2IIIne | 1.00 | 0.44 | 1.89 | |||
| 157832 | 259 | B5Vnne | 1.89 | V750 Ara | |||||
| 158319 | 260 | B4Ve | 0.9 | ||||||
| 158427 | 6510 | 261 | B2Vne | 1.18 | 0.58 | 2.23 | |||
| 158643 | 6519 | B9.5V | 1.32 | 0.56 | 3.70 | 51 Oph | Vega-type | ||
| 159489 | B3IVep | 0.35 | |||||||
| 160202 | 264 | B7Ve | 0.42 | ||||||
| 160886 | 885 | B3Vnne | 0.34 | V2243 Oph | |||||
| 161103 | B2IVe | 0.95 | |||||||
| 161261 | B9 | 0.1 | V2315 Oph | ||||||
| 161543 | 887 | B7.5e | V2385 Oph | ||||||
| 161711 | B9III/IVe | GT Dra | |||||||
| 161756 | 6621A | B6Ve | V3894 Sgr | ||||||
| 161756 | 6621B | B8Ve | V3894 Sgr | ||||||
| 161774 | 890 | B5Vnne | 0.55 | ||||||
| 161807 | B3Vne | 0.35 | 2.45 | ||||||
| 162352 | 892 | B1.5Vne | 0.5 | ||||||
| 162428 | 594 | B7IV/Ve | |||||||
| 162568 | 893 | B3Vne | 0.41 | ||||||
| 162732 | 6664 | B6IVe+sh | 0.4 | 0.76 | V744 Her,88 Her | ||||
| 163454 | 276 | B0.5Vpe | 2.57 | ||||||
| 163848 | 899 | B8Ve | |||||||
| 163868 | 277 | B3.5Vne | 0.59 | V3984 Sgr | |||||
| 164284 | 6712 | 278 | B2IV/Ve+sh | 0.77 | 0.52 | 2.10 | 66 Oph,V2048 Oph | ||
| 164447 | 6720 | 279 | B8Vne | 0.43 | 0.45 | V974 Her | |||
| 164906 | 280 | B1IV:pe: | 1.25 | 0.55 | 4.98 | ||||
| 165063 | B5Vne | 0.35 | |||||||
| 165285 | 281 | B1.5Vne | 1.5 | ||||||
| 165854 | B9e | ||||||||
| 165921 | B0Ve | 0.41 | 0.48 | V3903 Sgr | |||||
| 166014 | 6779 | B9.5III | 0.17 | 0.20 | o Her,103 Her | ||||
| 166256 | 283 | B9/A0e | |||||||
| 166443 | 596 | B1Ve | 1.53 | V4383 Sgr | |||||
| 166524 | B0Vpe | 1.09 | |||||||
| 166566 | 284 | B1IIIe | 0.51 | ||||||
| 166596 | 6804 | B2.5IIIp | V692 CrA | ||||||
| 167128 | 6819 | B3IIIep | 0.41 | 0.24 | 1.30 | QV Tel | |||
| 168135 | 289 | B8Ve | |||||||
| 168797 | 6873 | 601 | B3Ve | 0.08 | 0.18 | NW Ser | |||
| 168957 | 292 | B4Ve | 0.16 | ||||||
| 169033 | 6881 | 602 | B5Ve | 0.52 | |||||
| 169805 | 296 | B2Ve | 0.15 | ||||||
| 170061 | 298 | B0.5Vne | 0.3 | ||||||
| 170235 | 6929 | 299 | B2IVpe+sh | 0.35 | 0.38 | 2.22 | V4031 Sgr | ||
| 170682 | B4/5III | V3508 Sgr | |||||||
| 170835 | B2.5Vne | 1.3 |
| HD | HR | MWC | Sp | E(V-L) |
|
|
E(V-12) | other name | remarks |
| 171348 | 302 | B2Vne | 0.27 | V4400 Sgr | |||||
| 171406 | 6971 | B4Ve | 0.28 | V532 Lyr | |||||
| 171754 | 942 | B4Ve | |||||||
| 171757 | 943 | B2.5IIIne | 0.60 | ||||||
| 171780 | 6984 | 604 | B5Vne | -0.02 | 0.16 | ||||
| 172158 | 946 | B7.5Ve | 1.08 | ||||||
| 172252 | 947 | B1Vnpe | 0.35 | ||||||
| 172256 | 606 | B1.5Vne | 0.31 | V4131 Sgr | |||||
| 173219 | 304 | B1Vnep | 1.83 | V447 Sct | |||||
| 173370 | 7040 | B9Ve | 0.17 | 0.04 | 0.56 | 4 Aql | |||
| 173371 | 956 | B9IIIe | |||||||
| 173637 | 607 | B1IVe | 1.95 | ||||||
| 173948 | 7074 | 963 | B2II/IIIe+sh | 0.50 | |||||
| 174237 | 7084 | 608 | B2.5Ve | 0.96 | 0.18 | 1.06 | CX Dra | ||
| 174513 | 609 | B1Ve | 1.8 | V457 Sct | |||||
| 174571 | 610 | B3Vpe | 1.2 | 1.92 | |||||
| 174638 | 7106 | 306 | B7Ve | 0.22 | 0.45 | 1.14 | |||
| 175863 | 308 | B5Ve | 0.8 | ||||||
| 175869 | 7158 | B8IIIep | -0.02 | 0.46 | 64 Ser | ||||
| 176159 | 971 | B9e | V1437 Aql | ||||||
| 177015 | 309 | B5Vn | 0.87 | ||||||
| 177291 | 973 | B8Ve | 1.44 | V4409 Sgr | young? | ||||
| 177648 | 310 | B2Ve | 0.76 | ||||||
| 178175 | 7249 | 311 | B2Ve | 0.73 | 0.80 | 1.61 | V4024 Sgr | ||
| 178475 | 7262 | B5V | 0.21 | ||||||
| 179343 | 978 | B9V+sh | 0.15 | ||||||
| 179405 | B3e | ||||||||
| 181409 | 7335 | B2IVe | 0.30 | ||||||
| 181615 | 7342 | 313 | B2Vpe | 3.03 | 0.68 | 5.66 | HAEBE? | ||
| 182645 | 7378 | B7III | |||||||
| 183362 | 7403 | 318 | B3Ve+sh | 0.73 | 0.78 | 1.98 | V558 Lyr | ||
| 183656 | 7415 | 988 | B6Ve+sh | 0.25 | 0.54 | V923 Aql | |||
| 183914 | 7418 | 618 | B8Ve | 0.20 | 6 Cyg | ||||
| 184279 | 319 | B0.5Ve+sh | 0.9 | V1294 Aql | |||||
| 184915 | 7446 | B0.5III | 0.25 | 1.17 | |||||
| 185037 | 7457 | 619 | B8Vne | 0.66 | <0.05 | 11 Cyg | |||
| 187350 | 621 | B2IVne | 0.85 | ||||||
| 187567 | 7554 | 322 | B2.5IVe | 1.43 | 2.40 | V1339 Aql | |||
| 187811 | 7565 | 323 | B2.5Ve+sh | 0.58 | 0.15 | 0.67 | 12 Vul | ||
| 187851 | B2V | 0.71 | V396 Vul | ||||||
| 189687 | 7647 | 624 | B3IVe | 0.61 | 0.28 | 25 Cyg,V1746 Cyg | |||
| 190944 | 328 | B1.5Vne | 1.38 | 0.97 | 2.30 | ||||
| 191531 | 328 | B0.5IV | |||||||
| 191610 | 7708 | 329 | B3IVe | 0.76 | 0.33 | 1.60 | 28 Cyg,V1624 Cyg | ||
| 191639 | 7709 | B1Ve | 0.18 | 0.22 | BE Cap | ||||
| 192044 | 7719 | 331 | B7.5Ve | 0.21 | 0.43 | 0.89 | 20 Vul | ||
| 192445 | 332 | B2Ve | 0.33 | ||||||
| 192685 | 7739 | B3V | 0.15 | 0.2 | 1.31 | QR Vul | |||
| 193009 | 336 | B0Ve | 2.1 | V2113 Cyg | |||||
| 193182 | B7IV/Ve+sh | 0.25 | 0.15 | ||||||
| 193911 | 7789 | 341 | B8IIIne+sh | 0.11 | 0.43 | 0.90 | 25 Vul | ||
| 194244 | 7803 | B9Ve | |||||||
| 194335 | 7807 | 343 | B2IIIne | 0.98 | 0.35 | V2119 Cyg | |||
| 194883 | 345 | B2Ve | 1.6 | V2120 Cyg | |||||
| 195325 | 7836 | 1019 | B9e+sh | 0.17 | 1 Del | ||||
| 195407 | 346 | B0IV:pe | 1.51 | 1.23 | |||||
| 195554 | 7843 | 637 | B9Vne | ||||||
| 196712 | 7890 | 350 | B7IIIne | 0.05 | |||||
| 197038 | B7e | ||||||||
| 197419 | 7927 | 1026 | B2IV-Ve | 0.33 | V568 Cyg | ||||
| 197434 | 1027 | B8e | |||||||
| 198183 | 7963 | 352 | B5Ve | -0.02 | 0.32 | -0.06 | 54 Cyg, |
||
| 198512 | 354 | B1Vnnep | 1.8 | V2135 Cyg | |||||
| 198625 | 7983 | B4Ve | 0.12 | 0.25 | 1.45 | V2136 Cyg | |||
| 198895 | 355 | B1.5Ve | 3.4 | 1.56 | V417 Cep | ||||
| 198931 | 1032 | B1Ve | 1.60 | 1.92 | |||||
| 199218 | 8009 | 356 | B8Vnne | 0.24 | |||||
| 199356 | 357 | B2IVe | 1.1 | 0.65 | V2139 Cyg | ||||
| 200120 | 8047 | 359 | B1.5Ve+sh | 1.05 | 0.52 | 2.50 | 59 Cyg,V832 Cyg | ||
| 200310 | 8053 | 360 | B1Ve | 0.14 | 0.51 | 60 Cyg,V1931 Cyg | |||
| 201522 | B0Ve | 1.0 | |||||||
| 201733 | 8103 | 363 | B4IVp | 0.1 | 1.2 | V2148 Cyg | |||
| 202904 | 8146 | 364 | B2.5Vne | 1.09 | 0.46 | 66 Cyg | |||
| 203025 | 8153 | 365 | B2IIIe | 0.63 | |||||
| 203064 | 8154 | O7.5IIIe | 0.50 | 0.23 | 68 Cyg | ||||
| 203374 | 366 | B0IVpe | 1.1 | 1.91 | |||||
| 203467 | 8171 | 367 | B2.5Ve+sh | 0.73 | 0.03 | 0.88 | 6 Cep,V382 Cep | ||
| 203699 | B3IV | 0.18 | |||||||
| 203731 | 369 | B1Vne | 1.0 | V2153 Cyg | |||||
| 204116 | B1Ve | 1.18 | V2155 Cyg | ||||||
| 204185 | B2e | ||||||||
| 204722 | 370 | B2Ve | 1.95 | V2162 Cyg | |||||
| 204860 | B4Ve | 0.2 | V2163 Cyg | ||||||
| 205060 | 371 | B6Ve | 0.8 | ||||||
| 205551 | 8259 | 641 | B9IIIe | ||||||
| 205618 | 642 | B1.5Vne | 0.95 | V2166 Cyg | |||||
| 205637 | 8260 | 373 | B2.5Ve+sh | 0.81 | 1.20 | 0.54 | |||
| 206773 | 376 | B0Vpe | 1.6 | 0.29 | 2.33 | ||||
| 207232 | 377 | B7V | |||||||
| 208057 | 8356 | 644 | B3Ve | 0.04 | 0.24 | 16 Peg,OQ Peg | |||
| 208220 | B1IVe | 0.48 | |||||||
| 208392 | 380 | B1IIIe | 0.34 | EM Cep | |||||
| 208682 | 8375 | 381 | B2.5Ve+sh | 1.03 | 0.70 | 1.36 | |||
| 208886 | B7III/IVe | ||||||||
| 209014 | 8386 | B8Ve | 0.30 | 0.15 | 0.67 | ||||
| 209409 | 8402 | 384 | B7IVe+sh | 0.13 | 0.60 | 0.97 | 31 Aqr,o Aqr | ||
| 209522 | 8408 | 650 | B4IVne | -0.05 | 0.19 | UU PsA | |||
| 210129 | 8438 | 385 | B7Vne | 0.1 | 0.32 | 25 Peg | |||
| 211835 | 652 | B3Ve | V404 Lac | ||||||
| 212044 | 386 | B0Ve | 0.51 | 1.87 | V357 Lac | ||||
| 212076 | 8520 | 387 | B1.5Vne | 0.94 | 0.12 | 31 Peg,IN Peg | |||
| 212571 | 8539 | 388 | B1Ve+sh | 0.34 | 0.94 | 52 Aqr, |
|||
| 212666 | 1059 | B5.5e | |||||||
| 212791 | 653 | B6e | V408 Lac | ||||||
| 213088 | 389 | B9e |
| HD | HR | MWC | Sp | E(V-L) |
|
|
E(V-12) | other name | remarks |
| 213129 | 654 | B5.5e | |||||||
| 214167 | B1.5Ve | 0.2 | 8 Lac A | ||||||
| 214168 | 8603 | 390 | B2Ve | 1.19 | 0.18 | 8 Lac B | |||
| 214748 | 8628 | 392 | B8Ve | -0.03 | 0.34 | 0.63 | 18 PsA, |
Vega-type? | |
| 215227 | 656 | B5ne | 1.05 | ||||||
| 215605 | 658 | B2IVnne | 1.76 | ||||||
| 216057 | 8682 | 393 | B5Vne | 0.39 | |||||
| 216200 | 8690 | B3IV:e | 1.6 | 14 Lac,V360 Lac | |||||
| 216581 | B2.5V | ||||||||
| 216851 | 660 | B3Vn | V423 Lac | ||||||
| 217050 | 8731 | 394 | B3.5IIIpe+sh | 0.72 | 0.77 | 2.21 | EW Lac | ||
| 217061 | B1V | 0.39 | 0.43 | ||||||
| 217543 | 8758 | 395 | B3.5Vpe | 0.4 | |||||
| 217675 | 8762 | B6IIIpe+sh | 0.07 | 0.13 | o And,1 And | ||||
| 217891 | 8773 | 396 | B5Ve | 0.55 | 0.09 | 0.51 | |||
| 218393 | 397 | B3IVne | 1.0 | 0.33 | 1.25 | KX And | |||
| 218674 | B3IV/Ve+sh | 0.36 | KY And | ||||||
| 219688 | 8858 | B5V | -0.01 | 0.08 | |||||
| 220058 | 398 | B1nep | 0.1 | V810 Cas | |||||
| 220116 | 399 | B1e | 1.77 | V811 Cas | |||||
| 223044 | B3e | ||||||||
| 223387 | 401 | B0Ve | 0.9 | ||||||
| 224544 | 9068 | 406 | B6IVe+sh | 0 | 0.79 | ||||
| 224559 | 9070 | 407 | B3.5Vne | 0.24 | LQ And | ||||
| 224686 | 9076 | B8Ve | 0.06 | 0.04 | 0.22 |
|
Vega-type? | ||
| 224905 | B1Vn | 1.15 | |||||||
| 225095 | 409 | B2IVne | 0.66 | ||||||
| 225985 | 995 | B1Vpe | 0.9 | ||||||
| 227836 | 628 | B0/2:V:e | 1.8 |
V425 Cyg | |||||
| 228104 | 629 | B1IVpe | 0.95 | ||||||
| 228438 | 333 | B1Ve | 0.15 | ||||||
| 228860 | B0.5IVe | 1.08 | |||||||
| 229171 | B0.5IIIn | 1.00 | |||||||
| 230579 | 975 | B1.5IVne | 1.35 | ||||||
| 232552 | 19 | B0IVpe | 1.09 | ||||||
| 235668 | 646 | B2e | V2172 Cyg | ||||||
| 235795 | 1057 | B1:V:nne | 1.2 | ||||||
| 236689 | B1.5Vep | 0.25 | |||||||
| 236935 | 24 | B1Vne | 1.4 | ||||||
| 237056 | 720 | B0.5Vpe | 0.9 | ||||||
| 239758 | 643 | B2Vne | 1.1 | V435 Cep | |||||
| 244894 | 761 | B0.5Ve | 1.45 | ||||||
| 245493 | 764 | B2Vp | 0.2 | ||||||
| 246878 | B1Ve | 1.1 | |||||||
| 248753 | 128 | B1Vnne | 1.7 | V1167 Tau | |||||
| 249695 | 785 | B1.5Vpnne | 0.25 | ||||||
| 250028 | 786 | B2Ve | 1.7 | ||||||
| 250163 | 517 | B1Ve | 1.8 | ||||||
| 250289 | B2IIIe | 1 | |||||||
| 254647 | 798 | B0e | 0.6 | ||||||
| 256577 | B2IVp | 1.3 | |||||||
| 276738 | 735 | B6/7III/V | |||||||
| 298298 | B1Vpe | 0.6 | |||||||
| 300584 | B1Ve | 1.6 | |||||||
| 302724 | B2Ve | 1 | |||||||
| 302838 | B1Vne | 0.4 | |||||||
| 305382 | B2Ve | 1.8 | |||||||
| 306209 | B1Ve | 0.6 | |||||||
| 306657 | B2Ve | ||||||||
| 306791 | B2IIIe | ||||||||
| 306793 | B3Ve | ||||||||
| 306797 | B5e | V855 Cen | |||||||
| 306962 | B1IIIne | 1.2 | |||||||
| 306978 | B2Ve | ||||||||
| 307350 | B2IVne | 0.5 | |||||||
| 312973 | B0IVpe | 0.9 | |||||||
| 316568 | B2Vpe | 0.8 | AS 253 | ||||||
| 316587 | B1Vne | 1 | |||||||
| 316589 | B2IVe | 0.8 | |||||||
| 350559 | B7IIIe | ||||||||
| CD-30 5559 | B3Vep | 0.7 | |||||||
| CPD-60 3087 | B3Ve | ||||||||
| CPD-60 3108 | B2Vnpe | ||||||||
| CPD-60 3122 | B3nep | V845 Cen | |||||||
| CPD-60 3125 | B2.5Ve | ||||||||
| CPD-60 3126 | B1.5Vne | V846 Cen | |||||||
| CPD-60 3128 | B2.5Ve | ||||||||
| CPD-60 3129 | B2.5V | ||||||||
| CPD-60 3144 | B3Ve | ||||||||
| CPD-60 4551 | B1IIIne | 0.71 | V959 Cen | ||||||
| CPD-60 4708 | B2Vne | 0.38 | V696 Cen | ||||||
| BD-13 2040 | 180 | B7e | 0.6 | ||||||
| BD-13 4936 | 918 | B1Vne | 1.1 | ||||||
| BD+35 1169 | 500 | B1Vpe | 0.9 | ||||||
| BD+41 3731 | B2e | 0.17 | 0.85 | ||||||
| BD+47 3302 | B2Vnep | 0.8 | AS 458 | ||||||
| BD+49 3735 | B1.5Ve | 0.4 | AS 483,V397 Lac | ||||||
| BD+53 2964 | 1067 | B2IVpnne | 1 | ||||||
| BD+55 589 | 446 | B2IV/Ve | |||||||
| BD+56 473 | 441 | B0.5IIIe | 1.5 | V356 Per | |||||
| BD+56 484 | 444 | B1IIIe | 0.5 | V502 Per | |||||
| BD+56 493 | B1Vpe | 0.8 | |||||||
| BD+56 511 | B3III | -0.08 | |||||||
| BD+56 548 | 445 | B1.5IIIe | 1.78 | ||||||
| BD+56 573 | 40 | B2III/Ve | 1.38 | ||||||
| BD+56 579 | 710 | B7IV/Ve | |||||||
| BD+56 582 | B1III | 1.7 | |||||||
| BD+56 624 | 46 | B3IIIe | 1.5 | ||||||
| BD+57 515 | 28 | B2ep | 0.65 | ||||||
| BD+57 607 | 55 | Be | 0.3 | ||||||
| BD+58 458 | 42 | B1pe | 0.2 | ||||||
| BD+59 2829 | 3 | B0IVne | 0.3 | ||||||
| BD+61 2355 | B7IV | 0.36 | BHJ 9 | ||||||
| BD+61 2380 | B9Ve | -0.1 |
The columns in the Appendix I
give the HD number or other identification, the MK spectral type
of a star (as from the source catalogue), the calculated value of
colour excess E(V-L) (in magnitudes), the calculated value of intrinsic
V band polarization (in %), the weighted average value of
![]() (in kms-1), the average value of far IR excess
(E(V-12)) at 12
(in kms-1), the average value of far IR excess
(E(V-12)) at 12 ![]() m, the common name or other designation of the
star and any remarks. The references to the sources of the V and L photometry,
the observed polarization and the individual values of
m, the common name or other designation of the
star and any remarks. The references to the sources of the V and L photometry,
the observed polarization and the individual values of
![]() are given below.
are given below.
References to the sources of optical and IR photometry:
Dougherty et al. (1991); SIMBAD (1999);
Gezari, D. Y. et al. (1999); Hoffleit & Jaschek (1982);
Sterken (1990); Grillo et al. (1992);
Hillenbrand et al. (1992);
References to the sources of optical polarimetry:
Poeckert et al. (1979); McLean & Brown (1978);
Hall & Mikesell (1953); Ghosh et al. (1999);
WUPPOL (1999); Leroy (1993); McDavid (1999);
Serkowski et al. (1975); Quirrenbach (1997);
Clarke & Bjorkman (1998); Huang et al. (1989);
Bjorkman et al. (1997); Coyne et al. (1967);
Jian & Bhatt (1995); Yudin & Evans (1998);
Vosnchinnikov & Marchenko (1982); Bjorkman & Schulte-Ladbeck (1994);
McDavid (2000); Heiles (2000).
References to the sources of ![]() data:
data:
SIMBAD (1999);
Balona (1990);
Slettebak (1982);
van den Ancker et al. (1998);
Corporon & Lagrange (1999);
Elias et al. (1997);
Bjorkman et al. (1997);
WUPPOL (1999);
Brown & Verschueren (1997);
Howarth et al. (1997);
Prinja (1993);
Hirata (1993);
Quirrenbach (1993);
Mennickent et al. (1994);
Ballereau et al. (1995);
Hoffleit & Jaschek (1982);
Halbedel (1996);
Uesugi & Fukuda (1982);
Kaper (1999);
Henrichs (1999);
Dachs et al. (1981);
Steele et al. (1999);
Carpenter et al. (1984);
Levato & Maloroda (1970);
Dachs et al. (1981);
Coté & Waters (1987);
Lyubimkov et al. (1997);
Balona (1995);
Short & Bolton (1994);
Rivinius et al. (1999);
Prosser (1992);
Snow (1981);
Snow (1981);
Ghosh (1988);
Slettebak et al. (1997);
Briot (1986);
Chosh et al. (1999);
Doazan et al. (1981);
Wolff et al. (1978);
Wolff et al. (1982);
Finkenzeller (1985);
Balona et al. (1992);
Turner et al. (1978);
Slettebak (1966);
Jaschek & Jaschek (1993);
Conti & Ebberts (1977);
Herrero (1994);
Penny (1996);
Bernacca & Perinotto (1970);
Clark & Steele (2000)
| observed | interstellar | intrinsic | observed | interstellar | intrinsic | ||||||||||
| polarization | polarization | polarization | polarization | polarization | polarization | ||||||||||
| HD | D, pc |
|
pV, % | pV, % | HD | D, pc |
|
pV, % | pV, % | ||||||
| 144 | 301 |
|
73 | 0.73 | 85 | 0.30 | 24 | 47359 | 1820 |
|
8 | 0.5 | 170 | 0.7 | 20 |
| 4180 | 278 |
|
85 | 0.5 | 90 | 0.23 | 74 | 47761 | 751 |
|
169 | 1.8 | 175 | 0.6 | 152 |
| 5394 | 188 |
|
111 | 0.3 | 90 | 0.43 | 125 | 48282 | 425 |
|
165 | 0.6 | 35 | 1.0 | 146 |
| 6811 | 226 |
|
90 | 0.6 | 90 | 0.14 | 90 | 48917 | 800 | 0.51 |
18 | ||||
| 7636 | 559 |
|
80 | 2.3 | 85 | 0.51 | 55 | 49330 | 298 |
|
133 | 0.8 | 150 | 1.14 | 121 |
| 10144 | 44 |
|
136 | 0 | 0 | 49336 | 444 |
|
2 | 0.9 | 50 | 1.65 | 166 | ||
| 10516 | 220 |
|
28 | 0.4 | 105 | 2.17 | 26 | 49787 | 1445 |
|
0.7 | 160 | 0.7 | 70 | |
| 11415 | 136 |
|
125 | 0.2 | 105 | 0.28 | 139 | 49888 | 502 |
|
0.50 | 130 | 0.50 | 40 | |
| 12302 | 340 |
|
90 | 1.54 | 90 | 0.80 | 89 | 49977 | 676 |
|
152 | 0.30 | 130 | 1.95 | 155 |
| 12856 | 1700 |
|
108 | 2 | 100 | 0.91 | 179 | 50013 | 242 |
|
106 | 0 | 0.3 | 106 | |
| 13051 | 2041 | 2.21 | 88 | 2.2 | 100 | 0.92 | 49 | 50083 | 500 |
|
24 | 1 | 170 | 1.25 | 47 |
| 13758 | 1620 |
|
108 | 3.5 | 115 | 1.48 | 91 | 50658 | 253 |
|
16 | 0.2 | 50 | 0.6 | 4 |
| 13890 | 2000 |
|
107 | 3.3 | 115 | 0.95 | 71 | 50696 | 1740 |
|
139 | 0.8 | 150 | 0.6 | 64 |
| 14422 | 1950 |
|
117 | 3.5 | 115 | 0.47 | 11 | 51354 | 398 |
|
140 | 0.2 | 15 | 1.0 | 135 |
| 14605 | 1820 |
|
118 | 3.5 | 115 | 0.47 | 144 | 51480 | 160 |
|
173 | 0.4 | 130 | 0.55 | 17 |
| 15450 | 725 |
|
122 | 3.5 | 115 | 0.97 | 152 | 52244 | 1660 |
|
13 | 0.7 | 120 | 1.33 | 22 |
| 18552 | 341 | 0.38 | 104 | 52437 | 407 |
|
81 | 0.2 | 100 | 0.12 | 136 | ||||
| 18877 | 1820 |
|
126 | 2 | 120 | 0.45 | 160 | 52721 | 909 |
|
17 | 0.4 | 135 | 1.4 | 24 |
| 19243 | 617 |
|
129 | 1.9 | 119 | 0.78 | 158 | 52812 | 460 |
|
39 | 0.3 | 160 | 1.05 | 46 |
| 20017 | 503 |
|
126 | 2.6 | 120 | 0.62 | 156 | 52918 | 342 |
|
0.4 | 130 | 0.4 | 40 | |
| 20134 | 394 |
|
110 | 2.4 | 120 | 0.90 | 48 | 53367 | 830 |
|
30 | 0.2 | 130 | 0.75 | 32 |
| 20336 | 246 |
|
142 | 1.0 | 128 | 0.65 | 29 | 54309 | 380 |
|
1 | 0.3 | 30 | 0.55 | 167 |
| 20418 | 147 |
|
101 | 0.25 | 110 | 0.13 | 83 | 54464 | 1000 |
|
0 | 0 | |||
| 21212 | 407 |
|
136 | 2.7 | 123 | 2 | 154 | 54786 | 2100 |
|
116 | 0.5 | 170 | 1 | 102 |
| 21362 | 170 |
|
112 | 0.4 | 110 | 0.1 | 14 | 55135 | 420 |
|
0.3 | 130 | 0.30 | 40 | |
| 21455 | 177 |
|
106 | 0.5 | 111 | 0.10 | 78 | 55538 | 1800 |
|
171 | 0.5 | 170 | 0.65 | 172 |
| 21551 | 267 |
|
127 | 1.3 | 120 | 0.85 | 26 | 55606 | 2500 |
|
60 | 0 | 0.55 | 60 | |
| 21641 | 220 | 0.26 |
129 | 56014 | 483 |
|
85 | 0.4 | 90 | 0.25 | 76 | ||||
| 21650 | 314 |
|
151 | 0.9 | 130 | 0.6 | 17 | 56139 | 283 |
|
60 | 0.2 | 80 | 0.14 | 25 |
| 22192 | 215 |
|
45 | 1.0 | 117 | 1.7 | 35 | 56806 |
|
178 | 0.7 | 165 | 0.3 | 41 | |
| 22298 | 360 |
|
119 | 1.55 | 120 | 1.12 | 118 | 57150 | 260 |
|
87 | 0.15 | 30 | 0.77 | 92 |
| 22780 | 248 |
|
144 | 0.6 | 110 | 0.47 | 174 | 57219 | 256 |
|
32 | 0.15 | 30 | 0.03 | 113 |
| 23016 | 125 |
|
87 | 0.3 | 120 | 0.55 | 72 | 57386 | 1250 |
|
141 | 0.4 | 135 | 0.18 | 154 |
| 23302 | 114 |
|
128 | 0.3 | 120 | 0.09 | 162 | 57393 | 2400 |
|
78 | 0.3 | 130 | 0.6 | 65 |
| 23478 | 239 |
|
29 | 0.8 | 7 | 1.3 | 42 | 57539 | 483 |
|
0.5 | 120 | 0.5 | 30 | |
| 23480 | 110 |
|
135 | 0.3 | 120 | 0.18 | 162 | 58011 | 1085 |
|
111 | 0.35 | 120 | 0.1 | 73 |
| 23552 | 182 |
|
140 | 0.4 | 140 | 0.16 | 154 | 58050 | 691 |
|
78 | 1.1 | 25 | 1.12 | 156 |
| 23630 | 113 |
|
117 | 0.3 | 120 | 0.12 | 34 | 58343 | 290 |
|
164 | 0.5 | 170 | 0.40 | 157 |
| 23800 | 427 |
|
122 | 1.55 | 130 | 1.26 | 112 | 58715 | 52 |
|
90 | 0 | 0.14 | 90 | |
| 23862 | 119 |
|
90 | 0.3 | 120 | 0.38 | 69 | 58978 | 435 |
|
161 | 0.25 | 160 | 0.85 | 161 |
| 24479 | 100 |
|
146 | 0.27 | 136 | 0.21 | 43 | 59094 | 870 |
|
118 | 0.6 | 110 | 0.18 | 173 |
| 24534 | 826 | 0.88 | 43 | 1 | 57 | 0.48 | 178 | 59498 | 1050 |
|
115 | 0.6 | 120 | 0.12 | 82 |
| 25348 | 1260 |
|
124 | 0.5 | 95 | 1.16 | 135 | 60848 | 498 |
|
56 | 0.25 | 25 | 0.22 | 96 |
| 25799 | 360 |
|
102 | 0.8 | 95 | 0.45 | 179 | 60855 | 508 | 0.31 |
|||||
| 25940 | 170 |
|
145 | 0.25 | 165 | 0.17 | 110 | 61355 |
|
102 | 0.8 | 140 | 0.8 | 65 | |
| 26356 | 210 |
|
0.06 | 136 | 0.06 | 46 | 62532 | 1580 |
|
127 | 0.45 | 165 | 0.55 | 101 | |
| 26420 | 182 |
|
137 | 0.3 | 165 | 0.66 | 126 | 62654 | 1380 |
|
163 | 1 | 170 | 0.7 | 153 |
| 26906 | 550 |
|
144 | 1.1 | 155 | 1.22 | 134 | 62753 | 298 |
|
15 | 0.15 | 45 | 0.65 | 9 |
| 28497 | 483 |
|
128 | 0.3 | 180 | 1.02 | 120 | 62780 | 4170 |
|
128 | 0.5 | 70 | 1.90 | 135 |
| 29866 | 166 |
|
6 | 0.8 | 10 | 1.19 | 3 | 63150 | 1820 |
|
137 | 1 | 160 | 1.5 | 123 |
| 30076 | 412 |
|
169 | 0.3 | 180 | 0.17 | 148 | 63359 | 2630 |
|
25 | 0.8 | 150 | 0.9 | 52 |
| 32190 | 575 |
|
80 | 0.7 | 80 | 0.08 | 80 | 63462 | 315 |
|
0.2 | 100 | 0.2 | 10 | |
| 32343 | 206 |
|
168 | 0.4 | 165 | 0.12 | 178 | 64298 | 524 |
|
122 | 0.1 | 100 | 0.68 | 125 |
| 32990 | 302 |
|
88 | 0.7 | 80 | 0.69 | 96 | 65719 | 1660 |
|
14 | 0.5 | 15 | 0.15 | 11 |
| 32991 | 316 |
|
95 | 0.7 | 80 | 0.40 | 126 | 65875 | 315 |
|
15 | 0 | 0.15 | 15 | |
| 33152 | 955 |
|
4 | 1.4 | 150 | 1.67 | 30 | 66194 | 315 |
|
138 | 0.35 | 145 | 0.32 | 130 |
| 33232 | 324 |
|
140 | 1.0 | 165 | 0.92 | 112 | 69168 | 310 |
|
80 | 0.1 | 80 | 0.16 | 80 |
| 33328 | 538 |
|
78 | 0.3 | 110 | 0.24 | 31 | 69404 | 365 |
|
120 | 0.2 | 100 | 0.4 | 129 |
| 33461 | 372 |
|
165 | 1.2 | 165 | 0.64 | 165 | 69425 | 2290 |
|
131 | 1.5 | 110 | 1.11 | 7 |
| 33599 | 794 |
|
30 | 0.1 | 90 | 0.7 | 30 | 71934 | 830 |
|
13 | 0.25 | 180 | 0.6 | 18 |
| 33604 | 603 |
|
168 | 1.5 | 160 | 0.44 | 43 | 72014 | 315 |
|
126 | 0.1 | 130 | 0.46 | 125 |
| 33988 | 240 |
|
161 | 1 | 160 | 0.22 | 66 | 72063 | 2000 |
|
107 | 0.5 | 130 | 0.9 | 95 |
| 34921 | 1515 |
|
146 | 2 | 160 | 2 | 133 | 72067 | 490 |
|
160 | 0.2 | 180 | 0.2 | 92 |
| 34959 | 382 |
|
65 | 0.3 | 80 | 0.7 | 59 | 74401 | 1510 |
|
81 | 0.6 | 160 | 1.3 | 76 |
| 35165 | 581 |
|
6 | 0.1 | 10 | 0.7 | 5 | 75658 | 690 |
|
138 | 0.45 | 160 | 0.45 | 20 |
| 35345 | 1115 |
|
155 | 2.5 | 160 | 0.65 | 134 | 76534 | 411 |
|
124 | 1 | 130 | 0.53 | 46 |
| 35411 | 276 |
|
168 | 0.1 | 70 | 0.20 | 165 | 77032 | 1200 |
|
123 | 0.6 | 120 | 1.14 | 124 |
| 35439 | 340 |
|
122 | 0.3 | 80 | 0.46 | 142 | 77320 | 307 |
|
130 | 0.57 | 70 | 1.24 | 142 |
| 36012 | 391 |
|
72 | 0.3 | 80 | 0.10 | 12 | 78764 | 251 |
|
125 | 0.2 | 125 | 0.08 | 125 |
| 36576 | 575 |
|
75 | 1.15 | 25 | 1.17 | 113 | 79778 | 830 |
|
145 | 0.8 | 145 | 0.2 | 145 |
| 37115 | 543 |
|
89 | 0.4 | 60 | 0.37 | 121 | 80834 | 795 |
|
111 | 1.0 | 100 | 0.73 | 127 |
| 37202 | 128 |
|
31 | 0.3 | 20 | 1.13 | 34 | 81654 | 724 |
|
131 | 1.1 | 120 | 0.7 | 23 |
| 37330 | 493 |
|
63 | 0.4 | 65 | 0.26 | 60 | 82830 | 3980 |
|
128 | 1.4 | 10 | 2.0 | 110 |
| 37490 | 498 |
|
48 | 0.45 | 65 | 0.27 | 9 | 83043 | 1050 |
|
162 | 2.0 | 155 | 0.92 | 56 |
| 37657 | 363 |
|
174 | 0.4 | 160 | 1.32 | 178 | 83060 | 1260 |
|
108 | 1.7 | 110 | 0.5 | 25 |
| 37795 | 82 |
|
109 | 0 | 0.15 | 109 | 83597 | 2400 |
|
151 | 3.0 | 155 | 1.78 | 68 | |
| 37967 | 337 |
|
8 | 0.3 | 85 | 1.1 | 4 | 83953 | 152 |
|
176 | 0.05 | 75 | 0.32 | 174 |
| 38010 | 262 |
|
158 | 1.5 | 5 | 0.33 | 131 | 84523 | 525 |
|
122 | 0.5 | 120 | 0.25 | 28 |
| 38087 | 199 |
|
118 | 0.2 | 65 | 2.5 | 122 | 84567 | 550 |
|
74 | 0.5 | 75 | 0.25 | 73 |
| 38191 | 2400 |
|
156 | 1.5 | 150 | 0.5 | 174 | 86272 | 1050 |
|
118 | 0.8 | 100 | 0.5 | 149 |
| 38708 | 724 |
|
167 | 2.2 | 170 | 1.06 | 83 | 86612 | 193 |
|
10 | 0.03 | 10 | 0.01 | 10 |
| 39340 | 794 |
|
171 | 2.2 | 170 | 0.13 | 10 | 86689 | 3800 |
|
168 | 0.6 | 110 | 0.7 | 13 |
| 39478 | 912 |
|
2 | 170 | 2.0 | 80 | 87380 | 2890 |
|
127 | 1.0 | 130 | 0.2 | 84 | |
| 40193 | 650 |
|
70 | 0.4 | 40 | 0.4 | 96 | 87543 | 250 |
|
107 | 0.3 | 105 | 0.20 | 110 |
| 40978 | 460 |
|
6 | 0.5 | 180 | 0.58 | 11 | 87901 | 83.5 |
|
46 | 0.1 | 80 | 0.1 | 23 |
| 41335 | 282 |
|
147 | 0.05 | 60 | 0.60 | 147 | 89080 |
|
100 | 0.6 | 120 | 0.45 | 38 | |
| 42054 | 323 |
|
35 | 0 | 0 | 90187 | 3020 |
|
115 | 1.5 | 120 | 0.45 | 96 | ||
| 42545 | 238 |
|
0.1 | 45 | 0.1 | 135 | 90563 | 1100 |
|
135 | 1.5 | 120 | 0.9 | 164 | |
| 43285 | 228 |
|
61 | 0.1 | 45 | 0.08 | 129 | 91120 | 149 |
|
89 | 0 | 0.23 | 89 | |
| 43544 | 256 |
|
46 | 0.2 | 45 | 0.05 | 133 | 91188 | 794 |
|
105 | 1.2 | 150 | 1.25 | 68 |
| 43703 | 1400 |
|
142 | 0.5 | 155 | 1.3 | 137 | 91465 | 152 |
|
74 | 0.35 | 140 | 1.16 | 68 |
| 44458 | 513 |
|
79 | 0.35 | 50 | 0.72 | 91 | 92027 | 870 |
|
111 | 0.5 | 100 | 0.71 | 119 |
| 44506 | 617 | 0.39 |
92 | 92061 | 2890 |
|
99 | 0.9 | 100 | 0.05 | 80 | ||||
| 44637 | 398 |
|
1 | 1.3 | 175 | 0.6 | 14 | 92714 | 1200 |
|
31 | 0.8 | 100 | 1.1 | 16 |
| 45314 | 457 |
|
171 | 1.4 | 175 | 0.2 | 124 | 92938 | 140 |
|
147 | 0.4 | 140 | 0.24 | 45 |
| 45542 | 154 |
|
17 | 0.15 | 5 | 0.10 | 35 | 93030 | 135 |
|
139 | 0.4 | 140 | 0.02 | 67 |
| 45626 | 457 |
|
157 | 2 | 175 | 1.25 | 122 | 93237 | 307 |
|
137 | 0.5 | 140 | 0.25 | 131 |
| 45725 | 212 |
|
0.8 | 0.2 | 165 | 0.24 | 14 | 93561 |
|
105 | 0.8 | 140 | 1.0 | 80 | |
| 45726 | 212 |
|
155 | 0.2 | 165 | 0.13 | 81 | 93683 | 1260 |
|
146 | 1 | 80 | 1.8 | 158 |
| 45910 | 760 | 1.06 | 150 | 0.5 | 170 | 0.70 | 135 | 94648 | 1260 |
|
78 | 1 | 80 | 0.3 | 72 |
| 45995 | 435 |
|
132 | 0.4 | 180 | 0.91 | 119 | 96357 | 830 |
|
130 | 1 | 100 | 1.3 | 150 |
| 46380 | 575 |
|
178 | 0.6 | 10 | 1.28 | 172 | 96864 | 1380 |
|
150 | 1.5 | 120 | 1.4 | 3 |
| 47054 | 256 | 0.34 |
71 | 98624 | 2290 |
|
119 | 1 | 80 | 1.1 | 149 | ||||
| observed | interstellar | intrinsic | observed | interstellar | intrinsic | ||||||||||
| polarization | polarization | polarization | polarization | polarization | polarization | ||||||||||
| HD | D, pc |
|
pV, % | pV, % | HD | D, pc |
|
pV, % | pV, % | ||||||
| 98927 | 1510 |
|
63 | 1.0 | 80 | 0.8 | 43 | 160886 | 1000 |
|
59 | 1.3 | 57 | 0.34 | 141 |
| 99354 | 2750 |
|
72 | 1.3 | 90 | 0.84 | 35 | 161103 | 830 |
|
172 | 4.0 | 175 | 0.95 | 158 |
| 100199 | 2290 |
|
84 | 1.3 | 90 | 0.5 | 11 | 161261 | 452 |
|
82 | 0.75 | 85 | 0.1 | 57 |
| 100324 | 912 |
|
136 | 3.5 | 120 | 2 | 164 | 161774 |
|
164 | 0.9 | 160 | 0.55 | 171 | |
| 100889 | 93 |
|
33 | 0.07 | 35 | 0.04 | 128 | 161807 | 383 |
|
177 | 1.4 | 175 | 0.35 | 5 |
| 102742 | 1200 |
|
86 | 1.0 | 90 | 0.15 | 61 | 162352 |
|
173 | 1.5 | 175 | 0.5 | 166 | |
| 105435 | 121 |
|
137 | 0 | 0.33 | 137 | 162568 | 253 |
|
179 | 0.65 | 177 | 0.41 | 3 | |
| 105521 | 330 |
|
30 | 0.07 | 111 | 0.38 | 28 | 162732 | 368 |
|
67 | 0.45 | 160 | 0.76 | 69 |
| 105675 | 2890 |
|
59 | 1.2 | 90 | 1.55 | 38 | 163454 | 1200 |
|
50 | 1.3 | 170 | 2.57 | 63 |
| 105753 | 3980 |
|
74 | 1.2 | 90 | 0.7 | 41 | 163868 | 600 |
|
141 | 1.0 | 150 | 0.59 | 67 |
| 107348 | 118 |
|
132 | 0.07 | 140 | 0.04 | 22 | 164284 | 207 |
|
92 | 0.5 | 75 | 0.52 | 108 |
| 109387 | 153 |
|
24 | 0.1 | 60 | 0.24 | 12 | 164447 | 498 |
|
146 | 0.55 | 175 | 0.45 | 101 |
| 110335 | 317 |
|
89 | 1.45 | 75 | 1.05 | 160 | 164906 | 1050 |
|
174 | 0.9 | 180 | 0.55 | 94 |
| 110432 | 301 |
|
81 | 0.45 | 80 | 1.3 | 81 | 165063 | 377 |
|
147 | 0.8 | 160 | 0.35 | 100 |
| 110863 | 760 |
|
93 | 2.8 | 85 | 1.94 | 105 | 165285 | 1580 |
|
56 | 0.6 | 120 | 1.5 | 47 |
| 112078 | 122 |
|
169 | 0.05 | 125 | 0.07 | 13 | 165921 | 541 |
|
100 | 0.5 | 120 | 0.48 | 79 |
| 112091 | 111 |
|
128 | 0.05 | 130 | 0.12 | 127 | 166014 | 106 |
|
179 | 0 | 0.17 | 179 | |
| 112999 | 336 |
|
78 | 2.2 | 90 | 0.9 | 27 | 166443 | 1510 |
|
145 | 0.5 | 110 | 1.53 | 154 |
| 113120 | 483 |
|
115 | 1.1 | 105 | 0.4 | 149 | 166524 | 2290 |
|
105 | 0.8 | 50 | 1.09 | 127 |
| 113605 | 1445 |
|
80 | 2.0 | 90 | 0.7 | 28 | 166566 | 1380 |
|
45 | 1.0 | 30 | 0.51 | 84 |
| 113902 | 99 |
|
107 | 0.05 | 130 | 0.04 | 58 | 167128 | 228 |
|
3 | 0.9 | 10 | 0.24 | 151 |
| 114200 | 3630 |
|
92 | 1.2 | 100 | 0.4 | 64 | 168797 | 360 |
|
64 | 0.60 | 65 | 0.18 | 61 |
| 114800 | 382 |
|
109 | 1.8 | 75 | 1.7 | 153 | 168957 | 513 |
|
176 | 0.65 | 180 | 0.16 | 159 |
| 114981 | 935 |
|
32 | 0.15 | 35 | 0.02 | 152 | 169033 | 188 |
|
111 | 0.8 | 125 | 0.52 | 88 |
| 116781 | 1995 |
|
81 | 2.2 | 75 | 0.8 | 155 | 169805 | 1260 |
|
141 | 1 | 140 | 0.15 | 45 |
| 117111 | 1050 |
|
78 | 1.5 | 80 | 0.6 | 52 | 170061 |
|
71 | 1.5 | 70 | 0.3 | 156 | |
| 117357 | 1995 |
|
74 | 2.2 | 75 | 0.8 | 71 | 170235 | 603 |
|
175 | 0.5 | 4 | 0.38 | 163 |
| 118246 | 660 |
|
83 | 0.25 | 80 | 0.05 | 99 | 170835 | 427 |
|
21 | 0.9 | 180 | 1.3 | 35 |
| 120324 | 162 |
|
169 | 0.07 | 170 | 0 | 171348 | 476 |
|
174 | 0.9 | 180 | 0.27 | 152 | |
| 120991 | 630 |
|
84 | 0.4 | 80 | 0.09 | 102 | 171406 | 455 |
|
13 | 0.5 | 180 | 0.28 | 19 |
| 121556 | 760 |
|
129 | 1.6 | 80 | 1.73 | 162 | 171757 | 3980 |
|
36 | 0.8 | 60 | 0.6 | 166 |
| 121847 | 104 |
|
65 | 0.25 | 60 | 0.04 | 9 | 171780 | 318 |
|
171 | 0.4 | 180 | 0.16 | 106 |
| 122450 | 833 |
|
129 | 1.7 | 80 | 0.66 | 163 | 172158 | 2090 |
|
143 | 1.1 | 180 | 1.08 | 104 |
| 122669 | 1510 |
|
64 | 2.2 | 70 | 0.48 | 31 | 172252 | 725 |
|
148 | 4.5 | 150 | 0.35 | 117 |
| 122691 | 1660 |
|
87 | 2.2 | 70 | 1.2 | 132 | 172256 | 760 |
|
169 | 0.7 | 180 | 0.3 | 140 |
| 124367 | 149 |
|
120 | 0.3 | 70 | 0.35 | 150 | 173219 | 1260 |
|
41 | 2.0 | 45 | 1.83 | 156 |
| 124771 | 169 |
|
112 | 0.3 | 110 | 0.37 | 114 | 173370 | 145 |
|
81 | 0.12 | 73 | 0.04 | 118 |
| 125159 |
|
62 | 1 | 70 | 0.3 | 33 | 173637 | 1900 |
|
87 | 1.7 | 45 | 1.95 | 117 | |
| 127489 | 535 |
|
62 | 2 | 65 | 0.46 | 166 | 173948 | 556 |
|
21 | 0.15 | 20 | 0.50 | 20 |
| 127972 | 94.6 |
|
174 | 0.1 | 75 | 0.47 | 172 | 174237 | 667 |
|
80 | 0 | 0.18 | 80 | |
| 129954 | 351 |
|
65 | 1.3 | 80 | 0.67 | 17 | 174513 | 2180 |
|
1.8 | 45 | 1.8 | 135 | |
| 131492 | 256 |
|
65 | 0.9 | 75 | 0.5 | 175 | 174571 | 460 |
|
80 | 1.7 | 80 | 1.2 | 80 |
| 133738 | 115 |
|
52 | 0.15 | 60 | 0.81 | 51 | 174638 | 270 |
|
155 | 0.15 | 155 | 0.45 | 155 |
| 134401 | 1260 |
|
13 | 1.1 | 55 | 1.2 | 161 | 175863 | 400 |
|
0.8 | 110 | 0.8 | 20 | |
| 135160 | 558 |
|
54 | 1.5 | 60 | 0.4 | 168 | 175869 | 338 |
|
48 | 0.5 | 60 | 0.46 | 151 |
| 136415 | 156 |
|
83 | 0.3 | 65 | 0.36 | 97 | 177015 | 800 |
|
0 | 0.8 | 40 | 1.87 | 148 |
| 136556 | 1900 |
|
34 | 2 | 55 | 1.45 | 179 | 177648 | 279 |
|
40 | 0.5 | 25 | 0.76 | 50 |
| 137387 | 313 |
|
122 | 0.65 | 135 | 0.45 | 102 | 178175 | 469 |
|
0 | 0.72 | 45 | 0.80 | 148 |
| 137432 | 128 |
|
91 | 0.1 | 65 | 0.08 | 125 | 178475 | 255 |
|
138 | 0.3 | 140 | 0.21 | 135 |
| 137518 | 4170 |
|
41 | 1.5 | 55 | 1.0 | 154 | 181409 | 568 |
|
163 | 0.5 | 145 | 0.30 | 31 |
| 138749 | 95.3 |
|
90 | 0.05 | 100 | 0.15 | 87 | 181615 | 513 |
|
172 | 0.7 | 172 | 0.68 | 172 |
| 138769 | 133 |
|
66 | 0.05 | 45 | 0.05 | 85 | 183362 | 525 |
|
42 | 0.3 | 0 | 0.78 | 53 |
| 139790 | 1445 |
|
36 | 2.5 | 50 | 1.8 | 146 | 183656 | 295 |
|
60 | 0.4 | 70 | 0.54 | 53 |
| 140336 | 3800 |
|
49 | 1.7 | 55 | 0.6 | 156 | 184279 | 600 |
|
0.9 | 100 | 0.9 | 10 | |
| 140784 | 119 |
|
32 | 0.1 | 70 | 0.1 | 171 | 184915 | 446 |
|
172 | 2.4 | 180 | 1.17 | 99 |
| 140926 | 578 |
|
43 | 1.5 | 50 | 0.42 | 11 | 185037 | 226 | 77 | 0.15 | 75 | <0.05 | 121 | |
| 140946 | 1095 |
|
60 | 1.5 | 50 | 0.5 | 111 | 187350 | 322 |
|
82 | 1.6 | 90 | 0.85 | 7 |
| 141637 | 160 |
|
34 | 0.4 | 45 | 0.62 | 27 | 187567 | 476 |
|
114 | 1.35 | 70 | 1.43 | 31 |
| 141926 | 1445 |
|
66 | 2 | 50 | 1.05 | 110 | 187811 | 190 |
|
0.15 | 5 | 0.15 | 96 | |
| 142184 | 120 |
|
64 | 0.5 | 60 | 0.17 | 76 | 187851 | 368 |
|
24 | 0.55 | 40 | 0.71 | 12 |
| 142237 | 1095 |
|
55 | 2 | 50 | 0.65 | 129 | 189687 | 483 |
|
110 | 0.4 | 90 | 0.28 | 166 |
| 142926 | 148 |
|
160 | 0 | 0.16 | 160 | 190944 | 1510 |
|
24 | 0.4 | 15 | 0.97 | 28 | |
| 142983 | 157 |
|
138 | 0.65 | 110 | 0.73 | 162 | 191610 | 264 |
|
56 | 0.15 | 90 | 0.33 | 43 |
| 144320 | 1260 |
|
48 | 2 | 50 | 0.85 | 143 | 191639 | 860 |
|
4 | 0.3 | 180 | 0.22 | 10 |
| 144970 | 1660 |
|
44 | 2.5 | 50 | 1.0 | 32 | 192044 | 350 |
|
160 | 0.30 | 90 | 0.43 | 173 |
| 145846 | 630 |
|
55 | 3 | 50 | 0.85 | 86 | 192445 | 1860 |
|
174 | 0.7 | 175 | 0.33 | 86 |
| 146444 | 760 |
|
24 | 2.5 | 35 | 1.25 | 138 | 192685 | 368 |
|
0.2 | 57 | 0.2 | 148 | |
| 146463 | 725 |
|
31 | 2 | 50 | 1.5 | 148 | 193009 | 860 |
|
75 | 1.5 | 170 | 2.1 | 78 |
| 147274 | 2290 |
|
35 | 1 | 45 | 0.65 | 20 | 193182 | 285 |
|
134 | 0.35 | 140 | 0.15 | 119 |
| 147302 | 1320 |
|
52 | 2 | 50 | 0.35 | 60 | 193911 | 552 |
|
0.43 | 57 | 0.43 | 147 | |
| 147756 | 2090 |
|
24 | 1.5 | 25 | 0.1 | 127 | 194335 | 274 |
|
0.35 | 70 | 0.35 | 160 | |
| 148184 | 150 |
|
110 | 0.7 | 125 | 0.41 | 50 | 194883 | 769 |
|
1.6 | 160 | 1.6 | 70 | |
| 148259 | 457 |
|
19 | 1.6 | 20 | 0.3 | 114 | 195325 | 174 |
|
63 | 0.2 | 70 | 0.17 | 55 |
| 148877 |
|
39 | 1 | 45 | 0.25 | 156 | 195407 | 1360 |
|
44 | 1.6 | 65 | 1.23 | 14 | |
| 149298 | 1200 |
|
156 | 0.8 | 35 | 1.3 | 141 | 196712 | 377 |
|
95 | 0.4 | 95 | 0.05 | 2 |
| 149313 | 366 |
|
30 | 1.4 | 25 | 0.39 | 49 | 197419 | 360 |
|
0.33 | 45 | 0.33 | 135 | |
| 149671 | 211 |
|
48 | 0.5 | 40 | 0.16 | 89 | 198183 | 360 |
|
81 | 0.33 | 45 | 0.32 | 120 |
| 149729 | 1380 |
|
49 | 0.9 | 45 | 0.38 | 60 | 198512 | 1000 |
|
126 | 2.4 | 150 | 1.8 | 82 |
| 149757 | 140 |
|
126 | 0.7 | 90 | 0.82 | 153 | 198625 | 282 |
|
0.25 | 65 | 0.25 | 155 | |
| 152060 | 2190 |
|
23 | 0.8 | 35 | 1.2 | 175 | 198895 | 397 |
|
149 | 2.5 | 135 | 3.4 | 159 |
| 152478 | 230 |
|
19 | 0.3 | 25 | 0.97 | 17 | 198931 | 752 |
|
147 | 2.8 | 160 | 1.92 | 143 |
| 152541 | 380 |
|
21 | 0.6 | 26 | 0.35 | 14 | 199218 | 207 |
|
60 | 0.3 | 80 | 0.24 | 43 |
| 152979 | 1660 |
|
26 | 1.6 | 25 | 0.1 | 37 | 199356 | 645 |
|
151 | 2 | 160 | 0.65 | 118 |
| 153261 | 363 |
|
24 | 0.8 | 40 | 0.99 | 11 | 200120 | 345 |
|
22 | 0.3 | 65 | 0.52 | 5 |
| 153295 | 2290 |
|
33 | 0.8 | 35 | 1 | 32 | 200310 | 418 |
|
100 | 0.33 | 60 | 0.51 | 120 |
| 153879 | 1660 |
|
13 | 1.0 | 25 | 0.8 | 178 | 201522 | 418 |
|
15 | 0.33 | 60 | 1.0 | 6 |
| 154040 | 630 |
|
86 | 0.6 | 35 | 1.4 | 98 | 201733 | 336 |
|
172 | 0.3 | 62 | 1.2 | 168 |
| 154111 | 1380 |
|
35 | 1.6 | 30 | 0.4 | 104 | 202904 | 276 |
|
111 | 0.15 | 40 | 0.46 | 117 |
| 154154 | 1820 |
|
21 | 1.0 | 25 | 1.7 | 18 | 203025 | 525 |
|
11 | 0.8 | 20 | 0.63 | 113 |
| 154243 | 1050 |
|
22 | 0.8 | 90 | 2.0 | 14 | 203064 | 1030 |
|
55 | 0.15 | 65 | 0.23 | 49 |
| 154450 | 1820 |
|
90 | 1.25 | 140 | 1.7 | 67 | 203374 | 830 |
|
166 | 1 | 35 | 1.1 | 134 |
| 154911 | 2190 |
|
149 | 1.65 | 155 | 0.35 | 107 | 203467 | 331 |
|
122 | 0.5 | 120 | 0.03 | 166 |
| 155438 | 2750 |
|
28 | 1.1 | 25 | 0.6 | 33 | 203699 | 600 |
|
33 | 0 | 0.18 | 33 | |
| 155806 | 660 |
|
150 | 0.7 | 140 | 0.30 | 165 | 203731 | 309 |
|
167 | 0.27 | 65 | 1.0 | 164 |
| 155851 | 1445 |
|
146 | 1.25 | 140 | 1.0 | 154 | 204116 | 725 |
|
22 | 1.8 | 25 | 1.18 | 17 |
| 156325 | 386 |
|
156 | 0.5 | 140 | 1.6 | 161 | 204722 | 780 |
|
10 | 2.0 | 45 | 1.95 | 153 |
| 156468 | 1000 |
|
9 | 1.5 | 180 | 0.65 | 75 | 204860 | 483 |
|
0.2 | 45 | 0.2 | 135 | |
| 157042 | 221 |
|
151 | 0.25 | 30 | 0.44 | 136 | 205060 | 461 |
|
32 | 0.22 | 50 | 0.8 | 27 |
| 158319 | 725 |
|
70 | 1.5 | 55 | 0.9 | 132 | 205618 | 990 |
|
26 | 0.6 | 50 | 0.95 | 12 |
| 158427 | 74 |
|
174 | 0.15 | 30 | 0.58 | 166 | 205637 | 203 |
|
156 | 0 | 1.20 | 156 | |
| 158643 | 131 |
|
30 | 0.1 | 120 | 0.56 | 30 | 206773 | 498 |
|
169 | 1.75 | 170 | 0.29 | 163 |
| 159489 | 3800 |
|
22 | 1.0 | 20 | 0.35 | 27 | 208057 | 157 |
|
119 | 0.19 | 32 | 0.24 | 144 |
| 160202 | 532 |
|
161 | 1.7 | 165 | 0.42 | 87 | 208220 | 2600 |
|
42 | 2.0 | 35 | 0.48 | 87 |
| observed | interstellar | intrinsic | |||||
| polarization | polarization | polarization | |||||
| HD | D, pc |
|
pV, % | pV, % | |||
| 208392 | 910 |
|
44 | 1 | 45 | 0.34 | 41 |
| 208682 | 369 |
|
140 | 0.5 | 120 | 0.70 | 154 |
| 209014 | 311 |
|
15 | 0 | 0.15 | 15 | |
| 209409 | 117 |
|
177 | 0.2 | 125 | 0.60 | 6 |
| 209522 | 346 |
|
19 | 0 | 0.19 | 19 | |
| 210129 | 214 |
|
7 | 0.12 | 55 | 0.32 | 176 |
| 212044 | 860 |
|
52 | 1.7 | 47 | 0.51 | 124 |
| 212076 | 298 |
|
98 | 0.26 | 112 | 0.12 | 58 |
| 212571 | 338 |
|
168 | 0.3 | 127 | 0.94 | 177 |
| 214167 | 196 |
|
0.20 | 110 | 0.2 | 20 | |
| 214168 | 77 |
|
30 | 0.05 | 120 | 0.18 | 30 |
| 214748 | 228 |
|
155 | 0.30 | 100 | 0.34 | 3 |
| 215227 | 256 |
|
28 | 0.60 | 83 | 1.05 | 12 |
| 215605 | 1995 |
|
40 | 2.6 | 60 | 1.76 | 166 |
| 216057 | 185 |
|
44 | 0.75 | 50 | 0.39 | 146 |
| 216200 | 333 |
|
145 | 0.8 | 75 | 1.6 | 154 |
| 217050 | 337 |
|
75 | 0.8 | 75 | 0.77 | 67 |
| 217061 | 795 |
|
88 | 1.5 | 95 | 0.43 | 27 |
| 217543 | 273 |
|
0.4 | 85 | 0.4 | 175 | |
| 217675 | 212 |
|
90 | 0.45 | 85 | 0.13 | 161 |
| 217891 | 151 |
|
109 | 0.22 | 102 | 0.09 | 128 |
| 218393 | 446 |
|
55 | 0.9 | 65 | 0.33 | 179 |
| 218674 | 525 |
|
90 | 0.9 | 80 | 0.36 | 151 |
| 219688 | 98.7 |
|
152 | 0.05 | 152 | 0.08 | 152 |
| 220058 | 1995 |
|
67 | 1.2 | 65 | 0.1 | 121 |
| 220116 | 535 |
|
81 | 2.5 | 85 | 1.77 | 75 |
| 223387 | 1995 |
|
67 | 1.2 | 65 | 0.9 | 70 |
| 224544 | 571 |
|
66 | 0.65 | 100 | 0.79 | 41 |
| 224559 | 417 |
|
37 | 0.55 | 50 | 0.24 | 170 |
| 224686 | 115 |
|
86 | 0.04 | 88 | 0.04 | 84 |
| 224905 | 1510 |
|
100 | 1.5 | 75 | 1.15 | 143 |
| 225095 | 358 |
|
79 | 0.85 | 65 | 0.66 | 93 |
| 225985 | 2100 |
|
149 | 0.5 | 80 | 0.9 | 159 |
| 227836 | 2750 |
|
82 | 1.8 |
82 | ||
| 228104 | 1750 |
|
70 | 0.45 | 160 | 0.95 | 70 |
| 228438 | 3500 |
|
170 | 1.0 | 170 | 0.15 | 170 |
| 228860 | 1995 |
|
102 | 0.5 | 80 | 1.08 | 110 |
| 229171 | 1995 |
|
20 | 1.5 | 180 | 1.0 | 75 |
| 230579 | 1200 |
|
99 | 0.7 | 80 | 1.35 | 109 |
| 232552 | 306 |
|
117 | 1.2 | 110 | 1.09 | 125 |
| 235795 | 2180 |
|
40 | 2.0 | 48 | 1.2 | 144 |
| 236689 | 1580 |
|
91 | 2.5 | 90 | 0.25 | 101 |
| 236935 | 1510 |
|
91 | 3 | 95 | 1.4 | 82 |
| 237056 | 780 |
|
125 | 5.5 | 118 | 0.9 | 152 |
| 239758 | 2090 |
|
59 | 1.5 | 45 | 1.1 | 80 |
| 244894 | 2290 |
|
19 | 1 | 50 | 1.45 | 0 |
| 245493 | 1050 |
|
165 | 1 | 160 | 0.2 | 12 |
| 246878 | 2500 |
|
133 | 1 | 180 | 1.1 | 104 |
| 248753 | 395 |
|
139 | 0.9 | 165 | 1.7 | 127 |
| 249695 | 1820 |
|
176 | 1.2 | 170 | 0.25 | 54 |
| 250028 | 1000 |
|
164 | 3.5 | 175 | 1.7 | 138 |
| 250163 | 1450 |
|
136 | 2 | 165 | 1.8 | 100 |
| 250289 | 546 |
|
162 | 1.95 | 165 | 1 | 156 |
| 254647 | 2630 |
|
11 | 0.6 | 180 | 0.6 | 22 |
| 256577 | 1995 |
|
148 | 0.6 | 170 | 1.3 | 140 |
| 298298 | 1900 |
|
158 | 1.5 | 170 | 0.6 | 113 |
| 300584 | 1820 |
|
52 | 0.5 | 150 | 1.6 | 54 |
| 302724 | 1320 |
|
59 | 0.8 | 80 | 1 | 42 |
| 302838 | 2290 |
|
157 | 1.2 | 150 | 0.4 | 40 |
| 305382 | 1900 |
|
145 | 1.5 | 100 | 1.8 | 173 |
| 306209 | 3150 |
|
94 | 1.1 | 95 | 0.6 | 90 |
| 306962 |
|
80 | 1.4 | 100 | 1.2 | 55 | |
| 307350 | 1820 |
|
91 | 1.2 | 100 | 0.5 | 28 |
| 312973 | 1900 |
|
147 | 0.8 | 110 | 0.9 | 175 |
| 316568 | 1380 |
|
13 | 1.2 | 180 | 0.8 | 35 |
| 316587 | 3000 |
|
155 | 1.2 | 180 | 1 | 125 |
| 316589 | 2550 |
|
19 | 1.2 | 180 | 0.8 | 55 |
| CD-30 5559 |
|
171 | 0.9 | 150 | 0.7 | 25 | |
| CPD-60 4551 | 461 |
|
97 | 1.5 | 85 | 0.71 | 128 |
| CPD-60 4708 |
|
73 | 1.5 | 80 | 0.38 | 25 | |
| BD-13 2040 |
|
14 | 0.9 | 175 | 0.6 | 60 | |
| BD-13 4936 | 1250 |
|
101 | 0.9 | 80 | 1.1 | 35 |
| BD+35 1169 | 1500 |
|
133 | 1.4 | 150 | 0.9 | 105 |
| BD+41 3731 | 2500 |
|
125 | 0.9 | 90 | 0.85 | 169 |
| BD+47 3302 | 1650 |
|
0 | 1 | 20 | 0.8 | 155 |
| BD+49 3735 | 2400 |
|
35 | 1.4 | 40 | 0.4 | 15 |
| BD+53 2964 | 1650 |
|
61 | 2.0 | 50 | 1 | 125 |
| BD+56 473 | 1150 |
|
111 | 3.5 | 120 | 1.5 | 90 |
| BD+56 484 | 2290 |
|
124 | 3.5 | 120 | 0.5 | 170 |
| BD+56 493 | 2290 |
|
126 | 3.5 | 120 | 0.8 | 165 |
| BD+56 582 |
|
106 | 3.5 | 120 | 1.7 | 70 | |
| BD+56 624 |
|
107 | 3.5 | 120 | 1.5 | 61 | |
| BD+57 515 | 1900 |
|
111 | 4 | 115 | 0.65 | 80 |
| BD+57 607 |
|
117 | 4 | 115 | 0.3 | 177 | |
| BD+58 458 | 1500 |
|
115 | 4.5 | 115 | 0.2 | 115 |
| BD+59 2829 | 3150 |
|
74 | 1.3 | 80 | 0.3 | 40 |
|
|
The columns in this table give HD number or other identification, the
distance to the object in parsec (marked by italic when it was derived from
reddening or from an absolute magnitude-spectral type/luminosity
calibration), the value of observed V band polarization with its
standard deviation (
![]() in percents and
in percents and
![]() in degrees),
the estimated value of interstellar polarization (
in degrees),
the estimated value of interstellar polarization (
![]() in
percents and
in
percents and
![]() in degrees), the calculated value of
intrinsic polarization (
in degrees), the calculated value of
intrinsic polarization (![]() in percents and
in percents and
![]() in
degrees).
in
degrees).