A&A 368, 1133-1136 (2001)
DOI: 10.1051/0004-6361:20010060
V. V. Voitsekhovich - V. G. Orlov - L. J. Sanchez
Instituto de Astronomia, UNAM AP 70-264 Cd. Universitaria, 04510 Mexico D.F., Mexico
Received 10 November 2000 / Accepted 8 January 2001
Abstract
The influence of scintillations on image centroid measurements and on the
phase reconstruction from Hartmann-like wavefront sensors is investigated
quantitatively by means of computer simulations. It is shown that under the
conditions of astronomical observations, the magnitude of the effect is
between 10% (for excellent seeing) and 18% (for poor seeing). However,
because the magnitude of the effect increases with the increasing of the
turbulence strength, one can expect that under the strong-turbulence
conditions the influence of scintillations on the image centroid can be
quite strong. So, starting from agiven turbulence strength, it can be
impossible to make a successful phase reconstruction from image centroid
measurements. It is also shown that the scintillations affect in a different
and complicated way the reconstruction quality of different aberrations.
Nevertheless one can notice some general tendencies: The scintillations affect
more strongly the reconstruction quality of the tip-tilt and high-order
aberrations than the reconstruction quality of intermediate aberrations.
Key words: atmospheric effects - instrumentaion: adaptive optics - techniques: high angular resolution
Hartmann-like wavefront sensors are often-used in astronomical adaptive systems for measurements of turbulence-induced wavefront distortions (Voitsekhovich et al. 1988; Rigaut et al. 1991; Jiang et al. 1993; Li et al. 1993; Colucci et al. 1994; Rigaut et al. 1997). These sensors are popular in applications because they provide a direct and simple relationship between the measurements and phase gradients at the telescope aperture: It is assumed that the phase gradient averaged over a subaperture of a Hartmann mask is proportional to the corresponding image centroid offset. This simple relationship, however, is valid if the effect of amplitude fluctuations (scintillations) is not taken into account. It is widely accepted that under the weak-turbulence conditions which are of main interest for astronomical observations, the effect of scintillations on the image centroid is negligible (Roddier 1981) but this assumption has never been supported by quantitative calculations.
In this paper we calculate the magnitude of the effect of interest by means of computer simulations. The simulations are based on the recently proposed method of random wave vectors (RWV) (Kouznetsov et al. 1997; Voitsekhovich et al. 1999) that allows us to simulate the amplitude and phase samples with the desired statistics and cross-statistics.
The set of Hartmann measurements is composed from the measurements of separated image centroids. So, at first we consider the effect of scintillations on a single image centroid, and then we investigate how the scintillations affect the quality of phase reconstruction from Hartmann data.
Let the wave
![]() pass through a thin lens of
diameter d and focal length f. The centroid
pass through a thin lens of
diameter d and focal length f. The centroid
![]() of the
image formed by this wave at the lens focal plane can be written as
(Tatarski 1968):
of the
image formed by this wave at the lens focal plane can be written as
(Tatarski 1968):
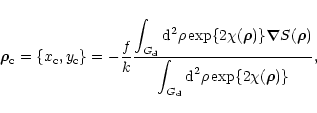 |
(1) |
However, in experiments related to the phase reconstruction from centroid
measurements it is always assumed that the effect of amplitude fluctuations
on the image centroid is negligible. Mathematically this assumption can be
written as
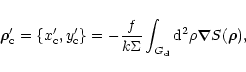 |
(2) |
Since in the problems related to propagation through atmospheric
turbulence, the quantities
![]() and
and
![]() are random, we can define the relative error
are random, we can define the relative error ![]() of image centroid
measurements associated with scintillations as
of image centroid
measurements associated with scintillations as
![\begin{displaymath}\sigma =\frac{1}{2}\left[ \frac{\sqrt{\left\langle \left(
x_{...
...{\sqrt{\left\langle
y_{\rm c}^{2}\right\rangle }}\right] \cdot
\end{displaymath}](/articles/aa/full/2001/12/aa10457/img15.gif) |
(3) |
In order to calculate the error ![]() we apply the method of
random wave vectors (RWV) (Kouznetsov et al. 1997; Voitsekhovich
et al. 1999) that allows us to simulate the phase and
log-amplitude samples with desired statistics and
cross-statistics. The detailed description of RWV method and
step-by-step simulation procedure can be found in Kouznetsov et al. (1997). The present simulations are performed for the Hufnagel
model of Cn2 profile (turbulence strength profile) that is
given by (Hufnagel 1974)
we apply the method of
random wave vectors (RWV) (Kouznetsov et al. 1997; Voitsekhovich
et al. 1999) that allows us to simulate the phase and
log-amplitude samples with desired statistics and
cross-statistics. The detailed description of RWV method and
step-by-step simulation procedure can be found in Kouznetsov et al. (1997). The present simulations are performed for the Hufnagel
model of Cn2 profile (turbulence strength profile) that is
given by (Hufnagel 1974)
| = | C0r0-5/3k-2 | ||
![$\displaystyle \times\left[ \left( \frac{
z}{z_{0}}\right)^{10}\exp \left\{ -\frac{z}{z_{1}}\right\} +\exp \left\{ -
\frac{z}{z_{2}}\right\} \right] ,$](/articles/aa/full/2001/12/aa10457/img17.gif) |
(4) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10457f1.eps}\end{figure}](/articles/aa/full/2001/12/aa10457/Timg18.gif) |
Figure 1:
Relative error |
| Open with DEXTER | |
So, using Eqs. (1-3) and the samples simulated by the RWV method, we
calculate the relative error ![]() defined by Eq. (3). The number of
samples used in the simulation is 5000. The simulation results are
shown in Fig. 1 where the relative error
defined by Eq. (3). The number of
samples used in the simulation is 5000. The simulation results are
shown in Fig. 1 where the relative error ![]() is plotted versus the
ratio of lens diameter d to the Fried parameter r0. In Fig. 1 we show
the error of interest for three cases of seeing conditions: poor seeing (
r0=0.07 m), good seeing (r0=0.1 m), and excellent seeing (
r0=0.15 m).
Because in the astronomical community it is widely accepted to characterize
the seeing by the image FWHM rather than by the Fried parameter, we present
a relationship between two parameters in Table 1. Table 1 includes two very
different telescope diameters (1 m and 10 m) in order to stress that,
for the considered range of telescope sizes, the relationship of interest is
affected slightly by the telescope diameter.
is plotted versus the
ratio of lens diameter d to the Fried parameter r0. In Fig. 1 we show
the error of interest for three cases of seeing conditions: poor seeing (
r0=0.07 m), good seeing (r0=0.1 m), and excellent seeing (
r0=0.15 m).
Because in the astronomical community it is widely accepted to characterize
the seeing by the image FWHM rather than by the Fried parameter, we present
a relationship between two parameters in Table 1. Table 1 includes two very
different telescope diameters (1 m and 10 m) in order to stress that,
for the considered range of telescope sizes, the relationship of interest is
affected slightly by the telescope diameter.
As one can see from Fig. 1, the error initially grows to a maximum magnitude, and then slowly approaches to an asymptotic level. This behavior is mainly determined by the cross-correlation between the log-amplitude and phase gradient fluctuations that have the same salient features: it starts from zero, reaches its maximum magnitude under some separation between the observation points, and then starts to decrease. So, in the initial phase, while the lens size is smaller than the log-amplitude phase gradient cross-correlation length, the error increases because the log-amplitude and phase gradient fluctuations become more and more correlated with the increasing lens size. After reaching its maximum magnitude, the error starts to decrease due to the progressive decorrelation between the log-amplitude and phase gradient fluctuations. Physically, it means that the main contribution to the error comes from the aperture zones within which the log-amplitude and phase gradient are still correlated. With increasing lens size this contribution starts to be smaller and smaller, as is reflected in the behavior of the error.
In the Hartmann test a set of image centroid measurements
H is
used to reconstruct the phase at the aperture. In real experiments these
measurements are always affected by scintillations that can be written
mathematically as
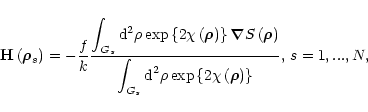 |
(5) |
However, in order to provide a successful phase reconstruction, one always
uses a scintillation-free approximation
![]() of Hartmann
measurements that can be written as
of Hartmann
measurements that can be written as
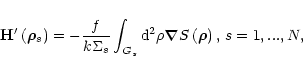 |
(6) |
So, there is always some scintillation-related error of phase reconstruction that arises from the difference between Eqs. (5) and (6). In our case, when the log-amplitude and phase fluctuations are random, this error is a statistical quantity, and can be considered as a variance of the difference between the phases restored from the sets of scintillation-affected and scintillation-free Hartmann measurements. For the completeness of analysis it is preferable to calculate not only the total error of phase reconstruction, but also the error for each aberration that allows one to see the reconstruction quality of separated aberrations. Such an investigation can be done if, for example, the Zernike phase expansion is included in the analysis (Voitsekhovich 1996).
Expanding the phase
![]() over the set of Zernike
polynomials, one can write
over the set of Zernike
polynomials, one can write
| = | 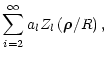 |
||
| al | = | (7) |
The Zernike coefficients al to be obtained from the Hartmann data ![]() can be written as
can be written as
![\begin{displaymath}a_{l}=T\left[ {\bf H}\right] ,
\end{displaymath}](/articles/aa/full/2001/12/aa10457/img30.gif) |
(8) |
In the present paper we use the procedure of least-square fit to the phase
gradient. In terms of the Zernike expansion, this procedure can be written as
![$\displaystyle \sum_{s=1}^N \sum_{l=2}^L \left[ a_{l}\vec{ \nabla }Z_{l}\left( \...
...ho }
_{s}/R\right) -\mathbf{H}\left( \vec{\rho }_{s}\right) \right] ^{2}=\min .$](/articles/aa/full/2001/12/aa10457/img31.gif) |
(9) |
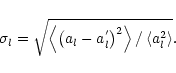 |
(10) |
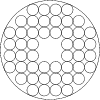 |
Figure 2: Hartmann mask configuration |
| Open with DEXTER | |
The simulation has been performed with a 48-subpupil Hartmann mask for a 2 m
telescope diameter. The mask configuration is shown in Fig. 2, and the
number of samples used in the simulation is 5000. The simulation
results are plotted in Fig. 3. As for the case of a single centroid error,
we present the results for three cases of seeing conditions: poor seeing
(
r0=0.07 m), good seeing (r0=0.1 m), and excellent seeing (
r0=0.15 m). One can see that the error depends in a complicated way on the Zernike
mode number that is due to a different complexity of the geometric structure
of Zernike polynomials. Nevertheless, one can notice some general tendencies.
For the lowest-order aberrations (tip-tilt, N2 and N3), the error is
between 10-18% (depending on the seeing conditions). Then, for the
second-order aberrations (defocus and astigmatism, NN 4-6), it drops
abruptly in 2-3 steps. With the increase in the aberration number,
the error increases (with some oscillations), and for high-order
aberrations it reaches practically the same magnitude as for the case of
tip-tilt. So, generally speaking, the scintillations more strongly affect
the reconstruction quality of the tip-tilt and high-order aberrations, while
for intermediate aberrations the effect is less pronounced.
 |
Figure 3:
Relative error
|
| Open with DEXTER | |
In this paper we have applied the RWV method that was developed for investigations related to weak-turbulence propagation. Because weak-turbulence conditions are of strong interest in astronomical observations, our quantitative analysis was restricted to this case only. Nevertheless, the results obtained allow us to draw some qualitative conclusions related to the strong-turbulence propagation that is of importance for a number of another applications. It was shown that the magnitude of the effect increases with increasing turbulence strength. So, one can expect that under the strong-turbulence conditions, the influence of scintillations on the image centroid can be quite strong, and starting from a given turbulence strength, it can make impossible a successful phase reconstruction from image centroid measurements. The quantitative results corresponding to the strong turbulence case can be obtained applying another simulation technique, for instance that based on propagation through multiple phase screens (Martin & Flatte 1988).