A&A 368, 451-463 (2001)
DOI: 10.1051/0004-6361:20000558

BeppoSAX study of the broad-band properties of luminous globular cluster X-ray sources

L. Sidoli1 - A. N. Parmar1 - T. Oosterbroek1 - L. Stella2 - F. Verbunt3 - N. Masetti4 - D. Dal Fiume4


1 - Astrophysics Division, Space Science Department of ESA, ESTEC, Postbus 299, 2200 AG Noordwijk,
The Netherlands
2 - Osservatorio Astronomico di Roma, Via Frascati 33, Monteporzio Catone, 00040 Roma, Italy
3 - Astronomical Institute, Utrecht University, PO Box 80000, 3508 TA Utrecht, The Netherlands
4 - Istituto Tecnologie e Studio Radiazioni Extraterrestri, CNR, Via Gobetti 101, 40129 Bologna, Italy

Received 16 October 2000 / Accepted 12 December 2000

Abstract
We have performed a detailed study of the broadband spectra of the luminous ( $\mathrel{\hbox{\rlap{\lower.55ex \hbox {$\sim$ }} \kern-.3em \raise.4ex \hbox{$>$ }}}$1036 erg s-1) globular cluster X-ray sources using BeppoSAX. With the exception of X 2127+119, located in NGC 7078, all the other spectra are well represented by a two component model consisting of a disk-blackbody and Comptonized emission. The measured low-energy absorptions are in good agreement with those predicted from optical measurements of the host globular clusters. This implies that there is little intrinsic X-ray absorption within the binaries themselves, and that the above spectral model provides a good representation of the low-energy continua. The sources can be divided into two groups. In the first group, composed of 3 ultra-compact (orbital period <1 hr) sources, the disk-blackbody temperatures and inner-radii appear physically realistic and the Comptonization seed photons temperatures and radii of the emission areas are consistent with the disk temperatures and inner radii. For all the other sources, the disk-blackbody parameters appear not to be physically realistic and the Comptonization parameters are unrelated to those of the disk-blackbody emission. If this is a spectral signature of ultra-compact binaries, this implies that no other ultra-compact binaries are present among those studied here. It is unclear why this difference between the two types of binaries should exist. One possibility may be related to the mass ratio, which is similar in the ultracompact systems and binaries containing black holes. In the latter systems the soft components are also well-fit with disk-blackbody models, which appear to have physically realistic parameters.

Key words: accretion, accretion disks - stars: neutron - globular clusters - X-rays: general


   
1 Introduction

The nature of the X-ray sources in globular clusters has provoked great observational and theoretical interest. Surveys of the dozen brightest $(\mathrel{\hbox{\rlap{\lower.55ex \hbox {$\sim$ }} \kern-.3em \raise.4ex \hbox{$>$ }}}$1036 erg s-1) globular cluster X-ray sources have shown that they share many similarities with the low-mass X-ray binaries (LMXBs) found in the rest of the Galaxy - for example the presence of X-ray bursts and a lack of coherent pulsations in their persistent emission (Hertz & Wood 1985; Parmar et al. 1989; Verbunt et al. 1995). The presence of Type I bursts indicates that the luminous systems contain accreting neutron stars rather than black holes, and they are generally considered to be similar systems to the galactic X-ray burst sources. Their formation is, however, about a factor $\sim$200 more efficient inside globular clusters than in the galaxy itself.

LMXB X-ray spectra are generally modeled by combining one or more spectral components. At luminosities $\sim$1037 erg s-1 these often consist of a modified blackbody and some form of power-law like component thought to result from the Comptonization of cooler photons. At lower luminosities, the spectra appear to simplify and are often fit with a power-law with an exponential cut-off at high energies (White et al. 1988).

In this paper we present the results of a systematic survey of the luminous globular cluster X-ray sources undertaken as part of the BeppoSAX Core Program. We pay particular attention to the spectral properties of the persistent emission. A long-term goal of such studies is to understand how the spectral shape may be used to derive information on physically interesting parameters such as the mass accretion rate, the neutron star mass, radius and spin-rate, the system inclination and the viscosity of the material in the accretion disk. For surveys of LMXBs, the study of those located in globular clusters provides a number of advantanges: (1) the distances to the many globular clusters have been independently determined through main-sequence modeling and other methods (see e.g., Carretta et al. 2000). This allows more accurate estimates of luminosity than is typical for galactic LMXBs. (2) The mean cluster abundances have been determined, allowing any dependence of X-ray properties on abundance to be examined. (3) The cluster reddenings have been measured so providing an independent estimate of low-energy absorption. For a number of clusters the reddening is significantly less than typical for galactic LMXBs.

Results of the BeppoSAX observations of Terzan 1, Terzan 2, NGC 6441, and NGC 7078 are to be found in Guainazzi et al. (1999, 1998), Parmar et al. (1999) and Sidoli et al. (2000), respectively. In addition, NGC 6440, Terzan 6, and Liller 1 were observed by BeppoSAX in other programs. Results are reported in in't Zand et al. (1999, 2000) and Masetti et al. (2000), respectively. For these sources data were extracted from the SSD BeppoSAX archive and reprocessed using the SAX Data Analysis System (SAXDAS).

   
2 Globular cluster properties

Table 1 includes informations on the globular clusters which are known to contain luminous X-ray sources and have been analysed here. Most of the cluster distances, metallicities and extinctions are taken from Djorgovski (1993). In the case of Terzan 1 more recent estimates of the distance and extinction obtained using HST are used (Ortolani et al. 1999). For the highly absorbed globular cluster Terzan 6 the results of Barbuy et al. (1997) are used, while the metallicity of Liller 1 is taken from the infrared measurements of Frogal et al. (1995).

The metallicities of the studied globular clusters range from strongly underabundant compared to solar (NGC 7078, [Fe/H] = -2.17), to around solar (Liller 1, [Fe/H] = +0.25). Such a wide range of metallicity should allow any dependence of the X-ray properties on this parameter to be probed. However, we caution that the material being accreted does not necessarily have the same metallicity as the host globular cluster since the companion star may have undergone a non-standard evolution during which its envelope composition was altered.

The extinctions to the studied globular clusters range from low ( $A_{\rm v} = 0.1$, NGC 1851) to strongly absorbed ( $A_{\rm v} \sim 10$, Liller 1). The amount of extinction strongly affects the low-energy cut-off of the X-ray data and so the sensitivity to any low-energy spectral components. As an example, the X-ray source in NGC 1851 is visible using BeppoSAX down to 0.1 keV, while that in Liller 1 is only detected above 1 keV. A summary of all previous observations of the Globular Clusters luminous X-ray sources can be found in Sidoli et al. (2000b).

   
3 Observations

Results from the Low-Energy Concentrator Spectrometer (LECS; 0.1-10 keV; Parmar et al. 1997), Medium-Energy Concentrator Spectrometer (MECS; 1.8-10 keV; Boella et al. 1997), High Pressure Gas Scintillation Proportional Counter (HPGSPC; 5-120 keV; Manzo et al. 1997) and Phoswich Detection System (PDS; 15-300 keV; Frontera et al. 1997) on-board BeppoSAX are presented. All these instruments are coaligned and collectively referred to as the Narrow Field Instruments (NFI). The MECS and the LECS are grazing incidence telescopes with imaging gas scintillation proportional counters in their focal planes. The non-imaging HPGSPC consists of a single unit with a collimator that was alternatively rocked on- and 180$^\prime$ off-source every 96 s during most of the observations. During the observations in the year 2000 th collimator remained on-source. The PDS consists of four independent non-imaging units arranged in pairs each having a separate collimator. Each collimator was alternatively rocked on- and 210$^\prime$ off-source every 96 s during the observations.


 

 
Table 1: BeppoSAX observations of luminous globular cluster X-ray sources. T is the MECS exposure and R the energy range used for spectral fitting. LMHP indicate whether data from the LECS, MECS, HPGSPC, and PDS respectively, were included in the fits

Globular		 X-ray $P_{\rm orb}$ BeppoSAX Observation T R Inst. d Cluster $A_{\rm v}$
Cluster Source (hr) Start Stop (ks) (keV)   (kpc) [Fe/H]  

NGC 1851		 X 0512-401 <0.85 2000 Feb. 23 12:44 Feb. 25 07:44 72.2 0.1-25 LM-P 12.2 -1.29 0.1
Terzan 2 X 1724-304   1996 Aug. 17 04:29 Aug. 18 05:05 37.1 0.3-100 LMHP 10.0 -0.25 4.0
Liller 1 X 1730-335   1998 Feb. 27 03:30 Feb. 27 19:22 16.2 1.0-10 LM- 7.9 +0.25 $\sim$10
      1998 Mar. 02 19:57 Mar. 03 12:35 29.8 1.0-10 LM-      
Terzan 1 X 1732-304   1999 Apr. 03 12:52 Apr. 04 15:29 47.1 2.0-10 -M- 5.2 -0.71 6.8
NGC 6440 X 1745-203   1998 Aug. 26 02:11 Aug. 26 14:36 21.6 0.4-100 LMHP 7.0 -0.34 3.5
NGC 6441 X 1746-370 5.7 1999 Apr. 04 18:07 Apr. 05 20:23 49.9 0.25-30 LMHP 10.7 -0.53 1.3
Terzan 6 X 1747-313 12.4 1998 Sep. 06 06:16 Sep. 06 19:02 28.9 0.5-50 LMHP 7.0 -0.61 7.4
NGC 6624 X 1820-303 0.2 1997 Oct. 02 06:45 Oct. 02 19:90 22.3 0.3-30 LMHP 8.1 -0.37 0.9
      1998 Apr. 17 04:14 Apr. 18 03:12 37.5 0.3-30 LMHP      
      1998 Sep. 23 12:44 Sep. 24 15:30 48.3 0.3-30 LMHP      
NGC 6712 X 1850-087 0.3 1997 Apr. 24 11:47 Apr. 25 11:09 42.0 0.3-50 LMHP 6.8 -1.01 1.4
NGC 7078 X 2127+119 17.1 1999 Nov. 16 01:15 Nov. 17 00:50 35.5 0.1-100 LM-P 10.5 -2.17 0.2


Table 1 lists the BeppoSAX observations used in this survey together with some basic information about each globular cluster (see Sect. 2). The observations of Terzan 2 and NGC 6712 were made prior to the failure of one of the MECS units. Data from the entire observations were accumulated, except for the following sources: (1) X 1730-335 (the Rapid Burster, hereafter RB). BeppoSAX carried out a total of 7 observations, partly analysed by Masetti et al. (2000), which were extracted from the archive and examined for the presence of bursts. Only two observations included sufficiently long quiescent intervals for this study (see Table 1). (2) For the 5.7 hour dip source X 1746-371 the dipping and bursting intervals discussed in Parmar et al. (1999) were excluded. (3) The eclipse observed from the 12.4 hr eclipsing system X 1747-313 (In't Zand et al. 2000) was excluded. (4) The bursts seen from X 0512-401, X 1724-304, and X 1745-203 were excluded. Table 1 also indicates the instruments that were used in the spectral analysis of each source. In the case of the faintest source studied (Terzan 1, 0.014 MECS counts s-1) only the MECS was used, while for the slightly brighter Liller 1 observations the LECS and MECS were used. If available, all the NFI were used for the brightest sources.

Since previous analyses used different software and calibration releases, all relevant data were re-extracted. As usual, good data were selected from intervals when the elevation angle above the Earth's limb was >$4^{\circ}$ for the LECS and >$5^{\circ}$ for other instruments and when the instrument configurations were nominal. This was done by using the SAXDAS 2.0.0 data analysis package. LECS and MECS data were extracted centered on the source positions using radii of 8$^\prime$ and 4$^\prime$, respectively, corresponding to about 95% of the total source photons. In the case of the RB extraction radii of 4$^\prime$ and 2$^\prime$ were used in order to minimize the contribution from the 32$^\prime$ distant bright X-ray source 4U 1728-337. Similarly, data from the non-imaging instruments were not included in the RB fits. Background subtraction for the imaging instruments was performed using standard files; this is not a critical procedure for the bright sources studied here (with the exception of Terzan 1). Background subtraction for the non-imaging instruments was carried out using the offset pointing intervals. In the case of observations were the HPGSPC remained coaligned, background subtraction was performed using data obtained when the instrument was looking at the dark Earth.

The overall spectra extracted as described above were first investigated by simultaneously fitting data from as broad a band as possible. The LECS and MECS spectra were rebinned to oversample the full width half maximum of the energy resolution by a factor 3 and to have additionally a minimum of 20 counts per bin to allow use of $\chi^2$ statistics. The HPGSPC and PDS spectra were rebinned using the standard techniques in SAXDAS. Data were selected from within the energy ranges 0.1-8.0 keV (LECS), 1.8-10 keV (MECS), 8.0-20 keV (HPGSPC), and 15-100 keV (PDS) whenever a sufficient number of counts were obtained (see Table 1). The photo-electric absorption cross sections of Morrison & McCammon (1983) and the solar abundances of Anders & Grevesse (1989) are used throughout. Factors were included in the spectral fitting to allow for normalization uncertainties between the instruments. These factors were constrained to be within their usual ranges during the fitting (Fiore et al. 1999). An additional uncertainty of 1% was added quadratically to the uncertainties to account for systematic uncertainties in instrumental responses. Since we wish to investigate the spectral properties of the sources, we first attempted to find a general spectral model that could be successfully applied to all the sources. Many luminous LMXB are fit with a two component model consisting of a blackbody, or blackbody-like component which might represent emission from an optically thick accretion disk or from the neutron star surface, together with a Comptonized component which may be interpreted as emission from a hot inner disk region or a boundary layer between the disk and the neutron star. For the soft component we tried both a single blackbody model and a disk-blackbody component, in the formulation of Mitsuda et al. (1984) and Makishima et al. (1986). The disk-blackbody model assumes that the gravitational energy released by the accreting material is locally dissipated into blackbody radiation, that the accretion flow is continuous throughout the disk, and that the effects of electron scattering are negligible. There are only two parameters in this model, $r_{\rm in}({\cos}\,i)^{0.5}$ where $r_{\rm in}$ is the innermost radius of the disk, i is the inclination angle of the disk and $kT_{\rm in}$ the blackbody effective temperature at $r_{\rm in}$. Some limitations of this model are discussed in Merloni et al. (2000).

For the Comptonized component the XSPEC model COMPTT (Titarchuk 1994; Hua & Titarchuk 1995; Titarchuk & Lyubarskij 1995), which self-consistently calculates the spectrum produced by the Comptonization of soft photons in a hot plasma, was used. This model contains as free parameters the temperature of the Comptonizing electrons, $kT{\rm _e}$, the plasma optical depth with respect to electron scattering ${\rm\tau_p}$ and the input temperature of the soft photon (Wien) distribution ( $kT{\rm _0}$). A spherical geometry was assumed for the comptonizing region.

Fit result to the broad-band spectra with the single blackbody plus Comptonization and disk-blackbody plus Comptonization are reported in Tables 2 and 3 respectively. A single temperature blackbody plus a cut-off power-law model was also tried, but with unacceptable results in the majority of the sources. Since the disk-blackbody plus Comptonization emission (Table 3) always gives a better (or equally good) fit than single blackbody plus Comptonization emission (Table 2), we will refer to it as the "standard'' model.


 

 
Table 2: BeppoSAX spectral results using the COMPTT and single-blackbody model. For globular clusters with multiple observations, the results are given in the same order as in Table 1. L is the 0.1-100 keV (assumed isotropic, in units of 1035 ergs-1) source luminosity using the distances given in Table 1 and assuming that the measured $N_{\rm H}$ is interstellar. The units of $N_{\rm H}$ are 1022 atom cm-2. $f_{\rm bb}$ is the absorption corrected 0.1-100 keV ratio of blackbody to COMPTT fluxes. All uncertainties are quoted at 90% confidence

Globular		 L $N_{\rm H}$ kT0 $kT{\rm _e}$ ${\rm\tau_p}$ $kT_{\rm bb}$ $R_{\rm bb}$ $f_{\rm bb}$ $\chi^2$/dof
Cluster     (keV) (keV)   (keV) (km)    

NGC 1851		 43 $0.003 \pm ^{0.005} _{0.003}$ $0.20 \pm ^{0.02} _{0.03} $ $2.4 \pm ^{0.2} _{0.1}$ $17.4 \pm ^{1.0} _{1.3}$ $0.56 \pm ^{0.04} _{0.02}$ $6.7 \pm ^{0.86} _{1.4}$ 0.14 153.2/97
Terzan 2 200 $ 0.83 \pm 0.06$ $1.11 \pm ^{0.15} _{0.03}$ $36 \pm ^{110} _{6}$ $2.8 \pm ^{0.4} _{2.4}$ $0.66 \pm ^{0.07} _{0.06}$ $10.7 \pm ^{0.35} _{0.80}$ 0.15 197.1/178
Liller 1 8.7 $1.4 \pm ^{1.0} _{0.4}$ <4.2 $2.5 \pm ^{2.3} _{0.7}$ $17 \pm ^{23} _{10}$ <1.5 <4.0 <0.14 100.7/90
  2.5 $1.3 \pm ^{0.9} _{1.1}$ $0.43 \pm ^{0.22} _{0.40}$ $9.1 \pm ^{100} _{6.8}$ $ 7.3 \pm ^{7.7} _{4.3}$ ... ... ... 71.0/57
Terzan 1 0.059 <0.66 <0.48 >2.2 <20 ... ... ... 18.4/11
NGC 6440 66 $0.38 \pm 0.06$ $0.50 \pm ^{0.03} _{0.04} $ $9.6 \pm 0.1$ $8.6 \pm ^{0.70} _{0.80} $ $1.3 \pm ^{0.3} _{0.1}$ $0.87 \pm ^{0.26} _{0.33}$ 0.05 101.5/107
NGC 6441 140 $0.20 \pm ^{0.25} _{0.06} $ $0.51 \pm ^{0.04} _{0.07}$ $2.35 \pm ^{0.09} _{0.04}$ $ 17.2 \pm ^{0.30} _{0.75}$ $0.27 \pm ^{0.27} _{0.08}$ $28 \pm ^{61} _{11}$ 0.04 117.6/106
Terzan 6 59 $1.3 \pm ^{0.01} _{0.02}$ $1.34 \pm ^{0.21} _{0.02}$ $16.0 \pm ^{0.54} _{1.0}$ $2.0 \pm ^{0.20} _{0.1}$ $ 0.65 \pm {0.05}$ $6.7 \pm ^{1.0} _{1.4}$ 0.29 144.5/119
NGC 6624 420 $0.10 \pm ^{0.11} _{0.03}$ $0.38 \pm 0.02$ $2.97 \pm ^{0.03} _{0.08}$ $13.3 \pm 0.2$ $0.21 \pm ^{0.01} _{0.05}$ $88 \pm 2$ 0.05 268.2/120
  500 <0.015 $0.38 \pm ^{0.03} _{3.0} $ $3.0 \pm ^{0.01} _{0.03}$ $13.3 \pm{0.1}$ $1.5 \pm ^{0.01} _{0.06}$ $1.9\pm ^{0.07} _{0.01}$ 0.05 232.5/117
  560 $0.25 \pm ^{0.02} _{0.01}$ $0.07 \pm ^{0.02} _{0.02}$ $2.7 \pm ^{0.15} _{0.01}$ $15.8 \pm ^{0.2} _{1.0}$ $0.64 \pm ^{0.16} _{0.01}$ $14.4 \pm ^{0.3} _{5.7}$ 0.09 588.4/134
NGC 6712 13 $0.17 \pm ^{0.05} _{0.01} $ $0.60 \pm ^{0.20} _{0.08}$ $91 \pm ^{10} _{80}$ $1.2 \pm ^{0.05} _{0.65}$ $0.43 \pm ^{0.02} _{0.01}$ $8.9 \pm ^{1.0} _{0.2}$ 0.34 181.1/154
NGC 7078 90 $0.20 \pm ^{0.05} _{0.20}$ $0.042 \pm ^{0.030} _{0.039}$ $37 \pm ^{30} _{35}$ $ 2.9 \pm ^{+\infty} _{0.4}$ $1.1 \pm 0.05$ $3.3 \pm ^{0.80} _{0.30}$ 0.24 375.5/124



 

 
Table: BeppoSAX spectral results using the standard COMPTT and disk-blackbody model. For globular clusters with multiple observations, the results are given in the same order as in Table 1. L is the 0.1-100 keV (assumed isotropic, in units of 1035 erg s-1) source luminosity using the distances given in Table 1 and assuming that the measured $N_{\rm H}$ is interstellar. The units of $N_{\rm H}$ are 1022 atom cm-2. f is the absorption corrected 0.1-100 keV ratio of disk-blackbody to COMPTT fluxes. i is the inclination angle of the disk. All uncertainties are quoted at 90% confidence

Globular		 L $N_{\rm H}$ kT0 $kT{\rm _e}$ ${\rm\tau_p}$ $kT_{\rm in}$ $r_{\rm in} (\cos i)^{0.5}$ f $\chi^2$/dof
Cluster     (keV) (keV)   (keV) (km)    

NGC 1851		 47 $0.026 \pm ^{0.030} _{0.005}$ $0.33 \pm ^{0.06} _{0.09} $ $2.8 \pm ^{0.20} _{0.50}$ $14.0 \pm ^{0.5} _{0.9}$ $0.30 \pm ^{0.07} _{0.21}$ $17 \pm ^{99} _{2.8}$ 0.14 126.1/97
Terzan 2 220 $ 0.78 \pm 0.05$ $0.63 \pm 0.02$ $27 \pm ^{10} _{5}$ $3.8 \pm 0.7$ $ 3.3 \pm 0.3$ $0.28 \pm {0.05}$ 0.12 191.5/178
Liller 1 9.6 $2.8 \pm ^{0.5} _{1.6}$ $0.44 \pm ^{0.24} _{0.44}$ $3.0 \pm ^{1.3} _{0.5}$ $6.08 \pm ^{0.42} _{0.25}$ <0.50 <37000 <0.05 100.6/90
  2.5 $1.3 \pm ^{0.9} _{1.1}$ $0.43 \pm ^{0.22} _{0.40}$ $9.1 \pm ^{100} _{6.8}$ $ 7.3 \pm ^{7.7} _{4.3}$ ... ... ... 71.0/57
Terzan 1 0.059 <0.66 <0.48 >2.2 <20 ... ... ... 18.4/11
NGC 6440 71 $0.47 \pm 0.07$ $0.50 \pm 0.04 $ $8.7 \pm ^{1.3} _{0.8}$ $9.9 \pm ^{0.8} _{1.4} $ $1.98 \pm ^{0.33} _{0.13}$ $0.47 \pm ^{0.15} _{0.20}$ 0.14 84.8/107
NGC 6441 140 $0.26 \pm 0.02 $ $0.54 \pm ^{0.04} _{0.06}$ $25 \pm ^{225} _{24.5}$ $ 0.40 \pm ^{1.6} _{0.40}$ $2.82 \pm 0.05$ $0.92 \pm ^{0.03} _{0.04}$ 10 107.3/106
Terzan 6 67 $1.39 \pm 0.08$ $0.66 \pm ^{0.06} _{0.10}$ $8.3 \pm ^{1.7} _{1.3}$ $ 6.3 \pm ^{2.7} _{0.4}$ $2.65 \pm ^{0.15} _{0.06}$ $0.60 \pm ^{0.09} _{0.03}$ 2.16 136.5/119
NGC 6624 480 $0.16 \pm ^{0.003} _{0.003}$ $0.574 \pm ^{0.004} _{0.004} $ 2.72 0.01 0.01 $15.3 \pm ^{0.05} _{0.05}$ $0.57 \pm ^{0.05} _{0.05}$ $22 \pm{0.13}$ 0.36 152.1/120
  570 $0.16 \pm ^{0.07} _{0.007}$ $0.460 \pm ^{0.02} _{0.07}$ $2.86 \pm ^{0.07} _{0.01}$ $13.8 \pm 0.1$ $0.37 \pm ^{0.011} _{0.005}$ $45 \pm ^{40} _{3}$ 0.18 182.2/117
  660 $0.27 \pm ^{0.01} _{0.04}$ $0.0639 \pm ^{0.020} _{0.040}$ $2.77 \pm ^{0.13} _{0.06}$ $15.7 \pm ^{1.43} _{0.10}$ $1.06 \pm ^{0.47} _{0.021}$ $4.9 \pm ^{0.8} _{1.8}$ 0.12 627.7/134
NGC 6712 19 $0.39 \pm ^{0.01} _{0.03} $ $0.81 \pm ^{0.11} _{0.19}$ $71 \pm ^{7} _{25}$ $1.70 \pm ^{0.15} _{1.00}$ $0.63 \pm ^{0.05} _{0.02}$ $4.5 \pm ^{0.15} _{0.75}$ 0.76 160.0/154
NGC 7078 65 $0.06 \pm ^{0.01} _{0.03}$ $0.036 \pm ^{0.0095} _{0.006}$ $92 \pm ^{4.6} _{3.4}$ $ 2.6 \pm ^{0.1} _{0.2}$ $1.92 \pm 0.04$ $1.1 \pm{0.009}$ 2.0 284.8/124


   
4 Spectral fit results: the standard model

The results of fitting the standard model to all of the extracted spectra are given in Table 3. All spectral uncertainties and upper-limits are given at 90% confidence. The fits to all the spectra are acceptable with the exception of NGC 7078 where the $\chi^2$ is 284.8 for 124 degrees of freedom (dof), and the second and third observation of the source in NGC 6624. Since a different model is a better representation of the NGC 7078 X-ray spectrum, probably due to the ADC nature of this source (see Sidoli et al. 2000), we exclude it from the discussion, though the results of the fitting procedures have been included in Tables 2 and 3, for completeness. We note that an acceptable fit (a $\chi^2$ of 100.0 for 109 dof) can also be obtained without the disk-blackbody component for NGC 6440. In the case of Liller 1 and Terzan 1 the sources are too faint to derive accurate spectral parameters. Moreover Liller 1 was not sampled at energies greater than 10 keV due to the reasons explained in Sect. 3. We include results from these sources in Tables 2 and 3 for completeness, but do not consider them further. Figure 1 shows the photon spectra of the remaining sources derived using the standard model. This figure clearly illustrates the importance of the broad-band coverage afforded by BeppoSAX in clearly separating the two components. Bolometric luminosities have been calculated using the energy range 0.1-100 keV and assuming that the observed $N_{\rm H}$ is interstellar. The results in Sect. 4.1 indicate that for the majority of sources this assumption is valid.


  \begin{figure} \par\includegraphics[height=4.3cm,angle=-90]{h2504f1a.ps}\include... ...0]{h2504f1g.ps}\includegraphics[height=4.3cm,angle=-90]{h2504f1h.ps}\end{figure} Figure 1: The BeppoSAX spectra of each of the globular cluster X-ray sources obtained using the standard model, in order of increasing 0.1-100 keV luminosity. The contributions of the two components (where evident) are shown separately. Except for NGC6441 the COMPTT is the one extending to higher energies
Open with DEXTER

   
4.1 Low-energy absorption

We first compared the fitted values of low-energy absorption, $N_{\rm H}$, with the values predicted using the relation between the optical extinction, $A_{\rm v}$, and absorption of $N_{\rm H}[{\rm cm}^{-2}/A_{\rm v}] = 1.79~10^{21}$ derived by Predehl & Schmitt (1995). If there is no additional absorption present in the X-ray binaries themselves, and their low-energy X-ray continua have been properly characterized, then a good agreement is expected between the values derived from the globular cluster $A_{\rm v}$ measurements, and those from the LMXB X-ray spectra. Figure 2 shows the measured values of $N_{\rm H}$ taken from Table 3 plotted against the optically derived values of $N_{\rm H}$. The straight line shows the locus of points with equal optical and X-ray derived $N_{\rm H}$ values.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h2504f2.ps} \end{figure} Figure 2: The measured values of $N_{\rm H}$ (Table 3) plotted against the optically derived values of $N_{\rm H}$. The straight line shows the location of points with equal optical and X-ray derived $N_{\rm H}$ values. Here and in all other figures, the light diamonds mark the X-ray binaries known to harbor sub-giant companions ( $P_{\rm orb}>10$ hr), the triangles the ultra-compact binaries ( $P_{\rm orb}<1$ hr), while the squares indicate all other sources. The meaning of the symbols is the same in all the figures
Open with DEXTER

In general, there is good agreement between the two absorption measurements. In the case of X 1745-203, located in NGC 6440 the X-ray derived $N_{\rm H}$ is $\sim$0.75 that expected (a difference of 1.5 1021 atom cm-2). This may suggest the presence of an additional soft X-ray component that, not being included in the spectral model, leads to an underestimate of the absorbing column. Alternatively, the overall X-ray continuum model might be incorrect. We note that also the blackbody plus COMPTT model does not provide a good estimate of the column density, being even much lower. In't Zand et al. (1999) find that the spectrum of X 1745-203 may also be modeled using either a broken power-law and blackbody, or a high-energy cut-off power-law, or a bremsstrahlung and blackbody. In these 3 cases, the derived values of $N_{\rm H}$ are in the range 6.7-9.0 1021 atom cm-2, similar to that predicted from the $A_{\rm v}$ measurement of 6.2 1021 atom cm-2. In the case of X 1850-087 located in NGC 6712 the X-ray derived $N_{\rm H}$, of 3.9 1021 atom cm-2, is significantly higher than that derived from the optical of 2.5 1021 atom cm-2. This may suggest the presence of extra absorbing material in this system. However, when fitting this spectrum with a single blackbody plus Comptonization, a much lower column density is found ( 1.7 1021 atom cm-2).

   
4.2 Disk-blackbody component

The soft emission from luminous globular cluster sources is succesfully fit with a multicolor disk-blackbody component. If we interprete this model "literally", its normalization translates into a lower limit for the innermost radius $r_{\rm in}$ of the accretion disk, $R_{\rm in}=r_{\rm in}({\cos}\,i)^{0.5}$. Except for NGC 1851 and NGC 6624 (where the inclination cannot be constrained), the values observed are generally low, thus requiring a quite high inclination angle of the binary systems, for $r_{\rm in}$ to be larger than the last stable orbit for an accretion disk around a neutron star ( $6GM/c^{2} \sim 9$ ( $M/M_{\odot}$) km). We note that still higher inclinations would be derived if the Merloni et al. (2000) correction to the disk-blackbody model were taken into account. For several globular cluster sources, a confirmation of their high inclination angles comes from X-ray and optical observations. In particular, the presence of strong sinusoidal-like modulations in the X-ray flux (as in the case of the ADC source NGC 7078), partial X-ray eclipses of the central source by the companion star (Terzan 6), X-ray dips (NGC 6441) are all indicative of inclination angles >60-70$^{\circ}$ (Frank et al. 1987). The temperature $kT_{\rm in}$ at the inner disk radius is 0.5-3.5 keV, with the three ultra-compact binaries (NGC 1851, NGC 6712, NGC 6624; $P_{\rm orb}<1$ hr) displaying significantly lower temperatures (<1 keV) compared to all other sources (1.5-3.5 keV). The variation of $kT_{\rm in}$ and inner radius of the accretion disk is displayed in Fig. 3, while the variation with the disk luminosity, measured in the 0.1-100 keV energy range, is shown in Figs. 4 and 5.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h2504f3.ps} \end{figure} Figure 3: Variation of the disk-blackbody temperature $kT_{\rm in}$ and the lower limit to the inner radius of the accretion disk
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h2504f4.ps} \end{figure} Figure 4: Variation of the lower limit to the inner radius of the accretion disk and the luminosity of the disk-blackbody component, in the 0.1-100 keV band (in units of 1035 erg s-1)
Open with DEXTER

In the disk-blackbody model, the bolometric luminosity, $L_{\rm bol}$, of the accretion disk can be related to the temperature $kT_{\rm in}$ and the mass M of the compact object (see e.g., Eqs. (9) and (11) in Makishima et al. 2000) as $L_{\rm bol}\propto M^{2}\cdot T_{\rm in}^{4}$. A summary of the parameters derived from the disk-blackbody component is shown in Fig. 5, where the globular cluster sources appear to be divided into two groups: the ultra-compact binaries, with $kT_{\rm in}\mathrel{\hbox{\rlap{\lower.55ex \hbox {$\sim$ }} \kern-.3em \raise.4ex \hbox{$<$ }}}$1 keV, the inferred masses of which are compatible with that of a neutron star, and sources with $kT_{\rm in} \mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\dis... ...er{\offinterlineskip\halign{\hfil$\scriptscriptstyle ...1 keV, located on grids with much lower inferred masses for the compact object. Since all these X-ray binaries (except Terzan 6) are known to harbor a neutron star, due to their Type I X-ray bursting activity, either the multi-colour disk-blackbody is not an accurate model for the soft part of the spectrum, or their luminosity has been underestimated, possibly due to a very high inclination angle of the binary systems. Another explanation may be that the parameters derived in the framework of the disk-blackbody model cannot be related directly to physical quantities (see Merloni et al. 2000).


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h2504f5.ps}\end{figure} Figure 5: Relation between the disk-blackbody luminosity measured in the 0.1-100 keV energy range (in units of 1035 erg s-1) and the temperature $kT_{\rm in}$ at the inner accretion disk radius. Dash-dotted lines represent loci of constant mass for the neutron star (in units of solar masses), while the solid lines show loci of constant $\eta $, that is the luminosity normalized to the Eddington luminosity (assumed to be 1.5 1038 erg s-1 for a solar mass compact object)
Open with DEXTER

   
4.3 Comptonization component

Thermal Comptonization (Titarchuk 1994) provides a good fit to the high energy region of the globular cluster sources spectra. The relations between the different parameters derived from the spectral analysis are shown in Figs. 6-11. The Comptonizing plasma has temperatures $kT_{\rm e}$ ranging from few keV up to the extremely high value of $\sim$92 keV in the case of the ADC source in NGC 7078. The seed photons in all sources have temperatures kT0<1 keV while the Comptonization parameter y, defined as $y=4kT_{\rm e}\tau^{2}/m_{\rm e}{\rm c}^{2}$, is in the range $\sim$1-7, except for the very low value of $\sim$0.03 for the source in NGC 6441, that might be not in the right regime, since y$\ll$1 and $\tau $<1. The trend of y with the luminosity is shown in Fig. 6, suggesting that at least for some sources a correlation exists.The dependence of the plasma optical depths $\tau $ and of the electron temperatures $kT_{\rm e}$from the total luminosities are shown in Figs. 7 and 8. Following in't Zand et al. (1999), an equivalent spherical radius $R_{\rm W}$ of the emission area of the seed photons can be defined as $R_{\rm W}=3\ 10^4 d \sqrt{\frac{f_{\rm comptt}}{1+y}}/(kT_{0})^2$ km, where d is the distance (in kpc), $f_{\rm comptt}$ is the comptonized flux (in erg cm-2 s-1, corrected for the interstellar absorption, 0.1-100 keV band) and kT0 is the seed temperature in keV. $R_{\rm W}$ ranges from few km up to $\sim$1300 km (NGC 7078) and seems to correlate with the total luminosity (see Fig. 9), as $R_{\rm W}$ $\propto$ L0.5 .

This might suggest that the seed photons originate from the boundary layer (the radial extent and height of which become larger with increasing accretion rates; e.g. Popham & Sunyaev 2000) rather than from the accretion disk. The comparison between $R_{\rm W}$ and the lower limit $R_{\rm in}$ to the inner radius of the accretion disk is shown in Fig. 10. In this respect, the comparison between the temperatures $kT_{\rm0}$ of the seed photons and the temperature $kT_{\rm in}$ is interesting (see Fig. 11): among the globular cluster sources, only the ultra-compact binaries (located in NGC 1851, NGC 6624 and NGC 6712) display temperatures $kT_{\rm0}$ consistent with the temperature of the inner regions of the accretion disk.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h2504f6.ps} \end{figure} Figure 6: The Comptonization parameter y versus the total luminosity in the 0.1-100 keV band (in units of 1035 erg s-1)
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h2504f7.ps}\end{figure} Figure 7: The optical depth $\tau $ of the Comptonizing plasma versus total luminosity (0.1-100 keV, in units of 1035 erg s-1)
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.8cm,angle=0]{h2504f8.ps} \end{figure} Figure 8: The electron temperature $kT_{\rm e}$ versus the total luminosity (0.1-100 keV, in units of 1035 erg s-1)
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.8cm,angle=0]{h2504f9.ps}\end{figure} Figure 9: The radius $R_{\rm W}$ of the emission area of the seed photons versus the total luminosity in the 0.1-100 keV band (in units of 1035 erg s-1). Sources with larger luminosities (i.e. accretion rates) display larger radii of the seed photons regions
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.7cm,angle=0]{h2504f10.ps}\end{figure} Figure 10: Plot of the ratio between the lower limit $R_{\rm in}$ of the inner radius of the accetion disk and the radius $R_{\rm W}$ of the emission area of the seed photons, versus $R_{\rm W}$
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.1cm,angle=0]{h2504f11.ps}\end{figure} Figure 11: Comparison between the temperature of the seed photons, as estimated from the Comptonization model, and the temperature $kT_{\rm in}$ at the inner radius of the accretion disk. The three ultra-compact binaries, indicated by the triangles, have all a temperature of the seed photons consistent with originating from the accretion disk, while all other sources display a much higher inner disk temperature
Open with DEXTER

   
4.4 Connection with the globular clusters metallicity

The galactic globular clusters hosting bright LMXBs are found to be both denser (except NGC 6712) and more metal-rich (except NGC 7078) (see Fig. 12), indicative of the fact that both the high density stellar environment and the metallicity could play a role in the formation mechanism of LMXBs, thought to be via tidal captures or "two plus one" stellar encounters (see Bellazzini et al. 1995).


  \begin{figure} \par\includegraphics[width=7.7cm,angle=0]{h2504f12.ps}\end{figure} Figure 12: Globular clusters concentrations "c'' ( $c={\rm Log}$(cluster tidal radius)/Log(core radius)) versus their metallicities ([Fe/H]). The 12 galactic globular clusters hosting bright LMXBs (squares) are located in the upper right region, being denser and more metal-rich than the other galactic globular clusters (marked by crosses) (see Bellazzini et al. 1995)
Open with DEXTER

Besides the formation mechanism, it is interesting to investigate if the metallicity of the accreting matter (assumed to be the same of the hosting globular cluster) plays a role in the LMXBs spectral properties. In Figs. 13-19 several parameters derived from the spectral analysis are plotted versus the metallicity ([Fe/H]) of the hosting globular cluster. The positive correlation between disk temperature $kT_{\rm in}$ and the metallicity displayed in Fig. 13 is opposite to the results of Irwin & Bregman (1999), who studied in the ROSAT energy band the dependence of the X-ray properties of LMXBs on the metallicity of their environment, and found that the spectra of LMXBs become softer as the metallicity of their environment increases. However, we note that our correlation has a quite large probability of 11% to be obtained by chance; moreover, it might be spurious also for the reason that the three ultra-compact binaries, where the accreting matter should be essentially helium, are not expected to show a trend with the metallicity of the hosting globular cluster. Note that the same effect may be present when considering the apparent correlation between the total X-ray luminosity and the metallicity (see Fig. 15, probability of chance correlation of 20%). Moreover, no correlation is evident within the much more numerous X-ray sources residing in the M 31 globular clusters (Verbunt et al. 1984), in the same range of metallicity. An apparent anticorrelation of the temperature of the seed photons kT0 with the metallicity is present, for sources in globular clusters more metallic than 0.1 solar (see Fig. 17). For the electron temperature $kT_{\rm e}$ and the optical depth of the comptonizing plasma $\tau $ there are no obvious correlations with the metallicity of the accreting matter.

  \begin{figure} \par\includegraphics[width=8.5cm,angle=0]{h2504f13.ps} \end{figure} Figure 13: Variation of the disk-blackbody temperature $kT_{\rm in}$ with the globular cluster metallicity ([Fe/H]). The accretion disk temperatures become higher as the metallicity increases. However this correlation may be spurious, since the three ultra-compact binaries, where the accreting matter is essentially helium, are not expected to show a trend with the metallicity
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.8cm,angle=0]{h2504f14.ps} \end{figure} Figure 14: Variation of the lower limit to the disk-blackbody inner radius with the globular cluster metallicity ([Fe/H])
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.7cm,angle=0]{h2504f15.ps}\end{figure} Figure 15: Total luminosity (0.1-100 keV, in units of 1035 erg s-1) versus globular clusters metallicity ([Fe/H]). A possible correlation exists, with higher luminosities as the metallicity increases. However the same caution as for the possible correlation of $kT_{\rm in}$ with [Fe/H] should be reminded (see Fig. 13)
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.8cm,angle=0]{h2504f16.ps}\end{figure} Figure 16: The electron temperature $kT_{\rm e}$ versus the globular cluster metallicity ([Fe/H])
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.4cm,angle=0]{h2504f17.ps}\end{figure} Figure 17: The temperature kT0 of the seed photons in the Comptonization model, versus the globular cluster metallicity ([Fe/H]). An anticorrelation exists for globular clusters more metallic than about 0.1 solar
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.4cm,angle=0]{h2504f18.ps}\end{figure} Figure 18: The plasma optical depth $\tau $ versus the globular cluster metallicity ([Fe/H])
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.5cm,angle=0]{h2504f19.ps}\end{figure} Figure 19: The radius $R_{\rm W}$ of the region of the seed photons versus the globular cluster metallicity ([Fe/H]). The correlation in the metallicity range 0.1-1 solar originates from the anticorrelation between kT0 and the metallicity in that range
Open with DEXTER

   
4.5 Iron line emission

All the sources analysed here do not display significant iron line emission, except for the source in NGC 6624, where a very weak narrow line is detected. The addition of a narrow $K_{\rm\alpha}$ iron line to the standard model, resulted in the upper limits to the EWreported in Table 4.


 

 
Table 4: Equivalent Width of a narrow iron line (energy fixed at 6.7 keV) added to the standard model. Upper limits are at the 95% confidence level

Cluster		 EW (eV)

NGC 1851		 <11
Terzan 2 <25
Liller 1 <105
Terzan 1 <2200
NGC 6440 <45
NGC 6441 <15
Terzan 6 <25
NGC 6624 13 $\pm ^{12} _{11}$
NGC 6712 <13
NGC 7078 <33


   
5 Discussion

We have performed a systematic survey of the properties of the luminous X-ray sources located in globular clusters. A remarkable property of this sample of LMXBs containing neutron stars is their well known distance and interstellar absorption. This, together with the broad-band capabilities of the BeppoSAX Narrow Field Instruments, allowed us to properly model the 0.1-100 keV spectra, to accurately determine the X-ray luminosity for these sources and to study their general spectral properties in a range of luminosity spanning more than two order of magnitudes.

The spectral fitting gave satisfactory results with our spectral "standard" model, consisting of a disk-blackbody plus a Comptonized emission. Other two-component models, such as a cut-off power-law plus a single-blackbody or a single-blackbody plus Comptonization emission, almost always resulted in poorer quality fits.

However, although our standard model provides a good fit to the spectra of almost all the LMXBs studied, several problems arise with the physical interpretation of the resulting spectral parameters, especially when dealing with the disk-blackbody component.

Indeed, the resulting inner disk radii are too small, even for extreme inclination angles of the accretion disks, and, on the other hand, the inner disk temperature are high compared with other systems in the galactic plane, for which $kT_{\rm in}$$\sim$1.5 is usually found (e.g. Tanaka & Lewin 1995). For comparison, this same spectral model has been applied to the BeppoSAX data of two X-ray bursters, Ser X-1 and GX 3+1, finding a $r_{\rm in}({\cos}\,i)^{0.5}$ of $6.8\pm{0.8}$ km and $2.8\pm ^{1.4} _{1.2}$ km, respectively, and a disk temperature, $kT_{\rm in}$, of 1.46 and 1.95 keV (Oosterbroek et al. 2000).

The only globular cluster sources for which the multicolor disk-blackbody model seems to reasonably represent the likely physical parameters of the disk are the ultra-compact binaries, located in NGC 1851, NGC 6712 and NGC 6624. In these three sources the disk-blackbody provides reasonable disk radii, and lower inner disk temperatures. Moreover, since in these three sources the temperature of the seed photons kT0 and the radius $R_{\rm W}$are in agreement with $kT_{\rm in}$ and $r_{\rm in}$ respectively, it is tempting to identify the inner disk as the region for the seed photons of the Comptonization emission. However, we note that the finding of a lower disk temperature $kT_{\rm in}$ for the ultra-compact binaries could be partly due to the low interstellar absorption (as estimated from optical observations) towards these sources, with respect to other globular cluster sources (see Fig. 20).


  \begin{figure} \par\includegraphics[width=8.8cm,angle=0]{h2504f20.ps}\end{figure} Figure 20: The inner disk temperature $kT_{\rm in}$ versus the $N_{\rm H}$ estimated from the optical absorption (see Table 1)
Open with DEXTER

For sources where temperatures kT0 were significantly different from $kT_{\rm in}$ (NGC 6440, NGC 6441, Terzan 2 and Terzan 6), we tried also to fit their spectra with the "standard" model linking the temperatures kT0 and $kT_{\rm in}$ together. The main result of this fit with respect to those reported in Table 3 is the values of the disk-blackbody parameters: the temperatures $kT_0=kT_{\rm in}$were in the range 0.5-0.8 keV, the ratio f was less than 0.15 for all the three sources (remarkable, since previous analysis of the NGC 6441 spectrum resulted in a ratio f=10) and the disk-blackbody radii became 1-8.5 km. However, this alternative fit resulted in worse $\chi^2$ except for NGC 6440, for which an equally good $\chi^2$ was obtained.

Another problem with the standard model arises from the relative contribution of the disk to the Comptonized component. Indeed, the ratio f of the disk-blackbody 0.1-100 keV luminosity to the Comptonized one, should be $\sim$1 (Sunyaev & Shakura 1986). But we find f>1 for the sources NGC 7078 (the ADC source; $f\sim 2$), Terzan 6 ($f\sim 2$) up to the very high value of NGC 6441 (f=10). On the other hand, when a single-blackbody is used instead of the disk-blackbody, the ratio $f_{\rm bb}$ is always less than 1 (see Table 2). NGC 6441 is an intriguing source: if a blackbody is used instead of the disk-blackbody, the Comptonization dominates the emission and the high energy region of the spectrum, whereas when a disk-blackbody model is used, the opposite is valid.

For the LMXBs where the interpretation of the soft component as contributed by the inner disk is reasonable, it is possible to estimate the strength of the neutron star magnetic field. The total luminosity $L_{\rm tot}$ of an accreting neutron star can be expressed as the sum of the luminosity liberated in the accretion disk $L_{\rm disk}$ and the remaining luminosity dissipated at the neutron star radius $R_{\rm ns}$, where $L_{\rm tot}=GM_{\rm ns}\dot {M}/R_{\rm ns}$ and $L_{\rm disk}=GM_{\rm ns}\dot {M}/2R_{\rm m}$ (e.g., Priedhorsky 1986). $R_{\rm m}$ is the magnetospheric radius $R_{\rm m}=20\,B_8^{4/7}\,R_6^{10/7}\,M_2^{1/7}\,L_{37}^{-2/7}\,\xi$ km, where $B=B_8\,10^8$ G is the magnetic field, $R_{\rm ns}=R_6$10 km, $M_{\rm ns}=2\,M_2M_{\odot}$ is the neutron star mass, $L_{\rm tot}=10^{37}\,L_{37}$ erg s-1 and the parameter $\xi$ accounts for the disk geometry of the accretion and is $\xi\sim0.5{-}1$, (Ghosh & Lamb 1979, 1992). Thus, the magnetic field strength of a neutron star can be estimated from the luminosity of the disk.

In Fig. 21 a grid with different neutron star magnetic fields, calculated assuming R6=1, M2=1 and $\xi$=1, is superimposed on a plot of the ratio of disk to total luminosity, versus the total luminosity (0.1-100 keV). The ratio of $L_{\rm disk}$ to $L_{\rm tot}$ is a measure of $R_{\rm ns}/2R_{\rm m}$ (Priedhorsky 1986):

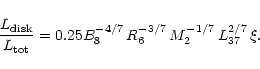\begin{displaymath}\frac{L_{\rm disk}}{L_{\rm tot}} = 0.25 B_8^{-4/7}\, R_6^{-3/7}\,M_2^{-1/7}\, L_{37}^{2/7}\,\xi . \end{displaymath} (1)

Assuming a 2$M_{\odot }$ neutron star, this ratio depends only on the magnetic field strength and total luminosity. The ratio of $L_{\rm disk}$ to $L_{\rm tot}$ reaches a maximum of 0.5 when $R_{\rm m}$ is equal to $R_{\rm ns}$; since the sources in NGC 6441, NGC 7078 and Terzan 6 have an unusually high disk-blackbody emission (as estimated from the disk-blackbody model used here), that led to ratios above the maximum allowed of 0.5, we will not consider them.

The magnetic field estimated in this way for the source X 1820-30 in NGC 6624 (2.1 108 G) is in agreement with the value derived from the saturation of the kHz QPO frequencies (Campana 2000). In the case of the RB, we find a magnetic field ($\sim$8 108 G) consistent, within a factor of 2, with that estimated by Masetti et al. (2000) using the propeller effect model.


  \begin{figure} \par\includegraphics[width=8.5cm,angle=0]{h2504f21.ps}\end{figure} Figure 21: An estimate of the neutron star magnetic field strength depending on the disk and total luminosities in the 0.1-100 keV, in units of 1037 erg s-1. Straight lines are loci of constant magnetic field (0.1, 0.5, 1, 2, 5 and 10 108 G, increasing from top to bottom), assuming a 2$M_{\odot }$ neutron star. A lower neutron star mass results in a shift of the magnetic field grid towards the bottom of this plot. Only sources with f<1 are reported
Open with DEXTER

   
6 Conclusions

We performed broad-band spectroscopy of the luminous X-ray sources located in a number of galactic globular clusters with BeppoSAX. The results can be summarized as follows:

The search for correlations of the spectral parameters with the metallicity of the hosting globular clusters led to the following results: In a literal interpretation of the disk-blackbody model, the luminosity of the accretion disk, for the sources with a ratio f<1, is used to derive an estimate of the neutron star magnetic field. We note that, for the two sources for which an independent estimate of the magnetic field exists (the RB and X1820-303, located in NGC 6624), there is a good agreement with the values derived here.

On the other hand, problems exist with a physical interpretation of the spectral parameters of the disk-blackbody component, since we obtained resonable values for the radii of the inner disks only in the case of the ultra-compact binaries. From the similarities between radii and temperatures of the inner accretion disk and the parameters of the "seed" photons in the Comptonization emission, we propose that in the ultra-compact binaries in NGC 1851, NGC 6712 and NGC 6624 the Componization is fed by the inner regions of the accretion disk, while this is not the case for all other sources (in NGC 6440, NGC 6441, Terzan 2 and Terzan 6). It is unclear why the disk-blackbody model gives physically reasonable results only in the case of the ultra-compact binaries. A possibility may be related to the mass ratio which is similar in the ultracompact binaries and binary systems containing black holes. Indeed, physically reasonable parameters are usually obtained from disk-blackbody fits to the soft emission from black hole X-ray binaries (see, e.g., Tanaka & Lewin 1995).

Acknowledgements
The BeppoSAX satellite is a joint Italian-Dutch programme. We thank the staffs of the BeppoSAX Science Data and Operations Control Centers for help with these observations. L. Sidoli acknowledges an ESA Fellowship.

References

 
Copyright ESO 2001