A&A 368, 561-568 (2001)
DOI: 10.1051/0004-6361:20010005
Cooling of hybrid neutron stars and hypothetical
self-bound objects with superconducting quark cores
D. Blaschke1,2
- H. Grigorian 1,3
- D. N. Voskresensky4
1 - Fachbereich Physik, Universität Rostock,
Universitätsplatz 1, 18051 Rostock, Germany
2 -
European Centre for Theoretical Studies ECT*, Villa Tambosi,
Strada delle Tabarelle 286, 38050 Villazzano (Trento), Italy
3 -
Department of Physics, Yerevan State University, Alex
Manoogian Str. 1, 375025 Yerevan, Armenia
4 -
Moscow Institute for Physics and Engineering,
Kashirskoe shosse 31, 115409 Moscow, Russia
Gesellschaft für Schwerionenforschung GSI,
Planckstrasse 1, 64291 Darmstadt, Germany
Received 19 September 2000 / Accepted 12 December 2000
Abstract
We study the consequences of superconducting quark cores (with
color-flavor-locked phase as representative example) for the evolution of
temperature profiles and cooling curves in quark-hadron hybrid stars
and in hypothetical self-bound objects having no hadron shell (quark core
neutron stars). The quark gaps are varied from 0 to
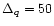 MeV.
For hybrid stars we find time scales of
MeV.
For hybrid stars we find time scales of 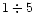 ,
,
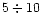 and
and 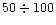 years for the formation of a quasistationary temperature distribution in the
cases
years for the formation of a quasistationary temperature distribution in the
cases
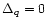 ,
0.1 MeV and
,
0.1 MeV and
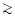 1 MeV, respectively.
These time scales are governed by the heat transport within quark cores
for large diquark gaps (
1 MeV, respectively.
These time scales are governed by the heat transport within quark cores
for large diquark gaps (
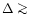 1 MeV) and within the hadron shell for
small diquark gaps (
1 MeV) and within the hadron shell for
small diquark gaps (
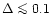 MeV).
For quark core neutron stars we find a time scale
MeV).
For quark core neutron stars we find a time scale 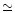 300 years for the
formation of a quasistationary temperature distribution in the case
300 years for the
formation of a quasistationary temperature distribution in the case
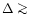 10 MeV and a very short one for
10 MeV and a very short one for
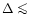 1 MeV.
If hot young compact objects will be observed they can be interpreted as
manifestation of large gap color superconductivity.
Depending on the size of the pairing gaps, the compact star takes different
paths in the
1 MeV.
If hot young compact objects will be observed they can be interpreted as
manifestation of large gap color superconductivity.
Depending on the size of the pairing gaps, the compact star takes different
paths in the
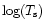 vs.
vs.
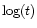 diagram where
diagram where 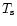 is the
surface temperature. Compared to the corresponding hadronic model which well fits existing data
the model for the hybrid neutron star (with a large diquark gap) shows too
fast cooling. The same conclusion can be drawn for the corresponding self-bound objects.
is the
surface temperature. Compared to the corresponding hadronic model which well fits existing data
the model for the hybrid neutron star (with a large diquark gap) shows too
fast cooling. The same conclusion can be drawn for the corresponding self-bound objects.
Key words: dense matter - stars: interiors - stars: evolution
- stars: neutron
1 Introduction
The interiors of compact stars are considered as systems where
high-density phases of strongly interacting matter do occur in nature,
see Glendenning (1996) and Weber (1999) for recent textbooks.
The consequences of different phase transition scenarios for the cooling
behaviour of compact stars have been reviewed recently
in comparison with existing X-ray data, see Page (1992), Schaab et al. (1997).
A completely new situation might arise if the scenarios suggested for
(color) superconductivity (Alford et al. 1998; Rapp et al. 1998) with large diquark pairing gaps (
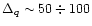 MeV) in quark matter are applicable to neutron
star interiors. Various phases are possible. The two-flavor (2SC) or the three-flavor (3SC)
superconducting phases allow for unpaired quarks of one color whereas in
the color-flavor locking (CFL) phase all the quarks are paired.
Estimates of the cooling evolution have been performed (Blaschke et al. 2000)
for a self-bound isothermal
quark core neutron star (QCNS) which has a crust but no hadron shell,
and for a quark star (QS) which has neither crust nor hadron shell.
It has been shown there in the case of the 2SC (3SC) phase of QCNS
that the consequences of the occurrence of gaps for the cooling curves are
similar to the case of usual hadronic neutron stars (enhanced cooling).
However, for the CFL case it has been shown that the cooling is
extremely fast since the drop in the specific heat of
superconducting quark matter dominates over the reduction of the
neutrino emissivity. As has been pointed out there, the abnormal rate of
the temperature drop is the consequence of the approximation of homogeneous
temperature profiles the applicability of which should be limited by the heat
transport effects. Page et al. (2000) estimated the cooling of hybrid neutron stars (HNS) where heat transport effects within the superconducting quark core have been
disregarded. Neutrino mean free paths in color superconducting quark matter have been
discussed in Carter & Reddy (2000) where a short period of cooling delay at the onset
of color superconductivity for a QS has been conjectured in accordance with
the estimates of Blaschke et al. (2000) in the CFL case for small gaps.
In the present paper we want to consider a more detailed
scenario for the thermal evolution of HNS and QCNS
which includes the heat transport in both the quark and the hadronic matter.
We will demonstrate how long it takes for the HNS and for the QCNS to
establish a quasistationary temperature profile and then we consider the
influence of both the diquark pairing gaps and the hadronic gaps
on the evolution of the surface temperature.
MeV) in quark matter are applicable to neutron
star interiors. Various phases are possible. The two-flavor (2SC) or the three-flavor (3SC)
superconducting phases allow for unpaired quarks of one color whereas in
the color-flavor locking (CFL) phase all the quarks are paired.
Estimates of the cooling evolution have been performed (Blaschke et al. 2000)
for a self-bound isothermal
quark core neutron star (QCNS) which has a crust but no hadron shell,
and for a quark star (QS) which has neither crust nor hadron shell.
It has been shown there in the case of the 2SC (3SC) phase of QCNS
that the consequences of the occurrence of gaps for the cooling curves are
similar to the case of usual hadronic neutron stars (enhanced cooling).
However, for the CFL case it has been shown that the cooling is
extremely fast since the drop in the specific heat of
superconducting quark matter dominates over the reduction of the
neutrino emissivity. As has been pointed out there, the abnormal rate of
the temperature drop is the consequence of the approximation of homogeneous
temperature profiles the applicability of which should be limited by the heat
transport effects. Page et al. (2000) estimated the cooling of hybrid neutron stars (HNS) where heat transport effects within the superconducting quark core have been
disregarded. Neutrino mean free paths in color superconducting quark matter have been
discussed in Carter & Reddy (2000) where a short period of cooling delay at the onset
of color superconductivity for a QS has been conjectured in accordance with
the estimates of Blaschke et al. (2000) in the CFL case for small gaps.
In the present paper we want to consider a more detailed
scenario for the thermal evolution of HNS and QCNS
which includes the heat transport in both the quark and the hadronic matter.
We will demonstrate how long it takes for the HNS and for the QCNS to
establish a quasistationary temperature profile and then we consider the
influence of both the diquark pairing gaps and the hadronic gaps
on the evolution of the surface temperature.
A detailed discussion of the neutrino emissivity of quark matter
without the possibility of color superconductivity has been given
first by Iwamoto (1982).
In his work the quark direct Urca (QDU)
reactions
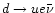 and
and
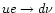 have been suggested as the most efficient processes.
Their emissivities have been obtained as
have been suggested as the most efficient processes.
Their emissivities have been obtained as![[*]](/icons/foot_motif.gif)
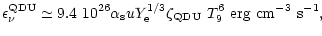 |
|
|
(1) |
where at a compression
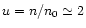 the
strong coupling constant is
the
strong coupling constant is
 and decreases
logarithmically at still higher densities.
The nuclear saturation density is
and decreases
logarithmically at still higher densities.
The nuclear saturation density is
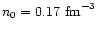 ,
,
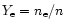 is the electron fraction, and
T9 is the temperature in units of 109 K.
If for somewhat larger density the electron fraction was too small
(
is the electron fraction, and
T9 is the temperature in units of 109 K.
If for somewhat larger density the electron fraction was too small
(
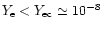 ),
then all the QDU processes would be completely
switched off (Duncan et al. 1983) and the neutrino emission would be
governed by two-quark reactions like the quark modified Urca (QMU)
and the quark bremsstrahlung (QB) processes
),
then all the QDU processes would be completely
switched off (Duncan et al. 1983) and the neutrino emission would be
governed by two-quark reactions like the quark modified Urca (QMU)
and the quark bremsstrahlung (QB) processes
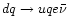 and
and
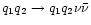 ,
respectively.
The emissivities of the QMU and QB processes have been estimated as
(Iwamoto 1982)
,
respectively.
The emissivities of the QMU and QB processes have been estimated as
(Iwamoto 1982)
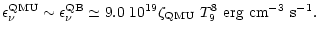 |
|
|
(2) |
Due to the pairing, the emissivities of QDU processes
are suppressed by a factor
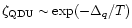 and the emissivities of QMU and QB processes are suppressed by a
factor
and the emissivities of QMU and QB processes are suppressed by a
factor
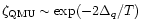 for
for
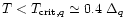 whereas for
whereas for
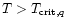 these factors are equal to unity.
The modification of
these factors are equal to unity.
The modification of
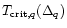 relative to the standard
BCS formula is due to the formation of correlations as, e.g., instanton-
anti-instanton molecules (Rapp et al. 2000).
For the temperature dependence of the gap below
relative to the standard
BCS formula is due to the formation of correlations as, e.g., instanton-
anti-instanton molecules (Rapp et al. 2000).
For the temperature dependence of the gap below
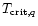 we use the
interpolation formula
we use the
interpolation formula
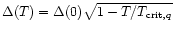 ,
with
,
with
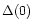 being the gap at zero temperature.
The contribution of the reaction
being the gap at zero temperature.
The contribution of the reaction
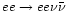 is very small (Kaminker & Haensel 1999)
is very small (Kaminker & Haensel 1999)
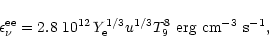 |
(3) |
but it can become important when quark processes are blocked out for large
values of
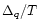 in superconducting quark matter.
For the quark specific heat we use
an expression (Iwamoto 1982)
in superconducting quark matter.
For the quark specific heat we use
an expression (Iwamoto 1982)
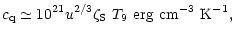 |
|
|
(4) |
where
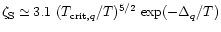 .
Besides, one should add the gluon-photon contribution (Blaschke et al. 2000)
.
Besides, one should add the gluon-photon contribution (Blaschke et al. 2000)
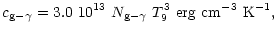 |
|
|
(5) |
where
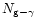 is the number of available massless gluon-photon states
(which are present even in the color superconducting phase),
as well as the electron one,
is the number of available massless gluon-photon states
(which are present even in the color superconducting phase),
as well as the electron one,
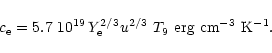 |
(6) |
The heat conductivity of the matter is the sum of
partial contributions (Flowers & Itoh 1981)
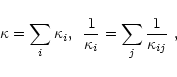 |
(7) |
where i,j denote the components (particle species).
For quark matter 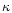 is the sum of the partial conductivities of the
electron, quark and gluon components (Haensel & Jerzak 1989; Baiko & Haensel 1999)
is the sum of the partial conductivities of the
electron, quark and gluon components (Haensel & Jerzak 1989; Baiko & Haensel 1999)
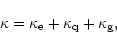 |
(8) |
where
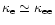 is determined by electron-electron scattering
processes since in superconducting quark matter the partial contribution
is determined by electron-electron scattering
processes since in superconducting quark matter the partial contribution
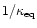 (as well as
(as well as
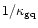 )
is additionally suppressed by a
)
is additionally suppressed by a
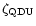 factor, as for the scattering on impurities in
metallic superconductors.
For
factor, as for the scattering on impurities in
metallic superconductors.
For
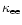 we have
we have
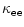 |
= |
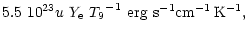 |
(9) |
and
where we have accounted for the suppression factor.
The contribution of massless gluons we estimate as
DU processes
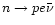 ,
,
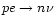 can occur when the proton fraction exceeds 11% (Lattimer et al. 1991).
It does not occur for the equation of state we use but there are examples
for the opposite case (Page et al. 2000). This is another difference of our
present work to the recent one of Page et al. (2000).
Next, we take into account the modified Urca (MU) processes
can occur when the proton fraction exceeds 11% (Lattimer et al. 1991).
It does not occur for the equation of state we use but there are examples
for the opposite case (Page et al. 2000). This is another difference of our
present work to the recent one of Page et al. (2000).
Next, we take into account the modified Urca (MU) processes
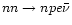 ,
,
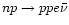 ,
and the reverse
processes. The final emissivity is given by
Friman & Maxwell (1979); Yakovlev et al. (1999)
,
and the reverse
processes. The final emissivity is given by
Friman & Maxwell (1979); Yakovlev et al. (1999)
Here
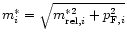 is the non-relativistic quasiparticle effective mass related to the
in-medium one-particle energies from a given
relativistic mean field model for i=n,p.
We have introduced the abbreviations
is the non-relativistic quasiparticle effective mass related to the
in-medium one-particle energies from a given
relativistic mean field model for i=n,p.
We have introduced the abbreviations
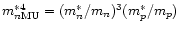 and
and
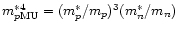 .
The suppression factors are
.
The suppression factors are
![$\zeta_{n{\rm MU}}=\zeta_n \zeta_p
\simeq {\exp}\{-[\Delta_n(T)+\Delta_p(T)]/T\}$](/articles/aa/full/2001/11/aah2452/img73.gif) ,
,
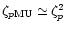 ,
and should be replaced by unity for
,
and should be replaced by unity for
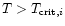 when for given
species i the corresponding gap vanishes.
For neutron and proton S-wave pairing,
when for given
species i the corresponding gap vanishes.
For neutron and proton S-wave pairing,
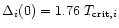 and for P-wave pairing of neutrons
and for P-wave pairing of neutrons
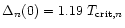 .
To be conservative we have used in (13) the free one-pion exchange
estimate of the NN interaction amplitude.
Restricting ourselves to a qualitative analysis we use here simplified
exponential suppression factors
.
To be conservative we have used in (13) the free one-pion exchange
estimate of the NN interaction amplitude.
Restricting ourselves to a qualitative analysis we use here simplified
exponential suppression factors 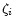 .
In a more detailed analysis these
.
In a more detailed analysis these 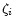 -factors have prefactors with
rather strong temperature dependences (Yakovlev et al. 1999). At temperatures
-factors have prefactors with
rather strong temperature dependences (Yakovlev et al. 1999). At temperatures
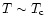 their inclusion only slightly affects the resulting cooling curves.
For
their inclusion only slightly affects the resulting cooling curves.
For
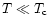 the MU process gives in any case a negligible contribution to
the total emissivity and thereby corresponding modifications can again be
omitted. Also for the sake of simplicity the general possibility of a
3P
the MU process gives in any case a negligible contribution to
the total emissivity and thereby corresponding modifications can again be
omitted. Also for the sake of simplicity the general possibility of a
3P
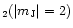 pairing which may result in a power-law behaviour of the
specific heat and the emissivity of the MU process Voskresensky & Senatorov (1987); Yakovlev et al. (1999) is disregarded since mechanisms of this type of pairing are up to now not
elaborated. Even more essential modifications of the MU rates may presumably come
from in-medium effects which could result in extra prefactors of
pairing which may result in a power-law behaviour of the
specific heat and the emissivity of the MU process Voskresensky & Senatorov (1987); Yakovlev et al. (1999) is disregarded since mechanisms of this type of pairing are up to now not
elaborated. Even more essential modifications of the MU rates may presumably come
from in-medium effects which could result in extra prefactors of
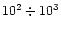 already at
already at
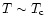 .
In order to estimate the role of the in-medium effects in the NN
interaction for the HNS cooling we have also performed calculations for the
so-called medium modified Urca (MMU) process (Voskresensky & Senatorov 1986; Migdal et al. 1990) by
multiplying the rates (13) by the appropriate prefactor
.
In order to estimate the role of the in-medium effects in the NN
interaction for the HNS cooling we have also performed calculations for the
so-called medium modified Urca (MMU) process (Voskresensky & Senatorov 1986; Migdal et al. 1990) by
multiplying the rates (13) by the appropriate prefactor
![\begin{displaymath}\epsilon_{\nu}^{\rm MMU}/\epsilon_{\nu}^{\rm MU}\simeq 10^{3}...
...)/\widetilde{\omega}^{8}(k\simeq p_{\rm F} )\right]
u^{10/3},
\end{displaymath}](/articles/aa/full/2001/11/aah2452/img83.gif) |
(14) |
where the value
![$\Gamma (g^{\prime})
\simeq 1/[1+1.4~u^{1/3}]$](/articles/aa/full/2001/11/aah2452/img84.gif) is due to the dressing of
is due to the dressing of 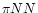 vertices and
vertices and
 is the effective pion gap which we took as function of density
from Fig. 2 of (Schaab et al. 1997).
For
is the effective pion gap which we took as function of density
from Fig. 2 of (Schaab et al. 1997).
For
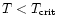 the most important contribution comes from the
neutron (Flowers et al. 1976; Voskresensky & Senatorov 1987; Yakovlev et al. 1999) and the proton (Voskresensky & Senatorov 1987) pair
breaking and formation processes.
Their emissivities we take from Ref. (Schaab et al. 1997) which is applicable for
both the cases of S- and P-wave nucleon pairing
the most important contribution comes from the
neutron (Flowers et al. 1976; Voskresensky & Senatorov 1987; Yakovlev et al. 1999) and the proton (Voskresensky & Senatorov 1987) pair
breaking and formation processes.
Their emissivities we take from Ref. (Schaab et al. 1997) which is applicable for
both the cases of S- and P-wave nucleon pairing
where
![\begin{displaymath}I({\Delta_i(T)}/{T})\simeq 0.89~\sqrt{T/\Delta_i(T)}
\exp[-2 \Delta_i(T)/T]~,
\end{displaymath}](/articles/aa/full/2001/11/aah2452/img94.gif) |
(17) |
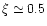 for 1S0 pairing
and
for 1S0 pairing
and
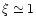 for 3P2 pairing.
A significant contribution of the proton channel is due to the NN
correlation effect taken into account in Voskresensky & Senatorov (1987).
For the nucleons (i=n,p), the specific heat is (Maxwell 1979)
for 3P2 pairing.
A significant contribution of the proton channel is due to the NN
correlation effect taken into account in Voskresensky & Senatorov (1987).
For the nucleons (i=n,p), the specific heat is (Maxwell 1979)
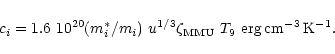 |
(18) |
The specific heat for the electrons is determined by (6) and that for
the photons for
 is given by (5) with the corresponding
number of polarizations
is given by (5) with the corresponding
number of polarizations
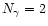 .
The total conductivity is
.
The total conductivity is
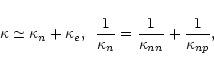 |
(19) |
where the partial contributions are (Flowers & Itoh 1981; Baiko & Haensel 1999)
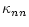 |
= |
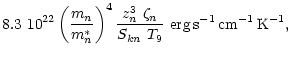 |
(20) |
| Skn |
= |
0.38 zn-7/2 + 3.7 zn2/5 , |
(21) |
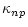 |
= |
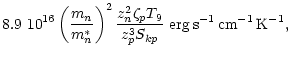 |
(22) |
| Skp |
= |
1.83 zn-2 + 1.43 zn2(0.4+zn8)-1 . |
(23) |
Here we have introduced the apropriate suppression factors 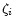 which act
in the presence of gaps for superfluid hadronic matter and we have used the
abbreviation
zi=(ni/(4 n0))1/3.
The heat conductivity of electrons is given by Eq. (9).
In some density interval
which act
in the presence of gaps for superfluid hadronic matter and we have used the
abbreviation
zi=(ni/(4 n0))1/3.
The heat conductivity of electrons is given by Eq. (9).
In some density interval
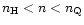 we have a mixed phase in the
HNS case. Although our treatment of the contribution of the mixed phase to the equation
of state is rather poor, for the discussion of the neutrino processes
we assume the mixed phase to be constructed as a lattice (for
we have a mixed phase in the
HNS case. Although our treatment of the contribution of the mixed phase to the equation
of state is rather poor, for the discussion of the neutrino processes
we assume the mixed phase to be constructed as a lattice (for
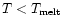 )
of color superconducting quark droplets embedded in the nucleonic Fermi sea
(superfluid for
)
of color superconducting quark droplets embedded in the nucleonic Fermi sea
(superfluid for
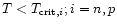 )
at densities near the
lower boundary density
)
at densities near the
lower boundary density 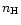 which is reorganized as a
lattice of nucleon droplets in the quark
Fermi sea near the upper boundary density
which is reorganized as a
lattice of nucleon droplets in the quark
Fermi sea near the upper boundary density 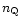 .
We suppose that the mixed phase contributes to the neutrino reactions and to the heat transport
as two homogeneous phases weighted according to their partial volumina and
thus suppress reactions on the impurities which could be as
efficient as one-nucleon/quark processes in the liquid phase (Reddy et al. 2000).
Thus we assume
.
We suppose that the mixed phase contributes to the neutrino reactions and to the heat transport
as two homogeneous phases weighted according to their partial volumina and
thus suppress reactions on the impurities which could be as
efficient as one-nucleon/quark processes in the liquid phase (Reddy et al. 2000).
Thus we assume
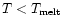 in our case.
In order to avoid a complicated analysis of the processes in the crust
we use an interpolated relation between the surface and the
crust temperatures (see Shapiro & Teukolsky 1983)
in our case.
In order to avoid a complicated analysis of the processes in the crust
we use an interpolated relation between the surface and the
crust temperatures (see Shapiro & Teukolsky 1983)
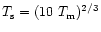 ,
where temperatures are given in K,
the so-called Tsuruta law (Tsuruta 1979).
More elaborated and complicated dependences of
,
where temperatures are given in K,
the so-called Tsuruta law (Tsuruta 1979).
More elaborated and complicated dependences of 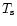 on
on 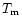 and the
parameters of the crust can be found in Gudmundsson et al. (1982);
Gudmundsson et al. (1982); Van Riper (1988); Potekhin et al. (1997).
As we have estimated, their inclusion does not affect qualitatively the
conclusions of this work. The mantle temperature
and the
parameters of the crust can be found in Gudmundsson et al. (1982);
Gudmundsson et al. (1982); Van Riper (1988); Potekhin et al. (1997).
As we have estimated, their inclusion does not affect qualitatively the
conclusions of this work. The mantle temperature
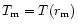 we take at the distance
we take at the distance 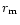 from the center where the density is equal to the critical one for the transition to the mixed (Aen) phase.
This is correct for time scales exceeding those determined by the heat
conductivity of the crust estimated as
from the center where the density is equal to the critical one for the transition to the mixed (Aen) phase.
This is correct for time scales exceeding those determined by the heat
conductivity of the crust estimated as
 10 yr for hadronic stars and
10 yr for hadronic stars and
 1 yr for strange stars (see Pizzochero 1991; Lattimer et al. 1991). Since the crust is rather thin and has a much smaller heat content than the
bulk of the star its contribution to the cooling delay for time intervals
shorter than the ones given above is negligible.
Due to these reasons and for the sake of
simplicity we disregard these effects in further considerations.
We also add the photon contribution to the emissivity at the surface
1 yr for strange stars (see Pizzochero 1991; Lattimer et al. 1991). Since the crust is rather thin and has a much smaller heat content than the
bulk of the star its contribution to the cooling delay for time intervals
shorter than the ones given above is negligible.
Due to these reasons and for the sake of
simplicity we disregard these effects in further considerations.
We also add the photon contribution to the emissivity at the surface
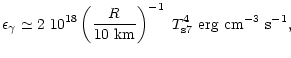 |
|
|
(24) |
where
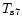 is the surface temperature in units of 107 K,
using it as the boundary condition in our transport code.
Thus simplifying we assume that the outer crust
and the photosphere are thin enough to approximate
is the surface temperature in units of 107 K,
using it as the boundary condition in our transport code.
Thus simplifying we assume that the outer crust
and the photosphere are thin enough to approximate
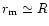 ,
where
R is the star radius. Then, the luminosity at
,
where
R is the star radius. Then, the luminosity at 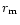 corresponds to the surface luminosity
of the photons from the star
corresponds to the surface luminosity
of the photons from the star
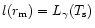 .
The equation of state is decribed according to the model (Chubarian et al. 2000)
incorporating three possible phases (depending on the star mass, the
value of the bag constant B and other parameters as the mass of the strange
quark, the compressibility of hadron matter etc.).
These phases are hadronic matter, quark-hadron mixed phase and pure quark
matter. As a representative example we consider below a star with a mass of
1.4
.
The equation of state is decribed according to the model (Chubarian et al. 2000)
incorporating three possible phases (depending on the star mass, the
value of the bag constant B and other parameters as the mass of the strange
quark, the compressibility of hadron matter etc.).
These phases are hadronic matter, quark-hadron mixed phase and pure quark
matter. As a representative example we consider below a star with a mass of
1.4 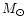 for the neutron star consisting of pure hadronic matter
(radius
for the neutron star consisting of pure hadronic matter
(radius 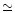 13 km), for the HNS (radius
13 km), for the HNS (radius 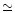 10 km) and for the
self-bound QCNS (radius
10 km) and for the
self-bound QCNS (radius 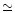 9 km).
The typical electron fraction is
9 km).
The typical electron fraction is
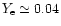 for the hadronic star which
does not allow for the occurrence of direct Urca processes.
For the HNS the electron fraction is
for the hadronic star which
does not allow for the occurrence of direct Urca processes.
For the HNS the electron fraction is
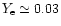 for
for
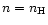 ,
where
,
where 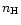 corresponds to the
critical density when first seeds of quark phase appear;
corresponds to the
critical density when first seeds of quark phase appear;
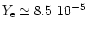 for
for
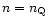 when hadron seeds
disappear, i.e. at the boundary of the quark core,
and
when hadron seeds
disappear, i.e. at the boundary of the quark core,
and
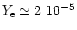 for
for
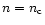 ,
i.e. for the
baryon density in the star center.
The radius corresponding to
,
i.e. for the
baryon density in the star center.
The radius corresponding to
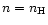 is
is
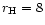 km and that
corresponding to
km and that
corresponding to
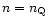 is
is
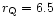 km.
We take the same dependences
km.
We take the same dependences
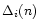 for i=n,p as in Fig. 6
of Schaab et al. (1997). As an alternative example we also consider the model with suppressed gaps to estimate the effect of possible uncertainties.
In the mixed phase we take
for i=n,p as in Fig. 6
of Schaab et al. (1997). As an alternative example we also consider the model with suppressed gaps to estimate the effect of possible uncertainties.
In the mixed phase we take
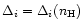 for the hadron sub-system and
for the hadron sub-system and
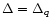 for the quark one,
and in the quark phase we for simplicity take
for the quark one,
and in the quark phase we for simplicity take
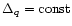 .
For QCNS besides the case when
.
For QCNS besides the case when 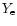 is determined from our calculation
we consider also
is determined from our calculation
we consider also
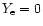 as an extreme example of the case
as an extreme example of the case
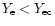 ,
in order to understand its possible consequencies. Then
direct Urca does not occur also in the quark phase.
Due to the inhomogeneous distribution of matter
inside the star and finite heat conductivity the temperature profile
T(r,t) during the cooling process can differ from the isothermal
equilibrium one for which the temperature on the inner crust boundary
(
,
in order to understand its possible consequencies. Then
direct Urca does not occur also in the quark phase.
Due to the inhomogeneous distribution of matter
inside the star and finite heat conductivity the temperature profile
T(r,t) during the cooling process can differ from the isothermal
equilibrium one for which the temperature on the inner crust boundary
(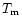 )
and the central one (
)
and the central one (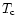 )
are connected by the relation
)
are connected by the relation
![$T_{\rm m}=T_{\rm c} \exp [\Phi(0) - \Phi(R)]$](/articles/aa/full/2001/11/aah2452/img137.gif) ,
where
,
where
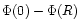 is the difference of the gravitational potentials
in the center and at the surface of the star, respectively.
The flux of energy l(r) per unit time through a spherical slice at
the distance r from the center is proportional to the gradient of the
temperature on both sides of the spherical slice,
is the difference of the gravitational potentials
in the center and at the surface of the star, respectively.
The flux of energy l(r) per unit time through a spherical slice at
the distance r from the center is proportional to the gradient of the
temperature on both sides of the spherical slice,
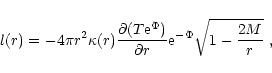 |
(25) |
the factor
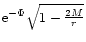 corresponds to the relativistic correction of the time scale and the
unit of thickness. The equations for energy balance and thermal energy transport are
(Weber 1999)
corresponds to the relativistic correction of the time scale and the
unit of thickness. The equations for energy balance and thermal energy transport are
(Weber 1999)
where n=n(r) is the baryon number density, A=A(r) is the total baryon
number in the sphere with radius r and
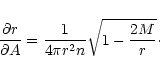 |
(28) |
The total neutrino emissivity
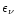 and the total specific heat
cV are given as the sum of the corresponding partial contributions
defined in the previous section for a composition ni(r) of constituents
i of the matter under the conditions of the actual temperature profile
T(r,t). The accumulated mass M=M(r) and the gravitational potential
and the total specific heat
cV are given as the sum of the corresponding partial contributions
defined in the previous section for a composition ni(r) of constituents
i of the matter under the conditions of the actual temperature profile
T(r,t). The accumulated mass M=M(r) and the gravitational potential
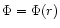 can be determined by
can be determined by
where
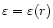 is the energy density profile
and the pressure profile p=p(r) is defined by the condition of
hydrodynamical equilibrium
is the energy density profile
and the pressure profile p=p(r) is defined by the condition of
hydrodynamical equilibrium
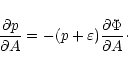 |
(31) |
The boundary conditions for the solution of (26) and
(27) read
l(r=0)=l(A=0)=0 and
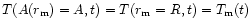 ,
respectively.
In our examples we choose the initial temperature to be 1 MeV.
This is a typical value for the temperature
,
respectively.
In our examples we choose the initial temperature to be 1 MeV.
This is a typical value for the temperature
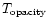 at which the star becomes transparent for neutrinos.
Simplifying we disregard the neutrino influence on transport.
These effects dominate for
at which the star becomes transparent for neutrinos.
Simplifying we disregard the neutrino influence on transport.
These effects dominate for
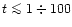 min,
when the star cools down to
min,
when the star cools down to
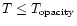 and become unimportant for later times.
and become unimportant for later times.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{h2452f1.eps}
\end{figure}](/articles/aa/full/2001/11/aah2452/Timg159.gif) |
Figure 1:
Early evolution of temperature profiles for a HNS of
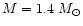 with large (lower panel), small (middle) and vanishing
(upper panel) diquark pairing gaps
with large (lower panel), small (middle) and vanishing
(upper panel) diquark pairing gaps |
| Open with DEXTER |
With the above inputs we have solved the evolution equation for the
temperature profile. In order to demonstrate the influence of the size of the diquark and nucleon
pairing gaps on the evolution of the temperature profile we have
performed solutions with different values of the quark and nucleon gaps.
The representative examples are shown in Fig. 1.
Nucleon gaps are taken the same as in Fig. 6 of Schaab et al. (1997).
The quark gaps larger than 1 MeV show the same typical behaviour as
for the gap
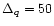 MeV. The gaps much smaller than 1 MeV exhibit
the typical small gap behaviour as for
MeV. The gaps much smaller than 1 MeV exhibit
the typical small gap behaviour as for
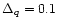 MeV in our example.
For large quark gaps, the hadron phase cools down
on the time scale
MeV in our example.
For large quark gaps, the hadron phase cools down
on the time scale
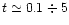 yr due to the heat transport to the
star surface whereas the quark core keeps the heat during this time.
Therefore, if an independent measurement of the core
temperature was possible, e.g. by neutrinos, then a core temperature stall
during first several years of cooling
evolution would be a case for quark core superconductivity with large
pairing gaps. Then the quark core begins to cool down slowly from its mixed phase boundary,
the cold from hadrons via mixed phase spreads to the center,
demonstrating that the direct neutrino radiations during all the time
are unefficient within the quark core.
The homogeneous temperature profile is recovered at typical times of
yr due to the heat transport to the
star surface whereas the quark core keeps the heat during this time.
Therefore, if an independent measurement of the core
temperature was possible, e.g. by neutrinos, then a core temperature stall
during first several years of cooling
evolution would be a case for quark core superconductivity with large
pairing gaps. Then the quark core begins to cool down slowly from its mixed phase boundary,
the cold from hadrons via mixed phase spreads to the center,
demonstrating that the direct neutrino radiations during all the time
are unefficient within the quark core.
The homogeneous temperature profile is recovered at typical times of
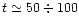 yr.
For
yr.
For
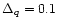 MeV the QDU processes and the heat conductivity within
the quark core are quite efficient.
Therefore at very small times (
MeV the QDU processes and the heat conductivity within
the quark core are quite efficient.
Therefore at very small times (
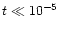 yr) the temperature profile
within the quark core is a homogeneous one whereas during the next
yr) the temperature profile
within the quark core is a homogeneous one whereas during the next
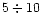 yr the hadron shell is cooled down from the both sides,
the mixed phase boundary at
yr the hadron shell is cooled down from the both sides,
the mixed phase boundary at
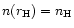 and the star surface.
Thus, for
and the star surface.
Thus, for
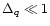 MeV the interior
evolution of the temperature has an influence on the surface temperature from
the very early times.
Actually the shortest time scale which determines the slowing of the
heat transport within the crust is in this case
MeV the interior
evolution of the temperature has an influence on the surface temperature from
the very early times.
Actually the shortest time scale which determines the slowing of the
heat transport within the crust is in this case 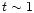 yr.
Thus at much smaller times one has
yr.
Thus at much smaller times one has
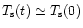 with a
drop of T(r,t) in the vicinity of
with a
drop of T(r,t) in the vicinity of
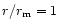 .
Due to the relatively small
heat content of the crust this peculiar effect is disregarded here.
Qualitatively the same behaviour is illustrated for normal quark matter
with the only difference that quantitatively the quark processes are more
efficient at
.
Due to the relatively small
heat content of the crust this peculiar effect is disregarded here.
Qualitatively the same behaviour is illustrated for normal quark matter
with the only difference that quantitatively the quark processes are more
efficient at
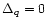 and the cold thereby traverses the hadron
phase more rapidly, at typical times
and the cold thereby traverses the hadron
phase more rapidly, at typical times
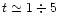 yr.
A detailed comparison of the cooling evolution
(
yr.
A detailed comparison of the cooling evolution
(
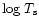 vs.
vs.
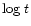 )
of HNS for different values of
quark and hadron gaps is given in Fig. 2.
We have found that the curves for
)
of HNS for different values of
quark and hadron gaps is given in Fig. 2.
We have found that the curves for
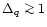 MeV are very close to
each other demonstrating typical large gap behaviour.
As representative example we again take
MeV are very close to
each other demonstrating typical large gap behaviour.
As representative example we again take
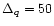 MeV.
The behaviour of the cooling curve for
MeV.
The behaviour of the cooling curve for
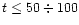 yr is in straight
correspondence with the heat transport processes discussed above.
The subsequent time evolution is governed by the processes in the hadronic
shell and by a delayed transport within the quark core with a dramatically
suppressed neutrino emissivity from the color superconducting region.
In order to demonstrate this feature we have performed a calculation with
the nucleon gaps (
yr is in straight
correspondence with the heat transport processes discussed above.
The subsequent time evolution is governed by the processes in the hadronic
shell and by a delayed transport within the quark core with a dramatically
suppressed neutrino emissivity from the color superconducting region.
In order to demonstrate this feature we have performed a calculation with
the nucleon gaps (
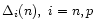 )
being artificially suppressed
by a factor 0.2. Then up to
)
being artificially suppressed
by a factor 0.2. Then up to
![$\mbox{log}(t[{\rm yr}]) \mathrel{\mathchoice {\vcenter{\offinterlineskip\halign...
...r{\offinterlineskip\halign{\hfil$\scriptscriptstyle ...](/articles/aa/full/2001/11/aah2452/img175.gif) the behaviour of the cooling
curve is analogous to the one we would have obtained for pure hadronic matter.
The curves labelled "MMU'' are calculated with the rates of modified Urca
processes of Eq. (13) multiplied by the factor (14),
i.e. with inclusion of appropriate medium modifications in the NN
interaction.
the behaviour of the cooling
curve is analogous to the one we would have obtained for pure hadronic matter.
The curves labelled "MMU'' are calculated with the rates of modified Urca
processes of Eq. (13) multiplied by the factor (14),
i.e. with inclusion of appropriate medium modifications in the NN
interaction.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{h2452f2.eps}
\end{figure}](/articles/aa/full/2001/11/aah2452/Timg176.gif) |
Figure 2:
Evolution of the surface temperature 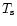 of HNS
with
of HNS
with
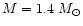 for
for
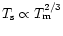 .
Data points
are from Schaab et al. (1999) (full symbols) and from Yakovlev et al. (2000)
(empty symbols). .
Data points
are from Schaab et al. (1999) (full symbols) and from Yakovlev et al. (2000)
(empty symbols).  is the typical time which is necessary for the cooling
wave to pass through the crust
is the typical time which is necessary for the cooling
wave to pass through the crust |
| Open with DEXTER |
As can be seen from Fig. 2, these effects have an influence on the cooling
evolution only for
![$\mbox{log}(t[{\rm yr}]) \mathrel{\mathchoice {\vcenter{\offinterlineskip\halign...
...r{\offinterlineskip\halign{\hfil$\scriptscriptstyle ...](/articles/aa/full/2001/11/aah2452/img177.gif) since our specific
model equation of state does not allow for large nucleon densities in the
hadron phase for the
since our specific
model equation of state does not allow for large nucleon densities in the
hadron phase for the
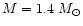 neutron star under discussion.
The effect would be more pronounced for larger star masses, a softer
equaton of state for hadron matter and smaller values of the gaps in the
hadronic phase.
The unique asymptotic behaviour at
neutron star under discussion.
The effect would be more pronounced for larger star masses, a softer
equaton of state for hadron matter and smaller values of the gaps in the
hadronic phase.
The unique asymptotic behaviour at
![$\mbox{log}(t[{\rm yr}]) \geq 5$](/articles/aa/full/2001/11/aah2452/img178.gif) for all
the curves corresponding to finite values of the quark and nucleon gaps is
due to a competition between normal electron contribution to the specific
heat and the photon emissivity from the surface since small exponentials
switch off all the processes related to paired particles.
This tail is very sensitive to the interpolation law
for all
the curves corresponding to finite values of the quark and nucleon gaps is
due to a competition between normal electron contribution to the specific
heat and the photon emissivity from the surface since small exponentials
switch off all the processes related to paired particles.
This tail is very sensitive to the interpolation law
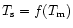 used to
simplify the consideration of the crust.
The curves coincide at large times due to the uniquely chosen relation
used to
simplify the consideration of the crust.
The curves coincide at large times due to the uniquely chosen relation
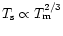 .
The curves for
.
The curves for
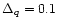 MeV demonstrate an intermediate cooling
behaviour between those for
MeV demonstrate an intermediate cooling
behaviour between those for
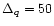 MeV and
MeV and
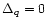 .
Heat transport becomes not efficient after first
.
Heat transport becomes not efficient after first 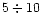 yr.
The subsequent 104 yr evolution is
governed by QDU processes and quark specific heat being only moderately
suppressed by the gaps and by the rates of NPBF processes in the
hadronic matter (up to
yr.
The subsequent 104 yr evolution is
governed by QDU processes and quark specific heat being only moderately
suppressed by the gaps and by the rates of NPBF processes in the
hadronic matter (up to
![$\mbox{log}(t[{\rm yr}]) \leq 2.5$](/articles/aa/full/2001/11/aah2452/img180.gif) ).
At
).
At
![$\mbox{log}(t[{\rm yr}]) \geq 4$](/articles/aa/full/2001/11/aah2452/img181.gif) begins the photon cooling era.
The curves for normal quark matter (
begins the photon cooling era.
The curves for normal quark matter (
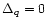 )
are governed by
the heat transport at times
)
are governed by
the heat transport at times
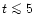 yr and then by QDU processes and the
quark specific heat. The NPBF processes are important up to
yr and then by QDU processes and the
quark specific heat. The NPBF processes are important up to
![$\mbox{log}(t[{\rm yr}])\leq 2$](/articles/aa/full/2001/11/aah2452/img183.gif) ,
the photon era is delayed up to
,
the photon era is delayed up to
![$\mbox{log}(t[{\rm yr}])\geq 7$](/articles/aa/full/2001/11/aah2452/img184.gif) .
For times smaller than
.
For times smaller than 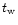 (see Fig. 2) the heat transport is delayed within
the crust area (Lattimer et al. 1991). Since we, for simplicity, disregarded this
delay in our heat transport treatment, for such small times the curves should
be interpreted as the
(see Fig. 2) the heat transport is delayed within
the crust area (Lattimer et al. 1991). Since we, for simplicity, disregarded this
delay in our heat transport treatment, for such small times the curves should
be interpreted as the
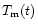 dependence scaled to guide the eye by the same
law
dependence scaled to guide the eye by the same
law
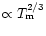 ,
as
,
as 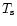 .
.
As can be seen from the lower panel of Fig. 3 for our large gap example
(
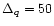 MeV), where
MeV), where
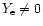 is determined from equation of
state, the QCNS cools down rather smoothly from its surface during the first
300 yr.
is determined from equation of
state, the QCNS cools down rather smoothly from its surface during the first
300 yr.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{h2452f3.eps}
\end{figure}](/articles/aa/full/2001/11/aah2452/Timg188.gif) |
Figure 3:
Early evolution of temperature profiles for a QCNS of
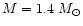 with large (lower panel), and small
(upper panel) diquark pairing gaps
with large (lower panel), and small
(upper panel) diquark pairing gaps |
| Open with DEXTER |
All the small gap examples exhibit about the same behaviour as the case
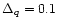 MeV which we present in the upper panel of Fig. 3.
Opposite to the large gap case, the transport processes are very efficient
and a homogeneous temperature profile is recovered at
MeV which we present in the upper panel of Fig. 3.
Opposite to the large gap case, the transport processes are very efficient
and a homogeneous temperature profile is recovered at
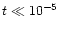 yr.
In reality in the latter case
yr.
In reality in the latter case
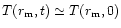 at times
at times 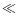 1 yr with a drop of T(r) in a narrow
interval near
1 yr with a drop of T(r) in a narrow
interval near
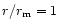 and we disregard this peculiar behaviour
as we have explained this above discussing HNS.
and we disregard this peculiar behaviour
as we have explained this above discussing HNS.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{h2452f4.eps}
\end{figure}](/articles/aa/full/2001/11/aah2452/Timg191.gif) |
Figure 4:
Evolution of the surface temperature 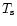 for the QCNS
with
for the QCNS
with
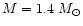 for
for
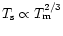 |
| Open with DEXTER |
In Fig. 4 we demonstrate the evolution of the surface temperature
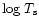 vs.
vs.
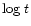 for representative cases.
The curve for
for representative cases.
The curve for
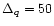 MeV (
MeV (
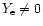 )
shows a 300 yr delayed cooling
which then is controlled by the electron specific heat and the photon
emissivity from the surface, as it was stated in Blaschke et al. (2000).
However, in difference with the corresponding curve of
Blaschke et al. (2000)
we have a much larger typical cooling time scale (
)
shows a 300 yr delayed cooling
which then is controlled by the electron specific heat and the photon
emissivity from the surface, as it was stated in Blaschke et al. (2000).
However, in difference with the corresponding curve of
Blaschke et al. (2000)
we have a much larger typical cooling time scale (
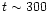 yr)
since in that work the simplifying approximation of a homogeneous
temperature profile has been used.
For the low gap limit
yr)
since in that work the simplifying approximation of a homogeneous
temperature profile has been used.
For the low gap limit
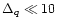 MeV in this particular QCNS case
there is no heat transport delay and our results coincide with those
obtained in Blaschke et al. (2000).
Unimportant differences are only due to the inhomogeneous density profile and
a different value of
MeV in this particular QCNS case
there is no heat transport delay and our results coincide with those
obtained in Blaschke et al. (2000).
Unimportant differences are only due to the inhomogeneous density profile and
a different value of
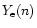 which follows in our case
from an actual calculation for the given equation of state.
The curve corresponding to
which follows in our case
from an actual calculation for the given equation of state.
The curve corresponding to
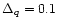 MeV (
MeV (
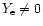 )
from very early times is due to a competition between QDU emissivity and the
quark specific heat, both being only moderately suppressed
whereas late time asymptotics, as in the large gap example, relates to the
photon era. A similar trend is present for normal quark matter
staying below the corresponding curves for
)
from very early times is due to a competition between QDU emissivity and the
quark specific heat, both being only moderately suppressed
whereas late time asymptotics, as in the large gap example, relates to the
photon era. A similar trend is present for normal quark matter
staying below the corresponding curves for
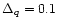 MeV
due to the absence of the
MeV
due to the absence of the 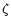 suppression factors
in the former case. At t> 108 yr
both cases have a different photon era asymptotic behaviour
whereas all finite gap curves have the same large time asymptotics when
suppression factors
in the former case. At t> 108 yr
both cases have a different photon era asymptotic behaviour
whereas all finite gap curves have the same large time asymptotics when
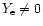 .
At
.
At
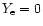 the QDU processes are absent and the large time
asymptotics are governed by the gluon-photon specific heat which is a
nonlinear function of the temperature and the photon emissivity.
Due to this nonlinearity the large time asymptotics are
different in all the cases under consideration.
All the results for
the QDU processes are absent and the large time
asymptotics are governed by the gluon-photon specific heat which is a
nonlinear function of the temperature and the photon emissivity.
Due to this nonlinearity the large time asymptotics are
different in all the cases under consideration.
All the results for
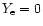 (including case of large gaps) coincide with
those obtained in Blaschke et al. (2000) although the sharp fall of the curve for the
large gap case is in reality controlled by the heat conductivity of the crust
that will lead to a cooling delay within the first year of evolution
(Pizzochero 1991) as in Fig. 2 the curves for
(including case of large gaps) coincide with
those obtained in Blaschke et al. (2000) although the sharp fall of the curve for the
large gap case is in reality controlled by the heat conductivity of the crust
that will lead to a cooling delay within the first year of evolution
(Pizzochero 1991) as in Fig. 2 the curves for
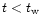 should be interpreted as
should be interpreted as
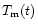 dependence scaled by the Tsuruta law.
For the CFL phase with large quark gap, which was expected to exhibit
the most prominent manifestations of colour superconductivity in HNS and
QCNS, we have found an essential delay of the cooling during the first
dependence scaled by the Tsuruta law.
For the CFL phase with large quark gap, which was expected to exhibit
the most prominent manifestations of colour superconductivity in HNS and
QCNS, we have found an essential delay of the cooling during the first
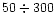 yr due to a dramatic suppression of the heat conductivity in
the quark matter region.
This delay makes the cooling of QCNS not as rapid as
one could expect when ignoring the heat transport.
In HNS compared to QCNS (large gaps) an additional delay of the subsequent
cooling evolution comes from the processes in pure hadronic matter.
In spite of that we found still too fast cooling for those objects.
Therefore, with the CFL phase of large quark gap it seems
rather difficult to explain the majority of the presently known
data both in the cases of the HNS and QCNS, whereas in the case
of pure hadronic stars the available data are much better fitted within the
same model for the hadronic matter we used here.
For 2SC (3SC) phases we expect analogous behaviour to that demonstrated
by
yr due to a dramatic suppression of the heat conductivity in
the quark matter region.
This delay makes the cooling of QCNS not as rapid as
one could expect when ignoring the heat transport.
In HNS compared to QCNS (large gaps) an additional delay of the subsequent
cooling evolution comes from the processes in pure hadronic matter.
In spite of that we found still too fast cooling for those objects.
Therefore, with the CFL phase of large quark gap it seems
rather difficult to explain the majority of the presently known
data both in the cases of the HNS and QCNS, whereas in the case
of pure hadronic stars the available data are much better fitted within the
same model for the hadronic matter we used here.
For 2SC (3SC) phases we expect analogous behaviour to that demonstrated
by
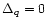 since QDU processes on unpaired quarks are then allowed.
We however do not exclude that new observations may lead to
lower surface temperatures for some supernova remnants and will be
better consistent with the model which also needs further improvements.
On the other hand, if future observations will show very large temperatures
for young compact stars they could be interpreted as a manifestation of
large gap color superconductivity in the interiors of these objects.
since QDU processes on unpaired quarks are then allowed.
We however do not exclude that new observations may lead to
lower surface temperatures for some supernova remnants and will be
better consistent with the model which also needs further improvements.
On the other hand, if future observations will show very large temperatures
for young compact stars they could be interpreted as a manifestation of
large gap color superconductivity in the interiors of these objects.
Acknowledgements
Research of H.G. and D.B. was supported in part by the Volkswagen Stiftung
under grant no. I/71 226 and by DFG under grant no. 436 ARM 17/1/00.
H.G. acknowledges the hospitality of the Department of Physics at the
University of Rostock where this research has been performed. D.N.V.
is grateful for hospitality and support of GSI Darmstadt.
D.B. acknowledges support of the Department of Energy for his participation in the INT program
on "QCD at Nonzero Baryon Density'' (INT-00-1) at the University of
Washington as well as a fellowship at the ECT* Trento where this work was
completed. We thank Th. Klähn for his contributions during early stages of this work;
M. Colpi, M. Prakash, K. Rajagopal, S. Reddy, A. Sedrakian and F. Weber
for their discussions during the Workshop "Physics of Neutron Star
Interiors'' at the ECT*.
-
Alford, M., Rajagopal, K., & Wilczek, F. 1998, Phys. Lett. B, 422, 247
In the text
NASA ADS
-
Baiko, D. A., & Haensel, P. 1999,
Acta Phys. Polon. B, 30, 1097
In the text
-
Blaschke, D., Klähn, T., & Voskresensky, D. N. 2000, ApJ, 533, 406
In the text
NASA ADS
-
Carter, G. W., & Reddy, S. 2000, Phys. Rev. D, 62, 103002.
In the text
- Chubarian, E., Grigorian, H.,
Poghosyan, G., & Blaschke, D. 2000, A&A, 357, 968
In the text
NASA ADS
-
Duncan, R. C., Shapiro, S. L., & Wasserman, I. 1983, ApJ, 267, 358
In the text
NASA ADS
-
Flowers, E., & Itoh, N. 1981, ApJ, 250, 750
In the text
NASA ADS
-
Flowers, E., Ruderman, M., & Sutherland, P. 1976, ApJ, 205, 541
In the text
NASA ADS
-
Friman, B., & Maxwell, O. 1979, ApJ, 232, 541
In the text
NASA ADS
-
Glendenning, N. K. 1996, Compact Stars (New York: Springer)
In the text
-
Gudmundsson, E. H., Pethick, C. J., & Epstein, R. I. 1982, ApJ, 259, L19
In the text
NASA ADS
-
Gudmundsson, E. H., Pethick, C. J., & Epstein, R. I. 1982, ApJ, 27, 286
In the text
-
Haensel, P., & Jerzak, A. J. 1989, Acta Phys. Pol. B, 20, 141
In the text
- Iwamoto, N. 1982, Ann. Phys., 141, 1
In the text
-
Kaminker, A. D., & Haensel, P. 1999, Acta Phys. Pol. B, 30, 1125
In the text
-
Lattimer, J. M., Pethick, C., Prakash, M., & Haensel, P. 1991, Phys. Rev. Lett., 66, 2701
In the text
NASA ADS
- Maxwell, O. V. 1979, ApJ, 231, 201
In the text
NASA ADS
- Migdal, A. B., Saperstein, E. E.,
Troitsky, M. A., & Voskresensky, D. N. 1990, Phys. Rep., 192, 179
In the text
- Page, D. 1992, High Energy Phenomenology,
ed. M. A. Perez & R. Huerta (Singapore: World Scientific), 347
In the text
-
Page, D., Prakash, M., Lattimer, J. M., & Steiner, A. 2000, Phys. Rev. Lett., 85, 2048
In the text
NASA ADS
-
Potekhin, A. Y., Chabrier, G., & Yakovlev, D. G. 1997, A&A, 323, 415
In the text
NASA ADS
-
Pizzochero, P. M. 1991, Phys. Rev. Lett., 66, 2425
NASA ADS
-
Rapp, R., Schäfer, T., Shuryak, E. V., & Velkovsky, M. 1998,
Phys. Rev. Lett., 81, 53
In the text
NASA ADS
-
Rapp, R., Schäfer, T., Shuryak, E. V., & Velkovsky, M. 2000, Ann. Phys., 280, 35
In the text
-
Reddy, S., Bertsch, G., & Prakash, M. 2000, Phys. Lett. B, 475, 1
In the text
NASA ADS
-
Schaab, Ch., Voskresensky, D., Sedrakian, A. D.,
Weber, F., & Weigel, M. K. 1997, A&A, 321, 591
In the text
NASA ADS
-
Schaab, Ch., Sedrakian, A., Weber, F., & Weigel, M. K. 1999,
A&A, 346, 465
NASA ADS
-
Shapiro, S., & Teukolsky, S. A. 1983, Black Holes, White
Dwarfs and Neutron Stars (New York: Wiley), ch. 10
In the text
-
Tsuruta, S. 1979, Phys. Rep., 56, 237
In the text
-
Van Riper, K. A. 1988, ApJ, 329, 339
In the text
NASA ADS
- Voskresensky, D. N.,
& Senatorov, A. V. 1987, Sov. J. Nucl. Phys., 45, 411
In the text
- Voskresensky, D. N.,
& Senatorov, A. V. 1986, JETP, 63, 885
In the text
- Weber, F. 1999, Pulsars as Astrophysical
Laboratories for Nuclear and Particle Physics
(Bristol: IoP Publishing)
In the text
-
Yakovlev, D. G., Levenfish, K. P., & Shibanov, Yu. A. 1999, Phys. Usp., 42, 737
In the text
Copyright ESO 2001
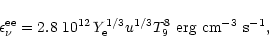
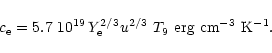
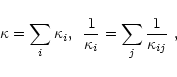
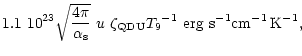
![\begin{displaymath}\epsilon_{\nu}^{\rm MMU}/\epsilon_{\nu}^{\rm MU}\simeq 10^{3}...
...)/\widetilde{\omega}^{8}(k\simeq p_{\rm F} )\right]
u^{10/3},
\end{displaymath}](/articles/aa/full/2001/11/aah2452/img83.gif)
![\begin{displaymath}I({\Delta_i(T)}/{T})\simeq 0.89~\sqrt{T/\Delta_i(T)}
\exp[-2 \Delta_i(T)/T]~,
\end{displaymath}](/articles/aa/full/2001/11/aah2452/img94.gif)
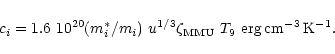
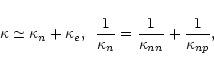
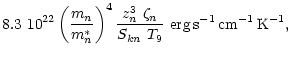
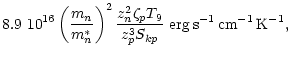
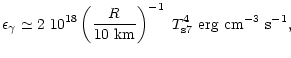
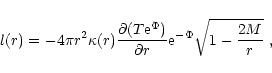
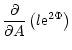
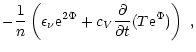
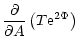
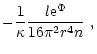
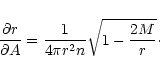
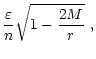
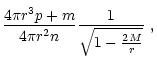
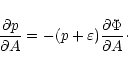
![\begin{figure}
\par\includegraphics[width=8cm,clip]{h2452f1.eps}
\end{figure}](/articles/aa/full/2001/11/aah2452/Timg159.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{h2452f2.eps}
\end{figure}](/articles/aa/full/2001/11/aah2452/Timg176.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{h2452f3.eps}
\end{figure}](/articles/aa/full/2001/11/aah2452/Timg188.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{h2452f4.eps}
\end{figure}](/articles/aa/full/2001/11/aah2452/Timg191.gif)