A&A 368, 471-483 (2001)
DOI: 10.1051/0004-6361:20000559

The circumstellar structure of the Be shell star $\mathsf{\phi}$ Persei[*]

II. Modeling

W. Hummel1,3 - S. Stefl2


1 - Institut für Astronomie und Astrophysik und Universitäts-Sternwarte München, Scheinerstr. 1, 81679 München, Germany
2 - Astronomical Institute, Academy of Sciences of the Czech Republic, 25165 Ondrejov
3 - European Southern Observatory, Karl-Schwarzschildstr. 2, 85745 Garching, Germany

Received 18 May 2000 / Accepted 12 December 2000

Abstract
We model Fe II 5317 emission lines and phase resolved He I 6678 and 5876 emission lines of the bright B2e&sdO shell binary $\phi $ Per to find the size and shape of the excitation region inside the circumprimary disk. We find the Fe II 5317 emission to originate within 9 stellar radii in an axisymmetric disk around the primary. Orbital phase variations of He I 6678 are fit in terms of a disk sector with disk radius of 10 stellar radii and opening angle of $\simeq$ $120\hbox{$^\circ$ }$ facing the secondary. This region can be alternatively described by an intersection of a sphere around the secondary and the circumprimary disk with a penetration depth of about 7 R*. Similar fit values are found for He I 5876. The enigmatic orbital phase precedence of shell occurrence in the He I emission features is discussed. We favor a model in which the inner He I shell is deformed because of differential rotation in combination with a finite recombination time.

Key words: line: formation, profiles stars: circumstellar matter, emission-line, Be, binaries, spectroscopic


  
1 Introduction

$\phi $ Per (HR 496; HD 10516) is a bright (V=4 $.\!\!^{\rm m}$07) B2e&sdO binary with a period of 127 days. The optical spectrum is dominated by the early-type spectrum of the primary and numerous emission lines formed in a circumprimary gaseous disk. Spectroscopic evidence for the secondary was found by Thaller et al. (1995).

In a detailed spectroscopic study, Poeckert (1981) found an He II emission varying in anti-phase to the primary's motion and argued for a further disk around the secondary. $\phi $ Per became again a matter of interest when Gies et al. (1993) found a peculiar emission feature in the He I 6678 line. The authors argued for two physical components, one originating in the disk around the primary and a second component originating in the disk around the secondary or in a Roche lobe overflow stream near L1. In addition to these suggestions, Suzuki et al. (1997) proposed the Balmer emission to originate in a disk around the primary and in a ring around the whole binary system.

The spectral variability of this binary has recently been studied in the first paper of this series (Stefl et al. 2000; hereafter P1). In P1 we found strong indications that the orbital phase variation of the He I emission feature is due to a partial photoionization in the circumprimary disk by the secondary. Furthermore we argued that the emission feature originates as a whole in one disk around the primary and that the division into physically different components as proposed by Gies et al. (1993) is no longer required. Another spectroscopic peculiarity is the orbital phase interval for shell occurrence. Poeckert (1981) found the deep shell absorption components in He I 4026 and 4471 to occur only in a phase range around the superior conjunction of the primary (at 0 $.\!\!^{\scriptscriptstyle\rm p}$0, see also the special note on the definition of the orbital phase zero point in P1), while in P1 we found the maximum shell absorption in He I 6678 at 0 $.\!\!^{\scriptscriptstyle\rm p}$8.

Our interpretation of the orbital phase variations of emission features in P1 are based on heuristic arguments. In this study we verify our suggestions by modeling the phase dependent variations of representative emission lines. The aim of this study is to find the geometrical size and shape of the He I 6678 and He I 5876 emission regions inside the circumprimary disk. A preliminary sketch of our suggested emission region is given in Fig. 10 of P1.

Our basic model assumptions and calculation procedures are described in Sect. 2. We then describe the modeling of the simplest case of emission line (Fe II 5317). For the He I 6678 emission feature, we first model the emission alone (Sect. 4.1). In the second step we take several absorption effects into account (Sect. 4.2). Based on these findings we model our He I 5876 line profiles. The final results are discussed in Sect. 6.

  
2 Model construction

We consider $\phi $ Per as a close binary system. Prominent emission lines in the optical region originate from a gaseous disk around the primary which is seen nearly equator-on ( $i=80\hbox{$^\circ$ }$). As a first approximation we assume the disk to have the same physical properties as disks in ordinary single Be stars. This assumption is justified by the morphologic similarity of emission line profiles between $\phi $ Per and e.g. $\Psi$ Per (Poeckert 1981; Hummel & Vrancken 1995; hereafter HV1) but also by the model results of Poeckert & Marlborough (1979) who fit three of the Balmer emission lines by a model of the quasi-Keplerian disk in the equatorial plane of the primary. We furthermore assume the disk to be isothermal. The isothermal approximation was recently verified for Be star circumstellar disks (Millar & Marlborough 1998). As often assumed, the gas temperature of the disk is approximated by 2/3 of the effective temperature of the primary (Poeckert & Marlborough 1982; van Kerkwijk et al. 1995) giving a relatively high gas temperature of the disk of $T_{\rm gas}=19\,000$ K for $T_{\rm eff}=28\,500$ K.

The disk rotation is not Keplerian, but the impact of the secondary on the gravitation potential and the kinematics is taken into account as deviations from a purely Keplerian flow. We further assume the disk to be axisymmetric in density. The latter assumption seems to be no longer justified, when the Fe II emission lines became asymmetric after 1996 (P1). We model therefore only observations collected before 1996. Finally, we assume the disk to be in the equatorial plane of the primary which coincides with the orbital plane of the double star.

Among the variety of orbital and stellar parameters derived for $\phi $ Per (see Table 1) we use those of Gies et al. (1998).

 

 
Table 1: List of parameters as derived from different investigators

parameter		 Poeckert Bozic et al. Gies et al.
  (1981) (1995) (1998)

i/$^\circ$		 80    
$M_1 \sin^3 i$/$M_{\odot}$ 21 16.35 8.91
$M_2 \sin^3 i$/$M_{\odot}$ 3.4 1.69 1.09
q 6.3 9.67 8.174
$R_1^{{\rm equ}}$/$R_{\odot}$   10 8
$a \sin i$/$R_{\odot}$ 148.4 278.2 228.3
K1/km s-1 16.8 10.4 9.97
K2/km s-1 105.3 100.8 81.3

$a_1 \sin i$/$R_{\odot}$		 20.6 26.07 24.88
$a_2 \sin i$/$R_{\odot}$   252.13 206.55
a/$R_{\odot}$   282.49 231.82
a1/$R_{\odot}$   26.47 25.27
a2/$R_{\odot}$   256.02 206.55
a/R*   28.25 28.98
a1/ $R_* = \overline{PC}$   2.647 3.159
a2/ $R_* = \overline{SC}$   25.602 25.82
$K_2/a_2 \sin i$   3.998 3.1975


  
2.1 Reduced potential

The circumprimary disk of $\phi $ Per is embedded in a binary system hence the rotation velocity of the circumstellar gas is no longer given by the Keplerian rotation:

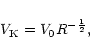\begin{displaymath}V_{{\rm K}} = V_0 R^{-\frac{1}{2}}, \end{displaymath} (1)

where

 \begin{displaymath} R = \frac{r}{R_*} = \frac{\sqrt{x^2+y^2}}{R_*}, \end{displaymath} (2)

and x and y are the Cartesian coordinates in the central plane of the circumstellar disk. The -y-axis points to the observer. In spite of simplicity we assume an angularly symmetric velocity field in the co-rotating frame of the binary. Deviations from axisymmetry in the velocity law has impact on the phase dependence of the radial velocity curve (Suzuki 1980) of $\simeq$25 km s-1. We neglect these effects in the calculations but keep them in mind when interpreting results concerning the radial velocity curve in the co-rotating frame of the binary. For the radial dependence of the rotation velocity of the circumprimary gas we adopt the velocities from the tables of Huang (1967) for $\mu = M_2 / (M_1+M_2) = 0.1$. We thereby assume that the observed value of $v \sin i = 450$ km s-1 corresponds to the projected ( $i=80\hbox{$^\circ$ }$) rotation velocity of the innermost orbit (r=R*) in the reduced potential ( $M_r = M_1 (1 - \mu)$). For the radius R* < r < L1=19.1 R* we interpolate and extrapolate the tabulated values of Huang (1967) in terms of a radial perturbation of the Keplerian flow using the following empirical expression (Fig. 1):

 \begin{displaymath} V_{{\rm rot}} = 450 R^{-\frac{1}{2}} - \left[ 3.4781 R - 1.031 \right], \end{displaymath} (3)

where $V_{{\rm rot}}$ is expressed in kms-1 and R is given in units of the stellar radius R* (Eq. (2)). The line-of-sight component is given by

 \begin{displaymath} V_{{\rm rot}}^{{\rm lof}} = V_{{\rm rot}} \sin \phi \sin i. \end{displaymath} (4)

The radial slope of $V_{{\rm rot}}(R)$ is steeper than for Keplerian orbits. For diagnostic reasons, Huang's values can be expressed in terms of a power-law $V_{{\rm rot}}(R) \sim R^{-j}$ with j=0.85 but with a worse fit.


  \begin{figure} \par\includegraphics[width=8.7cm,height=4.1cm,clip]{h2216-fig01.ps} \end{figure} Figure 1: Rotation velocity of the circumprimary gas as a function of radius. 1) Keplerian rotation; 2) Keplerian approximation using the reduced mass $M=M_1 \sqrt {1-\mu }$; 3) numerical results for the restricted three-body problem along the components separation ( $\blacksquare $, after Huang 1967) and polynomial fit used in our code
Open with DEXTER

  
2.2 Binary motion

Given a Cartesian coordinate system $(x,\,y)$ originating in the center of the primary (P), the y-axis is the line-of-sight and the -y-axis is pointing to the observer (see Fig. 2), each point (A) in the disk can be expressed as

\begin{displaymath}x = r \cos \phi_{{\rm A}} \\ y = r \sin \phi_{{\rm A}} \end{displaymath} (5)

and the position of the center of mass (C) is given by

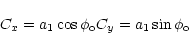\begin{displaymath}C_x = a_1 \cos \phi_{\rm o} \\ C_y = a_1 \sin \phi_{\rm o} \end{displaymath} (6)

where a1 is the distance between P and C and a1 + a2=a is the separation of the two stars. Each emitting particle in the circumprimary disk follows the radial velocity curve of the primary, hence

 \begin{displaymath} V_{{\rm orb}}^{{\rm lof}} = - K_1 \sin \phi_{\rm o} \sin i \end{displaymath} (7)

and the total line-of-sight projected velocity is given by

 \begin{displaymath} V_{{\rm tot}} = V_{{\rm orb}}^{{\rm lof}} + V_{{\rm rot}}^{{\rm lof}}. \end{displaymath} (8)

  
2.3 Parameterization

We model Fe II 5317 and in particular the orbital phase variations of He I emission lines as due to geometric effects. The aim of this study is to constrain the emission region of the individual emission lines. The formation of He I in the outer part of the circumprimary disk as due to illumination by the secondary would require to consider a detailed He multi-level model atom which is beyond the scope of this study. We therefore apply an improved method of Horne & Marsh (1986), adapted for the particular geometric situation of Be stars (Hummel & Vrancken 2000, hereafter HV2) and modify the kinematics and geometry according to the equations given above.

The scale height H(R) of the circumstellar disk is determined by the balance between z-component of the stellar gravitation vector and the gas pressure in the disk. H(R) is expected to be smaller with respect to a disk in the potential of a single star since also the gravitation contribution of the secondary acts towards the equatorial plane. The scale height in a binary system is given by:

 \begin{displaymath}H(R) = \frac{C_{{\rm s}}} {\sqrt{\frac{G M_1}{R^3} + \frac{G M_2}{b^3}}}, \end{displaymath} (9)

where the second term of the square root is the contribution by the secondary and

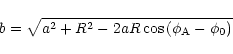\begin{displaymath}b = \sqrt{ a^2 + R^2 - 2 a R \cos \left( \phi_{{\rm A}}- \phi_0 \right) } \end{displaymath} (10)

is the distance between a point in the circumprimary disk (A in Fig. 2) and the secondary. The maximum contribution by the secondary to the disk height amounts less than 1% and can be neglected for the rest of this study.


  \begin{figure} \par\includegraphics[width=8cm,height=8cm,clip]{h2216-fig02.ps} \end{figure} Figure 2: Sketch of the binary system $\phi $ Per, not scaled. The Cartesian coordinate system originates in the center of the primary (P) and angles are measured from the negative y-axis towards the x-axis. The orbital phase angle ( $\phi _{\rm o}$) is zero at the phase of superior conjunction of the primary. C denotes the center of mass and A can be any point in the circumprimary disk, given either by $(r,\,\phi _{\rm A})$ or $(x,\,y)$. Angles increase counter-clockwise
Open with DEXTER

The radial velocity is given by Eq. (8). Further changes of the present application with respect to HV2 concerns the oscillator strength for Fe II 5317, He I 6678, 5876 and the corresponding laboratory wavelengths to be included in Eqs. (7) and (8) of HV2. The shear velocity is the first order term in the velocity expansion in the central plane of the disk and gives a reliable approximation for the local velocity gradient along the line of sight (Horne & Marsh 1986, HV2)

 \begin{displaymath} V_{{\rm sh}} = \frac{\partial V_{{\rm rot}}(R)}{\partial R} \Delta R \end{displaymath} (11)

and approximating

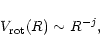\begin{displaymath}V_{{\rm rot}}(R) \sim R^{-j}, \end{displaymath} (12)

the shear velocity is given by

 \begin{displaymath} V_{{\rm sh}} = - \frac{j H(R)}{R} V_{{\rm rot}}(R) \sin i \tan i \sin \phi \cos \phi. \end{displaymath} (13)

For evaluating $V_{{\rm sh}}$ we use the approximative Eq. (13) with j=0.85 instead of inserting Eq. (3) into Eq. (11).

For $i=80\hbox{$^\circ$ }$ and neglecting the rotational flattening of the central star the obscuration radius $R_{\rm o}$ reaches 8.6 R*at $\phi=0$. One of two other characteristic values for the model is the inclination limit of Eq. (13) of HV2:

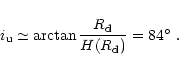\begin{displaymath}i_{\rm u} \simeq \arctan{\frac{R_{\rm d}}{H(R_{\rm d})}} = 84\hbox{$^\circ$ }. \end{displaymath} (14)

For $i>i_{\rm u}$ the central part of model profiles becomes biased due to the neglected curvature terms in the velocity field and the related line optical depth. The z-component of the projected scale height $H(R_{\rm d})$ at the stellar disk for $i=80\hbox{$^\circ$ }$ is

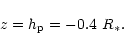\begin{displaymath}z = h_{{\rm p}} = -0.4~R_*. \end{displaymath} (15)

This means that for $R_{\rm d}=10$ and $i=80\hbox{$^\circ$ }$ the scale height of the disk $H(R_{\rm d})$ is projected below the equatorial plane and does not increase the effective stellar surface contribution to shell absorption (see HV2 and Hanuschik (1996) for details). The upper limit for radial extension of the circumprimary disk is given by the Roche radius, which is about $R_{\rm R} = 16.8~R_*$ (Paczynski 1971) for a mass ratio of q=8.174, while L1 is located a little bit further away from the primary at L1=19 R*.

This model is applied to three different observational data sets, all of them described in detail in P1.

  
3 The FeII 5317 formation region

First, we fit the high resolution Fe II 5317 emission lines of $\phi $ Per collected before 1996. Poeckert (1981) found the Fe II emission lines to be symmetric and phase-independent. He concludes that Fe II is emitted in the innermost regions of the disk around the primary. Our observations of Fe II 5317 as well as our low resolution Fe II profiles before 1996 are in full agreement with Poeckert's findings. Since Bozic et al. (1995) found the Fe II emission lines to vary with the radial velocity curve of the primary we constructed an averaged Fe II emission profiles by adding the three phase-corrected high-resolution line profiles of highest S/N from P1 (at 0 $.\!\!^{\scriptscriptstyle\rm p}$333, 0 $.\!\!^{\scriptscriptstyle\rm p}$516 and 0 $.\!\!^{\scriptscriptstyle\rm p}$729).


 

 
Table 2: Final best-fit parameters for the net emission line profile

Fe II 5317 -- axisymmetric model

model		 n0 m $S^{\rm L}$ $R_{\rm i}$ $R_{\rm d}$     $\chi^2$
  cm-3     R* R*      

C1 $^{{\rm a)}}$		 1.40e4 5.25 1.3e-2 1.0 12.4     5.6e-5
C2 $^{{\rm b)}}$ 1.39e4 5.25 1.5e-2 1.0 9.3     3.8e-5

He I 6678 -- sector model

model		 n0 m $S^{\rm L}$ $R_{\rm i}$ $R_{\rm d}$ $\Delta \phi $ $\phi_2-\phi_1$ $\chi^2$

SE1		 9.0e-5 0.5 1.00 5.3 10.4 .135 112 1.96e-3
SE2 9.0e-2 0.5 2e-3 5.3 10.4 .135 112 2.78e-3
SE3 $^{{\rm c)}}$ 9.0e-2 0.5 2e-3 5.3 10.4 .135 112 2.5e-3
SE4 $^{{\rm d)}}$ 9.0e-2 0.5 2e-3 5.3 10.4 .135 112 2.5e-3

He I 6678 -- sphere model

model		 n0 m $S^{\rm L}$ $R_{\rm i}$ $R_{\rm d}$ $\Delta \phi $ $R_{\rm e}$ $\chi^2$

SP1		 1.1e-4 0.5 1.0 1.0 10.0 0.16 25.6 $^{{\rm e)}}$ 2.00e-3
SP2 1.1e-1 0.5 2e-4 1.0 10.0 0.16 25.6 2.81e-3

He I 5876 -- sector model

model		 n0 m $S^{\rm L}$ $R_{\rm i}$ $R_{\rm e}$ $\Delta \phi $ $\phi_2-\phi_1$ $\chi^2$

SE5 $^{{\rm f)}}$		 8.62e+2 0.5 3e-3 6 12 0.0 180 3.2e-2

Notes:
$^{{\rm a)}}$ Keplerian rotation used.
$^{{\rm b)}}$ Numerical velocity field after Huang (1967) used.
$^{{\rm c)}}$ A phase shift of $2\pi$ is used for the bended boundary.
$^{{\rm d)}}$ A phase shift of $2\pi$ is used for both boundaries $\phi _1$ and $\phi _2$; the shadow radius $R_{\rm o} = 8.6~R_*$.
$^{{\rm e)}}$ The binary separation is a = 29 R*.
$^{{\rm f)}}$ A phase shift of $0.8 * 2\pi$ is used for both boundaries $\phi _1$ and $\phi _2$.


For the modeling, we assume that Fe II is emitted in an angularly symmetric disk around the primary with a radial dependence of the angular velocity relation given by line 3 in Fig. 1. We include self-absorption in the disk, shell absorption, and stellar obscuration by taking into account the shadow of the star projected onto the equatorial plane (see HV2 for details).

Figure 3 shows a fit to our mean high resolution Fe II line profile. Best-fit parameters are the emission radius $R_{\rm d} \simeq 9~R_*$, and the emissivity $\eta = 0.015 F_{{\rm c}} R^{-5.25}$, where $F_{{\rm c}}$ is the flux of the local stellar continuum (see Table 2, model C2).

We fit the Fe II line profile also using a conventional Keplerian velocity law $V \sim R^{-0.5}$ (dotted profile in Fig. 3). The quality of the fit is comparable to the previous model where we used a numerical velocity law (line 3 in Fig. 1). The best fit parameters differ considerably (see Table 2, model C1), in particular the emission radius $R_{\rm d}$. Although a similar fit can be achieved also with a Keplerian rotation, we prefer the numerical velocity law for the rest of this study since it is physically more plausible and the resulting parameters are more realistic.


  \begin{figure} \par\includegraphics[width=8.7cm,height=4.4cm,clip]{h2216-fig03.ps} \end{figure} Figure 3: Average Fe II emission and model fits, using $R_{\rm d} = 12.4$ for the model with Keplerian rotation (model C1, dotted line) and $R_{\rm d}=9.3$ for the model (C2, thin solid line) using the velocity field after Huang (1967)
Open with DEXTER

  
4 The HeI 6678 formation region

Of all He I lines so far detected to be in emission, the He I 6678 line is most suitable to model the geometrical distribution of the emission since it is the first emission line for which we could obtain sufficient observational phase coverage and it is also the strongest He I line in emission, while the absorption component is less developed. Our first guess on the location of the emission is that the whole emission feature originates in the circumprimary disk in a non-axisymmetric manner with a strong concentration towards the secondary. This approach is based on the spectral analysis of our observations described in P1. The excitation mechanism is not known, most probably it is photoionization due to the radiation field of the much hotter secondary rather than the collisional heating due to a stellar wind of the secondary. For the photoionization it is also not quite clear if the excitation is due to the continuum flux (the maximum is expected to be around $\lambda \simeq 377$ Å for $T_{{\rm eff}}=53\,000$ K) or if the observed He I is caused by a selective excitation due to a single hypothetical fluorescence line in the secondary spectrum. If He I is excited by a single fluorescence line, we would expect an inhomogeneous distribution (meaning not symmetric with respect to $\overline {PS}$ in Fig. 2) of the He I emission, since the wavelength difference between the incoming radiation and the He I transition has to coincide with the corresponding kinematical lines of a constant radial velocity inside the disk of the primary. On the other hand, if the photoionization of He I is caused by the continuum flux maximum from the secondary, which is much broader in wavelength than a single fluorescence line we would expect the He I emission region to be distributed more or less symmetrically with respect to a central symmetry line of the system. It cannot be definitively decided from the available observations which of the both excitation scenarios is applicable. Since the orbital phase variations of He I 6678 and He I 5876 look rather similar and coincide in phase we favor the latter scenario. This means for the modeling that He I is excited by the continuum radiation of the secondary, and we assume the incoming exciting radiation to be independent of wavelength.

4.1 Pure emission region

4.1.1 Sector model
For modeling the He I 6678 emission line region we simply limit our integration of the disk surface by two angles $\phi _1$ and $\phi _2$ instead of the full interval of $2\pi$ (Fig. 4). So far we only consider the line radiation emitted from a disk sector, stationary in the orbital co-rotating frame and facing the secondary star. We neglect the effects of stellar obscuration and shell absorption since the shadow of the star projected onto the equatorial plane ( $R_{\rm o} = 8.6~R_*$ at i=80$^\circ$) is smaller than the estimated inner emission radius of $R_{\rm i} \simeq 7~\mbox{$\space R_{\star}$ }$ (HV1) for He I. Self-absorption (shear broadening) is taken into account.
  \begin{figure} \par\includegraphics[width=8cm,height=10.2cm,clip]{h2216-fig04.ps} \end{figure} Figure 4: Sketch of the sector model. The emission region is constrained by $R_{\rm i}$, $R_{\rm d}$, and $\phi _1$ and $\phi _2$. We allow for a phase shift $\Delta \phi $ between the symmetry line of the system $\overline {PS}$ and the sector half width at $\phi = (\phi _1 + \phi _2)/2$
Open with DEXTER

For fitting the phase-resolved emission lines we adjusted the inner radius $R_{\rm i}$, the outer radius $R_{\rm d}$, the full opening angle of the sector $\phi_2-\phi_1$ and the parameterized occupation density n0 manually. From preliminary studies it turned out that the synthetic line profiles do much less respond to changes in the radial emission exponent m with respect to the line profile study of HV2. This effect is due to large inner rim $R_{\rm i} \simeq 5$ of the emission region, matching only the low angular velocity parts of the disk. The emissivity is therefore kept constant with radius ( $\eta = R^{-m}$, m=0.5).

All other physical parameters are from Gies et al. (1998) (see Table 1). We additionally allowed for a phase shift $\Delta \phi $ between $\overline {PS}$ and the center of the emission ( $=(\phi_1+\phi_2)/2$) (see Fig. 4). The necessity of such a phase shift can be seen in the phase resolved observations (Fig. 5) where the symmetric profiles occur after 0 $.\!\!^{\scriptscriptstyle\rm p}$0 and 0 $.\!\!^{\scriptscriptstyle\rm p}$5. Secondly we used a simplex method for the multi-parameter fitting to improve the fit quality. This step was carried out several times to check on possible ambiguous solutions in the multiple parameter space and in order to test and improve the quality of our final model.

A best fit to the He I $\lambda$6678 emission lines in frame of this simple sector model is shown in Fig. 5a. The resulting parameters are given in Table 2. The general behavior of orbital phase variations is well matched. A phase shift of $\Delta \phi \simeq 0.13$ between $\overline{SP}$ and the emission region is required to improve the fit quality, since the profile asymmetry changes at $\simeq$ $0\hbox{$.\!\!^{\scriptscriptstyle\rm p}$ }1$ and $\simeq$ $0\hbox{$.\!\!^{\scriptscriptstyle\rm p}$ }6$


  \begin{figure*} \mbox{\includegraphics[width=5.1cm,height=11.5cm,clip]{h2216-SE1... ...raphics[width=5.1cm,height=11.5cm,clip]{h2216-SE3-fig13.ps} } \par \end{figure*} Figure 5: Bold profiles: phase resolved observations of He I 6678 emission lines, corrected for phase shifted stellar absorption and phase binned. The lowermost line profile is the orbital mean profile. Details on the observations are given in P1. Thin: phase dependent theoretical emission line profiles for He I 6678. a) the sector model (SE1). b) as a), except the shell absorption is taken into account in the model profiles (SE2). c) as b), except the differential rotation is taken into account to test the preceding shell absorption (SE3). Parameters for all three models SE1, SE2 and SE3 are given in Table 2
Open with DEXTER


  \begin{figure*}\mbox{\includegraphics[width=5.1cm,height=11.5cm]{h2216-SE3b-fig1... ...\includegraphics[width=5.1cm,height=11.5cm]{h2216-SP2-fig16.ps} }\end{figure*} Figure 6: Bold profiles: as Fig. 5. Thin profiles: a) sector model (SE4), differential deformation of the incoming boundary $\phi _1$ is also taken into account. b) phase dependent theoretical emission line profiles for He I 6678 from the sphere model (SP1). c) as a), except the shell absorption is taken into account in the model profiles (SP2). Parameters for all models SE4, SP1 and SP2 are given in Table 2
Open with DEXTER

  
4.1.2 Sphere model
One systematic difference between our model profiles of the simple sector model and the observations are the emission bumps in the model profiles (Fig. 5a) before and after the phase of maximum emission elongation. It is very probable that the emission bump can only be fully resolved in high resolution spectra like those of Gies et al. (1993) and that they are identical to what those authors call the faint component. Moreover also our high resolution profiles of He I 5876 (Fig. 12) also show some fine structure.

Certainly the bumps in the calculated profiles originate close to $\phi _1$ and $\phi _2$, but it cannot directly be decided if they originate close the Ri or $R_{\rm d}$ (see Fig. 4). We therefore modify the sector model in two different ways:

We modify the emission region in such a way that we only allow He I to be emitted in those regions which do not exceed a certain distance $R_{\rm e}$ from the secondary (Fig. 7):

 \begin{displaymath} R_{\rm d} \cap R_{\rm e}. \end{displaymath} (16)

The emission region suppresses emission from regions around ( $\phi_1,R_{\rm i}$) and ( $\phi_2,R_{\rm i}$). Such a distribution can be expected, if the He I excitation is only due to the radiation field of the secondary independently on the kinematics and the density distribution in the circumprimary disk. Following the discussion in P1 on the predicted Strömgren sphere of the secondary we will refer to this model as the sphere-model.

Model profiles for the best-fit parameters are given in Fig. 6b. Best-fit parameters are given in Table 2. The radius of the excitation sphere around the secondary is found to be $R_{\rm e} = 25.6~R_*$, while the binary separation is given as $\overline{PS}=29~R_*$, hence the He I 6678 is found to be emitted from the outer disk radius $R_{\rm d}=10$ down to R = 2.4 R* in frame of the sphere model, meaning a maximum penetration depth of 7.6 R*. There is no striking difference between model profiles from the sector model and those from the sphere model, meaning that both models are valid parameterizations of the true emission distribution.

In a further diagnostic model we suppressed the emission region around the outer corners at ( $\phi_1,R_{\rm d}$) and ( $\phi_2,R_{\rm d}$). The inner edge of the He I emission region is still $R_{\rm i}$ but the outer edge is a curve from ( $\phi_1,R_{\rm i}$) to ( $(\phi_1+\phi_2)/2,R_{\rm d}$) to ( $\phi_2,R_{\rm i}$). This geometric constraint results in a crescent like shape. The resulting model profiles only show single-peak profiles without emission bumps in the wings. This comparison clearly demonstrates that the emission bumps are produced at the outer rim of the emitting part of the circumprimary disk (at $\simeq$ $(R_{\rm d},\phi_1)$ and $\simeq$ $(R_{\rm d},\phi_2)$) and are a natural consequence of the relatively large sector angle $\Delta \phi \simeq 110\hbox{$^\circ$ }$. In the test model with the crescent like shape the emission regions around ( $R_{\rm d}, \phi_1$) and ( $R_{\rm d}, \phi_2$) are omitted, hence the bumps do no longer appear in the theoretical profiles. The latter model with the crescent like shape is therefore rejected for the rest of this study.


  \begin{figure} \par\includegraphics[width=8.5cm,height=9.5cm,clip]{h2216-fig05.ps} \end{figure} Figure 7: Sketch of the ionization sphere model. The emission region is constrained by $R_{\rm d} \cap R_{\rm e}$
Open with DEXTER

4.1.3 Comparison with observed peak-velocity relation
In Fig. 8 we show the peak radial velocities of the theoretical profiles from model SE1 and SP1 as a function of orbital phase together with the observed relation. Both parametric variants of the assumed He I 6678 emission region match well the the "box-diagram'' (P1) of the radial velocity curve of the emission peaks. The fine structure in the orbital phase diagram is most probably related to deviations from axial symmetry in the velocity law (Suzuki 1980) which is not taken into account in the model.


  \begin{figure} \par\includegraphics[width=7.6cm,height=8cm,clip]{h2216-fig06.ps} \end{figure} Figure 8: Comparison between the observed peak radial velocity as a function of phase and the the same relation as derived from the model profiles. Solid line corresponds to model SE1 and the bold dashed line corresponds to model SP1
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.6cm,height=8cm,clip]{h2216-fig07.ps} \end{figure} Figure 9: Comparison between the observed peak intensity as a function of phase and the the same relation as derived from the model profiles. Solid line corresponds to model SE1 and the bold dashed line corresponds to model SP1
Open with DEXTER

4.2 Emission and absorption

Up to now we modeled exclusively the He I emission for He I 6678, since the absorption is of minor importance with respect to He I 5876. The different absorption processes which can occur in Be star circumstellar disks have been described in detail by HV2. We recall here solely the concept of the obscuration radius $R_{\rm o}(\phi)$, which determines the shadow of the star projected to the equatorial plane of the disk. The oval shape of $R_{\rm o}(\phi)$ points to the observers direction. Note that emission depends on the occupation number ratio of upper and lower atomic level, absorption is dependent on the absolute lower level occupation. The region of absorption and emission is therefore not necessarily identical, but depends on the local degree of excitation. Note also the difference between the shell absorption and self absorption in the disk. The latter occurs in the emission region of the disk and is taken into account via Eq. (13). Shell absorption (absorption troughs below the stellar continuum) reprocesses stellar radiation directly and can only occur in the oval-shape shell region (specified by the obscuration radius $R_{\rm o}$) pointing to the observer; its not moving with orbital phase. Therefore orbital phase variations of shell lines give more immediate information on the azimuthal excitation structure of the disk.

4.2.1 Sphere model
For this model we simply assume that absorption occurs where also emission occurs, meaning that the absorption region is also given by Eq. (16). The shell effect itself, however, does only occur when the obscuration region ( $R<R_{\rm o}(\phi)$) matches the He I excitation region. Since the He I excitation region approaches the star up to a distance of 2 R* we can expect shell absorption for some phase interval around the superior conjunction.

In Fig. 6 we "switched on'' the absorption in the sphere model (SE2) and fit our phase resolved observations. As has been discussed by HV2, the treatment of absorption additionally constrains the emissivity, hence lower values of the foot point emissivity $S^{\rm L}$are required to fit the absorption cores. Best fit model parameters are given in Table 2. The absorption component appears for a wide phase range of 0 $.\!\!^{\scriptscriptstyle\rm p}$0 to 0 $.\!\!^{\scriptscriptstyle\rm p}$2, when the He I region and the obscuration radius most overlap. Shell absorption occurs as predicted only when the $R_{\rm d} \cap R_{\rm e}$-region intersects the shell region at superior conjunction of the primary advanced by $\Delta \phi $. The shell lines of He I 6678 occur, however, at phase $\simeq$ $0\hbox{$.\!\!^{\scriptscriptstyle\rm p}$ }9$.

4.2.2 Sector model
Taking the shell absorption into account in the sector model would have minor impact on line profiles, since the obscuration radius of $R_{\rm o}=8.6$ does only intersect the inner parts of the whole He I emission region extended from R=5 to R=10.

For the model construction, we assume the lower He I level to be excited down to R=R* within the sector $[\phi_1 \cdots \phi_2]$. The emission is assumed to be formed for $R>R_{\rm i} = 5.3$, meaning we set $S^{\rm L}=0$ for R<5.3. This construction is justified by the observed behavior of the He I 6876 line. It would be consistent with a situation when the population of the upper level of the He I 6876 line increases with R inside the sector.

As in the sphere model the shell absorption is only efficient when the sector, moving with orbital phase, matches the obscuration region which always points to the observer. This happens near the phase of superior conjunction. Best fit model profiles of the sector model (SE2) are given in Fig. 5b, parameters are given in Table 2.

The resulting line profiles show the same trend as those of the sphere model, except that shell absorption occurs over a longer phase interval, including the phase-binned profile at $0\hbox{$.\!\!^{\scriptscriptstyle\rm p}$ }975$, since the sector model covers geometrically a larger phase interval than the sphere model, in particular at small radii.

The absorption in the model profiles is mostly due to the shell absorption of the primary alone; stellar obscuration by the primary does effectively not occur since the emission region is located beyond the obscuration radius at $R_{\rm o}=8.6$.


  \begin{figure} \par\includegraphics[width=8cm,height=8.5cm,clip]{h2216-fig08.ps} \end{figure} Figure 10: Absorption component of the He I 6678 emission in the sector model (SE2). Upper left: residual intensity of the shell component; lower left: radial velocity of the shell component; right: shell profiles as a function of orbital phase. Note that the shell region must overlap with the He I excitation region to produce shell absorption
Open with DEXTER

In Fig. 10 we give a zoom view on the most interesting phases of a pure absorption sector model ( $S^{\rm L}=0$ throughout the disk). Note that the shell absorption does only occur when the sector overlaps with the obscuration region. The sharp rim of the sector causes an occurrence of shell lines in the well defined phase interval 0 $.\!\!^{\scriptscriptstyle\rm p}$85-01 $.\!\!^{\scriptscriptstyle\rm p}$15. The radial velocity of the shell component follows the radial velocity curve of the primary but diverges when the sector enters or leaves the obscuration region and alters the shell profile.

A systematic difference between our models and the observations account for the phase shift between emission and absorption. The absorption caused by the shell effect in the inner disk regions of the sector reaches maximum at 0 $.\!\!^{\scriptscriptstyle\rm p}$9, meaning before the symmetry of emission at and before the nominal phase of superior conjunction. This is at variance to epoch 1976-1978 when the He I 4026 and 4471 show shell absorption in the phase interval 0 $.\!\!^{\scriptscriptstyle\rm p}$94-0 $.\!\!^{\scriptscriptstyle\rm p}$04 and 0 $.\!\!^{\scriptscriptstyle\rm p}$94-0 $.\!\!^{\scriptscriptstyle\rm p}$14, respectively (see Poeckert 1981, his Figs. 4 and 5)

This is a critical test of our modeling. If absorption in the He I lines is due to shell absorption it must occur inside the obscuration radius, meaning that the inner He I absorption region precedes the outer emission parts. In the frame of our sector model this means that the sector boundaries are bended towards earlier phases in the inner disk regions. We will address this effect in the next section. In the following subsection we test if the phase shift can be explained by a deformation of the recombination front due to differential rotation in the circumprimary disk.

  
4.3 Differential rotation, advection

The sector/sphere model of the He I excitation region implies that the fast orbiting gas is excited when it enters the region facing the secondary and recombines immediately after having left the Strömgren sphere or the sector. The orbiting He gas is excited once per revolution time in a cyclic manner. For a finite recombination time the He excitation is transported with the orbiting gas out of the sector. This advection becomes important in the inner region of the disk when the gas leaves the sector region with a higher angular velocity than in the outer disk. The gas particles in a Keplerian disk pass an angular distance of

 \begin{displaymath} \Delta \phi_{\rm K} (R) = \Omega(R) \Delta t = - \Omega_0 R^{-\frac{3}{2}} \Delta t \end{displaymath} (17)

during $\Delta t$, where

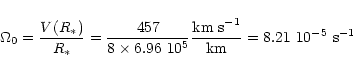\begin{displaymath}\Omega_0= \frac{V(R_*)}{R_*} =\frac{457}{8 \times 6.96~10^{5}} \frac{{\rm km~s}^{-1} }{\rm km} = 8.21~10^{-5}~{\rm s}^{-1} \end{displaymath} (18)

is the angular velocity at R* in rad and $\Delta \phi_{\rm K}$ is the angular distance. For the reduced potential (Eq. (4)) we get a slightly different expression for Eq. (17):

 \begin{displaymath} \Delta \phi_{{\rm B}} (R) = \left( - \Omega_0 R^{-\frac{3}{2}} -3.4781 + 1.031 R^{-1} \right) \Delta t . \end{displaymath} (19)

The deformation of a radial sector boundary due to the differential rotation can be expressed by a phase shift:

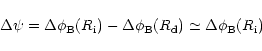\begin{displaymath}\Delta \psi = \Delta \phi_{{\rm B}} (R_{\rm i}) - \Delta \phi_{{\rm B}} (R_{\rm d}) \simeq \Delta \phi_{{\rm B}} (R_{\rm i}) \end{displaymath} (20)

neglecting $\Delta \phi_{{\rm B}}$ at $R=R_{\rm d}$. From the expression above the radiative time scale $\Delta t$ can be derived. In Fig. 11 we plot four recombination fronts for phase shifts between the inner and the outer emission radius of $\Delta \psi = 0\hbox{$.\!\!^{\scriptscriptstyle\rm p}$ }0, 0\hbox{$.\!\!^{\scriptscriptstyle\rm p}$ }5, 1\hbox{$.\!\!^{\scriptscriptstyle\rm p}$ }0$ and 2 $.\!\!^{\scriptscriptstyle\rm p}$0. The phase shifts correspond to recombination times of $\Delta t = 0$h, 10.6h, 21.3h, and 42.5h.


  \begin{figure} \par\includegraphics[width=8.05cm,height=8cm,clip]{h2216-fig09.ps} \end{figure} Figure 11: Sketch of the bended sector model. The He I emission region is enclosed by $R_{\rm i}$ and $R_{\rm d}$ in radius and by a constant phase ( $\phi _{\rm 1}$) and a bended line due to the differential rotation. The He I shell absorption region is enclosed by R* and $R_{\rm d}$ in radius, by a constant phase ( $\phi _{\rm a}$), a bended line due to the differential rotation and the obscuration area. Four bended boundaries are given for recombination times corresponding to a phase shift of $\Delta \phi = 0.0, 0.5, 1$ and 2 between $\phi _2 (R_{\rm d})$ and $\phi _2 (R_{\rm i})$. The oval obscuration region points to the observerlocated at the bottom (-y) and the orbital phase is 0 $.\!\!^{\scriptscriptstyle\rm p}$87
Open with DEXTER

For an electron density of $n_{\rm e} = 10^{12}$ cm-3, typical for Be star circumstellar disks (e.g Poeckert & Marlborough 1979) the mean free photon path can be estimated to be

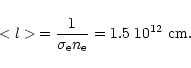\begin{displaymath}<l> \,= \frac{1}{\sigma_{\rm e} n_{\rm e}} = 1.5~10^{12}~{\rm cm}. \end{displaymath} (21)

The mean escape time for photons would be

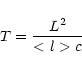\begin{displaymath}T = \frac{L^2}{<l> c} \end{displaymath} (22)

where $L \simeq H(R*)$ is the total travel length. T is of the order of several seconds. It is too small with respect to the required time of $\simeq$20h. For line radiation there is $<l>\, = \frac{1}{\kappa n}$, where

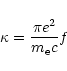\begin{displaymath}\kappa = \frac{\pi e^2}{m_{\rm e}c} f \end{displaymath} (23)

and f is the oscillation strength (=0.711 at He I 6678 and 0.609 at He I 5876) and n is the number of absorbers. For $T_{{\rm disk}}=20\,000$ K, a number density of n= 1013 cm-3 (Poeckert & Marlborough 1979) and solar abundance (Y = 0.089) we find a He I fraction of 10-4 and a relative level population of 10-9 for the lower level of the 6678 Å transition under conditions of LTE, meaning n=103 cm-3. Using the minimum travel length of the scale height L= H(R*) we find a maximum radiative recombination time of several months. This means that the excitation of the circumprimary gas can be transported with the disk and that advection is a favorable mechanism to understand the precedence of the shell absorption.

Model profiles (model SE3) including the effect of rotational deformation of the shell absorption region with $\Delta \phi =1$ are shown in Fig. 5c. Parameters are given in Table 2.

Shell absorption does now occur on a larger phase interval including the intended phase of 0 $.\!\!^{\scriptscriptstyle\rm p}$9. Our simple treatment of a finite recombination time is able to account for a shell-precedence of about $0\hbox{$.\!\!^{\scriptscriptstyle\rm p}$ }1$. This model cannot suppress shell absorption between $0\hbox{$.\!\!^{\scriptscriptstyle\rm p}$ }3$ and $0\hbox{$.\!\!^{\scriptscriptstyle\rm p}$ }0$. A possible deformation of the excitation front ($\phi_1(R)$) due to a finite excitation time when the gas enters the Strömgren sphere could play a similar role. Without a detailed physical justification but for diagnostic reasons we modify model SE3 and apply the distorted emission front also to the $\phi _1$ boundary of the disk region (SE4). Model profiles taken the finite excitation time into account are given in Fig. 6 where we used also a bended shape for the $\phi _1$ azimuthal boundary. The shell absorption for this model (SE4) fades out earlier in phase with respect to model SE3 but not sufficiently early to account for a complete absence of shell absorption around $0\hbox{$.\!\!^{\scriptscriptstyle\rm p}$ }1{-}0\hbox{$.\!\!^{\scriptscriptstyle\rm p}$ }0$.

Our applied phase shift of $\Delta \phi = 1\hbox{$.\!\!^{\scriptscriptstyle\rm p}$ }0$ (corresponding to a mean total exit time of 21h) is too small to reduce the shell absorption at phase $0\hbox{$.\!\!^{\scriptscriptstyle\rm p}$ }0$. Phase shifts larger than $\Delta \phi = 1\hbox{$.\!\!^{\scriptscriptstyle\rm p}$ }0$ become physically questionable.

For $\Delta \psi > 2 \pi$ the orbiting gas would be re-excited before it was completely recombined. The observational counterpart for such a scenario would be no longer appearance and disappearance of shell lines but orbital phase variations of permanently present shell lines.

At variance, orbital phase variation of the scale height H(R) can impact the phase variations of spectral features (e.g. Gies et al. 1998). Since only one species is affected by the radiation field of the secondary a heating mechanism is not likely. Since H(R) scales only as $\sim$$\sqrt(T)$ a rather large temperature gradient along the orbital trajectories must be present for significant variations of H(R) with orbital phase. It is also difficult to explain the shell phase shift in terms of a variation of H(R) with orbital phase. A diminishing of H(R) on the side facing the secondary could be achieved by the gravitation of the secondary, however, as shown in Eq. (9) its influence is too low. Hence orbital phase variation of H(R) is less favorable to explain the phase shift of the shell absorption.

5 The HeI 5876 formation region

The few available phase dependent He 5876 emission lines are spectroscopically nearly fully resolved. The log of observations is given in P1. The He I 5876 emission feature shows similar orbital phase variations as He I 6678, however, the shell absorption is much deeper and the profile wing shows a peculiar bump near quadratures (0 $.\!\!^{\scriptscriptstyle\rm p}$74 and 0 $.\!\!^{\scriptscriptstyle\rm p}$34). In spite of our fractional orbital phase coverage of He 5876 observations we fit He 5876 emission lines, starting with the parameter set of the best fit emission region for He I 6678. For the comparison we subtracted a mean photospheric absorption profile obtained in a similar way as for He I 6678 in P1. In Fig. 12 we show a reasonable estimate of a few He I 5876 emission lines using the sector model (model SE5). The parameters are given in Table 2. For the He I 5876 fit we are not able to find shell profiles with a similar flux minimum as observed at 0 $.\!\!^{\scriptscriptstyle\rm p}$74. We therefore have to increase the disk inclination from $i=80\hbox{$^\circ$ }$ to i=84$^\circ$. As is explained in detail by Hanuschik (1996), HV2 and in Sect. 2.3, the primary becomes obscured by the vertical extension of the disk at $R_{\rm d}$.

For i=84$^\circ$ $H(R_{\rm d})$ is projected to $h_{\rm p}=0.36$, hence about $\frac{3}{4}$ of the star is obscured by $H(R_{\rm d})$ and the effective stellar surface contributing to the shell absorption is considerably enlarged.

As shown in Fig. 12 observed profiles at $\simeq$ $0\hbox{$.\!\!^{\scriptscriptstyle\rm p}$ }7$ and $0\hbox{$.\!\!^{\scriptscriptstyle\rm p}$ }34$ are assigned a larger weight with respect to $0\hbox{$.\!\!^{\scriptscriptstyle\rm p}$ }54$ which gives a fit of lower quality for most of the parameter combinations we tested. For diagnostic reasons we also give the model profile for $0\hbox{$.\!\!^{\scriptscriptstyle\rm p}$ }0$ (stars in Fig. 12 for 0 $.\!\!^{\scriptscriptstyle\rm p}$74) which is slightly asymmetric due to the deformation of the recombination front. Nevertheless our model is able to account for the strong gradient of the shell intensity in the small orbital phase interval of $[0\hbox{$.\!\!^{\scriptscriptstyle\rm p}$ }736{-}0\hbox{$.\!\!^{\scriptscriptstyle\rm p}$ }740 ]$.


  \begin{figure} \par\includegraphics[width=8.7cm,height=7cm,clip]{h2216-fig10.ps} \end{figure} Figure 12: Fit of the He I 5876 emission feature at four different orbital phases. Model parameters are given in Table 2. The dotted line in the figure for $P=0\hbox{$.\!\!^{\scriptscriptstyle\rm p}$ }74$ is the model profile for phase 0 $.\!\!^{\scriptscriptstyle\rm p}$0
Open with DEXTER

  
6 Discussion

6.1 Sphere model versus sector model

The sphere model, originally introduced in order to search for the origin of the inner emission bumps in the He I 6678 lines, does also match the general characteristics of the orbital phase variations of the He I 6678 line. Its only drawback is of technical reasons: it is easier to simulate effects of differential rotation in the sector model than in the sphere model. The disk radius $R_{\rm d}$ in both models amounts to 10 R* for He I 6678 (see also Table 2). Moreover this radius agrees well with that derived from Fe II ( $R_{\rm d}=9.3$) and that of He I 5876 ( $R_{\rm d}=10$). These values are also in agreement with interferometric results (Quirrenbach et al. 1997; Hummel & Vrancken 2000a). The larger disk radii derived by HV1 are due to the assumption of Keplerian rotation which is not valid in $\phi $ Per. In single Be stars measured disk radii are interpreted as those of the emission region in a physically more extended disk. Since the excitation of He I is most probably due to photoionization caused by the secondary we expect a larger He I emission radius ($R_{\rm d}$) than the Balmer and Fe II emission radius in the particular case of $\phi $ Per. This is not observed. This means that the derived disk radius of $R_{\rm d} \simeq 10$ seems to be a real physical cut of the density distribution in the circumprimary disk. The disk is well embedded in the Roche radius of about $R_{\rm R}=16.8$. The optical observations bear no indication for any Roche lobe overflow.

Both parameterizations of the He I 6676 emission region qualitatively match the box-diagram of the radial velocity and verify our suggestion of one emission region inside one disk around the primary. There is no further disk required to explain the orbital phase variations of the He I emission feature.

6.2 The phase shift of the shell absorption

One of the most enigmatic behavior of the He I emission feature is the preceding phase shift of the shell absorption. Poeckert (1981) detected the shell absorption at 0 $.\!\!^{\scriptscriptstyle\rm p}$0, meaning at phase of superior conjunction of the primary. In our observations 1992-1996 (P1) shell absorption occurs no longer at phase 0 $.\!\!^{\scriptscriptstyle\rm p}$0 but at 0 $.\!\!^{\scriptscriptstyle\rm p}$8-0 $.\!\!^{\scriptscriptstyle\rm p}$9. One explanation for the present phase shift could be differential rotation in connection with a finite excitation/recombination time as discussed already in Sect. 4.3. However, though our estimate shows reasonable agreement between the observed phase shift and the required mean free photon path, this explanation fails for the observed zero phase shift during 1975 (Poeckert 1981).

Another idea for the phase shift would be an inclined rotation axis of the primary with respect to the orbital plane of the secondary. For a large disk one could expect warping effects, but in this case the disk inclination would be variable with orbital phase and shell events should appear two times per phase (Hummel 1998) what is not observed. Furthermore the disk is well embedded in the potential of the primary and we suppose that L1 at R= 19 R* is too far beyond the disk radius of $R_{\rm d}=10~R_*$ to warp the disk. If the inclined disk is stable against perturbations induced by the secondary we would nevertheless observe phase dependent variations of the intensity above those which have been modeled since the disk would be illuminated from the upper and from the lower side during one orbital period. None of these effects can be drawn from the observations. We therefore conclude that the secondary orbits well in the equatorial plane of the primary. Shell events may also be induced by a variation of the disk scale height induced by a variation of the disk radius (Hanuschik 1996, HV2). Indeed the high inclination makes $\phi $ Per a candidate. However, we do not favor this idea. First, the disk around $\phi $ Per cannot vary its radial size as free as disks around single Be stars. Second, given a constant disk radius over an orbital period the shell events would mean a lower disk scale height along the separation line $\overline{SP}$ and a larger disk height after the gas has passed the point of closest approach to L1. Since the scale height scales as $\sqrt{T}$, a relatively large kinetic temperature change is required at the location where the orbiting gas recedes the secondary.

A final idea would be that the growing long-term variations in $\phi $ Per first detected by the V/R peak variations of Fe II lines (see P1) have already been present before 1996 but with a lower amplitude and confined to the innermost disk regions with R<5 R*. In that way the He I emission due to the secondary is not influenced and the peaks of the Fe II lines originating mostly at $R_{\rm d}$ are also not affected by the early beginning of the long-term variations.

Indeed the Fe II emission lines though symmetric and with V=R show different profiles shapes at the bottom of the profiles which has not been mentioned yet.

A final idea on the shell phase shift concerns the precession of density waves. In Paper I we identified the long-term variations of $\phi $ Per with a global density wave (Okazaki 1992). We furthermore derived a phase position at which $\overline{SP}$ matches the angular position of the high density region of $\simeq$ $0\hbox{$.\!\!^{\scriptscriptstyle\rm p}$ }2$ in 1998 (see Fig. 4 of P1) and a V/R-ratio minimum in Fe II around Oct 1999 (see Fig. 3 of P1). The latter finding means an approximative phase position of either $\simeq$ $0\hbox{$.\!\!^{\scriptscriptstyle\rm p}$ }25$ or $\simeq$ $0\hbox{$.\!\!^{\scriptscriptstyle\rm p}$ }75$ for the high density region, however together with the first finding the $\simeq$ $0\hbox{$.\!\!^{\scriptscriptstyle\rm p}$ }75$ position is not likely. So far the observations indicate a prograde pattern precession if we assume that the disk rotates in the same direction as the secondary. Extrapolating back to 1995 a phase position of $0\hbox{$.\!\!^{\scriptscriptstyle\rm p}$ }05$- $0\hbox{$.\!\!^{\scriptscriptstyle\rm p}$ }1$ can be estimated for the high density region, meaning that this region partly overlaps with the oval shell region. This inhomogeneous density distribution inside the shell area would enhance shell profiles at orbital phases $0\hbox{$.\!\!^{\scriptscriptstyle\rm p}$ }9$ (see Fig. 10). No advection would be required. This interpretation can easily be tested by a further phase resolved observation of He I shell components during superior conjunction of the primary. There should be no longer a phase shift of the shell occurrence since the high density region of the density wave should have been precessed completely out of the shell region.

6.3 Comparison between HeI 6678 and HeI 5876

Emission line series have been modeled independently, since no assumptions have been made whether both lines match the same region inside the circumprimary disk. Note that He I 6678 is modeled with the nominal inclination of i=80$^\circ$ while for He I 5876 a slightly larger inclination of i=84$^\circ$ is required to match the deep central depression. Therefore the shell component in the He I 5876 model profiles is more due to the disk height projection effect, while in the He I 6678 model the conventional shell region in the equatorial plane produces the shell component in the emission line. From the emission radii we conclude that the He I 5876 formation region is on average slightly closer to the secondary. The largest difference in model parameters occurs in the azimuthal opening angle which is 180$^\circ$ for He I 5876 but only about 110$^\circ$ for He I 6678. The large opening angle is necessary for He I 5876 to fit the shell components at $P\simeq 0\hbox{$.\!\!^{\scriptscriptstyle\rm p}$ }7$. If we had emphasized a better fit for the emission dominant line profiles at $0\hbox{$.\!\!^{\scriptscriptstyle\rm p}$ }34$ and $0\hbox{$.\!\!^{\scriptscriptstyle\rm p}$ }54$ (Fig. 12) a smaller opening angle similar to that for He I 6678 would have been more appropriate.

7 Conclusion

The main conclusions drawn from our modeling are:

Acknowledgements
Financial support by the Deutsche Forschungsgemeinschaft DFG project number 436 TSE 113/19 and the Grant Agency of the Czech Republic (202/97/0326) is gratefully acknowledged.

References

 

Copyright ESO 2001