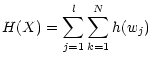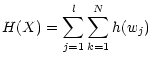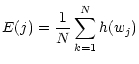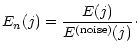Up: Entropy and astronomical data
Subsections
The multiscale entropy has been defined by:
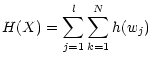 |
|
|
(55) |
with
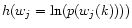 .
In order to study the behavior of the information at a given scale, we
prefer to calculate the mean entropy vector E defined by:
.
In order to study the behavior of the information at a given scale, we
prefer to calculate the mean entropy vector E defined by:
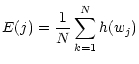 |
|
|
(56) |
E(j) gives the mean entropy at scale j. From the mean entropy vector,
we have statistical information on each scale separately.
Having a noise model, we are able to calculate (generally from simulations)
the mean entropy vector
 resulting from pure noise.
Then we define the normalized mean entropy vector by
resulting from pure noise.
Then we define the normalized mean entropy vector by
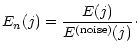 |
|
|
(57) |
Figure 9 shows the result of a simulation.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10414f9.ps}\end{figure}](/articles/aa/full/2001/11/aa10414/Timg148.gif) |
Figure 9:
Mean entropy versus the scale of 5 simulated images containing
undetectable
sources and noise. Each curve corresponds to the multiscale transform
of one image. From
top to bottom, the image contains respectively 400, 200, 100,
50 and 0 sources |
Five simulated images were created by adding n sources to a
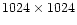 image
containing Gaussian noise of standard deviation equal to 1 (and
arbitrary mean). The n sources
are identical, with a maximum equal to 1, standard deviation equal to 2,
and zero covariance terms.
Defining the signal-to-noise ratio (SNR) as the ratio between
the standard deviation in the smallest box which contains at least 90%
of the flux of the source, and the noise standard deviation, we have a SNR
equal to 0.25. The sources are not detectable in the simulated
image, nor in its wavelet transform. Figure 10 shows a region
which contains a source at the center.
It is clear there is no way to find
this kind of noisy signal. The five images were created using a number
of sources
respectively equal to 0, 50, 100, 200 and 400, and the simulation was
repeated ten times with different noise maps in order to have an error bar on
each entropy measurement. For the image which contains 400
sources, the number of pixels affected by a source is less than 2.5%.
image
containing Gaussian noise of standard deviation equal to 1 (and
arbitrary mean). The n sources
are identical, with a maximum equal to 1, standard deviation equal to 2,
and zero covariance terms.
Defining the signal-to-noise ratio (SNR) as the ratio between
the standard deviation in the smallest box which contains at least 90%
of the flux of the source, and the noise standard deviation, we have a SNR
equal to 0.25. The sources are not detectable in the simulated
image, nor in its wavelet transform. Figure 10 shows a region
which contains a source at the center.
It is clear there is no way to find
this kind of noisy signal. The five images were created using a number
of sources
respectively equal to 0, 50, 100, 200 and 400, and the simulation was
repeated ten times with different noise maps in order to have an error bar on
each entropy measurement. For the image which contains 400
sources, the number of pixels affected by a source is less than 2.5%.
When the number of sources increases, the difference between the multiscale
entropy curves increases. Even if the sources are very faint, the presence
of signal can be clearly detected using the mean entropy vector. But it is
obvious that the positions of these sources remain unknown.


Up: Entropy and astronomical data
Copyright ESO 2001