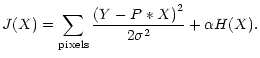Up: Entropy and astronomical data
The term "entropy'' is due to Clausius (1865), and the concept of
entropy was introduced by Boltzmann into statistical mechanics
in order to measure the number of microscopic ways that a given macroscopic
state can be realized. Shannon (1948) founded the mathematical theory of
communication when he suggested that the information gained in a
measurement depends on the number of possible outcomes out of
which one is realized. Shannon also suggested that
the entropy can be used for maximization of the bit transfer rate under
a quality constraint. Jaynes (1957)
proposed to use the entropy measure
for radio interferometric image deconvolution, in
order to select between a set of possible solutions that contains the
minimum of information or, following his entropy definition,
which has maximum entropy. In principle, the solution verifying such
a condition should be the most reliable. A great deal of work has been
carried out
in the last 30 years on the use of entropy for the general problem
of data filtering and deconvolution (Ables 1974; Bontekoe et al. 1994; Burg 1978; Frieden 1978a; Gull & Skilling 1991; Mohammad-Djafari 1994,1998; Narayan & Nityananda 1986; Pantin & Starck 1996; Skilling 1989; Weir 1992).
Traditionally information and entropy are determined from events and the
probability of their occurrence. But signal and noise, rather than
events and occurrences of events, are the basic building-blocks
of signal and data analysis in the physical sciences. Instead of the
probability of an event, we are led to consider the probabilities of our
data being either signal or noise.
Observed data Y in the physical sciences
are generally corrupted by noise, which is often additive and which
follows in many cases a Gaussian distribution, a Poisson distribution, or
a combination of both. Other noise models may also be considered.
Using Bayes' theorem to evaluate the probability distribution of the
realization of the original signal X,
knowing the data Y, we have
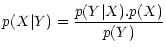 |
|
|
(1) |
p(Y|X) is the conditional probability distribution of getting the data
Y given an original signal X, i.e. it represents the distribution
of the noise. It is given, in the case of uncorrelated Gaussian
noise with variance 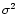 ,
by:
,
by:
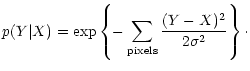 |
|
|
(2) |
The denominator in Eq. (1) is independent of X and
is considered as a constant. This is the case of stationary noise.
p(X) is the a priori distribution
of the solution X. In the absence of any information on the solution
X except its positivity, a possible course of action
is to derive the probability
of X from its entropy, which is defined from information theory.
The main idea of information theory (Shannon 1948) is to establish
a relation between the received information and the probability of
the observed event (Bijaoui 1984). If we
denote
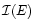 the information
related to the event E, and p the probability of this
event happening, then we consider that
the information
related to the event E, and p the probability of this
event happening, then we consider that
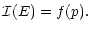 |
|
|
(3) |
Then we assume the two following principles:
- The information is a decreasing function of the probability. This
implies that the more information we have, the less will be the probability
associated with one event;
- Additivity of the information. If we have two independent events
E1 and E2, the information
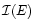 associated with the occurrence
of both is equal
to the addition of the information of each of them:
associated with the occurrence
of both is equal
to the addition of the information of each of them:
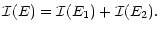 |
|
|
(4) |
Since E1 (of probability p1) and E2 (of probability p2) are
independent, then the probability of both happening is equal to the
product of p1 and p2. Hence
| f(p1 p2) = f(p1) + f(p2) . |
|
|
(5) |
Then we can say that the information measure is
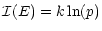 |
|
|
(6) |
where k is a constant. Information must be positive, and kis generally fixed at -1.
Another interesting measure is the mean information which is denoted
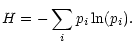 |
|
|
(7) |
This quantity is called the entropy of the system and was established by
Shannon (1948).
This measure has several properties:
- It is maximal when all events have the same probability
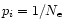 (
(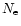 being the number of events), and is equal to
being the number of events), and is equal to
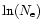 .
It is in this
configuration that the system is the most undefined;
.
It is in this
configuration that the system is the most undefined;
- It is minimal when one event is sure. In this case, the system is
perfectly known, and no information can be added;
- The entropy is a positive, continuous, and symmetric function.
If we know the entropy H of the solution (the next section
describes different ways to calculate it),
we derive its probability by
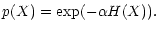 |
|
|
(8) |
Given the data, the most probable image is obtained by maximizing
p(X|Y). Taking the logarithm of Eq. (1), we
thus need to maximize
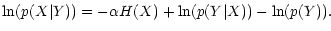 |
|
|
(9) |
The last term is a constant and can be omitted.
Then, in the case of Gaussian noise, the solution is found by minimizing
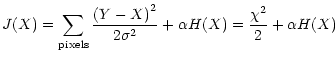 |
|
|
(10) |
which is a linear combination of two terms: the entropy of the signal,
and a quantity corresponding to 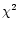 in statistics measuring the
discrepancy between the data and the predictions of the model.
in statistics measuring the
discrepancy between the data and the predictions of the model.
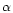 is a parameter that can be viewed alternatively as
a Lagrangian parameter or a value fixing the relative weight between
the goodness-of-fit and the entropy H.
is a parameter that can be viewed alternatively as
a Lagrangian parameter or a value fixing the relative weight between
the goodness-of-fit and the entropy H.
For the deconvolution problem, the object-data relation is given by the
convolution
where P is the point spread function, and the solution is found (in the case
of Gaussian noise) by minimizing
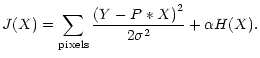 |
|
|
(12) |
The way the entropy is defined is fundamental, because from its definition
will depend the solution. The next section discusses the different approaches
which have been proposed in the past.
Multiscale Entropy, presented in Sect. 3,
is based on the wavelet transform and noise modeling.
It is a means of measuring information in a data set, which takes
into account important properties of the data which are related to
content. We describe how it can be used for signal and image filtering,
and in Sect. 4 for image deconvolution. The case of multi-channel data
is considered in Sect. 5.
We then proceed to the use of multiscale entropy
for description of image content. We pursue three
directions of enquiry, respectively described in Sects. 6, 7 and 8.
In Sects. 6 and 7, we determine whether signal is present in the image
or not, possibly at or below the image's noise level; and how multiscale entropy is very well
correlated with the image's content in the case of astronomical
stellar fields. Knowing that multiscale entropy represents well the
content of the image, we finally use it to define the optimal compression
rate of the image. In all cases, a range of examples illustrate these
new results.


Up: Entropy and astronomical data
Copyright ESO 2001
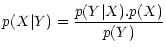
![]() the information
related to the event E, and p the probability of this
event happening, then we consider that
the information
related to the event E, and p the probability of this
event happening, then we consider that