A&A 368, 74-85 (2001)
DOI: 10.1051/0004-6361:20000553
M. Massarotti1,2 - A. Iovino1 - A. Buzzoni1,3
1 - Osservatorio Astronomico di Brera, Via Brera 28, 20121 Milano, Italy
2 -
Università di Napoli, Dipartimento di Scienze Fisiche, Mostra d'Oltremare, 80125 Napoli, Italy
3 -
Telescopio Nazionale Galileo, Roque de los Muchachos Astronomical Obs.,
PO Box 565, 38700 Santa Cruz de La Palma (TF), Spain
Received 20 September 2000 / Accepted 12 December 2000
Abstract
We discuss the stability of the photometric redshift estimate obtained
with the SED fitting method with respect to the choice of the galaxy
templates. Within the observational uncertainty and photometric
errors, we find satisfactory agreement among different sets of
theoretical and empirical templates using the Hubble Deep Field North
as a target galaxy sample. Our results suggest that, especially at
high redshift, the description of the physical processes of photon
absorption in the interstellar and intergalactic medium plays a
dominant role in the redshift estimate. The specific choice of the
template set, as long as this includes both normal and starburst
galaxies, is in comparison a minor issue.
Key words: galaxies: distances and redshifts - galaxies: evolution - intergalactic medium - dust, extinction - methods: data analysis - techniques: photometric
Physical properties of high-redshift galaxies have been extensively
explored in recent years thanks to a number of deep spectroscopic
surveys carried out with the largest ground optical telescopes
(e.g. Lilly et al. 1995; Cowie et al. 1996; Ellis et al. 1996). These
surveys have enabled to trace well galaxy evolution up to
![]() .
.
Beyond this redshift limit, however, ground-based spectroscopy is
forcedly confined to the brightest objects, a few magnitudes above the
limit achieved by deep photometry. For the time being, spectra of
galaxies fainter than ![]() ab mag are still difficult to
obtain, and one must therefore rely on multicolor observations coupled
to photometric redshift techniques to estimate redshifts for the
majority of galaxies in this magnitude range.
ab mag are still difficult to
obtain, and one must therefore rely on multicolor observations coupled
to photometric redshift techniques to estimate redshifts for the
majority of galaxies in this magnitude range.
Photometric redshift techniques have already been applied by many authors to the ultra-deep images in the Hubble Deep Field North (HDFN, Williams et al. 1996), addressing in fine detail the study of the galaxy luminosity function, the star formation rate (SFR), the UV cosmological density, and the clustering properties (Madau et al. 1996; Connolly et al. 1997; Sawicki et al. 1997; Franceschini et al. 1998; Pascarelle et al. 1998; Connolly et al. 1998; Miralles & Pelló 1998; Arnouts et al. 1999).
Two main approaches have been used in the literature to measure photometric redshifts: the so-called training-set method (e.g. Connolly et al. 1997; Wang et al. 1999), and the spectral energy distribution (SED) fitting method (e.g. Sawicki et al. 1997; Giallongo et al. 1998; Benítez 2000).
In the training-set method the relation between colors (sometimes also magnitudes) and redshift is calibrated using a spectroscopic galaxy sample. The accuracy of this method depends on the number and completeness of the reference templates, and obviously increases when acquiring new spectroscopic data. It becomes less reliable at high redshifts because of incompleteness and increasing redshift uncertainty of the most distant reference galaxies (see Benítez 2000; Fernández-Soto et al. 2000 for a full discussion of the method drawbacks).
In the SED fitting method, on the other hand, photometric redshift is
obtained by comparing observed galaxy fluxes,
![]() at
the ith photometric band, with a library of reference fluxes,
at
the ith photometric band, with a library of reference fluxes,
![]() ,
depending z on redshift, and T a suitable set
of parameters, that account for galaxy morphological type, age,
metallicity, dust reddening etc. In this way, for each galaxy one can
perform a
,
depending z on redshift, and T a suitable set
of parameters, that account for galaxy morphological type, age,
metallicity, dust reddening etc. In this way, for each galaxy one can
perform a ![]() confidence test obtaining the values of z and Tthat minimize flux residuals between observations and reference
templates. In addition to the best-z estimate, the method
identifies an "optimum template'', supplying information on galaxy
age and morphology, although special caution must obviously be taken
in using this piece of information, because of possible numerical
degeneracies in the parameter space.
confidence test obtaining the values of z and Tthat minimize flux residuals between observations and reference
templates. In addition to the best-z estimate, the method
identifies an "optimum template'', supplying information on galaxy
age and morphology, although special caution must obviously be taken
in using this piece of information, because of possible numerical
degeneracies in the parameter space.
In this paper we will discuss in some detail the performance of the SED fitting method as a function of the template set chosen to reproduce galaxy colors. The primary aim is to assess the effects of different template properties on the numerical stability and physical consistency of the method. In our opinion, this "sanity check'' must be preliminary to any direct comparison of photometric and spectroscopic redshift determinations, as different template sets can give statistically similar results when applied to the same spectroscopic subsample, but produce a different redshift distribution on the entire photometric catalog (Yee 1998).
The plan of the paper is as follows. We will first recall in Sect. 2 some key steps in the method. The theoretical and empirical template libraries are introduced in Sect. 3, while Sect. 4 presents results obtained by comparing the different galaxy template sets. The role of physical processes in the interstellar and intergalactic medium is discussed in Sect. 5, where we show their relevant impact on redshift estimate. Section 6 finally summarizes our conclusions.
Before proceeding with our discussion, it might be useful to briefly remind how the SED fitting algorithm works.
As a first step one has to convert galaxy observed magnitudes for each
ith photometric band into incoming apparent flux,
![]() .
This is equivalent to reconstruct the
SED of target galaxies at very low spectral resolution by sampling
their luminosity at the effective wavelength of the photometric bands
available.
.
This is equivalent to reconstruct the
SED of target galaxies at very low spectral resolution by sampling
their luminosity at the effective wavelength of the photometric bands
available.
For each object, the sampled flux has then to be compared with the
reference spectral libraries of template galaxies,
![]() ,
computing a
,
computing a ![]() merit function of the
fitting residuals such as
merit function of the
fitting residuals such as
In the equation, N is the number of photometric bands, and
![]() is the observational uncertainty in the ith band. The
scale factor s is chosen in such a way as to minimize
is the observational uncertainty in the ith band. The
scale factor s is chosen in such a way as to minimize ![]() for
each template:
for
each template:
We will search the galaxy redshift in the range
![]() with a step of 0.02.
with a step of 0.02.
As in the current literature, a further constraint has been added to
the fit imposing that the age of the best template cannot be older
than the Hubble time at the selected redshift (in our calculations we
assumed a
![]() ,
q0=0.0 cosmology with
,
q0=0.0 cosmology with
![]() ). It can be verified, however, that redshift estimates
do not depend critically on the details of the cosmological model, and
this constraint could be dropped with no serious impact on the
final output.
). It can be verified, however, that redshift estimates
do not depend critically on the details of the cosmological model, and
this constraint could be dropped with no serious impact on the
final output.
The major advantage of the first choice is that the observed SEDs for a suitable set of local galaxies, spanning the whole range of Hubble morphological types, gives by definition a physically consistent picture of the real galaxies, at least the nearby ones. On the other hand, there is no obvious argument supporting a straightforward extension of the current galaxy properties to high-redshift objects. At earlier cosmological epochs, evolution could play a substantial role in changing both morphological and spectrophotometric properties of distant galaxies (see Buzzoni 1998 for a critical discussion on the subject).
In this respect, synthesis models should be preferred, as they do try to take into account evolution. Of course, some differences exist among current theoretical codes, especially in the SED predictions for the UV range (Charlot et al. 1996), and these differences should be carefully examined when trying to match high-redshift observations to derive z from multicolor photometry. Optical (or even infrared) observations of high-redshift objects sample UV restframe emission.
We should also recall that at high z the restframe
wavelength range explored by a given photometric system becomes narrower.
For example, at ![]() the whole HST WFPC2 photometric
system (i.e.
U300, B450, V606 plus the I814 band) is
just probing the wavelength range shortward of the galaxy 4000 Å Balmer break, while for
the whole HST WFPC2 photometric
system (i.e.
U300, B450, V606 plus the I814 band) is
just probing the wavelength range shortward of the galaxy 4000 Å Balmer break, while for ![]() the spectral window shrinks even
more to a scarce
the spectral window shrinks even
more to a scarce ![]() Å interval around 1800 Å in the
galaxy restframe (cf. Fig. 1). Note in addition that, at least
for early-type galaxies, SED drops to nominal values shortward of the
Balmer discontinuity, so that
Å interval around 1800 Å in the
galaxy restframe (cf. Fig. 1). Note in addition that, at least
for early-type galaxies, SED drops to nominal values shortward of the
Balmer discontinuity, so that ![]() corrections become increasingly
positive with z. As we can see in Fig. 1, the effect can
reach up to two orders of magnitude for elliptical galaxies, and this
can result in a strong bias against their detection at high redshifts.
corrections become increasingly
positive with z. As we can see in Fig. 1, the effect can
reach up to two orders of magnitude for elliptical galaxies, and this
can result in a strong bias against their detection at high redshifts.
Another problem to be addressed when comparing photometric
observations of high-redshift galaxies with reference templates is
the role of intervening interstellar (ISM) and intergalactic medium
(IGM), which strongly modulates the observed galaxy SED. Interstellar
dust attenuates the galaxy luminosity by an amount that greatly
depends on the specific galaxy environment (Gordon et al. 1997; Bruzual
et al. 1988; Kuchinski et al. 1998). The IGM, on the other hand,
drastically absorbs galaxy emission shortward of the Ly-![]() limit (the well known Ly-
limit (the well known Ly-![]() forest effect, e.g. Madau
1995). Unfortunately, present knowledge of these physical processes
does not yet permit any firm and univocal correction of the data,
leaving room for a variety of operational approaches (Sawicki
et al. 1997; Giallongo et al. 1998; Miralles & Pelló 1998).
forest effect, e.g. Madau
1995). Unfortunately, present knowledge of these physical processes
does not yet permit any firm and univocal correction of the data,
leaving room for a variety of operational approaches (Sawicki
et al. 1997; Giallongo et al. 1998; Miralles & Pelló 1998).
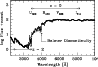 |
Figure 1: Restframe portion of galaxy SED explored by the WFPC2 photometric system at z = 0 and z = 2. As an illustrative example a template model for local elliptical galaxies is shown |
| Open with DEXTER | |
In our study we will include three sets of theoretical galaxy models, namely those provided by the code of Bruzual & Charlot (1993, hereafter BC), Buzzoni (1989, 1995, 2000; BUZ) and Fioc and Rocca-Volmerange (1997; FRV), as well as the empirical template set of Coleman et al. (1980; CWW) extensively used by previous authors (Sawicki et al. 1997; Fernández-Soto et al. 1999, hereafter FSLY; Benítez 2000; Thompson et al. 2000).
For each galaxy we are mainly interested in a measure of its redshift, but an age estimate and a morphological classification parameter are also a result of the SED fitting technique. In order to ensure an homogeneous sampling of the galaxy distinctive parameters, a selected grid of reference models for each of the three synthetic libraries has therefore been considered.
According to the leading physical processes in the galaxy stellar populations we can identify two main evolutionary regimes that induce relevant differences in galaxy luminosity:
i) "Early'' galaxy evolution - In the first Gyr of life, most
of the galaxy luminosity is provided by short-living stars of high
mass (
![]() ,
Buzzoni 2000). These are strong UV emitters
and dominate galaxy luminosity at short wavelength. Given their short
lifetime, these stars track actual star formation activity in the host
galaxy through a measure of its integrated UV flux. Synthesis models
all converge toward a unified starburst scenario for t < 1 Gyr,
despite any later morphological evolution that could then
differentiate among spirals, ellipticals and irregulars (Buzzoni 1998;
Leitherer et al. 1999).
,
Buzzoni 2000). These are strong UV emitters
and dominate galaxy luminosity at short wavelength. Given their short
lifetime, these stars track actual star formation activity in the host
galaxy through a measure of its integrated UV flux. Synthesis models
all converge toward a unified starburst scenario for t < 1 Gyr,
despite any later morphological evolution that could then
differentiate among spirals, ellipticals and irregulars (Buzzoni 1998;
Leitherer et al. 1999).
ii) "Late'' galaxy evolution - It comprises all the objects
older than 1 Gyr, displaying morphological features accounted for by
the standard Hubble classification. Disregarding any specific detail
of star formation and morphology, the stellar bulk in old galaxies is
dominated by stars with
![]() experiencing a full
red-giant-branch (RGB) phase tipping with a degenerate-core Helium
flash (Renzini & Buzzoni 1986).
experiencing a full
red-giant-branch (RGB) phase tipping with a degenerate-core Helium
flash (Renzini & Buzzoni 1986).
For each of our synthesis codes, we first set up an "old-galaxy'' template library, tuning up reference models for present-day galaxies along the whole Hubble sequence, and consistently tracking back-in-time evolution up to t = 1 Gyr. For ages less than 1 Gyr all our synthesis codes have been complemented by the starburst models at t = 50, 100, 500, and 800 Myr from Leitherer et al. (1999), better suitable to describe high-mass stellar evolution.
Note that having used Leitherer et al. (1999) starburst models to describe young galaxies does not influence our results, as all the codes do actually converge, for early ages, to the redshift results provided by the Leitherer et al. (1999) models.
An important issue to optimize computing resources and prevent redundant oversampling in the parameter space is the age step in the grid of template models.
| Template | Age | U-V | B-V | V-K | SFR | IMF(*) | Remarks |
| (z = 0) | |||||||
| Bruzual & Charlot (1993): | |||||||
| E/S0 | 12 Gyr | 1.58 | 1.00 | 3.22 | Sca |
|
|
| Sab | 12 Gyr | 1.09 | 0.81 | 2.95 | Sca |
|
|
| Scd | 12 Gyr | 0.78 | 0.66 | 2.74 | Sca |
|
|
| Im | 1.4 Gyr | 0.13 | 0.28 | 1.89 | const. | Sca |
|
| Buzzoni (2000): | |||||||
| E | 15 Gyr | 1.48 | 0.94 | 3.27 | single burst | Sal | two-zone model, |
|
|
|||||||
|
|
|||||||
| Sb | 15 Gyr | 0.58 | 0.63 | 2.79 |
|
Sal | three-zone model, |
|
|
|||||||
|
|
|||||||
| Sc | 15 Gyr | 0.36 | 0.53 | 2.62 |
|
Sal | three-zone model, |
|
|
|||||||
|
|
|||||||
| Im | 15 Gyr | 0.16 | 0.43 | 2.39 |
|
Sal |
|
| Fioc & Rocca Volmerange (1997): | |||||||
| E | 15 Gyr | 1.40 | 0.91 | 3.19 | Schmidt law | R&B | Schmidt parameters (
|
|
|
|||||||
| Sb | 12 Gyr | 0.92 | 0.73 | 3.14 | Schmidt law | R&B | Schmidt parameters (
|
|
|
|||||||
| Sc | 12 Gyr | 0.59 | 0.58 | 2.94 | Schmidt law | R&B | Schmidt parameters (
|
|
|
|||||||
| Im | 4 Gyr | 0.20 | 0.36 | 2.26 | Schmidt law | R&B | Schmidt parameters (
|
|
|
|||||||
| Coleman et al. (1980): | |||||||
| E | - | 1.49 | 0.93 | - | - | - | M 31 model |
| Sbc | - | 0.59 | 0.58 | - | - | - | - |
| Scd | - | 0.37 | 0.49 | - | - | - | - |
| Im | - | -0.06 | 0.32 | - | - | - | - |
Leitherer et al. (1999): |
|||||||
| Starburst #1 | 800 Myr | -0.27 | 0.13 | 1.62 | const. | Sal |
|
| Starburst #2 | 500 Myr | -0.37 | 0.09 | 1.62 | const. | Sal |
|
| Starburst #3 | 100 Myr | -0.66 | 0.02 | 1.70 | const. | Sal |
|
| Starburst #4 | 50 Myr | -0.76 | 0.00 | 1.72 | const. | Sal |
|
| (*) Sal = Salpeter (1955), Sca = Scalo (1986), R&B = Rana & Basu (1992). |
Based on the theory of simple stellar populations (cf. e.g. Buzzoni
1989) we know that luminosity evolution proceeds in this case like
![]() ,
with
,
with ![]() varying in the range between unity
at UV wavelength and 0.7 in the infrared (K band). Even accounting
for a smoother evolution, e.g. for a continuous SFR, a
varying in the range between unity
at UV wavelength and 0.7 in the infrared (K band). Even accounting
for a smoother evolution, e.g. for a continuous SFR, a
![]() age sampling is sufficient to confidently appreciate any
0.1 mag change in apparent colors for high-z spirals and
ellipticals.
age sampling is sufficient to confidently appreciate any
0.1 mag change in apparent colors for high-z spirals and
ellipticals.
The adopted BC templates consist of models with four different SFR histories to match today's E/S0, Sa/Sb, Sc/Sd, and Im Hubble types. From the BUZ and FRV codes, we selected the original templates for E, Sb, Sc, Im morphological types. The BC models assume a Scalo IMF, while the FRV models assume a Rana & Basu (1992) mass distribution, and the BUZ models adopt a standard Salpeter IMF. For all the models we sampled the different Hubble types at t = 1.0, 1.4, 2.0, 4.0, 8.0, 10.0, 12.0 and 15.0 Gyr.
Table 1 gives a complete summary of the relevant distinctive properties of each theoretical library, reporting also the expected colors for present-day galaxies of different Hubble type.
The original CWW empirical template set consisted of four observed
galaxy spectra, E, Sbc, Scd and Im respectively. Sawicki
et al. (1997) and Benítez (2000) had already noticed that adding
starburst templates (sensibly bluer than any Im SED) to CWW greatly
alleviates the systematic discrepancies found in redshift distribution
of target galaxies beyond z>1.5. Similarly, the lack of starburst
templates could have biased FSLY results by inducing an artificial
peak in the galaxy distribution around
![]() .
In this work,
following the strategy adopted by Sawicki et al. (1997), we extended the
CWW empirical library by adding two starburst models from Leitherer
et al. (1999) at t = 50 and 500 Myr. This enlarged dataset will
hereafter be referred to as the CWW-extended (CWWE) set.
.
In this work,
following the strategy adopted by Sawicki et al. (1997), we extended the
CWW empirical library by adding two starburst models from Leitherer
et al. (1999) at t = 50 and 500 Myr. This enlarged dataset will
hereafter be referred to as the CWW-extended (CWWE) set.
Fluxes provided by synthetic SED models have to be corrected for ISM and IGM absorption effects. Both are wavelength dependent, the latter is also redshift dependent, and they can dramatically change the galaxy spectrum in the UV restframe.
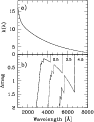 |
Figure 2: Panel a) the adopted dust attenuation law after Calzetti (1999). Panel b) the IGM attenuation in a magnitude scale at redshift 2.5, 3.5 and 4.5, as labelled, according to Madau (1995) |
| Open with DEXTER | |
Interstellar dust attenuation depends on the color excess parameter
E(B-V), scaling with dust column density, as well as on the
differential ISM opacity
![]() ,
which is related to the
physical properties of dust grains. The classical
relationship for intrinsic and emerging flux is:
,
which is related to the
physical properties of dust grains. The classical
relationship for intrinsic and emerging flux is:
We describe the IGM absorption as a function of redshift following Madau (1995) (Fig. 2, panel b).
To give an illustrative example of the combined action of dust and IGM, in Fig. 3 the BUZ Sb template has been reddened by different amounts of the color excess E(B-V) up to 0.3 magnitudes (upper panel). The effect of the IGM on the same spectrum is displayed on the contrary in the lower panel for the two cases of redshift z = 1.5 and z = 3.
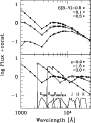 |
Figure 3:
The effect of internal reddening and IGM on the Sb reference
template from Buzzoni (2000). Dust attenuation for E(B-V) up to 0.3
mag, as labelled, is shown in the upper panel, while the expected
break induced by the Ly- |
| Open with DEXTER | |
The galaxy spectral break induced by the cosmological Ly-![]() forest turns out to be the most effective feature to estimate
redshifts beyond
forest turns out to be the most effective feature to estimate
redshifts beyond ![]() .
The so-called "dropout'' technique has
been widely used to select high-redshift objects in current deep
surveys (Steidel et al. 1995; Madau et al. 1996). Notice though that for
faint objects the strong signature due to the IGM external
feature can be confused with the 4000 Å Balmer break (which, on the
contrary is intrinsic to galaxy SED) resulting in a biased
redshift estimate.
.
The so-called "dropout'' technique has
been widely used to select high-redshift objects in current deep
surveys (Steidel et al. 1995; Madau et al. 1996). Notice though that for
faint objects the strong signature due to the IGM external
feature can be confused with the 4000 Å Balmer break (which, on the
contrary is intrinsic to galaxy SED) resulting in a biased
redshift estimate.
The HDFN photometric catalog produced by FSLY will be used as a target
dataset for our analysis. It has been widely adopted in the recent
literature (see, for instance, Arnouts et al. 1999; FSLY; Benítez
2000) and consists of 1067 objects observed with HST WFPC2 in the four
photometric bands U300, B450, V606, and I814, and
with the IRIM camera at KPNO in the infrared range (Johnson J, H,
and K, Dickinson et al. 2000). The FSLY catalog contains
fluxes,
![]() ,
and errors,
,
and errors, ![]() ,
for each galaxy in
all photometric bands (
,
for each galaxy in
all photometric bands (
![]() ). These quantities are those
used in Eqs. (1)-(2).
). These quantities are those
used in Eqs. (1)-(2).
The availability of IR observations is of special relevance for our
analysis because, even for galaxies at ![]() ,
it allows us to
sample restframe emission at optical wavelengths, longward of the
Balmer break. This greatly improves our chances to correctly
interpret galaxy colors and obtain a fair redshift estimate for the
most distant objects. As we can see in Fig. 1, within the
photometric errors, both elliptical and blue star-forming galaxies at
,
it allows us to
sample restframe emission at optical wavelengths, longward of the
Balmer break. This greatly improves our chances to correctly
interpret galaxy colors and obtain a fair redshift estimate for the
most distant objects. As we can see in Fig. 1, within the
photometric errors, both elliptical and blue star-forming galaxies at
![]() show basically the same SED within the wavelength range
covered by the HST photometric system. Only IR data can allow us to
break color degeneracy.
show basically the same SED within the wavelength range
covered by the HST photometric system. Only IR data can allow us to
break color degeneracy.
For our analysis we selected from the original FSLY dataset only those
objects with good photometry, that is with S/N>5 in at least two
bands, in order to rely confidently on at least one color. Out of a
total of 1067 galaxies, we were left with 1041 objects in our
subsample. As a result of our selection we will be biased against the
most distant objects beyond z > 5. For these galaxies the
Ly-![]() break enters the V606 band, making them detectable
only in the I814 band (IR observations are not deep enough, in
any case, to grant a good S/N detection for these distant objects).
break enters the V606 band, making them detectable
only in the I814 band (IR observations are not deep enough, in
any case, to grant a good S/N detection for these distant objects).
The 4000 Å Balmer break being one of the most useful spectral feature for photometric redshift determination, we will single out a "low-redshift'' subsample, including those galaxies for which the break is still within the HST photometric bands (this happens for z < 1.5), and a "high-redshift'' subsample (z > 1.5) for which the 4000 Å break enters the IR photometric bands.
It is of special relevance for our aim to preliminarily assess the effect of the observational uncertainties on the accuracy of redshift determination with the SED fitting method.
We used a simple bootstrap procedure to generate ten copies of the FSLY catalog, obtained by adding to each galaxy flux a correction randomly extracted from the Gaussian distribution of its photometric error.
For each of the reference template libraries we then compared, for
each object, the redshift obtained from the measured photometry
![]() and that from the bootstrapped galaxy photometry
and that from the bootstrapped galaxy photometry
![]() .
.
|
|
|
|
|
|
|
| z < 1.5 | z > 1.5 | ||||
| BUZ | -0.01 | 0.16 | 0.24 | 11% | 7% |
| BC | -0.01 | 0.16 | 0.23 | 12% | 8% |
| FRV | -0.01 | 0.17 | 0.21 | 11% | 7% |
| CWWE | 0.00 | 0.15 | 0.26 | 12% | 8% |
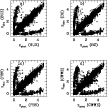 |
Figure 4: Comparison of the statistical uncertainty in the redshift estimate due to photometric errors for the BC, BUZ and FRV reference libraries, as well as for the CWWE empirical templates. Residuals are from a bootstrap simulation of the FSLY galaxy catalog (1041 objects for each of ten simulated catalog samples) |
| Open with DEXTER | |
We will eventually have:
and
where
![]() is the number of simulated
galaxies.
is the number of simulated
galaxies.
Moreover, we will check for the fraction of "discrepant''
(
![]() )
and "catastrophic''
(
)
and "catastrophic''
(
![]() )
outliers in the low- and
high-redshift galaxy subsamples.
)
outliers in the low- and
high-redshift galaxy subsamples.
Table 2 gives a summary of the bootstrap results obtained for each theoretical synthesis code as well as for the CWWE empirical templates. Figure 4 shows in addition the distribution of the redshift residuals.
Since photometric errors increase at fainter magnitudes, redshift
uncertainty is more pronounced for the most distant objects:
![]() at z<1.5, while
at z<1.5, while
![]() for the z>1.5subsample. The catastrophic outliers are always less than 10% of the
global sample, and there are no systematic effects, as expected.
for the z>1.5subsample. The catastrophic outliers are always less than 10% of the
global sample, and there are no systematic effects, as expected.
In addition to the photometric errors, also physical degeneracies in the z vs. color space domain of the models could themselves result in a source of numerical instability for the redshift estimates. In this regard, different model sets could in principle provide also different "bias patterns'' in the redshift distribution.
Quite interestingly, Table 2 shows that this is not the case for the four template sets accounted here. This might indicate that all reference libraries contain the same kind of degeneracy. In other words the galaxy colors are interpreted in the same way (from a statistical point of view) by the different template sets.
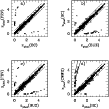 |
Figure 5:
Comparison of HDFN expected redshift distribution, for
different reference libraries. The solid line is for
|
| Open with DEXTER | |
In Fig. 4 the distribution of redshift residuals for
catastrofic outliers (
![]() )
has a well defined pattern,
and it is actually possible to identify two main sources for this
pattern. The first is the color degeneracy between redshift
)
has a well defined pattern,
and it is actually possible to identify two main sources for this
pattern. The first is the color degeneracy between redshift ![]() and
1.3 < z < 2.1, that, given the photometric bands available in
FSLY, shows up in all the templates. In the redshift interval
1.3 <
z < 2.1, the entire Lyman series has not yet entered the U300band (cf. Fig. 2), while the Balmer break is located between
the I814 and J bands. The uncertainty in the photometric
observations can easily cause a featureless objects to move within the
ranges
and
1.3 < z < 2.1, that, given the photometric bands available in
FSLY, shows up in all the templates. In the redshift interval
1.3 <
z < 2.1, the entire Lyman series has not yet entered the U300band (cf. Fig. 2), while the Balmer break is located between
the I814 and J bands. The uncertainty in the photometric
observations can easily cause a featureless objects to move within the
ranges ![]() and
1.3 < z < 2.1. The second major source of
the pattern visible in Fig. 4 are the biased z estimates
occuring when, due to large photometric errors, the Balmer break is
mistaken for the Lyman decrement or vice versa. When the photometric
errors in the IR bands are large enough to diluite/enhance a
real/fictitious Balmer decrement, the objects affected are shuffled
between the redshift ranges 0 < z < 1 and z > 2.5.
and
1.3 < z < 2.1. The second major source of
the pattern visible in Fig. 4 are the biased z estimates
occuring when, due to large photometric errors, the Balmer break is
mistaken for the Lyman decrement or vice versa. When the photometric
errors in the IR bands are large enough to diluite/enhance a
real/fictitious Balmer decrement, the objects affected are shuffled
between the redshift ranges 0 < z < 1 and z > 2.5.
We can now compare photometric redshifts obtained using different reference template libraries.
Given two independent redshift estimates, namely
![]() and
and
![]() from different libraries, we can again define
a simple statistical moment of the residual distribution in the form:
from different libraries, we can again define
a simple statistical moment of the residual distribution in the form:
while a variance can be computed as
where
![]() is the number of galaxies.
is the number of galaxies.
Also in this case, we should check for the fraction of discrepant
(
![]() )
and catastrophic
(
)
and catastrophic
(
![]() )
outliers in the low-
and high-redshift galaxy subsamples.
)
outliers in the low-
and high-redshift galaxy subsamples.
In addition, we should also test whether
![]() is
consistent with zero or there is some systematic drift in data
residuals. Mean standard deviation should be explored against
possible trends as a function of galaxy redshifts.
is
consistent with zero or there is some systematic drift in data
residuals. Mean standard deviation should be explored against
possible trends as a function of galaxy redshifts.
Figure 5 and Table 3 summarize the relevant
results. The agreement between BC, BUZ and FRV (panels a-c in
Fig. 5) seems quite good, with less than 5% of catastrophic
outliers, and ![]() below 0.15 over the entire redshift range.
below 0.15 over the entire redshift range.
|
|
|
|
|
|
|
| z < 1.5 | z > 1.5 | ||||
| BC vs. FRV | 0.02 | 0.09 | 0.12 | 3% | 3% |
| BC vs. CWWE | 0.03 | 0.12 | 0.17 | 6% | 5% |
| BUZ vs. BC | 0.00 | 0.12 | 0.13 | 4% | 3% |
| BUZ vs. FRV | 0.02 | 0.13 | 0.15 | 5% | 4% |
| BUZ vs. CWWE | 0.02 | 0.15 | 0.19 | 6% | 4% |
| FRV vs. CWWE | 0.01 | 0.12 | 0.18 | 6% | 5% |
The comparison with the CWWE template set gives slightly poorer values
for ![]() (cf. panel d in Fig. 5), especially for
the most distant galaxies in the FSLY sample, but again a small
fraction of discrepant redshift objects.
(cf. panel d in Fig. 5), especially for
the most distant galaxies in the FSLY sample, but again a small
fraction of discrepant redshift objects.
As we can appreciate in Table 3, there are only marginal
systematic drifts in the
![]() residuals.
residuals.
It should be noted that in the synthetic libraries the "primeval'' evolutionary scenario is described with the same templates (the four starburst models from Leitherer et al. 1999). On the other hand, even by replacing, for example, the "primeval'' BC library with the young galaxies provided by the BC code itself, results of the comparison with other models are left almost unchanged.
Comparing the results of Table 3 with those of Table 2,
it is clear that the whole SED fitting procedure is
largely insensitive to any specific choice of the model reference
library. Rather than depending on the detailed galaxy SED, the
redshift is mainly constrained by the recognition of the Balmer and/or
the Ly-![]() break in the galaxy flux distribution.
break in the galaxy flux distribution.
As a quite extreme but instructive example, in Fig. 6 we
tried a fit of the galaxy subsample with fiducial redshift z > 2(259 objects, as estimated in every one of our reference
libraries) using as a template set two Kurucz' (1992) model
atmospheres for stars of
![]() and
and
![]() .
These temperatures are roughly consistent with a B0-B2 spectral
type like for stars of 10-20
.
These temperatures are roughly consistent with a B0-B2 spectral
type like for stars of 10-20 ![]() that dominate starburst galaxy
luminosity in the early 10-100 Myr of life (Leitherer et al. 1999). The
redshift distribution relying on this "minimal'' template set well
agrees with that obtained using, for example, the FRV model library
(
that dominate starburst galaxy
luminosity in the early 10-100 Myr of life (Leitherer et al. 1999). The
redshift distribution relying on this "minimal'' template set well
agrees with that obtained using, for example, the FRV model library
(
![]() and no catastrophic outliers). At high redshifts,
therefore, the SED fitting method provides robust estimates of galaxy
redshifts, even when using an extremely poor library of templates. It
is clear, however, that such a simplified procedure cannot be of any
utility if we are interested in a more accurate analysis of
high-redshift data, such as to investigate age distribution or galaxy
morphology at different cosmological times.
and no catastrophic outliers). At high redshifts,
therefore, the SED fitting method provides robust estimates of galaxy
redshifts, even when using an extremely poor library of templates. It
is clear, however, that such a simplified procedure cannot be of any
utility if we are interested in a more accurate analysis of
high-redshift data, such as to investigate age distribution or galaxy
morphology at different cosmological times.
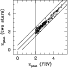 |
Figure 6:
SED fitting of the FSLY galaxy subsample beyond z>2. The
data distribution by matching the FRV template set is compared with a
"minimal'' reference library consisting of two Kurucz' (1992) model
atmospheres for stars of spectral type B0 and B2. The relative
|
| Open with DEXTER | |
Another interesting check of internal consistency of the SED fitting method deals with the age-redshift constraint. We discarded such constraint, by allowing the procedure to choose also galaxy models older than the Hubble time. Plotting the galaxy age information and the redshift information, both obtained from the photometric redshift algorithm, will allow to check for their reciprocal consistency.
For this exercise we grouped HDFN galaxies such as to guarantee at least 100 objects per redshift bin. Figure 7 reports our results according to the BC, BUZ and FRV codes.
Over the whole sample, the percentages of the fitting templates older than the actual Hubble time ( [H0, q0] = [50, 0.0]) with BC, BUZ and FRV codes are 3.9%, 8.5% and 5.7% respectively. For each theoretical code the empirical redshift-age relation is virtually compatible with any cosmological model with H0 = 50 and q0 < 0.5.
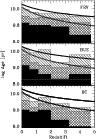 |
Figure 7: The expected age-redshift relation from the BC, BUZ and FRV best templates by imposing no cosmological constraint. HDFN galaxies have been grouped in order to guarantee at least 100 objects per redshift bin. Solid, grid, and diagonal-shaded histograms are the 50%, 75%, and 90% envelopes of galaxy age distribution. In each plot, solid and dotted lines are the theoretical age-z relation for H0 = 50 and q0 = 0.0 and 0.5, respectively |
| Open with DEXTER | |
Although wide general agreement exists among template libraries in
predicting galaxy redshift, it is worth investigating in some detail
the few striking cases of catastrophic discrepancies (i.e.
![]() ).
).
There are basically two groups of such outliers, as in the
distribution of redshift residuals due to photometric errors. The
first group consists of objects with featureless spectrum, that is
with no significant break signature (within the photometric
errors). This is typically the case of the faintest blue objects in
the HDFN sample. Due to color degeneracy between redshift ![]() and
1.3 < z < 2.1, these galaxies are shuffled within the two
intervals by different libraries. The redshift interval
1.3 < z <
2.1 is intrinsically critical for the SED fitting algorithm given the
photometric bands available to us. As already noted above, while the
entire Lyman series has not yet entered the U300 band
(cf. Fig. 2), the Balmer break is located between the
I814 and J bands. Therefore, redshift estimate entirely relies
on the recognition of the smooth SED, and little changes in the
reference templates can easily lead to diverging data interpretations.
and
1.3 < z < 2.1, these galaxies are shuffled within the two
intervals by different libraries. The redshift interval
1.3 < z <
2.1 is intrinsically critical for the SED fitting algorithm given the
photometric bands available to us. As already noted above, while the
entire Lyman series has not yet entered the U300 band
(cf. Fig. 2), the Balmer break is located between the
I814 and J bands. Therefore, redshift estimate entirely relies
on the recognition of the smooth SED, and little changes in the
reference templates can easily lead to diverging data interpretations.
The second class of catastrophic outliers comprises those objects for which the Balmer break is mistaken for the Lyman decrement or vice versa, according to the template library chosen, generating a series of biased z estimates beyond z > 2.5. This effect is especially evident when comparing CWWE vs. BC (cf. panel d in Fig. 5). A too scanty sampling of galaxy morphology, like in the CWWE templates, is the cause of the relative exacerbation of the effect. For example galaxies with no deep Balmer break and relatively blue optical colors can be interpreted as Lyman break galaxies, in absence of alternative intermediate age elliptical templates.
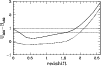 |
Figure 8:
The
U300-B450 apparent color as a function of
redshift for the CWW Im empirical template (solid line) and
Leitherer et al. (1999) 50 Myr starburst model (dashed line). In
absence of any starburst template, a fraction of star-forming
galaxies at |
| Open with DEXTER | |
More in general, a major source of catastrophic errors in the SED
fitting procedure can result from the lack of starburst templates in
the galaxy reference library. Standard Hubble types alone (even
including Im irregulars) are not "blue'' enough to reproduce the
colors of the most active star-forming objects seen at high
redshift. In Fig. 8 we show the
U300 - B450 apparent
color of the CWWE Im template (solid line) and that of the Leitherer
et al. (1999) 50 Myr starburst model (dotted line) as a function of
redshift. Lacking starburst templates can introduce a systematic shift
in the redshift estimate (
![]() )
for those galaxies with
)
for those galaxies with
![]() .
Even worst, in some cases one might
erroneously confuse UV-enhanced galaxies at
.
Even worst, in some cases one might
erroneously confuse UV-enhanced galaxies at ![]() with local
irregulars sampled in their optical SED. When comparing FSLY
photometric redshifts with spectroscopic redshifts both this effects
are evident.
with local
irregulars sampled in their optical SED. When comparing FSLY
photometric redshifts with spectroscopic redshifts both this effects
are evident.
Dust reddening and IGM absorption have a large impact on the detection of starburst-galaxies at high redshifts, as these effects can effectively masque the original starburst spectrum.
In a simple experiment using the CWWE library and imposing
E(B-V) =
0 in our fit, about 20% of galaxies in the FSLY catalog can suitably
be matched by (reddening-free) starburst templates. When dust
attenuation is accounted for, and E(B-V) is left to vary as a free
fitting parameter, this fraction raises to about ![]() of the whole
galaxy sample. A confident evaluation of the fraction of UV-enhanced
galaxies at the different distances would have a pervasive impact in a
number of cosmological problems, like for instance the study of the
cosmic SFR (Madau et al. 1996; Steidel et al. 1999; Thompson et al. 2000).
of the whole
galaxy sample. A confident evaluation of the fraction of UV-enhanced
galaxies at the different distances would have a pervasive impact in a
number of cosmological problems, like for instance the study of the
cosmic SFR (Madau et al. 1996; Steidel et al. 1999; Thompson et al. 2000).
To explore the selective influence of interstellar dust on the SED fitting procedure, we considered the FSLY subsample with fiducial z > 1.5 (as estimated in every one of our reference libraries) and compared it with the CWWE empirical library (see Fig. 9).
Out of 348 selected galaxies, 341 can be fitted by starburst templates, Scd spirals or later morphological types.
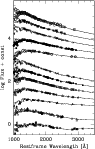 |
Figure 9: Restframe composite SED from the HST data for the 341 HDFN galaxies with fiducial z>1.5 compared with the CWWE reference templates. From top to bottom solid lines display the starburst template with t=500 Myr and E(B-V)=0.0,0.05,0.1,0.2,0.3, the t = 50 Myr starburst model with E(B-V)=0.0,0.05,0.1,0.2,0.3, the Scdand the Im CWW spectra |
| Open with DEXTER | |
In a dust-free fitting scheme (i.e. by assuming
E(B-V) = 0) we
derive the following relative partition among fiducial morphological
types:
[others:Scd:Im:Starbursts] = [7:34:160:147]
with about ![]() objects poorly fitted, that is at least 3-
objects poorly fitted, that is at least 3-![]() off in each band according to Eq. (1). Incidentally, if
we exclude from the template library the starburst models we obtain:
off in each band according to Eq. (1). Incidentally, if
we exclude from the template library the starburst models we obtain:
[others:Scd:Im] = [7:43:298]
but at the cost of almost doubling the fraction of poorly fitted
objects (![]() 24% of the total sample).
24% of the total sample).
If we leave E(B-V) as a free fitting parameter (in the range
![]() ), the quality of the fit improves remarkably
(only 5% of objects deviates by 3-
), the quality of the fit improves remarkably
(only 5% of objects deviates by 3-![]() or more), and an even
larger number of starburst candidates is obtained:
or more), and an even
larger number of starburst candidates is obtained:
[others:Scd:Im:Starbursts] = [7:25:41:275].
A dust-free fitting scheme also drastically increases the number of
catastrophic outliers (![]() 10% on the entire catalog,
cf. Fig. 10), and at z>1.5 the redshift of reddened
galaxies is overestimated by
10% on the entire catalog,
cf. Fig. 10), and at z>1.5 the redshift of reddened
galaxies is overestimated by
![]() since IGM
absorption, which is an increasing function of redshift, is forced to
mimic color reddening.
since IGM
absorption, which is an increasing function of redshift, is forced to
mimic color reddening.
In Fig. 9 the scatter of the HST data (blueshifted according
the
![]() value and normalized according the scaling
factor s of Eq. (2)) around the CWWE templates is shown
directly. As we can see, at
value and normalized according the scaling
factor s of Eq. (2)) around the CWWE templates is shown
directly. As we can see, at
![]() Å the best templates
are an accurate description of high-redshift galaxy
photometry. Notice however that at
Å the best templates
are an accurate description of high-redshift galaxy
photometry. Notice however that at
![]() Å the observed
fluxes deviate from the best templates: the experimental data do
contain the IGM absorption, while the best templates do not.
Å the observed
fluxes deviate from the best templates: the experimental data do
contain the IGM absorption, while the best templates do not.
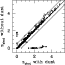 |
Figure 10:
The selective influence of galaxy internal reddening on the
SED fitting performance. The HDFN redshift distribution from the BC
template set is displayed with and without taking into account for ISM
absorption. This is done by leaving
E(B-V) = 0 or as a free fitting
parameter in the range
|
| Open with DEXTER | |
The effect of IGM at high redshifts is explored in
Fig. 11. Redshifts in the FSLY catalogue are determined
using the BUZ reference library with and without IGM taken into
account. A drift clearly appears beyond z > 1.5 when the
Ly-![]() break enters the U300 band. The shift is generated
by the wavelength difference between the 912 Å Lyman break in the
galaxy spectrum and the various steps of the Ly-
break enters the U300 band. The shift is generated
by the wavelength difference between the 912 Å Lyman break in the
galaxy spectrum and the various steps of the Ly-![]() forest. The
fraction of outliers amounts to about
forest. The
fraction of outliers amounts to about ![]() on the entire catalog
and to
on the entire catalog
and to ![]() 21% of the z>1.5 subsample.
21% of the z>1.5 subsample.
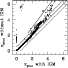 |
Figure 11:
Comparison of the HDFN redshift distribution obtained from
the BUZ reference library with and without taking into account the IGM
absorption. Long-dashed lines in the plot represent
|
| Open with DEXTER | |
We investigated the stability of photometric redshift estimates in the SED fitting method with respect to the galaxy template set chosen. We used as a target dataset the FSLY catalog in the HDFN and as libraries of galaxy colors those produced by the theoretical codes of Bruzual & Charlot (1993), Buzzoni (2000) and Fioc & Rocca-Volmerange (1997), as well as the empirical template set of Coleman et al. (1980). This way our model reference framework comprises (and enlarges) the sample of template libraries used by almost all the literature on the field.
The existence of non negligible photometric errors in the data is by
itself an important source of uncertainty in the redshift
estimates. Comparing the FSLY results with a number of bootstrap
simulation of the same galaxy sample we estimate that the internal
uncertainty in the SED fitting performance amounts to
![]() at z<1.5 and
at z<1.5 and
![]() at z>1.5, with
at z>1.5, with ![]() 8%
of catastrophic outliers. This result is almost independent from the
adopted model library and can be read as a lower limit to the
intrinsic accuracy of the fitting method given the photometric errors
of the FSLY catalogue.
8%
of catastrophic outliers. This result is almost independent from the
adopted model library and can be read as a lower limit to the
intrinsic accuracy of the fitting method given the photometric errors
of the FSLY catalogue.
The external redshift uncertainty, found by comparing results obtained
using different theoretical models, is typically
![]() at z<1.5 and
at z<1.5 and
![]() at z>1.5, with less than
at z>1.5, with less than ![]() of catastrophic outliers. Comparing theoretical models and the CWWE
empirical set we obtained
of catastrophic outliers. Comparing theoretical models and the CWWE
empirical set we obtained
![]() at z<1.5 and
at z<1.5 and
![]() at z>1.5, with less than
at z>1.5, with less than ![]() of catastrophic
outliers. Our results show that, given the photometric errors in the
data, the SED fitting procedure is to a large extent almost
insensitive to any specific choice of the model reference library.
of catastrophic
outliers. Our results show that, given the photometric errors in the
data, the SED fitting procedure is to a large extent almost
insensitive to any specific choice of the model reference library.
The lack of starburst templates in the model library, on the other
hand, introduces a systematic bias in the redshift estimate (
![]() )
and a sensible increase of catastrophic outliers as
UV-enhanced galaxies at
)
and a sensible increase of catastrophic outliers as
UV-enhanced galaxies at ![]() can be confused with local
irregulars sampled in their optical SED.
can be confused with local
irregulars sampled in their optical SED.
Not including in the fitting procedure ISM dust reddening or IGM opacity has a dramatic impact on the distribution of redshifts measured.
A dust-free fitting scheme drastically increases the number of
catastrophic outliers (![]() 10% on the entire catalog) and at
z>1.5 the redshift of dust reddened galaxies is overestimated by
10% on the entire catalog) and at
z>1.5 the redshift of dust reddened galaxies is overestimated by
![]() .
When dust attenuation is accounted
for, the fraction of galaxies matched by starburst templates raises
from
.
When dust attenuation is accounted
for, the fraction of galaxies matched by starburst templates raises
from ![]() 20% (by imposing
E(B-V) = 0) to
20% (by imposing
E(B-V) = 0) to ![]() 55% of the
whole HDFN sample.
55% of the
whole HDFN sample.
In an IGM-transparent fitting scheme a drift in the redshift
estimates clearly appears beyond z > 1.5 and the fraction of
outliers amounts to ![]() 21% of the high-redshift subsample.
21% of the high-redshift subsample.
Our results suggest that, especially at high redshifts, the description of physical processes of photon absorption in the interstellar and in the intergalactic medium plays a key role in the SED fitting method for interpreting photometric data. Any specific choice of the templates, as long as these describe both normal and starburst galaxies, has on the contrary a minor effect on the performance of the method.
Acknowledgements
It is a pleasure to thank S. Charlot for useful suggestions, and the referee, R. I. Thompson, for his comments. M. Massarotti acknowledges financial support by Osservatorio Astronomico di Brera and Fondazione Cariplo.