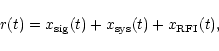 |
(1) |
A&A 368, 369-376 (2001)
DOI: 10.1051/0004-6361:20000552
P. A. Fridman
ASTRON, Postbus 2, 7990AA Dwingeloo, The Netherlands
Received 7 September 2000 / Accepted 8 December 2000
Abstract
A method of radio frequency interference (RFI) suppression in radio astronomy spectral observations based on the analysis of the probability distribution of an instantaneous spectrum is described. This method allows the separation of the Gaussian component due to the natural radio source and the non-Gaussian RFI signal. Examples are presented in the form of computer simulations of this method of RFI suppression and of WSRT observations with this method applied. The application of real time digital signal processing for RFI suppression is found to be effective for radio astronomy telescopes operating in a worsening spectral environment.
Key words: power spectrum - probability distribution - RFI excision
The increasing radio frequency interference (RFI) from transmissions and spurious signals of commercial telecommunication applications limit the real sensitivity of radio telescopes at certain frequencies. This radio-ecological environment at radio observatories appears to be worsening each year, while the observing systems get more sensitive. Further improvements in antenna quality and in receiver parameters do not give the expected results because of limitations due to RFI. Therefore it is very difficult to reach the design sensitivity, especially at low frequencies, even for radio telescopes situated in secluded areas (Spoelstra 1997; Kahlmann 1999; Cohen 1999).
Several methods of RFI excision have been proposed during recent years. The successful application of these methods depends on the type of radio telescope, type of observations, type of RFI, and there is no universal RFI mitigation algorithm.
1. Type of radio telescope - single dish, connected radio interferometer, VLBI. Single dish radio telescopes are especially vulnerable to RFI. Radio interferometric systems suffer from RFI to a lesser degree, (Thompson 1982), but auxiliary noise power measurements made at each antenna for calibration purposes are distorted by RFI;
2. Mode of observations - continuum or spectral. In continuum observations it is possible to sacrifice some part (5-10%) of the data stream polluted by a strong RFI and save the remained part without significant loss of sensitivity. In spectral observations RFI and signal-of-interest may occupy the same spectral region, so it is impossible to delete this particular part of the spectrum;
3. Type of RFI - impulse-like bursts, narrow-band or wide-band. Theoretical consideration and experimental data show that RFI may be basically represented as the superposition of two types of waveforms: impulse-like bursts and long narrowband and strongly correlated random oscillations (Middleton 1972,1977; Lemmon 1997). RFI of the first type can be effectively suppressed using fast real time thresholding before averaging at the total power detector or correlator (Fridman 1996; Weber et al. 1997). This is the processing in temporal domain.
RFI of the second type should be processed in the frequency domain, where there is a good contrast between a quasi-continuum spectrum of the system noise plus radio source signal and the narrow-band RFI signal. RFI in continuum observations may be excised using adaptive filtering methods (Fridman 1998), such that the parts of the spectrum affected by RFI are used with a smaller weighting than the other "unpolluted'' spectral regions during the averaging in the time-frequency plane. This sort of processing cannot be applied in spectral line observations, where RFI may contaminate the same spectral region that is of interest for the radio astronomer. In the case of the GLONASS navigational satellites (Ellington et al. 2000) the RFI was parametrically modelled and the model of RFI signal was subtracted from the radio telescope output so that the 1612 MHz OH spectral line was not distorted.
Adaptive interference cancellation (similar to adaptive noise cancellation, Widrow & Stearns 1985) can be useful for single dish observations with an auxuliary reference antenna, pointed "off-source''. The use of an auxiliary reference channel provides some benefits (Barnbaum & Bradley 1998), but not all radio telescopes are equipped or can be equipped with such a reference channel. Furthermore, the effectiveness of this adaptive noise cancelling strongly depends on the sensitivity of the reference channel. The reference channel should at least be as sensitive as the main channel for successful RFI suppression (Fridman 1997,2000).
A new method of post-correlation RFI removing was proposed (Briggs et al. 2000). Cross-correlation products of four signals (two main channels and two reference channels) are processed, using closure complex amplitude relations. RFI signal is estimated and subtracted from the outputs of main channels. So RFI suppression can be made off-line with the averaged data, see also references in (The Elizabeth and Frederick White Conference on Radio Frequency Interference Mitigation Strategies 1999).
Methods of spatial filtering in the temporal and frequency domains applicable for radio interferometers are discussed elsewhere (Leshem & van der Veen 1999). Spatial filtering methods use the difference in the direction-of-arrival of radio source and RFI. The RFI emission of well spatially localized sources could be suppressed in multielement radio interferometers using adaptive array philosophy, when zeros of a synthesized antenna pattern coincide with directions-of-arrival of undesirable signals (adaptive nulling techniques). This approach is popular while considering new projects of superlarge phased array radiotelescopes, (van Ardenne 1996; Bregman 2000). However, there are some limitations in using this techniques for the existing large radio interferometers like the WSRT, VLA, and GMRT: very sparse antenna arrays, phase-only computer control, complex impact on image postprocessing. Spatial filtering is effective when RFIs are strongly correlated at radio telescope antennas (like in a half-wavelength phased array). RFI at the adjacent antennas (hundreds meters separation) are highly correlated, but when the distance between antennas is more than 1 km (and especially for baselines 10-100 km) RFI at these points are less correlated, and effectiveness of the adaptive nulling is less, than for the continuous-like half-wavelength phased arrays. RFI at the sites of VLBI system, separated by hundreds and thousands of kilometers, are practically uncorrelated. So the impact of an RFI is an increased variance at correlator output, which is noticeable in the case of strong RFI (comparable with the system noise power).
In this paper, I consider a method of RFI excision based on the analysis of the probability distribution of the power spectrum at the radio telescope output. System and radio source noise generally has a Gaussian distribution with a zero mean. If a Fourier transformation is applied to such an "ideal'' signal, the real and imaginary components in every spectral bin are also Gaussian random values with zero mean. The instantaneous power spectrum, which is a square of magnitude of the complex spectrum, has an exponential distribution (or, in other terms, a chi-squared distribution with two degrees of freedom). Any changes of the input signal of this model, due to the presence of an RFI, yield a change of its statistics. The power spectrum in this case has a non-central chi-squared distribution with two degrees of freedom. Radio astronomy observations generally employ the averaging of the power spectrum over some integration period, which results in a conversion of the probability distribution of the averaged power spectrum into a Gaussian distribution.
Analysis of sample probability distribution before averaging allows an effective separation of these signals by means of real-time processing facilities employing digital signal processing. The method may be effective for single dish observations without a reference channel. The description of this separation by using the analysis of the power spectrum distribution will be presented below. I will also present some computer simulations, and some results from test observations at the Westerbork Synthesis Radio Telescope (WSRT).
A radio telescope receiver output signal is described as follows:
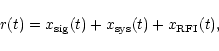 |
(1) |
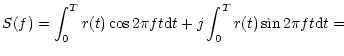 |
|||
| (2) |
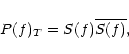 |
(3) |
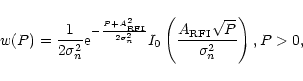 |
(4) |
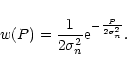 |
(5) |
| = | 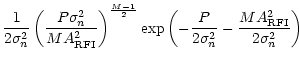 |
||
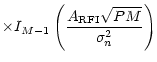 |
(6) |
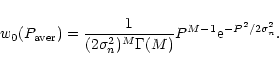 |
(7) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig1.eps}
\end{figure}](/articles/aa/full/2001/10/aah2442/Timg29.gif) |
Figure 1:
The non-central |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{fig2.eps}
\end{figure}](/articles/aa/full/2001/10/aah2442/Timg30.gif) |
Figure 2:
a) The non-central |
| Open with DEXTER | |
One observes that the presence of RFI changes the form of the distribution w(P) of the unaveraged periodogram. This property may be used for separating the (system + signal) noise component
![]() from the RFI component
from the RFI component
![]() .
.
The most promising method is to obtain an estimate of the sample probability distribution
![]() (histogram), and subsequently estimate the
(histogram), and subsequently estimate the
![]() and
and
![]() ,
which best fit this sample distribution (symbol
,
which best fit this sample distribution (symbol
![]() denotes sample average). However,
performing this processing in real-time with a sufficiently wide band (at the MegaHertz level) is a difficult task even for the most powerful modern Digital Signal Processors (DSPs).
denotes sample average). However,
performing this processing in real-time with a sufficiently wide band (at the MegaHertz level) is a difficult task even for the most powerful modern Digital Signal Processors (DSPs).
A more attractive practical approach is to use the sample moments of the power spectrum. The first four statistical parameters, mean, variance, skewness and excess, for distribution (4) are:
| mean | = | (8) | |
| var | = | (9) | |
| skew | = | ![$\displaystyle \frac{2\sigma _{n}^{2}+3{A}_{\rm RFI}^{2}}{[\sigma _{n}^{2}+{A}_{\rm RFI}^{2}]^{3/2}}\sqrt{\sigma _{n}^{2}},$](/articles/aa/full/2001/10/aah2442/img38.gif) |
(10) |
| exc | = | 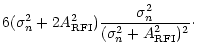 |
(11) |
Having the sample values of
![]() ,
this redundant system of nonlinear equations can be solved with respect to
,
this redundant system of nonlinear equations can be solved with respect to
![]() and
and
![]() ,
with the obvios constraints
,
with the obvios constraints
![]() .
Analysis of the "solution surface'' shows that the solution is unique. Even on the basis of only the first two equations, it is easy to derive that at each frequency
.
Analysis of the "solution surface'' shows that the solution is unique. Even on the basis of only the first two equations, it is easy to derive that at each frequency
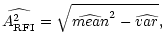 |
(12) | ||
| (13) |
Sometimes radio astronomers use a cross-correlation spectrum instead of the auto-correlation spectrum, with the aim of suppressing large system noise spectral component. The probability distribution and the statistical parameters for this case are given in the Appendix.
Some computer simulations have been done to investigate how effective the separation of the Gaussian noise component and the non-Gaussian RFI can be. Figure 3 represents a block diagram of the simulation program.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig3.eps}
\end{figure}](/articles/aa/full/2001/10/aah2442/Timg51.gif) |
Figure 3: A block diagram of the computer simulations |
| Open with DEXTER | |
The lower part of the block diagram in Fig. 3 shows the common way of doing spectral analysis: calculating of the power spectrum
![]() and subsequent averaging. At this point the two versions of the power spectrum
and subsequent averaging. At this point the two versions of the power spectrum
![]() are available: one without RFI excision, and another with RFI excision.
Figures 4-7 show the results of the some computer simulations.
are available: one without RFI excision, and another with RFI excision.
Figures 4-7 show the results of the some computer simulations.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig4.eps}
\end{figure}](/articles/aa/full/2001/10/aah2442/Timg55.gif) |
Figure 4: Computer simulations: a) the power spectrum with spectral line with no RFI; b) the input signal with no RFI; c) a two feature RFI power spectrum (logarithmic scale); d) the resulting input signal with RFI; e) the "cleaned'' power spectrum; g) the difference between a) and e) |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig5.eps}
\end{figure}](/articles/aa/full/2001/10/aah2442/Timg57.gif) |
Figure 5: Spectra of the statistical parameters for the model in Fig. 4c (with RFI): a) mean; b) variance; c) skewness; d) excess |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig6.eps}
\end{figure}](/articles/aa/full/2001/10/aah2442/Timg58.gif) |
Figure 6: Computer simulations: a) the power spectrum with spectral line with no RFI; b) the input signal with no RFI; c) a two feature RFI power spectrum (logarithmic scale); d) the resulting input signal with RFI; e) the "cleaned'' power spectrum; g) the difference between a) and e) |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig7.eps}
\end{figure}](/articles/aa/full/2001/10/aah2442/Timg59.gif) |
Figure 7: Spectra of the statistical parameters for the model in Fig. 6c (with RFI): a) mean; b) variance; c) skewness; d) excess |
| Open with DEXTER | |
Test observations were made with the WSRT to demonstrate the effectiveness of the proposed method with real radio astronomy signals. Digital spectral analysis was performed with the help of a SIGNATEC PMP-8 board with eight high performance Texas Instruments DSP TMS320C6201 processors (Fridman 2000). The baseband (0-1.25 MHz) signal at the analogue output of WSRT frequency conversion subsystem corresponding to one of the radio telescopes (RT6) is digitized in a 12-bit analogue-digital converter and then applied to the PMP-8, where the FFT and the averaged statistical parameters were calculated. The final presentation of the "dirty'' and the "clean'' spectra, and of their difference were done on a workstation.
Figures 8, 9, and 10 show the results of three test observations of Galactic spectral lines: 21 cm HI lines in the direction of Crab and Orion, and an 18 cm OH line in the W3(OH) radio source.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig8_2.eps}
\end{figure}](/articles/aa/full/2001/10/aah2442/Timg62.gif) |
Figure 8: RFI excision using the WSRT with bandwidth = 1.25 MHz, halfsampling frequency = 1.563 MHz, and frequency resolution = 3.052 kHz: a) a neutral hydrogen spectral line (21 cm) in the Galaxy towards the Crab nebula with RFI superposed at 1420.397 MHz; b) the same spectrum after RFI excision simultaneously made with frame a; c) a magnification of the spectral line region (channels 30-100) with spectra of a) and b) superposed on a record without any RFI |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig9_1.eps}
\end{figure}](/articles/aa/full/2001/10/aah2442/Timg63.gif) |
Figure 9: RFI excision using the WSRT with bandwidth = 1.25 MHz, halfsampling frequency = 1.563 MHz, and frequency resolution = 3.052 kHz: a) a neutral hydrogen spectral line (21 cm) in the Galaxy towards the Orion nebula with RFI superposed at 1420.350 MHz; b) the same spectrum after RFI excision simultaneously made with frame a; c) a magnification of the spectral line region (channels 60-120) with spectra of a) and b) superposed on a record without any RFI |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig10_1.eps}
\end{figure}](/articles/aa/full/2001/10/aah2442/Timg68.gif) |
Figure 10: RFI excision using the WSRT with bandwidth = 2.5 MHz, halfsampling frequency = 3.125 MHz, and frequency resolution = 6.104 kHz: a) a hydroxyl (OH) emission line (18 cm) in the Galaxy towards W3(OH) at 1665.8 MHz with RFI superposed; b) the same spectrum after RFI excision simultaneously made with frame a; c) a magnification of the spectral line region (channels 250-300) with spectra of a) and b) superposed on a record without any RFI |
| Open with DEXTER | |
![$\displaystyle p(z)=\frac{1}{\pi \sigma _{1}\sigma _{2}\sqrt{(1-\rho ^{2})}}K_{0}\left[\frac{\vert z\vert}{\sigma _{1}\sigma _{2}(1-\rho ^{2})}\right]$](/articles/aa/full/2001/10/aah2442/img70.gif) |
|||
![$\displaystyle \times\exp \left[\frac{\rho z}{\sigma _{1}\sigma _{2}(1-\rho ^{2})}\right],$](/articles/aa/full/2001/10/aah2442/img71.gif) |
(14) |
![\begin{displaymath}f(\xi )=[1-2i\xi \sqrt{\sigma _{1}\sigma _{2}}+\xi ^{2}\sigma _{1}\sigma _{2}(1-\rho ^{2})]^{-1/2}.
\end{displaymath}](/articles/aa/full/2001/10/aah2442/img72.gif) |
(15) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig11.eps}
\end{figure}](/articles/aa/full/2001/10/aah2442/Timg73.gif) |
Figure 11: The product probability distribution with the correlation factor as a parameter, a) a 3D presentation; and b) sections for different correlation factors |
| Open with DEXTER | |
For a product of two Gaussian values z = xy with non-zero means the formula for the PDF is too complex, but the characteristic function is simple enough to calculate the necessary central moments and hence the skewness and the excess. The central moments are more convenient to calculate using cumulants:
![]() .
For variances equal to 1, the means a1, a2, and the correlation coefficient
.
For variances equal to 1, the means a1, a2, and the correlation coefficient ![]() ,
the characteristic function is (Deustch 1962):
,
the characteristic function is (Deustch 1962):
| = | |||
![$\displaystyle \times\exp \left\{\frac{2i\xi a_{1}a_{2}-\xi ^{2}[a_{1}^{2}-2\rho a_{1}a_{2}+a_{2}^{2}]}{2[1-2i\xi \rho +\xi ^{2}(1-\rho ^{2})]}\right\}\cdot$](/articles/aa/full/2001/10/aah2442/img78.gif) |
(16) |
| (17) |
| (18) |
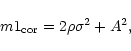 |
(19) |
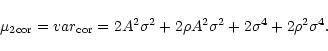 |
(20) |
| = | (21) | ||
| = | (22) |
| = | |||
| (23) | |||
| = | |||
| = | |||
| = | 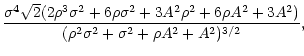 |
||
| (24) |
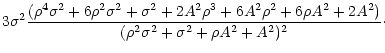 |
|||
| (25) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig12.eps}
\end{figure}](/articles/aa/full/2001/10/aah2442/Timg112.gif) |
Figure 12:
The skewness a) and the excess b) for a product with 2 degrees of freedom and |
| Open with DEXTER | |
Acknowledgements
The author would like to thank W.A. Baan for helpful suggestions and valuable discussions.