5 Spectroscopic luminosity ratio

Figure 4: Radial velocity curve of the HeI $\lambda$4471 line in the spectrum of HD149404 as a function of the orbital phase and assuming e = 0.0 (see Table3). The triangles correspond to the primary's RVs while the squares indicate the RVs of thesecondary

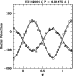Figure 5: Radial velocity curve determined by the mask cross-correlation method as a function of the orbital phase (assuming a circular orbit, see Table3)

In principle, a rough estimate of the visible luminosity ratio of the binary components can be inferred from the ratio of the equivalent widths of absorption lines in the primary's and secondary's spectra (e.g. Rauw et al. 2000a):

$$\frac{I_{\rm prim}}{I_{\rm sec}} = \left( \frac{EW_{\rm prim}... ... \left( \frac{EW_{\rm O9.5I}}{EW_{\rm O7.5I}} \right)_{\rm typ}$$

where $\left( \frac{EW_{\rm O9.5I}}{EW_{\rm O7.5I}} \right)_{\rm typ}$ stands for the ratio of the EWs of the lines as observed in typical single O9.5I (as a best substitute for O9.7I) and O7.5I stars. We measured the EW ratios of the HeI $\lambda \lambda$4026, 4471, HeII $\lambda$4542 and SiIV $\lambda \lambda$4089, 4116 absorption lines (see Table 5). The typical EW ratios were derived from the compilation of O-star equivalent widths published by Conti & Alschuler (1971) and Conti (1973, 1974). In the case of HD149404, the main limitation of the method stems from the strong orbital variability of the line strength (see Table5). For instance, the strength of the primary's SiIV lines around $\phi \sim 0.75$ is reduced by a factor 2 with respect to $\phi \sim 0.25$, while the strength of the secondary's SiIV lines simultaneously increases by about a factor 1.3. An easy way to account for the fading of the primary's lines around $\phi \sim 0.75$ and the simultaneous strengthening of the secondary's absorptions would be to assume that one of the two stars was brighter on the front side than on the rear. However, since the amplitude of the photometric variations is only a few percent, it seems rather unlikely that the observed EW variations reflect actual variations of the brightness of one of the binary components, otherwise a larger amplitude of the light curve would be expected.

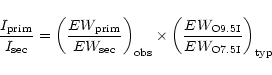
We notice that the total EW (primary + secondary) varies by only about 5% for the absorptions considered here. On the other side, we know that the HeI lines are most probably affected by an emission component and the EW of the primary's HeI lines are reduced around $\phi \sim 0.75$ (see Fig. 2). Therefore, blending with a most probably slightly red-shifted emission component not associated with either of the two stars could be an explanation for the observed variations.

Similar difficulties are encountered in the UV. Howarth et al. (1997) derived a mean raw UV magnitude difference of 0.8 with the secondary being the brighter component. Correcting this magnitude difference for the different spectral types, we obtain a UV luminosity ratio (primary/secondary) of roughly 0.6. Stickland & Koch (1996) reported a luminosity ratio of about 1.0 when the primary is moving towards us (our phase 0.25) and about 0.5 when it is moving away (our phase 0.75). Using the results for the HeII and SiIV lines from Table5, we calculate a mean luminosity ratio of about $1.4 \pm 0.4$ near $\phi \sim 0.25$ and $0.5 \pm 0.1$ near $\phi \sim 0.75$.

Assuming that the observed EWs are indeed reduced by a red-shifted emission component, we can derive the "actual" spectroscopic luminosity ratio using the mean EWs of each star's line when the star is moving towards us. In this way, we find an average ratio of $\overline{I}_{\rm prim}\,(0.25)/\overline{I}_{\rm sec}\,(0.75) = 0.90 \pm 0.16$ (see Table5).

Alternatively, the absorption enhancement seen when the lines are blueshifted could be due to material from a wind interaction region that would be swept up by the star during its orbital motion. In this case, the front sides of the stars would display abnormal line strengths and the actual luminosity ratio would best be derived from the mean EWs of the lines observed when the stars are moving away from us. This assumption yields an average ratio of $\overline{I}_{\rm prim}\,(0.75)/\overline{I}_{\rm sec}\,(0.25) = 0.75 \pm 0.23$ (see Table5). This result overlaps within the errors with the value of the $\overline{I}_{\rm prim}\,(0.25)/ \overline{I}_{\rm sec}\,(0.75)$ ratio. In this second scenario, each star would have to sweep up about the same amount of material in order to explain the roughly constant total EWs of the lines. Therefore, it seems more likely that the variations of the apparent luminosity ratio are rather due to an unresolved emission component and in the following we shall thus adopt a spectroscopic luminosity ratio of $0.90 \pm 0.16$.

 

 

Table 5: Luminosity ratios (primary/secondary) derived for different lines at different orbital phases. Typical uncertainties on the observed EW ratios are less than 10%. The colons indicate those measurements that have larger uncertainties due to heavier blending. The last two columns list the luminosity ratios derived from the mean EWs measured when the components are moving towards us (Col. 7) or when they are moving away from us (Col. 8); see the text for further details

HJD-2450000	1299.800	1584.857	1672.766		1304.796	1579.879
$\phi$	0.234	0.278	0.235		0.743	0.771		$\overline{I}_{\rm prim}\,(0.25)/ \overline{I}_{\rm sec}\,(0.75)$	$\overline{I}_{\rm prim}\,(0.75)/\overline{I}_{\rm sec}\,(0.25)$
HeI $\lambda$4026	1.70	1.13	1.95		0.28	0.41		0.86	0.66
HeI $\lambda$4471	1.35	1.19	1.51		0.35	0.47		0.84	0.60
HeII $\lambda$4542	1.71	1.22:	1.95			1.15:		1.19	0.66
SiIV $\lambda$4089	1.07	0.90	1.11		0.39	0.91:		0.83	0.61
SiIV$\lambda$4116	1.40	1.25	1.57		0.54			0.80	1.21