3 Data reduction

Standard photometry has been derived from the CCD images by using ARLO, an ad-hoc pipeline software developed under IRAF 2.10.4 (Casalegno 1998). A detailed description of the pipeline tasks, along with a discussion of the choice of critical input parameters is given in Casalegno et al. (1999). The implementation of the pipeline procedures was driven by two main requirements: the first, building an automated pipeline and the second, storing all the relevant data to perform an error analysis without necessarily going back to the original CCD frames. This is justified by the large amount of data involved, which consists of approximately 30000 images, taken with different telescopes/instruments and over a time span of more than ten years. Both aperture and PSF photometry were routinely performed on each CCD image.

Aperture photometry is computed by the IRAF package APPHOT, with the aperture radius chosen to be equal to 2.3 times the average full-width-half-maximum of the frame, as estimated by the previous IRAF tasks. This choice is driven by the competing requirements of minimizing light contamination from close objects and losing a negligible fraction of the seeing-dominated PSF profile. It turns out that the fraction of light lost with this choice of the radius is less than $1\%$. In no case is the aperture radius smaller than 4.5'', as suggested in Massey et al. (1989). This circle is supposed to encompass the seeing-independent part of the light distributed in the profile wings.

The fitting method implemented in IRAF is that of DAOPHOT (Stetson 1987). It uses a model for the PSF function made of an analytical part plus an empirical correction table, which is then fit via a least-square technique to derive the best stellar parameters. The choice of the stars being used for the definition of the average PSF profile is an automated procedure not requiring human interaction, as implemented in the ARLO pipeline. This feature has been demonstrated to work well for moderately crowded sky regions, whereas in heavily dense fields a more reliable PSF can be obtained by selecting the stars manually within the frame.

3.1 Instrumental magnitude errors

Both instrumental magnitude errors coming from the aperture and PSF methods are carried along during the reductions. The aperture photometry error, as computed by the PHOTCALC task, is given by $\sigma_{\rm ap} = C/S\cdot\sqrt{S/G +A\cdot\sigma^2_{\rm B}+A^2\cdot\sigma^2_{\rm B}/N}$, where $C= 2.5\cdot {\rm log}(e)$, G is the CCD gain, S the total counts from the star within the chosen aperture A (in fractional pixels), and $\sigma_{\rm B}$ is the standard deviation of the background over the N fractional pixels of a defined sky annulus around the main aperture. The first two terms inside the square root represent the error due to photon statistics from the star and the sky background respectively, while the third addendum accounts for the error due to subtraction of the mean sky.

The computation of the PSF photometric error involves several steps, as in this case the magnitude is calculated by an iterative least-square procedure (see Stetson 1987 for details). Briefly, the method consists in fitting the residuals of the pixel values after subtraction of the preliminary PSF profile; the standard error of the flux in each pixel is calculated from the readout noise and gain of the detector, and it is rigorously propagated through the least squares solution to predict the PSF magnitude error. After the fit has been perfomed, the rms value of the observed pixel residuals is computed. An average of these two estimates is returned as the final magnitude error, as implemented in the IRAF DAOPHOT package.

3.2 Transformation to the Johnson-Kron-Cousins system

Transformation of instrumental magnitudes onto the Johnson-Kron-Cousins system is achieved by imaging selected faint standard stars from the Landolt catalog. Exposures of the Landolt stars are taken several times during an observing night, with fairly large air mass distributions (typically $\sim$1.1-2). Particular attention has been paid in culling the Landolt list, with the purpose of covering an adequate range of colors. Moreover, stars with a poor observation history, although not completely excluded, were seldom used. Finally, we used Landolt fields with more than one standard star in the CCD frame, thereby mitigating the negative effect of one poor observation on the final parameters of the fit. Landolt stars are visually identified in each exposure. Then, the objects in the V and B frames are linked to the corresponding ones in the R frames. Finally, a fit of the observed to the standard magnitudes is performed using the IRAF task FITPARAM, and applying the following set of equations:

$$\left\{ \begin{array}{c} R=r+z_R+K_R\cdot X_R +\beta_R\cdot (... ...] B=b+z_B+K_B\cdot X_B + \beta_B\cdot (B-V) \end{array}\right.$$

where uppercase and lowercase letters indicate standard and instrumental magnitudes respectively, and X_R, X_V, X_B are the air masses computed for each exposure. The magnitude scale zero-point is given by the z terms, while the K terms represent the first order extinction coefficients, and the $\beta$ terms gauge the color component of the transformation between the standard and the instrumental systems. As prescribed by Harris et al. (1981), a least-square solution of the above set of equations is carried out to estimate at once both the nightly atmospheric extinction values and the color transformation between the instrumental and the standard system. The actual value of the estimated parameters might vary from night to night, reflecting the statistical properties of the least-square solution. However, since the parameters are correlated with each other by the model, small errors of the extinction values are well compensated by adjustments in the color term estimates, making the results for the program stars fairly stable. An alternative expression for the V equation, which have been implemented for part of the southern data reductions, makes use of the color (V-R) instead of (B-V), allowing one to account for a color term in the standardization of the v magnitude where a B-filter exposure is not available. We verified that the (B-V) and (V-R) colors of the Landolt stars retained in our list are comparable in range and that they are linearly related; therefore, the photometric response in the V band is equally well modelled by using either color. The task FITPARAM is used interactively, allowing visual inspection of the quality of the fit, and possibly reject dubious observations. If judged necessary, a temporal term of the form $\delta\times T_{\rm obs}$ is added to the equations. This was seldom used to model constant temporal variations in the night extinction coefficients, or the presence of linear drifts of the detector/filter system. A typical rms of a good fit is of the order of 0.02-0.03, whereas formal errors on the transformation coefficients are typically an order of magnitude smaller than their estimated values. When a satisfying fit could not be achieved the night was considered non photometric, and the newly observed program fields tagged for re-observation.

3.3 Photometric errors in the standard system

The final photometric error assigned to each object in a frame is computed by the IRAF task INVERFIT, with the default input option errors = "obserrors''. This error estimate is an empirical one which takes into account the variance of the observation only, without propagating the errors of the coefficients of the transformation to the standard system. We have tested the reliability of this error estimate by direct comparison of independent observations of the same sequence. The results show that the current estimation is a lower limit for the expected photometric error. In particular, the uncertainty of the zero-point estimation (e.g., z_V for the V passband, but the same reasoning applies to all filters) adds to the final error budget a contribution comparable with that induced by the photon noise error of the stellar source, according to the approximate formula:

$$\sigma_V^2 \simeq \left(\frac{K_B+1}{K_V+1}\right)^2\sigma^2_{\rm obs} + \left(\frac{K_V+1}{K_B+1}\right)^2\sigma^2_{z_V}.$$

Hence, while for stars fainter than $\sim$17 the main error constribution is from photon noise, for brighter stars the zero-point uncertainty is typically higher than the instrumental magnitude one, and the IRAF-computed error is significantly underestimated. A more rigorous error propagation formula will be used for future GSPC-II releases.

3.4 Astrometry

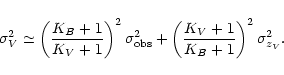
Astrometry of each CCD frame is carried out as part of the reduction pipeline using the Digital Sky Survey (DSS, Lasker 1994) as the reference catalog. The IRAF task employed is LYNXYMATCH (XYXYMATCH in the current IRAF version), which makes use of the triangularization algorithm (Groth 1986) to link reference to program stars in a completely automated fashion. If the algorithm fails, which occurred for about $25\%$ of all cases, the user is asked to interactively identify the stars and restart the procedure. The astrometric accuracy of a GSPC-II object is limited by that of the DSS, which is typically of the order of half an arcsecond. On the other hand, their relative astrometric precision is generally better than the absolute one, typically 0.2-0.3 arcsec and fairly homogeneous over the sky. It is to be noted however that for the $\sim$23 arcmin CCD format the final astrometric error is somewhat critical, ultimately depending upon the distribution of the DSS stars found by the triangles algorithm on the CCD frame. More explicitely, if the stars found in the DSS cover a small area of the CCD frame, the error propagation of the parameters of the linear transformation could generate large errors in the extrapolated CCD area. Hence, one can expect a few cases where even a search aperture radius of 2-3 arcsec cannot ensure a good matching of GSPC-II with plate objects. We are in the process of correcting these astrometric errors as they become evident through the GSC-II plate processing pipeline.

3.5 Applications to Schmidt photographic photometry

Our experience with the calibration of Schmidt survey plates has demonstrated that an accurate response function to incident light can be obtained by fitting the logarithmic integrated density of stellar objects to some externally derived magnitudes, as long as their Point Spread Function (PSF) on the photographic emulsion is reasonably stable and they are not highly saturated; requirements which are clearly met by the Schmidt images of the stars in the GSPC-II sequences. However, GSPC-II standard magnitudes need to be converted to the passband defined by the plate emulsion/filter combination, before they can be used for plate calibration. Color transformations of the form J=J(B-V,V), J=J(V-R,R) - where J stands for the blue POSS-II passband - were derived for each of the GSC-II passbands, by using the STSDAS package SYNPHOT and a library of empirical and theoretical spectra (Lejeune et al. 1997; Gunn & Stryker 1983). These transformations are strictly valid only within a particular color range ( -0.15 < V-R < 1.43), corresponding to mainly early- to medium-type main sequence stars. Similar constraints are enforced for the B-V color.

Another crucial aspect of the photometric calibration deals with off-axis aberrations. These become noticeable at a radius of $\sim$$2.7^\circ$ from the plate center and increases toward the edges, their main component being attributable to vignetting of the plate corrector, and therefore radially symmetric. Because of the non-linearity of the emulsion sensitivity, vignetting gives rise to a complex photometric response which needs to be properly calibrated by using photometric standards over a much larger plate area. To overcome this problem, we have recently secured special sets of calibration sequences, currently being used to build vignetting correction masks for each Schmidt survey/passband (García Yus 2000).

Figure 2: Visualization of the main steps of the night-reduction pipeline (left), and of how the frame data is channeled into different GSPC-II field containers and matched against each other (right)