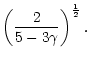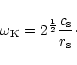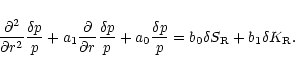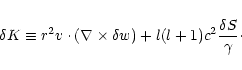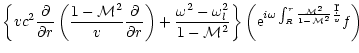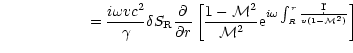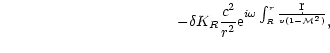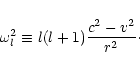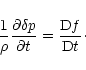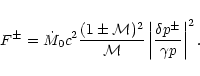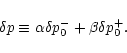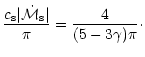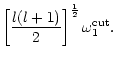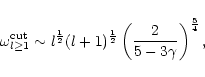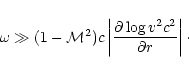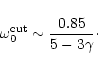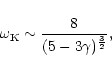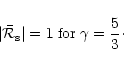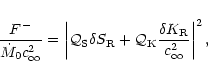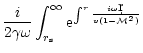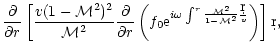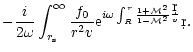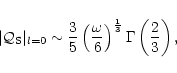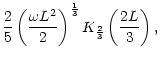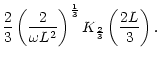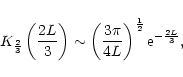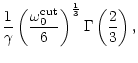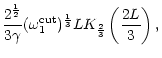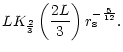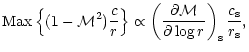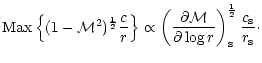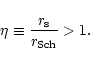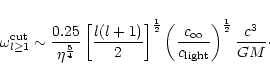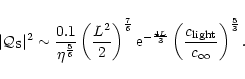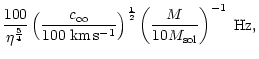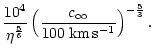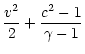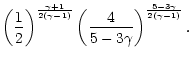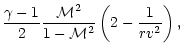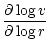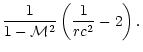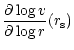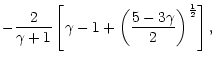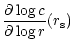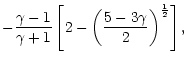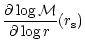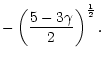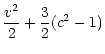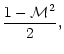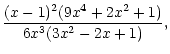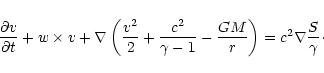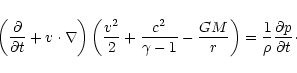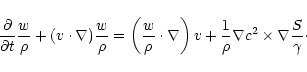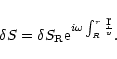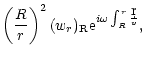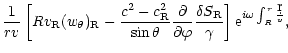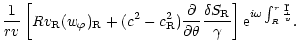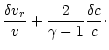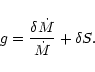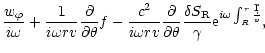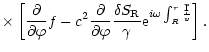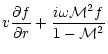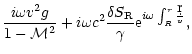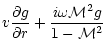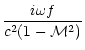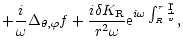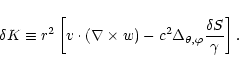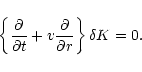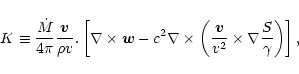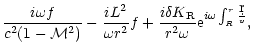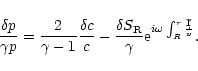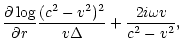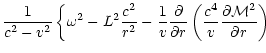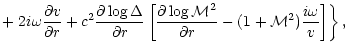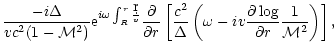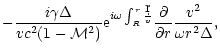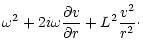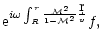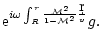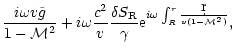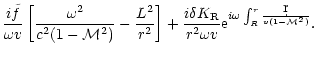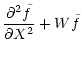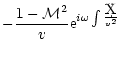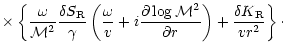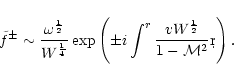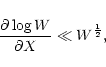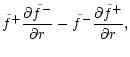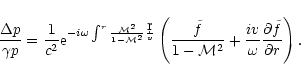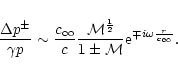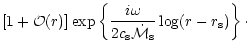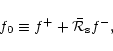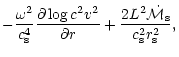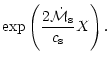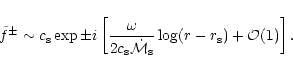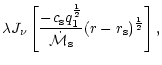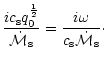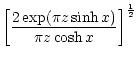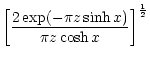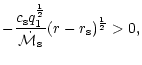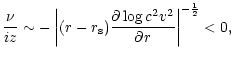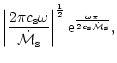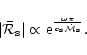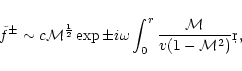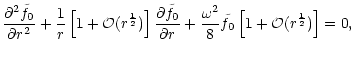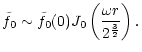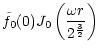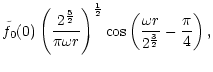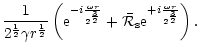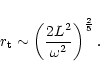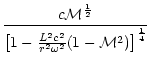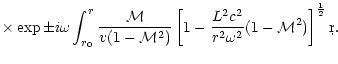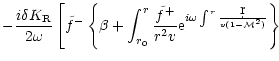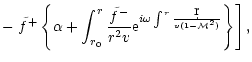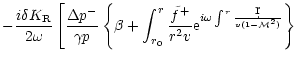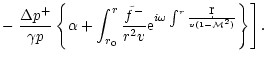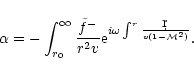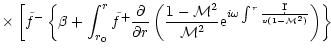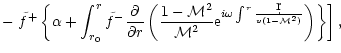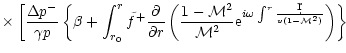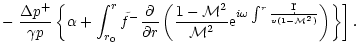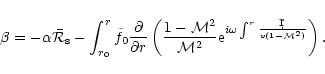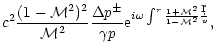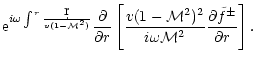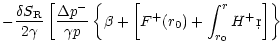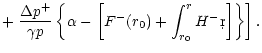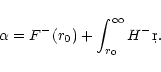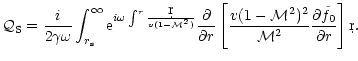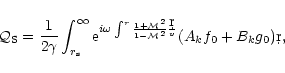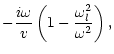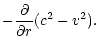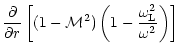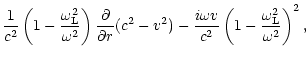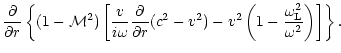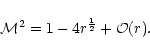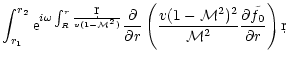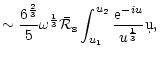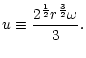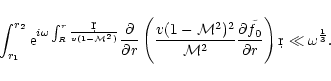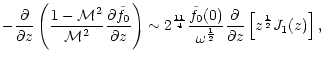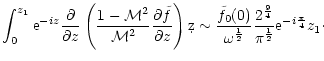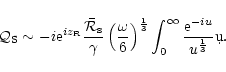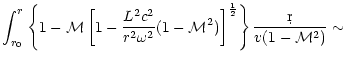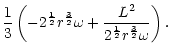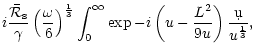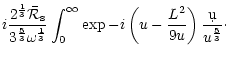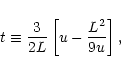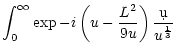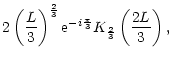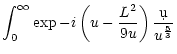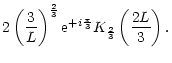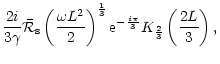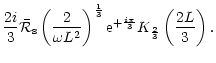A&A 368, 311-324 (2001)
DOI: 10.1051/0004-6361:20000506
Entropic-acoustic instability of shocked Bondi accretion
I.
What does perturbed Bondi accretion sound like?
T. Foglizzo
Service d'Astrophysique, CEA/DSM/DAPNIA, CE-Saclay, 91191
Gif-sur-Yvette, France
Received 17 October 2000 / Accepted 21 December 2000
Abstract
In the radial flow of gas into a black hole (i.e.Bondi accretion), the
infall of any entropy or vorticity perturbation produces acoustic waves
propagating outward. The dependence of this acoustic flux on the shape of
the perturbation is investigated in detail. This is the key process in the
mechanism of the entropic-acoustic instability proposed by Foglizzo & Tagger
(2000) to explain the instability of Bondi-Hoyle-Lyttleton accretion. These
acoustic waves create new entropy and vorticity perturbations when they
reach the shock, thus closing the entropic-acoustic cycle. With an adiabatic
index
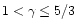 ,
the linearized equations describing the perturbations
of the Bondi flow are studied analytically and solved numerically. The
fundamental frequency of this problem is the cut-off frequency of acoustic
refraction, below which ingoing acoustic waves are refracted out. This
cut-off is significantly smaller than the Keplerian
frequency at the sonic radius and depends on the latitudinal number l of
the perturbations.When advected adiabatically inward, entropy and
vorticity perturbations trigger acoustic waves propagating outward,
with an efficiency which is highest for non radial perturbations l=1.
The outgoing acoustic flux produced by
the advection of vorticity perturbations is always moderate and peaks at
rather low frequency. By contrast, the acoustic flux
produced by an entropy wave is highest close to the refraction cut-off.
It can be very large if
,
the linearized equations describing the perturbations
of the Bondi flow are studied analytically and solved numerically. The
fundamental frequency of this problem is the cut-off frequency of acoustic
refraction, below which ingoing acoustic waves are refracted out. This
cut-off is significantly smaller than the Keplerian
frequency at the sonic radius and depends on the latitudinal number l of
the perturbations.When advected adiabatically inward, entropy and
vorticity perturbations trigger acoustic waves propagating outward,
with an efficiency which is highest for non radial perturbations l=1.
The outgoing acoustic flux produced by
the advection of vorticity perturbations is always moderate and peaks at
rather low frequency. By contrast, the acoustic flux
produced by an entropy wave is highest close to the refraction cut-off.
It can be very large if  is close to 5/3.
These results suggest that the shocked Bondi flow with
is close to 5/3.
These results suggest that the shocked Bondi flow with
 is
strongly unstable with respect to the entropic-acoustic mechanism.
is
strongly unstable with respect to the entropic-acoustic mechanism.
Key words: accretion, accretion disks - hydrodynamics -
instabilities - shock waves - binaries: close -
X-rays: stars
The time variability of the emission from X-ray binaries may be
related to hydrodynamic instabilities in the process of accretion onto
a compact star. The simplest accretion flow is the
stationary, spherically symmetric accretion of an adiabatic gas onto a
compact object, first studied by Bondi (1952).
The stability of Bondi accretion was established by Garlick (1979)
and Petterson et al.(1980) in the Newtonian limit, and by Moncrief (1980)
in the framework of general relativity. Kovalenko & Eremin (1998)
suggested that non radial perturbations might reach non linear amplitudes in
the supersonic part of the flow if the size of the accretor is small enough.
This effect was invisible in the 3-D numerical simulations of the Bondi flow
by Ruffert (1994a), which confirmed its stability. By contrast, a strong
instability appeared in the numerical simulations of Bondi-Hoyle-Lyttleton
accretion when a bow shock is present (e.g.Ruffert 1994b for
 ). The Bondi-Hoyle-Lyttleton accretion is named after the
pioneering works of Hoyle & Lyttleton (1939) and Bondi & Hoyle (1944)
concerning an accretor moving
at supersonic speed with respect to the gas. Foglizzo & Tagger (2000)
(hereafter FT2000) suggested that this instability might be explained
by what they called the entropic-acoustic instability. This generic
mechanism of instability in shocked converging flows is based on the cycle
of entropic and acoustic waves in the subsonic region of
the flow between the shock and the sonic surface surrounding the accretor.
The advection of entropy perturbations towards the accretor produces
outgoing acoustic waves which propagate towards the shock. Perturbed
by these acoustic waves, the shock produces new entropy perturbations, thus
closing the entropic-acoustic cycle. According to FT2000, this cycle is
unstable (i.e.the amplitude of the new entropy perturbation exceeds
the initial one) if the sound speed at the sonic point is much larger than
the sound speed at the shock. This mechanism might play a destabilizing
role in various
astrophysical environments such as wind accretion or disc accretion.
In this series of two papers, we describe the entropic-acoustic instability
in the Bondi flow, including a spherical shock as an outer boundary (as in
Foglizzo & Ruffert 1997). The study of this rather
academic configuration
serves two purposes:
). The Bondi-Hoyle-Lyttleton accretion is named after the
pioneering works of Hoyle & Lyttleton (1939) and Bondi & Hoyle (1944)
concerning an accretor moving
at supersonic speed with respect to the gas. Foglizzo & Tagger (2000)
(hereafter FT2000) suggested that this instability might be explained
by what they called the entropic-acoustic instability. This generic
mechanism of instability in shocked converging flows is based on the cycle
of entropic and acoustic waves in the subsonic region of
the flow between the shock and the sonic surface surrounding the accretor.
The advection of entropy perturbations towards the accretor produces
outgoing acoustic waves which propagate towards the shock. Perturbed
by these acoustic waves, the shock produces new entropy perturbations, thus
closing the entropic-acoustic cycle. According to FT2000, this cycle is
unstable (i.e.the amplitude of the new entropy perturbation exceeds
the initial one) if the sound speed at the sonic point is much larger than
the sound speed at the shock. This mechanism might play a destabilizing
role in various
astrophysical environments such as wind accretion or disc accretion.
In this series of two papers, we describe the entropic-acoustic instability
in the Bondi flow, including a spherical shock as an outer boundary (as in
Foglizzo & Ruffert 1997). The study of this rather
academic configuration
serves two purposes:
- (i)
- it is the first detailed description of the entropic-acoustic
instability in a specific flow, beyond the general concepts and
approximations of FT2000.
The Bondi flow is simple enough to allow for an analytical treatment of 3D
perturbations, including non radial perturbations of entropy and
perturbations of vorticity;
- (ii)
- understanding the instability of the Bondi flow with a spherical
shock might be the first step towards a comprehension of the instability of
non radial shocked accretion flows such as supersonic Bondi-Hoyle-Lyttleton
accretion.
In this first paper, we investigate the key part of the entropic-acoustic
instability: the excitation of outgoing acoustic waves by the advection of
entropy and vorticity perturbations. As explained in FT2000, the efficiency
of this process is directly linked to the efficiency of the refraction of
acoustic waves, which is also studied. The efficiencies of these processes
depend a priori on the frequency  of the perturbation, its
wavenumbers in spherical coordinates (l,m), and the adiabatic index
of the perturbation, its
wavenumbers in spherical coordinates (l,m), and the adiabatic index
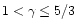 of the gas. The accretor is a compact object such as a
black hole, absorbing all the matter falling inside the sonic radius. The
shock, which plays no role in this first paper, is introduced in the second
paper of this series (Foglizzo 2001) in order to close the entropic-acoustic
cycle and enable a description of the eigenmodes of the global
instability.
of the gas. The accretor is a compact object such as a
black hole, absorbing all the matter falling inside the sonic radius. The
shock, which plays no role in this first paper, is introduced in the second
paper of this series (Foglizzo 2001) in order to close the entropic-acoustic
cycle and enable a description of the eigenmodes of the global
instability.
The present paper is organized as follows. Linearized equations are
established in Sect. 2. The refraction of acoustic waves is studied in
Sect. 3. The excitation of acoustic waves by the advection of entropy and
vorticity perturbations is examined in Sect. 4.
We consider the radial accretion flow of a gas with constant sound
velocity 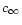 and density
and density
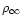 at
infinity, accelerated towards a point-like accretor of mass M,
which is totally absorbing. The
equations describing the unperturbed Bondi flow are recalled in
Appendix A. In what follows, densities and velocities are normalized by
at
infinity, accelerated towards a point-like accretor of mass M,
which is totally absorbing. The
equations describing the unperturbed Bondi flow are recalled in
Appendix A. In what follows, densities and velocities are normalized by
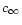 and
and
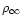 ,
and distances are normalized to the Bondi
radius
,
and distances are normalized to the Bondi
radius
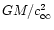 .
After this normalization, the unperturbed flow
depends on a single parameter
.
After this normalization, the unperturbed flow
depends on a single parameter 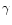 ,
the adiabatic index of the gas.
The sound velocity
,
the adiabatic index of the gas.
The sound velocity 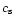 at the sonic radius
at the sonic radius 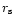 in the
Bondi flow diverges for
in the
Bondi flow diverges for
 :
:
The "natural" sonic frequency
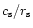 is directly related to the
Keplerian frequency
is directly related to the
Keplerian frequency
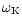 at the sonic radius:
at the sonic radius:
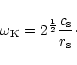 |
(3) |
The Euler equation, the equations of conservation of entropy and mass
in the Bondi flow are linearized for small perturbations in
Appendix B. After a Fourier transform in time, the perturbations are
projected onto a basis of spherical harmonics Ylm, where l,m are
the numbers associated to the latitudinal (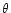 )
and longitudinal
(
)
and longitudinal
(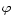 )
angles. Kovalenko & Eremin (1998) studied the same
set of equations in order to analyze the asymptotic behaviour of their
solutions near the origin r=0. By contrast, we are interested in the
effect of linear perturbations on the subsonic part of the flow (
)
angles. Kovalenko & Eremin (1998) studied the same
set of equations in order to analyze the asymptotic behaviour of their
solutions near the origin r=0. By contrast, we are interested in the
effect of linear perturbations on the subsonic part of the flow (
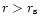 ).
A single differential equation of second
order is obtained in Appendix B.2, with the following structure:
).
A single differential equation of second
order is obtained in Appendix B.2, with the following structure:
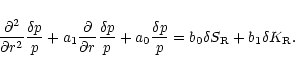 |
(4) |
The coefficients
a0,a1,b0,b1 are functions of r which depend
on the flow velocity and sound speed radial profiles in the
unperturbed Bondi flow.
Their rather lengthy expressions are given in Appendix B,
Eqs. (B.21) to (B.24).
The homogeneous equation corresponding to the left hand side of
Eq. (4) describes the propagation of acoustic waves in the
Bondi flow and their refraction by the sound speed gradients. The
important feature of Eq. (4) is the presence of source terms
on the right hand side:
(i) 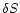 is the perturbation of entropy. For the sake of
simplicity, the ratio of the molecular weight
is the perturbation of entropy. For the sake of
simplicity, the ratio of the molecular weight 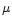 to the gas constant
to the gas constant
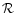 is set to
is set to
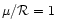 throughout this paper, with no loss
of generality.
throughout this paper, with no loss
of generality.
(ii) 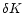 involves the curl of the vorticity vector
involves the curl of the vorticity vector
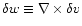 projected
along the flow velocity:
projected
along the flow velocity:
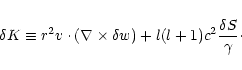 |
(5) |
The radial dependence of the three components of the vorticity vector
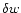 is explicitely integrated in Appendix B.1
(Eqs. (B.5) to (B.7)). Nevertheless, the vorticity
contributes to the excitation of acoustic waves only through the
radial part of its curl, as it appears in Eq. (5).
In an adiabatic flow, both
is explicitely integrated in Appendix B.1
(Eqs. (B.5) to (B.7)). Nevertheless, the vorticity
contributes to the excitation of acoustic waves only through the
radial part of its curl, as it appears in Eq. (5).
In an adiabatic flow, both 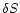 and
and 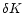 are conserved when
advected (see Appendix B.1). A more compact mathematical
formulation is obtained in Appendix B.2.2 by writing the
differential equation satisfied by the perturbation f of the Bernoulli
constant.
are conserved when
advected (see Appendix B.1). A more compact mathematical
formulation is obtained in Appendix B.2.2 by writing the
differential equation satisfied by the perturbation f of the Bernoulli
constant.
where the frequency
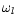 is defined as:
is defined as:
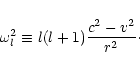 |
(7) |
The structure of this differential equation is the same as
Eq. (4), with much simpler coefficients. The right hand side of
Eq. (6) contains two source terms proportional to
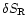 and
and
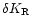 .
The pressure perturbation is related
to f by the following equation derived in Appendix B.1:
.
The pressure perturbation is related
to f by the following equation derived in Appendix B.1:
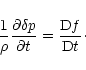 |
(8) |
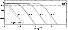 |
Figure 1:
Refraction coefficient
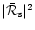 for
for
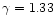 ,
l=0,1,2,3. The dotted line corresponds to the leading behaviour of ,
l=0,1,2,3. The dotted line corresponds to the leading behaviour of
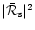 for
for
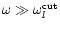 (Eq. (15))
(Eq. (15)) |
| Open with DEXTER |
The homogeneous equation associated with Eq. (6),
describing the propagation of acoustic waves is:
| |
|
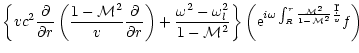 |
|
| |
|
 |
(9) |
This equation is of second order, which reflects the fact that pressure
perturbations can be decomposed into ingoing and outgoing acoustic waves.
Such an identification is possible only in the region of the flow where the
lengthscale of the flow gradients is longer than the wavelength of the
perturbation,
where a WKB treatment of the wave propagation can be used (see Appendix C).
This is always the case far from the accretor in the Bondi flow,
since the density and sound speed are uniform at infinity. We may
define
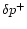 and
and
 as the solutions of the
homogeneous
equation propagating respectively inward and outward at infinity.
Following FT2000, the index + (resp. -) refers to
waves propagating in the same (resp. opposite) direction as the flow.
The acoustic flux carried by these acoustic waves is defined by
Eq. (6) of FT2000:
as the solutions of the
homogeneous
equation propagating respectively inward and outward at infinity.
Following FT2000, the index + (resp. -) refers to
waves propagating in the same (resp. opposite) direction as the flow.
The acoustic flux carried by these acoustic waves is defined by
Eq. (6) of FT2000:
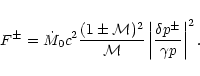 |
(10) |
Let us normalize
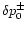 so that they carry the same acoustic
flux at infinity. Any linear combination
so that they carry the same acoustic
flux at infinity. Any linear combination 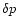 of the two independent
solutions
of the two independent
solutions
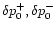 ,
with complex
coefficients
,
with complex
coefficients
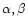 ,
is also a solution of Eq. (9):
,
is also a solution of Eq. (9):
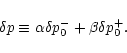 |
(11) |
There is, however, only one ratio
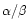 such that
such that 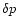 is regular at the sonic radius. Indeed, a local analysis of the solutions of
Eq. (6) for
is regular at the sonic radius. Indeed, a local analysis of the solutions of
Eq. (6) for
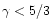 ,
at the sonic point
,
at the sonic point
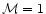 using
Frobenius series, reveals that there is only one solution crossing the
sonic point regularly, the other exhibiting a logarithmic singularity
(Bender & Orszag 1978, Chap. 3.3, p. 68). This regularity condition
reflects the fact that an incoming acoustic wave
using
Frobenius series, reveals that there is only one solution crossing the
sonic point regularly, the other exhibiting a logarithmic singularity
(Bender & Orszag 1978, Chap. 3.3, p. 68). This regularity condition
reflects the fact that an incoming acoustic wave
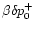 is only partially transmitted to the accretor: an outgoing acoustic wave of
amplitude
is only partially transmitted to the accretor: an outgoing acoustic wave of
amplitude
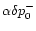 is refracted out.
Using the same notations as FT2000, the fraction
is refracted out.
Using the same notations as FT2000, the fraction
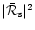 of refracted acoustic flux is deduced from
Eqs. (10) and (11):
of refracted acoustic flux is deduced from
Eqs. (10) and (11):
The refraction coefficient is therefore directly related to the regularity
of the solution at the sonic point.
The differential Eq. (9) is integrated using a
Runge-Kutta implicit method, from the sonic point to the WKB region.
The refraction coefficient is then computed by identifying the
ingoing and outgoing waves in the WKB region.
If
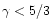 ,
a Frobenius expansion is used in the vicinity of
,
a Frobenius expansion is used in the vicinity of 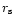 to
start the integration away from the singularity.
The calculation for
to
start the integration away from the singularity.
The calculation for
 and l=0 is similar to the case
and l=0 is similar to the case
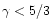 ,
except that the sonic point is at r=0.
If
,
except that the sonic point is at r=0.
If
 and
and 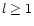 ,
the homogeneous solution presents an essential
singularity at the sonic point, where one branch converges to zero,
and the other diverges. Nevertheless, an asymptotic expansion of the
converging solution (see Eqs. (C.32) and (C.33))
allows a numerical integration from the vicinity of the origin
towards infinity. As expected by Kovalenko & Eremin (1998), no
overreflection occurs (
,
the homogeneous solution presents an essential
singularity at the sonic point, where one branch converges to zero,
and the other diverges. Nevertheless, an asymptotic expansion of the
converging solution (see Eqs. (C.32) and (C.33))
allows a numerical integration from the vicinity of the origin
towards infinity. As expected by Kovalenko & Eremin (1998), no
overreflection occurs (
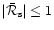 ). The typical frequency dependence
of
). The typical frequency dependence
of
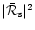 is shown in Fig. 1 for
is shown in Fig. 1 for
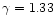 .
.
If
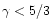 ,
the accretor is surrounded by a supersonic region
from which acoustic waves cannot escape. Only those waves with a high
enough frequency may penetrate this region, because lower frequency
waves are refracted out before the sonic radius. This leads us to expect
the refraction
,
the accretor is surrounded by a supersonic region
from which acoustic waves cannot escape. Only those waves with a high
enough frequency may penetrate this region, because lower frequency
waves are refracted out before the sonic radius. This leads us to expect
the refraction
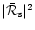 to decrease to zero at high frequency, and be
close to unity at low frequency (see Fig. 1). The refraction
cut-off
to decrease to zero at high frequency, and be
close to unity at low frequency (see Fig. 1). The refraction
cut-off
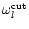 of a wave of latitudinal order l is defined as the
intermediate frequency corresponding to a refraction of half of the incoming
acoustic flux:
of a wave of latitudinal order l is defined as the
intermediate frequency corresponding to a refraction of half of the incoming
acoustic flux:
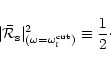 |
(14) |
Bessel functions are used in Appendix D to approximate the homogeneous
solution at high frequency, in order to obtain the leading order of
the asymptotic behaviour of
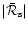 .
This latter decreases exponentially
above
.
This latter decreases exponentially
above
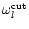 (see Fig. 1):
(see Fig. 1):
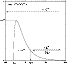 |
Figure 2:
Typical radial dependence of
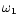 (here
(here
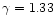 ),
showing the turning point ),
showing the turning point 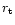 of a non radial acoustic wave l=1
below the cut-off frequency
of a non radial acoustic wave l=1
below the cut-off frequency
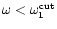 |
| Open with DEXTER |
The turning point of non radial perturbations appears
explicitly on Eq. (9). It corresponds to the radius
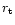 solution of
solution of
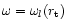 ,
where
,
where
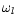 is
defined by Eq. (7) (see Fig. 2). For
is
defined by Eq. (7) (see Fig. 2). For
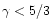 ,
this turning point is double when the frequency equals the
maximum of the function
,
this turning point is double when the frequency equals the
maximum of the function
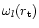 .
The refraction
coefficient is then equal to 1/2, according to Bender &
Orszag (1978, Chap. 10.6, p. 524):
.
The refraction
coefficient is then equal to 1/2, according to Bender &
Orszag (1978, Chap. 10.6, p. 524):
This result was checked by measuring numerically the refraction of
acoustic waves. Figure 3 shows the dependence of
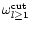 on
the adiabatic index
on
the adiabatic index 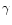 .
.
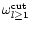 should scale as
should scale as
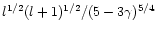 according to the asymptotic
behaviour of
according to the asymptotic
behaviour of
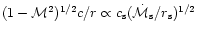 when
when
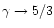 ,
deduced from Eqs. (A.12 to A.14). A refined comparison with
the results of numerical calculations of
,
deduced from Eqs. (A.12 to A.14). A refined comparison with
the results of numerical calculations of
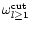 leads to
leads to
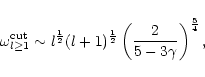 |
(19) |
over the range
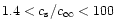 considered numerically.
The radius r1 such that
considered numerically.
The radius r1 such that
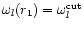 is the minimum
value of the turning radius rt (see Fig. 2).
is the minimum
value of the turning radius rt (see Fig. 2).
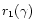 is independent of l,m and lies just outside the sonic
surface, and is well fitted by
is independent of l,m and lies just outside the sonic
surface, and is well fitted by
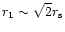 for
for 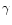 close to 5/3.
close to 5/3.
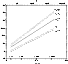 |
Figure 3:
The cut-off frequencies
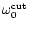 and
and
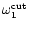 correspond to
correspond to
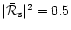 for l=0 and l=1 respectively. They
cannot be distinguished from their fittings (Eqs. (19) and
(21)) on this plot. These frequencies are compared to the sonic
frequency
for l=0 and l=1 respectively. They
cannot be distinguished from their fittings (Eqs. (19) and
(21)) on this plot. These frequencies are compared to the sonic
frequency
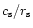 ,
the Keplerian frequency at the sonic radius ,
the Keplerian frequency at the sonic radius
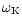 ,
and ,
and
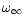 .
Frequencies are expressed in
units of .
Frequencies are expressed in
units of
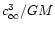 ,
as functions of ,
as functions of
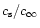 (or
(or 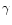 ,
or ,
or 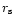 ) )
|
| Open with DEXTER |
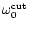 is computed numerically in Fig. 3, and corresponds
to a lower frequency than
is computed numerically in Fig. 3, and corresponds
to a lower frequency than
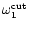 .
The value of
.
The value of
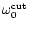 can be estimated analytically for
can be estimated analytically for
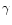 close to 5/3 from the criterion of validity of the WKB
approximation of acoustic waves, derived in Appendix C:
close to 5/3 from the criterion of validity of the WKB
approximation of acoustic waves, derived in Appendix C:
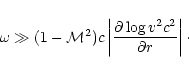 |
(20) |
Since the acoustic flux is conserved in the region
of validity of the WKB approximation, any refraction of acoustic waves
must occur outside this region. We deduce that
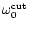 scales as the maximum of the function on the right hand
side of Eq. (20). When
scales as the maximum of the function on the right hand
side of Eq. (20). When 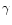 is close to 5/3, this
maximum scales as
is close to 5/3, this
maximum scales as
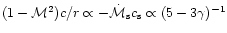 .
This is confirmed by numerical calculations of
.
This is confirmed by numerical calculations of
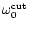 which indicate that
in the range of sound velocities
which indicate that
in the range of sound velocities
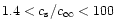 studied
numerically, the ratio
studied
numerically, the ratio
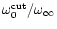 is constant within the
numerical errors:
is constant within the
numerical errors:
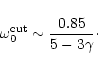 |
(21) |
The scaling of
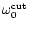 should be compared to the two other
particular frequencies of the flow near the sonic point,
should be compared to the two other
particular frequencies of the flow near the sonic point,
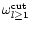 in
Eq. (19) and the local Keplerian frequency
in
Eq. (19) and the local Keplerian frequency
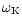 :
:
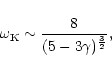 |
(22) |
and thus
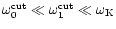 for
for 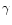 close to 5/3. The
values of
close to 5/3. The
values of
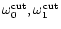 computed numerically are
compared to
computed numerically are
compared to
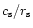 and to the Keplerian frequency in Fig. 3.
and to the Keplerian frequency in Fig. 3.
In a Bondi flow with
 ,
acoustic waves are perfectly
refracted at any frequency:
,
acoustic waves are perfectly
refracted at any frequency:
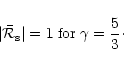 |
(23) |
This can be deduced
from the limit of flows with 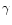 close to 5/3, because the
cut-off frequency
close to 5/3, because the
cut-off frequency
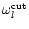 tends to infinity when
tends to infinity when
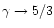 .
This is not surprising, since an ingoing acoustic wave of any frequency
always ultimately meets "a wall", i.e.a subsonic region
where the scale of the flow gradients are much shorter than the
wavelength.
.
This is not surprising, since an ingoing acoustic wave of any frequency
always ultimately meets "a wall", i.e.a subsonic region
where the scale of the flow gradients are much shorter than the
wavelength.
The WKB analysis at high frequency (Appendix C) indicates that ingoing and
outgoing acoustic waves are coupled together at
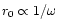 for
l=0,
and at their turning point
for
l=0,
and at their turning point
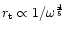 if
if 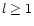 .
The continuity between the flow
.
The continuity between the flow
 and flows with
and flows with 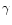 close
to 5/3 is checked by remarking that
close
to 5/3 is checked by remarking that
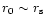 for
for
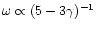 and
and
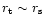 for
for
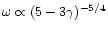 .
Comparing this
to
.
Comparing this
to
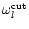 in Eqs. (21) and (19),
the cut-off frequency is simply interpreted as the
maximum frequency such that the coupling of acoustic perturbations
occurs in the subsonic flow.
in Eqs. (21) and (19),
the cut-off frequency is simply interpreted as the
maximum frequency such that the coupling of acoustic perturbations
occurs in the subsonic flow.
According to Eq. (6), it is natural to define
two dimensionless complex acoustic efficiencies
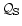 ,
,
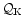 associated respectively to the two source terms
associated respectively to the two source terms
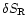 and
and
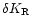 .
These definitions are made so that the acoustic flux F-of an outgoing sound wave triggered by the perturbations of
entropy and vorticity, measured far from the accretor is:
.
These definitions are made so that the acoustic flux F-of an outgoing sound wave triggered by the perturbations of
entropy and vorticity, measured far from the accretor is:
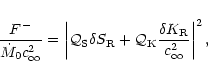 |
(24) |
The integral expressions for
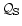 and
and
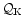 are derived in
Appendix D:
are derived in
Appendix D:
It is remarkable that both acoustic efficiencies are independent
of the longitudinal number m.
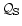 and
and
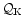 depend only on
depend only on
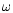 and l.
and l.
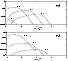 |
Figure 4:
Acoustic efficiencies
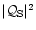 and
and
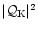 depending
on the frequency for
depending
on the frequency for
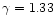 ,
l=0,1,2,3 ,
l=0,1,2,3 |
| Open with DEXTER |
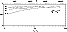 |
Figure 5:
The frequencies which maximize
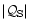 are
displayed in units of the refraction cut-off
are
displayed in units of the refraction cut-off
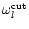 ,
for l=0,1,2,3as functions of ,
for l=0,1,2,3as functions of
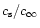 |
| Open with DEXTER |
The step of the numerical integration must be able to resolve both
acoustic and entropy waves. Far from the accretor, the wavelength of
the acoustic perturbation is asymptotically constant (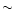
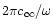 ), whereas the wavelength of the entropy perturbation
decreases to zero as
), whereas the wavelength of the entropy perturbation
decreases to zero as
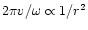 .
It is therefore
useful to transform the integrals in Eqs. (25) and
(26) to accelerate their convergence. This is done
in Appendix D by successive integrations by parts, thus obtaining
Eqs. (D.6) and (D.19).
If
.
It is therefore
useful to transform the integrals in Eqs. (25) and
(26) to accelerate their convergence. This is done
in Appendix D by successive integrations by parts, thus obtaining
Eqs. (D.6) and (D.19).
If
 ,
the integrals are transformed near the origin in
order to correctly treat the singularity.
,
the integrals are transformed near the origin in
order to correctly treat the singularity.
4.3 Asymptotic expansion of
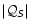 and
and
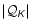 at high
frequency for
at high
frequency for 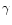 =
=
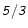
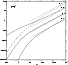 |
Figure 6:
Acoustic efficiency
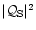 of entropy perturbations for
of entropy perturbations for
 ,
l=0,1,2,3. The full line corresponds to the numerical
calculation, the dotted line corresponds to the asymptotic estimate
at high frequency (Eqs. (28) and (29)) ,
l=0,1,2,3. The full line corresponds to the numerical
calculation, the dotted line corresponds to the asymptotic estimate
at high frequency (Eqs. (28) and (29)) |
| Open with DEXTER |
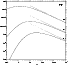 |
Figure 7:
Acoustic efficiency
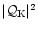 of vorticity perturbations for
of vorticity perturbations for
 ,
l=1,2,3. The full line corresponds to the numerical
calculation, the dotted line corresponds to the asymptotic estimate
at high frequency (Eq. (30)) ,
l=1,2,3. The full line corresponds to the numerical
calculation, the dotted line corresponds to the asymptotic estimate
at high frequency (Eq. (30)) |
| Open with DEXTER |
Special properties of the Bondi flow
 are related to
the position of the sonic radius, at the central singularity.
In particular, both cut-off frequencies
are related to
the position of the sonic radius, at the central singularity.
In particular, both cut-off frequencies
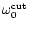 and
and
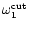 are infinite, which means that at any
frequency, incoming sound waves are totally refracted outward:
are infinite, which means that at any
frequency, incoming sound waves are totally refracted outward:
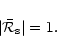 |
(27) |
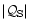 is estimated in Appendix E.1 at high frequency for
radial perturbations:
is estimated in Appendix E.1 at high frequency for
radial perturbations:
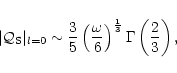 |
(28) |
where the Gamma function satisfies
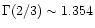 .
.
The case of non radial perturbations is derived in
Appendix E.2, where we define
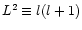 :
:
The asymptotic expansions in Eqs. (28), (29)
and (30), which involve no free scaling parameter, are
successfully compared to numerical calculations of
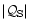 and
and
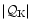 in
Figs. 6 and 7.
The radial case of Eq. (28) is recovered by taking the
continuous limit
in
Figs. 6 and 7.
The radial case of Eq. (28) is recovered by taking the
continuous limit 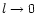 in Eq. (29).
Note that the asymptotic behaviour of the Bessel function
in Eq. (29).
Note that the asymptotic behaviour of the Bessel function
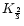 for large arguments (
for large arguments (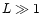 ),
),
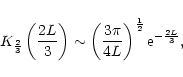 |
(31) |
makes the acoustic efficiencies decrease rapidly for high order l.
Remembering that the frequency of the entropy perturbation is directly
related to its radial wavelength (
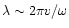 ),
our calculation of
),
our calculation of
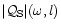 indicates that the
sound produced by the advection of an object of given mass in the
Bondi flow depends a lot on its shape. Virtually no sound comes out
if l is large and
indicates that the
sound produced by the advection of an object of given mass in the
Bondi flow depends a lot on its shape. Virtually no sound comes out
if l is large and 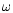 is small (e.g.a stretched spaghetti).
By contrast, the shape producing the highest acoustic flux corresponds to
a small l and a large
is small (e.g.a stretched spaghetti).
By contrast, the shape producing the highest acoustic flux corresponds to
a small l and a large 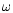 (e.g.a wide thin saucer).
(e.g.a wide thin saucer).
At high frequency, the coupling of entropy
and vorticity perturbations to acoustic waves comes essentially from the
region
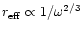 (i.e.the main contribution to the
integrals in Eqs. (25) and (26), computed
in Appendix E). The radial scaling at
high frequency is therefore
(i.e.the main contribution to the
integrals in Eqs. (25) and (26), computed
in Appendix E). The radial scaling at
high frequency is therefore
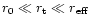 .
.
 |
Figure 8:
Maximum acoustic efficiency
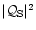 as a
function of
as a
function of
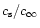 (i.e.of
(i.e.of
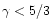 )
for l=0,1,2,3. The
dotted lines are deduced from the curves )
for l=0,1,2,3. The
dotted lines are deduced from the curves
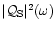 , ,
 (Fig. 6), where (Fig. 6), where 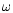 is replaced by
is replaced by
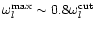 .
Curves corresponding to l=0
are marked with circles .
Curves corresponding to l=0
are marked with circles |
| Open with DEXTER |
 |
Figure 9:
Acoustic efficiencies
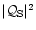 and
and
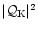 depending on the
frequency for
depending on the
frequency for
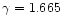 (i.e.
(i.e.
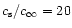 ), l=0,1,2.
Frequencies are expressed in units of ), l=0,1,2.
Frequencies are expressed in units of
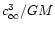 .
These efficiencies are very close to those obtained for .
These efficiencies are very close to those obtained for
 (dotted lines), truncated after the cut-off frequency
(dotted lines), truncated after the cut-off frequency
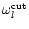 |
| Open with DEXTER |
For 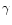 close to 5/3 and at frequencies lower than the cut off
frequency, we can use the approximation of
close to 5/3 and at frequencies lower than the cut off
frequency, we can use the approximation of
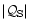 obtained for
obtained for
 .
According to Fig. 5, the maximum of
.
According to Fig. 5, the maximum of
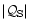 is reached
at the frequency
is reached
at the frequency
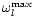 ,
with
,
with
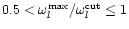 .
The asymptotic behaviour of
the maximum value of
.
The asymptotic behaviour of
the maximum value of
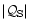 is therefore estimated by extrapolating Eqs. (28) and
(29) to the cut-off frequency:
is therefore estimated by extrapolating Eqs. (28) and
(29) to the cut-off frequency:
It is interesting to note in Fig. 8 that the most efficient
entropy perturbations at a given frequency when
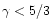 are non radial
(l=1), whereas radial ones are more efficient for
are non radial
(l=1), whereas radial ones are more efficient for
 (Fig. 6). This is directly related to
the fact that the critical refraction frequency is much higher for l=1
than for l=0 (Eqs. (19) and (21)). This is illustrated in
Fig. 9, where the acoustic efficiencies computed for
(Fig. 6). This is directly related to
the fact that the critical refraction frequency is much higher for l=1
than for l=0 (Eqs. (19) and (21)). This is illustrated in
Fig. 9, where the acoustic efficiencies computed for
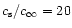 (
(
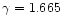 )
are very close to
their values for
)
are very close to
their values for
 ,
up to the refraction cut-off. In this
figure, the efficiency
,
up to the refraction cut-off. In this
figure, the efficiency
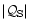 is higher for l=0 than for l=1 in the
limited range of frequencies
is higher for l=0 than for l=1 in the
limited range of frequencies
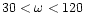 ,
but the overall maximum is
reached near
,
but the overall maximum is
reached near
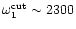 for l=1.
for l=1.
5 Conclusions
The acoustic response of the Bondi flow to pressure, entropy and
vorticity perturbations has been studied thoroughly.
Let us summarize the main results:
(i) the critical refraction frequency for acoustic waves
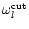 is quite different from the "natural" frequency
is quite different from the "natural" frequency
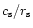 one might think of at first glance. Moreover
one might think of at first glance. Moreover
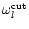 is also very
different for radial and non radial perturbations.
The two fundamental frequencies
is also very
different for radial and non radial perturbations.
The two fundamental frequencies
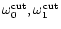 of this flow near the
sonic point were accurately determined (Eqs. (19) and (21)), and
are ordered as follows:
of this flow near the
sonic point were accurately determined (Eqs. (19) and (21)), and
are ordered as follows:
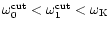 ,
with
,
with
(ii) two quantities conserved in the linear approximation
of the perturbed Bondi flow are source terms for acoustic waves: the
entropy perturbation 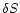 ,
and
a quantity
,
and
a quantity 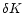 related to both vorticity and entropy
perturbations defined by Eq. (5).
related to both vorticity and entropy
perturbations defined by Eq. (5).
(iii) the acoustic efficiencies
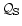 and
and
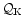 of
entropy and vorticity perturbations are independent of
the longitudinal number m.
of
entropy and vorticity perturbations are independent of
the longitudinal number m.
(iv)
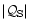 and
and
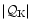 are highest for l=1 perturbations
if
are highest for l=1 perturbations
if
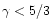 .
.
(v)
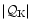 is highest at relatively low frequency, and is
always rather moderate (
is highest at relatively low frequency, and is
always rather moderate (
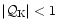 ).
).
(vi)
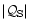 is highest at high frequency near the
refraction cut-off, and can be much larger than one if
is highest at high frequency near the
refraction cut-off, and can be much larger than one if 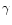 is
close to 5/3, i.e.if
is
close to 5/3, i.e.if
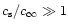 .
This confirms the physical
argument of FT2000 which stressed the importance of the enthalpy increase
between the outer part of the flow and the sonic point.
.
This confirms the physical
argument of FT2000 which stressed the importance of the enthalpy increase
between the outer part of the flow and the sonic point.
(vii) asymptotic scalings of
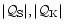 were obtained at
high frequency for
were obtained at
high frequency for
 (Eqs. (28) to (30)),
in excellent agreement with numerical calculations.
(Eqs. (28) to (30)),
in excellent agreement with numerical calculations.
The analytical expressions obtained for
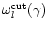 ,
and for
,
and for
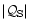 and
and
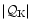 at high frequency for
at high frequency for
 ,
are accurate enough (see Figs. 3, 6
and 7) to be used as tests of the accuracy of 3D hydrodynamical
codes used for Bondi accretion, and particularly their limitations at
high frequency.
,
are accurate enough (see Figs. 3, 6
and 7) to be used as tests of the accuracy of 3D hydrodynamical
codes used for Bondi accretion, and particularly their limitations at
high frequency.
These results suggest that if a shock were present as outer
boundary, the entropic-acoustic cycle would be unstable with respect
to high frequency waves if the sound speed at the sonic point is high
enough, i.e.if 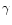 is close to 5/3. Indeed, an entropy
perturbation
is close to 5/3. Indeed, an entropy
perturbation
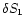 advected towards the accretor triggers an
outgoing acoustic flux
advected towards the accretor triggers an
outgoing acoustic flux
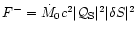 .
These acoustic waves propagate against the flow until they reach the shock,
where they produce new entropy perturbations
.
These acoustic waves propagate against the flow until they reach the shock,
where they produce new entropy perturbations
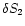 (see FT2000), with
(see FT2000), with
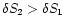 since
since
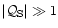 .
The eigenmodes corresponding to this unstable cycle will be investigated
in the second paper of this series (Foglizzo 2001). The fact that the
most unstable simulations of Bondi-Hoyle-Lyttleton accretion
also correspond to
.
The eigenmodes corresponding to this unstable cycle will be investigated
in the second paper of this series (Foglizzo 2001). The fact that the
most unstable simulations of Bondi-Hoyle-Lyttleton accretion
also correspond to
 (Ruffert & Arnett 1994; Ruffert 1994b)
already encourages us to look for an extrapolation of these results to the
case of non-radial shocked accretion flows.
(Ruffert & Arnett 1994; Ruffert 1994b)
already encourages us to look for an extrapolation of these results to the
case of non-radial shocked accretion flows.
In the flow
 ,
the fact that the outgoing acoustic flux
produced by entropy perturbations diverges at high frequency
(Eqs. (28) and (29)) is rather
surprising, and directly related to the hypothesis of a point-like
Newtonian accretor (
,
the fact that the outgoing acoustic flux
produced by entropy perturbations diverges at high frequency
(Eqs. (28) and (29)) is rather
surprising, and directly related to the hypothesis of a point-like
Newtonian accretor (
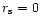 ).
In this section we show that
).
In this section we show that
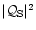 is naturally bounded
if the finite size of the accretor is taken into account.
Simple arguments are used in order to roughly estimate this upper bound in
the case of an accreting black hole, without computing the exact relativistic
corrections near its horizon.
is naturally bounded
if the finite size of the accretor is taken into account.
Simple arguments are used in order to roughly estimate this upper bound in
the case of an accreting black hole, without computing the exact relativistic
corrections near its horizon.
Let us denote by
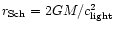 the Schwarzschild radius
of the black hole, where
the Schwarzschild radius
of the black hole, where
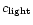 is the speed of light.
With a sound speed at infinity
is the speed of light.
With a sound speed at infinity
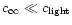 ,
Eq. (1)
guarantees that relativistic effects are negligible except for
,
Eq. (1)
guarantees that relativistic effects are negligible except for 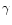 close to 5/3. Indeed Petrich et al.(1989) checked numerically
that relativistic corrections are small for
close to 5/3. Indeed Petrich et al.(1989) checked numerically
that relativistic corrections are small for
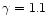 and
and
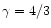 .
If
.
If
 ,
the sonic point is bound to lie
at a few Schwarzschild radii:
,
the sonic point is bound to lie
at a few Schwarzschild radii:
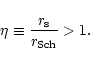 |
(38) |
Our description of non radial acoustic waves in the flow
 is not
affected by relativistic corrections as long as their turning point
is not
affected by relativistic corrections as long as their turning point 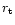 is far enough from the horizon. Since
is far enough from the horizon. Since
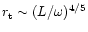 at high
frequency (Eq. (C.34)), a natural relativistic cut-off is
introduced for
at high
frequency (Eq. (C.34)), a natural relativistic cut-off is
introduced for
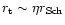 :
:
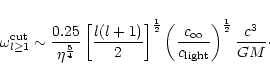 |
(39) |
The efficiency
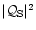 of the generation of non radial acoustic
waves close to this cut-off frequency is deduced from
Eq. (29):
of the generation of non radial acoustic
waves close to this cut-off frequency is deduced from
Eq. (29):
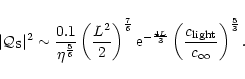 |
(40) |
The numerical values of the cut-off frequency and maximum acoustic
efficiency of the entropy perturbations l=1 are thus typically:
Therefore relativistic effects set an upper bound on the apparent
divergence of
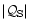 at high frequency for
at high frequency for
 .
Equation (42) indicates that entropy perturbations may excite
low degree acoustic waves very efficiently, up to non linear amplitudes
if the component l=1 of the entropy perturbations exceeds a few percent.
This efficiency is much smaller for inhomogeneities with a small
angular scale, since
.
Equation (42) indicates that entropy perturbations may excite
low degree acoustic waves very efficiently, up to non linear amplitudes
if the component l=1 of the entropy perturbations exceeds a few percent.
This efficiency is much smaller for inhomogeneities with a small
angular scale, since
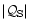 decreases exponentially when l increases (Eq. 40).
decreases exponentially when l increases (Eq. 40).
Non adiabatic processes are discussed by Chang & Ostriker (1985) in the
context of Bondi accretion. The efficiency
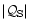 would be strongly
affected by a strong thermal conduction which smoothes out
entropy perturbations. This effect would be more pronounced for short
wavelength perturbations, which are also the most efficient for
would be strongly
affected by a strong thermal conduction which smoothes out
entropy perturbations. This effect would be more pronounced for short
wavelength perturbations, which are also the most efficient for 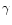 close to 5/3. Without
going into the details of such processes, our understanding of the
acoustic efficiency allows the following remark: if the inner
region of the flow were dominated by non adiabatic processes, the optimal
frequency for
close to 5/3. Without
going into the details of such processes, our understanding of the
acoustic efficiency allows the following remark: if the inner
region of the flow were dominated by non adiabatic processes, the optimal
frequency for
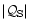 would be at most reduced to the maximum frequency of
acoustic waves refracted inside the adiabatic region of the flow.
Even when there is no shock, the mechanism of excitation of acoustic waves
from the advection of entropy perturbations opens interesting perspectives
to the problem of time delay in Cygnus X-1, approached numerically by
Manmoto et al.(1996). Interpreting their results in terms of acoustic
efficiency of entropy perturbations suggest that this physical process
survives the inclusion of rotation, radiative cooling and viscous
heating. The study of effects deserve a careful analysis which is beyond
the scope of the present paper.
would be at most reduced to the maximum frequency of
acoustic waves refracted inside the adiabatic region of the flow.
Even when there is no shock, the mechanism of excitation of acoustic waves
from the advection of entropy perturbations opens interesting perspectives
to the problem of time delay in Cygnus X-1, approached numerically by
Manmoto et al.(1996). Interpreting their results in terms of acoustic
efficiency of entropy perturbations suggest that this physical process
survives the inclusion of rotation, radiative cooling and viscous
heating. The study of effects deserve a careful analysis which is beyond
the scope of the present paper.
Acknowledgements
The author acknowledges stimulating discussions with Michel Tagger.
The Runge-Kutta algorithm used in this work for the numerical calculations
was kindly provided by Roland Lehoucq.
Appendix A: Description of the unperturbed Bondi flow
The Bernoulli equation and the conservation of mass are written after
normalizing velocities to the sound speed 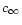 at infinity, and
distances to the Bondi radius
at infinity, and
distances to the Bondi radius
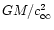
By taking the radial derivative of these equation, we obtain:
At the sonic point,
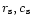 are defined by Eqs. (1) and (2).
A Taylor expansion of Eqs. (A.3) and
(A.4) leads to:
are defined by Eqs. (1) and (2).
A Taylor expansion of Eqs. (A.3) and
(A.4) leads to:
A.2 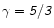
In accretion flows where
 ,
Eqs. (A.1) and
(A.2) become:
,
Eqs. (A.1) and
(A.2) become:
r,v,c can be expressed as explicit functions of the variable x defined by:
| x |
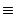 |
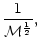 |
(A.10) |
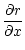 |
= |
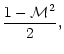 |
(A.11) |
| r |
= |
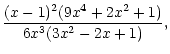 |
(A.12) |
| v2 |
= |
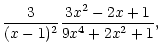 |
(A.13) |
| c2 |
= |
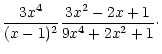 |
(A.14) |
B.1 Second order differential system
The Euler equation is written as follows:
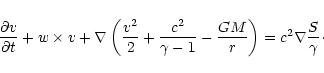 |
(B.1) |
Projecting the Euler equation onto the flow velocity, we obtain the
equation of evolution of the Bernoulli constant:
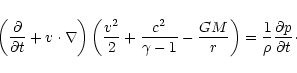 |
(B.2) |
By combining the curl of Euler equation and the mass conservation, we
obtain the equation for the evolution of the vorticity w:
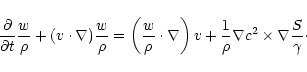 |
(B.3) |
We make a Fourier transform in time of the linearized equations
describing the radial flow perturbed in spherical coordinated
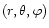 .
The linearized equation of entropy conservation can be directly
integrated:
.
The linearized equation of entropy conservation can be directly
integrated:
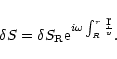 |
(B.4) |
The vorticity Eq. (B.3) can also be integrated when
linearized:
| wr |
= |
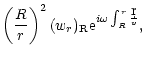 |
(B.5) |
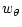 |
= |
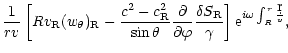 |
(B.6) |
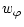 |
= |
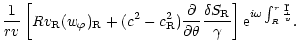 |
(B.7) |
Thus the product
r2wr is conserved during advection, as
remarked by Kovalenko & Eremin (1998).
In order to write the linearized Euler equation in the simplest form,
let us define the two functions f,g as follows:
f is the perturbation of the Bernoulli constant, which is directly
related to the pressure variations according to Eq. (B.2). g
is related to the perturbation of the mass accretion rate and entropy
through:
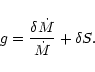 |
(B.10) |
By linearization of Eq. (B.1), we express the velocity
components
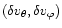 as follows:
as follows:
The radial part of the Euler equation, together with the continuity
equation, lead to the following differential system:
where
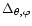 is the non radial part of the
Laplacian in spherical coordinates. The constant
is the non radial part of the
Laplacian in spherical coordinates. The constant
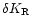 is
defined as follows:
is
defined as follows:
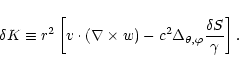 |
(B.15) |
We deduce from Eqs. ((B.6)-(B.7)) that 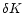 is conserved
when advected:
is conserved
when advected:
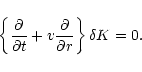 |
(B.16) |
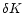 can be written independently of the system of coordinates,
as the first order perturbation of the quantity K defined by:
can be written independently of the system of coordinates,
as the first order perturbation of the quantity K defined by:
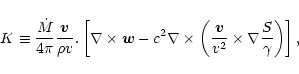 |
(B.17) |
but the conservation of K is established only in the linear approximation.
By projecting
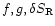 and the radial component of the curl
of the vorticity
and the radial component of the curl
of the vorticity
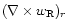 onto the spherical
harmonics
onto the spherical
harmonics
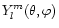 ,
which are the eigenvectors of the
Laplacian, we obtain:
,
which are the eigenvectors of the
Laplacian, we obtain:
where we have defined
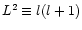 for the sake of the simplicity
of the equations.
for the sake of the simplicity
of the equations.
B.2 Second order differential equation
B.2.1 Pressure perturbation
The most natural function to describe the behaviour of acoustic waves
is the pressure perturbation
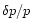 ,
which is related to the sound
speed perturbation through:
,
which is related to the sound
speed perturbation through:
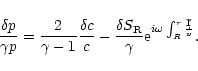 |
(B.20) |
Using this equation in Eqs. ((B.8)-(B.9)) enables us to
write (f,g) as functions of
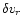 and
and 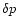 in
Eqs. ((B.18)-(B.19)), and thus obtain Eq. (4) with:
in
Eqs. ((B.18)-(B.19)), and thus obtain Eq. (4) with:
| a1 |
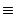 |
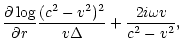 |
(B.21) |
| a0 |
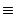 |
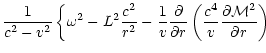 |
|
| |
|
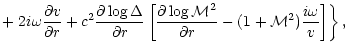 |
|
| |
|
|
(B.22) |
| b0 |
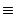 |
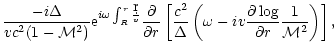 |
|
| |
|
|
(B.23) |
| b1 |
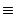 |
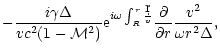 |
(B.24) |
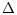 |
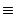 |
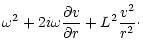 |
(B.25) |
The function 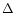 is introduced by our choice of writing the
differential equation satisfied by the pressure perturbation, which
is justified from the physical point of view. Note that
is introduced by our choice of writing the
differential equation satisfied by the pressure perturbation, which
is justified from the physical point of view. Note that 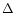 never vanishes as long as the real part of the frequency is different
from zero.
never vanishes as long as the real part of the frequency is different
from zero.
B.2.2 A more compact mathematical formulation
It is convenient to define (
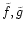 )
as:
)
as:
The differential system Eqs. ((B.18)-(B.19)) is then simpler:
The homogeneous differential Eq. ( 9) can
be transformed into a more compact form using the new variable X:
where
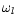 is defined by Eq. (7).
is defined by Eq. (7).
With this new variable, the sonic point 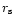 corresponds to
corresponds to
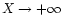 ,
while the spatial infinity corresponds to X=0.
,
while the spatial infinity corresponds to X=0.
C.1 WKB approximation far from the accretor
The general solution f of the homogeneous equation
associated to Eq. (B.32) is a linear
combination of ingoing (f+) and outgoing (f-) waves, which can
be approximated by the WKB method:
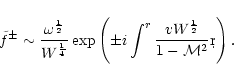 |
(C.1) |
This approximation is asymptotically valid for
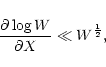 |
(C.2) |
which is satisfied at high frequency or far from the accretor.
The Wronskien 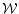 associated to the couple
(
associated to the couple
(
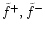 )
of solutions is:
)
of solutions is:
The pressure perturbation 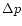 associated to a perturbation f
is deduced from Eq. (B.2):
associated to a perturbation f
is deduced from Eq. (B.2):
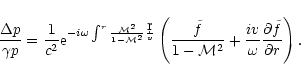 |
(C.5) |
The normalization factor
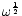 in
Eq. (C.1) is such that the pressure perturbations
in
Eq. (C.1) is such that the pressure perturbations
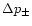 associated to these solutions by Eq. (B.2)
have the following asymptotic behaviour:
associated to these solutions by Eq. (B.2)
have the following asymptotic behaviour:
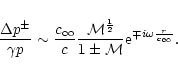 |
(C.6) |
Both carry the same acoustic flux
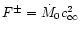 according
to Eq. (10).
according
to Eq. (10).
C.2 Definition of the refraction coefficient
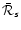 and estimate at high frequency
and estimate at high frequency
A Frobenius expansion in the vicinity of the sonic point (
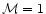 )
shows that
any solution of the homogeneous equation can be projected onto the
couple f1,f2 of solutions, where f1(r) is regular and f2(r)
is singular:
)
shows that
any solution of the homogeneous equation can be projected onto the
couple f1,f2 of solutions, where f1(r) is regular and f2(r)
is singular:
This defines a unique coefficient
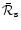 such that the solution
such that the solution
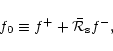 |
(C.9) |
is regular at the sonic point. The coefficient
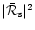 is the
refraction coefficient of sound waves. The linearity of the equations
guarantees of course that the solution
is the
refraction coefficient of sound waves. The linearity of the equations
guarantees of course that the solution
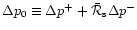 is also regular.
is also regular.
An expansion of W in the vicinity of the sonic point leads to:
| W |
= |
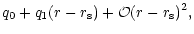 |
(C.10) |
| q0 |
 |
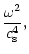 |
(C.11) |
| q1 |
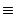 |
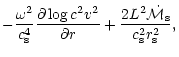 |
(C.12) |
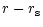 |
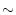 |
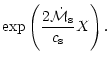 |
(C.13) |
The WKB approximation of
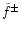 is valid at high frequency
is valid at high frequency
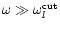 ,
for
,
for
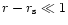 :
:
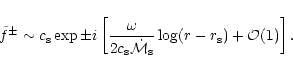 |
(C.14) |
The asymptotic solution to the differential Eq. (9)
can also be approximated by a Bessel function in the vicinity of the sonic
point, for
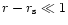 .
The regularity of f0 at the sonic radius
implies:
.
The regularity of f0 at the sonic radius
implies:
The Bessel and WKB approximations are both valid in the region where
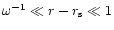 .
In this region, the matching of the two
approximations gives the normalization constant
.
In this region, the matching of the two
approximations gives the normalization constant 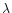 and the
refraction coefficient
and the
refraction coefficient
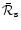 .
The asymptotic behavior of the Bessel
function, when both the imaginary order
.
The asymptotic behavior of the Bessel
function, when both the imaginary order 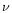 and the argument
tend to infinity, is obtained from Watson (1952, Chap. 8.6, p. 262).
The Bessel function
and the argument
tend to infinity, is obtained from Watson (1952, Chap. 8.6, p. 262).
The Bessel function
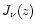 is written in terms of the Hankel
functions
is written in terms of the Hankel
functions
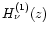 and
and
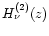 .
Let x,z be real numbers, with
.
Let x,z be real numbers, with 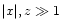 ,
such that the order
,
such that the order
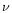 is purely imaginary
is purely imaginary
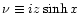 :
:
Applying these asymptotic expansions to Eq. (C.15), with
we obtain 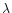 and
and
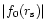 to first order at high frequency:
to first order at high frequency:
The exponential decrease of
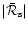 at high frequency is deduced from
Eqs. (C.18) and (C.19), by identifying the Hankel functions
with the ingoing and outgoing acoustic waves:
at high frequency is deduced from
Eqs. (C.18) and (C.19), by identifying the Hankel functions
with the ingoing and outgoing acoustic waves:
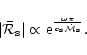 |
(C.24) |
The WKB approximation is valid in the range
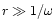 .
.
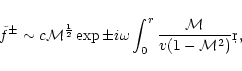 |
(C.25) |
where the normalization is chosen in agreement with
Eq. (C.1).
In the region
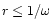 where the WKB approximation is not
valid, we approximate the solution by the Bessel function J0, which
is regular at the origin:
where the WKB approximation is not
valid, we approximate the solution by the Bessel function J0, which
is regular at the origin:
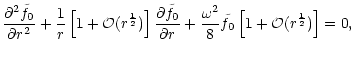 |
|
|
|
(C.26) |
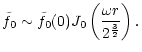 |
|
|
(C.27) |
The other Bessel solution, Y0, is singular with a logarithmic
divergence, as in the case of
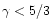 .
The Bessel approximation for
.
The Bessel approximation for
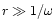 matches the WKB approximation:
matches the WKB approximation:
From this we deduce that:
The case of non radial perturbations needs to be treated separately,
because the behaviour of the solution is quite different near the
sonic point. If 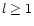 ,
there is always a turning point beyond which
the solution is evanescent, such that it decays exponentially on the
sonic point. The leading behaviour of
f0,g0 on this essential
singularity is the following, within a multiplicative constant:
,
there is always a turning point beyond which
the solution is evanescent, such that it decays exponentially on the
sonic point. The leading behaviour of
f0,g0 on this essential
singularity is the following, within a multiplicative constant:
The solutions of the other branch diverge exponentially on the sonic
point: as in the case of a regular sonic point, there is a unique
combination of ingoing and outgoing waves such that the solution does
not diverge at the sonic point.
The turning point 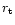 corresponds to the radius where W=0
in Eq. (B.32):
corresponds to the radius where W=0
in Eq. (B.32):
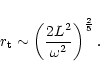 |
(C.34) |
The WKB approximation is valid for
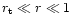 :
:
The outgoing pressure perturbation produced by the advection of a
perturbation
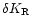 is computed by solving
Eq. (B.32), imposing the regularity at the sonic point and the
absence of an incoming sound wave from infinity. The general solution of
Eq. (B.32) with
is computed by solving
Eq. (B.32), imposing the regularity at the sonic point and the
absence of an incoming sound wave from infinity. The general solution of
Eq. (B.32) with
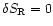 can be written as:
can be written as:
According to Eqs. (C.6) and ((C.7)-(C.8)), the
integrals involved in Eq. (D.2) are well defined both at
infinity and at the sonic radius. The condition that no sound wave
comes from infinity leads to:
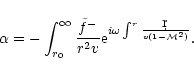 |
(D.3) |
The regularity at the sonic radius can be written:
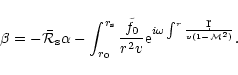 |
(D.4) |
Thus the efficiency of sound wave emission by the advection of
vorticity perturbations is:
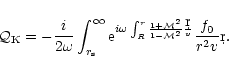 |
(D.5) |
This integral converges as 1/r3 at infinity. It can be transformed
using integrations by parts together with the homogeneous differential
system satisfied by
f0,g0, so that it converges rapidly at infinity,
thus allowing an easier numerical computation. The following expression
converges as 1/r5:
The outgoing pressure perturbation produced by an incoming entropy
perturbation
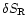 is also computed by solving
Eq. (B.32), imposing the regularity at the sonic point and
the absence of an incoming sound wave from infinity. The general
solution of Eq. (B.32) with
is also computed by solving
Eq. (B.32), imposing the regularity at the sonic point and
the absence of an incoming sound wave from infinity. The general
solution of Eq. (B.32) with
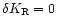 can be written as:
can be written as:
Since the integrals of Eq. (D.8) converge at the sonic
point, the regularity of the solution at the sonic point can be
written:
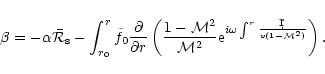 |
(D.9) |
In Eq. (D.8) the integrals diverge at infinity. Two
integrations by parts leads to define the two functions
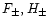 as follows:
as follows:
The pressure perturbation associated to the entropy perturbation
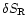 is:
is:
Far from the accretor, the pressure perturbation can be projected
onto the ingoing and outgoing sound waves. 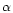 is chosen such
that there is no sound wave coming from infinity:
is chosen such
that there is no sound wave coming from infinity:
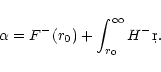 |
(D.13) |
Using Eqs. (D.9) and (D.13), and the fact that
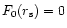 ,
we take the limit
,
we take the limit
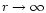 ,
,
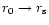 in
Eq. (D.12) and obtain:
in
Eq. (D.12) and obtain:
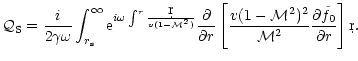 |
|
|
|
(D.14) |
This integral can be written with the following format, using the
homogeneous differential system (Eqs. (B.28), (B.29))
satisfied by
f0,g0:
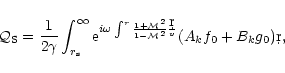 |
(D.15) |
where the functions
Ak(r),Bk(r) depend only on the unperturbed flow,
and the integral converges as 1/rk far from the accretor:
Two successive integrations by parts make the convergence of the
integral much faster, thus allowing an easier numerical calculation:
Appendix E: Asymptotic estimate of
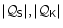 at high frequency
for
at high frequency
for
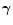 = 5/3
= 5/3
Equation (D.14) can be estimated in the limit
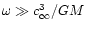 ,
when
,
when
 .
We treat the case of
radial (l=0) and non radial (
.
We treat the case of
radial (l=0) and non radial (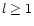 )
perturbations separately.
)
perturbations separately.
E.1 Radial perturbations
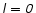
We use a local expansion of 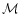 where
where 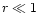 :
:
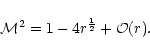 |
(E.1) |
Writing
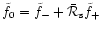 ,
we obtain
for
,
we obtain
for
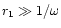 and
and 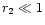 :
:
The range of validity
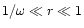 implies that
implies that
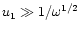 and
and
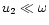 .
The contribution of the region
.
The contribution of the region
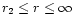 is negligible.
is negligible.
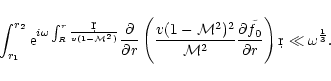 |
(E.3) |
The contribution of the region 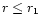 is estimated using the
asymptotic behaviour of the Bessel function J1:
is estimated using the
asymptotic behaviour of the Bessel function J1:
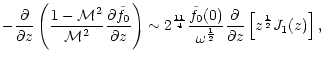 |
|
|
(E.4) |
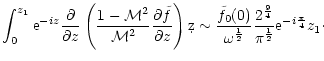 |
|
|
(E.5) |
Thus we deduce the acoustic efficiency at high frequency:
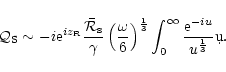 |
(E.6) |
The main contribution to the integral comes from the region where
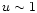 ,
i.e.
,
i.e.
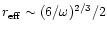 .
Equation (E.6) is rewritten in Eq. (28) using the Gamma
function.
.
Equation (E.6) is rewritten in Eq. (28) using the Gamma
function.
E.2 Non radial perturbations
As in the case of radial perturbations, the main contribution to the
integral comes from the region
accessible to the WKB approximation.
The outgoing wave is the main contributor to the integral
(D.14). Using the asymptotic development of v,c for
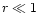 in Appendix A.2,
in Appendix A.2,
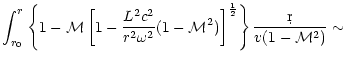 |
|
|
|
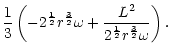 |
|
|
(E.7) |
With
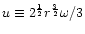 ,
the acoustic
efficiencies at high frequency are deduced from Eqs. (C.35),
(D.5), (D.14) and (E.7):
,
the acoustic
efficiencies at high frequency are deduced from Eqs. (C.35),
(D.5), (D.14) and (E.7):
Using the new variable
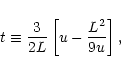 |
(E.10) |
the integrals in Eqs. (E.8)-(E.9) can be written using
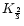 ,
the modified Bessel function of order 2/3
(Gradshteyn & Ryzhik 1980, p. 430):
,
the modified Bessel function of order 2/3
(Gradshteyn & Ryzhik 1980, p. 430):
Thus we obtain:
Here again, the main contribution to the integrals comes from the
region
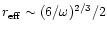 .
By contrast with
.
By contrast with
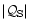 ,
,
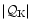 decreases at high frequency.
decreases at high frequency.
-
Bender, C. M., & Orszag, S. A. 1978, Advanced Mathematical Methods for
Scientists and Engineers (McGraw-Hill International Editions)
In the text
-
Bondi, H. 1952, MNRAS, 112, 195
In the text
NASA ADS
-
Bondi, H., & Hoyle, F. 1944, MNRAS, 104, 273
In the text
NASA ADS
-
Chang, K. M., & Ostriker, J. P. 1985, ApJ, 288, 428
In the text
NASA ADS
-
Foglizzo, T. 2001, A&A, in preparation, Paper II
In the text
-
Foglizzo, T., & Ruffert, M. 1997, A&A, 320, 342
In the text
NASA ADS
-
Foglizzo, T., & Tagger, M. 2000, A&A, 363, 174 (FT2000)
In the text
NASA ADS
-
Garlick, A. R. 1979, A&A, 73, 171
In the text
NASA ADS
-
Gradshteyn, I. S., & Ryzhik, I. M. 1980 (Academic Press, inc.)
In the text
-
Hoyle, F., & Lyttleton, R. A. 1939, Proc. Cam. Phil. Soc., 35, 405
In the text
-
Kovalenko, I. G., & Eremin, M. A. 1998, MNRAS, 298, 861
In the text
NASA ADS
-
Manmoto, T., Takeuchi, M., Mineshige, S., Matsumoto, R., & Negoro, H. 1996,
ApJ, 464, L135
In the text
NASA ADS
-
Moncrief, V. 1980, ApJ, 235, 1038
In the text
NASA ADS
-
Petrich, L. I., Shapiro, S. L., Stark, R. F., & Teukolsky, S. A. 1989,
ApJ, 336, 313
In the text
NASA ADS
-
Petterson, J. A., Silk, J., & Ostriker, J. P. 1980, MNRAS, 191, 571
In the text
NASA ADS
-
Ruffert, M. 1994a, ApJ, 427, 342
In the text
NASA ADS
-
Ruffert, M. 1994b, A&AS, 106, 505
In the text
NASA ADS
-
Ruffert, M., & Arnett, D. 1994, ApJ, 427, 351
In the text
NASA ADS
-
Watson, G. N. 1952, A Treatise on the Theory of Bessel Functions
(Cambridge University Press)
In the text
Copyright ESO 2001