A&A 368, 205-211 (2001)
DOI: 10.1051/0004-6361:20000563
Hypersonic collision of a blast wave on a low-mass star
D. García-Senz1,2 - N. Serichol1 - E. Bravo1,2
1 - Departament de Física i Enginyeria Nuclear, UPC, Sor
Eulàlia d'Anzizu s/n, B5, 08034 Barcelona, Spain
2 -
Institut d'Estudis Espacials de Catalunya, Gran Capità 2-4, 08034 Barcelona,
Spain
Received 4 October 2000 / Accepted 19 December 2000
Abstract
When a neutron star is born as a result of the accretion-induced collapse (AIC)
of a white dwarf, a small but significant fraction of its mass can be
simultaneously expelled at a velocity of around 104 kms-1. In this
paper
we study the collision between the gas ejected during the AIC of a white dwarf
and a 0.3  main-sequence star by using numerical
simulation techniques.
We found that, for a plausible combination of the orbital parameters and
impact energy, the low-mass star is completely destroyed. This scenario
can help to explain the origin of isolated millisecond pulsars.
main-sequence star by using numerical
simulation techniques.
We found that, for a plausible combination of the orbital parameters and
impact energy, the low-mass star is completely destroyed. This scenario
can help to explain the origin of isolated millisecond pulsars.
Key words: hydrodynamics - stars: supernovae: general - stars: pulsars: general
The issue of the origin of millisecond pulsars (MSP) has not yet been
satisfactorily settled. The favoured models assume that MSP
are the endpoint product of low-mass X-ray binary evolution. In these
models a persistent phase of accretion near the Eddington limit, which
causes the X-ray emission, would also be
responsible for the ultra-short spin of the pulsar (Bhattacharya 1996).
Another proposed model relies on the accretion-induced collapse of a
white dwarf. The starting configuration is a binary system composed of a
massive
white dwarf, the primary (
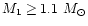 ), and a secondary star
(either evolved or unevolved) which come close enough as to allow the
exchange of matter through the inner Lagrangian point. Under the
appropriate conditions (mass accretion rate, initial configuration of the
system) the white dwarf would retain a fraction of the accreted matter, then
approaching the Chandrasekhar mass limit to finally collapse to a
neutron star (Canal et al. 1990). As a consequence of accretion, the former white
dwarf also increases its angular velocity. Conservation of angular momentum
during the collapse would give rise to a millisecond pulsar. As the implosion
process is thought to be rather quiet, the binary system has a good chance
of surviving in the end.
), and a secondary star
(either evolved or unevolved) which come close enough as to allow the
exchange of matter through the inner Lagrangian point. Under the
appropriate conditions (mass accretion rate, initial configuration of the
system) the white dwarf would retain a fraction of the accreted matter, then
approaching the Chandrasekhar mass limit to finally collapse to a
neutron star (Canal et al. 1990). As a consequence of accretion, the former white
dwarf also increases its angular velocity. Conservation of angular momentum
during the collapse would give rise to a millisecond pulsar. As the implosion
process is thought to be rather quiet, the binary system has a good chance
of surviving in the end.
If the origin of MSP is still vividly debated, the isolated
existence of a handful of them is even more
intriguing. In order for them to fit into the scenarios described
above, the key
question is how to get rid of the secondary once the MSP has formed. Nowadays
the most popular model invokes the ionization of the secondary by the
radiation of the pulsar (Ruderman et al. 1989). These models are supported by
the observation of a few
pulsars, such as PSR 1957+20, which have very low-mass orbiting companions
close enough to be heavily irradiated.
Nevertheless, there is no wide agreement and some authors claim that this
mechanism is not powerful enough to destroy the secondary (Ryba & Taylor 1991).
On the other hand, the AIC scenario could provide a natural way of removing the
secondary by direct interaction with the gas ejected during the implosion.
Unfortunately, several
calculations carried out in the past showed that, both for a main-sequence star
of 1  and for a red giant star of similar mass, even the
powerful blast wave caused by a type Ia supernova explosion is not
able to blow away the secondary. It would be extremely
difficult to shatter any secondary unless it had both a relatively large
radius and a low binding energy. Almost two decades ago, Iben & Tutukov (1984)
speculated that the collision of 0.1
and for a red giant star of similar mass, even the
powerful blast wave caused by a type Ia supernova explosion is not
able to blow away the secondary. It would be extremely
difficult to shatter any secondary unless it had both a relatively large
radius and a low binding energy. Almost two decades ago, Iben & Tutukov (1984)
speculated that the collision of 0.1  of gas ejected during the
AIC process, and moving near the escape velocity, would be enough to destroy
an unevolved star with
of gas ejected during the
AIC process, and moving near the escape velocity, would be enough to destroy
an unevolved star with
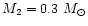 .
The main aim of this paper
is to
discern whether or not the collision of such a stream of gas would destroy the
low-mass secondary in the aforementioned conditions. The calculations were
carried out in three dimensions using a smoothed-particle hydrodynamics
(SPH) code. The orbit of the secondary is included for the first time
in the simulation of the impact. To some extent our work complete that
already done
by Fryxell & Arnett (1981), Livne et al. (1992) and, very recently, by
Marietta et al. (2000), which considered a
different kind of secondary star. In Sect. 2 we explain the details of the
initial configuration of our system and the relevant features of the method
of calculation. The evolution of the collision is presented in Sect. 3 and,
finally, our conclusions are summarized in Sect. 4.
.
The main aim of this paper
is to
discern whether or not the collision of such a stream of gas would destroy the
low-mass secondary in the aforementioned conditions. The calculations were
carried out in three dimensions using a smoothed-particle hydrodynamics
(SPH) code. The orbit of the secondary is included for the first time
in the simulation of the impact. To some extent our work complete that
already done
by Fryxell & Arnett (1981), Livne et al. (1992) and, very recently, by
Marietta et al. (2000), which considered a
different kind of secondary star. In Sect. 2 we explain the details of the
initial configuration of our system and the relevant features of the method
of calculation. The evolution of the collision is presented in Sect. 3 and,
finally, our conclusions are summarized in Sect. 4.
In the following we will assume that a compact binary system consisting of a
white dwarf of about 1.3  ,
composed
of oxygen, neon and
magnesium, plus a secondary of 0.35-0.4
,
composed
of oxygen, neon and
magnesium, plus a secondary of 0.35-0.4  has
come into being after one or two non-conservative mass-loss episodes
in previous common envelope stages (see Sect. 4 for a brief discussion).
Let us also assume that the
orbiting radius is small enough to keep the Roche lobe of the secondary
M2, in contact with its outer surface. Hence, for a given mass and radius
of the secondary the orbital separation and orbital velocity can be inferred.
Then, the accretion rate can be
approximated by (Ritter 1985):
has
come into being after one or two non-conservative mass-loss episodes
in previous common envelope stages (see Sect. 4 for a brief discussion).
Let us also assume that the
orbiting radius is small enough to keep the Roche lobe of the secondary
M2, in contact with its outer surface. Hence, for a given mass and radius
of the secondary the orbital separation and orbital velocity can be inferred.
Then, the accretion rate can be
approximated by (Ritter 1985):
![$\displaystyle \dot M_1=
[r_{g_1}^2R_1^2M_1\Omega_1-\dot J_{\rm syst}]\left\{\frac{G^{2/3}[(5+3\alpha_2)M_1-
6M_2]}{6(M_1+M_2)^{1/3}\omega^{1/3}} \right.$](/articles/aa/full/2001/10/aa10328/img6.gif) 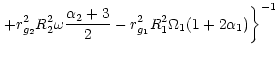 |
(1) |
where
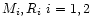 refer to mass and radius of the primary and secondary
respectively, and
refer to mass and radius of the primary and secondary
respectively, and
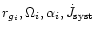 and
and
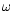 are the
gyration radius, spin angular frequency, mass-radius exponent, systemic loss
of angular momentum and orbital angular frequency respectively. Two sources
of loss of angular
momentum have been considered: gravitational wave radiation (Landau & Lifshitz
1987) and magnetic braking (Patterson 1984). Given the appropriate initial
conditions
(here
M10=1.35, 1.30
are the
gyration radius, spin angular frequency, mass-radius exponent, systemic loss
of angular momentum and orbital angular frequency respectively. Two sources
of loss of angular
momentum have been considered: gravitational wave radiation (Landau & Lifshitz
1987) and magnetic braking (Patterson 1984). Given the appropriate initial
conditions
(here
M10=1.35, 1.30  ,
M20=0.35, 0.4
,
M20=0.35, 0.4  ,
R20=0.56, 0.54
,
R20=0.56, 0.54 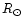 respectively, and
respectively, and
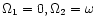 )
and supposing that the
flowing matter is accreted through a Keplerian disc with internal radius
R1, transferring part or all of its angular momentum to the white
dwarf, we can
roughly track the evolution of the primary prior to collapse. The mass-radius
relationship for the white dwarf is taken from
Nauenberg (1972) and is
)
and supposing that the
flowing matter is accreted through a Keplerian disc with internal radius
R1, transferring part or all of its angular momentum to the white
dwarf, we can
roughly track the evolution of the primary prior to collapse. The mass-radius
relationship for the white dwarf is taken from
Nauenberg (1972) and is
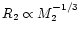 for the convective
secondary.
As can be seen in Fig. 1, the resulting
accretion rate decreases with time from few times
for the convective
secondary.
As can be seen in Fig. 1, the resulting
accretion rate decreases with time from few times
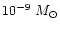 yr-1 to
yr-1 to
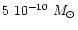 yr-1.
yr-1.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10328f1.eps}\end{figure}](/articles/aa/full/2001/10/aa10328/Timg16.gif) |
Figure 1:
Evolution of the accretion rate as a function
of the instantaneous mass of the white dwarf for two cases: M10=1.3  ,
M20=0.4 ,
M20=0.4  (continuum line), and
M10=1.35
(continuum line), and
M10=1.35  ,
M20=0.35 (thick line) ,
M20=0.35 (thick line) |
| Open with DEXTER |
According to Nomoto & Kondo (1991),
such a slow rate would lead to the collapse of the star provided
its initial mass is higher than 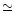 1.3
1.3  ,
otherwise the
nova-like phenomenon would prevent mass growth of the white dwarf. This
leaves white dwarfs composed of oxygen, neon and magnesium as the only
candidates for collapse (Gutiérrez et al. 1996). For example, for an
,
otherwise the
nova-like phenomenon would prevent mass growth of the white dwarf. This
leaves white dwarfs composed of oxygen, neon and magnesium as the only
candidates for collapse (Gutiérrez et al. 1996). For example, for an
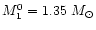 star, it would take about 50 Myr to accumulate enough
material to reach 1.4
star, it would take about 50 Myr to accumulate enough
material to reach 1.4  and ensure the implosion of the
primary. At
that moment the secondary mass would be
and ensure the implosion of the
primary. At
that moment the secondary mass would be 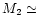 0.3
0.3  and it
would be orbiting
at 2.3
and it
would be orbiting
at 2.3 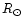 from the nascent neutron star with a
period of 0.34 days. Conservation of the
angular momentum, gained by the white dwarf during the accretion process, will
give rise to a pulsar spinning at a millisecond level after the
implosion.
The actual value of the
mass ejected during the collapse of the white dwarf is not known but
it is thought to be between
zero and a few tenths of
solar masses. The impacting velocity
has been taken to be close to the escape
velocity, around
from the nascent neutron star with a
period of 0.34 days. Conservation of the
angular momentum, gained by the white dwarf during the accretion process, will
give rise to a pulsar spinning at a millisecond level after the
implosion.
The actual value of the
mass ejected during the collapse of the white dwarf is not known but
it is thought to be between
zero and a few tenths of
solar masses. The impacting velocity
has been taken to be close to the escape
velocity, around 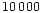 kms-1. This configuration,
summarized in Table 1, represents the starting point of our simulations.
kms-1. This configuration,
summarized in Table 1, represents the starting point of our simulations.
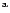 The parameters are: mass, radius and central density of the secondary, orbital
separation, period, rms velocity of the ejecta, incident mass, incident
momentum and ratio between the incident kinetic energy
and the binding energy of the secondary
respectively.
The parameters are: mass, radius and central density of the secondary, orbital
separation, period, rms velocity of the ejecta, incident mass, incident
momentum and ratio between the incident kinetic energy
and the binding energy of the secondary
respectively.
It is well known that low-mass stars have large convective envelopes. In fact,
for a 0.3  star, the whole interior is convective and its structure
can be approximated by a n=3/2 polytrope, which is less centrally
condensed than a radiative type n=3 polytrope of the same mass. Thus, low-mass
stars have a higher concentration of matter near the surface, which is where
the
ablation takes place in our scenario, being easier to destroy than more massive
stars.
Equilibrium models for these stars have recently been calculated by
Chabrier & Baraffe (1997). We have fitted one of their models with
star, the whole interior is convective and its structure
can be approximated by a n=3/2 polytrope, which is less centrally
condensed than a radiative type n=3 polytrope of the same mass. Thus, low-mass
stars have a higher concentration of matter near the surface, which is where
the
ablation takes place in our scenario, being easier to destroy than more massive
stars.
Equilibrium models for these stars have recently been calculated by
Chabrier & Baraffe (1997). We have fitted one of their models with
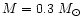 by an
n=3/2 polytrope (Fig. 2). The resulting structure was mapped to a
three-dimensional distribution of 22400 particles of equal mass. A wedge was
taken from the spherical
ejecta with size twice the radius of the secondary and thickness
of one-third of the orbital separation (Colgate 1970). The density
profile inside the ejecta
follows a power-law distribution
by an
n=3/2 polytrope (Fig. 2). The resulting structure was mapped to a
three-dimensional distribution of 22400 particles of equal mass. A wedge was
taken from the spherical
ejecta with size twice the radius of the secondary and thickness
of one-third of the orbital separation (Colgate 1970). The density
profile inside the ejecta
follows a power-law distribution
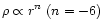 ,
and a homologous expansion
rate
,
and a homologous expansion
rate
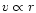 ,
which
is more realistic than the flat profile considered in most of the previous
works dealing
with collisions. Given the
total kinetic energy of the gas
(here, the specific kinetic energy was
,
which
is more realistic than the flat profile considered in most of the previous
works dealing
with collisions. Given the
total kinetic energy of the gas
(here, the specific kinetic energy was
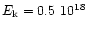 ergg-1),
this
resulted in a velocity range from 7900 kms-1 in the innermost part
of the shell to 14200 kms-1 at the outer edge.
The number of mass points in the chunk of the ejecta was 2200.
ergg-1),
this
resulted in a velocity range from 7900 kms-1 in the innermost part
of the shell to 14200 kms-1 at the outer edge.
The number of mass points in the chunk of the ejecta was 2200.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10328f2.eps}\end{figure}](/articles/aa/full/2001/10/aa10328/Timg32.gif) |
Figure 2:
Mass distribution for polytropes of index n=3/2 and n=3 with
total mass 0.3  |
| Open with DEXTER |
The interaction between the hypersonic ejecta and the secondary was simulated
using a SPH code. The orbital dynamics (spin of the secondary and orbital
rotation)
was also incorporated into the
simulation in order to take into account the gravitational attraction onto the
ablated matter, due to the 1.3  neutron star. The tidal torques
produced by the neutron star could be specially relevant in determining the
stability of the perturbed-expanded-secondary. The features of
the particle hydrocode are fairly standard (Hernquist & Katz 1989) and do not
warrant further explanation. Gravitation was calculated by means of a
multipolar expansion, retaining up to the quadrupole
term. The included physics is simple: the equation of state is that of an
ideal gas of ions and electrons plus radiation. Shocks were handled by using
the SPH form of the artificial viscosity. The secondary was composed entirely of
hydrogen whereas the ejecta was composed of oxygen, neon and
magnesium.
neutron star. The tidal torques
produced by the neutron star could be specially relevant in determining the
stability of the perturbed-expanded-secondary. The features of
the particle hydrocode are fairly standard (Hernquist & Katz 1989) and do not
warrant further explanation. Gravitation was calculated by means of a
multipolar expansion, retaining up to the quadrupole
term. The included physics is simple: the equation of state is that of an
ideal gas of ions and electrons plus radiation. Shocks were handled by using
the SPH form of the artificial viscosity. The secondary was composed entirely of
hydrogen whereas the ejecta was composed of oxygen, neon and
magnesium.
To test the stability of the initial configuration a model consisting of a
static point mass of 1.3  and
an orbiting secondary of 0.3
and
an orbiting secondary of 0.3  was run prior to the simulations given
in Table 1. We followed one complete orbit, during which the trajectory of
the secondary remained circular. No mass loss was observed during the evolution
in spite of the tidal deformation of the secondary and the numerical noise.
was run prior to the simulations given
in Table 1. We followed one complete orbit, during which the trajectory of
the secondary remained circular. No mass loss was observed during the evolution
in spite of the tidal deformation of the secondary and the numerical noise.
As can be seen in Table 1, there is a large ratio between the incident kinetic
energy and the
binding energy of the secondary. Therefore, even a low shock
efficiency could lead to the total or partial disruption of the star. As
was pointed out in previous calculations (i.e. Fryxell & Arnett 1981), the
effect of the supersonic collision is twofold. First, the direct momentum
transfer
from the gas to the star strips a portion of the envelope of the secondary,
also giving a radial velocity component of a few dozens of kilometres per
second to the remnant. Second, the energy deposition
which takes place in this inelastic collision ablates part of the envelope and
heats the core.
The evolution of the interaction is summarized in the nine snapshots shown
in Fig. 5. According to the simulation, the process can be roughly
separated
into four stages, represented by four limiting times:
1) 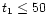 s: this is
the time taken by the ejecta to move a distance equal to its own width. During
this period there is an inelastic collision with the envelope of the star, in
which the incoming flow of gas transforms its kinetic energy into internal:
s: this is
the time taken by the ejecta to move a distance equal to its own width. During
this period there is an inelastic collision with the envelope of the star, in
which the incoming flow of gas transforms its kinetic energy into internal:
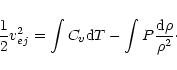 |
(2) |
The initial specific kinetic energy is in this way stored basically in the
radiation field. According to our simulation, the density increased by a
factor thirty while the temperature rose to 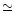 7 107 K,
which was not high enough to allow any substantial combustion of the
hydrogen in the scale of time considered. The outermost stellar material
was also compressed and heated. The overpressure gave rise to a
shock wave which began to move towards the centre of the secondary.
7 107 K,
which was not high enough to allow any substantial combustion of the
hydrogen in the scale of time considered. The outermost stellar material
was also compressed and heated. The overpressure gave rise to a
shock wave which began to move towards the centre of the secondary.
2)
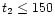 s: this is the time taken by the ejecta to cross the secondary.
The flow of gas wrapped around the low-mass star until it finally went out and the
interaction ceased. A fraction of the outermost zone
(
s: this is the time taken by the ejecta to cross the secondary.
The flow of gas wrapped around the low-mass star until it finally went out and the
interaction ceased. A fraction of the outermost zone
(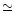 4% of the total mass of the secondary) was
stripped during the interaction, becoming unbound and leaving the star. On the
other hand, part of the impacting gas reversed its velocity and
moved back towards the neutron star.
4% of the total mass of the secondary) was
stripped during the interaction, becoming unbound and leaving the star. On the
other hand, part of the impacting gas reversed its velocity and
moved back towards the neutron star.
3)
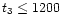 s: this is roughly the time necessary for the
induced shock to move a distance equal to the diameter of the secondary. The
propagation of the shock is depicted in Fig. 3, in which the density jump
is shown at four different times. By dividing the distance between the
second and fourth
peaks, at t=149 s and t=457 s respectively, by the elapsed time we got an
average shock velocity of
s: this is roughly the time necessary for the
induced shock to move a distance equal to the diameter of the secondary. The
propagation of the shock is depicted in Fig. 3, in which the density jump
is shown at four different times. By dividing the distance between the
second and fourth
peaks, at t=149 s and t=457 s respectively, by the elapsed time we got an
average shock velocity of
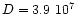 cms-1,
or a Mach number, Mn, of about 2. The
density jump predicted by the classical theory of shock waves
(Landau & Lifshitz 1987) is:
cms-1,
or a Mach number, Mn, of about 2. The
density jump predicted by the classical theory of shock waves
(Landau & Lifshitz 1987) is:
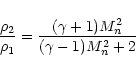 |
(3) |
taking
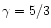 and Mn=2, the resulting density jump is 2.3, not much
different to the SPH result
and Mn=2, the resulting density jump is 2.3, not much
different to the SPH result
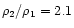 at t=250 s, as can be deduced
from Fig. 3. The shock wave is strong at early times but it becomes
weaker as the wave goes through the positive density gradient of the secondary. Radiative losses
also tend to damp the shock, especially at the beginning, when the Mach number
is higher. Nevertheless, the radiated energy is only a small fraction of the
internal and kinetic energy of the shocked gas.
We have estimated that even though radiative losses are large at the very
beginning, when the external piston is still working, they remain well below
at t=250 s, as can be deduced
from Fig. 3. The shock wave is strong at early times but it becomes
weaker as the wave goes through the positive density gradient of the secondary. Radiative losses
also tend to damp the shock, especially at the beginning, when the Mach number
is higher. Nevertheless, the radiated energy is only a small fraction of the
internal and kinetic energy of the shocked gas.
We have estimated that even though radiative losses are large at the very
beginning, when the external piston is still working, they remain well below
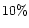 of the energy deposited by the wave once the shock was born.
In addition, the radiated energy is not lost by the star,
owing to
the small mean free path of the photons. Therefore, the main effect of
radiative losses is to slightly redistribute the energy deposited by the wave.
We have neglected them in a first approximation.
Once this stage was completed, a great deal of the original
kinetic energy carried by the ejecta was spread through the secondary by
the shock wave. At the same time, direct momentum transfer from the impacting
gas to the secondary and
the rocket effect due to the ablation imparted a radial velocity of about
50 kms-1 to the centre of mass of the remaining material (in the rest
frame of the neutron star). As a consequence its orbit began to become slightly eccentric. At t=1200 s
the mass lost was
of the energy deposited by the wave once the shock was born.
In addition, the radiated energy is not lost by the star,
owing to
the small mean free path of the photons. Therefore, the main effect of
radiative losses is to slightly redistribute the energy deposited by the wave.
We have neglected them in a first approximation.
Once this stage was completed, a great deal of the original
kinetic energy carried by the ejecta was spread through the secondary by
the shock wave. At the same time, direct momentum transfer from the impacting
gas to the secondary and
the rocket effect due to the ablation imparted a radial velocity of about
50 kms-1 to the centre of mass of the remaining material (in the rest
frame of the neutron star). As a consequence its orbit began to become slightly eccentric. At t=1200 s
the mass lost was 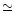 6% of the low-mass star.
6% of the low-mass star.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10328f3.eps}\end{figure}](/articles/aa/full/2001/10/aa10328/Timg42.gif) |
Figure 3:
Density jump caused by the propagation of the shock wave launched
by the collision through the secondary star at different times. The continuum
line, at t=0 s, is the initial unperturbed profile |
| Open with DEXTER |
4) in
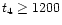 s a long period ensued in which the excess of internal
energy deposited by the shock wave was converted into kinetic. The secondary
began to oscillate with
radial pulsations while it remained orbiting and losing matter
to the nearby neutron star (last five snapshots in Fig. 5). As the
expelled material was carrying rotational and orbital angular momentum, part
of the debris formed an accretion disc around the neutron star. The secondary
finally achieved the curious "galaxy'' shape depicted in the last two
snapshots in Fig. 5. In our last model, at
s a long period ensued in which the excess of internal
energy deposited by the shock wave was converted into kinetic. The secondary
began to oscillate with
radial pulsations while it remained orbiting and losing matter
to the nearby neutron star (last five snapshots in Fig. 5). As the
expelled material was carrying rotational and orbital angular momentum, part
of the debris formed an accretion disc around the neutron star. The secondary
finally achieved the curious "galaxy'' shape depicted in the last two
snapshots in Fig. 5. In our last model, at 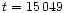 s, the low-mass star
had completed almost a third of the orbit, lost
s, the low-mass star
had completed almost a third of the orbit, lost 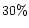 of its mass and
acquired an orbital eccentricity of
of its mass and
acquired an orbital eccentricity of 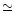 0.2.
0.2.
Unfortunately our computer resources did not allow us to continue the
simulation beyond this point. Once the accretion disc began to form,
the time-step
became too small to follow the phenomenon over a significant fraction of
the orbital motion. Nevertheless, the total destruction of the secondary is
the more probable outcome, as it can be deduced from Fig. 4. This figure
depicts the total energy profile and the radius of the secondary at
time 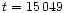 s. The Roche lobe radius at this time is
s. The Roche lobe radius at this time is
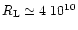 cm, which encloses only 0.09
cm, which encloses only 0.09  .
At this Lagrangian coordinate the total energy is nearly zero as can be seen
in the figure. Therefore, we
expect that the secondary will finally disappear after a few orbits, leaving
an accretion disc around the compact object.
.
At this Lagrangian coordinate the total energy is nearly zero as can be seen
in the figure. Therefore, we
expect that the secondary will finally disappear after a few orbits, leaving
an accretion disc around the compact object.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10328f4.eps}\end{figure}](/articles/aa/full/2001/10/aa10328/Timg46.gif) |
Figure 4:
Total energy profile and radial coordinate as a function of the
enclosed mass of the 0.3  secondary for both the initial time, t= 0 s, and
the final time considered,
secondary for both the initial time, t= 0 s, and
the final time considered, 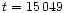 s s |
| Open with DEXTER |
We have carried out a complete simulation of the collision process
between the 0.1  of gas ejected during the accretion-induced
collapse of a white dwarf and a low-mass star (0.3
of gas ejected during the accretion-induced
collapse of a white dwarf and a low-mass star (0.3  ). The
calculation was done in three dimensions using an SPH hydrocode,
which allowed us to incorporate both the orbital elements of the compact
binary and the gravitational
force exerted by the neutron star. The main result of our work is that the
combination of the strong collision with the pulling force toward the compact
object is able to completely destroy the secondary star, leaving the neutron
star alone. Taking into account that the progenitor white dwarf was spun-up
by mass transfer in the previous stage to the collapse, the
final outcome of this scenario may be either an isolated millisecond pulsar
or a normal field pulsar, if magnetic dipole or gravitational radiation
were intense enough to slow down the initially fast rotation.
). The
calculation was done in three dimensions using an SPH hydrocode,
which allowed us to incorporate both the orbital elements of the compact
binary and the gravitational
force exerted by the neutron star. The main result of our work is that the
combination of the strong collision with the pulling force toward the compact
object is able to completely destroy the secondary star, leaving the neutron
star alone. Taking into account that the progenitor white dwarf was spun-up
by mass transfer in the previous stage to the collapse, the
final outcome of this scenario may be either an isolated millisecond pulsar
or a normal field pulsar, if magnetic dipole or gravitational radiation
were intense enough to slow down the initially fast rotation.
In the standard
explanation of the millisecond pulsars phenomenon, the combination of a
very short period and a small first period derivative is interpreted as an
old neutron star (i.e. with low magnetic field) which has been recycled by
further
mass accretion from the companion star. Nevertheless, in the framework of the
AIC of a white dwarf the
observed P-P
combination could be addressed if the neutron star were the result
of the collapse of a relatively low-magnetized white dwarf which gives rise
to a neutron star with a magnetic field
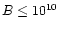 G
through flux conservation
(Michel 1987; Narayan & Popham 1989). On the other hand, gravitational
radiation might be intense after the collapse of the white dwarf, spinning
down the pulsar if the neutron star were born without complete spherical
symmetry. Small asymmetries could be present at the very beginning due to
both, initial eccentricity and internal
inhomogeneities formed during the collapse process itself.
Quadripolar
gravitational radiation induced by eccentricity could be intense at the
beginning, but it becomes less efficient as the period increases and
rotationally sustained eccentricity rapidly goes down.
The resulting
braking would probably not be able to take the pulsar out from the
millisecond region unless the initial eccentricity were rather large.
The amount of gravitational radiation due to the internal instabilities is
poorly known. In particular, the so called r-mode instability (Anderson et al.
1999) could be very efficient at removing rotational angular momentum and,
if the appropriate conditions are fulfilled, may decelerate the pulsar
to a period above 20 ms.
Nevertheless, that sort of instability largely relies on pieces of neutron
star physics, such as
the initial temperature distribution or the details of the cooling rate,
which are not yet completely understood.
Moreover, neutron stars which are the endproduct of the collapse of
ONeMg massive white dwarfs are thought to have lower entropy than that
resulting from the collapse of iron cores of massive stars (Woosley & Weaver
1986). Hence the
initial temperature distribution within the neutron star may also be
different. Thus, in spite of the aforementioned difficulties of the proposed
scenario and given that the standard scenario is not free of problems
either, the AIC route to produce steady millisecond rotators cannot be
ruled out at present time.
G
through flux conservation
(Michel 1987; Narayan & Popham 1989). On the other hand, gravitational
radiation might be intense after the collapse of the white dwarf, spinning
down the pulsar if the neutron star were born without complete spherical
symmetry. Small asymmetries could be present at the very beginning due to
both, initial eccentricity and internal
inhomogeneities formed during the collapse process itself.
Quadripolar
gravitational radiation induced by eccentricity could be intense at the
beginning, but it becomes less efficient as the period increases and
rotationally sustained eccentricity rapidly goes down.
The resulting
braking would probably not be able to take the pulsar out from the
millisecond region unless the initial eccentricity were rather large.
The amount of gravitational radiation due to the internal instabilities is
poorly known. In particular, the so called r-mode instability (Anderson et al.
1999) could be very efficient at removing rotational angular momentum and,
if the appropriate conditions are fulfilled, may decelerate the pulsar
to a period above 20 ms.
Nevertheless, that sort of instability largely relies on pieces of neutron
star physics, such as
the initial temperature distribution or the details of the cooling rate,
which are not yet completely understood.
Moreover, neutron stars which are the endproduct of the collapse of
ONeMg massive white dwarfs are thought to have lower entropy than that
resulting from the collapse of iron cores of massive stars (Woosley & Weaver
1986). Hence the
initial temperature distribution within the neutron star may also be
different. Thus, in spite of the aforementioned difficulties of the proposed
scenario and given that the standard scenario is not free of problems
either, the AIC route to produce steady millisecond rotators cannot be
ruled out at present time.
The combination of an accreting massive white dwarf plus a low-mass star
(0.3-0.4  )
orbiting in a close orbit with a period of about 0.5 days
could, however, be difficult to find in nature. First of all the
progenitor binary system must undergo, at least, a common envelope
episode in order to shrink the orbit and bring the stars
close enough to allow Roche lobe overflow of the secondary.
Recently, Sandquist et al. (1998) followed numerically the evolution of
binary systems consisting of an asymptotic giant branch star of 5
)
orbiting in a close orbit with a period of about 0.5 days
could, however, be difficult to find in nature. First of all the
progenitor binary system must undergo, at least, a common envelope
episode in order to shrink the orbit and bring the stars
close enough to allow Roche lobe overflow of the secondary.
Recently, Sandquist et al. (1998) followed numerically the evolution of
binary systems consisting of an asymptotic giant branch star of 5  and a 0.4
and a 0.4  secondary in an initially wide orbit. They concluded that
after one common envelope episode a compact binary would emerge consisting
of the core of the massive star and the low-mass secondary orbiting at a
distance of 4.37
secondary in an initially wide orbit. They concluded that
after one common envelope episode a compact binary would emerge consisting
of the core of the massive star and the low-mass secondary orbiting at a
distance of 4.37 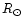 with a period of only 0.9 days. Even though
the mass
of the primary is larger in our case, 10-11
with a period of only 0.9 days. Even though
the mass
of the primary is larger in our case, 10-11  in order to get a
1.3-1.35
in order to get a
1.3-1.35  white dwarf, these stars probably undergo an additional
common envelope episode related to the carbon shell burning phase
(García-Berro & Iben 1994), thus
enhancing the possibility of the stars settling into a compact
orbit. A second
objection is related to the accretion rate from the secondary to the
massive white dwarf. As discussed in Sect. 2 the expected rate is rather low,
of the order of 10-9
white dwarf, these stars probably undergo an additional
common envelope episode related to the carbon shell burning phase
(García-Berro & Iben 1994), thus
enhancing the possibility of the stars settling into a compact
orbit. A second
objection is related to the accretion rate from the secondary to the
massive white dwarf. As discussed in Sect. 2 the expected rate is rather low,
of the order of 10-9  yr-1, which is currently thought to
lead to the total or partial expulsion of the accreted matter due to hydrogen
flashes on the white dwarf surface. Nevertheless, owing to the large initial
mass of the white dwarf it is necessary to accrete only 0.05-0.10
yr-1, which is currently thought to
lead to the total or partial expulsion of the accreted matter due to hydrogen
flashes on the white dwarf surface. Nevertheless, owing to the large initial
mass of the white dwarf it is necessary to accrete only 0.05-0.10  to reach the Chandrasekhar-mass limit. Therefore,
even a low effective accretion rate might lead to collapse. In addition,
some authors (see, for instance, Fig. 3 of Nomoto & Kondo 1991) claimed
that, for massive white dwarfs composed of
oxygen, neon and magnesium, very low accretion rates would lead directly to
the implosion of the object, due to depressurization induced by
electronic captures on 20Ne. The realization frequency of a
system consisting of a low-mass star in close orbit around a
massive ONeMg white dwarf is not incompatible with the rate of formation of
isolated millisecond pulsars. The formation rate in the first case is
roughly
to reach the Chandrasekhar-mass limit. Therefore,
even a low effective accretion rate might lead to collapse. In addition,
some authors (see, for instance, Fig. 3 of Nomoto & Kondo 1991) claimed
that, for massive white dwarfs composed of
oxygen, neon and magnesium, very low accretion rates would lead directly to
the implosion of the object, due to depressurization induced by
electronic captures on 20Ne. The realization frequency of a
system consisting of a low-mass star in close orbit around a
massive ONeMg white dwarf is not incompatible with the rate of formation of
isolated millisecond pulsars. The formation rate in the first case is
roughly
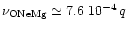 yr-1 (Iben & Tutukov 1984), where
q=M2/M1, is the main sequence mass-ratio of the two components. Taking
yr-1 (Iben & Tutukov 1984), where
q=M2/M1, is the main sequence mass-ratio of the two components. Taking
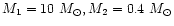 and, considering the difficulties
faced by the white dwarf to grow in mass owing to the involved accretion rates,
we would expect that
and, considering the difficulties
faced by the white dwarf to grow in mass owing to the involved accretion rates,
we would expect that
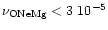 yr-1. A rough lower limit for the isolated MSP formation rate can be
inferred from
Lorimer (1997), who studied the formation rate of 16 low-mass binary pulsars
in the solar
neighbourhood, three of them isolated MSP, and gave a lower limit for that rate. Restricting his same
analysis just to
these three pulsars we infer
yr-1. A rough lower limit for the isolated MSP formation rate can be
inferred from
Lorimer (1997), who studied the formation rate of 16 low-mass binary pulsars
in the solar
neighbourhood, three of them isolated MSP, and gave a lower limit for that rate. Restricting his same
analysis just to
these three pulsars we infer
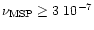 yr-1. Thus,
in view of the large factor between these two limits, it would be enough that
one among a few dozens of massive accreting ONeMg white dwarfs reached the
Chandrasekhar-mass limit to explain the observed population of isolated
millisecond pulsars
yr-1. Thus,
in view of the large factor between these two limits, it would be enough that
one among a few dozens of massive accreting ONeMg white dwarfs reached the
Chandrasekhar-mass limit to explain the observed population of isolated
millisecond pulsars
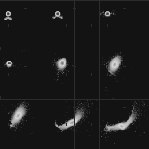 |
Figure 5:
Evolution of the interaction between the blast wave and the low-mass
star. The brightness is proportional to the logarithm of the density. Although
the neutron star cannot be seen it is located at the centre of curvature of
the ejecta at t=0 s (first snapshot), remaining there throughout the process. The
elapsed time is t= 0 s, 45 s, 149 s, 513 s, 2467 s, 4337 s, 6257 s, 12240 s
and 15048 s respectively |
| Open with DEXTER |
Regardless of the way the compact binary has finally formed, the result of our
simulation gives an alternative mechanism to the evaporative
irradiation of the secondary in order to get an isolated pulsar.
Moreover, different explosion strengths could destroy the secondary only
partially, leaving very low-mass remnants orbiting around the central pulsar.
Acknowledgements
This work was supported by CICYT funds PB98-1183-c03-02, AYA2000-1785
and CIRIT GRQ grants.
- Anderson, N., Kokkotas, K., & Schutz, B. F. 1999, ApJ, 510, 846
In the text
NASA ADS
-
Bhattacharya, D. 1996, in Compact Stars in Binaries, ed. J. V. Paradjis,
E. P. J. van den Heuvel, & E. Kuulkers (Dordrecht: Kluwer), 243
In the text
- Canal, R., Isern, J., & Labay, J. 1990, ARA&A, 28, 183
In the text
NASA ADS
- Chabrier, G., & Baraffe, I. 1997, A&A, 327, 1039
In the text
NASA ADS
- Colgate, S. 1970, Nature, 225, 247
In the text
- Fryxell, B., & Arnett, D. 1981, ApJ, 243, 994
In the text
NASA ADS
- García-Berro, E., & Iben, I. 1994, ApJ, 434, 306
In the text
NASA ADS
- Gutiérrez, J., García-Berro, E., Iben, I., et al. 1996, ApJ, 459, 701
In the text
NASA ADS
- Hernsquitz, L., & Katz, N. 1989, ApJS, 70, 419
In the text
NASA ADS
- Iben, I., & Tutukov, A. 1984, ApJS, 54, 335
In the text
NASA ADS
- Landau, L. D., & Lifshitz, E. M. 1987, Fluid Mechanics
(Oxford: Pergamon)
In the text
- Livne, E., Tuchman, Y., & Wheeler, J. C. 1992, ApJ, 399, 665
In the text
NASA ADS
- Lorimer, D. R. 1996, in Compact Stars in Binaries, ed. J. V. Paradjis,
E. P. J. van den Heuvel, & E. Kuulkers (Dordrecht: Kluwer), 235
- Marietta, E., Burrows, A., & Fryxell, B. 2000, ApJS, 128, 615
In the text
NASA ADS
- Michel, F. C. 1987, Nature, 329, 310
In the text
NASA ADS
- Nauenberg, M. 1972, ApJ, 175, 417
In the text
NASA ADS
- Narayan, R., & Popham, R. 1989, ApJ, 346, L25
In the text
NASA ADS
- Nomoto, K., & Kondo, Y. 1991, ApJ, 367, L19
In the text
NASA ADS
- Patterson, J. 1984, ApJS, 54, 443
In the text
NASA ADS
- Ritter, H. 1985, A&A, 148, 207
In the text
NASA ADS
- Ruderman, M., & Shaham, J. 1985, ApJ, 289, 244
NASA ADS
- Ryba, M. F., & Taylor, J. H. 1991, ApJ, 380, 557
In the text
NASA ADS
- Sandquist, E. L., Taam, R. E., Chen, X., Bodenheimer, P., & Burket, A. 1998, ApJ, 500, 909
In the text
NASA ADS
- Woosley, S. E., & Weaver, T. A. 1986, ARA&A, 24, 205
In the text
NASA ADS
Copyright ESO 2001
![$\displaystyle \dot M_1=
[r_{g_1}^2R_1^2M_1\Omega_1-\dot J_{\rm syst}]\left\{\frac{G^{2/3}[(5+3\alpha_2)M_1-
6M_2]}{6(M_1+M_2)^{1/3}\omega^{1/3}} \right.$](/articles/aa/full/2001/10/aa10328/img6.gif)
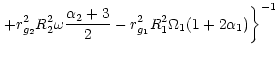
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10328f1.eps}\end{figure}](/articles/aa/full/2001/10/aa10328/Timg16.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10328f2.eps}\end{figure}](/articles/aa/full/2001/10/aa10328/Timg32.gif)
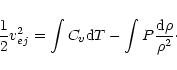
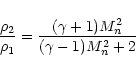
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10328f3.eps}\end{figure}](/articles/aa/full/2001/10/aa10328/Timg42.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10328f4.eps}\end{figure}](/articles/aa/full/2001/10/aa10328/Timg46.gif)
