A&A 368, 160-174 (2001)
DOI: 10.1051/0004-6361:20000409
L. Cidale1 - J. Zorec2 - L. Tringaniello1
1 - Facultad de Ciencias Astronómicas y Geofísicas, Universidad
de La Plata, Paseo del Bosque S/N, 1900 La Plata, Argentina
2 -
Institut d'Astrophysique de Paris, CNRS, 98bis Bd. Arago, 75014 Paris,
France
Received 3 October 2000 / Accepted 29 November 2000
Abstract
Low resolution spectra in the
![]() Å wavelength
range of 23 stars with the B[e] phenomenon are presented. Spectral
classification of 15 program stars was performed using the BCD
spectrophotometric system, based on the study of the Balmer discontinuity,
which is independent of interstellar and circumstellar dust extinctions and of
circumstellar gas emissions and/or absorptions. From calibrations of the
Å wavelength
range of 23 stars with the B[e] phenomenon are presented. Spectral
classification of 15 program stars was performed using the BCD
spectrophotometric system, based on the study of the Balmer discontinuity,
which is independent of interstellar and circumstellar dust extinctions and of
circumstellar gas emissions and/or absorptions. From calibrations of the
![]() BCD parameters we determined the (
BCD parameters we determined the (
![]() of the studied stars. For stars where this method could not be applied,
we tried to estimate the temperature of the central star by using the Balmer
and He I emission lines and/or their visible energy distribution. The
colour temperature and the temperatures obtained from the study of Balmer and
He I lines are consistent with each other. The new results are compared
with those obtained previously by other authors and discussed for each star
individually. For some stars, differences between the effective temperatures
derived using the BCD classification system and those obtained elsewhere,
based on photometric or spectroscopic analysis, imply spectral-type
classification disagreements ranging from 2-3 up to 6 B sub-spectral types.
The fundamental parameters of AS 119, CD-24
of the studied stars. For stars where this method could not be applied,
we tried to estimate the temperature of the central star by using the Balmer
and He I emission lines and/or their visible energy distribution. The
colour temperature and the temperatures obtained from the study of Balmer and
He I lines are consistent with each other. The new results are compared
with those obtained previously by other authors and discussed for each star
individually. For some stars, differences between the effective temperatures
derived using the BCD classification system and those obtained elsewhere,
based on photometric or spectroscopic analysis, imply spectral-type
classification disagreements ranging from 2-3 up to 6 B sub-spectral types.
The fundamental parameters of AS 119, CD-24![]() 5721, Hen2-91, HD 316375
and BD-11
5721, Hen2-91, HD 316375
and BD-11![]() 4747 were determined for the first time. A simple method was
introduced to calculate total (interstellar+circumstellar) dust extinction
towards the studied stars. For HD 53179, which is a double stellar system, and
for HD 45677 and HD 50138, which are suspected to be binaries, we predicted the
characteristics of the components that are consistent with the observed
4747 were determined for the first time. A simple method was
introduced to calculate total (interstellar+circumstellar) dust extinction
towards the studied stars. For HD 53179, which is a double stellar system, and
for HD 45677 and HD 50138, which are suspected to be binaries, we predicted the
characteristics of the components that are consistent with the observed
![]() parameters. However, the possible binarity of HD 45677 and HD
50138 still needs to be confirmed spectroscopically.
parameters. However, the possible binarity of HD 45677 and HD
50138 still needs to be confirmed spectroscopically.
Key words: stars: emission-line, B[e] - stars: fundamental parameters - stars: evolution
Among B and late O type stars with spectra showing more or less strong
hydrogen emission lines, there are some which also have forbidden emission
lines in the visual spectral range. In most of these cases, the presence of
forbidden transitions is accompanied by a strong infrared flux excess (Allen
& Swings 1976). According to the excitation of lines in the optical spectral
region, Allen & Swings (1976) divided these objects into three groups: group 1
comprises stars with rather weak Balmer, Fe II and occasionally [O
I] emission lines; in group 2 the stars show strong emission lines and
forbidden lines from ions with ionization potentials
![]() eV: [O
I], [S II], [Fe II], etc.; group 3 comprises stars with
ionization states
eV: [O
I], [S II], [Fe II], etc.; group 3 comprises stars with
ionization states
![]() eV: He II, O III, etc. By
comparing the spectral morphology in the
eV: He II, O III, etc. By
comparing the spectral morphology in the
![]() Å
wavelength interval of four B[e] objects with symbiotic and peculiar stars,
Ciatti et al. (1974) concluded that the various excitation conditions
coexisting in B[e] spectra are compatible with the presence of a hot radiation
source and a cool giant or supergiant component. These authors also suggest
that stars showing B[e] spectra may be a sequel of stellar evolution that
represents a state previous to a planetary nebula. However, Zickgraf (1998,
2000) showed that quite different type of objects and/or at different
evolutionary stages present the same B[e]-type characteristics. Detailed
reviews of these stars and their spectral properties are given in several
contributions in the "B[e] Stars" workshop (Hubert & Jaschek 1998). It thus
follows that the physical mechanisms producing the B[e] spectral aspects can
be different and that they may be present in stars, either single or binaries,
which are in quite different evolutionary stages. Lamers et al. (1998) referred
to these objects as presenting the "B[e] phenomenon", rather than considering
them as "B[e]-type" stars. They also divide them into five categories, each
distinguished by an evolutionary stage. However, in many cases the nature of
the central stars in objects with the B[e] phenomenon and their
evolutionary stage are little known. Similarly, nothing is known of the
specific relation between the physical circumstances leading to the appearance
of the B[e] phenomenon and the stellar evolution of these objects. To provide
new insight into the nature of the central stars, we observed the spectral
region near the Balmer discontinuity (BD) of a sample of southern objects with
the B[e] phenomenon. Such observations proved to be of great importance for
classical Be stars (highly rotating B stars with circumstellar envelopes,
Jaschek et al. 1981). When possible, we aim at determining the fundamental
parameters of B[e] stars by taking advantage of the BCD spectrophotometric
system.
Å
wavelength interval of four B[e] objects with symbiotic and peculiar stars,
Ciatti et al. (1974) concluded that the various excitation conditions
coexisting in B[e] spectra are compatible with the presence of a hot radiation
source and a cool giant or supergiant component. These authors also suggest
that stars showing B[e] spectra may be a sequel of stellar evolution that
represents a state previous to a planetary nebula. However, Zickgraf (1998,
2000) showed that quite different type of objects and/or at different
evolutionary stages present the same B[e]-type characteristics. Detailed
reviews of these stars and their spectral properties are given in several
contributions in the "B[e] Stars" workshop (Hubert & Jaschek 1998). It thus
follows that the physical mechanisms producing the B[e] spectral aspects can
be different and that they may be present in stars, either single or binaries,
which are in quite different evolutionary stages. Lamers et al. (1998) referred
to these objects as presenting the "B[e] phenomenon", rather than considering
them as "B[e]-type" stars. They also divide them into five categories, each
distinguished by an evolutionary stage. However, in many cases the nature of
the central stars in objects with the B[e] phenomenon and their
evolutionary stage are little known. Similarly, nothing is known of the
specific relation between the physical circumstances leading to the appearance
of the B[e] phenomenon and the stellar evolution of these objects. To provide
new insight into the nature of the central stars, we observed the spectral
region near the Balmer discontinuity (BD) of a sample of southern objects with
the B[e] phenomenon. Such observations proved to be of great importance for
classical Be stars (highly rotating B stars with circumstellar envelopes,
Jaschek et al. 1981). When possible, we aim at determining the fundamental
parameters of B[e] stars by taking advantage of the BCD spectrophotometric
system.
| Stars with the B[e] phenomenon | ||||||
| No. | Star | Ident. | Class | V | date | exp. |
| mag | UT | h | ||||
| 1 | RMC 4 | AzV 16 | sgB[e] | 13.2 | 09.08.98 | 1.00 |
| 2 | CPD
|
RMC 50 | sgB[e] | 11.5 | 08.08.97 | 1.00 |
| 3 | HD 269217 | MWC 106 | sgB[e] | 11.9 | 10.08.98 | 1.00 |
| 4 | BD
|
AS 116 | HAeBe | 10.4 |
12.10.97 | 0.25 |
| 5 | BD
|
AS 117 | HAeBe | 10.3 |
14.10.97 | 0.42 |
| 6 | AS 119 | unclB[e] | 11.0 | 14.10.97 | 0.67 | |
| 7 | HD 45677 | MWC 142 | unclB[e] | 8.1 | 12.10.97 | 0.25 |
| 8 | HD 50138 | MWC 158 | unclB[e] | 6.6 | 10.08.98 | 0.25 |
| 9 | HD 53179 | Z CMa | HAeBe | 9.9 | 14.10.97 | 0.50 |
| 10 | CD
|
AS 160 | unclB[e] | 10.9 | 14.10.97 | 0.83 |
| 11 | Hen 2-90 | ESO 132-1 | cPNB[e] | 13.0 | 10.08.98 | 1.44 |
| 12 | Hen 2-91 | unclB[e] | 14.4 | 09.08.98 | 1.44 | |
| 13 | CD
|
MWC 865 | unclB[e] | 11.4 | 08.08.98 | 0.58 |
| 14 | Hen 3-1356 | AS 222 | unclB[e] | 12.5 | 10.08.98 | 0.75 |
| 15 | HD 316248 | MWC 270 | cPNB[e] | 12.1 | 10.08.98 | 1.00 |
| 16 | HD 316375 | AS 246 | unclB[e] | 9.6 | 11.08.98 | 0.25 |
| 17 | HD 163296 | MWC 275 | HAeBe | 6.9 | 08.08.98 | 0.05 |
| 18 | HD 169515 | MWC 295 | symB[e] | 9.1 | 08.08.98 | 0.58 |
| 19 | MWC 297 | NZ Ser | HAeBe | 12.3 | 11.08.98 | 1.17 |
| 20 | BD
|
AS 321 | unclB[e] | 11.0 |
10.08.98 | 0.25 |
| 21 | AS 341 | symB[e] | 11.0 | 10.08.98 | 0.75 | |
| 22 | BD
|
MWC 314 | sgB[e] | 9.9 | 09.08.98 | 0.50 |
| 23 | HD 190073 | MWC 325 | HAeBe | 7.9 | 08.08.98 | 0.04 |
| Comparison B and Be stars | ||||||
| Star | Sp.T. | V | ESO | n | CASLEO | exp. |
| MK(
|
mag | (BCD) | (B&Ch) | h | ||
| HD 15318 | B9III | 4.28 | 21-24.11.80 | 10 | 09.08.98 | 0.02 |
| HD 32249 | B3V | 4.81 | 01-02.12.80 | 8 | 12.10.97 | 0.01 |
| HD 36512 | B0V | 4.62 | 03-12.10.79 | 10 | 12.10.97 | 0.01 |
| HD 120324 | B2IV-Ve | 3.04 | 12-14.04.82 | 8 | 10.08.98 | 0.02 |
| HD 144217 | B1V | 2.62 | 27-30.05.78 | 10 | 08.08.98 | 0.03 |
| HD 144218 | B2V | 4.92 | 27-30.05.78 | 10 | 08.08.98 | 0.07 |
| HD 149438 | B0V | 2.82 | 14-15.04.82 | 4 | 07.08.98 | 0.05 |
| HD 184915 | B0.5IIIe | 4.95 | 21-25.05.78 | 16 | 12.10.97 | 0.21 |
| HD 214923 | B8V | 3.40 | 03-07.10.79 | 8 | 09.08.98 | 0.02 |
| HD 224990 | B4III | 5.01 | 22-24.11.80 | 6 | 12.10.97 | 0.21 |
| Note: n = number of spectra used; exp. = exposure time in
hours; MK( V magnitudes are from CDS; |
||||||
The BCD (Barbier-Chalonge-Divan) spectrophotometric system, primarily a
stellar classification system, was introduced by Barbier & Chalonge (1941)
and Chalonge & Divan (1952). It is based on measurable quantities of the BD,
which can be obtained from low resolution spectra in the
![]() wavelength interval are then suitable. This system is useful for
stars ranging from spectral type O4 to F9 where the BD is larger than about
0.005 dex. In the
wavelength interval are then suitable. This system is useful for
stars ranging from spectral type O4 to F9 where the BD is larger than about
0.005 dex. In the
![]() region two spectrophotometric
parameters can be derived: D in dex and
region two spectrophotometric
parameters can be derived: D in dex and ![]() ,
this last is commonly
presented as the difference
,
this last is commonly
presented as the difference
![]() Å. D is the Balmer jump
measured at
Å. D is the Balmer jump
measured at
![]() Å, which is obtained by extrapolating the Paschen
continuum energy distribution in a
Å, which is obtained by extrapolating the Paschen
continuum energy distribution in a
![]() vs.
1/
vs.
1/![]() display (
display (
![]() is a comparison or reference flux
distribution).
is a comparison or reference flux
distribution). ![]() gives the mean spectral position of the BD. D is
a strong indicator of the effective photospheric temperature and
gives the mean spectral position of the BD. D is
a strong indicator of the effective photospheric temperature and ![]() easily leads us to the photospheric log g parameter. Stars with circumstellar
envelopes, whose densities are lower than the photospheric layers where Balmer
lines of the underlying star form, show two BD components. The first component
reflects the photospheric properties of the underlying star. The second BD is
due to the circumstellar matter. It can be either in emission or in absorption
and it is shifted to the blue from the first, photospheric BD. Both BD
components are then clearly distinguished, so that the BCD system is also
suitable for spectral classification of stars with circumstellar envelopes. On
the other hand, the photospheric BCD parameters are not affected either by
interstellar extinction or by circumstellar absorption and/or emission.
Moreover, as the
easily leads us to the photospheric log g parameter. Stars with circumstellar
envelopes, whose densities are lower than the photospheric layers where Balmer
lines of the underlying star form, show two BD components. The first component
reflects the photospheric properties of the underlying star. The second BD is
due to the circumstellar matter. It can be either in emission or in absorption
and it is shifted to the blue from the first, photospheric BD. Both BD
components are then clearly distinguished, so that the BCD system is also
suitable for spectral classification of stars with circumstellar envelopes. On
the other hand, the photospheric BCD parameters are not affected either by
interstellar extinction or by circumstellar absorption and/or emission.
Moreover, as the
![]() parameters are obtained from the continuum
energy distribution, they are related, on average, to physical properties of
deeper photospheric layers than any classification system based on spectral
line measurements. The advantages of determining fundamental parameters
with the BCD system and the uncertainties of these parameters are discussed in
Divan & Zorec (1982a) and Zorec & Briot (1991).
parameters are obtained from the continuum
energy distribution, they are related, on average, to physical properties of
deeper photospheric layers than any classification system based on spectral
line measurements. The advantages of determining fundamental parameters
with the BCD system and the uncertainties of these parameters are discussed in
Divan & Zorec (1982a) and Zorec & Briot (1991).
The present set of spectroscopic observations was obtained in October 1997
and August 1998 at the Complejo Astronómico El Leoncito (CASLEO,
Argentina). We used the Boller & Chivens Cassegrain spectrograph (B&Ch) with
a 600 lines mm-1 grating and a 512![]() 512 CCD detector attached to the
2.15 m telescope. The observed spectral range is
512 CCD detector attached to the
2.15 m telescope. The observed spectral range is
![]() Å where the 2 pixel resolution represents 4.53 Å, nearly the same as in the
original BCD system at
Å where the 2 pixel resolution represents 4.53 Å, nearly the same as in the
original BCD system at
![]() Å. Reductions were performed with the
IRAF software package (version 2.10.2). All but four of the spectra extracted
were corrected for atmospheric extinction and they were wavelength and flux
calibrated. The remaining four spectra, observed on 14.10.97, were not flux
calibrated, since the observation conditions did not allow us to obtain
suitable flux-calibrated comparison stars. For these stars we recovered
the BCD parameters by using HD 190073 as the comparison star. This star was
observed on the same night and has flux-calibrated spectra which were obtained
in Aug. 1998. Since the use of this star might lead to less precise
flux calibrations of spectra to determine the
Å. Reductions were performed with the
IRAF software package (version 2.10.2). All but four of the spectra extracted
were corrected for atmospheric extinction and they were wavelength and flux
calibrated. The remaining four spectra, observed on 14.10.97, were not flux
calibrated, since the observation conditions did not allow us to obtain
suitable flux-calibrated comparison stars. For these stars we recovered
the BCD parameters by using HD 190073 as the comparison star. This star was
observed on the same night and has flux-calibrated spectra which were obtained
in Aug. 1998. Since the use of this star might lead to less precise
flux calibrations of spectra to determine the
![]() parameters, we
studied only some wavelengths at both sides of the BD, as was usually done in
the original BCD reduction procedure (Chalonge & Divan 1952).
parameters, we
studied only some wavelengths at both sides of the BD, as was usually done in
the original BCD reduction procedure (Chalonge & Divan 1952).
In the original form of the BCD system, parameters are obtained by differential
spectrophotometry. In the present case, most of the BCD
![]() parameters were derived in an absolute way. In order to test the BCD parameters
derived using data obtained with the Boller & Chivens spectrograph against
those obtained in the original BCD system, we also observed some normal and
emission line B stars for which BCD data existed. We also reobserved stars with
the B[e] phenomenon already classified in this system and we included several
HAeBe stars. The log of observations done is displayed in Table 1.
Flux-calibrated spectra normalized to the flux at
parameters were derived in an absolute way. In order to test the BCD parameters
derived using data obtained with the Boller & Chivens spectrograph against
those obtained in the original BCD system, we also observed some normal and
emission line B stars for which BCD data existed. We also reobserved stars with
the B[e] phenomenon already classified in this system and we included several
HAeBe stars. The log of observations done is displayed in Table 1.
Flux-calibrated spectra normalized to the flux at
![]() Å of stars
whose BD we were able to study are shown in Fig. 1. The flux-uncalibrated
spectra of four program stars for which we also determined the BCD parameters
are shown in Fig. 2, while those of stars without measurable BD are shown in
Fig. 3.
Å of stars
whose BD we were able to study are shown in Fig. 1. The flux-uncalibrated
spectra of four program stars for which we also determined the BCD parameters
are shown in Fig. 2, while those of stars without measurable BD are shown in
Fig. 3.
![\begin{figure}
\par\includegraphics[width=18cm,clip]{MS10323f1.eps}\end{figure}](/articles/aa/full/2001/10/aa10323/Timg37.gif) |
Figure 1:
Energy distributions normalized to the flux at
|
| Open with DEXTER | |
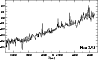 |
Figure 1: continued |
| Open with DEXTER | |
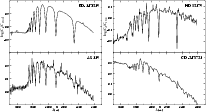 |
Figure 2:
Flux-uncalibrated spectra of four program stars for which BCD
parameters have also been determined [
|
| Open with DEXTER | |
Obviously, only stars with measurable BD can have fundamental parameters
determined using the calibrations of (
![]() ). A number of hot B[e]
stars, mainly of cPNB[e] and symB[e] class, either have a tiny BD or their
spectral region near the BD is crowded by strong emission lines, which prevent
any direct (
). A number of hot B[e]
stars, mainly of cPNB[e] and symB[e] class, either have a tiny BD or their
spectral region near the BD is crowded by strong emission lines, which prevent
any direct (
![]() )
determination. For the stars where these parameters
cannot be obtained directly, we used other methods to gain some insight into
their fundamental parameters, at least with regard to their effective
temperature.
)
determination. For the stars where these parameters
cannot be obtained directly, we used other methods to gain some insight into
their fundamental parameters, at least with regard to their effective
temperature.
![\begin{figure}
\par\includegraphics[width=18cm,clip]{MS10323f3.eps}\end{figure}](/articles/aa/full/2001/10/aa10323/Timg48.gif) |
Figure 3:
Energy distributions normalized to the flux at
|
| Open with DEXTER | |
Among the program stars, only 15 objects have a measurable Balmer
discontinuity. The results obtained are presented in Table 3. Those
![]() parameters which were derived in a differential way are
indicated by an asterisk. The
parameters which were derived in a differential way are
indicated by an asterisk. The
![]() ,
log g and the bolometric absolute
magnitude,
,
log g and the bolometric absolute
magnitude,
![]() ,
were determined using the
,
were determined using the
![]() calibration
(Divan & Zorec 1982a; Zorec 1986). In each case we assumed that stars are
single and that their photospheric-like spectrum can be represented by the
observed
calibration
(Divan & Zorec 1982a; Zorec 1986). In each case we assumed that stars are
single and that their photospheric-like spectrum can be represented by the
observed
![]() pair, and thus by (
pair, and thus by (
![]() ,
log g). The
absolute values of uncertainties of
,
log g). The
absolute values of uncertainties of
![]() ,
,
![]() and
and
![]() related to given
related to given
![]() observational errors are
observational errors are
![]() -dependent. For each
-dependent. For each
![]() fundamental parameter
obtained, Table 3 gives the
fundamental parameter
obtained, Table 3 gives the ![]() dispersion of the corresponding
dispersion of the corresponding
![]() values. In Table 3 we also
give the total extinction AV
(circumstellar+interstellar) obtained
as explained in Sect. 3.5.
values. In Table 3 we also
give the total extinction AV
(circumstellar+interstellar) obtained
as explained in Sect. 3.5.
Some program objects are binaries or supposed binaries. In Sect. 4.3 we
discuss the characteristics the components should have in order to produce,
within the observational uncertainties, the same
![]() parameters as
those observed.
parameters as
those observed.
The spectra of four stars (Nos. 11, 13, 15 and 21) are characterized by strong
emission lines in the
![]() 3500-4600 interval, which entirely
obliterate the stellar BD. The Balmer emission lines of these stars, seen up to
quantum numbers as high as n = 12, 14, can be considered nearly optically thin.
This is shown in Fig. 4, where we compare the average of their observed line
intensity ratios
3500-4600 interval, which entirely
obliterate the stellar BD. The Balmer emission lines of these stars, seen up to
quantum numbers as high as n = 12, 14, can be considered nearly optically thin.
This is shown in Fig. 4, where we compare the average of their observed line
intensity ratios
![]() (n > 5) with those
predicted by Osterbrock (1989) for emitting nebula in case B. Thus, to obtain
some insight into the excitation temperature of the Balmer emission lines
provided by the central stars, we assumed they are surrounded by a gaseous
circumstellar envelope (CE) or disk. The emitted flux in a line at wavelength
(n > 5) with those
predicted by Osterbrock (1989) for emitting nebula in case B. Thus, to obtain
some insight into the excitation temperature of the Balmer emission lines
provided by the central stars, we assumed they are surrounded by a gaseous
circumstellar envelope (CE) or disk. The emitted flux in a line at wavelength
![]() can then be written as:
can then be written as:
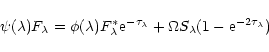 |
(1) |
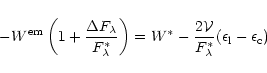 |
(2) |
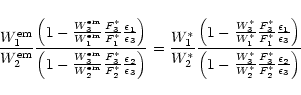 |
(3) |
The [
![]() ]
were established using Kurucz's
(1992) models of normal stellar atmospheres. The (
]
were established using Kurucz's
(1992) models of normal stellar atmospheres. The (
![]() )
relations were determined using observed values of the
)
relations were determined using observed values of the
![]() equivalent
widths of normal O, B and early A type stars (Boyarchuk 1957;
Buscombe 1969;
Kopylov 1958; Tereshchenko 1976). The effective temperatures used to obtain the
(
equivalent
widths of normal O, B and early A type stars (Boyarchuk 1957;
Buscombe 1969;
Kopylov 1958; Tereshchenko 1976). The effective temperatures used to obtain the
(
![]() )
relations for normal stars are from the BCD
)
relations for normal stars are from the BCD
![]() calibrations. To reveal a luminosity class effect in the
(
calibrations. To reveal a luminosity class effect in the
(
![]() )
relations, we grouped stars into three luminosity
class groups so that each of them becomes statistically significant: V,
IV-V+IV and III-IV+III+II-III. As the (
)
relations, we grouped stars into three luminosity
class groups so that each of them becomes statistically significant: V,
IV-V+IV and III-IV+III+II-III. As the (
![]() )
are not easy
to represent analytically, we used (
)
are not easy
to represent analytically, we used (
![]() )
relations, where
S70 is the value of the BD at
)
relations, where
S70 is the value of the BD at
![]() Å, which is used in
the BCD system as a continuous parameter of spectral classification for early
type stars (Zorec et al. 1983; Zorec & Briot 1991, 1997). The (
Å, which is used in
the BCD system as a continuous parameter of spectral classification for early
type stars (Zorec et al. 1983; Zorec & Briot 1991, 1997). The (
![]() )
relation is also straightforward to represent (Zorec et al. 1983).
Figure 5 shows the (
)
relation is also straightforward to represent (Zorec et al. 1983).
Figure 5 shows the (
![]() )
relations obtained for H
)
relations obtained for H![]() ,
H
,
H![]() and H
and H![]() lines of main sequence stars. The S70 and
lines of main sequence stars. The S70 and
![]() of
the studied stars with the B[e] phenomenon obtained by the present method are
given in Table 4. The dispersions are due to the use of several (Hni,Hnj,Hnk) combinations. No luminosity class effect on the
S70 and
of
the studied stars with the B[e] phenomenon obtained by the present method are
given in Table 4. The dispersions are due to the use of several (Hni,Hnj,Hnk) combinations. No luminosity class effect on the
S70 and
![]() values is detected.
values is detected.
Figure 4 strongly suggests that the CE of the studied stars are optically
thin in Balmer lines, at least from H![]() to H12. However, this condition
does not imply that the Balmer line formation regions have low densities. If
electron densities are
to H12. However, this condition
does not imply that the Balmer line formation regions have low densities. If
electron densities are
![]() 107 cm-3, the ratios of line
emission coefficient
107 cm-3, the ratios of line
emission coefficient
![]() can be considered
density- and temperature-independent (Drake & Ulrich 1980; Osterbrock 1989).
At
can be considered
density- and temperature-independent (Drake & Ulrich 1980; Osterbrock 1989).
At ![]()
![]() cm-3 there are collisional effects for the
higher hydrogen energy levels. Nevertheless, we tested that for optically thin
media, the low density approximation can still be used up to
cm-3 there are collisional effects for the
higher hydrogen energy levels. Nevertheless, we tested that for optically thin
media, the low density approximation can still be used up to
![]() 108 cm-3 to calculate the ratios
108 cm-3 to calculate the ratios
![]() for n
for n
![]() 12 without introducing larger errors in the estimation of
12 without introducing larger errors in the estimation of
![]() than those quoted in Table 4. For
than those quoted in Table 4. For
![]() 1012 cm-3,
the ratios of the line emission coefficients are essentially
temperature-dependent (Drake & Ulrich 1980). In our calculations we used
ratios of line emission coefficients for optically thin media and appropriate
for low (
1012 cm-3,
the ratios of the line emission coefficients are essentially
temperature-dependent (Drake & Ulrich 1980). In our calculations we used
ratios of line emission coefficients for optically thin media and appropriate
for low (
![]() 108 cm-3) and high (
108 cm-3) and high (
![]() 1012cm-3) densities. The electron temperature
1012cm-3) densities. The electron temperature ![]() needed to obtain the
temperature-dependent
needed to obtain the
temperature-dependent
![]() ratios was
approximated with
ratios was
approximated with
![]() .
For each star, the
effective temperature given in Table 4 is the average of the
.
For each star, the
effective temperature given in Table 4 is the average of the
![]() obtained with ratios of line emission coefficients corresponding to both
extreme electron density approximations. Finally, we note that no solution
could be obtained from (3) using
obtained with ratios of line emission coefficients corresponding to both
extreme electron density approximations. Finally, we note that no solution
could be obtained from (3) using
![]() ratios
for optically thick and dense CE.
ratios
for optically thick and dense CE.
| B&Ch | BCD | ||||
| Star | D | D | |||
| Å | dex | Å | dex | ||
| HD 15318 |
|
|
61 | 0.460 | |
| HD 32249 |
|
|
56 | 0.185 | |
| HD 36512 |
|
|
57 | 0.053 | |
| HD 120324 |
|
|
53 | 0.136 | |
| HD 144217 |
|
|
64 | 0.083 | |
| HD 144218 |
|
|
60 | 0.147 | |
| HD 149438 |
|
|
57 | 0.063 | |
| HD 184915 |
|
|
44 | 0.070 | |
| HD 214923 |
|
|
49 | 0.440 | |
| HD 224990 |
|
|
49 | 0.244 | |
| Star |
|
D | Spectral |
|
|
AV | Previous spectral | ||
| Å | dex | typea | K | mag | mag | classifications | |||
|
CPD
|
|
|
B5Ia |
|
- | - | 1.0 | B2-3 (10) | |
| HD 269217 |
|
|
B5-6Ia |
|
- | - | 0.4 | B3Ib: (8), B2-3 (10) | |
| BD
|
|
|
B3V |
|
4.3 |
|
1.1 | B7 (6), B3 (6) | |
| BD
|
* |
|
|
A1V: |
|
4.3 |
|
1.2 | A0 (6) |
| AS 119 | * |
|
|
B3IV |
|
3.7 |
|
2.7 | |
| HD 45677 |
|
|
B2IV-V |
|
3.9 |
|
1.4 | B2III-IV/B2V (11) | |
| HD 50138 |
|
|
B6III-IV |
|
3.4 |
|
0.4 | B6III-IV (11) | |
| HD 53179 | * |
|
|
F8III-IV | - | - | - | 2.3 | B5 (1), B5/8 (9) |
| CD
|
* |
|
|
B1.5V: |
|
4.4 |
|
1.7 | O9.5 (4) |
| Hen 2-91 | - |
|
B0 |
|
- | - | 5.8 | ||
| HD 316375 |
|
|
B2V |
|
4.2 |
|
0.7 | B8 (2) | |
| HD 163296 |
|
|
A0V: |
|
4.3 |
|
0.2 | A1V (5), A0/2V (9) | |
| HD 169515 | >80 |
|
O9.5V: |
|
- |
|
2.9 | O9.5Ib+O5.5V (3) | |
| BD
|
|
|
B9V |
|
4.2 |
|
2.8 | ||
| HD 190073 |
|
|
B9IV |
|
3.7 |
|
0.5 | A0III (7), A0IV(9) | |
|
Notes: "*" stars with flux-uncalibrated spectra; "a"
MK spectral types derived from the (
of Refs.: (1) Buscombe (1977), (2) Cannon & Walton Mayall (1949), (3) Chlebowski & Harnden (1989), (4) Drilling (1991), (5) Hauck & Jaschek (2000), (6) Miroshnichenko et al. (1999), (7) Ringuelet et al. (1987), (8) Smith & Bruhweiler (1999), (9) Thé et al. (1994), (10) Zickgraf et al. (1996), (11) Zorec et al. (1998). | |||||||||
Further information on the effective temperature of the star underlying the CE
can be obtained from the emitted flux in the He I recombination lines.
Hence, we assume that the number of photons emitted by the CE in a specific
recombination line is proportional to the number of ionizing photons emitted by
the star. It is then shown (Osterbrock 1989) that the ratio between the
luminosity of the star in the frequency of the line
![]() and
the number of ionizing photons
and
the number of ionizing photons
![]() (
(
![]() = 24.6 eV is the ionizing potential of
He I) is given by:
= 24.6 eV is the ionizing potential of
He I) is given by:
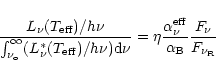 |
(4) |
 |
Figure 4:
Mean observed ratios
|
| Open with DEXTER | |
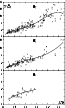 |
Figure 5:
(
|
| Open with DEXTER | |
In normal early type stars the colour temperature ![]() of the Paschen
continuum energy distribution closely corresponds to the effective stellar
temperature (Thomas 1983). In hot stars, where the dominant opacity source in
the CE is electron scattering, the observed Paschen energy distribution due
to the star+CE system should also closely reflect the underlying stellar
Paschen energy distribution. We may then try to infer the colour temperature
of the continuum energy distribution of those stars with the B[e] phenomenon
for which the methods used in the preceding subsections cannot be applied.
of the Paschen
continuum energy distribution closely corresponds to the effective stellar
temperature (Thomas 1983). In hot stars, where the dominant opacity source in
the CE is electron scattering, the observed Paschen energy distribution due
to the star+CE system should also closely reflect the underlying stellar
Paschen energy distribution. We may then try to infer the colour temperature
of the continuum energy distribution of those stars with the B[e] phenomenon
for which the methods used in the preceding subsections cannot be applied.
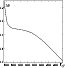 |
Figure 6:
Gradient index
|
| Open with DEXTER | |
The observed spectral range we have at our disposal to determine ![]() is extremely reduced and so it is possible that the inferred values of
is extremely reduced and so it is possible that the inferred values of ![]() may be highly uncertain. Although they probably do not represent the only
possible solution, we shall consider them as indicative of temperatures that
reproduce energy distributions which are compatible with those observed in the
studied wavelength interval. The wavelength interval analysed is
may be highly uncertain. Although they probably do not represent the only
possible solution, we shall consider them as indicative of temperatures that
reproduce energy distributions which are compatible with those observed in the
studied wavelength interval. The wavelength interval analysed is
![]() Å, where the theoretical energy distributions agree quite
well with observations of normal early type stars. As the studied stars are
probably heavily obscured and reddened by the interstellar and circumstellar
dust, photometric or spectrophotometric colour indices need to be defined so
that they are insensitive to these extinctions. The energy distributions to be
studied are so crowded with emission and/or absorption lines that colour
indices defined from monochromatic fluxes may well result in excessive
uncertainties. We then preferred to use gradients defined as:
Å, where the theoretical energy distributions agree quite
well with observations of normal early type stars. As the studied stars are
probably heavily obscured and reddened by the interstellar and circumstellar
dust, photometric or spectrophotometric colour indices need to be defined so
that they are insensitive to these extinctions. The energy distributions to be
studied are so crowded with emission and/or absorption lines that colour
indices defined from monochromatic fluxes may well result in excessive
uncertainties. We then preferred to use gradients defined as:
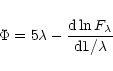 |
(5) |
| (6) |
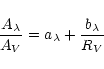 |
(7) |
As a byproduct, an estimate of the total dust extinction (ISM+circumstellar)
affecting the stellar energy distribution can be determined using the ![]() and
and ![]() gradients. Assuming that the luminosity class dependence of the
gradients. Assuming that the luminosity class dependence of the
![]() gradients can be neglected, we derived the total extinction in the V
magnitude from:
gradients can be neglected, we derived the total extinction in the V
magnitude from:
![]() ]
and
]
and
![]() ]. The errors in
determining
]. The errors in
determining ![]() by least squares are
by least squares are
![]() .
As
the model uncertainties regarding
.
As
the model uncertainties regarding ![]() are of the same order, the error
concerning the extinction is
are of the same order, the error
concerning the extinction is ![]() (AV)
(AV)
![]() mag. The ratios
mag. The ratios
![]() depend slightly on the value of
RV. In the above definitions we used
RV = 3.1. The
extinction AV obtained is commented briefly in Sect. 4.2.
depend slightly on the value of
RV. In the above definitions we used
RV = 3.1. The
extinction AV obtained is commented briefly in Sect. 4.2.
| 1 - Effective temperatures derived from Balmer lines | ||
| Star |
|
|
| dex | K | |
| Hen 2-90 |
|
|
| CD
|
|
|
| HD 316248 |
|
|
| AS 341 |
|
|
| 2 - Effective temperatures obtained from He I lines | ||||
| Star |
|
Star |
|
|
| K | K | |||
| Hen 2-90 |
|
AS 341 |
|
|
| CD
|
|
BD
|
|
|
| HD 316248 |
|
|||
| 3 - Colour temperatures | ||||
Star |
|
||
| K | |||
| RMC 4 | 1.31 | 1.35 |
|
| Hen 2-90 | 2.62 | 3.00 |
|
| CD
|
2.79 | 3.21 |
|
| Hen 3-1356 | 3.17 | 3.62 |
|
| HD 316248 | 2.24 | 2.60 |
|
| MWC 297 | 4.22 | 4.98 |
|
| AS 341 | 2.76 | 3.15 |
|
| BD
|
3.46 | 3.99 |
|
The main purpose of this work is to infer fundamental parameters of stars with
the B[e] phenomenon using the spectrophotometric BCD system. This system deals
with parameters, which are related to deeper atmospheric layers than those
where, on average, the spectral lines are formed. Since the BCD parameters are
not affected by either ISM or circumstellar extinctions, we hope they may help
us to obtain more precise information on the central stars of the studied
objects. However, with the aim of using the BCD system for different classes of
stars with B[e] phenomenon and for as many sets of objects as possible,
attainable from CASLEO during the allocated observing runs, we recorded a
number of spectra that finally had no measurable BD. Nevertheless, we then
tried to make the most of these spectra by using several methods to determine
temperatures, which may be related to or are indicative of the central star
effective temperature. As these temperatures are subject to more uncertainties
than those obtained from the BCD calibrations and because they do not represent
direct determinations of
![]() ,
we comment the results obtained for
both sets of objects separately. Finally, as Z CMa is a double star system
and two other program stars are suspected binaries, in this section we also
discuss the characteristics the binary components must have to lead to the
observed (
,
we comment the results obtained for
both sets of objects separately. Finally, as Z CMa is a double star system
and two other program stars are suspected binaries, in this section we also
discuss the characteristics the binary components must have to lead to the
observed (
![]() )
values and whether the conclusions drawn in this
paper by assuming they are single stars are misleading.
)
values and whether the conclusions drawn in this
paper by assuming they are single stars are misleading.
The new
![]() determinations for HD 45677 and HD 50138 are in good
agreement with previous ones obtained from the original, photographic BCD data
(Zorec et al. 1998; Lamers et al. 1998).
determinations for HD 45677 and HD 50138 are in good
agreement with previous ones obtained from the original, photographic BCD data
(Zorec et al. 1998; Lamers et al. 1998).
Comparing the new spectral classifications with the previous ones, found in
the literature, we can see that differences appear only for three stars. The
![]() obtained from the BCD calibrations for CPD
obtained from the BCD calibrations for CPD
![]() 116 (RMC
50; S65) and HD 269217 (R82) are lower than the value inferred for them by
Zickgraf et al. (1986), who mainly used a spectroscopic approach.
CPD
116 (RMC
50; S65) and HD 269217 (R82) are lower than the value inferred for them by
Zickgraf et al. (1986), who mainly used a spectroscopic approach.
CPD
![]() 116 has a deep second BD in absorption, as in classical Be
stars with a strong spectroscopic shell phenomenon (Divan & Zorec 1982b;
Moujtahid et al. 1998), that could erroneously be interpreted as representing
a B9 supergiant. This absorption, if any, is very small in HD 269217.
Measuring the BD carefully from the merging of Balmer lines, the earliest
spectral types we could assign to these stars are given in Table 3. On the
other hand, the B3 supergiant-type suggested for this star in the
literature requires
116 has a deep second BD in absorption, as in classical Be
stars with a strong spectroscopic shell phenomenon (Divan & Zorec 1982b;
Moujtahid et al. 1998), that could erroneously be interpreted as representing
a B9 supergiant. This absorption, if any, is very small in HD 269217.
Measuring the BD carefully from the merging of Balmer lines, the earliest
spectral types we could assign to these stars are given in Table 3. On the
other hand, the B3 supergiant-type suggested for this star in the
literature requires ![]() = 20-24 Å, which is not consistent with the
observed value of
= 20-24 Å, which is not consistent with the
observed value of ![]() .
HD 316375 has two well-separated BD components,
one of which is in emission, while the other is photospheric-like. The latter
unambiguously suggests a B2V spectral type, which is not consistent with the
B8-type assigned to the star in the HD catalogue and apparently have not
been superseded since then (see Table 3). Differences in the spectral
classification and effective temperature determination for
CPD
.
HD 316375 has two well-separated BD components,
one of which is in emission, while the other is photospheric-like. The latter
unambiguously suggests a B2V spectral type, which is not consistent with the
B8-type assigned to the star in the HD catalogue and apparently have not
been superseded since then (see Table 3). Differences in the spectral
classification and effective temperature determination for
CPD
![]() 116 and HD 269217, respectively members of SMC and LMC, could
perhaps be due to a chemical abundance effect which deserves further deeper
discussion. In this respect we note that the calibrations of BCD parameters
into MK spectral types and fundamental parameters we used in the present work
were made only with stars of our Galaxy.
116 and HD 269217, respectively members of SMC and LMC, could
perhaps be due to a chemical abundance effect which deserves further deeper
discussion. In this respect we note that the calibrations of BCD parameters
into MK spectral types and fundamental parameters we used in the present work
were made only with stars of our Galaxy.
The spectral type determined by Miroshnichenko et al. (1999) for
BD
![]() 1319, as well as the spectral type of CD
1319, as well as the spectral type of CD
![]() 5721 which
we inferred from Drilling's (1991) data, are photometric spectral types. As
BD
5721 which
we inferred from Drilling's (1991) data, are photometric spectral types. As
BD
![]() 1319 has neither emission lines near the BD nor any strong
indication for possible anomalous BD, its photometric classification should not
be disregarded. However CD
1319 has neither emission lines near the BD nor any strong
indication for possible anomalous BD, its photometric classification should not
be disregarded. However CD
![]() 5721 seems to have a small second BD in
emission and the photometric classification can lead to a slightly earlier
spectral type as compared with the spectrophotometric one. The spectral
type of BD
5721 seems to have a small second BD in
emission and the photometric classification can lead to a slightly earlier
spectral type as compared with the spectrophotometric one. The spectral
type of BD
![]() 1351 has also been discussed by Miroshnichenko et al.
(1999). Using photometric data these authors classify the star as B3-type,
while spectroscopic arguments, mainly the fit of wings of Balmer lines,
suggest a B7 spectral type. We note that in our spectra the Balmer lines H12
and H13 seem to be too deep if they are compared to Hn, with n < 12. Such
deep absorptions in H12 and H13 lines may imply that: a) all Balmer lines Hn
with n < 12 have emission components in their core, which cannot be seen in
all of them in our low resolution spectra; b) the spectral type of the central
star is cooler than B3; c) the circumstellar component of the BD rises at
1351 has also been discussed by Miroshnichenko et al.
(1999). Using photometric data these authors classify the star as B3-type,
while spectroscopic arguments, mainly the fit of wings of Balmer lines,
suggest a B7 spectral type. We note that in our spectra the Balmer lines H12
and H13 seem to be too deep if they are compared to Hn, with n < 12. Such
deep absorptions in H12 and H13 lines may imply that: a) all Balmer lines Hn
with n < 12 have emission components in their core, which cannot be seen in
all of them in our low resolution spectra; b) the spectral type of the central
star is cooler than B3; c) the circumstellar component of the BD rises at
![]() Å, which implies that the circumstellar regions
responsible for the Balmer continuum emission have electron densities
Å, which implies that the circumstellar regions
responsible for the Balmer continuum emission have electron densities
![]() 1013 cm-3 (see Moujtahid et al. 1999 for discussion of
1013 cm-3 (see Moujtahid et al. 1999 for discussion of ![]() inferred from the second component of the BD). For such densities the wings
of the higher members of the Balmer series can be optically thick. In this case
the use of model atmospheres for normal stars can lead to misleading spectral
type determinations. Simultaneous observations of the BD and of Balmer line
profiles towards the end of the Balmer series at phases of different emission
intensity, could help to determine more reliably the spectral type of the
central star.
inferred from the second component of the BD). For such densities the wings
of the higher members of the Balmer series can be optically thick. In this case
the use of model atmospheres for normal stars can lead to misleading spectral
type determinations. Simultaneous observations of the BD and of Balmer line
profiles towards the end of the Balmer series at phases of different emission
intensity, could help to determine more reliably the spectral type of the
central star.
Due to the characteristics of the
![]() calibration into MK
spectral types (double display of the
calibration into MK
spectral types (double display of the
![]() parameters, Chalonge &
Divan 1973), the BCD parameters obtained for Z CMa could correspond either to
a B2III or to a F8III-IV type star. The absorptions at
parameters, Chalonge &
Divan 1973), the BCD parameters obtained for Z CMa could correspond either to
a B2III or to a F8III-IV type star. The absorptions at ![]() 3933 Ca
II and
3933 Ca
II and ![]() 3968-70 H+Ca II lines suggest, however, that the
spectrum is probably F-type. In "normal" stars, the intrinsic gradient
3968-70 H+Ca II lines suggest, however, that the
spectrum is probably F-type. In "normal" stars, the intrinsic gradient
![]() defined in the
defined in the
![]() Å wavelength
interval can help to distinguish a B2 from a F8-type star (Chalonge & Divan
1973). The rather high interstellar+circumstellar dust extinction towards Z CMa
prevents the use of the observed gradient,
Å wavelength
interval can help to distinguish a B2 from a F8-type star (Chalonge & Divan
1973). The rather high interstellar+circumstellar dust extinction towards Z CMa
prevents the use of the observed gradient,
![]()
![]() m, to make such a choice. However, the total AV
extinction deduced from
m, to make such a choice. However, the total AV
extinction deduced from
![]() seems to be consistent with an
F8 spectral type, where
seems to be consistent with an
F8 spectral type, where
![]()
![]() m. Hence, we deduce
m. Hence, we deduce
![]() mag, which is
intermediate between the value
AV = 1.8 mag suggested by Hartmann et al. (1989)
and
AV = 2.8 mag derived by Berilli et al. (1992).
mag, which is
intermediate between the value
AV = 1.8 mag suggested by Hartmann et al. (1989)
and
AV = 2.8 mag derived by Berilli et al. (1992).
Another outstanding advantage of the BCD system is its simplicity. From the results obtained and the discussion above, we can see that the method leads to well-defined and model-independent fundamental stellar parameters. On the other hand, it has been shown (Zorec 1998) that reliable determinations of spectral type and luminosity class of stars with the B[e] phenomenon are helpful in determining their distance and in quantitatively separating the dust extinction due to the CE from the interstellar one. These quantities are relevant not only to discussion of the bolometric luminosity of the central object when studying the evolutionary stage of stars, but also to determination of the amount of dust in their circumstellar environment. Further details of this method will be presented in a separate paper (Zorec & Cidale 2000, in preparation).
In this subsection we merely wish to compare the temperature we obtained with some latest effective temperatures reported in the literature for these stars.
RMC 4: This object, a spectroscopic binary with an LBV-type component,
has been thoroughly discussed by Zickgraf et al. (1986, 1996) and classified
as a sgB[e] star. In order to fit the observed spectral line intensities and
the energy distribution, these authors iterated the effective temperature of
both components using models of stellar atmospheres. They obtained
![]() (B-comp.) = 27000 K and
(B-comp.) = 27000 K and
![]() (A-comp.) = 9500 K. Our estimate of
the colour temperature agrees with the effective temperature obtained by
Zickgraf et al. for the B component.
(A-comp.) = 9500 K. Our estimate of
the colour temperature agrees with the effective temperature obtained by
Zickgraf et al. for the B component.
Hen 2-90: This object is considered as a PN with a very dense and
compact nebula (Costa et al. 1993). In their analysis of the chemical
composition of the nebula, these authors used
![]() 104 K for the underlying star, which was determined using the Zanstra method. It is
nearly the same as the temperature obtained by Preite-Martinez et al. (1991)
with the energy-balance method. Our excitation temperatures, derived from
Balmer and He I lines and from the observed energy distribution, are
nearly the same, but lower than the previous ones. We note that
104 K for the underlying star, which was determined using the Zanstra method. It is
nearly the same as the temperature obtained by Preite-Martinez et al. (1991)
with the energy-balance method. Our excitation temperatures, derived from
Balmer and He I lines and from the observed energy distribution, are
nearly the same, but lower than the previous ones. We note that
![]()
![]() = 3.22 104 is probably justified, since in the
spectrum of this star we only see He I 4471 but no He II emission
line.
= 3.22 104 is probably justified, since in the
spectrum of this star we only see He I 4471 but no He II emission
line.
CD
![]() 11721: This object is considered as a HAeBe star
(Henning et al. 1998). Lorenzetti et al. (1999) guessed that the spectral
type of the central star might be hotter than B0. Depending on the authors, it
was classified: B0[e]p (de Winter & Thé 1990; Brooke et al. 1993; de Winter
& Pérez 1998), B4-5 (Benedettini et al. 1998), B7
(Hillenbrand et al. 1992)
and Aep (Natta et al. 1993). Lamers et al. (1998) considered it among the
unclB[e] stars. From Balmer and He I lines and from the energy
distribution we obtained a mean
11721: This object is considered as a HAeBe star
(Henning et al. 1998). Lorenzetti et al. (1999) guessed that the spectral
type of the central star might be hotter than B0. Depending on the authors, it
was classified: B0[e]p (de Winter & Thé 1990; Brooke et al. 1993; de Winter
& Pérez 1998), B4-5 (Benedettini et al. 1998), B7
(Hillenbrand et al. 1992)
and Aep (Natta et al. 1993). Lamers et al. (1998) considered it among the
unclB[e] stars. From Balmer and He I lines and from the energy
distribution we obtained a mean
![]() = 31600 K, which corresponds to
a B0-1 spectral type if
= 31600 K, which corresponds to
a B0-1 spectral type if
![]() is understood as
is understood as
![]() .
Using
.
Using
![]()
![]() and the measured gradients
and the measured gradients ![]() ,
,
![]() we
derived a total dust extinction
AV = 4.2 mag. This extinction was also
estimated by other authors:
AV = 7.1 mag (de Winter & Thé 1990),
we
derived a total dust extinction
AV = 4.2 mag. This extinction was also
estimated by other authors:
AV = 7.1 mag (de Winter & Thé 1990),
![]() mag (Brooke et al. 1993),
AV = 6.1 mag [=
1.6(ISM)+4.5(circumstellar)] (Natta et al. 1993) and
AV = 4.3 mag
(Hillenbrand et al. 1992). Our total AV is close to that obtained by
Hillenbrand et al. (1992) and to the AV(circumstellar) derived by
Natta et al. (1993), as the interstellar component of AV was
negligible. However, a low value of AV(ISM) should not be excluded,
because the interstellar extinction towards this star is roughly 1mag/kpc
(Neckel & Klare 1980) and many authors estimated the distance of
CD
mag (Brooke et al. 1993),
AV = 6.1 mag [=
1.6(ISM)+4.5(circumstellar)] (Natta et al. 1993) and
AV = 4.3 mag
(Hillenbrand et al. 1992). Our total AV is close to that obtained by
Hillenbrand et al. (1992) and to the AV(circumstellar) derived by
Natta et al. (1993), as the interstellar component of AV was
negligible. However, a low value of AV(ISM) should not be excluded,
because the interstellar extinction towards this star is roughly 1mag/kpc
(Neckel & Klare 1980) and many authors estimated the distance of
CD
![]() 11721 being less than 500 pc: d = 160 pc (Hillenbrand et al.
1992); d = 220 pc (Pezzuto et al. 1997); d = 400 pc (de Winter & Thé
(1990). On the other hand, distances of this object in the range
d = 2000-2600 pc
were suggested by Natta et al. (1993) and Shore et al. (1990).
11721 being less than 500 pc: d = 160 pc (Hillenbrand et al.
1992); d = 220 pc (Pezzuto et al. 1997); d = 400 pc (de Winter & Thé
(1990). On the other hand, distances of this object in the range
d = 2000-2600 pc
were suggested by Natta et al. (1993) and Shore et al. (1990).
Hen 3-1356: This rarely studied star was considered by Allen & Swings
(1976) to belong to "group 1", which except for the [O I] line is
nearly a classical Be star. Emission in the Balmer lines is seen up to
H![]() and there is a strong second BD in emission. The CE can then be
optically thick in the visual spectral range, so that the colour temperature
should be considered only as a lower limit for its effective temperature. The
visual energy distribution is strongly affected by the ISM and the
circumstellar dust extinction. From our data we obtained
AV = 4.9 mag.
and there is a strong second BD in emission. The CE can then be
optically thick in the visual spectral range, so that the colour temperature
should be considered only as a lower limit for its effective temperature. The
visual energy distribution is strongly affected by the ISM and the
circumstellar dust extinction. From our data we obtained
AV = 4.9 mag.
HD 316248: This PN, commonly known as M 1-26, was classified by Górny
et al. (1997) as an "e" type, which implies that the object is seen as a
compact disk without any structure. Using the Zanstra method, these authors
estimated
![]() K. Using a non-LTE spectroscopic approach,
Méndez et al. (1992) estimated
K. Using a non-LTE spectroscopic approach,
Méndez et al. (1992) estimated
![]() K. Our average
temperature determination, based on the Balmer and He I lines and the
energy distribution, is of the same order. The presence of He I and
He II emission lines in the spectrum confirms such a high
K. Our average
temperature determination, based on the Balmer and He I lines and the
energy distribution, is of the same order. The presence of He I and
He II emission lines in the spectrum confirms such a high
![]() .
.
MWC 297: In the current literature this star is considered as a HAeBe
object. It was classified as B0 by Henning et al. (1994), considered between a
late O and early B by Andrillat & Jaschek (1998) and B1.5Ve by Drew et al.
(1997). As discussed in Sect. 3.5, errors in determining the gradients
![]() and
and ![]() can easily explain the difference between the colour
temperature
can easily explain the difference between the colour
temperature
![]() K we obtained for this star and
K we obtained for this star and
![]() K, which suits a B1.5V spectral type.
However, we note that the
spectrum of MWC 297 shows a second BD component in quite strong emission, which
implies that the observed Paschen continuum may also be affected by some flux
excess, as in classical Be stars (Moujtahid et al. 1998, 1999). Due to this
excess the equivalent widths of photospheric-like lines are smaller by a factor
K, which suits a B1.5V spectral type.
However, we note that the
spectrum of MWC 297 shows a second BD component in quite strong emission, which
implies that the observed Paschen continuum may also be affected by some flux
excess, as in classical Be stars (Moujtahid et al. 1998, 1999). Due to this
excess the equivalent widths of photospheric-like lines are smaller by a factor
![]() (Zorec et al.
2000) as compared to that of the same star without flux excess (
(Zorec et al.
2000) as compared to that of the same star without flux excess (
![]() is the continuum optical depth of the CE at the line wavelength,
is the continuum optical depth of the CE at the line wavelength,
![]() is the flux excess and
is the flux excess and
![]() is the
stellar continuum flux). In the
is the
stellar continuum flux). In the
![]() spectral region used
by Drew et al. (1997) to compare the observed spectrum of MWC 297 with that of
stars without emission, there are lines which shallow up from spectral types
B0 to B3. If the spectral lines of MWC 297 are affected by the veiling effect
mentioned above, the spectral type of the star will be considered cooler and
the effective temperature underestimated. So, we can guess that the effective
temperature of MWC 297 could be in the interval 25000
spectral region used
by Drew et al. (1997) to compare the observed spectrum of MWC 297 with that of
stars without emission, there are lines which shallow up from spectral types
B0 to B3. If the spectral lines of MWC 297 are affected by the veiling effect
mentioned above, the spectral type of the star will be considered cooler and
the effective temperature underestimated. So, we can guess that the effective
temperature of MWC 297 could be in the interval 25000
![]() 32800 K, though probably
32800 K, though probably
![]() K, as we see He I 4471
in absorption but no He II lines. The energy distribution of this star
reveals strong dust extinction. Assuming
K, as we see He I 4471
in absorption but no He II lines. The energy distribution of this star
reveals strong dust extinction. Assuming
![]() K, we derived
AV = 6.9 mag, which is somewhat lower than
K, we derived
AV = 6.9 mag, which is somewhat lower than
![]() mag
estimated by Drew et al. (1997).
mag
estimated by Drew et al. (1997).
AS 341: Allen & Glass (1975) argued that this object might be of VV
Cephei type, where a hot B star has an M supergiant companion. From the
[O III] lines they derived a lower limit to the temperature of the
hottest component, which dominates the visible spectrum:
![]()
![]() 22000 K. From the Balmer and He I lines and from the continuum energy
distribution we obtained a mean value
22000 K. From the Balmer and He I lines and from the continuum energy
distribution we obtained a mean value
![]() = 31500 K. The star is
certainly rather hot since we see He I and He II lines.
= 31500 K. The star is
certainly rather hot since we see He I and He II lines.
BD
![]() 3887: In the latest and extensive study of
high-resolution spectroscopy of this LBV candidate, Miroshnichenko et al.
(1998) concluded that an effective temperature
3887: In the latest and extensive study of
high-resolution spectroscopy of this LBV candidate, Miroshnichenko et al.
(1998) concluded that an effective temperature
![]() K is the
most likely to represent its visible line spectrum and the energy distribution.
Using the He I lines we obtained
K is the
most likely to represent its visible line spectrum and the energy distribution.
Using the He I lines we obtained
![]() K. The stellar
K. The stellar
![]() must be rather high as there is no visible Mg II line in
the spectrum. The determination of the continuum energy distribution is
more uncertain in this star and the errors affecting
must be rather high as there is no visible Mg II line in
the spectrum. The determination of the continuum energy distribution is
more uncertain in this star and the errors affecting ![]() and
and ![]() are
twice as large than for other program stars, which produce
are
twice as large than for other program stars, which produce
![]() ,
the middle of the flat part of
,
the middle of the flat part of
![]() against
against
![]() in Fig. 6. Using the measured gradients
in Fig. 6. Using the measured gradients ![]() ,
,
![]() and the mean
value
and the mean
value
![]() K we obtain
AV = 5.3 mag, which is close
to the ISM extinction
AV = 5.7 mag determined by Miroshnichenko
(1996).
K we obtain
AV = 5.3 mag, which is close
to the ISM extinction
AV = 5.7 mag determined by Miroshnichenko
(1996).
HD 53179 (Z CMa) is a double star (Koresko et al. 1991; Lamzin et al.
1999) and HD 45677 and HD 50138 were suspected by Sheikina et al. (2000) to be
binaries. For HD 45677 there are period determinations of its photometric
variations (Halbedel 1989;
Miroshnichenko 1998). The spectral type obtained for
Z CMa and the fundamental parameters of HD 45677 and HD 50138 have been derived
in this paper assuming that these objects were single stars. The question may
then arise whether a stellar companion may modify interpretation of the
observed BCD data. As we have no spectroscopic data available to challenge the
stellar classifications obtained only from spectrophotometric observations, we
simply sought for binary components that within the standard uncertainties of
the BCD parameters [
![]() dex;
dex;
![]() Å (Divan & Zorec 1982a; Zorec & Briot 1991)] can produce the
observed (
Å (Divan & Zorec 1982a; Zorec & Briot 1991)] can produce the
observed (
![]() )
parameters.
)
parameters.
Parallaxes measured by the HIPPARCOS satellite show that HD 45677 (
![]() pc)
and HD 50138 (
pc)
and HD 50138 (
![]() pc) (Zorec 1998) are not inside the
southern filament of the Orion and Monoceros system of molecular clouds (
pc) (Zorec 1998) are not inside the
southern filament of the Orion and Monoceros system of molecular clouds (
![]() pc), in front
of which they project in the sky (Maddalena et al.
1986). Hence, they are isolated objects, but placed in the Gould belt plane
between the Orion and Vela complexes. Using the standard model of rotation of
our Galaxy (Wielen 1982), the observed radial velocities and proper motions of
these objects, we deduced that they could escape from the Ori A-B molecular
clouds and cover the distance separating them (
pc), in front
of which they project in the sky (Maddalena et al.
1986). Hence, they are isolated objects, but placed in the Gould belt plane
between the Orion and Vela complexes. Using the standard model of rotation of
our Galaxy (Wielen 1982), the observed radial velocities and proper motions of
these objects, we deduced that they could escape from the Ori A-B molecular
clouds and cover the distance separating them (
![]() 200 pc) in about
1-7 107 yr. Knowing that the oldest members of the Ori OB1 association
have ages roughly of 2 107 yr, we adopted this time as the age of our
stars. Thus, if each of our stars is supposed to be a binary, their components
have to be in the same evolutionary isochrone. From Schaller's et al. (1992)
grids of stellar models with metallicity Z = 0.02, we interpolated the masses,
effective temperatures and radii of stars lying on the t = 2 107 yr
isochrone. Then, to interpret the data, we assumed three configurations: a)
the secondary star is completely eclipsed by the primary and the bolometric
luminosity of the system is the observed one
200 pc) in about
1-7 107 yr. Knowing that the oldest members of the Ori OB1 association
have ages roughly of 2 107 yr, we adopted this time as the age of our
stars. Thus, if each of our stars is supposed to be a binary, their components
have to be in the same evolutionary isochrone. From Schaller's et al. (1992)
grids of stellar models with metallicity Z = 0.02, we interpolated the masses,
effective temperatures and radii of stars lying on the t = 2 107 yr
isochrone. Then, to interpret the data, we assumed three configurations: a)
the secondary star is completely eclipsed by the primary and the bolometric
luminosity of the system is the observed one
![]() ;
2)
both components are seen and they are well separated, so that
;
2)
both components are seen and they are well separated, so that
![]() is assumed to represent the bolometric luminosity of
the system; 3) the secondary eclipses the primary and the luminosity of the
configuration is
is assumed to represent the bolometric luminosity of
the system; 3) the secondary eclipses the primary and the luminosity of the
configuration is
![]() .
We note that
.
We note that
![]() is mainly due to the uncertainty on the
is mainly due to the uncertainty on the ![]() parameter
(
parameter
(
![]() ). In each of these cases we sought for components lying on
the 2 107 yr isochrone that reproduce the corresponding
). In each of these cases we sought for components lying on
the 2 107 yr isochrone that reproduce the corresponding
![]() luminosity. Finally, from the effective
temperatures of components we derived the discontinuities D(primary),
D(secondary) and, according to each binary configuration,
luminosity. Finally, from the effective
temperatures of components we derived the discontinuities D(primary),
D(secondary) and, according to each binary configuration,
![]() =
D(primary+secondary). Table 5 gives the averages and the 1
=
D(primary+secondary). Table 5 gives the averages and the 1![]() dispersions of the inferred parameters.
dispersions of the inferred parameters.
After trying to produce discontinuities of binary systems so that
![]() ,
we might expect dispersions of
,
we might expect dispersions of
![]() and differences
and differences
![]()
![]() higher than 0.015 dex, the
standard uncertainty of D, to be signs of the presence of binary components.
In Table 5 we see that for HD 45677 these deviations do not fulfil this
requirement, whereas in HD 50138
higher than 0.015 dex, the
standard uncertainty of D, to be signs of the presence of binary components.
In Table 5 we see that for HD 45677 these deviations do not fulfil this
requirement, whereas in HD 50138
![]() 0.015 dex and
0.015 dex and
![]() dex do not contradict the binarity hypothesis.
The bolometric magnitude variations
dex do not contradict the binarity hypothesis.
The bolometric magnitude variations
![]() mag assumed
here are smaller than the more or less regular visual photometric variations of
these stars (Miroshnichenko 1998). In HD 45677 these variations imply
periodicities, which according to the authors range from about 297
mag assumed
here are smaller than the more or less regular visual photometric variations of
these stars (Miroshnichenko 1998). In HD 45677 these variations imply
periodicities, which according to the authors range from about 297![]() (Halbedel 1989) to 1600
(Halbedel 1989) to 1600![]() (Miroshnichenko 1998). Spectroscopic
observations could perhaps confirm either periodic variation of radial
velocities, or at least the presence of double systems of spectral lines
consistent with masses similar to those predicted in Table 5. We finally
conclude that within the assumed
(Miroshnichenko 1998). Spectroscopic
observations could perhaps confirm either periodic variation of radial
velocities, or at least the presence of double systems of spectral lines
consistent with masses similar to those predicted in Table 5. We finally
conclude that within the assumed
![]() variations, the
possibility of some binarity does not notably change our previous spectral
classification and/or fundamental parameter determination for HD 45677. In HD
50138, however, depending on the predicted effective temperatures, there are
many possible spectral types for the primary, which range from B4 to B7.
variations, the
possibility of some binarity does not notably change our previous spectral
classification and/or fundamental parameter determination for HD 45677. In HD
50138, however, depending on the predicted effective temperatures, there are
many possible spectral types for the primary, which range from B4 to B7.
| Star |
|
|
|
|
| dex | K | |||
| HD 45677 | a
|
|||
| Primary |
|
|
||
| Secondary |
|
|
||
| HD 50138 | a
|
|||
| Primary |
|
|
||
| Secondary | 0.300:: |
|
||
|
a:
|
||||
Z CMa belongs to the FU Ori type objects (FUORs). It is a
pre-main-sequence double star system (0
![]() 1 separation), where the secondary (Z
CMa SE) dominates the optical continuum and the primary (Z CMa NW) shows an
emission line spectrum. The secondary not only dominates the IR, but also the
total luminosity of the system (
1 separation), where the secondary (Z
CMa SE) dominates the optical continuum and the primary (Z CMa NW) shows an
emission line spectrum. The secondary not only dominates the IR, but also the
total luminosity of the system (
![]() ,
Koresko et al. 1991;
Berilli et al. 1992; Garcia et al. 1999). Lamzin et al. (1999) have also
concluded that the secondary is probably the main source of the observed
optical variations. Z CMa shows wavelength-dependent spectral types, as is
usual for FUORs (Hessman et al. 1991). Though Z CMa is normally classified as
an Ae/Be star, with spectral types B5 or B5/8 (Buscombe 1977; Thé et al.
1994), it has features of a late B star and of an F-type spectrum (Strom et al.
1972). It may be, however, that the B-type classification depends upon the
strength of the Balmer absorption lines, which can be produced in an outflowing
wind (Covino et al. 1984). Hartmann et al. (1989) also suggested that Z CMa may
be a pre-main-sequence rotating accretion disk surrounding a central object
of mass
,
Koresko et al. 1991;
Berilli et al. 1992; Garcia et al. 1999). Lamzin et al. (1999) have also
concluded that the secondary is probably the main source of the observed
optical variations. Z CMa shows wavelength-dependent spectral types, as is
usual for FUORs (Hessman et al. 1991). Though Z CMa is normally classified as
an Ae/Be star, with spectral types B5 or B5/8 (Buscombe 1977; Thé et al.
1994), it has features of a late B star and of an F-type spectrum (Strom et al.
1972). It may be, however, that the B-type classification depends upon the
strength of the Balmer absorption lines, which can be produced in an outflowing
wind (Covino et al. 1984). Hartmann et al. (1989) also suggested that Z CMa may
be a pre-main-sequence rotating accretion disk surrounding a central object
of mass
![]() ,
which is consistent with our F-type spectral
classification. The strong accretion,
,
which is consistent with our F-type spectral
classification. The strong accretion,
![]() yr-1,
may presently be building up a large fraction of the stars.
yr-1,
may presently be building up a large fraction of the stars.
The measured total luminosity of the Z CMa system, as well as the inferred
mass and radius, are highly uncertain (Hartmann et al. 1989; Berilli et al.
1992) and can hardly be used as observational constraints to infer new
characteristics of the components. On the other hand, the (
![]() )
parameters are not calibrated for F-type stars into
)
parameters are not calibrated for F-type stars into
![]() .
We only know that there is a difference
.
We only know that there is a difference
![]() mag between
both components (Finkenzeller & Mundt 1984). Using this V
magnitude-restriction and assuming, only as a conjectural hypothesis, that the
components of Z CMa are "ordinary" stars, the obtained BCD parameters are
consistent with global "normal" MK spectral types which range from F8IV to
F8II-III. Within this same framework, the first of these classifications could
also correspond to an F8+K0 system and the second to an F6/7+G2/5
system.
mag between
both components (Finkenzeller & Mundt 1984). Using this V
magnitude-restriction and assuming, only as a conjectural hypothesis, that the
components of Z CMa are "ordinary" stars, the obtained BCD parameters are
consistent with global "normal" MK spectral types which range from F8IV to
F8II-III. Within this same framework, the first of these classifications could
also correspond to an F8+K0 system and the second to an F6/7+G2/5
system.
In this paper we present low resolution spectra of 23 stars with the
B[e] phenomenonin in the
![]() Å wavelength range.
Spectral classification and fundamental stellar parameters of 15 program stars
were studied using the BCD spectrophotometric system. The BCD system is
suitable for spectral classification of objects that display a measurable
Balmer discontinuity and among them also for those with CE. For stars with CE
we can determine the properties of the underlying star without concern for the
extra emissions and/or absorptions in the lines and in the continua, produced
in the visual spectral range by the circumstellar matter. The parameters
obtained (
Å wavelength range.
Spectral classification and fundamental stellar parameters of 15 program stars
were studied using the BCD spectrophotometric system. The BCD system is
suitable for spectral classification of objects that display a measurable
Balmer discontinuity and among them also for those with CE. For stars with CE
we can determine the properties of the underlying star without concern for the
extra emissions and/or absorptions in the lines and in the continua, produced
in the visual spectral range by the circumstellar matter. The parameters
obtained (
![]() ,
log g,
,
log g,
![]() )
are model-independent and
constitute a valuable tool to study the evolutionary stage of stars with the
B[e] phenomenon. The average absolute relative error of the effective
temperatures thus obtained is
)
are model-independent and
constitute a valuable tool to study the evolutionary stage of stars with the
B[e] phenomenon. The average absolute relative error of the effective
temperatures thus obtained is
![]()
![]() .
The fundamental parameters derived also help to determine, on the one hand,
reliable distances of these objects and on the other hand, the ISM and the
circumstellar dust extinction separately. The determination of distances of
stars with the B[e] phenomenon is now in progress and it will be presented in
another contribution. In the present work we also give an estimation of the
effective temperature of another 8 stars with the B[e] phenomenon which have
no measurable BCD parameters. These effective temperatures were determined by
studying the emission intensity of Balmer and He I lines and/or the
energy distribution in the Paschen continuum. The average error of the
effective temperatures obtained from lines is
.
The fundamental parameters derived also help to determine, on the one hand,
reliable distances of these objects and on the other hand, the ISM and the
circumstellar dust extinction separately. The determination of distances of
stars with the B[e] phenomenon is now in progress and it will be presented in
another contribution. In the present work we also give an estimation of the
effective temperature of another 8 stars with the B[e] phenomenon which have
no measurable BCD parameters. These effective temperatures were determined by
studying the emission intensity of Balmer and He I lines and/or the
energy distribution in the Paschen continuum. The average error of the
effective temperatures obtained from lines is
![]()
![]() .
The colour temperature and the temperatures obtained from the
study of Balmer and He I lines are consistent with each other within the
estimated errors in each determination. The new results were compared with
those obtained previously by other authors and discussed for each star
individually. For some stars, differences between the effective temperatures
derived using the BCD classification system and those obtained by other
authors, based on photometric or spectroscopic analysis, imply spectral-type
classification disagreements ranging from 2-3 up to 6 B sub-spectral types. The
fundamental parameters for AS 119, CD
.
The colour temperature and the temperatures obtained from the
study of Balmer and He I lines are consistent with each other within the
estimated errors in each determination. The new results were compared with
those obtained previously by other authors and discussed for each star
individually. For some stars, differences between the effective temperatures
derived using the BCD classification system and those obtained by other
authors, based on photometric or spectroscopic analysis, imply spectral-type
classification disagreements ranging from 2-3 up to 6 B sub-spectral types. The
fundamental parameters for AS 119, CD
![]() 5721, Hen 2-91, HD 316375 and
BD
5721, Hen 2-91, HD 316375 and
BD
![]() 4747 were obtained for the first time. A simple method was
introduced to calculate total (interstellar+circumstellar) dust extinction of
the studied stars. For HD 53179, which is a double stellar system, and for
HD 45677 and HD 50138, which are suspected binaries, we predicted the
characteristics of the components that are consistent with the observed
4747 were obtained for the first time. A simple method was
introduced to calculate total (interstellar+circumstellar) dust extinction of
the studied stars. For HD 53179, which is a double stellar system, and for
HD 45677 and HD 50138, which are suspected binaries, we predicted the
characteristics of the components that are consistent with the observed
![]() parameters. However, the possible binarity of HD 45677 and
HD 50138 still needs to be confirmed spectroscopically.
parameters. However, the possible binarity of HD 45677 and
HD 50138 still needs to be confirmed spectroscopically.
Acknowledgements
L. C. is grateful to the "Société de Secours des Amis des Sciences", Paris, for a grant which helped to complete the present work. We are deeply indebted to Dr. A. S. Miroshnichenko (referee) for his detailed reading of the manuscript and for his valuable suggestions that contributed to improve the presentation of this paper. We acknowledge the help of A. Garcia (IAP) in making the plots.