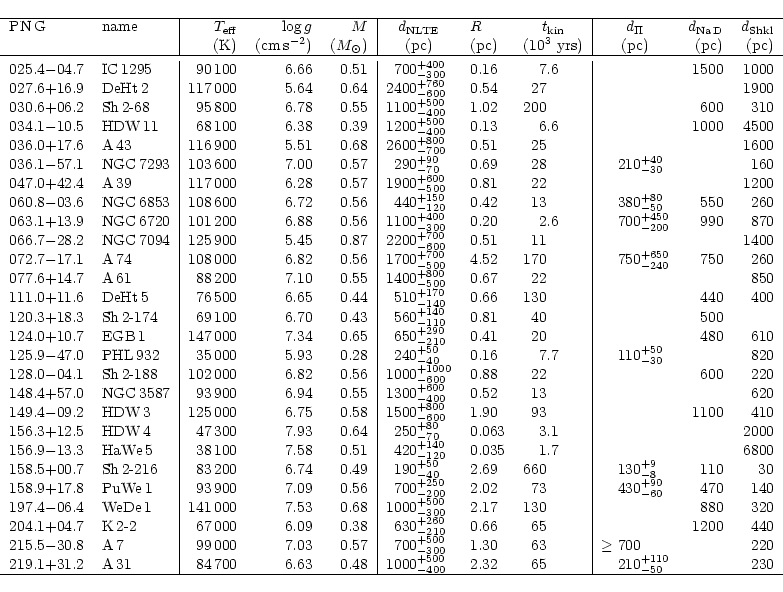
A&A 367, 973-982 (2001)
DOI: 10.1051/0004-6361:20000431

Spectroscopic investigation of old planetaries

V. Distance scales

R. Napiwotzki[*]

Dr. Remeis-Sternwarte, Sternwartstr. 7, 96049 Bamberg, Germany

Received 12 March 1999 / Accepted 4 December 2000

Abstract
We use the results of our recent NLTE model atmosphere analysis of central stars of old planetary nebulae (PN) to calculate distances. We perform a comparison with three other methods (trigonometric parallaxes, interstellar NaD lines, and Shklovsky distances) and discuss the problem of the PNe distance scale. The result of the comparison of our spectroscopic distances with the trigonometric distances is that the spectroscopic distances are 55% larger. Since using trigonometric parallaxes with large relative measurement errors can introduce systematic errors, we carried out a Monte Carlo simulation of the biases introduced by selection effects and measurement errors. It turns out that a difference between both distance scales of the observed size is expected for the present day data if the underlying distance scales are identical. Thus our finding is essentially a confirmation of the spectroscopic distance scale! Good agreement is found between the spectroscopic distances and distances derived from the interstellar NaD lines. All three independent methods of distance measurement indicate that the widely used ``statistical'' distance scales of the Shklovsky type are too short for old PNe. A correlation with nebular radii exists. The most likely explanation is an underestimate of the nebula masses for large PN. Implications for the nebula masses are discussed. Estimates of the PNe space density and birthrate, which are based on Shklovsky type distances, therefore give too large values.

Key words: stars: distances - planetary nebulae: general - white dwarfs - stars: fundamental parameters


1 Introduction

Distances of PNe are usually difficult to determine and are a long standing problem of PNe investigations. The vast majority of published distances of PNe are based on the Shklovsky (1956) method or derivatives of it (often called statistical distances). This method allows the calculation of PN distances from the measurement of the recombination line H$\beta$ and the angular diameter. However, Shklovsky distances are notoriously smaller than distances derived from model atmosphere analysis of the central stars (cf. Méndez 1988).

The question of PNe space densities and birth rates is closely related to the distance scale problem. Ishida & Weinberger (1987) compiled a list of nearby PNe, which contains mostly old, evolved nebulae (actually many of our PNe were selected from this list). Ishida & Weinberger collected distance determinations from literature and computed the space density and birth rates of this local sample of PNe. The derived birth rate of $8~10^{-12}~{\rm yr^{-1}~pc^{-3}}$ is too high to be in accordance with estimates of white dwarf birth rates ( $2.3~10^{-12}~{\rm yr^{-1}~pc^{-3}}$; Weidemann 1991). Since every central star of a PN (CSPN) should become a white dwarf this yielded a real dilemma. Taken at face value this would indicate that current white dwarf samples are very incomplete and the white dwarf birth rates are seriously underestimated. A certain fraction of white dwarfs may be hidden in binaries, indeed. Weidemann (1991) used a very local sample of white dwarfs (d<10pc) for his estimate and applied corrections for incompleteness and binarity. Pottasch (1996) reevaluated the PN space density and derived a value of $3~10^{-12}~{\rm yr^{-1}~pc^{-3}}$, lower than Ishida & Weinberger's result, but still higher than the estimated white dwarf birthrate. The difference in the PNe birthrate can be traced back to the use of different distance scales. While Ishida & Weinberger's collection is mainly based on statistical distance estimates (mainly Shklovsky distances and derivates of this method), Pottasch excluded statistical distance determinations.

In Paper IV of this series (Napiwotzki 1999) we presented the results of an NLTE model atmosphere analysis of 27 central stars of old PNe. This analysis of a reasonably sized sample of central stars of old PNe enables us to address the question of the distance scale of these objects. In Paper III (Napiwotzki & Schönberner 1995) we proposed the use of the interstellar NaD lines for distance determinations. These distances are free of assumptions about the nebula or the central star and are on average larger than the Shklovsky distances by a factor of 2.5 for our sample of old PNe. During the last years a number of trigonometric parallax measurements became available for a sample of central stars of old PNe (Harris et al. 1997; Pottasch & Acker 1998; Gutiérrez-Moreno et al. 1999). We will show that the CSPNe distances derived form our model atmosphere analysis, the NaD distances, and the trigonometric parallaxes are in agreement, but all three distances scales are much larger than those based on the Shklovsky method.

2 Distance scales

2.1 Spectroscopic distances


 

 
Table 1: Model atmosphere fluxes (in 108 ergcm-2s-1Å-1) at $\lambda _{{\rm eff}} = 5454$Å for the calculation of absolute magnitudes and distances. These values are calculated for a hydrogen-rich composition ( $n_{{\rm He}}/n_{{\rm H}} = 0.1$) and $\log g = 6.5$. However, the V band flux is quite insensitive to composition and $\log g$
$T_{{\rm eff}}$/K F5454 $T_{{\rm eff}}$/K F5454
40000 2.18 120000 6.37
50000 2.76 140000 7.21
60000 3.31 170000 8.50
70000 3.87 200000 9.67
80000 4.51 250000 11.93
90000 5.05 300000 13.98
100000 5.52    


Spectroscopic distances can be derived from the model atmosphere analyses described in Paper IV and offer an approach to the PN distance scale independent from the properties of the nebulae. After the stellar mass is estimated from a comparison with evolutionary models (cf. Paper IV) the distance can be calculated in a straightforward way from effective temperature, gravity, and the dereddened apparent magnitude of the stars:

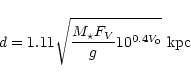1.
the stellar radius is computed from surface gravity and mass;
2.
the surface flux in the V band is calculated from model atmospheres, with the appropriate parameters (thus bypassing the uncertain bolometric corrections);
3.
and finally the absolute magnitude MV is derived and compared with the dereddend V0 magnitude of the star;
4.
This procedure can be condensed into one formula:

\begin{displaymath}d = 1.11 \sqrt{\frac{M_\star F_V}{g}10^{0.4V_0}}\ \rm kpc \end{displaymath} (1)

where $M_\star$ is the solar mass in $M_\odot$, g is the surface gravity in ${\rm cm}/{\rm s}^2$ and FV is the model atmosphere flux in 108 ergcm-2s-1Å-1. We use the monochromatic approximation of Heber et al. (1984) for FV with an effective wavelength $\lambda _{{\rm eff}} = 5454$Å, appropriate for hot stars. A short tabulation of model atmosphere fluxes is provided in Table 1.
This method is independent of any assumption about the PN, but obviously relies on the quality of the model atmospheres used for the analysis and, to a lesser extent, on the evolutionary models used for the mass determination. For our objects the apparent magnitudes were taken from Table 4 of Paper III. If a high quality measurement (indicator "A'') exists in the literature, it was adopted. Otherwise our spectrophotometric measurements were used. Since only very few reliable extinction measurements are available for our objects, we estimated the reddening from the galactic interstellar extinction model of Arenou et al. (1992). However, reddening is generally small and therefore only of moderate importance for our conclusions. The resulting distances are listed as $d_{{\rm NLTE}}$ in Table 2 together with the analysis results of Paper IV. Error limits were estimated from the analyses errors given in Paper IV, the estimated errors of the V measurements, and the reddening. The dominant error source is in most cases the gravity determination.
  
Table 2: Comparison of different distance determinations: from our NLTE analysis in Paper IV $d_{{\rm NLTE}}$, trigonometric distances $d_\Pi $ of Harris et al. (1997), from the interstellar NaD line $d_{{\rm Na\,D}}$, and the Shklovsky distances $d_{{\rm Shkl}}$ (the latter two are taken from Table 6 of Paper III). The kinematical ages calculated ( $t_{\rm kin}$) from the spectroscopic distances are also provided. Effective temperature $T_{{\rm eff}}$, surface gravity g, and stellar mass M were taken from Table 1 of Paper IV. For further input data cf. Table 6 of Paper III

\begin{displaymath}\begin{tabular}{ll\vert rrr\vert r@{}llr@{}l\vert r@{}lrr} \h... ...2.32 &65& &210&$^{+110}_{-50}$ & &230 \\ \hline \end{tabular}\end{displaymath}


2.2 Trigonometric distances

Recently Harris et al. (1997) published trigonometric parallaxes of 11 CSPNe. Eight of these stars belong to our sample (the value given for A7 is actually only an upper limit). Pottasch & Acker (1998) discussed HIPPARCOS parallaxes of three CSPNe including PHL932 which belongs to our sample. The resulting distance values are listed as $d_\Pi $ in Table 2 and are compared with the model atmosphere results in Fig. 1. The error limits were computed from the measurement errors of the parallaxes.

As it is evident from Fig. 1 and the following figures the error distribution of distance determinations is highly non-Gaussian with many outliers, which can skew the common weighting techniques to erroneous values. The reason is that the usually (implicitly) adopted Gaussian probability distribution gives high weight to deviant points. Therefore we decided to minimize the absolute deviations, which corresponds to a double sided exponential probability distribution and provides a more robust estimate (see discussion in Press et al. 1992). Since the distance errors are highly asymmetric, we did the comparison with the parallaxes, which have roughly symmetric error limits. Since we in all cases compare two measurements suffering from large uncertainties, we performed pro forma a linear regression with allowance for errors in both directions and with the intersection fixed at zero. The error ranges given below correspond to the $1\sigma$error of the mean.

The measured trigonometric distances are always smaller than the NLTE distances (cf. Fig. 1). The weighted mean of the distance ratios $r_{{\rm obs}}$, computed as described above, amounts to

 \begin{displaymath}r_{{\rm obs}} = \frac{d_{{\rm NLTE}}}{d_\Pi} = 1.55\pm 0.29. \end{displaymath} (2)

Taken at face value this in concordance with the conclusions of Jacoby & Van de Steene (1995), who compared trigonometric parallax measurements of Pier et al. (1993) with spectroscopic distances and concluded that the model atmosphere results overestimate the distances by $\approx$40%. However, one must consider that trigonometric parallaxes are on the one hand the most direct method for distance determinations, but on the other hand are also subject to heavy biases, which are introduced by random errors of measurement and on average cause the trigonometric parallaxes to be overestimated. This was discussed as early as 1953 by Trumpler & Weaver. Lutz & Kelker (1973) were the first to provide a quantitative correction, which is a function of the relative measurement error of the parallax $\sigma_\Pi /\Pi$. The original Lutz-Kelker correction is valid in a strict sense only, if nothing else is known about the star, which is usually an unrealistic assumption. Different kinds if corrections have to be applied if one deals with a volume limited sample, a magnitude limited sample, or if the "luminosity function'' of the parent population is known (Lutz 1983; Smith 1987).
  \begin{figure} \includegraphics[width=8.5cm]{h1441f1.ps}\par\end{figure} Figure 1: Distances computed from the results of the NLTE analysis compared to trigonometric distances. The error bars correspond to the measurement errors given in Table 2. The solid line indicates the average ratio of the NLTE distances and the trigonometric distances, the dotted line equality
Open with DEXTER

We took a different approach and performed a Monte Carlo simulation to derive biases caused by the selection of CSPNe for parallax measurements and the accompanying measurement errors. Our working hypothesis is that the spectroscopic distance scale is essentially correct, i.e. no systematic errors are present. The results of the Monte Carlo simulations are used to test if this hypothesis is compatible with observations.

In our simulation CSPNe were randomly created according to a simple model of the Galactic stellar density distribution and a theoretical post-AGB track. A spectroscopic analysis is simulated, i.e. random measurement errors are added. The star is selected for parallax measurement if the "spectroscopic distance'' is below a threshold value $d_{{\rm max}}$. A measurement error of the parallax $\sigma_\Pi$ is added to the true parallax and the resulting distance used for a comparison with the spectroscopic parallax, if the "measured parallax'' is larger than a threshold value $\Pi_{{\rm min}}$. $N_{{\rm sample}}$ stars are collected and the mean ratio $r_{{\rm MC}} = \frac{d_{{\rm NLTE}}}{d_\Pi}$ is computed analogous to the procedure applied for the observed data. This process is repeated $N_{{\rm total}}$ times and a probability distribution is evaluated. Sample probability distributions are given in Fig. 2 (these are discussed below). A detailed description of the Monte Carlo simulations, the input parameters, and their standard values is given in the Appendix.

  \begin{figure} \includegraphics[width=8.5cm]{h1441f2.ps}\par\end{figure} Figure 2: Results of Monte Carlo simulations for several values of the maximum allowed "spectroscopic'' distance $d_{{\rm max}}$. The distributions are normalized to an integrated area of 1. For cosmetic reasons we used $N_{{\rm total}}=10^6$ for this plot
Open with DEXTER

An investigation of the influence of the different input parameters on the results can be found in Table A.2. The derived bias between spectroscopic and trigonometric distances is most sensitive to the chosen threshold value $d_{{\rm max}}$ for the pre-selection of stars, the parallax measurement error $\sigma_\Pi$ and the threshold parallax $\Pi_{{\rm min}}$. Our standard model assumes $d_{{\rm max}} = 1000$pc. Note that one star in the Harris et al. (1997) sample has a much larger value of the spectroscopic distance (A74; $d_{{\rm NLTE}} = 1700$pc). For $\sigma_\Pi$ the mean of the error limits in Table 2, $\sigma_\Pi = 0.95$, was adopted. The threshold parallax was set to $\Pi_{{\rm min}} = 1.33$ (corresponds to A74). Our standard sample size, $N_{{\rm sample}} = 8$, corresponds to the observed sample and the simulation is carried out for $N_{{\rm total}} =100\,000$ samples.

The first qualitative conclusion, which can be drawn from Table A.2 and Fig. 2 is that the "measured'' ratio $r_{{\rm MC}}$ is always considerably larger than unity, although the underlying distance scales used in the Monte Carlo simulations are identical. Our standard model yields

\begin{displaymath}r_{{\rm MC}} = 1.32 \pm 0.25 \end{displaymath} (3)

(we give the median value and the range which contains 68.3% of all samples as $1\sigma$ limit). Although our measured value $r_{{\rm obs}} = 1.55\pm 0.29$ is larger it is still in the $1\sigma$ range of the standard simulation. If we increase $d_{\max}$ to 1500pc (keeping A74 in mind) the result of the Monte Carlo simulation increases to $ r_{{\rm MC}} = 1.50 \pm 0.38$close to the measured value. The impact of modifying $d_{\max}$ on the probability distribution is displayed in Fig. 2. If we on the other hand remove CSPNe with $d_{{\rm NLTE}}>1000$pc from our sample in Table 2 (NGC6720 and A74) we derive $ r_{{\rm MC}} = 1.42 \pm 0.29$close to the value predicted for $d_{\max}=1000$ pc.

A paradoxical effect results if the threshold parallax $\Pi_{{\rm min}}$ is increased: the bias increases for increasing $\Pi_{{\rm min}}$, if the spectroscopic threshold distance is left unchanged! E.g. for $\Pi_{{\rm min}}=3.0$mas we derive $r_{{\rm MC}} = 1.51\pm 0.35$. The reason is that we introduce a strong selection effect for stars with much too large measured parallaxes. This effect is only overcome, if $\Pi_{{\rm min}}$ is increased to even larger values ( $\Pi_{{\rm min}}\ge5$mas).

In principle, the expected bias can be reduced by lowering $d_{{\rm max}}$and $\sigma_\Pi$. However, if we e.g. adopt $d_{{\rm max}} = 750$pc and $\sigma_\Pi = 0.7$mas our observed sample is reduced to 3 stars!

We conclude that the mean value of $r_{{\rm MC}}$ derived from our observed sample (Table 2) is well within the range predicted by Monte Carlo simulations for perfect agreement of both distance scales. Thus the trigonometric parallax measurements provide no evidence that the spectroscopic distances are in error, but confirm the spectroscopic distance scale, instead! However, due to the statistical uncertainties we cannot provide a definitive proof of an agreement of better than about 20%.

2.3 Distances based on interstellar lines and extinction

Another method independent of assumptions about central star or nebula properties is based on interstellar lines. In Paper III we used the interstellar NaD lines at 5890/96Å for this purpose. The CSPNe are too hot to show any photospheric NaD lines and the PNe material is extremely dispersed. In their survey Dinerstein et al. (1995) detected circumstellar NaD lines in nine PNe. However, all investigated PNe were young objects, and if there is any neutral sodium at all in the circumstellar matter of the central star of old PNe, the column density would be very low and the resulting nebula contribution negligible. Naturally this method is restricted to stars at low galactic latitude. The distances derived in Paper III are given as $d_{{\rm Na\,D}}$ in Table 2.

Our NaD distances in Paper III were determined from the map of the interstellar NaD line strength of Binnendijk (1952). One might ask, whether the distance scale adopted in that work is still valid. To our knowledge no more recent collection of interstellar NaD equivalent widths is available. The reason is that using the equivalent width is out of fashion, because resolved interstellar lines in high resolution spectra provide more information. However, for our faint CSPNe equivalent widths are still a useful tool.

Binnendijk (1952) adopted spectroscopic distances of B stars, which were determined by the Yerkes group (Ramsey 1950; Duke 1951, and unpublished distances provided by W. W. Morgan). It is save to assume that systematic differences between these authors are small. We performed a check of the Ramsey (1950) and Duke (1951) distances. For this purpose we selected a representative subsample of 20 stars from each collection with Strömgren $uvby\beta$ measurements in the Hauck & Mermilliod (1998) catalogue. Temperatures and gravities were calculated with an updated version (Napiwotzki & Lemke, in prep.) of the photometric calibration of Napiwotzki et al. (1993). The new gravity calibration is based on accurate trigonometric parallaxes measurements of B stars with HIPPARCOS. Since the calibration doesn't cover O stars and supergiants, these stars were excluded from the comparison. Masses were derived by interpolation in the evolutionary tracks of Schaller et al. (1992) and distances $d_{uvby\beta}$computed as described in Sect. 2.1. Finally these distances were compared with the spectroscopic distances provided by Ramsey (1950) and Duke (1951) and mean ratios were computed as described in Sect. 2.2. The results are

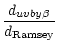$\displaystyle \frac{d_{uvby\beta}}{d_{{\rm Ramsey}}}$ = 0.92 (4)
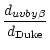$\displaystyle \frac{d_{uvby\beta}}{d_{{\rm Duke}}}$ = 1.17 (5)

or in other words the Ramsey distances are on average 8% longer, the Duke distances 14% shorter than the $uvby\beta$ distances.

Although the scatter of the individual determinations is large we can conclude that altogether systematic differences between the old Yerkes system and modern photometric distances, which are tied to accurate HIPPARCOS parallaxes, are small.

  \begin{figure} \includegraphics[width=8.5cm]{h1441f3.ps}\par\end{figure} Figure 3: Distances computed from the results of the NLTE analysis compared to NaD distances. The solid line indicates the average distance ratio
Open with DEXTER

Figure 3 shows that the agreement of the NaD distances with the model atmosphere analysis is good. The scatter is easily explained by the spatially highly variable extinction in the galactic plane. The average ratio of both distance scales amounts to

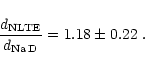\begin{displaymath}\frac{d_{{\rm NLTE}}}{d_{{\rm Na\,D}}} = 1.18\pm 0.22\ . \end{displaymath} (6)

The extinction distance method is an approach similar to our NaD method. The interstellar reddening of the central star or the PN is measured and compared to a distance-reddening relation derived from stars in the angular vicinity of the PN. Since reddening and distances of many stars have to be determined, it is unfortunately a costly method and has been applied to few PNe only. Extinction distances of two PNe of our sample were measured by Saurer et al. (1995). Results are $800\pm 300$pc for Sh2-188 and $800\pm 400$pc for HDW3. The Sh2-188 distance is in good agreement with our estimate of 1000+1000-600pc. Our HDW3 distance of 1500+800-600pc is moderately larger than the extinction distance. Saurer noted that his upper limit maybe uncertain because the interstellar extinction reaches a plateau value at 1200pc. However, the error bars overlap anyway.

2.4 Shklovsky distances

The Shklovsky (1956) method allows the calculation of PN distances from the measurement of the recombination line H$\beta$ and the angular diameter. The distance can be computed from (see e.g. Pottasch 1984, p. 115):

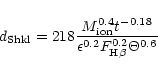\begin{displaymath}d_{{\rm Shkl}} = 218 \frac{M^{0.4}_{{\rm ion}} t^{-0.18}} {\epsilon^{0.2} F^{0.2}_{{\rm H}\beta}\Theta^{0.6}} \end{displaymath} (7)

with distance $d_{{\rm Shkl}}$ in pc, flux $F_{{\rm H}\beta}$in ergcm-2s-1, the angular diameter $\Theta$ in arcsec, the electron temperature t in 104K, the filling factor $\epsilon$, and the mass of the ionized nebular matter $M_{{\rm ion}}$ in $M_\odot$. The dependence of $d_{{\rm Shkl}}$on t and $\epsilon$ is only small, hence it suffices to use standard values (e.g. t = 1 and $\epsilon = 0.75$). However, major problems are caused by the need to assume a mass $M_{{\rm ion}}$ of the (ionized) nebula. The classical Shklovsky method adopts a constant mass, usually $M_{{\rm ion}} = 0.2~M_\odot$. However, for the few PNe with independent distance determinations a trend of increasing mass with increasing radius is observed (see e.g. Maciel & Pottasch 1980; Cahn et al. 1992). Thus Maciel & Pottasch (1980), Daub (1982), and Cahn et al. (1992) proposed modified Shklovsky methods employing an empirical mass-radius relationship. However, the Daub (1982) and Cahn et al. (1992) mass-radius relations adopted an upper limit for $M_{{\rm ion}}$, which means that for old, large PNe a constant mass of the order $0.2~M_\odot$ is applied, similar to the classical version. Recent approaches by Zhang (1995) and by Van de Steene & Zijlstra (1995) propose to use the correlation between the radio continuum brightness temperature and radius instead. However, this method needs an empirical calibration, too. In Table 2 we present Shklovsky distances $d_{{\rm Shkl}}$ collected from the literature. Most values were taken from the catalogue of Cahn et al. (1992). Please, consult Table 6 of Paper III for detailed references.
  \begin{figure} \includegraphics[width=8.5cm]{h1441f4.ps}\par\end{figure} Figure 4: Distances computed from the results of the NLTE analysis compared to Shklovsky distances. Filled diamonds: ordinary white dwarf CSPNe of spectral type DA and DAO, open circles: hybrid/high luminosity objects, open squares: non post-AGB objects. The dotted line indicates equality, the solid the average distance ratio for the ordinary white dwarf CSPNe
Open with DEXTER

A comparison of the Shklovsky and the model atmosphere distances is shown in Fig. 4. We distinguish between "ordinary'' white dwarf CSPNe of spectral type DA and DAO (filled symbols) and the hybrid/high luminosity objects A43, NGC7094, Sh2-68, and DeHt2 (open circles) and the non post-AGB objects (open squares). The evolutionary history of both latter classes are likely very different from standard evolution and may cause very different PN properties. The comparison shows that almost all Shklovsky distances of the ordinary white dwarf CSPNe are smaller than the model atmosphere distances. The average (weighted by the error limits of our analysis) amounts to

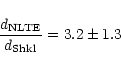\begin{displaymath}\frac{d_{{\rm NLTE}}}{d_{{\rm Shkl}}} = 3.2 \pm 1.3 \end{displaymath} (8)

where we have adopted an $1\sigma$ error of all Shklovsky distances of 30%.

Since $d_{{\rm NLTE}}/d_{{\rm Shkl}}$ is directly related to the ionized mass of the PN by the Shklovsky formula $M_{{\rm ion}} \sim d^{2.5}$, we interpret this as evidence that the ionized masses of the old PNe are much higher than the adopted typical mass of $0.2~M_\odot$. The distance scales would be in agreement if we increase the adopted PNe mass to $3.5~M_\odot$. However, the large scatter is a first indication that this is an oversimplification of the real situation, as we will show below. Note in passing that the non post-AGB objects (open squares in Fig. 4) have considerably lower values of $d_{{\rm NLTE}}/d_{{\rm Shkl}}$ (mostly <1) indicating masses lower than the adopted PN mass.

3 Discussion

We have now shown that the distances $d_{{\rm NLTE}}$ derived from our NLTE model atmosphere analyses are (within today's error limits) in good agreement with the trigonometric parallaxes measured by Harris et al. (1997) and Pottasch & Acker (1998) after biases are taken into account, and with distances derived from the strength of the interstellar NaD lines. Both distance scales are model independent and thus demonstrate that the NLTE analysis are not subject to large systematic errors. On the other hand Napiwotzki et al. (1999) have shown that state-of-the-art analyses of hot white dwarfs performed independently by different groups can yield surface gravities, which differ systematically by up to 0.1dex which translates into a distance error of 12%. Such errors of the model atmosphere distance scale would be compatible with the trigonometric and NaD distances of our stars. Much larger systematic errors can be excluded. The Shklovsky distance scale of old PNe is shown to be too short, most likely caused by an underestimate of the PNe masses.

  \begin{figure} \includegraphics[width=8.5cm]{h1441f5.ps}\par\end{figure} Figure 5: The individual ratios of $d_{{\rm NLTE}}$ and $d_{{\rm Shkl}}$ as function of the nebula radius. The meaning of the symbols is the same as in Fig. 4. The line indicates our fit (Eq. (9))
Open with DEXTER

Further insight can be gained when plotting (Fig. 5) the individual ratios $d_{{\rm NLTE}}/d_{{\rm Shkl}}$ as function of the PN radii (given in Table 2). A strong correlation is present. A simple (double logarithmic) linear fit results in

 \begin{displaymath}\log\frac{d_{{\rm NLTE}}}{d_{{\rm Shkl}}} = 0.388 +0.935 \log \frac{R}{{\rm pc}}\cdot \end{displaymath} (9)

This indicates that the PN masses increase with increasing radii. The trigonometric measurements essentially confirm this result (Fig. 6). The effect of the 35% shorter trigonometric distances in (Fig. 6) is small, because moderate changes of the distances essentially produce a shift parallel to our fit line.

How does our result compare with other tests of the Shklovsky distance scale? Ciardullo et al. (1999) determined PN distances from main sequence companions of the CSPN and concluded that statistical distance determinations overestimate the PN distances. Stasinska et al. (1991) and Pottasch & Zijlstra (1992) applied the Shklovsky method to PN in the bulge of our Galaxy. Stasinska et al. concluded that, besides considerable scatter, the mean Shklovsky distance reproduces the distance of the galactic bulge well, while Pottasch & Zijlstra claimed that the Shklovsky distances are systematically too high. Do these results contradict our findings in Fig. 5?

  \begin{figure} \includegraphics[width=8.5cm]{h1441f6.ps}\par\end{figure} Figure 6: Sames as Fig. 5 but this time we compare the distances from trigonometric and spectroscopic parallaxes $d_{{\rm\Pi }}$ with $d_{{\rm Shkl}}$. The Ciardullo et al. (1999) results are plotted as asterisks. For other symbols cf. Fig. 4. The line indicates the fit from Fig. 5
Open with DEXTER

Ciardullo et al. (1999) derived spectroscopic parallaxes of main sequence companions of 14 CSPN and compared their results (and 7 trigonometric parallaxes) with four different statistical distance scales based on the prescriptions of Cahn et al. (1992), Maciel & Pottasch (1980), van der Steene & Zijlstra (1995) and Zhang (1995). These are variants of the Shklovsky method (Eq. (2)) in which the ionized mass $M_{{\rm ion}}$ grows as a function of radius (Cahn et al. 1992; Maciel & Pottasch 1980; Zhang 1995) or of the radio brightness temperature of the PN. Cahn et al. (1992) assumed that the ionized mass of small, ionization bounded PNe grows with radius until an upper limit is reached for larger density bounded PN. This has the effect that these distance determinations for PNe in the sample discussed by Ciardullo et al. (1999) are essentially classical Shklovsky distances with $M_{{\rm ion}} = 0.135~M_\odot$. We performed a small correction to the Cahn et al. (1992) distances to transform them to the common $M_{{\rm ion}} = 0.2~M_\odot$ scale and added the Ciardullo et al. (1999) data points to Fig. 6. Two conclusions can be drawn:

1.
the Ciardullo et al. results agree very well with the correlation found for the spectroscopic distances in Fig. 5;
2.
the Ciardullo et al. distances are on average smaller than the Cahn et al. distances, indeed. The reason is that the PNe investigated by Ciardullo et al. are on average, smaller than the PNe in our sample.
PNe in the galactic bulge are very useful for several tests, because their distance is known from the distance of the bulge. Stasinska et al. (1991) and Pottasch & Zijlstra (1992) used this for tests of the Shklovsky distance scale (both groups adopted a distance of 7.8kpc). Stasinska et al. (1991) found reasonable agreement of Shklovsky distance: their distance distribution peaked between 8 and 9kpc with 77% of all PNe in the range $8.5\pm 3.5$kpc. Pottasch & Zijlstra (1992) on the other hand derived a peak value of 11.5kpc and a 75% range from 7 to 17kpc. The main difference between both works is that Pottasch & Zijlstra used only fluxes and angular diameters measured from radio observations, while Stasinska et al. combined radio and optical flux data and preferred optical angular diameters.

Since one wants to exclude foreground objects, PNe with an angular diameter larger than 20'' are excluded from bulge samples. This translates into a radius R = 0.41pc. Thus the old and large PNe of our sample (Table 2) are explicitly excluded from investigations of bulge PNe. Another strong selection effect against old PNe might already be at work, because of their low surface brightness combined with the large extinction. A lower limit of the angular diameter of $\approx$1'' is set by the need to resolve the PNe. This constrains the radii of bulge PNe, which could be used to test the Shklovsky method approximately to the range $0.04\,{\rm pc} < R < 0.41$pc. From Fig. 5 we would predict that the Shklovsky distances of bulge PNe are moderately too large, in qualitative agreement with the Pottasch & Zijlstra (1992) result. However, one should keep in mind that the stellar population of the galactic bulge is quite different from the local population. Therefore one should be aware that the properties of bulge PNe might be different from local samples.

The correlation given in Eq. (9) translates into a mass-radius relation

 \begin{displaymath}M_{{\rm ion}} = 1.87 R^{2.3} \end{displaymath} (10)

with M in $M_\odot$ and R in pc. Equation (10) implies that the ionized masses of old PN are quite high. For an old PN with R = 2pc one derives $M_{{\rm ion}} = 9.3~M_\odot$.

It is likely that during the PN evolution the complete material of the slow ($\approx$10kms-1) AGB wind material is swept-up by the faster ($\approx$ $20\ldots 40$kms-1) expanding planetary shell (Schmidt-Voigt & Köppen 1987; Marten & Schönberner 1991) and could finally be incorporated into the PN. However, $9~M_\odot$ is much larger than the mass a typical CSPN precursor ( $M = 1{\ldots} 2~M_\odot$) can loose during it's evolution. There are some points which should be considered when interpreting the mass-radius relation (Eq. (10)):

1.
the mass-radius relation would be modified if the filling factor $\epsilon$ (cf. Eq. (2)) changes during PN evolution;
2.
many PN of our sample (Table 2) have a large angular diameter (several arcminutes are not uncommon) and the surface brightness is very low. Thus it is often a challenging observational task to measure emission line fluxes of these objects. As a consequence the observational data provided in literature is often of low quality. We intend to determine reliable H$\beta$ fluxes of old PN from Table 2 to improve this situation;
3.
Old PN show often signs of an interaction with the surrounding interstellar medium (Borkowski et al. 1990; Tweedy & Kwitter 1996 and references therein). The PNe shape is distorted and it is difficult to estimate the angular diameter $\Theta$;
4.
On the other hand one may speculate that part of the ionized material is even swept-up interstellar matter. Note that an interstellar particle density of 1cm-3 corresponds to $0.05~M_\odot$/pc-3. If the interstellar matter corresponding to the nebular volume is incorporated into the nebula the mass of the R=2pc PN is increased by $1.7~M_\odot$. This might be an interesting topic for future investigations of the PNe interstellar matter interaction. However, more high quality observational material is necessary before one can start to attack this question.
If the mass-radius relation in Eq. (10) is confirmed one can use it in principle to produce a new variant of a statistical distance scale. However, the exponent ( $\beta = 2.3$) is uncomfortable close to the value $\beta = 2.5$ at which the method degenerates and unacceptable large errors have to be expected (cf. e.g. Kwok 2000, p. 177 f.).

4 Conclusions

We used the results of our model atmosphere analysis to compute distances of the central stars and showed that our model atmosphere distance scale is in good agreement with measured trigonometric parallaxes (after the effect introduced by biases has been taken into account via a Monte Carlo simulation) and distances derived from the interstellar NaD lines. All these three independent methods of distance measurement indicate that the widely used "statistical'' distance scales of the Shklovsky type are too short for old PNe. The most likely explanation is an underestimate of the nebula masses.

Estimates of the PNe space density and birthrate, which are based on Shklovsky type distances, therefore give too large values. If a more realistic distance scale is applied, discrepancies between white dwarf and PNe birthrates are resolved.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h1441f7.ps}\end{figure} Figure 7: Probability distribution for our standard model and for the possible future improvements discussed in the text
Open with DEXTER

Due to statistical uncertainties and biases of the trigonometric distances we could test the spectroscopic distance scale only on the 20% level. Do we have to wait for space missions like GAIA or SIM to improve this situation? A test on the 10% level might be achieved with state-of-the-art-techniques. Harris et al. (1997) announced that parallax measurement accuracies of 0.5mas are within reach, but this alone is not enough (cf. Table A.2). However, if a sample with $d_{{\rm NLTE}} < 750$pc is produced and the sample size is doubled to $N_{{\rm sample}} = 16$ the bias $r_{{\rm MC}}$ is reduced to 4% and the scatter to 10% (the probability distribution is compared with the present situation in Fig. 7). Thus, if we work on both fields, measuring of more accurate parallaxes and analyzing and selecting more candidates from spectroscopic investigations, this goal is within reach.

Acknowledgements
The author thanks Joachim Köppen for inspiring discussions and Detlef Schönberner, Uli Heber, and Klaus Werner for useful comments on previous drafts of this paper.

   
Appendix A: Monte Carlo simulation of the local PN population

Our Monte Carlo simulation of the local PN distribution proceeds in three steps:

1.
a star is created at a random position based on a simple 3D model of the galactic disk;
2.
a post-AGB age is randomly chosen and the absolute magnitude of the star is computed from a theoretical evolutionary track;
3.
a scheme which describes the selection of CSPNe for parallax measurements and the effects of measurement errors is applied.
The parameters of our standard model are provided in Table A.1 and the results of a parameter study which explores the effects of varying these parameters are listed in Table A.2.
 

 
Table A.1: Standard parameters for the Monte Carlo simulation
Sample sizes: 
$N_{{\rm total}}$ = 105 
$N_{{\rm sample}}$  = 8 
Sample selection: 
$V_{{\rm max}}$ = 17.5mag
$d_{{\rm max}}$ = 1000pc
$\Pi_{{\rm min}}$ = 1.33mas
$\sigma_\Pi$ = 0.95mas
$\sigma_{M_V}$ = 0.75mag
Stellar evolution: 
$M_{{\rm CSPN}}$  = 0.605$M_\odot$
$T_{{\rm min}}$ = 3000yrs
$T_{{\rm max}}$ = 50000yrs
Galactic model: 
R0 = 4500pc
$H_{{\rm star}}$ = 300pc
$H_{{\rm dust}}$ = 140pc
$\kappa_{{\rm dust}}$ = 1.0mag/kpc



 

 
Table A.2: Influence of parameter variations on the results of the Monte Carlo simulation
parameter values $d_{{\rm NLTE}}/d_\Pi$
std. model    $1.32 \pm 0.25$
$N_{{\rm sample}}$ 16  $1.30 \pm 0.19$
  32  $1.30 \pm 0.13$
  64  $1.30 \pm 0.09$
$V_{{\rm max}}$ 16.5mag $1.24 \pm 0.25$
  18.5mag $1.34 \pm 0.25$
$d_{{\rm max}}$ 750pc $1.14 \pm 0.20$
  1500pc $1.50 \pm 0.38$
  3000pc $1.64 \pm 0.51$
$\Pi_{{\rm min}}$ 1.5mas $1.37 \pm 0.26$
  2.0mas $1.51 \pm 0.30$
  3.0mas $1.51 \pm 0.35$
  4.0mas $1.32 \pm 0.30$
  5.0mas $1.22 \pm 0.24$
  7.0mas $1.16 \pm 0.21$
  10.0mas $1.14 \pm 0.20$
$\sigma_\Pi$ 0.1mas $1.06 \pm 0.16$
  0.2mas $1.07 \pm 0.16$
  0.3mas $1.10 \pm 0.16$
  0.4mas $1.13 \pm 0.17$
  0.5mas $1.16 \pm 0.17$
  0.7mas $1.23 \pm 0.20$
  1.2mas $1.38 \pm 0.31$
$\sigma_{M_V}$ 0.5mag $1.26 \pm 0.23$
  1.0mag $1.30 \pm 0.28$
$T_{{\rm min}}$ 1000yrs $1.31 \pm 0.26$
  5000yrs $1.31 \pm 0.26$
$T_{{\rm max}}$ 25000yrs $1.33 \pm 0.26$
  100000yrs $1.29 \pm 0.26$
$H_{{\rm star}}$ 150pc $1.28 \pm 0.26$
  600pc $1.34 \pm 0.26$
$H_{{\rm dust}}$ 60pc $1.32 \pm 0.25$
  210pc $1.31 \pm 0.25$
$\kappa_{{\rm dust}}$ 0.50mag/kpc $1.32 \pm 0.26$
  1.50mag/kpc $1.30 \pm 0.26$


Our simple description of the galactic disk is based on the Galaxy model of Bienaymé et al. (1987). An exponential density law with a scale height $H_{{\rm star}}$ of 300pc is adopted for the CSPN. This corresponds to a stellar population with an age of $3{\ldots}\,5~10^9$yrs. We included extinction by a dust component with a scale height $H_{{\rm dust}} =140$pc, which is the value appropriate for the interstellar matter. A dust opacity at the position of the sun $\kappa_{{\rm dust}} = 1$mag/kpc was chosen. The stellar and dust density decreases exponentially with the distance from the galactic center and a scale length R0 = 4.5kpc. For the distance of the sun from the galactic center we adopted the standard value of 8.5kpc. Let us note that Köppen & Vergely (1998) could successfully reproduce the extinction properties of galactic bulge PNe with our parameter values.

Our parameter study in Table A.2 shows that the influence of particular values of the parameters of our "galactic model'' are very small. Due to the exponential decrease of stellar density with height above the galactic plane the number of stars within a sphere with a given radius Rincreases less then R3. Since this lowers the number of far away stars, a lower bias is expected for lower values of the scale height. Extinction introduces another selection against far away stars (through the limiting magnitude). However, as Table A.2 proofs the effect of varying these parameters within reasonable limits is quite small.

For a given post-AGB age the absolute magnitudes of CSPNe can be computed from theoretical post-AGB tracks. In principle a mass distribution for the CSPNe should be used. However, since the mass distributions of CSPN and white dwarfs are quite narrow, we considered it sufficient to use only one theoretical track for simplicity. Spectroscopic studies of CSPNe (Paper IV), white dwarfs (Bergeron et al. 1992; Napiwotzki et al. 1999) and an investigation of PNe based on a distant independent method by Stasinska et al. (1997) derived peak masses in the range $0.55{\ldots} 0.60~M_\odot$. Thus we selected the $0.605~M_\odot$ post-AGB track of Blöcker (1995) for our simulation. The post-AGB age was varied within a given interval $T_{\rm min} {\ldots}\,T_{\rm max}$ which approximately reproduces the MV distribution of our CSPNe. However the simulation results are quite insensitive to their particular values (cf. Table A.2).

After "producing'' a CSPN we had to simulate the selection for parallax measurement and the distance determination with their measurement errors. The following scheme was adopted:

1.
we simulated a "spectroscopic analysis'' with a random measurement error. We adopted a standard value for the scatter of the absolute magnitude determination of $\sigma_{M_V} = 0.75$ (Gaussian error distribution). This corresponds to the mean of the errors given in Table 2;
2.
if the "spectroscopic analysis'' indicates that the distance of the CSPN is below a given maximum value $d_{{\rm max}}$ the star was selected for "parallax measurement'';
3.
the parallax is "measured'' with an Gaussian error distribution with $\sigma_\Pi$. Our standard value of $\sigma_\Pi$ is 0.95mas. That is the mean error of the parallax measurements provided in Table 2. A parallax measurement is used for distance determination if the value is larger than a lower limit $\Pi_{{\rm min}}$. We chose $\Pi_{{\rm min}} = 1.33$mas, corresponding to the value measured for A74;
4.
this process was repeated until $N_{{\rm sample}}$ distance determinations were performed. The standard value of $N_{{\rm sample}}$ is 8, the number of CSPNe with parallax measurements in Table 2. The mean value of $d_{{\rm NLTE}}/d_\Pi$ was computed with the same method as used for our observed sample (cf. Sect. 2.2.);
5.
to derive a proper statistic this simulation was repeated $N_{\rm total} = 10^5$ times. The best values given in Table A.2 and in Sect. 2.3 are the median values. $1\sigma$ values were computed from the condition that they should include 68.3% of the simulations. Results from repeated runs yielded results, which didn't deviate by more than 1%.
The effect of the most important input parameters, the threshold value $d_{{\rm max}}$ for the pre-selection of stars, the parallax measurement error $\sigma_\Pi$ and the threshold parallax $\Pi_{{\rm min}}$, is discussed in Sect. 2.2.

References

 

Copyright ESO 2001