A&A 367, 780-787 (2001)
DOI: 10.1051/0004-6361:20000500
L. C. Popovic - N. Stanic - A. Kubicela - E. Bon
Astronomical Observatory, Volgina 7, Belgrade, Yugoslavia
Received 9 October 2000 / Accepted 6 December 2000
Abstract
To investigate the structure of the Akn 120 emitting region
we have analysed
the spectral line profiles of H![]() ,
H
,
H![]() ,
Ly
,
Ly![]() ,
C III[1909], C IV[1549] and Mg II[2798] lines using
a Gaussian-decomposition approach.
The decomposed shape of the Akn 120 lines indicates three separated
broad
line-emitting regions,
in two of them, the systematic motions of
emitting gas are present.
It seems that one of the two regions has a high
random velocity of emitters (
,
C III[1909], C IV[1549] and Mg II[2798] lines using
a Gaussian-decomposition approach.
The decomposed shape of the Akn 120 lines indicates three separated
broad
line-emitting regions,
in two of them, the systematic motions of
emitting gas are present.
It seems that one of the two regions has a high
random velocity of emitters (![]() 2500 kms-1) and approaching
line-of-sight
velocities, and the other has a smaller random velocity of emitters
(
2500 kms-1) and approaching
line-of-sight
velocities, and the other has a smaller random velocity of emitters
(![]() 1000 kms-1) and receding line-of-sight velocities.
Also, we discuss the long-term H
1000 kms-1) and receding line-of-sight velocities.
Also, we discuss the long-term H![]() line shape variation
in the spectra of Akn 120.
The H
line shape variation
in the spectra of Akn 120.
The H![]() line (from 96 spectra) was fitted
with three broad and one
narrow Gaussians through the entire period considered (1977-1990). The
central broad as well as blue component of
H
line (from 96 spectra) was fitted
with three broad and one
narrow Gaussians through the entire period considered (1977-1990). The
central broad as well as blue component of
H![]() and shelf (Fe II template) cause the H
and shelf (Fe II template) cause the H![]() line shape variation.
Besides the Gaussian decomposition of the shapes of the three hydrogen lines
we propose here a disk model with two more regions
located symmetrically to the disk plane. Using the fitting method with the
disk model we obtained the parameters of the disk:
line shape variation.
Besides the Gaussian decomposition of the shapes of the three hydrogen lines
we propose here a disk model with two more regions
located symmetrically to the disk plane. Using the fitting method with the
disk model we obtained the parameters of the disk:
![]() ;
;
![]() ,
,
![]() .
.
Key words: galaxies: individual (Arakelian 120) - galaxies: Seyfert - line: profiles - accretion, accretion disks
The spectral line investigation of Active Galactic Nuclei (AGNs)
helps us to understand physical properties and kinematics of emitting gas.
The AGN radiation comes from a compact very
luminous center of a galaxy, and in their spectra narrow and broad emission lines
are observed. These lines come from a very extensive emitting line region,
where plasma has very different parameters; the electron density can range from
10
![]() to 10
to 10
![]() and electron temperatures from several hundreds
to tens of thousands Kelvin (see e.g. Osterbrock 1990).
It is widely accepted
that the "central engine'' consists of a massive
black hole fueled by an accretion disk. Also, observations
in a wide band of wavelengths (X, UV, optical) indicate that an accretion
disk should be present as a central part of the majority of AGNs.
and electron temperatures from several hundreds
to tens of thousands Kelvin (see e.g. Osterbrock 1990).
It is widely accepted
that the "central engine'' consists of a massive
black hole fueled by an accretion disk. Also, observations
in a wide band of wavelengths (X, UV, optical) indicate that an accretion
disk should be present as a central part of the majority of AGNs.
Emission line profiles of Active Galactic Nuclei usually show variabilities. Investigations of these variations could provide information about the structure, size and kinematics of the emitting gas in the central part of these objects (see e.g. Foltz et al. 1983; Peterson et al. 1985, 1989, 1998; Peterson & Gaskell 1991; Peterson 1993; Winge et al. 1996; Wandel et al. 1999, etc.). According to the standard model, the broad emission lines observed in spectra of AGNs originate in the high-velocity gas of the surrounding Broad Line Region (BLR) ionized by the UV and optical radiation of the compact central source. Fluctuation in the ionizing continuum cause the variations in emission line fluxes. Also, the structure of the BLR may be investigated through the analysis of the broad emission line profiles.
One of the Sy1 galaxies which has a large-amplitude variability in continuum
and in spectral line fluxes and shapes is Akn120 (Peterson et al. 1985;
Peterson & Cota 1987; Peterson et al. 1985, 1989, 1998; Korista 1992;
Winge et al. 1996; Popovic et al. 1998a; Doroshenko et al. 1999; Wandel
et al. 1999).
This galaxy has been monitored several times (see e.g. Peterson et al.
1998) in order to investigate complex variations in continuum flux and broad
line shape. These investigations show that the integrated flux in the broad
emission lines varies very much (Peterson et al. 1989; Winge et al. 1996)
and that the BLR is very small (Peterson et al. 1998; Wandel et al.
1999; Doroshenko et al. 1999). The analyses of emission line
shapes of Akn 120 have shown that Balmer lines are complex in
structure and variable (Korista 1992). The decomposition of H![]() and
other broad lines indicates the stratification in the BLR (Korista 1992).
The complex and strong profile variations of broad lines of Akn 120 indicate
very dynamic processes in the occuring the emitting gas.
In order to investigate the structure of the Akn 120 emitting region, we have
analysed the shapes of H
and
other broad lines indicates the stratification in the BLR (Korista 1992).
The complex and strong profile variations of broad lines of Akn 120 indicate
very dynamic processes in the occuring the emitting gas.
In order to investigate the structure of the Akn 120 emitting region, we have
analysed the shapes of H![]() ,
H
,
H![]() ,
Ly
,
Ly![]() ,
CIII[1909],
CIV[1549] and MgII[2789] lines. Moreover, H
,
CIII[1909],
CIV[1549] and MgII[2789] lines. Moreover, H![]() line profile variation
of Akn 120 is presented
from a set of 96 spectra observed at Crimean Astrophysical Observatory
(CrAO) in the period from 1971 till 1990.
Also, we have applied a disk model to modeling the complex hydrogen line
shapes.
line profile variation
of Akn 120 is presented
from a set of 96 spectra observed at Crimean Astrophysical Observatory
(CrAO) in the period from 1971 till 1990.
Also, we have applied a disk model to modeling the complex hydrogen line
shapes.
We have analyzed the spectra taken from two sources:
1) The 96 spectra of the H![]() line in the wavelength interval
4500-5300 Å that were observed at the
Crimean Astrophysical Observatory (CrAO) by K. K. Chuvaev on the 2.6 m
Shain telescope during the period 1971-1990 (HJD 2443435 till 2447944)
and 2) Ly
line in the wavelength interval
4500-5300 Å that were observed at the
Crimean Astrophysical Observatory (CrAO) by K. K. Chuvaev on the 2.6 m
Shain telescope during the period 1971-1990 (HJD 2443435 till 2447944)
and 2) Ly![]() ,
CIII[1909], CIV[1549] and Mg II[2798]
observed by the Hubble Space Telescope in 1994.
,
CIII[1909], CIV[1549] and Mg II[2798]
observed by the Hubble Space Telescope in 1994.
| group | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|
from HJD 2440000 + |
3435 | 3790 | 4173 | 4522 | 4881 | 5263 | 5619 | 5997 | 6853 | 7832 |
| till HJD 2440000 + |
3574 | 3934 | 4289 | 4672 | 5054 | 5412 | 5734 | 6088 | 7124 | 7944 |
| mean HJD 2440000 + |
3494 | 3879 | 4229 | 4577 | 4958 | 5331 | 5695 | 6058 | 7014 | 7888 |
| numbers of spectra |
14 | 14 | 9 | 5 | 15 | 12 | 11 | 6 | 6 | 4 |
The spectra of Ly![]() ,
CIII[1909], CIV[1549] and Mg II[2798] lines
have been elaborated by HST staff, while
all spectra of H
,
CIII[1909], CIV[1549] and Mg II[2798] lines
have been elaborated by HST staff, while
all spectra of H![]() were scanned on a two-coordinate CrAO microphotometer
(Popovic et al. 1998a; Doroshenko et al. 1999).
Further
treatment, including the correction for the film and sky background and instrumental
spectral sensitivity was performed. The wavelength and flux calibration were made
using the SPE data reduction package, developed by S. G. Sergeev. Wavelength
calibration was based on the night sky lines and narrow emission lines of the
galaxy. The redshift of Akn120 was taken to be z=0.03248 (Foltz et al. 1983).
were scanned on a two-coordinate CrAO microphotometer
(Popovic et al. 1998a; Doroshenko et al. 1999).
Further
treatment, including the correction for the film and sky background and instrumental
spectral sensitivity was performed. The wavelength and flux calibration were made
using the SPE data reduction package, developed by S. G. Sergeev. Wavelength
calibration was based on the night sky lines and narrow emission lines of the
galaxy. The redshift of Akn120 was taken to be z=0.03248 (Foltz et al. 1983).
In order to investigate the long-term variability of the
H![]() line shape and to take into consideration the gaps in
observations,
spectra were divided into 10 groups (see Table 1).
line shape and to take into consideration the gaps in
observations,
spectra were divided into 10 groups (see Table 1).
The spectra within the groups were averaged. In the mean spectra, noises and some short-term variability are to some extent suppressed and possible long-lasting features better expressed. The local continuum in four narrow zones around 4580, 4900, 5270 and 5630 Å was interpolated with a second-degree polynomial. The mean spectra were normalized to the OIII [5007] Å emission line flux. Notice that the narrow OIII lines (especially OIII 4959) are unusually weak in Akn 120, hence flux calibration based on the OIII line is less reliable than it normally would be.
The broad H![]() line has two peaks shifted blueward and redward from the
line center defined by the narrow emission lines. The
peaks are more or less clearly resolved. The H
line has two peaks shifted blueward and redward from the
line center defined by the narrow emission lines. The
peaks are more or less clearly resolved. The H![]() is
blended with OIII[4959,5007] and some other emission lines (Jackson &
Browne 1989; Meyers & Peterson 1985; Korista 1992).
is
blended with OIII[4959,5007] and some other emission lines (Jackson &
Browne 1989; Meyers & Peterson 1985; Korista 1992).
In order to decrease the number of free parameters, some relations among the
fitting Gaussians have been established a priori (Popovic &
Mediavilla 1997).
Namely, the three Gaussians
representing two narrow
OIII lines and a narrow H![]() component are preconditioned
to have the same systemic redshift (z=0.03248, according to Foltz
et al. 1983), and the intensity ratio of the two OIII
lines has been supposed to be 1:3.03. Also, the ratio of the full widths
of these two lines and narrow H
component are preconditioned
to have the same systemic redshift (z=0.03248, according to Foltz
et al. 1983), and the intensity ratio of the two OIII
lines has been supposed to be 1:3.03. Also, the ratio of the full widths
of these two lines and narrow H![]() component are fixed in proportion with
their wavelengths as
component are fixed in proportion with
their wavelengths as
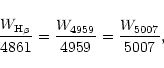 |
(1) |
Besides the three broad
Gaussians closely connected with H![]() a wide multi-peaked
structure (the shelf) can be noticed at the bottom.
The origin of the red shelf in Akn 120 and other AGN's H
a wide multi-peaked
structure (the shelf) can be noticed at the bottom.
The origin of the red shelf in Akn 120 and other AGN's H![]() line has
been discussed in several papers (Foltz et al. 1983; Mayers & Peterson
1985; Stirpe et al. 1989; van Groningen & de Bruyn 1989; Korista 1992;
Doroshenko et al. 1999).
Kollatschny et al. (1981) investigated the combined UV and optical
spectra of Akn 120, and noticed that UV and optical Fe II emission in
Akn 120 is very strong. Moreover, they found that Akn 120 shows unusually
strong Fe II emission in the UV spectra. On the other hand, calculations
performed by Joly (1988) indicate that multiplets 25 and 36 may have large
contributions in the red wing of H
line has
been discussed in several papers (Foltz et al. 1983; Mayers & Peterson
1985; Stirpe et al. 1989; van Groningen & de Bruyn 1989; Korista 1992;
Doroshenko et al. 1999).
Kollatschny et al. (1981) investigated the combined UV and optical
spectra of Akn 120, and noticed that UV and optical Fe II emission in
Akn 120 is very strong. Moreover, they found that Akn 120 shows unusually
strong Fe II emission in the UV spectra. On the other hand, calculations
performed by Joly (1988) indicate that multiplets 25 and 36 may have large
contributions in the red wing of H![]() .
It was our reason to accept the
red shelf Fe II template which has been proposed by Korista (1992). We have
supposed that the red shelf is composed of nine Fe II lines belonging to
the multiplets 25, 36 and 42. We took the relative strength of these lines
from Korista (1992) and we supposed that all Fe II lines
originate from the same conditions (in the same region), meaning that all
of them should have the same
.
It was our reason to accept the
red shelf Fe II template which has been proposed by Korista (1992). We have
supposed that the red shelf is composed of nine Fe II lines belonging to
the multiplets 25, 36 and 42. We took the relative strength of these lines
from Korista (1992) and we supposed that all Fe II lines
originate from the same conditions (in the same region), meaning that all
of them should have the same ![]() and shift.
and shift.
All other lines are also decomposed into a suitable number of Gaussians.
In order to see the structure of the central part of Akn 120
and to approach a model which can fit the shapes
of H![]() line
from the ten periods, we have first analysed the averaged profile of
H
line
from the ten periods, we have first analysed the averaged profile of
H![]() as well as averaged profiles of Ly
as well as averaged profiles of Ly![]() and
and
![]() line. In Figs. 1 and
2 one can see that either the H
line. In Figs. 1 and
2 one can see that either the H![]() or H
or H![]() broad line can be
decomposed into three broad Gaussian components. It is interesting that in
both lines we have similar decomposition, i.e. the
broadest component covers the other two broad components which are split in
the same way in both lines. In addition, the
blue components are more intensive that the red ones.
In the case of the averaged H
broad line can be
decomposed into three broad Gaussian components. It is interesting that in
both lines we have similar decomposition, i.e. the
broadest component covers the other two broad components which are split in
the same way in both lines. In addition, the
blue components are more intensive that the red ones.
In the case of the averaged H![]() line (Fig. 1),
the redshift of the blue component is 0.0310, and width is about
2400 kms-1, the red component is shifted to 0.0405 and has a width of about
1200 kms-1. The redshift of the broadest component is 0.0382, and its width is
about 5600 kms-1.
line (Fig. 1),
the redshift of the blue component is 0.0310, and width is about
2400 kms-1, the red component is shifted to 0.0405 and has a width of about
1200 kms-1. The redshift of the broadest component is 0.0382, and its width is
about 5600 kms-1.
Also, H![]() can be decomposed into four components (Fig. 2) where three
components are broad and one narrow. Near the observed wavelength
6800 Å, one of the two narrow forbidden N II lines (
can be decomposed into four components (Fig. 2) where three
components are broad and one narrow. Near the observed wavelength
6800 Å, one of the two narrow forbidden N II lines (
![]() 6548 Å and 6584 Å) can be found. The other one, three times weaker, is blended
with H
6548 Å and 6584 Å) can be found. The other one, three times weaker, is blended
with H![]() near position of the narrow H
near position of the narrow H![]() component.
The broadest line is shifted to d=0.0345, and has the
width of about 4900 kms-1. The blue component is shifted by 0.0292, and its
width is about 2100 kms-1; the red component is redshifted by
0.0374, and has a width of about 1600 kms-1.
component.
The broadest line is shifted to d=0.0345, and has the
width of about 4900 kms-1. The blue component is shifted by 0.0292, and its
width is about 2100 kms-1; the red component is redshifted by
0.0374, and has a width of about 1600 kms-1.
It can be seen from Figs. 1 and 2 that the H![]() has
one narrow peak with a width of about 590 kms-1, and H
has
one narrow peak with a width of about 590 kms-1, and H![]() also has one
narrow component with a width of about 450 kms-1.
also has one
narrow component with a width of about 450 kms-1.
The Ly![]() line allows us to probe the conditions in the very deep
regions of the AGN, where plasma undergoes very dynamic changes and turbulence.
Consequently, the red component is the broadest (width about
line allows us to probe the conditions in the very deep
regions of the AGN, where plasma undergoes very dynamic changes and turbulence.
Consequently, the red component is the broadest (width about
![]() 6600 kms-1,
shift is
6600 kms-1,
shift is ![]() 0.041),
but with the smallest intensity.
Even the blue peak is broader (
0.041),
but with the smallest intensity.
Even the blue peak is broader (![]() 2900 kms-1 and
2900 kms-1 and ![]() 0.031)
than the central one (
0.031)
than the central one (![]() 1000 kms-1
1000 kms-1 ![]() 0.0328),
see Fig. 3.
The central line,
unlike H
0.0328),
see Fig. 3.
The central line,
unlike H![]() and H
and H![]() ,
is the most intensive
component and, having the smallest line width, originates in the region with
the smallest velocity dispersion. It is evident that some absorption is
present in the red wing of the line, but as we are dealing only with origin and
behavior of the broad lines, in this paper we do not describe
it in detail.
,
is the most intensive
component and, having the smallest line width, originates in the region with
the smallest velocity dispersion. It is evident that some absorption is
present in the red wing of the line, but as we are dealing only with origin and
behavior of the broad lines, in this paper we do not describe
it in detail.
The CIII(1909) line (Fig. 4) also shows three broad components
(
![]() 3600 kms-1,
3600 kms-1,
![]() 0.03535;
0.03535;
![]() 1600 kms-1
1600 kms-1 ![]() 0.0317;
0.0317;
![]() 1550 kms-1,
1550 kms-1,
![]() 0.0212),
among which the
central is the most intens and the red is the widest. In this line the
blue component is of about equal relative intensity as the red one - unlike
the situation
in the previously
discussed lines.
0.0212),
among which the
central is the most intens and the red is the widest. In this line the
blue component is of about equal relative intensity as the red one - unlike
the situation
in the previously
discussed lines.
The CIV line (Fig. 5) also can be
decomposed into three Gaussian broad components
(
![]() 4800 kms-1,
4800 kms-1,
![]() 0.0336;
0.0336;
![]() 2300 kms-1
2300 kms-1 ![]() 0.0324;
0.0324;
![]() 1100 kms-1,
1100 kms-1,
![]() 0.0321),
but here there is no significant
difference between shifts of the red, central and blue Gaussian component,
except the fourth (smallest) Gaussian, which is within the level of
noises which we neglect.
0.0321),
but here there is no significant
difference between shifts of the red, central and blue Gaussian component,
except the fourth (smallest) Gaussian, which is within the level of
noises which we neglect.
MgII(2798) line (Fig. 6) is blended with many Fe lines, but it still could be
resolved in the same way as the other lines, showing three broad components
(
![]() kms-1,
kms-1,
![]() ;
;
![]() kms-1,
kms-1,
![]() ;
;
![]() kms-1,
kms-1,
![]() ). Also, one
very broad component (
). Also, one
very broad component (
![]() kms-1,
kms-1,
![]() )
is present which probably comes from Fe I and Fe II blends in the UV.
)
is present which probably comes from Fe I and Fe II blends in the UV.
All these lines are different from the Balmer ones in three aspects: 1) there are no narrow components; 2) the central components dominate by their relative intensity and not by the integrated radiation energy involved; and 3) the ratio of blue/red components is not always in favor of the blue; in the C III line, the components are very much equal, in the C IV line the blue component is much weaker than the red (although the distinction of their identities here is not certain).
As far as the blue/red component ratio is concerned, one can notice a sequence of increasing dissimilarity of the profile shape of these lines with respect to the Balmer ones: H I, Mg II, C III and C IV. Their respective ionization potentials follow the same sequence: 13.6 eV, 15.0 eV, 47.9 eV and 64.5 eV, respectively. This fact can indicate a stratification of the corresponding emissivities within the ionizing radiation field.
The similar Gaussian-decomposition structure in all observed spectral lines (expect, perhaps, the CIV line where the grouping of the three relevant Gaussians around a similar wavelength is unusual and unexpected) may be explained by the origin of the lines from the same BLR or the same BLR components (e.g. BLR1 and BLR2, see Gaskell 1999) but involving different radial distances from the central, ionizing, source.
In Fig. 7, we present all ten observed H![]() profiles
and an averaged profile obtained from these considered profiles
(full line in Fig. 7).
profiles
and an averaged profile obtained from these considered profiles
(full line in Fig. 7).
The shape of H![]() shows very strong variation (Fig. 7), especially in
the central part of the line. Here one should notice three
parts; sometimes a shoulder in the blue part of profile, a blue and a red
peak.
Low-quality data were rejected. The other problem is the very weak OIII (5007)
line which we used for flux calibration of H
shows very strong variation (Fig. 7), especially in
the central part of the line. Here one should notice three
parts; sometimes a shoulder in the blue part of profile, a blue and a red
peak.
Low-quality data were rejected. The other problem is the very weak OIII (5007)
line which we used for flux calibration of H![]() line region.
line region.
As one can see from Fig. 7, the H![]() line has two peaks displaced toward the
red and blue with respect to the redshifted center of the line. The highest
scatter of the profiles is within the H
line has two peaks displaced toward the
red and blue with respect to the redshifted center of the line. The highest
scatter of the profiles is within the H![]() core. This we take as real
change in the H
core. This we take as real
change in the H![]() flux and profile shape over time. The moderate scatter
of the curves near both edges of the interval of wavelengths may
partly reflect changes in two Fe II emission complexes around the observed
wavelengths 4727 Å and 5430 Å. However, it also can be caused by some uncertainties
in the reduction of the continuum.
flux and profile shape over time. The moderate scatter
of the curves near both edges of the interval of wavelengths may
partly reflect changes in two Fe II emission complexes around the observed
wavelengths 4727 Å and 5430 Å. However, it also can be caused by some uncertainties
in the reduction of the continuum.
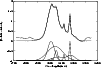 |
Figure 1:
Decomposition of the averaged shape of the H |
| Open with DEXTER | |
 |
Figure 2:
Decomposition of the averaged shape (dashed line) of
the H |
| Open with DEXTER | |
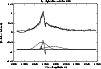 |
Figure 3:
Decomposition of the averaged shape of the the Ly |
| Open with DEXTER | |
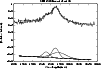 |
Figure 4: Decomposition of the averaged shape of the CIII[1909] line. The notation is the same as in Fig. 1 |
| Open with DEXTER | |
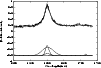 |
Figure 5: Decomposition of the averaged shape of the CIV[1549] line. The notation is same as in Fig. 1 |
| Open with DEXTER | |
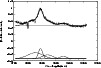 |
Figure 6: Decomposition of the averaged shape of MgII[2798] line. The notation is same as in Fig. 1. The dashed Gaussian component below may be contributed partly by Fe blends |
| Open with DEXTER | |
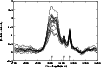 |
Figure 7:
The shape of H |
| Open with DEXTER | |
In all observed groups (ten groups in Table 1) the mean spectra
show the complex shape of the H![]() line of
Akn 120. The profiles can be decomposed into four components, where three
of them are broad.
Also, one red shelf composed of nine Fe II lines from multiplets 25, 36
and 42 is present in the red wing of H
line of
Akn 120. The profiles can be decomposed into four components, where three
of them are broad.
Also, one red shelf composed of nine Fe II lines from multiplets 25, 36
and 42 is present in the red wing of H![]() .
.
The temporal changes of the shifts, widths and sizes (
![]() )
of the
three broad Gaussians of the
H
)
of the
three broad Gaussians of the
H![]() line are shown in Figs. 8-10.
line are shown in Figs. 8-10.
As shown in Fig. 8, the shift of the blue and red
Gaussian components show similar
behaviour during time. Also, the shift of these two components is
relatively stable, while the shift of the broadest (central) component shows
significant variation.
On the other hand, the widths (Fig. 9), which indicate the
random velocities in the regions, show very clearly the existence of three
regions or separated velocity fields.
Two of them (shifted red and blue) are quite stable,
while the broadest shows very large changes. From the changes in intensity of the
components (Fig. 10) one can see that the broadest and blue components
display a
stronger variability in intensity than does the red one. It may indicate that these
regions are closer to the center of AGN. The structure of the
emitting region in Akn 120 may be such that we
observe two regions which are in the streams
(as proposed by Zheng
et al. 1990), and one central region
which is close to or belongs to
an emitting disk (as proposed by Allion
et al. 1988). It seems that the core of the H![]() line originates in
the two shifted regions and the wings arise from the disk and a central,
highly turbulent region which may be disk-like.
line originates in
the two shifted regions and the wings arise from the disk and a central,
highly turbulent region which may be disk-like.
In all the considered periods, the H![]() line has
two (sometimes three) peaks.
The nature of the double-peaked lines in AGNs has been discussed in several
papers (see e.g. Chen & Halpern 1989; Chen et al. 1989; Zheng et al. 1990;
Zheng et al. 1991; Goad & Wanders 1996; Popovic et al. 1998b;
Gaskel et al. 1983,
1996).
The origin of double peaked lines in AGNs can be
explained by:
line has
two (sometimes three) peaks.
The nature of the double-peaked lines in AGNs has been discussed in several
papers (see e.g. Chen & Halpern 1989; Chen et al. 1989; Zheng et al. 1990;
Zheng et al. 1991; Goad & Wanders 1996; Popovic et al. 1998b;
Gaskel et al. 1983,
1996).
The origin of double peaked lines in AGNs can be
explained by:
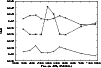 |
Figure 8: Redshifts of the three broad Gaussians for 10 groups of Akn 120 spectra (+ = blue peak, x = red peak, * = the broadest Gaussian) |
| Open with DEXTER | |
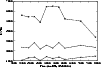 |
Figure 9: Same as in Fig. 11, but for the Gaussians' width (in kms-1) |
| Open with DEXTER | |
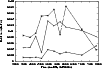 |
Figure 10:
The areas under the broad Gaussian components of the H |
| Open with DEXTER | |
We started from the following: 1)
the long-period variation of H![]() indicated that three emission regions
in the central part of Akn 120 exist in all periods considered, Figs. 8-10.
The variation in the
blue and central components, may indicate that they come from regions
which are closer to the central mass, whereas the red component may be produced
by a
stream which is partly obscured by the disk and the central region, and we see
only part of the "red stream'';
2) the shape of Ly
indicated that three emission regions
in the central part of Akn 120 exist in all periods considered, Figs. 8-10.
The variation in the
blue and central components, may indicate that they come from regions
which are closer to the central mass, whereas the red component may be produced
by a
stream which is partly obscured by the disk and the central region, and we see
only part of the "red stream'';
2) the shape of Ly![]() indicates (especially its wings)
that the radiation of the disk is present in this line.
Taking these two facts into account, we conclude
that a model with an accretion disk and two regions symmetrical to
the
disk may well fit the line profiles of the hydrogen lines.
indicates (especially its wings)
that the radiation of the disk is present in this line.
Taking these two facts into account, we conclude
that a model with an accretion disk and two regions symmetrical to
the
disk may well fit the line profiles of the hydrogen lines.
Also, the blue-boosted and redshifted broad Gaussian components in all
Akn 120 lines considered (except the C IV line)
may indicate that an accretion disk is present. But,
concerning the variation on longer time-scales, the bumps in the sides of lines
vary independently (Gaskell & Snedden 1999). The disk
model cannot explain the shape of all the spectral lines
(see e.g. Fig. 7).
Here, we apply
the disk model (Chen & Halpern 1989) to explain the wing shapes.
First, we subtracted the narrow lines from H![]() ,
an absorption line
from Ly
,
an absorption line
from Ly![]() and narrow O III lines as well as an Fe II template from
H
and narrow O III lines as well as an Fe II template from
H![]() .
Then, we fitted these line profiles by a disk model (Chen
& Halpern 1989; Chen et al. 1989) plus one or two Gaussians.
The emissivity of the
disk as a function of radius is given as
.
Then, we fitted these line profiles by a disk model (Chen
& Halpern 1989; Chen et al. 1989) plus one or two Gaussians.
The emissivity of the
disk as a function of radius is given as
| (2) |
The results of the fit are presented in Figs. 11-13.
We fitted the Ly![]() profile with the disk model with
parameters:
profile with the disk model with
parameters: ![]() 10
10![]() ,
,
![]() 120
120 ![]() and
and
![]() 1150
1150 ![]() and one Gaussian component, which
indicates a random velocity, w, of 1800 kms-1. For Balmer lines,
we could not fit the
lines with the disk model and one Gaussian component.
We propose that the
the central part of these lines corresponds to the other two regions.
Balmer lines
were fitted with the next parameters of the disk:
and one Gaussian component, which
indicates a random velocity, w, of 1800 kms-1. For Balmer lines,
we could not fit the
lines with the disk model and one Gaussian component.
We propose that the
the central part of these lines corresponds to the other two regions.
Balmer lines
were fitted with the next parameters of the disk:
![]() for both lines
and for H
for both lines
and for H![]() -
-
![]() 200
200 ![]() and
and
![]() 1000
1000 ![]() ,
the blue Gaussian component has
,
the blue Gaussian component has ![]() 1900 kms-1and the red has
1900 kms-1and the red has ![]() 1500 kms-1; for H
1500 kms-1; for H![]() -
-
![]() 165
165 ![]() and
and
![]() 1000
1000 ![]() ,
the blue Gaussian component has
,
the blue Gaussian component has ![]() 2100 kms-1
and the red has
2100 kms-1
and the red has ![]() 1700 kms-1.
1700 kms-1.
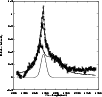 |
Figure 11:
Observed Ly |
| Open with DEXTER | |
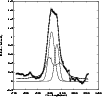 |
Figure 12:
Same as in Fig. 10, but for H |
| Open with DEXTER | |
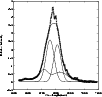 |
Figure 13:
Same as in Fig. 10, but for H |
| Open with DEXTER | |
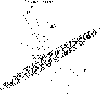 |
Figure 14: The scheme of the proposed model for Akn 120 |
| Open with DEXTER | |
In general, we accept the idea that there are two distinct components of a BLR (Gaskell 1999) or that some other type of stratification exists in a BLR (Korista 1992)
As long as we remain in the Gaussian-decomposition approach, we are ready to
interpret the two broad Gaussians corresponding to the blue and red Balmer
line
profile peaks as originating from somewhere outside the accretion
disk - probably from a biconical BLR configuration (BLR1 and BLR2 in Fig. 14).
In H![]() the blue Gaussian is
always stronger and the two change independently. The third, the broadest and
the most stable Gaussian, may represent the energy irradiated by the accretion
disk. However, with its predestined mono-peaked shape a Gaussian cannot reflect the
detailed disk profile: "blue boosted, red shifted'' (e.g. Stuchlik 1998). Only
in the unique case of an extremely turbulent accretion disk do the two
profile peaks
merge (van Groningen 1983) and a Gaussian may, in an approximation, represent
the disk component of a spectral line profile.
the blue Gaussian is
always stronger and the two change independently. The third, the broadest and
the most stable Gaussian, may represent the energy irradiated by the accretion
disk. However, with its predestined mono-peaked shape a Gaussian cannot reflect the
detailed disk profile: "blue boosted, red shifted'' (e.g. Stuchlik 1998). Only
in the unique case of an extremely turbulent accretion disk do the two
profile peaks
merge (van Groningen 1983) and a Gaussian may, in an approximation, represent
the disk component of a spectral line profile.
The main conclusion which can be drawn from the present analysis of
the H![]() ,
H
,
H![]() ,
Ly
,
Ly![]() ,
CIII[1909], CIV[1549] and
MgII[2798] lines,
is that these lines mainly exhibit blue boosted - red shifted
behavior.
It has led us to propose the disk model (see van Gronongen 1983;
Allion 1988; Chen &
Halpern 1989) which can describe the line wings and the double-stream model.
The
Ly
,
CIII[1909], CIV[1549] and
MgII[2798] lines,
is that these lines mainly exhibit blue boosted - red shifted
behavior.
It has led us to propose the disk model (see van Gronongen 1983;
Allion 1988; Chen &
Halpern 1989) which can describe the line wings and the double-stream model.
The
Ly![]() can be produced
in the inner parts of this disk while its core originates
in the stream near the central mass and the other component cannot be seen.
The H
can be produced
in the inner parts of this disk while its core originates
in the stream near the central mass and the other component cannot be seen.
The H![]() and H
and H![]() originate from the outer parts of the same assumed disk as well as in outer
part of the streams.
The wings of
H
originate from the outer parts of the same assumed disk as well as in outer
part of the streams.
The wings of
H![]() ,
H
,
H![]() and Ly
and Ly![]() can be fitted by a disk model.
The parameters of the disk are:
can be fitted by a disk model.
The parameters of the disk are:
![]() ,
,
![]() 120
120
![]() and
and
![]() 1200
1200 ![]() .
The scheme of the emitting region
in Akn 120 used in our analyse is given in Fig. 14. As one can see from
the Fig. 14, we propose a model with a disk, or a related (BLR3)
central region (probably disk-like) which
surrounds a part of the disk,
and also two regions located in the axial streams (BLR1 and BLR2),
where one of
them (redshifted, BLR2)
is partly obscured by the accretion disk and central region.
Taking into account the estimated
mass for Akn 120 (
.
The scheme of the emitting region
in Akn 120 used in our analyse is given in Fig. 14. As one can see from
the Fig. 14, we propose a model with a disk, or a related (BLR3)
central region (probably disk-like) which
surrounds a part of the disk,
and also two regions located in the axial streams (BLR1 and BLR2),
where one of
them (redshifted, BLR2)
is partly obscured by the accretion disk and central region.
Taking into account the estimated
mass for Akn 120 (
![]() )
given by Wandel et al. (1999)
we can obtain the dimension
of the radiating
disk of about 12 light days, which is in agreement with the estimation given
in Wandel et al. (1999), where the estimated dimension of Akn 120 BLR is about
11.748 light days.
)
given by Wandel et al. (1999)
we can obtain the dimension
of the radiating
disk of about 12 light days, which is in agreement with the estimation given
in Wandel et al. (1999), where the estimated dimension of Akn 120 BLR is about
11.748 light days.
Acknowledgements
This work was supported by the Ministry of Science and Technology of Serbia through the project "Astrometrical, Astrodynamical and Astrophysical Researches'' and The Federal Ministry of Developement, Sciences and Environmental Protection of Yugoslavia. L. C. P. and N. S. are grateful to Dr. Nina Polosuhkina and Valya Doroshenko for help and suggestions. L. C. P. acknowledges support by the Berlin Brandenburg Academy of Science and Humanities in the framework of its Balkan-Initiative and thanks the AIP for the hospitability during his stay at the Institute.