We present a first attempt at reproducing the morphology and kinematical properties of the DG Tau microjet using a 3D hydrodynamical numerical simulation of a precessing, variable velocity jet. Synthetic maps and position-velocity diagrams in H
A&A 367, 959-966 (2001)
DOI: 10.1051/0004-6361:20000415
A. Raga1,2 - S. Cabrit2 - C. Dougados3,4 - C. Lavalley3
1 - Instituto de Astronomía, UNAM, Apartado Postal 70-264,
04510 D. F., Mexico
2 -
Observatoire de Paris, DEMIRM, UMR 8540 du CNRS, 61 avenue
de l'Observatoire, 75014 Paris, France
3 -
Laboratoire d'Astrophysique, Observatoire de Grenoble,
CNRS/UJF UMR 5571, BP 53, 38041 Grenoble Cedex 9, France
4 -
Canada-France-Hawaii Telescope Corporation, PO Box 1597,
Kamuela HI 96743, USA
Received 1 September 2000 / Accepted 30 November 2000
Abstract
We present a first attempt at reproducing the morphology and
kinematical properties of the DG Tau microjet using a 3D
hydrodynamical numerical simulation of a precessing, variable velocity
jet. Synthetic maps and position-velocity diagrams in H![]() and
[O I]
and
[O I]![]() 6300 are calculated and compared with recent
imaging and spectro-imaging observations (Lavalley-Fouquet et al. 2000; Dougados et al. 2000).
Several observed properties are
qualitatively reproduced, such as the knot separation, width, and
asymmetric morphology, and the increase in ionization fraction and
decrease in electronic density away from the star. However, the
predicted kinematics in the region between the two jet knots differs
from the observed behaviour. This discrepancy probably results from
our simple assumption of a sinusoidal velocity variability, and points to a
more complex velocity time-variability in the jet from DG Tau.
6300 are calculated and compared with recent
imaging and spectro-imaging observations (Lavalley-Fouquet et al. 2000; Dougados et al. 2000).
Several observed properties are
qualitatively reproduced, such as the knot separation, width, and
asymmetric morphology, and the increase in ionization fraction and
decrease in electronic density away from the star. However, the
predicted kinematics in the region between the two jet knots differs
from the observed behaviour. This discrepancy probably results from
our simple assumption of a sinusoidal velocity variability, and points to a
more complex velocity time-variability in the jet from DG Tau.
Key words: hydrodynamics - stars: individual: DG Tau - ISM: HH objects - ISM: individual objects: HH 158 - ISM: jets and outflows
Even though most systems of Herbig-Haro (HH) objects are ejected by
optically invisible, deeply embedded infrared or radio sources, some HH
objects have a visible, T Tauri star as their source (see, e.g., Mundt &
Fried 1983; and the catalogue of Reipurth 1999). Several T Tauri stars also
show a collimated emission-line region extending away from the star for a
few seconds of arc. These so-called "microjets'' are identified through
long-slit spectroscopy (Solf 1989, 1997; Hirth et al. 1994, 1997), and are
believed to be the base of the HH flows sometimes observed at larger
distances from the star. Thus, microjets allow us to probe the jet structure
on smaller physical sizes (![]() 1016 cm at the distance of the Taurus
cloud) and shorter time scales (a few years) than in usual HH flows.
1016 cm at the distance of the Taurus
cloud) and shorter time scales (a few years) than in usual HH flows.
The best studied microjet so far is the one from DG Tau. Discovered by Mundt
& Fried (1983), it was then studied through long-slit spectroscopy (Mundt
et al. 1987; Solf & Böhm 1993; Solf 1997) and imaged with the Hubble
Space Telescope (Kepner et al. 1993; Stapelfeldt et al. 1997). Detailed
spectro-imaging studies of the two-dimensional jet structure on
sub-arcsecond scales were presented by Lavalley et al. (1997),
Lavalley-Fouquet et al. (2000), and Bacciotti et al. (2000). These studies
reveal several interesting properties including: (1) the presence of two
knots at 1
![]() and 3
and 3
![]() 6 from the star with morphology and kinematics
suggestive of bow shocks created by jet variability; (2) a line excitation
apparently dominated by shocks, with ionization fraction increasing away
from the star (Lavalley-Fouquet et al. 2000); (3) a larger jet width at
lower radial velocities,
with indications of a very low-velocity halo surrounding
the jet in [O I]; (4) wiggles in the jet beam.
6 from the star with morphology and kinematics
suggestive of bow shocks created by jet variability; (2) a line excitation
apparently dominated by shocks, with ionization fraction increasing away
from the star (Lavalley-Fouquet et al. 2000); (3) a larger jet width at
lower radial velocities,
with indications of a very low-velocity halo surrounding
the jet in [O I]; (4) wiggles in the jet beam.
The latter property of the DG Tau microjet is especially striking in
0
![]() 1 resolution adaptive-optics images recently obtained by Dougados
et al. (2000). The [O I] image shows that the
microjet ejected by DG Tauri has a curved structure, which enters a
bow-shaped knot along the northern bow wing. This kind of structure (in
which a jet enters a bow-shaped knot along one of the bow wings) is also
observed in other HH jets. For example, in HH 46/47 the jet enters the 47A
condensation along its western edge. Even though the spatial scale of this
HH flow is approximately one order of magnitude larger than the one of the
DG Tauri microjet, the morphological similarity between the two objects is
remarkable (see Heathcote et al. 1996; Dougados et al. 2000).
Interestingly, the two other microjets imaged by
Dougados et al. (2000), driven by CW Tau and RW Aur, are very straight and
much narrower than the DG Tau microjet. It is tempting to speculate that
precession of the jet axis might be responsible for both the observed
curvature and the larger width of the DG Tau jet, compared to these other
two microjets.
1 resolution adaptive-optics images recently obtained by Dougados
et al. (2000). The [O I] image shows that the
microjet ejected by DG Tauri has a curved structure, which enters a
bow-shaped knot along the northern bow wing. This kind of structure (in
which a jet enters a bow-shaped knot along one of the bow wings) is also
observed in other HH jets. For example, in HH 46/47 the jet enters the 47A
condensation along its western edge. Even though the spatial scale of this
HH flow is approximately one order of magnitude larger than the one of the
DG Tauri microjet, the morphological similarity between the two objects is
remarkable (see Heathcote et al. 1996; Dougados et al. 2000).
Interestingly, the two other microjets imaged by
Dougados et al. (2000), driven by CW Tau and RW Aur, are very straight and
much narrower than the DG Tau microjet. It is tempting to speculate that
precession of the jet axis might be responsible for both the observed
curvature and the larger width of the DG Tau jet, compared to these other
two microjets.
In this paper, we present a first attempt at reproducing the morphology and kinematics of the DG Tau microjet by a time-variable jet, using a 3D gasdynamic numerical simulation. We do not include a magnetic field in this simulation, as there are no direct measurements of the magnetic field strengths in HH jets (see, e.g., Hartigan et al. 1994), and there also is no clear theoretical consensus about the geometry and strength of the magnetic field in these objects. In the simulation, we introduce a sinusoidal variability of the ejection velocity, in order to form knots with the appropriate separations. We also introduce a precession of the outflow axis, to produce the observed curvature of the jet beam.
The precession results in off-centre positions for the jet beam as it enters the successive working surfaces of the flow, and broadens the working surface to a diameter comparable to the local width of the precession cone. This effect has been studied before in the context of extragalactic jets, having received the uncomfortable name of "dentist's drill model'' (Cox et al. 1991). Even though there are a number of papers about HH jets with variable ejection directions (Raga et al. 1993; de Gouveia dal Pino et al. 1995; Cliffe et al. 1996; Suttner et al. 1997), none of them have discussed the "dentist's drill'' effect (with the exception of the discussion of 2D simulations of Biro et al. 1995), which has remained in the (almost) exclusive realm of extragalactic jets.
We first derive the parameters adopted for modeling the DG Tauri microjet (Sect. 2), and then discuss a 3D numerical simulation carried out with these parameters (Sect. 3). Predicted intensity maps and position-velocity diagrams are presented in Sect. 4. Finally, we discuss the relative success of the model at explaining the observational characteristics of DG Tauri, in particular the velocity gradients along and perpendicular to the jet axis (Sect. 5).
From the numerical point of view, this work is similar to the one of Raga et al. (2001), who presented a variable ejection jet model for the "triple source'' radio continuum jet in Serpens (see, e.g., Curiel et al. 1993). The comparison between the model and the DG Tauri microjet presented in this paper is a natural step forward from the previous work in that it involves a comparison of predicted and observed emission line fluxes and line profiles, while the previous work was restricted to a comparison of only the predicted and observed radio continuum fluxes.
In a series of papers, we have presented spectro-imaging observations
obtained with the TIGRE and OASIS integral field spectrographs at the
Canada-France-Hawaii Telescope (Lavalley et al. 1997; Lavalley-Fouquet et al.
2000)
and adaptive optics narrow-band images, also obtained
at the same telescope (Dougados et al. 2000) in the H![]() ,
[O I] 6300,
[N II] 6583 and [S II] 6717, 31 lines. These data provide extensive
information about the physical conditions, radial velocities and proper
motions of the DG Tauri microjet, which we use to choose the parameters for
a gasdynamic numerical simulation.
,
[O I] 6300,
[N II] 6583 and [S II] 6717, 31 lines. These data provide extensive
information about the physical conditions, radial velocities and proper
motions of the DG Tauri microjet, which we use to choose the parameters for
a gasdynamic numerical simulation.
We adopt a distance of 140 pc to the Taurus star formation region,
and we consider that the jet is pointing towards the observer
at a
![]() angle with respect to the plane of the sky
(following Lavalley-Fouquet et al. 2000, who determined this angle
from radial velocity and proper motion measurements).
angle with respect to the plane of the sky
(following Lavalley-Fouquet et al. 2000, who determined this angle
from radial velocity and proper motion measurements).
In order to deduce the parameters for a proposed ejection velocity variability, we use the following arguments.
In 97/01 and 98/01, the DG Tauri microjet showed two main knots with a
projected separation of ![]() 2
2
![]() 7 (see Fig. 1 of Dougados et al. 2000
and Fig. 1 of Lavalley-Fouquet et al. 2000). The leading,
bow-shaped knot of the microjet
has a proper motion velocity of
7 (see Fig. 1 of Dougados et al. 2000
and Fig. 1 of Lavalley-Fouquet et al. 2000). The leading,
bow-shaped knot of the microjet
has a proper motion velocity of ![]() 200 kms-1(cf. Fig. 4 of Dougados et al. 2000), which when corrected for projection
effects gives a 300 kms-1 velocity for the material in
the working surface. This working surface velocity
should have a value close to the mean velocity v0 of the time-dependent
ejection velocity (see Kofman & Raga 1992), so that we obtain
a v0=300 kms-1 estimate for the mean velocity. From this value for
v0 and the knot separation (
8.5 1015 cm after correction for
projection effects) one obtains a
200 kms-1(cf. Fig. 4 of Dougados et al. 2000), which when corrected for projection
effects gives a 300 kms-1 velocity for the material in
the working surface. This working surface velocity
should have a value close to the mean velocity v0 of the time-dependent
ejection velocity (see Kofman & Raga 1992), so that we obtain
a v0=300 kms-1 estimate for the mean velocity. From this value for
v0 and the knot separation (
8.5 1015 cm after correction for
projection effects) one obtains a
![]() yr timescale.
yr timescale.
Another estimate of v0 and
![]() can be obtained from the average of
the radial velocities immediately upstream and downstream of the main
bow shock,
can be obtained from the average of
the radial velocities immediately upstream and downstream of the main
bow shock, ![]() -350 and -180 kms-1, respectively (see Fig. 2 of
Lavalley-Fouquet et al. 2000; and Fig. 7 of the present paper). After
correction for projection, one finds v0 = 360 kms-1 and
-350 and -180 kms-1, respectively (see Fig. 2 of
Lavalley-Fouquet et al. 2000; and Fig. 7 of the present paper). After
correction for projection, one finds v0 = 360 kms-1 and
![]() yr. We thus adopt v0 = 300 kms-1 and
yr. We thus adopt v0 = 300 kms-1 and
![]() yr for our model.
yr for our model.
We should note that the leading, bow-shaped knot of the
DG Tau microjet clearly does not correspond to the leading knot of
this outflow, as at least three more knots are detected at larger
distances from the source. Using the proper motions and radial velocities
of these knots measured by Eislöffel & Mundt (1998) and the separations
between the successive knots, one obtains estimates for a variability
timescale of ![]() 10 yr, which are consistent with the value
of
10 yr, which are consistent with the value
of
![]() which we have adopted.
which we have adopted.
Finally, fits to the observed line ratios in the two bright knots of the
DG Tauri microjet suggest shock velocities of ![]() 70-100 kms-1(Lavalley-Fouquet et al. 2000) which also agree with the radial velocity
jump observed across the main bow shock. We therefore choose a
70-100 kms-1(Lavalley-Fouquet et al. 2000) which also agree with the radial velocity
jump observed across the main bow shock. We therefore choose a
![]() km s-1 half-amplitude for the ejection velocity variability.
km s-1 half-amplitude for the ejection velocity variability.
We then carry out a numerical simulation in which the modulus of the
ejection velocity vj varies with time following
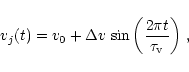 |
(1) |
Also, the beam of the DG Tauri microjet describes a curved path in the
plane of the sky, and enters the bow shock along one of the bow shock
wings (see Dougados et al. 2000). In order to reproduce this kind of
structure in our numerical simulation, we introduce a precession of
the jet beam. It is difficult to estimate the parameters of this
precession from the observations, but through a number of numerical
simulations we have determined that a precession cone of half-opening
angle
![]() and precession period
and precession period
![]() yr produces
results which are compatible with the curved beam structure
and wiggling observed in the DG Tauri microjet (Dougados et al. 2000;
Lavalley-Fouquet et al. 2000).
yr produces
results which are compatible with the curved beam structure
and wiggling observed in the DG Tauri microjet (Dougados et al. 2000;
Lavalley-Fouquet et al. 2000).
We assume that the jet has a top-hat initial cross section, with a radius
![]() cm (corresponding to half of the
cm (corresponding to half of the
![]() measured at the base of the DG Tau jet by Dougados et al. 2000).
We choose a
measured at the base of the DG Tau jet by Dougados et al. 2000).
We choose a
![]() cm initial density, which is a factor
of a hundred lower than the initial density determined by
Lavalley-Fouquet et al. (2000), but which is necessary in order not to have
highly unresolved cooling regions behind the shocks in the flow.
cm initial density, which is a factor
of a hundred lower than the initial density determined by
Lavalley-Fouquet et al. (2000), but which is necessary in order not to have
highly unresolved cooling regions behind the shocks in the flow.
As an example, we note that the cooling distance behind the bow shock
of the knot located
z=7 1015 cm from the source
in Fig. 4 has a value of ![]() 1.5 1014 cm
(which is the cooling distance to 104 K of a plane-parallel
shock of velocity 100 km s-1 and pre-shock density 100 cm-3,
according to the tabulation of Hartigan et al. 1987). This cooling
distance is only slightly larger than the resolution of our numerical
sumulations (see the following section). However, there is of
course a wide range of different cooling distances in the many
shocks which appear in our simulations.
1.5 1014 cm
(which is the cooling distance to 104 K of a plane-parallel
shock of velocity 100 km s-1 and pre-shock density 100 cm-3,
according to the tabulation of Hartigan et al. 1987). This cooling
distance is only slightly larger than the resolution of our numerical
sumulations (see the following section). However, there is of
course a wide range of different cooling distances in the many
shocks which appear in our simulations.
Finally, we assume that the surrounding environment is homogeneous, with a
![]() cm-3 density. Both the environment and the jet are
assumed to be initially neutral, and with a 103 K temperature.
cm-3 density. Both the environment and the jet are
assumed to be initially neutral, and with a 103 K temperature.
We compute a 3D gasdynamic jet simulation with the parameters derived in Sect. 2 using the "yguazú-a'' adaptive grid code. The details of this code are discussed by Raga et al. (2000). For the present application we use the version of the code described by Raga et al. (2001), who modeled the radio continuum emission from a jet with a variable ejection direction+velocity. In this version of the code, the 3D gasdynamic equations are integrated together with an equation for the ionization of hydrogen. Using the computed temperature, electron density and neutral fraction, a time-dependent cooling function is calculated (with the contribution from atoms other than hydrogen parametrized as described by Raga et al. 1999), and included in the energy equation.
The 3D numerical simulation is done on a 5-level, binary adaptive grid with a maximum resolution (in the three dimensions) of 1.17 1014 cm. This maximum resolution is only allowed in the region occupied by jet material, and the shortest grid spacing allowed for the environment is a factor of two higher than this value. The full computational domain is 7.5 1015 cm by 7.5 1015 cm by 1.5 1016 cm along x-y-z. The jet is injected at the origin of the coordinate system, with the axis of the precession cone being parallel to the z-direction, and the initial direction of the jet lying on the xz-plane, pointing towards the +x-direction (with the ejection direction starting to rotate towards the +y-direction). The parameters of the flow and the time-dependent ejection velocity are discussed in Sect. 2.
![\begin{figure}
\par\includegraphics[width=0.48\textwidth, angle=0]{aa10248f1.eps}\end{figure}](/articles/aa/full/2001/09/aa10248/Timg22.gif) |
Figure 1: Stratification of the jet flow obtained for a t=12 yr time integration. The left frame shows the pressure stratification (factor of two contours), the contact discontinuity separating the jet and the environmental material (thick contour), and the grid points chosen by the adaptive grid algorithm on the xz-plane. The other three frames show cuts along the z-axis of number density (of atoms and ions), z-velocity and temperature of the flow |
| Open with DEXTER | |
The flow stratification resulting from this simulation for a t=12 yr time-integration is shown in Fig. 1. This figure shows the pressure stratification (on the xz-plane) and density, z-velocity and temperature as a function of position along the z-axis (at x = 0). At this time we see that the leading working surface is getting to the edge of the computational domain, and that a second working surface has already formed.
Even though the flow has a jet-to-environment density ratio of 10 and is
highly radiative, a cocoon of jet material fills an approximate cylindrical
region of ![]() 10 times the initial jet radius (see Fig. 1). This is an
interesting characteristic of the flow, resulting from both the precession
and the velocity time-variability. This cocoon shows an inner conical
shock structure, which corresponds to a "tail shock'' that trails the
leading working surface.
10 times the initial jet radius (see Fig. 1). This is an
interesting characteristic of the flow, resulting from both the precession
and the velocity time-variability. This cocoon shows an inner conical
shock structure, which corresponds to a "tail shock'' that trails the
leading working surface.
From this numerical simulation, we have carried out predictions of emission maps and position-velocity diagrams, which we discuss in the following section.
From the numerical simulation described in Sects. 2 and 3, we compute
H![]() and [O I] 6300 intensity maps and position-velocity diagrams.
For each time frame, our gasdynamic code gives the temperature, density and
hydrogen ionization fraction for all grid points. With this data, and
assuming that the neutral fraction of oxygen follows the hydrogen neutral
fraction (due to the high charge exchange rate between these two species),
we can compute the H
and [O I] 6300 intensity maps and position-velocity diagrams.
For each time frame, our gasdynamic code gives the temperature, density and
hydrogen ionization fraction for all grid points. With this data, and
assuming that the neutral fraction of oxygen follows the hydrogen neutral
fraction (due to the high charge exchange rate between these two species),
we can compute the H![]() (considering both the effective recombination
rate and the contribution due to collisional excitations from the ground
state) and the [O I] 6300 emission coefficients (using the parameters of
Mendoza 1983, with a linear fit to the temperature dependence of
collision strengths). We have assumed an abundance of
6.6 10-4for oxygen (relative to hydrogen, by number), and a 3 10-4abundance for carbon (which is considered only as a source of free
electrons for the regions with neutral hydrogen). Once the emission
coefficients have been computed, we can obtain predictions of intensity
maps and position-velocity diagrams by carrying out the appropriate
line-of-sight integrations.
(considering both the effective recombination
rate and the contribution due to collisional excitations from the ground
state) and the [O I] 6300 emission coefficients (using the parameters of
Mendoza 1983, with a linear fit to the temperature dependence of
collision strengths). We have assumed an abundance of
6.6 10-4for oxygen (relative to hydrogen, by number), and a 3 10-4abundance for carbon (which is considered only as a source of free
electrons for the regions with neutral hydrogen). Once the emission
coefficients have been computed, we can obtain predictions of intensity
maps and position-velocity diagrams by carrying out the appropriate
line-of-sight integrations.
![\begin{figure}
\par\includegraphics[width=0.48\textwidth, angle=0]{aa10248f2.eps}\end{figure}](/articles/aa/full/2001/09/aa10248/Timg23.gif) |
Figure 2:
[O I] 6300 intensity maps predicted from the numerical
simulation for t=12, 14, 16, 18, 20 and 22 yr integration times.
A
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=0.48\textwidth, angle=0]{aa10248f3.eps}\end{figure}](/articles/aa/full/2001/09/aa10248/Timg24.gif) |
Figure 3:
[O I]6300 position-velocity diagrams predicted from the numerical
simulation for t=12, 14, 16, 18, 20 and 22 yr integration times.
A
|
| Open with DEXTER | |
Figure 2 shows the [O I] 6300 intensity maps predicted for several
different integration times, assuming a
![]() angle between
the z-axis and the plane of the sky, as appropriate for the
DG Tauri microjet (see Sect. 2). The corresponding [O I] 6300 position-velocity
diagrams are shown in Fig. 3. The line profiles were computed for a
spectrograph slit of 2'' width (corresponding to
angle between
the z-axis and the plane of the sky, as appropriate for the
DG Tauri microjet (see Sect. 2). The corresponding [O I] 6300 position-velocity
diagrams are shown in Fig. 3. The line profiles were computed for a
spectrograph slit of 2'' width (corresponding to
![]() 4 1015 cm at the distance of DG Tauri)
straddling the projection of the z-axis on the plane of the sky.
4 1015 cm at the distance of DG Tauri)
straddling the projection of the z-axis on the plane of the sky.
In Fig. 2, we see the leading working surface, which already starts to leave the computational grid at t=16 yr. The emission from the bow shock of this working surface is very weak because the shock is non-radiative (as it has a cooling distance of the order of ten times the jet radius, and a cooling timescale of 22 years, as can be seen from the 300 kms-1shock velocity model of Hartigan et al. 1987). The second working surface monotonically becomes fainter with increasing time starting from the t=12 yr map (Fig. 2). The third working surface is clearly visible in the t=18 yr map, showing a time evolution which is most similar to the one of the second working surface (as can be seen by comparing the t=20 with the t=12 yr maps, or the t=22 with the t=14 yr maps).
In the intensity maps, we also see the effects of the precession
of the jet beam. As the precession and velocity variability have
![]() yr (see Sect. 2), the two variabilities are synchronized.
At the time one of the working surfaces is starting to appear
(see, e.g., the t=16 and 18 yr intensity maps of Fig. 2), the
ejection direction approximately lies on the xz-plane, pointing
towards the +x-direction.
yr (see Sect. 2), the two variabilities are synchronized.
At the time one of the working surfaces is starting to appear
(see, e.g., the t=16 and 18 yr intensity maps of Fig. 2), the
ejection direction approximately lies on the xz-plane, pointing
towards the +x-direction.
The jet beam joining the source and the working surface, however, is formed by material ejected in between the times when the working surfaces appear, when the ejection direction points mostly in the -x-direction. This results in the formation of working surfaces with an extension in the +x-direction, which have the jet beam entering them along the -x-directed bow wing (see, e.g., the t=14 and 16 yr maps of Fig. 2). This is an example of the so-called "dentist's drill'' effect, which results in a relatively wide working surface being formed by a much thinner jet (see Cox et al. 1991).
In order to have predictions that can be compared with the
spectroscopic data of Lavalley-Fouquet et al. (2000) and
the HST STIS spectra of Bacciotti et al. (2000), the position-velocity
diagrams of Fig. 3 have been convolved with a FWHM=50 kms-1Gaussian "instrumental profile''. These diagrams show the "saw tooth''
signature expected for jets with a variable ejection velocity
(see, e.g., Raga et al. 1990). As the precession cone has
a small (
![]() ,
see Sect. 2) opening angle, no clear
effects of the precession are seen in the position-velocity diagrams.
An interesting result is that we see a slow component of the
emission line profiles (at radial velocities between 0 and
-50 km s-1 in all time frames) which comes from the cocoon
of warm jet and environmental gas which surrounds the jet beam.
,
see Sect. 2) opening angle, no clear
effects of the precession are seen in the position-velocity diagrams.
An interesting result is that we see a slow component of the
emission line profiles (at radial velocities between 0 and
-50 km s-1 in all time frames) which comes from the cocoon
of warm jet and environmental gas which surrounds the jet beam.
![\begin{figure}
\par\includegraphics[width=0.48\textwidth, angle=0]{aa10248f4.eps}\end{figure}](/articles/aa/full/2001/09/aa10248/Timg27.gif) |
Figure 4:
Results from the model for a t=18 yr time integration.
The graph shows the
H |
| Open with DEXTER | |
Finally, in Fig. 4 we show the H![]() intensity map predicted
for t=18 yr, together with the electron density,
hydrogen ionization fraction and [O I] 6300/H
intensity map predicted
for t=18 yr, together with the electron density,
hydrogen ionization fraction and [O I] 6300/H![]() line ratio
averaged across the width of the spectrograph slit (which straddles
the z-axis and has a projected width of 2 1015 cm,
as described above). The electron density and hydrogen ionization fractions
have been calculated by carrying out averages along lines of sight,
weighted by the
line ratio
averaged across the width of the spectrograph slit (which straddles
the z-axis and has a projected width of 2 1015 cm,
as described above). The electron density and hydrogen ionization fractions
have been calculated by carrying out averages along lines of sight,
weighted by the
![]() product (where
product (where ![]() is the electron
density, and
is the electron
density, and
![]() is the neutral hydrogen density). These values
therefore correspond in an approximate way to the values that would
be obtained from analyses of line ratios involving low ionization species
(see Bacciotti & Eislöffel 1999; Lavalley-Fouquet et al. 2000),
which have emission coefficients which approximately scale as
is the neutral hydrogen density). These values
therefore correspond in an approximate way to the values that would
be obtained from analyses of line ratios involving low ionization species
(see Bacciotti & Eislöffel 1999; Lavalley-Fouquet et al. 2000),
which have emission coefficients which approximately scale as
![]() (these emission coefficients, however, also have
explicit dependencies on temperature).
(these emission coefficients, however, also have
explicit dependencies on temperature).
The numerical simulation reproduces qualitatively well several
characteristics of the DG Tauri microjet. For example, the [O I] 6300 PUEO
image of the DG Tauri microjet (Dougados et al. 2000)
has a morphology that resembles the
ones obtained from the numerical model for t=16 or 18 yr integration
times (Fig. 2). The observed and predicted maps have main bow shocks with
similar widths (and at similar distances from the source), show a knot that
is beginning to emerge from the source region, and have a jet beam that
enters the main bow shock along one of its wings. Furthermore, Fig. 4
shows that the simulation also reproduces well the increase in ionization
fraction away from the star, and the accompanying factor of ![]() 10
decrease in electronic density, derived for the DG Tau microjet by
Lavalley-Fouquet et al. (2000) through an analysis of forbidden
emission line ratios. The predicted [O I]/H
10
decrease in electronic density, derived for the DG Tau microjet by
Lavalley-Fouquet et al. (2000) through an analysis of forbidden
emission line ratios. The predicted [O I]/H![]() ratio lies in the same
range as in the observations.
ratio lies in the same
range as in the observations.
![\begin{figure}
\par\includegraphics[width=0.48\textwidth, angle=0]{aa10248f5.eps}\end{figure}](/articles/aa/full/2001/09/aa10248/Timg31.gif) |
Figure 5:
PV diagrams perpendicular to the jet in [O I] and H |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=0.48\textwidth, angle=0]{aa10248f6.eps}\end{figure}](/articles/aa/full/2001/09/aa10248/Timg32.gif) |
Figure 6:
PV diagrams perpendicular to the jet in [O I] and H |
| Open with DEXTER | |
A comparison of the observed and predicted position-velocity diagrams
perpendicular to the jet axis, presented in Fig. 5, also reveals
interesting qualitative similarities.
At all distances, there is a clear trend both in the observed and predicted
diagrams that the transverse spatial extent of the emitting region is
larger at lower radial velocities. Such a behaviour has been observed in
knots ranging in distance from 1
![]() to 10
to 10
![]() along the DG Tau jet
(Bacciotti et al. 2000; Lavalley et al. 1997; Mundt et al. 1987). In the
simulation, this property arises from the presence of bow shock wings
trailing behind each internal working surface, which produce laterally
extended emission of lower radial velocities than the jet beam, down to
along the DG Tau jet
(Bacciotti et al. 2000; Lavalley et al. 1997; Mundt et al. 1987). In the
simulation, this property arises from the presence of bow shock wings
trailing behind each internal working surface, which produce laterally
extended emission of lower radial velocities than the jet beam, down to
![]() -100 kms-1. The magnitude of this effect is particularly well
reproduced for the main bow shock structure at
-100 kms-1. The magnitude of this effect is particularly well
reproduced for the main bow shock structure at
![]() cm. Hence, we are able to produce the large width observed
at that position even with an intrinsically narrow jet. A detailed
comparison with the innermost part of the DG Tau jet is more difficult
given the very complex kinematics in this region (which include a broad
range of velocities not well reproduced by our simulation, see below).
cm. Hence, we are able to produce the large width observed
at that position even with an intrinsically narrow jet. A detailed
comparison with the innermost part of the DG Tau jet is more difficult
given the very complex kinematics in this region (which include a broad
range of velocities not well reproduced by our simulation, see below).
The increase in jet width caused by the precession
can be judged by comparing Fig. 5 with similar diagrams for a non-precessing
jet simulation, with otherwise identical parameters, shown in Fig. 6.
The effect is most apparent in the faint jet section between the two
internal working surfaces, and also in the high-velocity apex
of the working surface at 7 1015 cm from the source.
A stronger broadening would be obtained for larger opening
angles of the precession cone (for the model shown in Fig. 5,
we have used a half-opening angle
![]() ,
see Sect. 2).
This broadening of the working surfaces, together with the entrance
of the jet beam along one of the bow shock wings (see Fig. 2)
is what has been called the "dentist's drill'' effect in
the extragalactic jet literature (see Sect. 1 and Cox et al. 1991).
,
see Sect. 2).
This broadening of the working surfaces, together with the entrance
of the jet beam along one of the bow shock wings (see Fig. 2)
is what has been called the "dentist's drill'' effect in
the extragalactic jet literature (see Sect. 1 and Cox et al. 1991).
Another nice feature of the simulation is that the warm jet cocoon left
behind by the leading working surface produces a low velocity emission
component (radial velocity < -100 kms-1), most apparent in [O I], which is
very extended laterally. A low-velocity [O I] "halo'' component of similar
velocity and extent is indeed observed (Lavalley et al. 1997;
Lavalley-Fouquet et al. 2000) and might be explained by such a jet cocoon.
This halo is very weak in both the observed and predicted H![]() position-velocity maps.
position-velocity maps.
Interestingly, a comparison of the observed and predicted position-velocity
diagrams parallel to the jet axis is less successful. In Fig. 7, we
show the [O I] 6300 and H![]() position-velocity diagrams obtained in
98/01 for the DG Tau microjet (Lavalley-Fouquet et al. 2000), as well as
the corresponding predictions obtained from the numerical model for a
t=18 yr time integration (cf. Fig. 3). From this figure, it is clear that
the observed and predicted kinematics are quite different from each other,
except toward the main bow shock located at
position-velocity diagrams obtained in
98/01 for the DG Tau microjet (Lavalley-Fouquet et al. 2000), as well as
the corresponding predictions obtained from the numerical model for a
t=18 yr time integration (cf. Fig. 3). From this figure, it is clear that
the observed and predicted kinematics are quite different from each other,
except toward the main bow shock located at
![]() cm.
cm.
![\begin{figure}
\par\includegraphics[width=0.48\textwidth, angle=0]{aa10248f7.eps}\end{figure}](/articles/aa/full/2001/09/aa10248/Timg35.gif) |
Figure 7:
PV diagrams parallel to the jet in [O I] and H |
| Open with DEXTER | |
For example, the region within ![]() 0
0
![]() 5 from DG Tauri shows an
"acceleration'', with the mean velocity of the line profile becoming
more negative away from the star. This effect is not seen in the
numerical simulation, which shows a decreasing radial velocity modulus
for increasing distances from the source. This steep velocity
decrease, resulting from the fast jet catching up with previous slower
ejecta, is actually responsible for the formation of the new knot at
5 from DG Tauri shows an
"acceleration'', with the mean velocity of the line profile becoming
more negative away from the star. This effect is not seen in the
numerical simulation, which shows a decreasing radial velocity modulus
for increasing distances from the source. This steep velocity
decrease, resulting from the fast jet catching up with previous slower
ejecta, is actually responsible for the formation of the new knot at
![]() 1015 cm from the star.
1015 cm from the star.
At distances
![]() cm (1
cm (1
![]() 5) from the source,
the predicted position-velocity diagram does show an increasing
velocity vs. position, from
5) from the source,
the predicted position-velocity diagram does show an increasing
velocity vs. position, from ![]() -150 kms-1 up to the bow shock
velocity. A comparable increase is indeed observed in the [O I] line
profiles of the DG Tauri microjet (see Fig. 7). However, observed line
profiles in this region also exhibit, especially in H
-150 kms-1 up to the bow shock
velocity. A comparable increase is indeed observed in the [O I] line
profiles of the DG Tauri microjet (see Fig. 7). However, observed line
profiles in this region also exhibit, especially in H![]() ,
a
high-velocity component at an almost constant radial velocity of
,
a
high-velocity component at an almost constant radial velocity of
![]() -300 kms-1 which is not reproduced by our simulation.
-300 kms-1 which is not reproduced by our simulation.
We have tried to run other numerical simulations with sinusoidal,
time-dependent ejection velocities, but we have been unable to find a set
of parameters that better reproduces the observed position-velocity
diagrams. An example of the results obtained for an alternative set of
parameters is shown in the bottom frames of Fig. 7 (corresponding to a
t=16 yr time-integration of a model with v0=350 kms-1,
![]() kms-1,
kms-1,
![]() yr and with the other parameters
identical to those discussed in Sect. 2). For this alternative model, we are
showing a time-step where the next working surface has not yet formed. As a
result, the radial velocity is steadily increasing all the way from the
origin to the working surface, with the velocity just upstream of the main
working surface being close to the maximum jet speed (a similar evolution
stage is encountered at t=14 yr for our first model; cf. Fig. 3). For
these alternative parameters, the maximum radial velocity is
yr and with the other parameters
identical to those discussed in Sect. 2). For this alternative model, we are
showing a time-step where the next working surface has not yet formed. As a
result, the radial velocity is steadily increasing all the way from the
origin to the working surface, with the velocity just upstream of the main
working surface being close to the maximum jet speed (a similar evolution
stage is encountered at t=14 yr for our first model; cf. Fig. 3). For
these alternative parameters, the maximum radial velocity is ![]() -350kms-1, close to what is observed in DG Tau. However, the emission knot
observed closer to the star is then left unexplained.
-350kms-1, close to what is observed in DG Tau. However, the emission knot
observed closer to the star is then left unexplained.
We conclude that a sinusoidal time-variable jet velocity seems to be unable to reproduce the kinematics of both emission knots in the DG Tau microjet, in particular the fact that the jet radial velocity appears almost constant between the two knots. Another type of variability (linear increase, saw-tooth) and/or the presence of several modes would be necessary to explain the observed radial velocity structure.
We have used various observations of the DG Tauri microjet in order to determine the parameters for a velocity variability and a precession of the ejection (as well as the initial radius and density of the jet). With these parameters, we have computed a 3D gasdynamic simulation, from which we carry out predictions of emission line maps and position-velocity diagrams. A comparison of these predictions with the observations shows interesting successes and failures of the model.
As expected, we can produce knots with appropriate morphologies as a result of the ejection velocity variability. Through the precession, we can produce knots that are much broader than the jet diameter (as a result of the "dentist's drill'' effect), with the jet beam entering along one of the "wings'' of the knot emission. This is in good qualitative agreement with the observations of the DG Tauri microjet. The observed increase in ionization fraction, and decrease in electronic density, away from the star is also qualitatively reproduced.
The position-velocity diagrams perpendicular to the jet axis also
show interesting agreement with recent spectro-imaging observations of
DG Tauri (Lavalley-Fouquet et al. 2000). In
particular, the models produce both a fast component of low
[O I] 6300/H![]() ratio (tracing the jet beam and the internal
working surfaces), and a much broader, low velocity component with a
high [O I] 6300/H
ratio (tracing the jet beam and the internal
working surfaces), and a much broader, low velocity component with a
high [O I] 6300/H![]() ratio (coming from the warm cocoon around
the jet). This broader "wake'' could possibly explain the
low-velocity [O I] halo observed in DG Tau (Lavalley et al. 1997),
although an explanation in terms of an intrinsic transverse jet structure is
definitely not excluded by our observations.
ratio (coming from the warm cocoon around
the jet). This broader "wake'' could possibly explain the
low-velocity [O I] halo observed in DG Tau (Lavalley et al. 1997),
although an explanation in terms of an intrinsic transverse jet structure is
definitely not excluded by our observations.
The predicted radial velocity gradients along the jet axis,
however, differ in an appreciable way from the observed
behaviour. For example, in the region within ![]() 1'' from the
source, an "acceleration'' (towards more negative velocities) is
observed in the DG Tauri microjet. Our model does predict such
"accelerations'' (see, e.g., the t=14 yr position-velocity diagram
of Fig. 3), but occuring over considerably larger distances. Also,
observations show a high-velocity component of almost constant radial
velocity
1'' from the
source, an "acceleration'' (towards more negative velocities) is
observed in the DG Tauri microjet. Our model does predict such
"accelerations'' (see, e.g., the t=14 yr position-velocity diagram
of Fig. 3), but occuring over considerably larger distances. Also,
observations show a high-velocity component of almost constant radial
velocity ![]() -300 km s-1 between the two working surfaces,
while our model predicts a much lower velocity in this region once the
second working surface has formed.
-300 km s-1 between the two working surfaces,
while our model predicts a much lower velocity in this region once the
second working surface has formed.
Such discrepancies with the observed velocity gradients can be attributed to the simplifying assumption in the present model that the ejection velocity variability is sinusoidal. A better agreement with the observations might be obtained by considering other types of velocity variabilities which could range from an asymmetric "rapid rise/slow decay'' periodic variability to a more general, non-periodic ejection velocity history. This will require introducing more free parameters, for which additional observational constraints are needed.
Presently, there is no clear idea about the nature of the
perturbations that could produce the ejection velocity
time-variability necessary for reproducing the observed knot
structure. The precession of the outflow axis necessary for modelling
the structure of the jet could be the result of a precession of the
accretion disk caused by the presence of a companion star, but in
order to produce the ![]() 10 yr precession period (implied by the
curved jet structure), a binary orbit with a very short period of
10 yr precession period (implied by the
curved jet structure), a binary orbit with a very short period of
![]() 0.5 yr would be necessary (as the disk precession period is of
0.5 yr would be necessary (as the disk precession period is of
![]() 20 times the orbital period, according to Terquem et al. 1999;
Bate 2000). Fortunately, the evolutionary timescales of the
DG Tauri microjet are so rapid that we should have the exciting
opportunity of discovering the precise nature of the variability of
the ejection through direct observations and 3D hydrodynamic modelling
of this object over the next two decades.
20 times the orbital period, according to Terquem et al. 1999;
Bate 2000). Fortunately, the evolutionary timescales of the
DG Tauri microjet are so rapid that we should have the exciting
opportunity of discovering the precise nature of the variability of
the ejection through direct observations and 3D hydrodynamic modelling
of this object over the next two decades.
Acknowledgements
The work of AR was supported by the CONACyT grants 32753-E and 27546-E. AR also acknowledges support from a Fellowship of the John Simon Guggenheim Memorial Foundation, and the Observatoire de Paris for an Enseignant Invité position. We would like to thank Adam Frank (the referee) for helpful comments about this paper.