A&A 367, 1061-1069 (2001)
DOI: 10.1051/0004-6361:20000548
An analysis of satellite calibration methods for
CCD astrometry of Saturn's satellites
K. X. Shen1,2,3 - G. Dourneau4 -
R. C. Qiao1,3 - J. R. Liu1,3
1 - Shannxi Astronomical Observatory, Lintong, Shannxi 710600, PR China
2 -
Chinese National Astronomical Research Center
3 -
United Laboratory for Optical Astrometry,
The Chinese Academy of Science, PR China
4 -
Observatoire de l'Université Bordeaux I, BP 89,
33270 Floirac, France
Received 25 July 2000 / Accepted 28 November 2000
Abstract
This paper presents an analysis of astrometric reduction methods for the
calibration of a CCD target. To compare these methods, we collected about
3000 recent CCD observations between 1990-1997.
We discuss the comparison of the four main contemporary theories describing
the eight major satellites of Saturn, used in recent CCD astrometric
reduction. We show that these theories developed by Taylor & Shen (1988),
Dourneau (1993), Harper & Taylor (1999) and Duriez & Vienne (1997),
give a rather good representation of the orbits of the eight main satellites,
especially for satellites III-VI. In the CCD astrometric reduction,
we point out a bias of the
theories on the derived satellite positions, which can reach about 0
 03.
Duriez and Vienne's TASS theory (1997), built with significantly higher consistency
than the other three,
generally leads to the lowest residuals for the observations analysed here.
Due to its high quality, we recommend use of this theory for CCD reduction.
Systematic errors affecting satellites' derived positions should be small,
due to the quality of the TASS theory.
This procedure might be an alternative to the multi-theory reduction method
previously proposed by Qiao et al. (1999).
Observations of satellites obtained from CCD reduction using TASS are expected
to be significantly more accurate (0
03.
Duriez and Vienne's TASS theory (1997), built with significantly higher consistency
than the other three,
generally leads to the lowest residuals for the observations analysed here.
Due to its high quality, we recommend use of this theory for CCD reduction.
Systematic errors affecting satellites' derived positions should be small,
due to the quality of the TASS theory.
This procedure might be an alternative to the multi-theory reduction method
previously proposed by Qiao et al. (1999).
Observations of satellites obtained from CCD reduction using TASS are expected
to be significantly more accurate (0
 015) than observations reduced from any other
theory (about 0
015) than observations reduced from any other
theory (about 0
 05).
05).
Key words: planetes & satellites: Saturn - astrometry - methods: observational
The CCD technique in astrometry, which has been used for about a decade, has some
intrinsic difficulties in dealing with astrometric reduction. This is a consequence of the
small size of the CCD target, generally associated with the use of a long-focus
telescope. In order to obtain profitable data, we must know precisely the
focal length of the telescope and the orientation of the target at each observation.
In recent years, much effort has been devoted to finding more reliable methods
of calibration. Jones et al. (1989) used the wide double star 61 Cygni to determine
the calibration parameters of CCD exposures.
Colas & Arlot (1991) chose to use globular clusters such as M 15, for
which astrometric catalog data are available. Neither of these methods
are quite satisfactory
from an astrometric perspective. So, other
methods were proposed, using the bright moons of Saturn, whose positions are
derived from well-known ephemeris data (Harper et al. 1997). Such methods have
already been used in some previous astrophotographic observations (Veillet & Dourneau 1982), but present a problem because errors of satellite ephemerides
affect their derived positions (Pascu et al. 1987).
In the present paper, we confirm this error from our analysis of observations.
In order to reduce systematic errors which affect satellite observations
reduced from the use of only one theory, Qiao et al. (1999) proposed
the multi-theory method.
This method uses the four contemporary dynamical satellite theories developed by
Taylor & Shen (1988), Dourneau (1993), Harper & Taylor (1993) and
Duriez & Vienne (1997).
Satisfactory observations of satellites were provided by the multi-theory
method, providing observed-minus-computed residuals which can reach 0
 08.
In this paper, we will analyze the accuracy of various CCD reduction methods
based on the four satellite theories, including the multi-theory method that we will use
as a reference for comparison. From a detailed analysis of these theories,
we will try to suggest a CCD reduction method
determining more accurately the positions of saturnian satellites.
08.
In this paper, we will analyze the accuracy of various CCD reduction methods
based on the four satellite theories, including the multi-theory method that we will use
as a reference for comparison. From a detailed analysis of these theories,
we will try to suggest a CCD reduction method
determining more accurately the positions of saturnian satellites.
The theories that we will analyze in this paper are the four main contemporary
theories mentioned above. Three of these theories, developed by Dourneau (1993),
Taylor & Shen (1988) and Harper & Taylor (1997) are constructed from previous
theories developed by Struve (1898) and later improved by Struve (1931) and
Kozai (1957). The differences between these three theories are in
the quantity and the quality of observations used to adjust the theoretical constants.
Also, the number of adjusted constants and the accuracy of the adjustment method
significantly differs between theories.
For example, Taylor & Shen (1988) used photographic observations over
the 1967-1983 period to determine a limited number of satellite orbital elements.
Dourneau (1987) corrected more than a hundred theoretical constants relative
to the eight major saturnian satellites from a century of observations,
including all published photographic and visual micrometric data from 1886 to 1985.
In this paper, we used the last version of this theory, in which Dourneau (1993)
corrected some more libration parameters of the four inner satellites.
This new version recently allowed a determination of the masses of these satellites
(Dourneau & Baratchart 1999). Harper & Taylor also corrected a great number
of constants of the major saturnian satellites.
They referred to the Strugnell & Taylor (1990) catalog of satellite
observations from 1874 to 1989, including Pascu's unpublished (1982) observations
made at U.S. Naval Observatory.
The new version of this theory (Harper & Taylor 1999), used in our paper, is
fitted to some additional recent CCD observations from 1990 to 1997 for all satellites,
Hyperion excepted. For Hyperion, this new version is derived from the
synthetic theory developed by Taylor (1992). It includes additional terms for
the perturbations of Titan and is based on observations from 1967 to 1982.
From this analysis, we can expect Dourneau's and Harper & Taylor's theories to be
rather similar, except for Hyperion. Also, both of these theories, based on a long
period of observation, should be significantly more reliable than Taylor & Shen's,
adjusted to a limited collection of observed data.
TASS theory (Théorie Analytique des Satellites de Saturne) has been presented in various
successive papers by Vienne & Duriez (1991, 1992, 1995). They propose new analytical
expressions for orbital elements, including additional perturbations of satellites.
TASS has a very good internal consistency of a few kilometers, significantly better
than the other three, more classical, contemporary theories.
Shen & Qiao (1996) have shown
that TASS accuracy is now greater than the precision of photographic observations.
In this paper, we have used the newest TASS 1.7 version (Duriez & Vienne 1997)
including Hyperion and adjusted to the observed data of the Strugnell & Taylor (1990)
catalog.
The four contemporary theories will be compared further in this paper to
the observations that we have collected and that we will present now.
In this work, we have collected about 3000 CCD observations of Saturn's satellite
positions. The first 500 of them were reported in our previous paper (Qiao
et al. 1999). They were made in the period 1994-1996 with the 1.56 m
telescope at the Sheshan Station near Shanghai, China. The approximate focal
length of the telescope was about 15.6 m and the size of the square pixels of
the CCD cell was
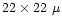 m. In addition, we collected another 2500 CCD positions,
successively obtained from 1990 to 1997 by Beurle
et al. (1993) and Harper et al. (1997, 1999), with the 1 m Jacobus Kapteyn
telescope on the island of La Palma, Spain. All these observations are
gathered in 21 datasets listed in Table 1. The first column gives names of
datasets in which H and Q, respectively, denote Harper and Qiao's
observations.
For each dataset, Cols. 7-9 specify how many times each
calibration satellite, Tethys, Dione and Rhea, was observed.
Titan, used as a reference satellite, is not specified, but the number of its
observations is the total of all mentioned calibration satellite numbers.
The last column indicates the number of nights of observation for each dataset.
Qiao's datasets always involve only one night, while Harper datasets can
involve several nights. However, during each dataset, the CCD camera
was kept fixed on the telescope, without any manipulation of the target.
m. In addition, we collected another 2500 CCD positions,
successively obtained from 1990 to 1997 by Beurle
et al. (1993) and Harper et al. (1997, 1999), with the 1 m Jacobus Kapteyn
telescope on the island of La Palma, Spain. All these observations are
gathered in 21 datasets listed in Table 1. The first column gives names of
datasets in which H and Q, respectively, denote Harper and Qiao's
observations.
For each dataset, Cols. 7-9 specify how many times each
calibration satellite, Tethys, Dione and Rhea, was observed.
Titan, used as a reference satellite, is not specified, but the number of its
observations is the total of all mentioned calibration satellite numbers.
The last column indicates the number of nights of observation for each dataset.
Qiao's datasets always involve only one night, while Harper datasets can
involve several nights. However, during each dataset, the CCD camera
was kept fixed on the telescope, without any manipulation of the target.
The images of satellites on CCD frames provide raw measured intersatellite
rectangular coordinates 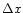 and
and 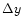 of the observed satellite B
relative to the reference satellite A. From these rectangular coordinates,
measured in pixels, we can derive other measured coordinates, such as
position angle
of the observed satellite B
relative to the reference satellite A. From these rectangular coordinates,
measured in pixels, we can derive other measured coordinates, such as
position angle 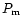 and separation
and separation 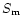 ,
commonly associated with old micrometric
observations.
,
commonly associated with old micrometric
observations.
Table 1:
Collected datasets of Saturn's satellite CCD observations,
denoted by H and Q respectively for Harper et al. (1997, 1999)
and Qiao et al. (1999) observations.
Values of the calibration parameters computed
in this paper from the four contemporary satellite theories are given and
can be compared with previous values adopted by the authors. Respective
numbers of calibration satellites and nights of observation are specified
for each dataset
| Datasets |
Calibration parameters |
Number of |
Number of |
| |
T&S |
H&T |
TASS |
Dourneau |
Adopted |
calibration
satellites |
nights of |
| |
above:
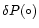 below: k(''/pixel)
below: k(''/pixel) |
Values |
Tethys |
Dione |
Rhea |
observation |
| H90A |
1.1624 |
1.1729 |
1.1711 |
1.1802 |
1.1746 |
40 |
31 |
47 |
9 |
| |
0.302802 |
0.302871 |
0.302820 |
0.302764 |
0.302844 |
|
|
|
|
| H90B |
1.2056 |
1.2165 |
1.2104 |
1.2255 |
1.2089 |
6 |
6 |
6 |
7 |
| |
0.302907 |
0.302950 |
0.302877 |
0.302843 |
0.302802 |
|
|
|
|
| H90C |
1.1050 |
1.1075 |
1.1015 |
1.1191 |
1.0900 |
1 |
2 |
3 |
2 |
| |
0.302882 |
0.302845 |
0.302796 |
0.302706 |
0.302902 |
|
|
|
|
| H91 |
0.2403 |
0.2739 |
0.2660 |
0.3035 |
0.2682 |
18 |
17 |
18 |
6 |
| |
0.302945 |
0.303078 |
0.302975 |
0.302956 |
0.302936 |
|
|
|
|
| H93 |
2.4404 |
2.4513 |
2.4503 |
2.4636 |
2.4525 |
28 |
30 |
30 |
7 |
| |
0.309729 |
0.309822 |
0.309733 |
0.309747 |
0.309693 |
|
|
|
|
| H94 |
0.0954 |
0.0952 |
0.0948 |
0.1077 |
0.0959 |
12 |
19 |
20 |
2 |
| |
0.309801 |
0.309910 |
0.309762 |
0.309810 |
0.309801 |
|
|
|
|
| Q940811 |
-5.4787 |
-5.6171 |
-5.5880 |
-5.7072 |
-5.4898 |
0 |
4 |
16 |
1 |
| |
0.249382 |
0.250093 |
0.249974 |
0.250128 |
0.249900 |
|
|
|
|
| Q940813 |
-5.5157 |
-5.5407 |
-5.5625 |
-5.5639 |
-5.5750 |
15 |
39 |
39 |
1 |
| |
0.249335 |
0.249578 |
0.249663 |
0.249645 |
0.249400 |
|
|
|
|
| Q941022 |
2.1273 |
2.1019 |
2.0945 |
2.0842 |
2.1540 |
4 |
23 |
23 |
1 |
| |
0.249917 |
0.249936 |
0.249936 |
0.249832 |
0.249713 |
|
|
|
|
| Q941023 |
2.2191 |
2.1866 |
2.2012 |
2.1832 |
2.2064 |
14 |
14 |
14 |
1 |
| |
0.250023 |
0.250290 |
0.250027 |
0.250204 |
0.249857 |
|
|
|
|
| Q941024 |
1.4426 |
1.4362 |
1.4396 |
1.4192 |
1.4520 |
5 |
0 |
5 |
1 |
| |
0.249697 |
0.249931 |
0.249820 |
0.249882 |
0.249850 |
|
|
|
|
| Q941025 |
2.1946 |
2.1938 |
2.1906 |
2.1815 |
2.2044 |
6 |
6 |
6 |
1 |
| |
0.249869 |
0.249954 |
0.249827 |
0.249868 |
0.249820 |
|
|
|
|
| H95 |
0.1328 |
0.1533 |
0.1464 |
0. 1562 |
0.1529 |
36 |
42 |
56 |
13 |
| |
0.330323 |
0.330431 |
0.330322 |
0.330340 |
0.330352 |
|
|
|
|
| Q950815 |
2.2064 |
2.2383 |
2.2054 |
2.2062 |
2.2485 |
9 |
19 |
20 |
1 |
| |
0.249034 |
0.250035 |
0.250272 |
0.250293 |
0.249800 |
|
|
|
|
| Q950816 |
2.2625 |
2.2675 |
2.2622 |
2.2516 |
2.2585 |
0 |
7 |
7 |
1 |
| |
0.249838 |
0.250082 |
0.249998 |
0.250055 |
0.249850 |
|
|
|
|
| Q950922 |
2.3784 |
2.1750 |
2.2882 |
2.1338 |
2.2450 |
3 |
9 |
9 |
1 |
| |
0.249881 |
0.249893 |
0.249785 |
0.249798 |
0.249950 |
|
|
|
|
| Q961018 |
7.6132 |
7.7188 |
7.7433 |
7.7602 |
7.5142 |
12 |
12 |
0 |
1 |
| |
0.252047 |
0.251500 |
0.251384 |
0.251383 |
0.251170 |
|
|
|
|
| Q961019 |
7.4846 |
7.4885 |
7.4920 |
7.4787 |
7.4782 |
13 |
14 |
13 |
1 |
| |
0.251185 |
0.251469 |
0.251381 |
0.251522 |
0.251275 |
|
|
|
|
| H97A |
0.5764 |
0.5789 |
0.5663 |
0.5438 |
0.5684 |
89 |
42 |
84 |
1 |
| |
0.330173 |
0.330407 |
0.330346 |
0.330497 |
0.330407 |
|
|
|
|
| H97B |
0.6159 |
0.5871 |
0.6040 |
0.5814 |
0.6126 |
68 |
68 |
61 |
1 |
| |
0.330227 |
0.330497 |
0.330383 |
0.330560 |
0.330389 |
|
|
|
|
| H97C |
0.6544 |
0.6437 |
0.6502 |
0.6502 |
0.6449 |
35 |
35 |
26 |
1 |
| |
0.330210 |
0.330435 |
0.330349 |
0.330418 |
0.330349 |
|
|
|
|
 |
(1) |
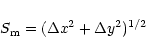 |
(2) |
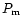 refers to the vertical axis of the CCD frame,
and
refers to the vertical axis of the CCD frame,
and 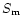 is expressed in pixels. From such raw data, we can derive
observed coordinates to be compared to computed coordinates, such as position
angle P, referred to the true pole of date, and separation S, expressed in
arc seconds, by the following relations:
is expressed in pixels. From such raw data, we can derive
observed coordinates to be compared to computed coordinates, such as position
angle P, referred to the true pole of date, and separation S, expressed in
arc seconds, by the following relations:
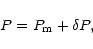 |
(3) |
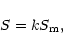 |
(4) |
in which 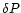 and k are defined as calibration
parameters of CCD exposures.
k represents the scale of the CCD frame, expressed in arcsecond per pixel.
and k are defined as calibration
parameters of CCD exposures.
k represents the scale of the CCD frame, expressed in arcsecond per pixel.
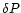 is the correction to the position angle of the true pole of date with respect
to the north-south axis of the CCD array, measured positive towards the east.
Observed coordinates P and S can be compared to topocentric computed
coordinates
is the correction to the position angle of the true pole of date with respect
to the north-south axis of the CCD array, measured positive towards the east.
Observed coordinates P and S can be compared to topocentric computed
coordinates 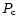 and
and 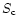 ,
expressed in the true equator and equinox of date.
We applied to these computed coordinates corrections for light-time,
refraction and stellar aberration.
Both calibration parameters k and
,
expressed in the true equator and equinox of date.
We applied to these computed coordinates corrections for light-time,
refraction and stellar aberration.
Both calibration parameters k and 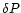 are determined in the reduction process
from their initial values k0 and
are determined in the reduction process
from their initial values k0 and
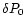 .
k0 is evaluated from the
approximate value of the focal length of the telescope, and
.
k0 is evaluated from the
approximate value of the focal length of the telescope, and
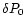 from some
index points marked on the telescope and on the CCD device, so that:
from some
index points marked on the telescope and on the CCD device, so that:
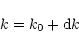 |
(5) |
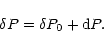 |
(6) |
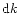 and
and 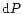 are corrections to initial values derived from the adjustment
between observed and computed satellite positions.
This adjustment consists of minimizing residuals between observed and computed
coordinates:
are corrections to initial values derived from the adjustment
between observed and computed satellite positions.
This adjustment consists of minimizing residuals between observed and computed
coordinates:
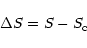 |
(7) |
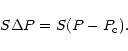 |
(8) |
Calibration parameter corrections 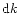 and
and 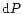 are solutions of the
least-squares method of adjustment.
We use an iterative procedure, by introducing computed
corrections for a new adjustment, until the convergence of calibration
parameters is achieved. We achieve the iterative procedure when corrections become
lower than 10-9 arcsecond for both coordinates.
Generally, the convergence occurred after no more than three iterations.
are solutions of the
least-squares method of adjustment.
We use an iterative procedure, by introducing computed
corrections for a new adjustment, until the convergence of calibration
parameters is achieved. We achieve the iterative procedure when corrections become
lower than 10-9 arcsecond for both coordinates.
Generally, the convergence occurred after no more than three iterations.
Calibration parameters for each dataset of observations presented
in Table 1 have been computed from the CCD reduction method described
in the subsection above. Different values were obtained with the various theories used.
Calibration parameters are supposed to be constant for each dataset,
as the CCD cell was not moved from the telescope.
We have successively computed the values of calibration parameters
from the four contemporary theories. These values are given in
Cols. 2-5 of Table 1. For comparison, the sixth column indicates values
previously adopted by Harper et al. (1997, 1999) and by Qiao et al.
(1999)
from their own respective methods. In these papers, Qiao derived calibration
parameters from
the multi-theory method including the four contemporary theories and Harper used
his own theory (Harper & Taylor 1993).
Table 1 shows that the values of the calibration parameters we have computed
for Harper's observations (Col. 3) are slightly different to the values he had
previously adopted (Col. 6). This can be explained as we have used in this paper
the newest version of this theory (Harper & Taylor 1999).
In order to extend the comparison of our
calibration parameter values with other ones, we have determined for the
particular Q961019 dataset of Table 1, made on the 19th of October 1996,
the scale and the position angle of the CCD frame
from other methods presented above in the introduction.
We have successively used the double star 61 Cygni, the globular cluster M 15, and
the multi-theory method. The values obtained are presented in Table 2.
Significant discrepancies can be observed between the values derived from these
different methods. Values obtained from the globular cluster M 15 and the multi-theory
method are in good agreement, but they appear significantly different from
those obtained from the double star 61 Cygni.
In Table 1, we can also observe
discrepancies between the values of the calibration parameters that we derived
from the different four contemporary theories, however, they appear much smaller than
those obtained from previous methods, as shown in Table 2.
In addition, we have determined that a difference between two scales
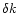 of 10-4''/pixel, generally observed in Table 1, can lead to
differences in the derived satellite positions of about 0
of 10-4''/pixel, generally observed in Table 1, can lead to
differences in the derived satellite positions of about 0
 1.
However, we need satellite positions with a greater accuracy in order to improve
analytical theories, particularly TASS. Mutual events are of great
interest for this purpose (Thuillot et al. 2000) but they are
unfortunately very rare. Because photographic plates are no longer manufactured,
the recent CCD observation technique could be the solution of the future.
However, the astrometric reduction used in this technique must be improved.
This is one of the special aims of this paper.
1.
However, we need satellite positions with a greater accuracy in order to improve
analytical theories, particularly TASS. Mutual events are of great
interest for this purpose (Thuillot et al. 2000) but they are
unfortunately very rare. Because photographic plates are no longer manufactured,
the recent CCD observation technique could be the solution of the future.
However, the astrometric reduction used in this technique must be improved.
This is one of the special aims of this paper.
As a preliminary analysis of calibration parameters, given in Tables 1
and 2, CCD reduction methods using satellite theories seem to give more
coherent values than other methods using reference stars. This can be
explained, as these stars are not located in the field of the observed
satellites. Moving the telescope may cause flexions and then significant
changes in calibration parameters (Colas & Arlot 1991).
Because CCD target are too small to allow reduction
from field stars, we prefer CCD reduction methods using satellite theories.
To improve these methods, we will compare the four
available theories, so as to discover if some, more accurate than others,
could be used in preference to any other one.
Table 2:
Calibration parameters k and 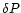 obtained from different CCD
astrometric reduction methods for the dataset Q961019 of Table 1
obtained from different CCD
astrometric reduction methods for the dataset Q961019 of Table 1
| Method |
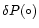 |
k(''/pixel) |
| Double stars(1) |
7.5782 |
0.250522 |
| Double stars(2) |
7.4654 |
0.251103 |
| Globular cluster M 15 |
7.4782 |
0.251161 |
| Multi-theory |
7.4782 |
0.251275 |
| |
|
|
| (1) 3 images of 61 Cygni used. |
| (2) 10 images of 61 Cygni used. |
Using the iterative procedure to determine the calibration parameters
described above, we computed observed-minus-computed residuals from intersatellite
positions, in separation (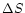 )
and
position angle (
)
and
position angle (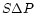 ), both expressed in arcseconds.
These residuals are given in Table 3 for each theory and for each satellite,
Titan excepted, as it was used as a reference.
Residuals were calculated from satellite observed positions obtained
from CCD reduction using the theory mentioned in the first line of Table 3, compared
to computed positions obtained from the same theory. Residuals higher than 0
), both expressed in arcseconds.
These residuals are given in Table 3 for each theory and for each satellite,
Titan excepted, as it was used as a reference.
Residuals were calculated from satellite observed positions obtained
from CCD reduction using the theory mentioned in the first line of Table 3, compared
to computed positions obtained from the same theory. Residuals higher than 0
 8
were eliminated.
A preliminary analysis of Table 3 shows the very high quality of the ephemeris
of satellites Tethys, Dione and Rhea, with residuals lower than 0
8
were eliminated.
A preliminary analysis of Table 3 shows the very high quality of the ephemeris
of satellites Tethys, Dione and Rhea, with residuals lower than 0
 1,
whichever theory used. Titan, used as the reference, also can be
considered as one of the satellites with the best-known theory.
Enceladus presents higher residuals, from 0
1,
whichever theory used. Titan, used as the reference, also can be
considered as one of the satellites with the best-known theory.
Enceladus presents higher residuals, from 0
 1 to 0
1 to 0
 2.
Mimas, Hyperion and Iapetus have much less accurate theories, with residuals
between 0
2.
Mimas, Hyperion and Iapetus have much less accurate theories, with residuals
between 0
 1 and 0
1 and 0
 5.
5.
Table 3 shows some significant discrepancies between residuals obtained from each
different theory.
TASS is the theory which generally gives the smallest residuals for
satellites with the best-known theories, with values from 0
 07 to 0
07 to 0
 08.
However, for these satellites, all other theories also give very satisfactory residuals,
from 0
08.
However, for these satellites, all other theories also give very satisfactory residuals,
from 0
 07 to 0
07 to 0
 1 and the differences with TASS appear quite small.
For other satellites, TASS is not always the best theory.
Harper & Taylor's (1999) theory generally gives the best residuals
for Mimas and Enceladus.
Dourneau's theory also gave better residuals in separation than TASS for Enceladus.
For Iapetus, TASS presents the best residuals, with 0
1 and the differences with TASS appear quite small.
For other satellites, TASS is not always the best theory.
Harper & Taylor's (1999) theory generally gives the best residuals
for Mimas and Enceladus.
Dourneau's theory also gave better residuals in separation than TASS for Enceladus.
For Iapetus, TASS presents the best residuals, with 0
 1 in
1 in 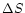 and 0
and 0
 2 in
2 in 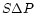 .
.
Table 3:
Statistics of observed-minus-computed residuals, expressed in arcseconds, for
all observations of Table 1, for each theory and for each satellite,
Titan excepted (used as the reference satellite).
The numbers of observed coordinates used are in parenthesis
Table 3.1. Residuals in separation 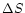 |
| |
T&S |
H&T |
TASS |
Dourneau |
| Mimas |
.3127(54) |
.2465(58) |
.2716(57) |
.2857(58) |
| Enceladus |
.2054(204) |
.1666(197) |
.1795(199) |
.1704(197) |
| Tethys |
.0905(413) |
.0746(413) |
.0722(413) |
.0814(413) |
| Dione |
.0967(438) |
.0800(438) |
.0750(438) |
.0865(438) |
| Rhea |
.0864(503) |
.0702(503) |
.0679(503) |
.0784(503) |
| Hyperion |
.3538(135) |
.2492(218) |
.1227(218) |
.4266(141) |
| Iapetus |
.3076(233) |
.1493(230) |
.1081(230) |
.1864(230) |
Table 3.2. Residuals in position angle 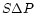 |
| |
T&S |
H&T |
TASS |
Dourneau |
| Mimas |
.3220(54) |
.1508(58) |
.1508(57) |
.1644(58) |
| Enceladus |
.1404(204) |
.1100(197) |
.1286(199) |
.1312(197) |
| Tethys |
.0803(413) |
.0728(413) |
.0717(413) |
.0877(413) |
| Dione |
.0699(438) |
.0694(438) |
.0678(438) |
.0734(438) |
| Rhea |
.0960(503) |
.0832(503) |
.0828(503) |
.0957(503) |
| Hyperion |
.3877(135) |
.1660(218) |
.1979(218) |
.5205(141) |
| Iapetus |
.5302(223) |
.2378(230) |
.2064(230) |
.2252(231) |
Thus, as a general result of the analysis of residuals presented in
Table 3, TASS can be considered as the best theory.
Both the theory developed by Harper & Taylor and by Dourneau
are rather close and can be placed in second position after TASS,
with a slight advantage for Harper & Taylor, especially for Hyperion.
Such a classification is not surprising, as we
have seen in Sect. 2 above that Dourneau's and
Harper & Taylor's theories were built from very similar adjustments
for all satellites, Hyperion excepted.
For this satellite, the residuals from Dourneau are the highest (0
 5),
but from Harper & Taylor they are very close to the lowest ones from TASS (0
5),
but from Harper & Taylor they are very close to the lowest ones from TASS (0
 2).
This can be explained as Dourneau did not include short-period terms
in the expressions for Hyperion, and we have used in this paper
the new version (Harper & Taylor 1999)
derived from the theory improved by Taylor (1992).
But we have noted above that discrepancies between residuals obtained from each of the four
theories remain very small for satellites with the best-known theories.
Then, for these satellites, it seems very difficult to appreciate the respective
quality of TASS, Harper & Taylor and Dourneau theories. The comparison of their
respective residuals in Table 3 is generally under the 0
2).
This can be explained as Dourneau did not include short-period terms
in the expressions for Hyperion, and we have used in this paper
the new version (Harper & Taylor 1999)
derived from the theory improved by Taylor (1992).
But we have noted above that discrepancies between residuals obtained from each of the four
theories remain very small for satellites with the best-known theories.
Then, for these satellites, it seems very difficult to appreciate the respective
quality of TASS, Harper & Taylor and Dourneau theories. The comparison of their
respective residuals in Table 3 is generally under the 0
 01 level
and any of these theories can reach such a precision.
But Table 3 clearly shows that Taylor & Shen's theory
results in higher residuals than all the other
theories for all satellites and especially for Mimas and
Iapetus (0
01 level
and any of these theories can reach such a precision.
But Table 3 clearly shows that Taylor & Shen's theory
results in higher residuals than all the other
theories for all satellites and especially for Mimas and
Iapetus (0
 3 to 0
3 to 0
 5).
5).
In conclusion, this analysis has shown that all four contemporary theories
analyzed in this paper are adequate to represent accurate
orbits of Tethys, Dione, Rhea and Titan. Thus, these satellites
can reasonably be used as calibration satellites. For
other satellites, we can conclude that ephemerides from all theories
still need to be improved, especially for Taylor & Shen and also,
in the particular case of Hyperion, for Dourneau.
Now, we propose to compare the residuals for all the observations of
the calibration satellites given in Table 1, relative to each theory.
A few low-quality observed positions with residuals greater than 3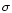 were eliminated. The residuals obtained are presented in Table 4.
They confirm the previous analysis of Table 3.
TASS appears again as the best theory in both coordinates for
calibration satellites, with very low values,
between 0
were eliminated. The residuals obtained are presented in Table 4.
They confirm the previous analysis of Table 3.
TASS appears again as the best theory in both coordinates for
calibration satellites, with very low values,
between 0
 07 and 0
07 and 0
 08. For these satellites, Table 4 also
confirms that the three other theories present very
satisfactory accuracy, whichever theory was used, with residuals
between 0
08. For these satellites, Table 4 also
confirms that the three other theories present very
satisfactory accuracy, whichever theory was used, with residuals
between 0
 07 and 0
07 and 0
 09, hardly higher than those
from TASS. Harper & Taylor's theory appears here very close to TASS.
All four theories of calibration satellites seem
to have about equivalent accuracy (of 0.08'', within
only 0.02''). Thus, this last value of 0
09, hardly higher than those
from TASS. Harper & Taylor's theory appears here very close to TASS.
All four theories of calibration satellites seem
to have about equivalent accuracy (of 0.08'', within
only 0.02''). Thus, this last value of 0
 02 could be considered
as a preliminary evaluation of the consistency of
CCD astrometric reduction methods using any of these four
theories of motion. Further, in this paper, we shall try
to evaluate more precisely such consistency
using different methods.
02 could be considered
as a preliminary evaluation of the consistency of
CCD astrometric reduction methods using any of these four
theories of motion. Further, in this paper, we shall try
to evaluate more precisely such consistency
using different methods.
Now, we propose to analyze and compare various CCD reduction methods
using different satellite theories.
First, we will try to point out the possible bias that any
theory used in the reduction can introduce in the
derived satellite positions. So, for all observations
of calibration satellites presented in Table 1, we determined the five different
positions, successively obtained from the reduction using the four theories
and from the multi-theory method.
Then, we computed residuals by comparing
these five observed positions to positions
computed from each theory.
Table 5 presents the derived residuals.
We can see that particular residuals in the diagonal of Table 5,
obtained from the comparison of satellite observed positions to computed positions,
derived using the same theory, were already given in Table 4.
It is interesting to note in Table 5 that diagonal residuals
generally appear as the smallest ones.
This points out a significant bias of theories towards corresponding
satellite positions affected with systematic errors.
Future adjustment of theories could be affected if such biased
satellite positions are used.
Table 5:
Residuals between satellite observed positions,
reduced from the four theories and from the multi-theory method,
and computed positions derived from these four theories.
Residuals are computed for all observations of calibration satellites
given in Table 1 and are expressed in arcseconds
Table 5.1. Residuals in separation 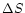 |
| Reduction |
Computation |
| method |
theories |
| |
TASS |
H&T |
Dourneau |
T&S |
| TASS |
0.0715 |
0.0840 |
0.0769 |
0.0923 |
| H&T |
0.0865 |
0.0748 |
0.0851 |
0.1131 |
| Dourneau |
0.0871 |
0.0915 |
0.0819 |
0.1137 |
| T&S |
0.1082 |
0.1245 |
0.1205 |
0.0910 |
| Multi-theory |
0.0728 |
0.0871 |
0.0879 |
0.1030 |
Table 5.2. Residuals in position angle 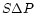 |
| Reduction |
Computation |
| method |
theories |
| |
TASS |
H&T |
Dourneau |
T&S |
| TASS |
0.0749 |
0.0762 |
0.0873 |
0.0843 |
| H&T |
0.0762 |
0.0759 |
0.0881 |
0.0847 |
| Dourneau |
0.0845 |
0.0850 |
0.0846 |
0.0972 |
| T&S |
0.0833 |
0.0837 |
0.1015 |
0.0835 |
| Multi-theory |
0.0751 |
0.0757 |
0.0833 |
0.0831 |
We shall try to evaluate the bias pointed out above.
We have determined, for each satellite,
differences between the four successive positions, obtained from each theory
in the CCD reduction, and positions derived from the multi-theory method,
used as a reference method, described above in the introduction.
These differences, computed for each night of observation listed in Table 1,
are visualized in Figs. 1 and 2 for both coordinates,
separation 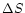 and position
angle
and position
angle 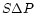 ,
respectively.
,
respectively.
![\begin{figure}
\par\includegraphics[height=18cm,clip]{shen_f1.ps}\end{figure}](/articles/aa/full/2001/09/aa10144/Timg26.gif) |
Figure 1:
Differences in separation 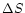 between satellite positions
reduced from the four successive theories and from the multi-theory method.
Ordinates are in arcseconds. Abscissas give the sequence of nights of observation
between satellite positions
reduced from the four successive theories and from the multi-theory method.
Ordinates are in arcseconds. Abscissas give the sequence of nights of observation |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[height=18cm,clip]{shen_f2.ps}\end{figure}](/articles/aa/full/2001/09/aa10144/Timg27.gif) |
Figure 2:
Differences in position angle 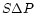 between satellite positions
reduced from the four successive theories and from the multi-theory method.
Ordinates are in arcseconds. Abscissas give the sequence of nights of observation
between satellite positions
reduced from the four successive theories and from the multi-theory method.
Ordinates are in arcseconds. Abscissas give the sequence of nights of observation |
| Open with DEXTER |
From a preliminary analysis, all differences appearing
in Figs. 1 and 2 are lower than 0
 1, with an exception for
some rare points relative to Taylor & Shen's theory.
Most differences remain lower than 0
1, with an exception for
some rare points relative to Taylor & Shen's theory.
Most differences remain lower than 0
 02, whatever the theory used.
This confirms our preliminary evaluation of the consistency of reduction methods
using satellite theories obtained above from residuals of Table 4.
However, some exceptions appear, especially in Fig. 1.
If observed positions successively reduced from the four theories present a rather
good coherency in position angle, generally within 0
02, whatever the theory used.
This confirms our preliminary evaluation of the consistency of reduction methods
using satellite theories obtained above from residuals of Table 4.
However, some exceptions appear, especially in Fig. 1.
If observed positions successively reduced from the four theories present a rather
good coherency in position angle, generally within 0
 02 (cf. Fig. 2),
they can present some higher discrepancies in separation.
For this coordinate, Fig. 1 emphasizes
differences between 0
02 (cf. Fig. 2),
they can present some higher discrepancies in separation.
For this coordinate, Fig. 1 emphasizes
differences between 0
 05 and 0
05 and 0
 1, especially for Harper & Taylor
and Taylor & Shen's theories.
In addition, it is interesting to note that these differences generally are
positive for Harper & Taylor and negative for Taylor & Shen,
pointing out a possible systematic bias in satellite observed positions
reduced from both of these theories.
Such a bias can be confirmed from the analysis of Table 6
which presents mean values of differences visualized in Figs. 1 and 2,
with their root mean square (rms) errors, for all observations of each satellite.
Table 6 shows that mean values are always positive for Harper & Taylor
and negative for Taylor & Shen,
confirming the bias relative to these theories pointed out in Fig. 1.
One of the highest bias concerns Harper & Taylor's theory, with about 0
1, especially for Harper & Taylor
and Taylor & Shen's theories.
In addition, it is interesting to note that these differences generally are
positive for Harper & Taylor and negative for Taylor & Shen,
pointing out a possible systematic bias in satellite observed positions
reduced from both of these theories.
Such a bias can be confirmed from the analysis of Table 6
which presents mean values of differences visualized in Figs. 1 and 2,
with their root mean square (rms) errors, for all observations of each satellite.
Table 6 shows that mean values are always positive for Harper & Taylor
and negative for Taylor & Shen,
confirming the bias relative to these theories pointed out in Fig. 1.
One of the highest bias concerns Harper & Taylor's theory, with about 0
 03 in separation.
It may be related to possible systematic scale errors in the observations,
already mentioned by Harper & Taylor (1993).
In addition, Table 6 shows that for each satellite,
TASS generally presents the lowest mean differences, under 0
03 in separation.
It may be related to possible systematic scale errors in the observations,
already mentioned by Harper & Taylor (1993).
In addition, Table 6 shows that for each satellite,
TASS generally presents the lowest mean differences, under 0
 005,
and the lowest rms errors, under 0
005,
and the lowest rms errors, under 0
 02.
This means that observed positions reduced from TASS are the most coherent with
those reduced from the multi-theory method.
As this method was proposed by Qiao et al. (1999) for reducing systematic errors
of each theory in satellite positions,
we can expect that positions reduced from TASS would also have no significant
systematic errors.
02.
This means that observed positions reduced from TASS are the most coherent with
those reduced from the multi-theory method.
As this method was proposed by Qiao et al. (1999) for reducing systematic errors
of each theory in satellite positions,
we can expect that positions reduced from TASS would also have no significant
systematic errors.
To further evaluate the accuracy of satellite observations
reduced from different theories, we propose to use rms errors of
mean differences given in Table 6, generally higher than the corresponding mean differences.
These errors are lowest for TASS. The CCD reduction using this theory
should then provide the most consistent satellite observations,
as rms errors in Table 6 are under 0
 015 in both coordinates.
Thus, for TASS, this last value appears somewhat better than our preliminary
evaluation (0
015 in both coordinates.
Thus, for TASS, this last value appears somewhat better than our preliminary
evaluation (0
 02) concerning reduction methods involving any satellite theory.
However, when theories other than TASS are used in the reduction,
the accuracy of observations, also evaluated from rms errors of Table 6,
appears significantly higher:
about 0
02) concerning reduction methods involving any satellite theory.
However, when theories other than TASS are used in the reduction,
the accuracy of observations, also evaluated from rms errors of Table 6,
appears significantly higher:
about 0
 03 for Harper & Taylor and Dourneau, and 0
03 for Harper & Taylor and Dourneau, and 0
 04 for Taylor & Shen.
04 for Taylor & Shen.
We have analysed the four contemporary satellite
theories developed by Taylor & Shen (1988),
Dourneau (1993), Duriez & Vienne (1997) and Harper & Taylor
(1999),
to get some information about their respective reliability.
We have shown that these four theories can derive quite satisfactory orbits
for Tethys, Dione, Rhea and Titan, which can be used as calibration satellites
for computing calibration parameters in CCD reduction.
For these satellites, whichever theory used in the CCD reduction, we can expect
to obtain observed positions with a good accuracy.
However, we have pointed out a bias of the theories used in the CCD reduction
in the corresponding derived satellite
positions, rather significant for Harper & Taylor and Taylor & Shen,
with values of about 0
 03.
In order to limit systematic errors, especially those introduced when only one theory
is used in the reduction process, we had proposed in a previous work (Qiao et al. 1999)
the multi-theory reduction method using all four contemporary theories together.
In this paper, we have shown that the CCD reduction using the TASS theory is in
better agreement with the multi-theory method than all other reduction methods.
So, when used in the CCD reduction, TASS should not introduce any significant bias
in the satellite positions.
Also, we have made some attempts to evaluate the accuracy of satellite positions
reduced from the multi-theory method and from CCD reduction
using the four successive contemporary theories.
From the CCD observed data from 1990 to 1997 analyzed in this paper,
we have shown that, for calibration satellites,
observations reduced from TASS seem to present the best consistency (0
03.
In order to limit systematic errors, especially those introduced when only one theory
is used in the reduction process, we had proposed in a previous work (Qiao et al. 1999)
the multi-theory reduction method using all four contemporary theories together.
In this paper, we have shown that the CCD reduction using the TASS theory is in
better agreement with the multi-theory method than all other reduction methods.
So, when used in the CCD reduction, TASS should not introduce any significant bias
in the satellite positions.
Also, we have made some attempts to evaluate the accuracy of satellite positions
reduced from the multi-theory method and from CCD reduction
using the four successive contemporary theories.
From the CCD observed data from 1990 to 1997 analyzed in this paper,
we have shown that, for calibration satellites,
observations reduced from TASS seem to present the best consistency (0
 015),
while those reduced from Harper & Taylor and Dourneau generally have a consistency of
0
015),
while those reduced from Harper & Taylor and Dourneau generally have a consistency of
0
 03 or better, and Taylor & Shen of about 0
03 or better, and Taylor & Shen of about 0
 05.
05.
In conclusion, the analysis we have performed has shown that the multi-theory
method appears to be useful in CCD reduction,
owing to its ability to provide satellite observations without
any significant systematic error.
However, such satellite observations reduced from the multi-theory method
can be affected by the significant errors introduced by the less accurate theories
such as Taylor & Shen.
So, we suggest the use of the highly consistent TASS theory alone
for computing calibration parameters in CCD reduction.
The observations should then have a consistency of about 0
 015 and they
should not present any significant systematic errors.
Our suggestions about CCD reduction methods should help observers
to publish in the future more accurate reduced positions of Saturn's satellites.
However, we advise them to publish in addition all their raw data,
measured in pixels on the CCD frame.
This will allow subsequent users of the satellite observations to adopt a
given method of reduction, as these methods should be improved in the near
future, particularly when larger CCD targets will be used.
For instance, wider fields will allow classical reduction from
reference field stars. This will resolve many model-dependant
systematic errors from future positions of Saturn's satellites.
015 and they
should not present any significant systematic errors.
Our suggestions about CCD reduction methods should help observers
to publish in the future more accurate reduced positions of Saturn's satellites.
However, we advise them to publish in addition all their raw data,
measured in pixels on the CCD frame.
This will allow subsequent users of the satellite observations to adopt a
given method of reduction, as these methods should be improved in the near
future, particularly when larger CCD targets will be used.
For instance, wider fields will allow classical reduction from
reference field stars. This will resolve many model-dependant
systematic errors from future positions of Saturn's satellites.
Acknowledgements
We wish to thank Prof. B. C. Qiao and his staff
at the Sheshan Station of Shanghai Observatory. Also, we thank the staff at the Yunnan
Astrometrical Observatory for their help during observations.
We are grateful to Dr. D. Harper for providing us with the new version of satellite
theories, as well as to Dr. D. B. Taylor for his newest version of Hyperion's theory.
This work was carried out with the
financial support of the National Science Foundation of China (NSFC).
- Beurle, K., Harper, D., Jones, D. H. P., et al. 1993, A&A, 269, 564
In the text
NASA ADS
- Colas, F., & Arlot, J. E. 1991, A&A, 252, 402
In the text
NASA ADS
- Dourneau, G. 1987, Observation et étude du
mouvement des huit premiers satellites de Saturne, Thèse de doctorat
d'État, Université Bordeaux I
In the text
- Dourneau, G. 1993, A&A, 267, 292
In the text
NASA ADS
- Dourneau, G., & Baratchart, S. 1999, A&A, 350, 680
In the text
NASA ADS
- Duriez, L., & Vienne, A. 1991, A&A, 243, 263
NASA ADS
- Duriez, L., & Vienne, A. 1997, A&A, 324, 366
In the text
NASA ADS
- Harper, D., & Taylor, D. B. 1993, A&A, 268, 326
In the text
NASA ADS
- Harper, D., Murray, C. D., Beurle, K., et al. 1997, A&A, 121, 65
In the text
- Harper, D., Beurle, K., Williams, I. P., et al. 1999, A&AS, 136, 257
In the text
NASA ADS
- Harper, D., & Taylor, D. B., 1999, personal communication
In the text
- Jones, D. H. P., Sinclair, A. T., & Williams, I. P. 1989, MNRAS, 237, 15P
In the text
NASA ADS
- Pascu, D. 1982, data held at the U.S. Naval Observatory, Washington, DC
In the text
- Pascu, D., Seidelman, P. K., Schmidt, R. S., Santoto,
E. J., & Hershey, J. L. 1987, AJ, 93, 963
In the text
NASA ADS
- Qiao, R. C., Shen, K. X., Liu, J. R., & Harper, D. 1999, A&AS, 137, 1
In the text
NASA ADS
- Shen, K. X., & Qiao, R. C. 1996, Proceeding of
the 172nd Symposium of the IAU, 141
In the text
- Strugnell, P. R., & Taylor, D. B. 1990, A&AS, 83, 289
In the text
NASA ADS
- Taylor, D. B., & Shen, K. X. 1988, A&A, 200, 269
In the text
NASA ADS
- Taylor, D. B. 1992, A&A, 265, 825
In the text
NASA ADS
- Thuillot, W., Arlot, J. E., Ruatti, C., et al. 2000, A&A, to be published
In the text
- Vienne, A., & Duriez, L. 1991, A&A, 246, 619
In the text
NASA ADS
- Vienne, A., & Duriez, L. 1992, A&A, 257, 351
In the text
- Vienne, A., & Duriez, L. 1995, A&A, 297, 588
In the text
NASA ADS
- Woltjer, J. 1928, Ann. Sterw. Leiden., XVI, 3
Copyright ESO 2001

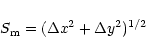
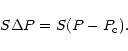
![\begin{figure}
\par\includegraphics[height=18cm,clip]{shen_f1.ps}\end{figure}](/articles/aa/full/2001/09/aa10144/Timg26.gif)
![\begin{figure}
\par\includegraphics[height=18cm,clip]{shen_f2.ps}\end{figure}](/articles/aa/full/2001/09/aa10144/Timg27.gif)