A&A 367, 674-693 (2001)
DOI: 10.1051/0004-6361:20000433

Low-excitation atomic gas around evolved stars

II. ISO observations of O-rich nebulae[*]

A. Castro-Carrizo1 - V. Bujarrabal1 - D. Fong2 - M. Meixner2 - A. G. G. M. Tielens3 -
W. B. Latter4 - M. J. Barlow5


1 - Observatorio Astronómico Nacional, Apartado 1143, 28800 Alcalá de Henares, Spain
2 - University of Illinois, 1002 W. Green St., Urbana, Il 61801, USA
3 - Kapteyn Astronomical Institute, PO Box 800, 9700 AV Groningen, The Netherlands
4 - SIRTF Science Center/IPAC, CalTech, MS 314-6, Pasadena, CA 91125, USA
5 - Department of Physics and Astronomy, University College London, Gower Street, London WC1E6BT, UK

Received 11 July 2000 / Accepted 24 November 2000

Abstract
We have observed atomic fine-structure lines in the far-infrared (FIR) from 12 oxygen-rich evolved stars. The sample is composed of mostly proto-planetary nebulae (PPNe) and some planetary nebulae (PNe) and asymptotic giant branch (AGB) stars. ISO LWS and SWS observations of [O I], [C II], [N II], [Si I], [Si II], [S I], [Fe I], and [Fe II] lines were obtained. Taking into account also the sample presented by Fong et al. (Paper I) of carbon-rich evolved stars, we find that PPNe emit in these low-excitation atomic transitions only when the central star is hotter than $\sim$10000 K. This result suggests that such lines predominantly arise from photodissociation regions (PDRs), and not from shocked regions. The line widths determined from our Fabry-Perot data also suggest that the FIR lines arise from relatively quiescent PDR gas, as opposed to shocked gas. Our results are in reasonable agreement with predictions from PDR emission models, allowing the estimation of the density of the emitting layers by comparison with the model results. On the other hand, the comparison with predictions of the emission from J-type and C-type shocked regions suggests that detected lines do not come from shocks. The [C II] line flux has been used to measure the mass of the low-excitation atomic component in PPNe, since this transition has been found to be a useful model-independent probe to estimate the total mass of these PDRs. The derivation of the mass formula and assumptions made are also discussed.

Key words: atomic data - stars: AGB and post-AGB - (Stars:) circumstellar matter - stars: mass-loss - (ISM:) planetary nebulae


1 Introduction

The very fast evolution from the AGB to the planetary nebula (PN) stage produces very important changes in both the central star and the surrounding envelope, during a transition time as short as $\sim$1000 yr. The star evolves from a large and cool red giant to a tiny and very hot blue dwarf. At the same time, the cool circumstellar envelope becomes a bright and highly excited planetary nebula. The chemical composition of the envelope changes significantly. AGB circumstellar envelopes are molecule rich and molecular emission is the main probe for their mass, dynamics, and shape. On the other hand, PNe are mostly composed of highly ionized atoms, due to the strong UV emission from their central stars; the nebular emission is therefore dominated by recombination lines (e.g. H$\alpha$) and forbidden lines of ionized atoms (e.g. [O III]). Highly excited atomic lines are also emitted from shocked regions in post-AGB nebulae. See Kwok (1993) and Pottasch (1984) as general references of this circumstellar evolution.

The objects in the intermediate evolutionary stage, protoplanetary nebulae (PPNe), often show intermediate properties between those kinds of objects. Many PPNe are intense emitters of CO lines, but in others the CO emission is very weak or even undetected. A few relatively evolved PPNe or young PNe (like M2-9) already show emission from ionized gas. The transition from molecular gas toward ionized gas must occur through a phase of PDR (photo-dominated or photodissociation region), in which the molecules have been dissociated but the gas (e.g. H) is largely neutral (e.g. Tielens & Hollenbach 1985). In the late stellar evolution, this region of low-excitation atomic gas must be a characteristic of protoplanetary nebulae. It is also important to note that the well known presence of shocks in PPNe and young PNe could play a role in the molecule dissociation, leading to the formation of relatively wide regions of atomic-rich gas (Hollenbach & McKee 1989). Therefore, low-excitation atomic gas may be dominant in both PDRs and shocked regions.

The low-excitation atomic gas in PPNe and young PNe had been scarcely studied before the arrival of the systematic observations with the ISO satellite. The main reason is that, when the temperature is low, atoms only emit in the far-infrared (FIR), by means of their fine-structure forbidden lines. Few works studied the properties of FIR lines in evolved objects. The supergiant $\alpha$ Ori was theoretically studied by Rodgers & Glassgold (1991). Some PNe have also been studied through Kuiper Airborne Observatory observations of some lines, like [O I]63 $\mu $m, [O I]145 $\mu $m and [C II]158 $\mu $m; see Dinerstein (1991) and Dinerstein et al. (1995).

The young PN NGC6302 has been studied from ISO observations of FIR atomic lines (Pottasch & Beintema 1999). In this work only highly ionized atoms were considered, mainly yielding a study of the properties of the inner H II region. The PDR around Betelgeuse has been revisited by Justtanont et al. (1999) through FIR lines of Fe+, Si+ and O0, who compared the new ISO observations with the model developed by Rodgers & Glassgold (1991). The observations of [ CI]609 $\mu $m by Huggins et al. (1994), in agreement with those of HI by Bowers & Knapp (1987), show that CI is an important constituent of the gas and is probably the major carrier of carbon from the chromosphere to the outer envelope, exceeding its number of atoms by a factor $\sim$5 the number of CO molecules. However, Betelgeuse remains the only O-rich star with a wind containing detectable CI; note that in C-rich sources CI seems to come from photodissociation of molecules other than CO (Knapp et al. 2000) that are not abundant in O-rich envelopes. HI has been also observed in Mira, probably caused by photodestruction of H2 by interstellar UV radiation (Bowers & Knapp 1988); we also note that Mira's hot companion (Karovska 1999) could contribute to molecular dissociation. Finally, fluorescent or absorption optical and UV lines of relatively heavy and rare atoms, like K, Na, and Mn, are also observed in envelopes around some red stars (mainly red supegiants and C-rich AGB stars, e.g. Eriksson et al. 1986; Guilain & Mauron 1996), but under physical and chemical conditions very different from those discussed here.

In spite of these papers, our general problem, the presence of low-excitation atomic gas in evolved nebulae, remained to be studied, particularly from the observational point of view. The purpose of our work is a systematic study of the fine-structure emission of low-excitation atoms by means of ISO observations. We present a quite complete set of observations and, after comparing with theoretical calculations and discussing the main nebular parameters that enter the interpretation of such lines, study the origin and properties of the low-excitation atomic gas in evolved nebulae. Far-infrared [O I], [C II], [N II], [Ne II], [Si II], [S I], [Fe I] and [Fe II] lines were observed in a sample composed of 24 objects, mostly PPNe but also including for comparison some AGB stars and PNe. Our results are presented in two papers, in one of them we discuss the observations and astrophysical results for carbon-rich objects (Fong et al. 2001, hereafter Paper I, in this volume); this second paper is devoted to the case of oxygen-rich stars. The separation of our sources in these two classes is mostly motivated because theoretical calculations of PDR models are very different. Both the necessary treatments of the chemistry and the obtained physical parameters are very different for the O-rich and C-rich sources. In fact, while the O-rich models used here have been developed from the work of Tielens & Hollenbach (1985), C-rich PDR models have been shown for the first time in our work in Paper I (Latter & Tielens in preparation).


 

 
Table 1: Observational parameters
Source OFF RA (J2000) DEC (J2000) AOT $T_{\rm int}$ Obs. Date
OH26.5+0.6   18:37:32.5 -05:23:59.0 LWS02 804 2mar97
IRAS18348-0526 $\surd$ 18:37:32.5 -05:18:59.0 LWS02 666 2mar97
        SWS02 970 2mar97
Mira   02:19:20.7 -02:58:26.2 LWS04 1070 04jul97
IRAS02168-0312, oCeti            
Betelgeuse   05:55:10.3 07:24:25.0 LWS02 1524 12sep97
IRAS05524+0723, $\alpha$ Orionis $\surd$ 05:55:10.3 07:29:25.0 LWS02 664 12sep97
        SWS02 970 09sep97
RSct   18:47:29.0 -05:42:16.6 LWS02 1814 19sep96
IRAS18448-0545 $\surd$ 18:47:28.9 -05:37:16.5 LWS02 912 19sep96
        SWS02 968 19sep96

AFGL2343

   19:13:58.6 00:07:30.6 LWS04 1060 02oct96
IRAS19114+0002 $\surd$ 19:13:58.5 00:12:30.6 LWS04 528 02oct96
    19:13:58.5 00:07:31.6 SWS02 862 02oct96
        SWS07 1106 02oct96
HD161796   17:44:55.4 50:02:38.4 LWS04 1024 18oct96
IRAS17436+5003       SWS07 1808 20aug96

89Her

   17:55:25.1 26:02:58.6 SWS02 570 23sep96
IRAS17534+2603            
M1-92   19:36:18.9 29:32:50.0 LWS01 2204 19apr97
IRAS19343+2926       LWS02 814 19apr97
Minkowski's Footprint $\surd$ 19:36:18.7 29:37:49.9 LWS02 548 19apr97
        LWS04 832 19apr97
        LWS04 1308 19apr97
        SWS02 968 19apr97
        SWS07 7712 25apr97
M2-9   17:05:37.9 -10:08:32.4 LWS04 1388 23sep96
IRAS17028-1004 $\surd$ 17:05:37.8 -10:04:32.4 LWS04 816 23sep96
Butterfly Nebula       SWS02 1046 29sep96
        SWS07 2840 23sep96
Hb12   23:26:14.7 58:10:54.6 LWS02 592 27aug97
IRAS23239+5754       SWS07 1244 31jan97
Mz-3   16:17:12.6 -51:59:08.2 LWS04 2174 10sep96
IRAS16133-5151 $\surd$ 16:17:12.3 -51:54:08.2 LWS04 1332 10sep96
        SWS07 2130 10sep96
NGC6302   17:13:44.4 -37:06:11.2 LWS04 656 06oct96
IRAS17103-3702 $\surd$ 17:13:44.6 -37:11:11.2 LWS04 528 06oct96
        LWS04 686 30mar98
        SWS07 1668 12oct96
        SWS07 766 20mar97


2 ISO observations and data analysis

We have observed a sample of 12 O-rich evolved objects, mostly PPNe but also including a few PNe and AGB stars for comparison. The observed sources are OH26.5+0.6, Mira, Betelgeuse, RSct, AFGL2343, HD161796, 89Her, M1-92, M2-9, Hb12, Mz-3, and NGC6302 (see Table 1). Betelgeuse is a red supergiant and AFGL2343 a probable hypergiant (deJager1998). We have included AFGL2343 in our sample because, like other hypergiants, it has ejected a dense envelope with similar characteristics to those of PPNe (e.g. Hrivnak et al. 1989). Also we observed off-source positions to determine the contribution from interstellar cloud emission.

Our purpose was to study low-excitation atomic gas through detections of the following atomic fine-structure lines: [O I] (63.2 $\mu $m, 145.5 $\mu $m), [C II] (157.7 $\mu $m), [N II] (121.9 $\mu $m), [Si I] (68.5 $\mu $m, 129.7 $\mu $m), [Si II] (34.8 $\mu $m), [S I] (25.2 $\mu $m), [Fe I] (24.0 $\mu $m, 34.7 $\mu $m) and [Fe II] (26.0 $\mu $m, 35.3 $\mu $m). For that we used both ISO spectrometers, LWS (43-196.7 $\mu $m) and SWS (2.4-45 $\mu $m), with different optical elements, grating and Fabry-Perot (FP). Particularly we used the following Astronomical Observation Templates (AOTs), which are described in Paper I: LWS01, LWS02, and SWS02 corresponding to grating modes, and LWS04 and SWS07 to Fabry-Perot. Only the Fabry-Perot spectrometers, LWS04 and SWS07, allowed us to obtain enough spectral resolution ($\sim$35 km s-1 and 10 km s-1 respectively) to get some information about the kinematic behavior of the emitting gas. The typical rms obtained, in units of 10-12 erg cm$^{-2}\,$s$^{-1}~\mu$m-1, ranges from 0.1 (with the SWS02) to 1000 (with the SWS07). Note that the intensity in the peak of the most intense lines that we have detected is $\sim$10-8 erg cm$^{-2}\,$s$^{-1}~\mu$m-1 for PNe, and $\sim$10-9-10-10 erg cm$^{-2}\,$s$^{-1}~\mu$m-1 for PPNe. This shows the difficulty of the detections, especially with the Fabry-Perot modes. For a few sources, we also present observations of the line [Ne II]12.8 $\mu $m, which have been described in Paper I (Appendix A). Note that in PDRs the photons can not ionize Ne, so that [Ne II] emission probably comes from H II regions. (The case of [N II] could be similar.) We present these data in order to analyze the kinematical behavior in those regions further in than PDRs, what could give us some information in comparison with the profiles of the lines that come from PDRs.

In Table 1 we present observational parameters, such as coordinates, the AOTs used, and both integration time and date of every observation. We have marked with a $\surd$ the second column (headed by OFF) when also off-source points were observed, and in those cases the off-source coordinates are shown. The sources have been always ordered according to the temperature of the central star increasing (in following sections we will see the convenience of this). In the first column of Table 1 we give the most usual name of each source, followed by other names often found in the literature, including the IRAS name. After this table every source will be named only by its most usual name.

In Table 2 we show the observational data results of the complex reduction, which is outlined in Paper I and which uses the packages LIA, OSIA, and ISAP. We give the AOT or mode of observation, the wavelength ($\mu $m) of the observed transition, the total flux ( $F_{\rm obs}$) of every detected line (in units of 10-13erg cm$^{-2}\,$s-1) with its corresponding error range ($\sigma$), and the noise (rms) of the observed intensity (in units of 10-12erg cm$^{-2}\,$s$^{-1}~\mu$m-1). ISAP gives $F_{\rm obs}$ and $\sigma$ from a Gaussian fit of the observational data. Undetected lines are shown as 3$\sigma$ upper limits in the column headed by Flux. An asterisk in the last column of the table indicates that these lines were taken from ground observations. Double and triple asterisk indicates that those data were obtained by other authors.


 

 
Table 2: Observational results. (a) ISM origin (see Sect. 2.1). (**) Data from the ISO Data Archive
SourceAOTLine Fluxrms
    10-13 erg10-12 erg
  ($\,\mu$m) cm2scm$^{2}~\mu$m
OH26.5+0.6S02[Fe I]24.042<610
  [S I]25.249<610
  [Fe II]25.988<810
  [Fe I]34.714<23
  [Si II]34.815 $24 \pm 3^{\rm a}$3
  [Fe II]35.349<47
 L02[O I]63.184 $62 \pm 10^{\rm a}$3
  [O I]145.530<100.6
  [C II]157.741 $430 \pm 5^{\rm a}$0.4
OffL02[O I]63.184$69 \pm 3$1
  [C II]157.741$366 \pm 5$0.4
MiraL01[O I]63.184$70 \pm 10$**
  [C II]157.741<4**
 L04[O I]63.184<50200
  [C II]157.741<3060
BetelgeuseS02[Fe I]24.042$35 \pm 4$20
  [S I]25.249$25 \pm 4$20
  [Fe II]25.988$339 \pm 8$40
  [Fe I]34.714<59
  [Si II]34.815$115 \pm 4$10
  [?]34.98$20 \pm3$9
  [Fe II]35.349$90 \pm 4$20
 L02[O I]63.184$193 \pm 6$2
  [N II]121.889<30.2
  [Si I]129.682<30.1
  [O I]145.530 $2.7 \pm 0.5$0.1
  [C II]157.741$12 \pm 1$0.1
OffL02[O I]63.184<80.9
  [C II]157.741 $6.2 \pm 0.6$0.07
RSctS02[Fe I]24.042<0.92
  [S I]25.249<12
  [Fe II]25.988<0.51
  [Fe I]34.714<23
  [Si II]34.815 $7 \pm 2^{\rm a}$4
  [Fe II]35.349<23
 L02[O I]63.184 $18 \pm 3^{\rm a}$0.8
  [N II]121.889 $6.1 \pm 0.6^{\rm a}$0.07
  [Si I]129.682<10.06
  [O I]145.530<20.1
  [C II]157.741 $45 \pm 1^{\rm a}$0.09
OffL02[O I]63.184$14 \pm 3$0.8
  [Si I]129.682<20.1
  [C II]157.741 $47.0 \pm 0.4$0.05



 
Table 2: (continued) Observational results. (a) ISM origin (see Sect. 2.1). (**)Data from the ISO Data Archive
SourceAOTLine Fluxrms
    10-13 erg10-12 erg
  ($\,\mu$m) cm2scm2$\mu $m
AFGL2343S02[Fe I]24.042<510
  [S I]25.249<48
  [Fe II]25.988<48
  [Fe I]34.714<710
  [Fe II]35.349<710
 S07[S I]25.249<9400
  [Si II]34.815<10300
 L01[O I]63.184<20**
  [C II]157.741 $13 \pm2^{\rm a}$**
 L04[O I]63.184<100500
  [Si I]68.473<100400
  [N II]121.889<2060
  [Si I]129.682<4080
  [O I]145.530<2040
  [C II]157.741<4070
OffL04[O I]63.184<100400
  [C II]157.741<5080
HD161796S07[S I]25.249<10600
  [Fe II]25.988<201000
  [Si II]34.815<10300
 L04[O I]63.184<60300
  [O I]145.530<1020
  [C II]157.741<2050
89HerS02[Fe I]24.042<0.61
  [S I]25.249<12
  [Si II]34.815<68
 L01[O I]63.184<9**
  [N II]121.889<3**
  [O I]145.530<1**
  [C II]157.741< 2**



 
Table 2: (continued) Observational results. (b) Significant ISM contribution (see Sect. 2.1). (*) Ground observations, see Appendix A in Paper I. (***) Data from Liu et al. (2001)

Source

 AOTLine Fluxrms
     10-13 erg10-12 erg
   ($\,\mu$m) cm2scm2$\mu $m
M1-92 --[Ne II]12.8<5*
  S02[Fe I]24.042<0.71
   [S I]25.249<0.50.9
   [Fe II]25.988 $5.9 \pm0.5$2
   [Fe I]34.714<35
   [Si II]34.815$20 \pm2$5
   [Fe II]35.349<23
  S07[Si II]34.815<6200
  L01[O I]63.184 $41 \pm4^{\rm b}$0.1
   [C II]157.741 $7 \pm1^{\rm b}$0.2
  L02[O I]63.184 $29 \pm5^{\rm b}$2
   [O I]145.530<20.1
   [C II]157.741 $8.5 \pm0.6^{\rm b}$0.05
  L04[O I]63.184<20100
Off L02[O I]63.184$20 \pm3$1
   [C II]157.741$15 \pm1$0.1
M2-9 S02[Fe I]24.042<12
   [S I]25.249<0.81
   [Fe II]25.988$26 \pm2$4
   [Fe I]34.714<47
   [Si II]34.815$63 \pm3$7
   [Fe II]35.349$12 \pm2$6
  S07[Fe I]24.042<10500
   [S I]25.249<10700
   [Fe II]25.988<20900
   [Fe I]34.714<10300
   [Si II]34.815$90 \pm10$400
   [Fe II]35.349<20500
  L01[O I]63.184$510 \pm10$***
   [O I]145.530 $19.3\pm0.9$***
   [C II]157.741$40 \pm1$***
  L04[O I]56.311<100700
   [O I]63.184$560 \pm40$400
   [Si I]68.473<80300
   [N II]121.889<3070
   [Si I]129.682<2040
   [O I]145.530<3060
   [C II]157.741<4070
Off L04[O I]63.184<3001000
   [Si I]129.682<1030
   [C II]157.741<3050
Hb12 --[Ne II]12.814$240 \pm 3$*
  S07[S I]25.249<301000
   [Si II]34.815$38 \pm 10$400
  L02[O I]63.184$72 \pm 5$2
   [O I]145.530 $6.7 \pm 0.6$0.09
   [C II]157.741 $45 \pm 2^{\rm b}$0.2
Off L01[O I]63.184$9 \pm 2$***
   [O I]145.530<2***
   [C II]157.741$28 \pm 1$***



 
Table 2: (continued) Observational results. (b) Significant ISM contribution (see Sect. 2.1). (***) Data from Liu et al. (2001)
Source AOTLine Fluxrms
     10-13 erg10-12 erg
   ($\,\mu$m) cm2scm2$\mu $m
Mz-3 S07[Fe I]24.042<10600
   [S I]25.249<201000
   [Fe II]25.988<10500
   [Si II]34.815<9300
  L01[O I]63.184 $220 \pm 10$***
   [N II]121.889$111 \pm 5$***
   [O I]145.530$7 \pm 1$***
   [C II]157.741 $160 \pm 3^{\rm b}$***
  L04[O I]63.184<100300
   [N II]121.889$76 \pm 8$200
   [O I]145.530<2030
   [C II]157.741 $129 \pm 7^{\rm b}$8
Off L01[O I]63.184$56 \pm 3$***
   [N II]121.889$45 \pm 4$***
   [O I]145.530<3***
   [C II]157.741$204 \pm 3$***
  L04[O I]63.184<80300
   [C II]157.741$138 \pm 6$100
NGC6302 S07[S I]25.249<201000
   [Fe II]25.988<9400
   [Si II]34.815 $230 \pm 10$400
  L01[O I]63.184 $2900 \pm 100$***
   [N II]121.889$91 \pm 6$***
   [O I]145.530$118 \pm 5$***
   [C II]157.741 $250 \pm 10^{\rm b}$***
  L04[O I]63.184 $3200 \pm 100$600
   [O I]145.530$98 \pm 8$20
   [C II]157.741 $260 \pm 20^{\rm b}$70
Off L01[O I]63.184$40 \pm 10$***
   [N II]121.889<6***
   [O I]145.530<4***
   [C II]157.741$137 \pm 6$***
  L04[O I]63.184<100500
   [C II]157.741<90200


2.1 ISM contamination

Let us now discriminate when the detections of the source observations come from the envelopes or from the ISM, by comparison of both source and off-source observations. In case that off-source transitions were detected with a total line flux higher than half of the flux obtained on-source, we have concluded that the emission comes from galactic interstellar clouds. When both FP and grating modes were used to observe the same line, we have taken the observations from grating modes to calculate the flux, $F_{\rm obs}$, because of the better sensitivity of those modes. We have compared the intensities of all the LWS-FP (L04) data presented here with those of LWS-grating (L01 or L02) observations, including data from the ISO data archive or from Liu et al. (2001) (except for the off-source observations of M2-9). We only give these grating data when they are relevant to determine the origin of the emission. Some SWS-FP (S07) data have not been compared with any kind of SWS-grating data. Note that in a few cases the FP intensities are not compatible with the grating data, due to the poor sensitivity of the FP.

We did not observe [Si II] nor [Fe II] in off-source points. So when [Si II] was detected but the [C II] and [O I] were assumed to come from ISM, we have supposed that also such detections arise from galactic clouds in the ISM. Those are the cases of OH26.5+0.6 and RSct. However for a similar case in M1-92, we have assumed that the [Si II] and [Fe II] emission comes from its envelope. First note that the [Si II]34.8 $\mu $m/[Fe II]25.9 $\mu $m ratio is quite different when both transitions come from galactic clouds or from one of our sources. In M2-9, where both lines have been found to come from the envelope, we obtained a ratio equal to 2.4, that is similar to that ratio of 3.4 found in M1-92. Usually in ISM this [Si II]/[Fe II] ratio is much larger. For instance, from our RSct observation we got galactic contamination, where such a ratio is higher than 14. Fuente et al. (2000) found a ratio higher than 6.1 in prototypical PDRs of the ISM. Moreover, note also that from the M1-92 observation we got an [O I] detection quite more intense than that from the off-source observation. We accordingly conclude that although we have strong galactic contamination, part of the detected fine-structure line emission comes from M1-92. Another particular case is Betelgeuse, where in spite of the off-source detection of [C II], we believe that its envelope emits through all the transitions (see Sect. 4). For NGC6302 and for Hb12 we think that the [C II] detection is real, in spite of the off-source emission, since the on-source intensity is twice as intense and other lines are detected from the nebula (see also Sect. 3.2). Note also that the [O I]63 $\mu $m/[C II]158 $\mu $m intensity ratio is much higher when the emission comes from our evolved objects than when it comes from the ISM. In all the off-source detections such a ratio is <1, whereas for source detections [O I]/[C II] is > or $\gg$1. A large [Si II]/[O I] ratio can also help us to identify source emission. In Mz-3 the same FIR lines were detected in both the nebula and an off-source point, but from the very different [O I]/[C II] ratios observed in both points it follows that part of the emission must come from the nebula. We have checked that contamination probably comes from the Galactic Center (discussion in Sect. 3.2 and Liu et al. 2001). Finally there are two detected lines, [O I]63 $\mu $m in Mira and [C II]158 $\mu $m in AFGL2343, that have not been confirmed by observations from off-source points. In these cases we use the [O I]/[C II] ratios to infer that Mira is probably emitting through [O I]63 $\mu $m, but that the [C II] line of AFGL2343 comes from ISM. (Note that such lines are grating data found in the public ISO archive, whereas our FP observations were not sensitive enough to detect them.)


  \begin{figure} \par\includegraphics[width=15cm,clip]{HR2319F1.ps}\end{figure} Figure 1: Comparison of the observed data and the convolved model fit (solid)
Open with DEXTER

3 Fabry-Perot line profile analysis

For our sources we expect expansion velocities from 15 km s-1 to 25 km s-1, and even more if the known post-AGB outflows also emit through these lines. Only from the FP modes (LWS04 and SWS07) we can obtain kinematical information (see the spectral resolutions in Sect. 2). Among the oxygen-rich sources we detected lines by means of FP modes in M2-9, Mz-3, Hb12 and NGC6302. Despite our conclusion that the Mz-3 emission is very contaminated (see Sect. 2), the profiles of its lines have been analyzed, including that detected in the off-source observation. In Table 3 we show the lines detected by FP modes in those sources, and the line parameters obtained by different fit procedures.


 

 
Table 3: Line fitting parameters
  Convolved Model Line Fit  ISAP Gaussian Fit  12CO Line Parameters
            
SourceLineVLine CenterPeak FluxTotal Flux VTotal Flux $V_{\exp}$ $V_{\rm LSR}$
  (HWHM)( $V_{\rm LSR}$)10-11 erg10-13 erg (HWHM)10-13 erg (HWZP) 
  (km s-1)(km s-1)cm2 s $\,\mu$mcm2 s (km s-1)cm2 s (km s-1)(km s-1)
            
            
M2-9[Si II]34.8$15\pm4$$77\pm3$$160\pm30$$65\pm26$ $22\pm2$$90 \pm10$ 780
 [O I]63$25\pm9$$75\pm3$$390\pm80$$640\pm270$ $30\pm1$$560 \pm40$   
            
Mz-3[N II]121$51\pm12$$-50\pm6$$17\pm2$$77\pm24$ $53\pm2$$76 \pm 8$ 6(2-1)-17
 [C II]158$37\pm2$ $-62\,\pm<3$$27\pm1$$130\pm8$ $40 \pm1$$129\pm7$   
(Off) $41\pm3$ $-62\,\pm<3$$23\pm1$$120\pm10$ $46\pm1$$112\pm7$   
            
Hb12[Ne II]12.8$24\,\pm<1$ $1\,\,\pm<1$$890\pm10$       
 [Si II]34.8$19\pm9$$-6\pm5$$100\pm40$$47\pm43$ $15 \pm1$$38 \pm 10$ 16[N II]-2
          (Core) 
NGC6302[Si II]34.8$24\pm3$$-32\pm1$$430\pm40$$250\pm50$  $21.5\pm0.4$$230 \pm 10$ 23(2-1)-40
 [O I]63$26\pm3$ $-32\,\pm<3$ $2000\pm100$ $3500\pm400$  $35.5\pm0.4$ $3200 \pm 100$   
 [O I]145$23\pm5$$-27\pm3$$31\pm2$$110\pm20$ $30\pm1$$98 \pm 8$   
 [C II]158$31\pm7$$-23\pm3$$61\pm5$$240\pm60$ $37\pm1$$210\pm20$   


3.1 Line profile fits

Since the observed lines are slightly broader than the instrumental profile of the FP spectrometers, we can try to deconvolve such an instrumental contribution in order to estimate the real kinematical profile of the emitting gas. So, for those lines spectrally resolved we have convolved a parametrized initial flat-top parabolic profile with the known instrumental response, using the method described in Paper I. From the comparison of this convolution with the observed data we have obtained parameters of the emission profile, and so of the kinematics of the emitting gas. In Fig. 1 we present some fits between the convolved model lines and the observed data. In Table 3 the results of such a procedure are also shown. In the Cols. 3, 4, 5 and 6 of that table we give the parameters of the theoretical emission lines whose convolution with the instrumental profile best fits to the observed data (shown in Fig. 1). They are the half width at half maximum of the line (km s-1), the central velocity (LSR), the intensity at the maximum, and the line total flux. In the next two columns of the table we give results of the Gaussian fits performed with ISAP, without removing any instrumental contribution. Such results are the integrated flux of the line and the equivalent expansion velocity of the emitting region. Finally we show data on 12CO lines found in the literature, except for Hb12 where parameters of [N II] emission are shown. The comparison with those will help us to determine the origin of the emitting low-excitation atomic regions, PDRs or shocks.

3.2 Kinematics of the low-excitation atomic gas

PDRs lie at the interface between the atomic and the molecular gas, so we would expect that the FIR cooling lines associated with circumstellar PDRs to have outflow velocities that are comparable to the molecular expansion velocities seen in 12CO. The main component of the CO line profiles traces the quiescent gas remnant of the old AGB envelope expanding isotropically at $\sim$15-20 km s-1. On the other hand, in many PPNe we can find a striking bipolar structure indicating the presence of strong shocks between fast bipolar post-AGB winds and the AGB envelope that was expanding much slower. In principle, shocks can also dissociate the molecular gas. If the emission of low-excitation atomic gas comes from those shocked regions, we expect expansion velocities $\sim$100 km s-1.

The expansion velocities we derived from the convolved model fits are in general comparable to those observed in CO, taking into account the large uncertainties of the deconvolution process. This suggests that the atomic line emission in general arises from PDRs instead of shocked regions, where higher velocities would be expected. Detailed discussions of the line fits and fit parameters obtained for individual objects are given below.

In some cases we infer information on the emitting atomic region from the LSR line velocity. Taking into account that the LWS-FP and SWS-FP wavelength calibration is $\sim$10 km s-1  and $\sim$3 km s-1, respectively, we can only consider velocity discrepancies greater than the calibration errors to be significant in the line center comparisons.

M2-9 -- The expansion velocity of M2-9 from the 12CO(J=1-0) line (see Zweigle et al. 1997) is relatively small when compared with typical AGB expansion velocities. The outflow velocity of the [O I] 63$\,\mu$m  line is 3.5 times larger than the 12CO value, which is concentrated in a clumpy torus. The velocities obtained from both the [O I] and [Si II] lines are very similar to those found for the main components of H$\alpha$ (Trammell et al. 1995), that expand bipolarly. This contrast in velocities suggests the presence of some shocked gas contribution to the FIR line emission, but the low velocity values involved indicate that no strong shock has taken place in the emitting region.

Mz-3 -- Both FP lines, [C II]158$\,\mu$m and [N II]122$\,\mu$m, most likely originate from the ISM because: 1) The [C II]158 $\,\mu$m  line was detected at the off-source position with roughly equal strength as pointing at the source, 2) the fitted model line centers are offset from the systemic $V_{\rm LSR}$ of the central star by $\sim$40 km s-1, and 3) the large width can be explained from its location near the Galactic Center (Galactic coordinates: 331.73, -1.01), where molecular clouds along the line of sight typically exhibit such broad lines profiles (see Bronfman et al. 1989). Anyway, the intensities of the reliable grating lines suggest that part of that emission must come from the source (Sect. 2.1). That could also broaden the line.

Hb12 -- 12CO  has not been detected in Hb12, so we are using the core of the optical [N II] line (Miranda & Solf 1989) and our [Ne II] data for comparison. For [N II], we have only taken the contribution of the compact 0.9'' central region expanding at $\sim$16 km s-1. The [Si II] line width compares reasonably well with the parameters of the optical [N II] and IR [Ne II] lines.

NGC6302 -- All of the convolved model FIR line widths compare well with the 12CO  line values, with the exception of the [C II]158$\,\mu$mline. This is 5-8 km s-1 broader than the other FIR lines and than the 12CO  line. From the grating data we got that the [C II] line flux is twice as large as that from the off-source point. However the less sensitive FP observations failed to detect [C II] at the selected off position. As we discussed in Sect. 2, we think that the [C II] detection in NGC6302 is real, although the interstellar contamination (Galactic coordinates: 349.51, 1.06) may broaden the line. The differences among line widths and the offset from the systemic $V_{\rm LSR}$ ($\sim$8-15 km s-1) may be related to an insufficient sensitivity of the FP spectrometers or to the interstellar contamination.

4 Dependence of the atomic line emissionon the stellar parameters

In this first analysis we relate the observed data of our nebulae to the evolutionary stage of the stars that are in their center. Note that the evolution of a star from the AGB to a white dwarf is connected with changes of some stellar parameters, such as the increase of the effective temperature $T_{\rm eff}$.

In Table 4 we present the spectral types of the central stars, their $T_{\rm eff}$, the distances to them, and their luminosities. Those parameters are relevant for this first interpretation of our data. They were chosen after an extensive review of the bibliography and the corresponding references are shown in the caption of the table. The luminosity (L) is always taken from measurements of the total spectral energy distribution of the stellar radiation and consistently with the adopted distance (D). Since sources are ordered by increasing stellar surface temperature, the first (two) objects are AGB stars, the last one is a hot young planetary nebula (PN), and most of them (eight without Betelgeuse, that we will discuss below) are PPNe (i.e. nebulae around post-AGB stars cooler than 50000 K).


 

 
Table 4: Parameters of the central stars for the oxygen-rich envelopes. Those for the carbon-rich sources are in Paper I. We classify as PPNe those post-AGB objects cooler than 50000 K. References: (S) Simbad; (H) Hipparcos data; (a) Kholopov et al. 1985; (b) Lorenz-Martins & De Araujo 1997; (c) Van Langevelde et al. 1990; (d) Justtanont et al. 1996, Le Sidaner & Le Bertre 1996; (e) Feast 1996; (f) Skinner et al. 1997; (g) Shenton et al. 1994; (h) Alcolea & Bujarrabal 1991; (i) Hrivnak et al. 1989; (j) Reddy & Hrivnak 1999; (k) Meixner et al., in preparation; (l) Waters et al. 1993; (m) Alcolea & Bujarrabal 1995; (n) Calvet & Cohen 1978; (o) Bujarrabal et al. 1998a; (p) Swings & Andrillat 1979; (q) Schwartz et al. 1997; (r) Ciatti et al. 1978; (s) Zhang & Kwok 1991; (t) Cahn et al. 1992; (u) Cohen et al. 1978; (v) Bujarrabal & Bachiller 1991, Quinn et al. 1996; (w) van der Veen et al. 1989; (x) Ashley & Hyland 1988; (y) Gómez et al. 1989; (z) Pottasch et al. 1984
name     Spectral Temperature D L comments
        type (K) (kpc) (103 $L_{\odot}$)  
                 
OH26.5+0.6       M $^{\rm S,a}$ 2000$^{\rm b}$ 1.4$^{\rm c}$ 20$^{\rm d}$ AGB star
Mira       M7III$^{\rm S}$ 3000 $^{\rm S,a}$ 0.13$^{\rm H}$ 8 $^{\rm e}$ AGB star
Betelgeuse       M2 Iab$^{\rm S}$ 3500 $^{\rm S,a}$ 0.13$^{\rm H}$ 50$^{\rm f}$ UV excess, supergiant
RSct       G0-K2$^{\rm g}$ 5000$^{\rm g}$ 0.43$^{\rm H}$ 4.6$^{\rm h}$ RVTau variable
AFGL2343       GIa$^{\rm i}$ 6750$^{\rm j}$ 5.6$^{\rm H}$ 600 $^{\rm i,j}$ hypergiant, PPN?
HD161796       F2-5Ib$^{\rm i}$ 7000$^{\rm i}$ 1$^{\rm H}$ 3$^{\rm k}$ IRAS17436+5003
89Her       F2Ibe $^{\rm h,l}$ 7000 $^{\rm h,l}$ 0.98$^{\rm H}$ 9 $^{\rm h,m}$ high-latitude yellow giant
M1-92       B1$^{\rm n}$ 22000$^{\rm n}$ 2.5$^{\rm o}$ 10 $^{\rm n,o}$ Minkowski's Footprint
M2-9       Be,BI $^{\rm n,p}$ 25000 $^{\rm n,p}$ 0.64$^{\rm q}$ 0.55$^{\rm q}$ Butterfly Nebula
Hb12       WN7$^{\rm r}$ 32000$^{\rm s}$ 2$^{\rm t}$ 3$^{\rm s}$ PPN, young PN
Mz-3       O9$^{\rm u}$ 32000$^{\rm u}$ 1.8$^{\rm v}$ 5$^{\rm w}$ PPN, young PN
NGC6302       pec.,Ne $^{\rm x,S}$ 300000 $^{\rm x,y}$ 2.2$^{\rm y}$ 13 $^{\rm y,z}$ young PN



  \begin{figure} \includegraphics[angle=-90,width=17.9cm,clip]{HR2319F2.ps}\end{figure} Figure 2: Distribution in the H-R diagram of the observed sources
Open with DEXTER

One of the main results of this work is obtained by direct comparison of the observed data with the stellar parameters (listed in Table 4), which are shown in Fig. 2. In that figure we can see the distribution of stars, whose envelopes were observed, in an H-R diagram. In order this analysis to be more reliable, our sample has been enlarged with similar observations from 12 C-rich evolved stars, which are presented in Paper I. The nebula detected in some of the observed atomic transitions are marked with filled symbols (see Table 2 and analysis in Sect. 2).

Figure 2 shows that only nebulae surrounding stars with an effective surface temperature $\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\displaystyle ... 10000 K are detected, and moreover note that, as $T_{\rm eff}$ increases above 10000 K, the line emission is more intense and the number of lines detected is higher. The only exceptions to this statement are the detection of many fine-structure lines in Betelgeuse, and the probable detection of [O I]63 $\mu $m in Mira. Betelgeuse is a red supergiant star which is known to show a strong excess of UV emission, probably produced by a hot chromosphere (Skinner et al. 1997). This particular excess causes intense atomic emission, studied in detail by Rodgers & Glassgold (1991) and Justtanont et al. (1999). On the other hand, Mira has a hotter binary companion that could be the responsible of the detected line (Sect. 1).

To strengthen the dependence of the emission on the stellar temperature, note that among emitters and non-emitters there are objects with very similar characteristics from the point of view of the morphology, presence of shocks, chemistry, and total nebular mass, but with different low-excitation atomic emission and different $T_{\rm eff}$ of the central star. Note the case of AFGL618 and AFGL2688, that is discussed in Paper I. Here we mention the lack of detection in AFGL2343, because this source is a hypergiant with a large luminosity and a very massive envelope, and in HD161796, that also is expected to show a dense inner envelope (see Sect. 5). However, as for the rest of the non-detections, the central stars of these nebulae are quite cool. Finally we note that the distances to the hottest stars in our sample are not systematically smaller than those to cool stars, so the non-detections are not due to a bias in the source selection yielding higher dilution factors for cool stars.

We interpret this result as showing that the total mass of the region of low-excitation atomic gas strongly depends on the temperature of the star in the center of the nebula. This argues that such a region is a PDR. Thus, the molecular dissociation, which gives rise to this atomic region, is mainly due to stellar UV photons, and not to shocks nor interstellar radiation.

5 Comparison with PDR emission theory

5.1 PDR model and parameter analysis

We have just seen that the good correlation between the emission by low-excitation atomic lines and the stellar temperature strongly suggests that this emission is associated with the formation of a PDR in the nebulae, caused by UV radiation from the central stars. Accordingly, to validate this argument we will first compare our measured line intensities with the predictions of PDR models. For such a purpose we have used the last improved version of the models of Tielens & Hollenbach (1985), that was published by van den Ancker (1999). The models solve the chemical and thermal balance in the gas, and predict the emission from these regions primarily as a function of the incident far-ultraviolet (FUV) flux (G) and of the density (n) in that region. These models were developed for the interstellar medium and assume ISM gas abundances, in particular $\rm C/O <1$. While these abundances may not be completely appropriate for these O-rich nebulae, they are adequate for this global comparison. Hollenbach et al. (1991) discussed these models for lower-density regions (102 cm $^{-3}\leq~n~\leq~$105 cm-3) and lower incident FUV fluxes (G caused by cooler stars), which is appropriate for some of our sources. Moreover Spaans et al. (1994) showed that, although the amount of FUV photons produced by a cool star ($\sim$6000 K) is much lower than that of a hot star ($\sim$30000 K), the efficiency of the heating through very small grains and large molecules is decreased by no more than an order of magnitude. So the temperature at the front edge of the PDR does not fall bellow 125 K for a central star of $\sim$6000 K. The conditions in which the low-excitation atomic gas exists, favors especially the emission of fine-structure transitions, since the involved collisional energies are similar to these fine-structure energies. Tielens & Hollenbach (1985) also showed that fine-structure lines are the most important coolants in atomic PDRs, the heating being due to far-ultraviolet photons. Those lines are excited collisionally at a range of temperatures of $\sim$102-103 K.

Predicted intensities are presented in the same format that is used by van den Ancker (1999), since the sample of calculations used here is very similar to that presented by this author and, moreover, this representation stresses the presence of the two main parameters in the models, the value of the FUV intensity at the edge of the PDR, G, and the representative density n.


 

 
Table 5: Parameters used for the comparison of our observations with PDR models and derived densities (Sect. 5). Moreover we show low-excitation atomic gas masses derived from the Eq. (6), with the approximations there assumed, which have been also multiplied by the corresponding correction factor $F_{\rm c}$. Details about this calculations are in Sect. 7. Mass estimates of the molecular regions from 12CO emission and of the ionized gas are given by comparison. ISM cont indicates that the mass upper limit cannot be very restrictive because of a strong ISM contamination. References: (a) Justtanont et al. 1996; (b) assumed values (few stellar radii); (c) Skinner et al. 1997; (d) Alcolea & Bujarrabal 1991; (e) Hawkings et al. 1995; (f) Meixner et al. 2000; (g) Bujarrabal et al. 1998b; (h) Zweigle et al. 1997; (i) Hora & Latter 1996; (j) Quinn et al. 1996; Górny et al. 1999; (k) Gómez et al. 1989; (l) Josselin et al. 2000; (m*) mass of the CI region, Huggins et al. 1994; (n) Bujarrabal et al. 1990; (o) Bujarrabal et al. 2000; (p) Huggins et al. 1996; (q) Miranda & Solf 1989; (r) Bujarrabal & Bachiller 1991
name $\theta_i$ Ri (4 $\pi\theta_i^{2}$)-1 $F_{\rm UV}$ G n   M $M_{\rm mol}$ $M_{\rm ion}$  
  ('') (cm) (sr-1)   (G0) (cm-3)   ($M_{\odot}$) ($M_{\odot}$) ($M_{\odot}$)  
                       
OH26.5+0.6 0.02$^{\rm a}$ 5 1014 8.5 1012 5.3 10-12 0.1            
Mira 0.26$^{\rm b}$ 5.0 1014 5.0 1010 1.8 10-7 1 103     <2 10-4 0.00015l    
Betelgeuse 0.5$^{\rm c}$ 9.7 1014 1.4 1010 3.2 10-6 3 104 >106   2 10-4 0.0004$^{\rm m*}$    
RSct 6$^{\rm d}$ 3.9 1016 9.4 107 0.00046 3 102 <104   <2 10-3 0.002$^{\rm n}$   ISM cont
AFGL2343 1.2$^{\rm e}$ 1.0 1017 2.35 109 0.0080 9 104 <3 104   <1 4.8$^{\rm o}$   ISM cont
HD161796 0.8$^{\rm f}$ 1.2 1016 5.3 109 0.0099 4 104 <105   <0.05 0.68$^{\rm o}$    
89Her 0.1$^{\rm d}$ 1.5 1015 3.4 1011 0.0099 8 106 <106   <5 10-3 0.0043$^{\rm o}$    
M1-92 1.5$^{\rm g}$ 5.6 1016 1.5 109 0.57 3 105 <104   <0.2 0.9$^{\rm g}$   ISM cont
M2-9 3$^{\rm h}$ 2.9 1016 3.8 108 0.65 8 104 3 104   0.04 0.005$^{\rm h}$ 0.004$^{\rm p}$  
Hb12 7$^{\rm i}$ 2.1 1017 6.9 107 0.75 1 104 2 103   0.3 <0.001$^{\rm p}$ 0.015$^{\rm q}$  
Mz-3 7$^{\rm j}$ 1.9 1017 6.9 107 0.75 2 104 3 103   <0.7 0.5$^{\rm r}$ 0.2$^{\rm p}$ ISM cont
NGC6302 5$^{\rm k}$ 1.6 1017 1.35 108 0.99 1 105 105   1.3 0.1$^{\rm p}$ 0.2$^{\rm p}$  


In order to compare our observations with the predictions, we need first to define both initial parameters, G and n, and then we will determine them for our sources. We use for such a purpose:

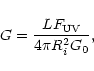\begin{displaymath}G = \frac{L F_{\rm UV}}{4 \pi R_i^2 G_0}, \end{displaymath} (1)

where L is the luminosity of the source (see Table 4); $F_{\rm UV}$ is the fraction of the star's output in the far ultraviolet, where stars are assumed to emit as black bodies with known temperatures (Table 4); G0 equals $\rm 1.6~10^{-3}\,erg\,s^{-1}~cm^{-2}$, a unit of average interstellar radiation field flux in the far ultraviolet energy range, from 6 eV to 13.6 eV (Habing 1968); and Ri is the inner radius from the star to the PDR in the circumstellar envelope. Note that the calculated value for G is independent of the distance assumed because both L and Ri2 depend directly on the distance squared, D2.

According to the above $F_{\rm UV}$ definition, such a parameter is the ratio of the black body intensity integrated from photon energies of 6 eV and higher to the black body intensity integrated over all photon energies. We assume that photon energies higher than 13.6 eV are eventually down converted to the far ultraviolet in the inner H II region.

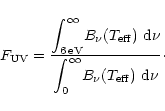\begin{displaymath}F_{\rm UV} = { \displaystyle{\int_{\rm 6\,eV}^\infty} B_\nu(T... ...aystyle{\int_{0}^\infty} B_\nu(T_{\rm eff})~{\rm d}\nu} \cdot \end{displaymath} (2)

The effective temperature of the central star is the only parameter in $F_{\rm UV}$. Analysis by Spaans et al. (1994) shows that using a black body as opposed to a model atmosphere gives reasonably accurate results for our purposes.

The PDR inner radius, Ri, is derived from the distance and the angular inner radius, $\theta_i$. We determined $\theta_i$ using images and/or spectral energy distribution fits from the literature. Ideally what we want is an image of a PDR gas tracer, such as H2 2.12 $\mu $m emission. If an H2 2.12 $\mu $m vibrationally excited emission image existed, we adopted the average radius of the H2 emission ring or shell for the inner radius because the H2 emission in a PDR is expected near the surface of the PDR (that we have only found for Hb12). However, if we could not find an H2 2.12 $\mu $m image, then we assumed that the PDR exists outside the H II region and inside the molecular gas region. From a molecular gas region tracer, we use the inner radius of a CO line map (e.g. M2-9 or M1-92). From an H II region tracer, we use the outer radius of either a radio continuum image if one exists (as for NGC6302), or of an optical image as a last resort (e.g. Mz-3). In the case of proto-planetary nebulae, where there is no ionized gas and moreover the CO line images do not resolve the inner radii, we use the inner radii of dust shells as imaged in the mid-infrared or fitted to marginally resolved mid-infrared images and spectral energy distributions (e.g. AFGL2343 or HD161796). In a few cases, only fits from spectral energy distributions exist (as for RSct and 89Her) and we adopt inner radii from them. For AGB stars we took a standard value for $R_i\sim 5~10^{14}$ cm, that corresponds to the typical extent of the inner regions of the envelope previous to dust condensation. This value is assumed because of the uncertain positioning of the inner edge in this case and must be considered as just representative and very uncertain. (Though we show these parameters for both AGBs, see Table 5, finally we will not compare these undetected cases with the model predictions.)

The theoretical models used here, both those for PDRs and for shocked regions (see next section), predict the emitted intensity $I_{\rm calc}$(erg cm-2 s-1 sr-1) from a plane-parallel layer. In order to compare with our measured line fluxes, $F_{\rm obs}$(erg cm-2s-1), we need to find an equation that relates both quantities geometrically. In our case, the geometry is better approached by a spherical shell. When the spherical layer is sufficiently thin, we can assume that the intensity predictions for the plane-parallel slab can be applied to the radial intensity of the shell. In the optically thin limit, that applies to most of the observed lines (Sect. 7.1), the total flux emitted by the shell, $F_{\rm obs}$, and this radial intensity, $I_{\rm calc}$, are related by the equation:

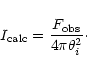\begin{displaymath}I_{\rm calc} = {F_{\rm obs} \over 4 \pi \theta_i^2}\cdot \end{displaymath} (3)

The conversion factor here comes from the geometrical relation between the shell width and its volume. In an optically thick case, this factor depends on the macroscopic velocity field. When the macroscopic velocity is much higher than the local velocity dispersion and the logarithmic velocity gradient is equal to one, the conversion factor is approximately the same as in Eq. (3). (As we will see in Sect. 7.1, this kinetics is likely present in our sources and will be indeed used in our excitation calculations.) It can be shown that for larger (smaller) representative values of the logarithmic gradient, the conversion factor from $F_{\rm obs}$ to $I_{\rm calc}$ is larger (smaller) than our canonical formula. Accordingly we will systematically use Eq. (3) to convert our measurement to intensities comparable to the model predictions. We also note that, as we saw for G, this conversion factor is independent of the distance to the source. Hence, our comparison of observations with the PDR and shock theory is independent of the distance to the source.

In Table 5 we show the adopted values for $\theta_i$(''), Ri(cm), and the calculated values of $F_{\rm UV}$ and G(G0). From the comparison of the data of every source with the predictions of the models for PDRs (see Fig. 3, and discussion below), we can derive typical densities for the emitting region, that are also shown in this table.


  \begin{figure} \par\includegraphics[width=17.5cm,clip]{HR2319F3.ps}\par\end{figure} Figure 3: Comparison of observations of fine-structure atomic lines with PDR model predictions. The compared sources are: (3) Betelgeuse, (4) RSct, (5) AFGL2343, (6) HD161796, (7) 89Her, (8) M1-92, (9) M2-9, (10) Hb12, (11) Mz-3, and (12) NGC6302. Detections are represented by filled circles and upper limits by open circles. Predictions of the models without including photoelectric heating are presented by an asterisk and a diamond, for calculations with n = 2.3105 and 107 cm-3, respectively, and G=105G0. See details in the text for the conversion of the observed fluxes into the predicted characteristic brightness
Open with DEXTER

5.2 Comparison with observations and discussion

Figure 3 compares theoretical curves from PDR theory with our data from the oxygen-rich envelopes for the nine observed atomic line transitions (shown in Table 2). The figure plots the predicted line intensity ( $I_{\rm calc}$) vs. the incident far-ultraviolet radiation at the edge of the PDRs (G, Table 5), for a set of different densities (n) and for every observed transition. To plot also our observations we have to calculate $I_{\rm calc}$ from the observed flux ( $F_{\rm obs}$ listed in Table 2) according to the Eq. (3). The sources are represented by numbers, according to the description of the figure caption. Detections are plotted as filled circles and non detections as open circles. For some sources, some of the transitions have been observed by different AOTs, then we have chosen the line intensities obtained by the grating spectrometers instead of those Fabry Perot, due to the worse sensitivity of these. When no flux was detected, we plot the upper limit from Table 2. When the line is detected in both the source and off-source positions at comparable levels, we take as an upper limit the absolute value of ON-OFF multiplied by 2. In this second case, our ability to detect the line is limited by confusion with the background. Without a line map of the region, it is difficult to assess the expected point-to-point variation in the background line emission. On the other hand, when the line flux of the source observation is bigger than twice the flux of the OFF observation, we assume that such an emission comes from the source, though contaminated. In that case we consider the flux emitted by the source as ON-OFF. Such are the cases of Betelgeuse and NGC6302 for the line [ CII]158 $\mu $m, already discussed in Sect. 2.1. Finally, for those sources with lines that do not have off-source observations, but we judge to be possibly originating from the ISM (e.g. [Si II] in OH26.5+0.6 and RSct) we simply do not plot the value because we have no way to evaluate an error. In Fig. 3 we have not represented observational data of envelopes surrounding AGB stars, because it is not expected to find PDRs produced by this kind of stars, not even for Mira, since in that case emission seems to be caused by its binary companion.

We conclude from Fig. 3 that the comparison between observations and PDR theory is quite satisfactory. The densities required to explain the data are quite compatible for the different lines. The adopted densities are given in Table 5. Note that the observed [Si II] intensities in O-rich sources are somewhat larger than predicted. This may be due to the low Si abundance assumed in the model, since a strong depletion onto grains of refractory material was assumed.

The main disagreement between our observations and these theory predictions is that PDR models, in the way we are using them, do not account for the strong contrast found between the atomic emission of nebulae around stars with more or less than about 10000 K of surface temperature (Sect. 4). As we can see in Table 5 and Fig. 3, the G values calculated for the different nebulae do not strongly decrease for stars cooler than 10000 K. In fact, since the envelopes of the cooler stars (with less $F_{\rm UV}L$) are nearer the center (less Ri), the far-ultraviolet radiation seen from the PDR (G) remains more or less the same. So, from this kind of representation ( $I_{\rm calc}$ vs. G and n, with $G~\sim~$constant) we only can attribute the non detections to that the emitting regions are very diffuse. On the other hand, we do not expect the gas to be systematically less dense in the nebulae surrounding the cooler stars. We know that some of the young PPNe observed (like HD161796 and AFGL2343) are very massive, and the gas in them is surely denser than it will be in the future, caused by the dilution associated with expansion. So in the inner part of the envelope we could expect a small PDR, but quite dense. The calculations seem not to be able to reproduce the PDRs in these young and cool objects.

The reason for this disagreement could be the initial assumptions of the models. G represents the number of UV photons with energy larger than 6eV, that are able to extract electrons from grains and contribute to photoelectric heating. However, the photodissociation of CO depends on the density of photons with energy over 11eV. The fraction of the UV radiation represented by G that is able to dissociate CO depends a lot on $T_{\rm eff}$, when the star is not very hot. Therefore, for relatively cool stars, our formulation is overestimating the rates of molecular photodissociation. Spaans et al. (1994) have shown that for $T_{\rm eff}$ between $\sim$10000 K and 30000 K (the value used by Tielens & Hollenbach 1985) the distribution of the kinetic temperatures and abundances through PDR does not vary a lot. But for $T_{\rm eff}$ smaller than $\sim$10000 K, the depth of the atomic-rich layer significantly decreases. Our simplified comparison with PDR models do not account for this phenomenon and, therefore, the predictions used in Fig. 3 can overestimate the atomic line intensities for $T_{\rm eff}\,<\,$10000 K.

Another factor to consider is that PDR models calculate the physical and chemical conditions in the gas assuming equilibrium, i.e. that the time evolution of the G and n values is small enough to allow the abundances to readapt to changes in these parameters. However, the equilibrium can be not always satisfied in PPNe, that are evolving very fast. As we see in the detailed calculations of the radiation field of cool stars by Spaans et al. (1994, see their Fig. 3), the characteristic photodissociation time of CO by a star cooler than 10000 K and $G\sim10^5\,G_0$ is $\sim$100-1000yr. This calculation holds for the unattenuated radiation field, so it is an upper limit to the true lifetimes in the regions emitting in atomic lines, that extend up to $A_{v}\sim2$ (Spaans et al. 1994, see their Fig. 8). Let us take as an example HD161796, with $T_{\rm eff}\sim7000$ K and $G\sim4~10^4\,G_0$ (Table 5). The expected CO lifetime for the unattenuated field is $\sim$500 yr. However, the radius of the inner shells (about 1.2 1016 cm) and the nebula expansion velocities (15 km s-1, from the CO profiles, excluding high-velocity outflows) suggest that the nebula left the AGB phase only about 250 yr ago. Moreover, it is obvious that during most of this time the stellar temperature was lower than the present value of 7000 K. Therefore, it is very probable that objects with stellar temperatures lower than $\sim$10000 K have not had time, during their life as PPNe, to photodissociate most of their molecular gas, even in the innermost nebular shells. This would indicate that the existing PDR models probably tend to overestimate the atomic line intensities for PPNe with stellar components cooler than 10000 K.

5.3 Photoelectric heating by O-rich grains

Since the physical nature of circumstellar dust grains around O-rich stars is not completely understood, the coupling between the FUV radiation field and the gas is unclear. For the O-rich PDR models, the photoelectric heating was assumed to be similar to the diffuse ISM, hence the photoelectric heating described in Tielens & Hollenbach (1985) was used. Such a formalism does not explicitly include the effects of PAH heating nor a grain size distribution; however, the effects of PAHs may have been implicitly included, since the dust properties were chosen to match the heating rate of the diffuse ISM. PAH features were seen in NGC 6302 (Beintema 1998), but their photoelectric contribution is probably insignificant. No PAH features are present in the spectra of the other sources in our sample. Very small (<100 Å) silicates could also heat the gas through photoelectric effect (Watson 1973). The sizes of circumstellar silicate grains are not well constrained. Assuming the grains found in O-rich environments are composed mainly of Mg-silicates, their lower size limit was theoretically derived to be $\sim$150 Å  (Salpeter 1974) and observationally modeled with a lower cutoff of $\sim$800 Å  in supergiants (Seab & Snow 1989). The smallest Mg-silicates are still larger than the 100 Å  limit, above which grains contribute negligibly to the photoelectric heating (Bakes & Tielens 1994). Thus, there is a distinct possibility that in O-rich nebulae there is no photo-electric heating because of the dust grain population.

We have briefly explored PDR model calculations in which the photoelectric heating is turned off. In this case, the gas heating is mainly driven by FUV pumping of H2, neutral carbon ionization and, further into the molecular cloud, collisions with dust grains. We computed three models with the same model parameters as the set of models we present here except that the photoelectric heating is turned off. We chose a typical incident $F_{\rm UV}$ flux for our sources, $G = 10^5\,G_0$, and three densities (n) of 103, 2.3 105, and 107 cm-3. The 2.3 105, and 107 cm-3 models are represented by an asterisk and a diamond respectively on the PDR model graphs (Fig. 3). The 103 cm-3 model results are not plotted on the PDR model graphs because the line intensities fall below the lowest intensity. In all three density cases, the calculated line fluxes for the models without photoelectric heating were at about a factor of ten lower than the models with photoelectric heating. The [OI] 63 and 146 $\mu $m lines show the most dramatic drop by a factor of 20 and 10, respectively.

The main reason for this drop in line intensity is a drop in kinetic gas temperature by at least a factor of ten. Photoelectric heating is by far the most important heating process in a PDR. Without photoelectric heating, FUV excitation of H2 followed by collisional deexcitation heats the gas. However, this process is only efficient at high densities (n=107 cm-3). In addition, this H2 heating is important only at the surface, dropping steadily until AV =2 where it becomes insignificant. The result is a much steeper temperature profile than when photoelectric heating is included. In fact, the temperature of the gas is quite low where most of the fine-structure line emission arises in a PDR with photoelectric heating. At the lower densities the situation is worse because the heating arises from the recombination of C+ and collisions with dust which results in very low temperatures ($\leq$40 K) incapable of producing significant fine-structure line emission.

If photoelectric heating is not important in these O-rich nebulae, then the average densities of detected sources would have to be around 107 cm-3 to produce these line emissions. This density is a factor of 10 higher than the highest density estimate for the C-rich evolved stars in which we know that photoelectric heating plays an important role because of the presence of PAHs (see Paper I). For their C-rich nebulae, NGC7027 and AFGL618, Justtanont et al. (2000) model the rotational CO lines and the atomic fine-structure lines as arising from a PDR associated with a halo of $\sim$105 cm-3 gas surrounding a denser toroid (107 cm-3). While the denser gas dominates the CO emission, its filling factor is too small to explain the observed fluxes of the atomic fine-structure lines and the latter almost exclusively originate in the lower density gas. Now, it would be curious if atomic fine-structure emission of the O-rich sources in our sample were to be associated with the denser regions while in the C-rich samples, the lower density gas dominated. Especially peculiar because we see a similar [O I]+[C II]/FIR ratio (i.e., a similar efficiency of heating of the atomic gas) in both samples. Hence it seems likely that photoelectric heating is important in the PDRs of these O-rich objects.

Now we have to consider what types of grains in an O-rich environment can produce photoelectric heating. In O-rich environments, the dominant grains expected to form are silicates and oxides, which are considered to be insulators. Grains composed of insulating material will not be subject to the photoelectric effect (Evans 1993), although low photoelectric yields have been measured in lunar dust ($\sim$50% silicate; Draine 1978). To account for the photoelectric heating required in these O-rich environments some sort of conducting grains must be present in sufficient abundance to produce the observed heating. One possible candidate is metallic Fe grains. Theoretically, at the pressures of circumstellar outflows, one expects the incorporation of Fe into the silicate structure to form Fe and Mg silicates. Observationally, there is also some indirect evidence for the incorporation of Fe in amorphous silicates. However, several of the sources in our sample (NGC6302, AFGL2343, HD161796, and 89Her) show evidence for crystalline Mg-rich, Fe-poor silicates ( $\rm Fe/Mg<0.05$; Molster 2000). The excess Fe may well be in the form of metallic iron, either expressed in the form of a metallic surface layer if the crystallization process took place after silicate formation, or in the form of separate iron particles if incorporation of the iron in the silicate structure was kinetically inhibited (Molster et al. 1999). Small iron grains or iron structures on small crystalline silicates might well be very efficient in photoelectric heating of the gas. In summary, we conclude that photoelectric heating is probably active in PDRs around O-rich post-AGB stars. Although the grain composition is uncertain in such an environment, the choice of ISM grain properties (as in the models by Tielens & Hollenbach 1985) seems reasonable.

6 Comparison with line emission theoryfor shocked regions

When the post-AGB fast wind ($\sim$100 km s-1) collides with the remnant of the AGB envelope, that has been expanding very slowly ($\sim$10 km s-1), typical chemical and physical processes of shocked regions start developing. Under these conditions, the shocked gas can also emit in atomic FIR lines. In principle a very large ratio of [O I]63 $\mu $m/[C II]158 $\mu $m ( $\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\displaystyle ...10) intensities could indicate that the emission comes from shocks instead of PDRs. On the other hand, when shocked regions emit strongly in ionized atoms, particularly in [Si II]35 $\mu $m, we can identify such shocks as J-type shocks. Few ions exist in C-type shocks, so their fine-structure emission is very weak. (A detailed description of J-type shocks and predictions for fine-structure line emission, in contrast with that expected from PDRs or from C-type shocks, was performed by Hollenbach & McKee 1989.) In order to compare with the shock theory curves we will use the same line intensities as calculated above for comparison with the PDR theory. In this case we need to plot $I_{\rm calc}$ vs. $\sum I_{\rm calc}$ for all detected lines to get information about the kind of shock capable of generating these intensities. The summation of line intensities is different for objects with detections and those without. For objects with detections, the summation of line intensities is the sum of only the detected lines; it does not include the upper limits for the non-detected lines in. For objects with non detections, the summation includes all the upper limits, except for the upper limits estimated from $\rm (ON-OFF)\times2$. These upper limits tended to be significantly higher than the others and would make the summation artificially high.

The theoretical curves are adapted from van den Ancker (1999) for both J- and C-type shocks, for all the observed lines. The theoretical predictions of the line [C II]158 $\mu $m and of [O I]63 $\mu $m are drawn in Fig. 4, respectively for J- and C-type shock models. The J-shock model extends over a shock velocity range of 40-100 km s-1, and over a particle density range of 103-106 cm-3. The C-shock model extends over 5-40 km s-1 and 104-106 cm-3.


  \begin{figure} \par\includegraphics[angle=-90,width=8.7cm,clip]{HR2319F4a.ps}\includegraphics[angle=-90,width=8.7cm,clip]{HR2319F4b.ps}\end{figure} Figure 4: Top: comparison of the observations of the line [C II]158 $\mu $m with model predictions for J-type shocks. Botton: comparison of the observations of the line [O I]63 $\mu $m with model predictions for C-type shocks. In both figures numbers represent sources according to Fig. 3. Comparison with the rest of the observed lines have been also performed, and are described in the text (Sect. 6). We indicate the shock velocity in km s-1 and the pre-shock density in cm-3. Sources are marked by diamonds when only upper limits were obtained for all lines ($\sum I$). Marks are filled (empty) for detected (undetected) lines
Open with DEXTER

The comparison of our data with the theory of atomic line emission from shock excited regions is obviously less satisfactory than it was with the PDR theory. The first impression of such a comparison with all the observed lines is that we cannot find definite shock characteristics that can explain the detected intensities (and upper limits) consistently for all lines observed in every source. Anyway, we note the difficulty of modeling shocked regions and so the unreliability of using predictions systematically. In the case of J-type shocks, the observed [C II] intensity (which is known to be a good tracer of PDRs) is too large for all the models here taken into account, even those with very high shock velocity. Although we found for NGC6302 and M2-9 quite large [O I]/[C II] intensity ratios, they do not seem to be large enough to be due to J-type shocks. Moreover, the intensities of the lines [Si II] and [S I] seem to suggest low shock velocities, contrary to what the [C II] line indicated. In the case of C-type shocks, there is a clear contradiction between the very low shock velocities suggested by the [O I] lines and that required to explained the [S I] line. C-type shocks do not explain the observed ionized atoms. (Note that circles in Fig. 4 represent sources that have been detected in some FIR line, so when we have upper limits only lower I are expected, but not lower $\sum I$.)

Finally we also note that the moderate velocities, deduced from our Fabry-Perot observations, comparable to those found from CO lines, do not suggest the presence of strong shocks in the atomic emission region (Sect. 3.2). Only for M2-9 we did infer some shock contribution, due to that the fine-structure lines are broader than the CO lines. The [O I]/[C II] ratio is $\sim$14, which is compatible with what is expected for shocks. Moreover we have detected intense [Si II] and [Fe II] lines, as would be expected from J-type shocks. So, we suggest that a part of the fine-structure emission from M2-9 is produced by shocks.

7 Calculation of the low-excitation atomic mass in PPNe

One of the highlights of this work is the calculation of the mass in the low-excitation atomic regions, since this is the first estimation of PDR masses in post-AGB envelopes. This low-excitation atomic region is practically coincident with the PDR: the region of photodissociation in which molecules, in particular CO, are dissociated but the gas is mostly neutral. Note that the interphase between exclusively molecular and low-excitation atomic regions is complex, because different molecules and atoms coexist. In this section, when we mention PDR we refer exclusively to the low-excitation atomic region, i.e. where CO is dissociated. On the other hand, it is known that in the H II region (the innermost layers, when it exists) the temperature rises rapidly (up to typically 10000 K) and the presence of high-frequency photons produce highly ionized atoms; in fact we can define "highly ionized atoms'' as those that require ionizing photons with an energy higher than 13.6 eV.

Probably the best tracer of this low-excitation atomic regions is the [C II] line emission at 157.7 $\,\mu$m, for its high abundance and extended presence in the PDR, and for the easiness of its analysis. It is known that C+ appears almost at the same time that CO is photodissociated, since the C0 region is very thin (e.g. Tielens & Hollenbach 1985). On the other hand, C+ itself has an ionization potential that is higher than that of H but (slightly) smaller than that of He. Therefore, C+ is soon photoionized in the H+ region, completely disappearing in the He+ one (e.g. Bowers & Deeming 1984).

The [C II]157.7 $\,\mu$m line is particularly well suited for measuring the emitting mass, i.e. the low-excitation atomic mass, in our nebulae if in addition the two following conditions are fulfilled. First, this transition corresponds to a small energy (91.2 K). According to the densities and temperatures that we expect in most nebulae (see Sect. 5 and Tielens & Hollenbach 1985), the excitation temperature $T_{\rm ex}$ of this line should be significantly higher than 91.2 K. This condition would allow us to calculate the total mass of the PDR independently of the excitation temperature of the line. Secondly, we need to know if this transition is optically thin. In principle the [C II] line is forbidden and therefore its opacity is expected to be low in all relevant cases, which will be also discussed below. If both conditions are fulfilled, the observed line intensity becomes practically independent of the density and temperature (see formulae below), depending only on the total emitting mass (provided that we know the relative abundance of carbon nuclei).

7.1 Justification of assumptions

In order to check the two above hypotheses, we have constructed a code able to calculate the excitation of the two fine-structure levels of C+. Since we are dealing with relatively cold material, we will neglect higher levels, so the statistical equilibrium equations must be applied to only two levels and one transition. The (eventual) effects of opacity are treated using the well known LVG or Sobolev approximation. For this we will assume that the logarithmic gradient of the macroscopic velocity is equal to 1, a value that greatly simplifies the calculations. The dynamics of PPNe are complex and it is not possible to define a typical velocity gradient in them. But in some well studied cases (see e.g. Bujarrabal et al. 1998; Olofsson et al. 1999), the bulk of the nebular material is found to be in expansion with a velocity increasing proportionally to the distance to the star, which supports the simplified velocity field assumed here. In any case, the LVG approximation takes into account the effects of opacity in a reasonable way and is known to yield a quite accurate description of the typical excitation state of a cloud, even if the conditions of applicability of the approximation are only marginally satisfied. (Of course, the LVG approximation cannot describe the line excitation when the opacity is extremely high, but as we will see this is not our case.) We will assume the universal abundance of carbon nuclei with respect to the total number density (also taken in the PDR calculations for O-rich objects): $X{\rm (C)} = 3~10^{-4}$. In the PDR (i.e. in our region of low-excitation atoms), we can take $X{\rm (C^+)}\sim X{\rm (C)}$, as discussed above.

The background radiation is assumed to be described by a blackbody field with 5 K temperature. Note that in a two-level atom the background radiation can always be approximated by the blackbody radiation law; the assumed value of the temperature corresponds to the increase with respect to the cosmic background expected for the typical FIR dust emission observed in our objects. We note that this assumption is relevant only for the weak [C II] emission corresponding to very low $T_{\rm ex}$ (and probably high opacity), a case that is particularly difficult to treat theoretically and that does not seem to occur in our nebulae.

For the collisional transition probability between the two levels of C+, J=3/2 and J=1/2, we take the simplified formulae given by Hollenbach & McKee (1989), based on calculations by Bahcall & Wolf (1968), Launay & Roueff (1977) and Flower & Launay (1977). For collisions with electrons, the e- abundance is assumed to be equal to that of C, since all electrons essentially come from the carbon ionization. It is easily verified that, under the conditions assumed here, the transition probabilities due to collisions with electrons are more than one order of magnitude smaller than those due to collisions with neutrals. Electron collisions are accordingly neglected in the calculations presented here. The H2 relative abundance in the PDRs may vary, depending on the depth in which the emitting gas is placed and the temperature of the exciting star. In any case, in most of the [C II] emitting gas in PDRs, hydrogen is in atomic form (Tielens & Hollenbach 1985; Spaans et al. 1994). We will assume that it is the case for our calculations for the generic case, but note that the difference with respect to other cases is small due to the small difference between the collisional rates for H and H2 collisions.

We have calculated excitation temperatures ( $T_{\rm ex}$) of the 157.7 $\,\mu$m line for a grid of densities and kinetic temperatures, where the $T_{\rm k}$ ranges between 100 and 1000 K, as predicted by PDR models (Tielens & Hollenbach 1985). The range of densities covers those estimated from the comparison of our observations with model calculations (Sect. 5). Our calculations indicate that in most of our cases (and also in those in Paper I), which show relatively high densities ( $\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\displaystyle ...103 cm-3), the excitation temperature is much higher than 91.2 K. Then, our first assumption for calculations of the total mass from [C II] data is satisfied. Below, we will discuss the corrections we can apply in the case of low-density PDRs to the simple calculation obtained with this approximation. We have checked with our LVG code and the universal abundance of C that the observed intensities can be explained with opacities clearly <1. On the other hand, we are going to use a simpler and perhaps more reliable procedure to discuss the low-opacity assumption, just only from the observed flux and an assumed excitation temperature. We will take as an example the case of our most intense emitter, NGC6302 (in principle the worst case). For its density, close to 106 cm-3, the excitation temperature is close to 500 K. The intensity emitted by the PDR, $I_{\rm calc}$ (erg cm-2s-1 sr-1, obtained from $F_{\rm obs}$), directly comparable to the PDR model output and observational data points in Fig. 3, is:

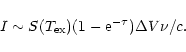\begin{displaymath}I \sim S(T_{\rm ex}) (1 - {\rm e}^{-\tau}) \Delta V \nu/c. \end{displaymath} (4)

S is the (representative) source function, $\tau$ is the opacity, $\nu$ is the transition frequency, and $\Delta V$ is the velocity dispersion of the atomic emission in this source, that we take $\sim$50 km s-1. Substituting those figures, we derive a low opacity $\sim$0.01. Therefore, we conclude that even in our most intense sources the opacity is lower than one. We can check that this argument can also be used for sources described in Paper I. For instance, the case of NGC7027 is quite similar to that of NGC6302 treated here, except for that the [C II] line is a little less intense and the line width is also smaller (see figures in Paper I). We also get for NGC7027 a [C II] opacity clearly lower than 1. Note that the fact that the lines are so broad (in comparison with ISM, with a few km s-1) is crucial for the [C II] emission to be very optically thin; indeed in models developed for PDRs in the ISM, the predicted opacities remain closer to unity. So the second assumption also seems to be fulfilled.

7.2 Mass formula

When both the opacity is low and the excitation temperature is high, the line emissivity is easily described. In the general case, the population of the second level can be written from the total particle density only knowing the statistical weight of every level, the assumed abundance X(C+), and the excitation temperature. The whole dependence on $T_{\rm ex}$ can be taken out through a function $F_{\rm c}(T_{\rm ex}$) that becomes 1 when $T_{\rm ex}\gg91.2$ K. Therefore substituting the energy separation between levels and the statistical weights (g1 = 2 and g2 = 4), when $T_{\rm ex}\gg91.2$ K the population of the second level becomes n2=2 n X(C)/3. So, in an optically thin and high excitation case, the number of photons emitted by an unit of volume of the PDR in a second is:

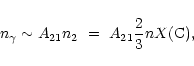\begin{displaymath}n_{\gamma} \sim A_{21} n_{2}~=~A_{21} \frac{2}{3} n X({\rm C}), \end{displaymath} (5)

where A21 is the Einstein coefficient for the spontaneous emission (we took A21 = 2.29 10-6s-1, Kaufman & Sugar 1986). Multiplying by the emitting volume and by the energy of each photon, taking into account the contribution of helium to the mean particle mass, and dividing by $4\pi D^{2}$, then we obtain $F_{\rm obs}$ from the total emitting mass M.

Therefore we can express M only from the detected $F_{\rm obs}$ of [CII]158 $\mu $m and the assumed distance, D, after substituting the rest of the known values (taking X(C)=310-4),

\begin{displaymath}M({\rm g}) = 4.64\,10^{43} F_{\rm obs}^{[{\mbox {\scriptsize... ...}]158~\mu {\rm m}}({\rm erg~cm^{-2}\,s^{-1}}) D({\rm kpc})^2. \end{displaymath} (6)

M is expected to be a good estimate of the total mass of the low-excitation atomic region in PPNe and young PNe.

We have mentioned that, when the excitation temperature is not very high, we should correct the above mass estimate multiplying by a certain correction factor $F_{\rm c}$. $F_{\rm c}\ge1$ always, and $F_{\rm c}\sim1$ for $T_{\rm ex}\gg91.2$ K. $F_{\rm c}$ can be calculated simply through the dependence of the population of the second level with $T_{\rm ex}$. Note that $T_{\rm ex}$ depends on the density and the kinetic temperature of the gas.

  \begin{figure} \par\includegraphics[angle=-90,width=8.8cm,clip]{HR2319F5.ps}\end{figure} Figure 5: Calculated values of the correction factor, $F_{\rm c}$, to multiply Eq. (6) in order to correct the simplified calculation of the mass for cases where the excitation temperature is not very high, usually because of the very low density of the gas
Open with DEXTER

In Fig. 5, we see the calculated values of $F_{\rm c}$ for a grid of parameters; the corrections are relatively low even for our sources with the lowest densities. For instance, for Hb12, that probably has a low representative density, $n\sim2~10^3$ cm-3, and taking a $T_{\rm k} = 300$ K (calculated by the PDR models for this source) we get a $F_{\rm c}\sim1.5$. Note that the correction factor does not depend a lot on the assumed kinetic temperature, provided that it is $\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\displaystyle ...100 K. However, for densities $\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\displaystyle ...102 cm-3, the C II emissivity becomes very low and the correction $F_{\rm c}$ becomes too high; under these circumstances the method is uncertain (because of the strong dependence of $F_{\rm c}$ on the physical parameters) and cannot in fact be applied, they correspond to regions from which the FIR [C II] line is very weak.

7.3 Masses of the low-excitation atomic gas

In the last columns of Table 5 we have listed for our sources the masses of the low-excitation atomic gas calculated in the way explained above, also taking into account the values of $F_{\rm c}$, as well as estimates of the molecular mass in those nebulae, obtained from CO line observations whose references are in the caption, and estimates of the ionized mass. Both molecular and ionized masses have been adapted consistently with our choices of distances to every source (see Table 4). In the cases where there was no detection of the [C II] line we have used the upper limits shown in the forth column of Table 2, or those obtained following the criterion explained in Sect. 5.2. The adopted correction factors were calculated from the densities determined from the PDR models fitting (Sect. 5), and assuming $T_{\rm k} = 500$ K. No correction was applied when $F_{\rm c}$ is smaller than 1.5 and for non detections, since due to the effects explained in Sect. 5, the density limits determined for most of those cases can be too restrictive. We had derived (see Sects. 2 and 3) that the observed [C II] emissions from NGC6302 and from Hb12 mainly come from the sources, although they are partly contaminated by ISM emission. So, to estimate its low-excitation atomic mass we have taken as $F_{\rm obs}$ (in Eq. (6)) the difference between the flux detected on and off-source, both from the grating spectrometer data. We followed the same procedure for Betelgeuse. For the red giants we only have very uncertain upper limits and so we did not fit them to the PDR models (Sect. 5). Therefore, we have not calculated masses for the their undetected PDRs. However we have estimated the atomic masses of Betelgeuse (and Mira) under our standard assumptions, in spite of the peculiar PDR, because of its intense FIR line emission. The atomic mass estimated for the envelope around Betelgeuse from our [C II] data (Table 5) is relatively low, although only a factor 2 smaller than the mass derived from [C I] (Huggins et al. 1994) and comparable to that deduced from other fine-structure lines (Justtanont et al. 1999; Rodgers & Glassgold 1991). This result may seem surprising, since the above authors suggest that the different lines come from quite different regions. We also note the relatively low atomic mass measured for M1-92 (Bujarrabal et al. 1998a,b), which is a known molecule-rich object ( $M_{\rm mol}\sim1$ $M_{\odot}$). For Mz-3 we have a poor mass upper limit because of the strong ISM contamination. However, for sources like M2-9 and 89Her, see Zweigle et al. (1997) and Alcolea & Bujarrabal (1995), in which the molecular mass is comparable to the atomic one, a global deficiency of (detected) nebular mass still exists. In the most evolved object of our sample, NGC6302, the atomic PDR mass is very high, representing the dominant nebular component.

8 Conclusions

We have observed atomic fine-structure lines in the far-infrared from 12 O-rich evolved stars including proto-planetary nebulae, as well as, for comparison, some red stars and young planetary nebulae. Considering also the analogous observations of 12 C-rich evolved stars by Fong et al. (2001), Paper I, we conclude that only nebulae that surround stars with $T_{\rm eff}\,\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\di... ...terlineskip\halign{\hfil$\scriptscriptstyle ... K have been detected. Among the observed PPNe there are objects with very similar characteristics from the point of view of the morphology, presence of shocks, chemistry, and total nebular mass, but with different $T_{\rm eff}$ of the central star and different atomic line intensities. This strengthens the dependence of the emission on the stellar temperature, and so seems to imply that low-excitation atomic emission comes from PDRs.

The comparison of our data with PDR line emission models is quite satisfactory. The main disagreement comes from the contrast of the emission from stars that are hotter and cooler that 10000 K, since models do not predict such a contrast. For the sources cooler than 10000 K models predict stronger atomic PDR emission than what has been observed. The origin of this seems to be that, for envelopes around cool stars, we compare our data with PDR models that can overestimate the number of photons capable of dissociating CO. Moreover the characteristic time of the CO dissociation is relatively long compared to the evolution time of the star from the AGB. This phenomenon cannot be accounted for in models that calculate the chemical abundances and gas temperature under equilibrium conditions.

The emission predicted by models of shocked regions cannot reproduce the observed line intensities consistently for all lines. Moreover, our observations with high spectral resolution indicate smaller velocities than expected in shocked regions. So we conclude that the contribution of shocked material to the observed emission by low-excitation atoms is only marginal.

We can calculate the total mass of the low-excitation atomic gas, from the detected [C II] flux, provided that we know the distance to the source and assuming a relative abundance of carbon nuclei. The calculation follows a simple formula and is argued to be quite model independent. The masses obtained in such a way for the observed young PN and a PPN are very high, namely Hb12 and NGC6302, $\sim$1 $M_{\odot}$. In these nebulae, most of the material seems to be forming a well developed PDR. However, in some PPNe, like M1-92 and HD161796, the PDR mass is very low, being the molecular gas the dominant component of the nebulae. In other objects, like M2-9 and 89Her, the mass of both the molecular and atomic gas is very low, and there is a global defficiency of the gas detected to date.

Acknowledgements
A. Castro-Carrizo and V. Bujarrabal have been partially supported by the CYCIT and the PNIE under grants PB96-104, 1FD97-1442 and ESP99-1291-E. D. Fong and M. Meixner have been supported by NASA JPL 961504 and NASA NAG 5-3350. M. Meixner has also been supported by NSF AST-97-33697. W. B. Latter and A. G. G. M. Tielens acknowledge additional support from NASA grant 399-20-61 from the Long Term Space Astrophysics Program. We are grateful to N. Trams, A. Heras and D. Kunze for their help in the analysis of the data. We also thank A. K. Speck for the enlightening discussions about properties of dust and J. Alcolea for his help during the first phases of the project. The ISO Spectral Analysis Package (ISAP) is a joint development by the LWS and SWS Instrument Teams and Data Centers. Contributing institutes are CESR, IAS, IPAC, MPE, RAL and SRON. OSIA is a joint development of the SWS consortium. Contributing institutes are SRON, MPE, KUL and the ESA Astrophysics Division.

References

 

Copyright ESO 2001