A&A 367, 388-404 (2001)
DOI: 10.1051/0004-6361:20010063
A. M. Hidalgo-Gámez1 - K. Olofsson1 - J. Masegosa2
1 - Astronomiska observatoriet, Box 515, 751 20 Uppsala, Sweden
2 -
Instituto de Astrofísica de Andalucía, CSIC, Apdo. 3004, 18080 Granada, Spain
Received 9 November 1999 / Accepted 18 October 2000
Abstract
Deep groundbased spectra of Hubble V and Hubble X, the two
largest and
brightest H II regions in the Local Group dwarf galaxy,
NGC 6822, are presented.
The extinction, excitation and ionization are studied
on scales as small as 4 pc.
The chemical composition of some elements within the regions
as well as possible small scale variations in the
abundances of helium, nitrogen, oxygen and neon over the face of the
two regions are investigated.
The detection of the emission lines
![]() OI
OI![]() and
and ![]() ClIII
ClIII![]() are probably related to shock-heating
from gas
ejected from supernova explosions and planetary nebula
ejections, respectively, although the
contribution to the total ionization is very small.
No significant differences in chemical composition was found
between Hubble V and Hubble X.
However, some small scale variations in the abundances of oxygen,
and possibly nitrogen and helium, over the face
of both H II regions were noted, although different physical
conditions could apply within the regions, such as local fluctuations in the temperature.
are probably related to shock-heating
from gas
ejected from supernova explosions and planetary nebula
ejections, respectively, although the
contribution to the total ionization is very small.
No significant differences in chemical composition was found
between Hubble V and Hubble X.
However, some small scale variations in the abundances of oxygen,
and possibly nitrogen and helium, over the face
of both H II regions were noted, although different physical
conditions could apply within the regions, such as local fluctuations in the temperature.
Key words: galaxies: evolution - galaxies: irregular - galaxies: stellar content - ISM: H II regions
Much effort has been devoted to the study of the chemical abundances of dwarf irregular galaxies (dI) (e.g. Pagel & Edmunds 1981; Ferguson et al. 1998). Most investigations focused on the measurement of the oxygen abundances of H II regions, with subsequent interpretation within the closed box model of chemical evolution (Tinsley 1978). It is usually assumed in these studies (Kinman & Davidson 1981; Shield 1990; Dinerstein 1990) that the metallicity of the H II regions is homogeneous on both small and large scales.
In contrast to the spiral galaxies, where important gradients in the chemical abundances are found (e.g. Belley & Roy 1992), the situation of the chemical homogeneity of the ISM in dI is still under debate. The absence of strong dynamical instabilities in dI, e.g. turbulent gas motions, make the mixing of the elements less efficient (Roy & Kunth 1995). To add to the complexity, the internal dynamics and star formation triggering processes and environments could imply a very different history of chemical evolution for each galaxy. For a number of galaxies studied, the difference in the oxygen abundances comparing H II regions are smaller than the error in the measurements, e.g. DDO 50 (Masegosa et al. 1991) and NGC 2366 (González-Delgado et al. 1994), while for some others the differences are larger, e.g. IC 10 (Lequeux et al. 1979) and WLM (Hodge & Miller 1995). One reason for the lack of agreement could be the relatively poor quality of the data used in the abundance determinations. This situation is greatly improved with the new observational facilities currently available and new studies of galaxies undergoing star formation, such as NGC 4214 (Kobulnicky & Skillman 1996) and NGC 5253 (Kobulnicky et al. 1997), have been carried out. For these two galaxies, no inhomogeneities along the slit were found, and only a local enhancement of nitrogen was detected in NGC 5253.
This paper focuses on the distribution of chemical elements
within two H II regions of the dI NGC 6822.
Similar studies were carried out
by Kobulnicky & Skillman (1996) and Kobulnicky et al. (1997).
The main difference between the latter studies and the
present investigation is that, here, the metallicity determination has been
limited to the locations in the H II regions where the emission
line
[OIII]![]() 4363 Å was detected, while in previous studies the
determination of the abundances were extended to the whole region observed.
For
those locations where the [OIII] line was not detected, Kobulnicky et al. used
an empirical method in the derivation of the oxygen abundances based on a
typical value of the electron temperature.
If the uncertainties associated
with the abundances from the empirical methods are too high, no firm
conclusions on possible abundance variations
can be drawn.
Another difference between the investigations by Kobulnicky &
Skillman (1996), Kobulnicky et al. (1997) and the one
presented here, concerns the size of the galaxies involved.
Both NGC 4214 and
NGC 5253 have optical radii of 5-6 times larger than NGC 6822,
the galaxy which is the subject of this investigation,
and the size might play an important role in the chemical homogenization of
the ISM.
In order to bring more clarity to the problem of the presence or
absence of chemical
inhomogeneities, good quality data, such as is presented here, should be
included in the investigation.
Another investigation is presently being undertaken by the authors which
includes
some other dwarf galaxies, such as IC 4662 and IC 10.
4363 Å was detected, while in previous studies the
determination of the abundances were extended to the whole region observed.
For
those locations where the [OIII] line was not detected, Kobulnicky et al. used
an empirical method in the derivation of the oxygen abundances based on a
typical value of the electron temperature.
If the uncertainties associated
with the abundances from the empirical methods are too high, no firm
conclusions on possible abundance variations
can be drawn.
Another difference between the investigations by Kobulnicky &
Skillman (1996), Kobulnicky et al. (1997) and the one
presented here, concerns the size of the galaxies involved.
Both NGC 4214 and
NGC 5253 have optical radii of 5-6 times larger than NGC 6822,
the galaxy which is the subject of this investigation,
and the size might play an important role in the chemical homogenization of
the ISM.
In order to bring more clarity to the problem of the presence or
absence of chemical
inhomogeneities, good quality data, such as is presented here, should be
included in the investigation.
Another investigation is presently being undertaken by the authors which
includes
some other dwarf galaxies, such as IC 4662 and IC 10.
NGC 6822 (DDO 209) is a Local Group dI with a barred structure (de Vaucouleurs et al. 1991). NGC 6822 was chosen because of its proximity to the Galaxy, which makes this object one of the best candidates for a thorough study of chemical composition. NGC 6822 is one of the best studied Local Group dI (e.g. Marconi et al. 1995; Gallart et al. 1996; Petitpas & Wilson 1998; Cohen & Blakeslee 1998). This galaxy is also the closest dI to the Milky Way at a distance of 0.48 Mpc (Hidalgo-Gámez & Olofsson 1998). The absolute magnitude is Mb = -14.75 and the optical radius is 1.08 kpc (Hidalgo-Gámez & Olofsson 1998). Recent observations at many different wavelengths have been performed; radio (Israel 1997), infrared (Gallagher et al. 1991), UV (Longo et al. 1991) and X-ray (Eskridge & White 1997). A total of 157 H II regions have been catalogued throughout the galaxy (Hodge et al. 1989).
The two largest and brightest H II regions, located at
the northern part of this elongated
galaxy, with only 320 pc separating them, are the
ones under study here:
Hubble V and Hubble X.
They have been selected because their large sizes and high surface
brightnesses offer a unique opportunity to study possible
variations in the chemical abundance of the elements within
the H II regions.
Even though they are the brightest regions in
NGC 6822 they are not comparable in luminosity to the most
powerful and bright H II regions observed such as the Orion nebula or 30 Dor.
The
H![]() luminosity of Hubble V is 4 1038 ergs-1, which is only
about 5
luminosity of Hubble V is 4 1038 ergs-1, which is only
about 5![]() of the Orion complex (Hodge et al. 1989).
These authors also determined
the optical sizes, which are 112 pc for Hubble V and 143 pc for Hubble X.
of the Orion complex (Hodge et al. 1989).
These authors also determined
the optical sizes, which are 112 pc for Hubble V and 143 pc for Hubble X.
The oxygen abundance of these two H II regions have previously been determined by e.g. Peimbert & Spinrad (1970), Lequeux et al. (1979), Pagel et al. (1980), Talent (1980), Skillman et al. (1989). In all these studies, relatively old instrumentation was used. Even though the mean chemical abundances of many elements of Hubble V and Hubble X agree well with the ones determined in those investigations (see Sect. 5.4), the older instrumentation could not allow spatially resolved studies of the abundances.
Because of the good quality of the data presented here, a two-dimensional mapping of Hubble V and Hubble X of regions of 4 pc could be performed and therefore details on small scales could be resolved. Apart from a determination of the elemental abundances of the two regions, a mapping of the extinction, excitation and ionization throughout both regions is possible, as well as a study of the spatial distribution of chemical elements throughout the regions. This concerns in particular nitrogen and oxygen which are the elements with the most reliable data.
The next section is devoted to the description of the acquisition of the data and its reduction. In Sect. 3 the analysis is outlined. Section 4 is devoted to the extinction determination as well as the correction for underlying stellar absorption in the spectra. The results and discussions are presented in Sect. 5. Conclusions are presented in Sect. 6.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig1.eps}\end{figure}](/articles/aa/full/2001/08/aa9350/Timg14.gif) |
Figure 1:
The continuum-subtracted H |
| Open with DEXTER | |
| H II region | PA | ||
| Hubble V | 19 |
|
270
|
| Hubble X | 19 |
|
270
|
Continuum-subtracted H![]() images of Hubble V and Hubble X
are presented
in Figs. 1a and b.
The observations were carried out on the 10th of August,
1997 with the ESO 3.6 m
telescope at La Silla, Chile.
EFOSC1 was used to obtain spectra as well as H
images of Hubble V and Hubble X
are presented
in Figs. 1a and b.
The observations were carried out on the 10th of August,
1997 with the ESO 3.6 m
telescope at La Silla, Chile.
EFOSC1 was used to obtain spectra as well as H![]() and
continuum
images.
The coordinates for the spectroscopical slit position centers and
position angles are given in Table 1.
The images were used as an aid for positioning the slit.
A
and
continuum
images.
The coordinates for the spectroscopical slit position centers and
position angles are given in Table 1.
The images were used as an aid for positioning the slit.
A
![]() pixel CCD (No. 26 in the ESO-listing) was used as a detector.
The total field-of-view of the CCD is
pixel CCD (No. 26 in the ESO-listing) was used as a detector.
The total field-of-view of the CCD is
![]() and the pixel size is 27
and the pixel size is 27 ![]() m.
Two grisms
were used for the observations.
They covered a range in wavelength
between
3720-5530 Å in the blue (grism 6) and 5150-6900 Å in the
red (grism 10).
The resolution was 8 Å for both grisms.
The original starting
wavelength of the grism of the blue spectral regions was 3740 Å and, in
order to
include the forbidden emission line
m.
Two grisms
were used for the observations.
They covered a range in wavelength
between
3720-5530 Å in the blue (grism 6) and 5150-6900 Å in the
red (grism 10).
The resolution was 8 Å for both grisms.
The original starting
wavelength of the grism of the blue spectral regions was 3740 Å and, in
order to
include the forbidden emission line
![]() OII
OII![]()
![]() 3727 Å, a displacement towards the blue
was introduced which resulted in a central wavelength of 4500 Å.
The slit, with a
width of 1
3727 Å, a displacement towards the blue
was introduced which resulted in a central wavelength of 4500 Å.
The slit, with a
width of 1
![]() 5 (in order to match the seeing conditions) and a length
of 3
5 (in order to match the seeing conditions) and a length
of 3
![]() 1 for the blue (the movable slit) and 3
1 for the blue (the movable slit) and 3
![]() 9 for the red, passed through
the H II regions in the E-W direction.
For the standard stars the slit was opened to 5''.
The total integration time for Hubble V was 50
9 for the red, passed through
the H II regions in the E-W direction.
For the standard stars the slit was opened to 5''.
The total integration time for Hubble V was 50![]() in the blue and 40
in the blue and 40![]() in
the red and for Hubble X, 40
in
the red and for Hubble X, 40![]() and 30
and 30![]() ,
respectively.
For the target objects,
the blue and red spectral regions were observed consecutively in order to
ensure that the same location in each H II region was observed.
Two subexposures were obtained in order to check for cosmic events.
The sky was clear at the zenith position but there were some clouds just
above the horizon. The seeing conditions were stable throughout the
night, in particular during the observations of NGC 6822 with a seeing of
1
,
respectively.
For the target objects,
the blue and red spectral regions were observed consecutively in order to
ensure that the same location in each H II region was observed.
Two subexposures were obtained in order to check for cosmic events.
The sky was clear at the zenith position but there were some clouds just
above the horizon. The seeing conditions were stable throughout the
night, in particular during the observations of NGC 6822 with a seeing of
1
![]() 25.
The airmasses were
1.22 and 1.09 for the blue and the red, respectively, for Hubble V.
The corresponding values for Hubble X were 1.03 and 1.06.
The observations were performed outside the paralactic angle.
Due to the rather low air masses, small, or no corrections for
differential refraction were applied.
It was found, following Table 2 of Fillipenko (1982), that the loss
of light in the vicinity of
25.
The airmasses were
1.22 and 1.09 for the blue and the red, respectively, for Hubble V.
The corresponding values for Hubble X were 1.03 and 1.06.
The observations were performed outside the paralactic angle.
Due to the rather low air masses, small, or no corrections for
differential refraction were applied.
It was found, following Table 2 of Fillipenko (1982), that the loss
of light in the vicinity of ![]() OII
OII![]()
![]() 3727 Å was 2%.
In such cases, corrections were made.
3727 Å was 2%.
In such cases, corrections were made.
| Line | Hubble V | Hubble X |
| (Å) | (%) | (%) |
| 61 | 41 | |
| 53 | 44 | |
| HeI |
81 | 47 |
| 75 | 50 | |
| H |
73 | 68 |
| H |
64 | 19 |
| 75 | 85 | |
| HeI |
67 | 68 |
| H |
15 | 12 |
| 22 | 33 | |
| 8 | 6 | |
| HeI |
81 | 49 |
| 94 | 94 | |
| H |
16 | 6 |
| 29 | 91 | |
| HeI |
40 | 42 |
| 67 | 29 | |
| 80 | 41 |
The data was reduced with the software package
MIDAS.
Bias and flat-fielding
were performed in the standard way, with bias-frames and continuum lamps.
Considering the negligible changes in the flat frames over several consecutive
nights, a
single flat frame for each grism was used, averaging a total of 19 and 23
flat-frames for the blue and red spectral regions, respectively.
No sky flats were performed and the spectral response of
the CCD was corrected by averaging the values in the spatial direction.
The final frames, obtained by dividing the normalized flat-fields by the
averaged ones, were
completely flat along the spatial direction but with some small structures in
the spectral direction, even though the median was 1.00 in all cases.
All the flat-frames were observed through the 1
![]() 5 slit.
He-Ar
lamps were used for the wavelength calibration.
Due to the long exposures
needed in order to obtain a high signal-to-noise ratio, 2-3
arc-frames were obtained during each night, with different inclinations in
order to check for flexures.
No flexures were found along the lines, nor in
the arc-frames or in the sky lines observed in the spectra.
The calibrations resulted in rms of 0.28 and 0.40 using the blue and red
grisms, respectively.
The sky subtraction was performed using the batch in MIDAS, where four
points were needed.
The method defined two regions of the sky, normally one at each side
of the emission region.
Hubble V was quite well centered on the slit and there
was a sufficient number of pixels for an accurate sky subtraction.
In the case of Hubble X,
a displacement was evident towards one edge of the slit and only 20 pixels
were available near this edge.
In any case, due to the large number of
pixels at the other edge, an acceptable sky subtraction could be performed.
Only
the sky lines located near 6300 Å remained.
The flux calibrations were performed with spectra of the standard stars
LTT 1788 and LTT 1020.
The accuracy of the calibrations was 5% in the blue
and 8% in the red spectral region.
The atmospheric extinction correction was
made using the tables of La Silla.
5 slit.
He-Ar
lamps were used for the wavelength calibration.
Due to the long exposures
needed in order to obtain a high signal-to-noise ratio, 2-3
arc-frames were obtained during each night, with different inclinations in
order to check for flexures.
No flexures were found along the lines, nor in
the arc-frames or in the sky lines observed in the spectra.
The calibrations resulted in rms of 0.28 and 0.40 using the blue and red
grisms, respectively.
The sky subtraction was performed using the batch in MIDAS, where four
points were needed.
The method defined two regions of the sky, normally one at each side
of the emission region.
Hubble V was quite well centered on the slit and there
was a sufficient number of pixels for an accurate sky subtraction.
In the case of Hubble X,
a displacement was evident towards one edge of the slit and only 20 pixels
were available near this edge.
In any case, due to the large number of
pixels at the other edge, an acceptable sky subtraction could be performed.
Only
the sky lines located near 6300 Å remained.
The flux calibrations were performed with spectra of the standard stars
LTT 1788 and LTT 1020.
The accuracy of the calibrations was 5% in the blue
and 8% in the red spectral region.
The atmospheric extinction correction was
made using the tables of La Silla.
One of the main goals of this paper is to study the spatial
distribution of chemical elements within the H II regions.
The two-dimensional
spectra (Figs. 2a and b, only available electronically)
were divided into three-row spectra (hereafter, 3r-spectra).
The spatial resolution of three pixels corresponds to a seeing
of about 1
![]() 5, since
the pixel size is 0
5, since
the pixel size is 0
![]() 61/pixel for EFOSC1.
A 3r-spectrum corresponds to a linear scale of
4.3 pc at the distance of NGC 6822.
The total number of 3r-spectra covering the H II regions was 44 for the
blue and 54 for the red spectral regions of Hubble V.
The corresponding numbers for Hubble X were 34 and 33.
The number of
3r-spectra are based on different lines in each spectral range,
H
61/pixel for EFOSC1.
A 3r-spectrum corresponds to a linear scale of
4.3 pc at the distance of NGC 6822.
The total number of 3r-spectra covering the H II regions was 44 for the
blue and 54 for the red spectral regions of Hubble V.
The corresponding numbers for Hubble X were 34 and 33.
The number of
3r-spectra are based on different lines in each spectral range,
H![]() in the red
and [OII]
in the red
and [OII]![]() 3727 Å in the blue, which are, normally, the
most conspicuous emission lines in this type of object.
A crucial task is to ascertain that, using both grisms, the pointing is towards
the same location within the H II regions.
The alignment of both the blue and the red was performed with the aid
of
the continuum between 5200 Å and 5400 Å which is the range where
the blue and the red regions overlap.
A displacement of 15 pixels resulted for Hubble V between the
blue and the red.
Even though the overlapping was not perfect
this resulted in a deviation of less than one pixel.
The situation is more favourable for Hubble X where a
displacement of only one pixel was necessary in order to align both
the and the red.
The problem with
overlap is quite common when one-arm spectrographs are used, such as EFOSC1.
This is due to small movements of the observational setup
(instrument+CCD+telescope) between the observations
using the blue and the red grisms.
3727 Å in the blue, which are, normally, the
most conspicuous emission lines in this type of object.
A crucial task is to ascertain that, using both grisms, the pointing is towards
the same location within the H II regions.
The alignment of both the blue and the red was performed with the aid
of
the continuum between 5200 Å and 5400 Å which is the range where
the blue and the red regions overlap.
A displacement of 15 pixels resulted for Hubble V between the
blue and the red.
Even though the overlapping was not perfect
this resulted in a deviation of less than one pixel.
The situation is more favourable for Hubble X where a
displacement of only one pixel was necessary in order to align both
the and the red.
The problem with
overlap is quite common when one-arm spectrographs are used, such as EFOSC1.
This is due to small movements of the observational setup
(instrument+CCD+telescope) between the observations
using the blue and the red grisms.
The faintest lines were considered real detections when the
intensity was
1![]() higher than the average noise level in the vicinity of the line.
Moreover, in order to estimate the uncertainties due to the determination
of the continuum level and to avoid misidentification of noisy peaks with
weak lines, each 3r-spectrum was analysed several times using several
different continuum levels.
Only spectral lines which were detected in two
of these were considered real detections.
At the resolution of 8 Å it was found that some of the
emission lines
were blended, especially
higher than the average noise level in the vicinity of the line.
Moreover, in order to estimate the uncertainties due to the determination
of the continuum level and to avoid misidentification of noisy peaks with
weak lines, each 3r-spectrum was analysed several times using several
different continuum levels.
Only spectral lines which were detected in two
of these were considered real detections.
At the resolution of 8 Å it was found that some of the
emission lines
were blended, especially ![]() SII
SII![]()
![]()
![]() 6716,6730 Å,
6716,6730 Å,
![]() NII
NII![]()
![]() 6548 Å with H
6548 Å with H![]() as well as
as well as
![]() OI
OI![]()
![]() 6300 Å with
6300 Å with ![]() SIII
SIII![]()
![]() 6312 Å.
For the blended
lines a special routine in the software was used which fits
two Gaussian
profiles to the doublet to provide the intensity of each line.
These intensities were
compared with those obtained from the transition
probability between lines of
the same ionization stage and the total intensity of the doublet.
Differences
in the intensity values were added to the uncertainties
(see Sect. 3.2).
In most cases, the agreement was good.
A set of intensities, normalized to the H
6312 Å.
For the blended
lines a special routine in the software was used which fits
two Gaussian
profiles to the doublet to provide the intensity of each line.
These intensities were
compared with those obtained from the transition
probability between lines of
the same ionization stage and the total intensity of the doublet.
Differences
in the intensity values were added to the uncertainties
(see Sect. 3.2).
In most cases, the agreement was good.
A set of intensities, normalized to the H![]() emission line, for
each 3r-spectrum was finally obtained.
Due to a difference of half a pixel between the blue and the red
spectral regions of Hubble V, the red region of each 3r-spectrum was
normalized to the
H
emission line, for
each 3r-spectrum was finally obtained.
Due to a difference of half a pixel between the blue and the red
spectral regions of Hubble V, the red region of each 3r-spectrum was
normalized to the
H![]() line intensities.
line intensities.
Another point of interest is how to derive the average
metallicity for each
H II region.
In order to reach an average, new spectra were obtained by
summing all the rows where the emission from the forbidden
line ![]() OIII
OIII![]()
![]() 4363 Å was detected.
These are named spatially-averaged spectra, and refer to the total nebular
emission
from each H II region within the slit.
They
correspond to a total of 51 rows for Hubble V and 33 for Hubble X, which give
total physical sizes of 215 pc and 139 pc, respectively.
The spatially-averaged spectra are presented in Figs. 3a and b.
4363 Å was detected.
These are named spatially-averaged spectra, and refer to the total nebular
emission
from each H II region within the slit.
They
correspond to a total of 51 rows for Hubble V and 33 for Hubble X, which give
total physical sizes of 215 pc and 139 pc, respectively.
The spatially-averaged spectra are presented in Figs. 3a and b.
![\begin{figure}
\par\includegraphics[width=8.8cm]{9350f3a.eps}\vspace*{2mm}
\includegraphics[width=8.8cm]{9350f3b.eps}\end{figure}](/articles/aa/full/2001/08/aa9350/Timg26.gif) |
Figure 3: The spatially-averaged spectrum of a) Hubble V and b) Hubble X. The figures are scaled in order to emphasize weaker spectral features |
| Open with DEXTER | |
For any conclusive answer regarding possible variations in the chemical abundance in H II regions, a careful estimate of the uncertainties of the continuum and line intensities is of the utmost importance. In this analysis, different sources of uncertainty have been considered: uncertainties in the level of the spectral continuum with respect to the line, uncertainties due to the different corrections (in particular the extinction correction), uncertainties introduced by the reduction procedure and uncertainties due to the blending of spectral lines. The uncertainty introduced by photon counting was found to be very small in the parts of the spectra devoted to the analysis. This is due to the low level of noise and this possible source of error is therefore neglected.
It was noticed that the major contributor to the uncertainty for each 3r-spectrum was the determination of the continuum level. The uncertainties were estimated using the dispersion of the raw intensity of each line. Even though the uncertainties associated with the extinction correction were important and accounted for in the error analysis, they were in most cases smaller than the uncertainties associated with the continuum.
The reduction procedure can also introduce uncertainties.
From our analysis it has been estimated that an important source of
uncertainty
in the resulting intensities is the deviation of
the response curve of the standard star from the observed flux data.
The deviations were estimated to be 8% in the vicinity of the
H![]() line, 4%
close to
line, 4%
close to ![]() OII
OII![]()
![]() 3727 Å and the
3727 Å and the
![]() OIII
OIII![]()
![]() 5007 Å line and 20% close to
5007 Å line and 20% close to
![]() SII
SII![]()
![]() 6716 Å.
6716 Å.
For the blended lines an additional error term was added.
In this case, the
lines were deblended by a special routine in the software.
This term takes into account the goodness of the deblending procedure
performed by the software.
Uncertainties of 49% for
![]() NII
NII![]()
![]() 6548 Å, 16% for
6548 Å, 16% for
![]() SII
SII![]()
![]() 6716 Å and 36% for
6716 Å and 36% for
![]() SII
SII![]()
![]() 6730 Å were obtained for Hubble V.
The corresponding uncertainties for Hubble X were 54% for
6730 Å were obtained for Hubble V.
The corresponding uncertainties for Hubble X were 54% for
![]() NII
NII![]()
![]() 6548 Å, 6% for
6548 Å, 6% for ![]() SII
SII![]()
![]() 6716 Å and 9%
for
6716 Å and 9%
for ![]() SII
SII![]()
![]() 6730 Å.
6730 Å.
All these uncertainties were summed for each spectrum.
Table 2 presents the error
percentage of the emission lines for each region.
It should be noted that
these numbers correspond to those 3r-spectra with the lowest signal-to-noise
ratio
in the emission line ![]() OIII
OIII![]()
![]() 4363 Å.
Therefore, they must be considered
as the maximum statistical errors affecting the 3r-spectra.
These spectra contain, mainly, the outer part of the H II regions
and the
errors at the central parts, which will be the
regions under consideration in this investigation (see Sect. 5.3), are smaller.
4363 Å.
Therefore, they must be considered
as the maximum statistical errors affecting the 3r-spectra.
These spectra contain, mainly, the outer part of the H II regions
and the
errors at the central parts, which will be the
regions under consideration in this investigation (see Sect. 5.3), are smaller.
Systematic errors are much more difficult to assess. These should, in particular, be introduced during observation. A possible source of error is bad columns on the CCD. No evidence of systematic errors was found during the course of this work although systematic errors cannot be completely ruled out.
In order to derive the abundances of the elements from the intensities of the lines, two main corrections must be applied: the spectra must be corrected for underlying stellar absorption and extinction.
The absorption
features arising from the stellar component can severely affect
some emission line intensities.
The absorption affects, mainly,
the Balmer lines but other lines are also affected.
In this analysis, an elaborate absorption correction was applied.
The line intensities were corrected using the expression of
McCall et al. (1985)
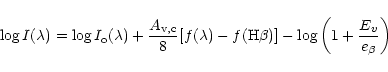
![\begin{eqnarray*}A_{\rm v,c} = {-8.0 \over \lbrack f(\lambda) - f({\rm H}\beta) ...
...a)}
\over 1 + {E_{\rm v}({\rm H}_\beta) \over e_\beta}} \right]
\end{eqnarray*}](/articles/aa/full/2001/08/aa9350/img33.gif)
Following the absorption correction a new normalization to the H![]() line and a reddening correction was applied.
line and a reddening correction was applied.
Besides the dust within the Galaxy, which has not been
corrected for in this analysis since this is only a matter of
scaling,
dust could reside within the emission region itself.
In addition, dust may be uniformly distributed outside the
nebula but within NGC 6822, and
made up of clumpy dust grains (Caplan & Deharveng 1986).
Since the extinction
is wavelength dependent, it will affect the relative intensities
of the lines and for an
appropriate determination of the physical properties of the
H II regions,
a correction for this effect should be applied.
There are two different
methods at hand.
The first is based on a comparison of the intensities from the
radio continuum and e.g. the optical H![]() line.
Since the extinction is negligible in the radio wavelength
region,
the total extinction in the H
line.
Since the extinction is negligible in the radio wavelength
region,
the total extinction in the H![]() line is obtained directly
(see e.g. Skillman 1984; Masegosa 1988 for details).
The second method is based on the Balmer emission line
decrement.
The strength of the Balmer lines depends only
weakly on the electron temperature (
line is obtained directly
(see e.g. Skillman 1984; Masegosa 1988 for details).
The second method is based on the Balmer emission line
decrement.
The strength of the Balmer lines depends only
weakly on the electron temperature (![]() ), thus the
ratio between observed and theoretical line intensities
gives a measurement of the amount of extinction.
), thus the
ratio between observed and theoretical line intensities
gives a measurement of the amount of extinction.
In this investigation, the Balmer decrement is used for
the extinction correction.
The expression used was
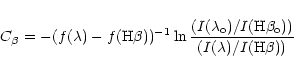
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig4.ps} \end{figure}](/articles/aa/full/2001/08/aa9350/Timg39.gif) |
Figure 4:
a) The extinction across the face of Hubble V.
The extinction coefficient, |
| Open with DEXTER | |
Due to the overlapping problem in the spectra of Hubble V mentioned
previously (see Sect. 3.1), the extinction
coefficient was determined from the intensity of the H![]() line instead of the H
line instead of the H![]() line.
Following the reddening correction of the lines, the
red part was normalized by the theoretical
value of the ratio H
line.
Following the reddening correction of the lines, the
red part was normalized by the theoretical
value of the ratio H![]() /H
/H![]() .
Case B recombination was assumed with an
.
Case B recombination was assumed with an ![]() of
10000 K, which is close to the
of
10000 K, which is close to the ![]() determined with the use
of the oxygen lines for both regions.
For Hubble X, the extinction coefficient was determined using
the H
determined with the use
of the oxygen lines for both regions.
For Hubble X, the extinction coefficient was determined using
the H![]() line.
As Caplan & Deharveng (1986) pointed out, the best
way of distinguishing between internal and external extinction
is by comparing the
extinction derived from the optical Balmer decrement and the
radio wavelength region.
The latter part of the spectrum
is evidently not attainable in this investigation.
In order to obtain some clues
about the location of the dust in the two H II regions,
the
line.
As Caplan & Deharveng (1986) pointed out, the best
way of distinguishing between internal and external extinction
is by comparing the
extinction derived from the optical Balmer decrement and the
radio wavelength region.
The latter part of the spectrum
is evidently not attainable in this investigation.
In order to obtain some clues
about the location of the dust in the two H II regions,
the ![]() ,
based on the H
,
based on the H![]() line,
and the H
line,
and the H![]() /H
/H![]() emission line ratio, normalized to their corresponding maxima, are compared (Figs. 4a and b for Hubble V and X,
respectively).
The
emission line ratio, normalized to their corresponding maxima, are compared (Figs. 4a and b for Hubble V and X,
respectively).
The ![]() derived from the H
derived from the H![]() line is preferred
since the
line is preferred
since the ![]() based on the H
based on the H![]() line mimics
the behaviour of the H
line mimics
the behaviour of the H![]() intensity, independent of the origin of the extinction.
Although only a limited amount of
information could be extracted, some conclusions could be drawn.
While the H
intensity, independent of the origin of the extinction.
Although only a limited amount of
information could be extracted, some conclusions could be drawn.
While the H![]() /H
/H![]() ratio is approximately constant
throughout Hubble V, the
ratio is approximately constant
throughout Hubble V, the
![]() varies.
The same is true for Hubble X.
This is an indication of external extinction because, if the
extinction would be internal to the nebula, these two parameters
should follow a similar behaviour.
It must be pointed out that the zero values
in the
varies.
The same is true for Hubble X.
This is an indication of external extinction because, if the
extinction would be internal to the nebula, these two parameters
should follow a similar behaviour.
It must be pointed out that the zero values
in the ![]() in Figs. 4a and b are mainly due to the fact
that, for these spectra, no extinction correction
was made due the low signal-to-noise ratio.
Therefore, the zero points for the extinction are arbitrary.
From the figures, it is also possible to draw some conclusions
about the distribution of the dust.
The situation is quite similar in both regions, with
non-distinct clumps
present in Hubble X and a big clump of dust throughout most of the eastern
part of Hubble V.
in Figs. 4a and b are mainly due to the fact
that, for these spectra, no extinction correction
was made due the low signal-to-noise ratio.
Therefore, the zero points for the extinction are arbitrary.
From the figures, it is also possible to draw some conclusions
about the distribution of the dust.
The situation is quite similar in both regions, with
non-distinct clumps
present in Hubble X and a big clump of dust throughout most of the eastern
part of Hubble V.
Another indicator of internal extinction is the possible correlation
between the emission line
ratio ![]() OIII
OIII![]() /
/![]() OII
OII![]() and
and ![]() (González-Delgado et al. 1994)
because the dust could be mixed with the ionized gas.
Such a correlation does not exist, either for Hubble V or for
Hubble X.
The linear correlation coefficients are found to be
(González-Delgado et al. 1994)
because the dust could be mixed with the ionized gas.
Such a correlation does not exist, either for Hubble V or for
Hubble X.
The linear correlation coefficients are found to be
![]() and
and
![]() ,
respectively, which confirms
the external origin of the reddening.
,
respectively, which confirms
the external origin of the reddening.
The extinction coefficients for all the Balmer lines in both regions
were determined from the spatially-averaged spectra.
The results are presented in Table 3.
There are some indications of decreasing values with increasing
wavelengths.
However, some exceptions, especially for ![]() ,
based on the
H
,
based on the
H![]() /H
/H![]() ratio in Hubble X, are seen.
The increasing values of
ratio in Hubble X, are seen.
The increasing values of ![]() toward shorter wavelengths
is probably a result of underlying stellar absorption and cannot be
explained by the uncertainties in the measurements, which are much smaller.
toward shorter wavelengths
is probably a result of underlying stellar absorption and cannot be
explained by the uncertainties in the measurements, which are much smaller.
The colour excess E(B-V) (de Vaucouleurs et al. 1991) determined in this investigation for the two H II regions correspond to 1.8 mag and 2.5 mag, respectively, in the B-band. These rather high values indicate the presence of a dust component external to the regions but internal to the galaxy. The absorption within the Galaxy in the B-band is only 0.86 mag. The E(B-V) values derived by Wilson (1992) and Marconi et al. (1995) agree with the high values obtained here, but do not agree with the E(B-V) values obtained from previous spectroscopical investigations.
We emphasize the use of the H![]() emission line in the
reddening correction of Hubble V instead of H
emission line in the
reddening correction of Hubble V instead of H![]() due to the
lack of a perfect overlapping between the red and the blue part of
the spectrum.
It is well known that the H
due to the
lack of a perfect overlapping between the red and the blue part of
the spectrum.
It is well known that the H![]() line is more
affected by underlying stellar absorption, but comparing the values of the
extinction coefficients (Table 3) determined with all the Balmer lines
observed, no significant differences are obtained, with the
exception of spectral lines with wavelengths shorter than H
line is more
affected by underlying stellar absorption, but comparing the values of the
extinction coefficients (Table 3) determined with all the Balmer lines
observed, no significant differences are obtained, with the
exception of spectral lines with wavelengths shorter than H![]() .
.
All results presented in the following sections include error estimates associated with the reddening correction.
| line | Hubble V | Hubble X |
| H |
2.0 |
- |
| H |
1.92 |
1.16 |
| H |
2.05 |
0.99 |
| H9 | 5.21 |
5.08 |
| H10 | 5.28 |
4.84 |
| H11 | 5.23 |
3.22 |
| H12 | 5.03 |
5.82 |
Only those 3r-spectra for which the emission line
![]() OIII
OIII![]()
![]() 4363 Å was detected were
used in the determination of the chemical abundances.
In Sect. 5.3 a
discussion of the limits of the signal-to-noise ratio is presented.
The total
number of 3r-spectra was 17 for Hubble V and 16 for Hubble X.
A five-level atom two-zone model was used to derive the
chemical abundances (Bergvall 1999).
The
4363 Å was detected were
used in the determination of the chemical abundances.
In Sect. 5.3 a
discussion of the limits of the signal-to-noise ratio is presented.
The total
number of 3r-spectra was 17 for Hubble V and 16 for Hubble X.
A five-level atom two-zone model was used to derive the
chemical abundances (Bergvall 1999).
The ![]() in the high ionization zone (O++) is
estimated using an iterative process based on the
in the high ionization zone (O++) is
estimated using an iterative process based on the ![]() OIII
OIII![]() line
ratios (Osterbrock 1989).
This method is often referred to as the temperature-sensitive
method.
The temperature of the low ionization zone (O+)
was estimated using the relation of Vila-Costas & Edmunds
(1993).
line
ratios (Osterbrock 1989).
This method is often referred to as the temperature-sensitive
method.
The temperature of the low ionization zone (O+)
was estimated using the relation of Vila-Costas & Edmunds
(1993).
The output from the model are the ![]() of the high and low
ionization zones of
the nebula, the ionic abundances of the lines as well as the
total oxygen abundance and the abundance ratio log(N/O).
Also, the oxygen abundance from semiempirical methods
(Skillman 1989; McGaugh 1994) are provided for
comparison.
The electron density,
of the high and low
ionization zones of
the nebula, the ionic abundances of the lines as well as the
total oxygen abundance and the abundance ratio log(N/O).
Also, the oxygen abundance from semiempirical methods
(Skillman 1989; McGaugh 1994) are provided for
comparison.
The electron density, ![]() ,
of the regions is determined from
the ratio of the lines
,
of the regions is determined from
the ratio of the lines
![]() SII
SII![]()
![]() 6716, 6730 Å.
In cases of a poor signal-to-noise ratio in these lines, or if the lines
where not
properly resolved, the
6716, 6730 Å.
In cases of a poor signal-to-noise ratio in these lines, or if the lines
where not
properly resolved, the ![]() was assumed to be 100 cm-3.
This value is typical for this class of objects.
No error estimates were used in the derivation of
these quantities; instead
an alternative approach was made.
The intensity of each line was increased by its error
percentage.
With these updated intensities, new ionic
abundances were obtained
and the uncertainties were estimated from the difference
between the two values.
was assumed to be 100 cm-3.
This value is typical for this class of objects.
No error estimates were used in the derivation of
these quantities; instead
an alternative approach was made.
The intensity of each line was increased by its error
percentage.
With these updated intensities, new ionic
abundances were obtained
and the uncertainties were estimated from the difference
between the two values.
It may appear that applying a two-zone ionization model to individual H II regions of less than 5 pc in size could give unrealistic results, since in the most unfavourable cases, a large portion of the ionization zone could reside outside the region considered. This would of course result in erroneous emission line ratios. As a check, new frames covering the pixels corresponding to four individual consecutive spectra, randomly chosen, for Hubble V and Hubble X, respectively, were obtained and two new sets of intensities were derived, as previously described (see Sect. 3). The chemical abundances were compared with the average values of the abundances derived from the four individual spectra. While the average oxygen abundance is 12+log(O/H) = 8.16 for Hubble V, the oxygen abundance derived from the individual spectra is 8.20. For Hubble X, the value is 8.10 in both cases. These results indicate that the differences are smaller than the errors in the abundance determinations.
The atomic abundances of the elements are derived from the ionic ones and the ionization correction factors (ICFs) which take into account the non-observable ions for each element.
For some elements, such as oxygen, no correction needs to be applied since all important ionization stages are within the wavelength range studied.
The ICF for helium is somewhat problematic since quite
contradictory results exist.
Izotov et al. (1997) proposed that no ICF was necessary for
helium.
On the other hand, Pagel et al. (1992) proposed the following
expression
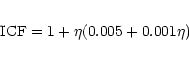
The most commonly used ICF for nitrogen is N(O)/N(O+) (Torres-Peimbert & Peimbert 1977) because of the affinity of the ionization potential between the two species, and also because of the lack of more highly ionized nitrogen in H II regions when only photoionization prevails. Garnett (1989) studied the applicability of this ICF and concluded that it could be applied to regions with metallicities lower than that of the LMC (12+log(O/H) = 8.3).
A derivation of the total abundance of neon can also be problematic
since, in this
investigation, only Ne++ appears in the wavelength region observed.
The ICF proposed is based on the proximity of the ionization
potentials
between neon and oxygen and is given by
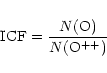
| Ion | Hubble V | ( |
Hubble X | ( |
|
| 3727 | 1.6 | .1 | 2.3 | .1 | |
| H12 | 3750 | 0.020 | .001 | 0.015 | .001 |
| H11 | 3771 | 0.027 | .001 | 0.041 | .008 |
| H10 | 3798 | 0.040 | .002 | 0.039 | .003 |
| He I | 3819 | 0.007 | .001 | 0.008 | .006 |
| H9 | 3835 | 0.063 | .002 | 0.057 | .006 |
| 3869 | 0.376 | .007 | 0.338 | .010 | |
| He I + H8 | 3889 | 0.189 | .004 | 0.207 | .008 |
| 3970 | 0.268 | .003 | 0.258 | .008 | |
| + H7 | |||||
| Fe I | 4002 | - | - | 0.005 | .002 |
| He I | 4026 | 0.016 | .001 | 0.013 | .001 |
| 4068 | 0.009 | .001 | 0.012 | .006 | |
| + 4076 | |||||
| H |
4101 | 0.253 | .002 | 0.280 | .006 |
| H |
4340 | 0.469 | .005 | 0.49 | .01 |
| 4363 | 0.055 | .003 | 0.048 | .001 | |
| He I | 4471 | 0.039 | .001 | 0.037 | .003 |
| 4658 | 0.002 | - | - | - | |
| + C IV | |||||
| 4711 | 0.004 | .001 | - | - | |
| + He I | |||||
| H |
4861 | 1 | .1 | 1 | .1 |
| He I | 4921 | 0.011 | .004 | 0.006 | .001 |
| 4959 | 1.7 | .1 | 1.41 | .08 | |
| 5007 | 5.1 | .3 | 4.2 | .2 | |
| 5198 | - | - | 0.005 | .001 | |
| 5517 | 0.001 | .000 | 0.023 | .001 | |
| 5537 | 0.003 | .000 | 0.02 | .01 | |
| HeI | 5875 | 0.063 | .001 | 0.120 | .004 |
| 6300 | 0.011 | .007 | 0.029 | .009 | |
| 6312 | 0.006 | .004 | 0.012 | .004 | |
| 6363 | 0.004 | .001 | 0.009 | .002 | |
| 6548 | 0.006 | .004 | - | - | |
| H |
6562 | 1.50 | .07 | 2.859 | .400 |
| 6583 | 0.031 | .009 | 0.073 | .008 | |
| He I | 6678 | 0.016 | .003 | 0.030 | .005 |
| 6716 | 0.05 | .01 | 0.11 | .03 | |
| 6730 | 0.03 | .01 | 0.07 | .02 | |
|
1.9 | 1.4 | |||
|
|
234 | 165 | |||
|
|
17 | 15 | |||
| log F(H |
-12.16 | -12.41 |
In order to check for the reliability
of the results, the signal-to-noise ratio of each 3r-spectrum are plotted
in Figs. 5a and b (only available electronically).
The signal-to-noise ratio of the three emission lines,
H![]() ,
H
,
H![]() and
and
![]() OIII
OIII![]()
![]() 4363 Å, follows a similar behaviour and only
the absolute values change.
The physical size of each region is measured from the geometrical
center of the nebula determined from the H
4363 Å, follows a similar behaviour and only
the absolute values change.
The physical size of each region is measured from the geometrical
center of the nebula determined from the H![]() emission
in the spectra.
The western part corresponds to positive values.
A region between -80 and -20 pc and -80 and -30 pc could be
defined for Hubble V and Hubble X, respectively, where
log(
emission
in the spectra.
The western part corresponds to positive values.
A region between -80 and -20 pc and -80 and -30 pc could be
defined for Hubble V and Hubble X, respectively, where
log(![]() )
is higher than 0.9 (based on the intensity of
the H
)
is higher than 0.9 (based on the intensity of
the H![]() emission line) or 0.5 (based on the intensity of
emission line) or 0.5 (based on the intensity of
![]() OIII
OIII![]()
![]() 4363 Å), where the signal-to-noise ratio
was considered acceptably high for a meaningful analysis (Rola &
Pelat 1994).
4363 Å), where the signal-to-noise ratio
was considered acceptably high for a meaningful analysis (Rola &
Pelat 1994).
Therefore, the study of possible spatial variations in the
physical
properties of Hubble V and Hubble X is considered limited by the
signal-to-noise ratio obtained and only applies to the parts of each
H II region where this ratio is sufficiently high.
It should be pointed out that in the case of Hubble V (Fig. 5a)
some limitations exist.
From the figure it is evident that the signal-to-noise ratio of the
![]() OIII
OIII![]()
![]() 4363 Å line shows a steep gradient
close to -80 pc.
Also, this line is practically undetected close to -35 pc and
closer to the geometrical center the signal-to-noise ratio
is generally low.
The situation for Hubble X (Fig. 5b) is more favourable.
4363 Å line shows a steep gradient
close to -80 pc.
Also, this line is practically undetected close to -35 pc and
closer to the geometrical center the signal-to-noise ratio
is generally low.
The situation for Hubble X (Fig. 5b) is more favourable.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig6.ps} \end{figure}](/articles/aa/full/2001/08/aa9350/Timg53.gif) |
Figure 6:
The fractional ionization
of Hubble V a) and X b) defined as;
[OIII] |
| Open with DEXTER | |
The ionization structure of Hubble V and
Hubble X was studied.
The low and high ionization zones are plotted in Figs. 6a and b.
They correspond to the regions of the maximum intensity of O+ and
O++, respectively.
A general definition of a
high ionization region could be those geometrical locations where the ratio
O++![]() O+ is higher than unity.
The high ionization region is limited to between -90 and
-10 pc in Hubble V and to -70 and -20 pc in Hubble X.
In both
H II regions, the high ionization region coincides with
the peaks in the excitation parameter (see the next section).
It is also evident from Figs. 6a and b that the O+ zone
coincides quite well with
the N+ zone.
This gives strong support for the use of the ratio
N(O)/N(O+) as an ICF for nitrogen (see Sect. 5.2.2).
O+ is higher than unity.
The high ionization region is limited to between -90 and
-10 pc in Hubble V and to -70 and -20 pc in Hubble X.
In both
H II regions, the high ionization region coincides with
the peaks in the excitation parameter (see the next section).
It is also evident from Figs. 6a and b that the O+ zone
coincides quite well with
the N+ zone.
This gives strong support for the use of the ratio
N(O)/N(O+) as an ICF for nitrogen (see Sect. 5.2.2).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig7.ps} \end{figure}](/articles/aa/full/2001/08/aa9350/Timg54.gif) |
Figure 7:
The excitation parameter, defined as
|
| Open with DEXTER | |
The excitation parameter is defined as the ratio of the two
emission lines ![]() OIII
OIII![]()
![]() 5007/H
5007/H![]() .
Peaks in the excitation parameter are seen
at -65 and -55 pc in Hubble V and Hubble X
(Figs. 7a and b), respectively.
This could be an indication of the location of the
OB association within the nebula, which is ionizing the
region.
.
Peaks in the excitation parameter are seen
at -65 and -55 pc in Hubble V and Hubble X
(Figs. 7a and b), respectively.
This could be an indication of the location of the
OB association within the nebula, which is ionizing the
region.
When comparing the two regions, it is evident
that they show quite a high level of excitation, with Hubble V
displaying somewhat higher absolute values across the
face of the object.
There could be two reasons for this:
The most recent episode of star formation is younger
in Hubble V or the ionizing stars are hotter, and therefore,
more massive.
A comparison of the equivalent width of H![]() ,
,
![]() ,
supports the first possibility, provided this parameter
traces the age of the region for a given
IMF (Copetti et al. 1986).
This is in agreement with the conclusion by Wilson (1992).
The age of Hubble X is determined by the latter from
colour-magnitude diagrams
and suggests that it is 1.6 Myr older than the age of the last
event of star formation in Hubble V.
Also, the OB association in Hubble V contains four
more massive stars than that of Hubble X.
,
supports the first possibility, provided this parameter
traces the age of the region for a given
IMF (Copetti et al. 1986).
This is in agreement with the conclusion by Wilson (1992).
The age of Hubble X is determined by the latter from
colour-magnitude diagrams
and suggests that it is 1.6 Myr older than the age of the last
event of star formation in Hubble V.
Also, the OB association in Hubble V contains four
more massive stars than that of Hubble X.
The non reddening-corrected H![]() /H
/H![]() ratio is
also presented in Figs. 7a and b.
The H
ratio is
also presented in Figs. 7a and b.
The H![]() /H
/H![]() ratios
of both regions are rather high, values of 5 and 4.5 for
Hubble V and
Hubble X were derived, respectively.
These numbers are close to those reported in the literature
for these regions.
Talent (1980)
obtained non-corrected intensities of 5.4 and 4.5 for Hubble V
and Hubble X, respectively.
It should be emphasized again that these values are not
corrected for galactic extinction (see Sect. 4.2).
ratios
of both regions are rather high, values of 5 and 4.5 for
Hubble V and
Hubble X were derived, respectively.
These numbers are close to those reported in the literature
for these regions.
Talent (1980)
obtained non-corrected intensities of 5.4 and 4.5 for Hubble V
and Hubble X, respectively.
It should be emphasized again that these values are not
corrected for galactic extinction (see Sect. 4.2).
The ![]() OIII
OIII![]() /
/![]() OII
OII![]() ratio is also an
indicator of excitation
and has a maximum at -65 pc in the case of Hubble V.
The same number for Hubble X is -50 pc.
These positions coincide very well with the maxima of
the excitation parameter and is
expected since the O+-zone is largely temperature
independent.
ratio is also an
indicator of excitation
and has a maximum at -65 pc in the case of Hubble V.
The same number for Hubble X is -50 pc.
These positions coincide very well with the maxima of
the excitation parameter and is
expected since the O+-zone is largely temperature
independent.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig8.ps} \end{figure}](/articles/aa/full/2001/08/aa9350/Timg56.gif) |
Figure 8:
The electron temperature, |
| Open with DEXTER | |
It is well known that temperature fluctuations in the nebular gas could mimic variations in the abundance of chemical elements. Temperatures derived from the nebular continuum are distinctly lower than those derived from the collisionally-excited emission lines, which could be the cause of the different temperature measurements (Peimbert 1967). González-Delgado et al. (1994) studied the giant H II region NGC 2363 located in the irregular galaxy NGC 2366. They compared the average temperatures derived from the Paschen continuum emission and the [OIII] lines and found differences of at least 2000 K using the two methods. Liu & Danziger (1993) derived the same result from a study of 14 planetary nebulae (PNe). On the other hand, Liu et al. (1995) used only the Balmer discontinuity in a study of the Orion nebula and found that the temperature seems constant, close to 9000 K, over a large portion of the nebula. Obviously, the situation is rather confusing and, in this analysis, insufficient spectral information was available, e.g. from the Balmer or Paschen discontinuities and no such comparison could be made.
Figures 8a and b show the distribution of the ![]() over the face
of Hubble V and Hubble X, respectively,
for which average values of 11500 K and 12000 K were derived.
For the spatially-averaged spectra,
the
over the face
of Hubble V and Hubble X, respectively,
for which average values of 11500 K and 12000 K were derived.
For the spatially-averaged spectra,
the ![]() are
are
![]() K and
K and
![]() K for Hubble V and X, respectively (see Table 5) and are
marked in the figures with horizontal lines.
The spatial distribution of
oxygen, determined with the use of the temperature-sensitive method
(Osterbrock 1989) over the face of
Hubble V is presented in Fig. 9a.
The same is given for Hubble X in Fig. 9b.
As expected, the
K for Hubble V and X, respectively (see Table 5) and are
marked in the figures with horizontal lines.
The spatial distribution of
oxygen, determined with the use of the temperature-sensitive method
(Osterbrock 1989) over the face of
Hubble V is presented in Fig. 9a.
The same is given for Hubble X in Fig. 9b.
As expected, the ![]() and oxygen abundance are distributed in
the same manner.
It is evident that some
variations in oxygen abundance are found.
They could reflect real variations in oxygen abundance or
small temperature fluctuations.
An average value of 8.15 is obtained for both regions,
which agrees well
with the abundances obtained from the spatially-averaged spectra (Table 5).
We note the very small uncertainties derived for the center
of Hubble X.
and oxygen abundance are distributed in
the same manner.
It is evident that some
variations in oxygen abundance are found.
They could reflect real variations in oxygen abundance or
small temperature fluctuations.
An average value of 8.15 is obtained for both regions,
which agrees well
with the abundances obtained from the spatially-averaged spectra (Table 5).
We note the very small uncertainties derived for the center
of Hubble X.
In order to study metallicity gradients within extragalactic H II regions, the distribution of some other elements, such as helium and nitrogen, should be investigated. Many studies have been devoted to the abundances of these elements in galaxies with moderately low metallicity, e.g. Garnett (1989), Garnett (1990) and Izotov et al. (1997). Apart from oxygen, only a few studies have been performed on the variation and possible inhomogeneities of these elements within the H II regions (Kobulnicky & Skillman 1996; Kobulnicky et al. 1997). Some other traditionally controversial topics, such as the origin of nitrogen or the abundance of primordial helium, have been analysed instead.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig9.ps} \end{figure}](/articles/aa/full/2001/08/aa9350/Timg59.gif) |
Figure 9:
The spatial distribution of (O/H) in Hubble V
a) and Hubble X b).
The region with sufficiently high signal-to-noise ratio is
considered to be
between -80 and -20 pc for Hubble V and between -80 and -30 pc
for Hubble X.
The horizontal lines correspond to the average value (solid) determined
from the spatially-averaged spectra with a 1 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig10.ps} \end{figure}](/articles/aa/full/2001/08/aa9350/Timg60.gif) |
Figure 10:
The spatial distribution of (He/H), by number, in
Hubble V a) and Hubble X b).
The horizontal lines correspond to the average value (solid) determined
from the spatially-averaged spectra with a 1 |
| Open with DEXTER | |
The emission lines used for a determination of helium abundances
are normally HeI![]() 4471 Å, HeI
4471 Å, HeI![]() 5875 Å and
HeI
5875 Å and
HeI![]() 6678 Å.
Other HeI (and, if present, HeII) lines can also be used.
Taking into consideration that some lines could be
affected by fluorescence and underlying stellar
absorption (Izotov et al. 1997), a weighted average
value for the helium line intensity was obtained.
Only two of the above mentioned lines were used for the abundance
determination.
The line He
6678 Å.
Other HeI (and, if present, HeII) lines can also be used.
Taking into consideration that some lines could be
affected by fluorescence and underlying stellar
absorption (Izotov et al. 1997), a weighted average
value for the helium line intensity was obtained.
Only two of the above mentioned lines were used for the abundance
determination.
The line He![]() 5875 Å was excluded from the
abundance determination due to its proximity
to the NaI
5875 Å was excluded from the
abundance determination due to its proximity
to the NaI
![]() 5890, 5896 Å lines.
The latter can be of stellar as well as interstellar origin.
5890, 5896 Å lines.
The latter can be of stellar as well as interstellar origin.
| Hubble V | Hubble X | |
|
11800 ( |
11950 ( |
|
|
48500 ( |
46000 ( |
| 12+log(O/H) | 8.10 ( |
8.12 ( |
| ICF(N) | 3.2 ( |
5.0 ( |
| 12+log(N/H) | 6.5 ( |
6.4 ( |
| log(N/O) | -1.58 ( |
-1.7 ( |
| ICF(Ne) | 1.4 ( |
1.2 ( |
| 12+log(Ne/H) | 7.3 ( |
7.4 ( |
| log (Ne/O) | -0.78 ( |
-0.8 ( |
| He/H | 0.079 ( |
0.10 ( |
| Y | 0.240 ( |
0.289 ( |
| 12+log(O/H)
|
8.07 | 8.09 |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig11.ps} \end{figure}](/articles/aa/full/2001/08/aa9350/Timg63.gif) |
Figure 11:
The spatial distribution of (N/H) in
Hubble V a) and Hubble X b).
The horizontal lines correspond to the average value (solid) determined
from the spatially-averaged spectra with a 1 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig12.ps} \end{figure}](/articles/aa/full/2001/08/aa9350/Timg64.gif) |
Figure 12:
The spatial distribution of (Ne/H) in
Hubble V a) and Hubble X b).
The horizontal lines correspond to the average value (solid) determined
from the spatially-averaged spectra with a 1 |
| Open with DEXTER | |
Figures 10a and b show the spatial distribution of helium, by number, over the face of both Hubble V and Hubble X. The situation for Hubble V (Fig. 10a) is somewhat confusing. The figure shows strong variations in the (He/H) ratio over the face of the object. In the eastern part, the values are rather close to those predicted by the hot Big Bang model. However, considering the low signal-to-noise ratio in parts of the spectra of Hubble V, this behaviour is to be expected. The helium abundance within Hubble X (Fig. 10b), on the other hand, is constant at (He/H) = 0.10.
The distribution of nitrogen in both regions is presented in Figs. 11a and b. In the parts of the H II regions considered, the nitrogen abundance is more or less constant, close to log(N/H) = -5.60 and -5.50 for Hubble V and Hubble X, respectively. These values agree with those derived from the spatially-averaged spectra (Table 5). The derived numbers are rather typical for this class of objects (e.g. Izotov et al. 1997). Some variations could be argued for, especially the overabundance of nitrogen close to -30 pc in Hubble V (Fig. 11a). However, considering the uncertainties, no firm conclusions regarding the presence of fluctuations in nitrogen abundance in the region could be drawn, since this could be an effect of the low signal-to-noise ratio.
The spatial distribution of neon over the face of the two
H II regions is presented in Figs. 12a and b.
The lines used for the determination of the abundance of neon,
![]() NeIII
NeIII![]()
![]() 3869 Å and
3869 Å and ![]() NeIII
NeIII![]()
![]() 3970 Å, could be
affected by metal-line blanketing.
Due to the relatively low metallicity of these regions, this
effect should not be too crucial
for this analysis, even though some uncertainties are introduced.
The average
values obtained, log(Ne/H) = -4.70 and -4.60
for Hubble V and Hubble X, respectively, show good agreement
with the spatially-averaged abundances (Table 5).
3970 Å, could be
affected by metal-line blanketing.
Due to the relatively low metallicity of these regions, this
effect should not be too crucial
for this analysis, even though some uncertainties are introduced.
The average
values obtained, log(Ne/H) = -4.70 and -4.60
for Hubble V and Hubble X, respectively, show good agreement
with the spatially-averaged abundances (Table 5).
As previously mentioned, a spectrum for each region was obtained
by summing all the pixels where the line
![]() OIII
OIII![]()
![]() 4363 Å was
detected.
The total number of pixels
for Hubble V and Hubble X corresponded to sizes of 75 and 67 pc,
respectively.
These two spatially-averaged spectra were corrected for extinction
and absorption as described previously.
Table 4 presents
the intensities, normalized to H
4363 Å was
detected.
The total number of pixels
for Hubble V and Hubble X corresponded to sizes of 75 and 67 pc,
respectively.
These two spatially-averaged spectra were corrected for extinction
and absorption as described previously.
Table 4 presents
the intensities, normalized to H![]() ,
and the total error estimate of
each line, as described in Sect. 3.
The extinction parameters,
determined using H
,
and the total error estimate of
each line, as described in Sect. 3.
The extinction parameters,
determined using H![]() for Hubble V and H
for Hubble V and H![]() for
Hubble X, are also given.
The equivalent width and the flux of H
for
Hubble X, are also given.
The equivalent width and the flux of H![]() as well as the
signal-to-noise ratio
measured in the vicinity of the line
as well as the
signal-to-noise ratio
measured in the vicinity of the line ![]() OIII
OIII![]()
![]() 4363 Å
are presented in the table as well.
4363 Å
are presented in the table as well.
| 1 | 2 | 3 | 4 | 5 | ||
| HV | 0.32 | 1.04 | ||||
| HX | 0.75 | |||||
| HV | 12180 | 11510 | 11000 | 11410 | 11450 | |
| HX | 10900 | 11500 | 10920 | |||
| 12+log(O/H) | HV | 8.09 | 8.20 | 8.19 | 8.28 | 8.22 |
| HX | 8.27 | 8.09 | 8.31 | |||
| log(N/O) | HV | -1.77 | -1.69 | -1.7* | ||
| HX | -1.74 | |||||
| log(Ne/O) | HV | -0.66 | -0.85 | |||
| HX | -0.66 | -0.75 | ||||
| N(He)/N(H) | HV | 0.094 | 0.081 | |||
| HX | 0.084 |
The total helium abundance was obtained, as in the case
of the 3r spectra, from the weighted
sum of the helium abundance from the lines He![]() 4771 Å
and He
4771 Å
and He![]() 6678 Å.
No ICF was used for the reasons discussed in Sect. 5.2.1.
Both (He/H) and Y (the mass fraction of helium) are compiled in Table 5.
6678 Å.
No ICF was used for the reasons discussed in Sect. 5.2.1.
Both (He/H) and Y (the mass fraction of helium) are compiled in Table 5.
The ratio log(N/O) has been determined for both regions (Table 5). From a comparison with a sample of dI (Garnett 1990) and blue compact galaxies (BCG) (Izotov & Thuan 1999) it can be concluded that Hubble X has a value slightly lower than the average derived from those investigations, which is log(N/O) = -1.5.
The ratio log(Ne/O) is -0.78 and -0.8 for Hubble V and Hubble X, respectively. A comparison of the sample of dI by McCall et al. (1985) and BCG (Izotov & Thuan 1999) was made. It can be concluded that the spatially-averaged ratio is normal for this type of object. One should also note the small difference in the total neon abundance between the two regions which is in good agreement with the results from the spatially-averaged oxygen abundance.
A number of studies focused on NGC 6822 was selected for comparison, such as Peimbert & Spinrad (1970), Lequeux et al. (1979), Talent (1980), Pagel et al. (1980), and Skillman et al. (1989). The extinction coefficients and the elemental abundances from those investigations are presented in Table 6. The oxygen abundance is reported in all the studies selected.
From an inspection of Tables 5 and 6 it is clear that the
abundances
obtained in this study agree well with those presented by
Pagel et al. (1980).
It should be pointed out that despite the relatively high extinction
found for both regions, quite different from the
one obtained by Pagel et al. (1980), the ![]() 's and oxygen abundances
for both H II regions are similar in both investigations.
This is also true for log(N/O) of Hubble X.
The differences obtained in the extinction values could be
due to a different positioning of the slit within the H II regions.
's and oxygen abundances
for both H II regions are similar in both investigations.
This is also true for log(N/O) of Hubble X.
The differences obtained in the extinction values could be
due to a different positioning of the slit within the H II regions.
The major source of ionization in this type of object is
photoionization by hot stars.
However, a contribution to the total ionization by other sources,
such as PN ejection, shock-heating from
SN ejecta
and non-thermal radiation, cannot, a priori, be ruled out.
The intensity of some emission lines are strongly enhanced in
the presence of other sources of ionization.
The emission lines
![]() OI
OI![]()
![]()
![]() 6300, 6363 Å and
6300, 6363 Å and
![]() ClIII
ClIII![]()
![]()
![]() 5517, 5537 Å, are clearly present in
the spectra of Hubble V and Hubble X.
The
5517, 5537 Å, are clearly present in
the spectra of Hubble V and Hubble X.
The ![]() OI
OI![]() lines, especially, indicate the presence of
shock-heating or non-thermal emission.
The latter source can be ruled out due to the absence of highly ionized
species, such as FeX, or broad emission lines, which are
typical of active galaxies.
lines, especially, indicate the presence of
shock-heating or non-thermal emission.
The latter source can be ruled out due to the absence of highly ionized
species, such as FeX, or broad emission lines, which are
typical of active galaxies.
Considering the uncertainties associated with the weak ![]() OI
OI![]() lines, their
intensities measured in the H II regions studied here could be
explained by
pure photoionization (Stasinska 1990) and therefore no
correction for shock-heating to the line intensities was
considered necessary.
The
lines, their
intensities measured in the H II regions studied here could be
explained by
pure photoionization (Stasinska 1990) and therefore no
correction for shock-heating to the line intensities was
considered necessary.
The ![]() ClIII
ClIII![]() lines are mainly
reported in studies of PNe (e.g. Saurer 1998)
but also in some BCG, as evident in the sample of Izotov et al. (1997).
A possibility is that these lines appear because of the
high
lines are mainly
reported in studies of PNe (e.g. Saurer 1998)
but also in some BCG, as evident in the sample of Izotov et al. (1997).
A possibility is that these lines appear because of the
high
![]() in the regions.
The ionization potential of
in the regions.
The ionization potential of ![]() ClIII
ClIII![]() is about
40 eV, which is smaller than that of He II (54.4 eV).
In this
case, the lines could be ionized if the radiation is hard enough
and is observable only when the data is of sufficiently high quality due to
their low abundances.
is about
40 eV, which is smaller than that of He II (54.4 eV).
In this
case, the lines could be ionized if the radiation is hard enough
and is observable only when the data is of sufficiently high quality due to
their low abundances.
In order to check whether PNe contribute to the total emission,
diagnostic diagrams of Baldwin et al. (1981) were obtained for
all the spectra where the lines were present.
The diagrams which included the emission line ratios of
![]() OII
OII![]()
![]() 3727 Å,
3727 Å, ![]() OIII
OIII![]()
![]() 5007 Å,
5007 Å,
![]() OI
OI![]()
![]() 6300 Å,
6300 Å,
![]() NII
NII![]()
![]() 6583 Å, H
6583 Å, H![]() and H
and H![]() were used.
It was obvious that, in all diagnostic diagrams, the observed
line ratios were located within the position of ordinary
H II regions ionized by hot stars.
The same is true for
the spectra where the
were used.
It was obvious that, in all diagnostic diagrams, the observed
line ratios were located within the position of ordinary
H II regions ionized by hot stars.
The same is true for
the spectra where the ![]() ClIII
ClIII![]() line were detected.
Even if the line
ratios correspond to H II regions, the PNe could be
positioned
behind these, considering the weakness of the
line were detected.
Even if the line
ratios correspond to H II regions, the PNe could be
positioned
behind these, considering the weakness of the ![]() ClIII
ClIII![]() lines.
Thus, the origin of
the
lines.
Thus, the origin of
the ![]() ClIII
ClIII![]() lines could be nebular or due to PNe, but the
relative
amounts are difficult to assess.
A comparison with photoionization models does not give a
definitive answer due to uncertainties in the
modeling as well as in the measurements.
lines could be nebular or due to PNe, but the
relative
amounts are difficult to assess.
A comparison with photoionization models does not give a
definitive answer due to uncertainties in the
modeling as well as in the measurements.
Whatever the origin of chlorine, the abundance of
![]() ClIII
ClIII![]() can be estimated.
These lines are not included
in the software used for the abundance determination, but
assuming that the
can be estimated.
These lines are not included
in the software used for the abundance determination, but
assuming that the ![]() is roughly the same as that for the
is roughly the same as that for the
![]() OIII
OIII![]() region (Izotov et al. 1997), the expression for
the nebular P3 transitions from Aller (1984) could be used.
The expression is
region (Izotov et al. 1997), the expression for
the nebular P3 transitions from Aller (1984) could be used.
The expression is
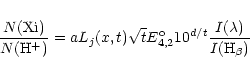
The abundances obtained can be compared to those of a sample of
BCG (Izotov et al. 1997).
The average value of Cl++ for the 11 galaxies
where ![]() ClIII
ClIII![]() is detected is 2.65 10-8, which is an intermediate value
between those for Hubble V and Hubble X.
Also, the ratio log(Cl++/O++) can be determined.
Values of -4.01 and -3.10 are obtained for Hubble V and Hubble X, respectively. No direct comparison
could be made with the results of the sample of Izotov et al. because they
used the
atomic abundances of chlorine but without giving any details regarding
the explicit form of the ICF used.
is detected is 2.65 10-8, which is an intermediate value
between those for Hubble V and Hubble X.
Also, the ratio log(Cl++/O++) can be determined.
Values of -4.01 and -3.10 are obtained for Hubble V and Hubble X, respectively. No direct comparison
could be made with the results of the sample of Izotov et al. because they
used the
atomic abundances of chlorine but without giving any details regarding
the explicit form of the ICF used.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig13.ps}\end{figure}](/articles/aa/full/2001/08/aa9350/Timg71.gif) |
Figure 13:
The spatial distribution of log(N/O) in
Hubble V a) and Hubble X b).
The horizontal lines correspond to the average value (solid) determined
from the spatially-averaged spectra with a 1 |
| Open with DEXTER | |
There are some gaseous mixing processes which act on scales of a few tens of parsecs. Local enrichment of gas ejected at SN explosions may be the most important, but also turbulent diffusion and fluid instabilities could have an effect on timescales of 107-108 yr (Roy & Kunth 1995) for H II regions of sizes of the order of 1 kpc. The regions studied in this analysis are about a factor of two smaller, which suggests that the timescales involved should be shorter by a factor of about ten. Even if turbulent diffusion and fluid instabilities are considered more efficient in large disk galaxies they cannot be completely ruled out in the case of dwarf galaxies.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig14.ps} \end{figure}](/articles/aa/full/2001/08/aa9350/Timg72.gif) |
Figure 14:
The spatial distribution of log(Ne/O) in
Hubble V a) and Hubble X b).
The horizontal lines correspond to the average value (solid) determined
from the spatially-averaged spectra with a 1 |
| Open with DEXTER | |
The most remarkable characteristic of the oxygen distribution
in Hubble V (Fig. 9a) is a deviation from the average value at
-43 pc of 0.16 dex from the spatially-averaged value.
A similar behaviour
is noticed in Hubble X (Fig. 9b) at -68 pc of 0.13 dex from the
spatially-averaged value.
Considering the relatively small uncertainties measured at both locations,
which
included all the possible sources of uncertainty affecting the determination
of the chemical abundances, the overabundances could not be ascribed to
uncertainties in the oxygen abundance.
This could represent real local
overabundances of oxygen or could be an effect of local temperature
fluctuations.
If local enrichment from massive stars is the cause of the
increase of the oxygen abundance, neon should show a
similar behaviour, due to the fact that both elements are, mainly, the
result of type II SN explosions with stars more massive than
![]() 10
10 ![]() as progenitors.
This is, however, difficult to assess, due to the high
uncertainties involved, especially in the case of Hubble V.
as progenitors.
This is, however, difficult to assess, due to the high
uncertainties involved, especially in the case of Hubble V.
As previously mentioned, an overabundance of nitrogen is detected at -30 pc in Hubble V (Fig. 11a). Also, at this location, one sees a variation in the helium abundance (Fig. 10a). The differences with respect to the average values are 0.15 dex in the nitrogen abundance and 0.25 dex in the helium abundance. This location also shows a difference in the log(N/O) ratio with respect to the spatially-averaged value, evident in Fig. 13a. The distribution of log(N/O) resembles that of log(N/H). At the most western part, the large scatter is probably due to the low abundance of oxygen. The high value of the oxygen abundance at -45 pc corresponds to a low value in the log(N/O) ratio, which indicates a real overabundances in oxygen. Figure 13b shows the log(N/O) ratio for Hubble X and it is clear that no major deviations from the average value are found across the H II region.
A possible explanation for the overabundances in helium and nitrogen could involve Wolf-Rayet stars. It is well known that winds from these stars could pollute the ISM (e.g. Maeder 1991). As previously mentioned, features typical of this type of star are absent from the spectra of Hubble V and X. Considering the typical temperature of the winds expelled from the stars, the cooling time needed to observe the elements in the optical region is longer (107 years) than the typical lifetime of the spectral features, assuming a short episode of star formation (which is of the order of 105 years). The lack of helium or nitrogen overabundances in the so-called Wolf-Rayet galaxies (Kobulnicky et al. 1997) is suggestive of such a situation.
Figures 14a and b show the spatial distribution of log(Ne/O) over the face of Hubble V and X, respectively. A deviation from a constant value could be interpreted as a variation in the distribution of oxygen or neon due to mechanisms other than gas ejection from massive stars. The results show that the log(Ne/O) ratio is largely constant, especially in Hubble X, which indicates a similar origin for both elements. The local underabundance in the log(Ne/O) ratios at -47 pc and -22 pc in Hubble V could indicate a real depletion of neon, with respect to oxygen. One can also note that these locations are not spatially coincident with the higher-than-average locations in oxygen abundance (Fig. 9a). This could rule out a local enrichment from massive stars.
Another objective of this paper is to study possible variations in the chemical content, comparing H II regions in dI. A more detailed discussion will be presented in a second paper (Hidalgo-Gámez et al. 2001).
Different mechanisms at different length- and timescales are responsible for a chemically well-mixed medium (Roy & Kunth 1995). Epicyclic mixing for rotating disk galaxies or the presence of bars and superbubble expansion, among other phenomena, would erase any abundance variations on timescales less than 109 yr. In the case of low-mass dwarf galaxies, some of the above mentioned mechanisms are less efficient or do not operate at all and the mixing of the elements in the ISM would be severely delayed. Other processes, such as selective loss of chemical elements through galactic winds and the low efficiency of mixing in a hot interstellar medium would make the variations larger in dwarf galaxies with long dormant phases between star-forming events. The derived parameters for the two H II regions are presented in Table 5. It is clear that the oxygen abundance in both regions is about the same, within the uncertainties. For nitrogen and neon no major differences between the regions are found. The situation for helium is different. As evident from Table 5, the (He/H) abundance ratio in Hubble V is about 2/3 that of Hubble X. This difference is certainly larger than the uncertainties in the measurements and should be considered real. The reason for the different values derived is unclear, especially in light of the fact that the other elements are similar if the two H II regions are compared. Uncertainties in the ICF can be ruled out since no HeII lines are observed in either spectra which implicate that the ICF should be close to one.
One possible explanation for the similarity in internal
physical properties
is probably the proximity between
Hubble V and X, about 320 pc.
Both H II regions are located in the same part of the
galaxy, the northern edge of the bar.
An argument favouring the efficient mixing of chemical elements
between these H II regions is the existency of a bar
which will flatten the abundance gradient, not only
along, but also across the bar.
Moreover, from the properties of the OB associations found
in NGC 6822 (Wilson 1992) the star formation processes are
similar.
Also, the star formation history of both regions could be very
similar.
Israel et al. (1996) derived a recent star formation rate of
0.02 ![]() yr-1 kpc-2 from infrared data for both
regions.
With this in mind, and considering the proximity of the two
regions, it could be
concluded that the mixing of the elements in the medium in the
vicinity of
Hubble V and Hubble X has been very efficient and the
abundances of chemical elements are very similar, with
differences of the same order as the error estimates.
Apart from possible inhomogeneities from previous events of
star formation in the region, ongoing events could pollute
the ISM of each region.
Comparing the ages, 6.6 and 8.2 Myr, respectively, and the time the
elements ejected from SNe need in order to reach the temperature of the
ISM (typically of the order of 50 Myr), it is clear that those elements
are too hot to be observed in the optical region.
The possible chemical inhomogeneities
detected in the optical region will be due to poor mixing of the
elements from previous star-forming events.
yr-1 kpc-2 from infrared data for both
regions.
With this in mind, and considering the proximity of the two
regions, it could be
concluded that the mixing of the elements in the medium in the
vicinity of
Hubble V and Hubble X has been very efficient and the
abundances of chemical elements are very similar, with
differences of the same order as the error estimates.
Apart from possible inhomogeneities from previous events of
star formation in the region, ongoing events could pollute
the ISM of each region.
Comparing the ages, 6.6 and 8.2 Myr, respectively, and the time the
elements ejected from SNe need in order to reach the temperature of the
ISM (typically of the order of 50 Myr), it is clear that those elements
are too hot to be observed in the optical region.
The possible chemical inhomogeneities
detected in the optical region will be due to poor mixing of the
elements from previous star-forming events.
A detailed study of the distribution of helium, nitrogen, oxygen and neon within the two major H II regions, Hubble V and Hubble X, in the dI galaxy NGC 6822 was made. Due to the high quality of the data, elemental abundances in regions of approximately 4.3 pc were derived. The study of local enrichment in galaxies at small scales has been made previously, mainly for oxygen. Studies of variations in the helium, nitrogen and oxygen abundances in this type of object on scales as small as 4 pc have not previously been reported in the literature. Indications of variations in the chemical abundances of oxygen, and possibly nitrogen, were found within the two H II regions. This could be real local chemical overabundances or could simply reflect local temperature fluctuations. Also, the extinction of Hubble V and Hubble X was studied and indicated an origin external to the H II regions. The physical properties of Hubble V and Hubble X are similar. This is related to the timing of the last episode of star formation, the star formation rates and the chemical abundances. This suggests that, due to the proximity of the two H II regions, they could have influenced each other dynamically.
Acknowledgements
Dr. N. Bergvall, Dr. P. Leisy, Sr. V. Ortega, Mr. A. Pharasyn, Sr. Roman, Sr. Santillán, Dr. Sánchez-Salcedo and Dr. G. Östlin are acknowledged for their different contributions to this work. This paper has benefited much from the comments of Prof. J.-R. Roy. A.M.H.G was partially supported by NOTSA and the Uppsala Astronomical Observatory. A.M.H.G. thanks the Mathematics and Statistics Department of the University of Newcastle-upon-Tyne and Instituto de Astrofísica de Andalucía. Finally, an anonymous referee is thanked for many valuable comments and suggestions which have improved the quality of this paper. This research made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{fig2.eps}
\end{figure}](/articles/aa/full/2001/08/aa9350/Timg75.gif) |
Figure 2: The two-dimensional spectra of Hubble V a) and Hubble X b). In both regions the entire spectral range, between 3720 Å and 6800 Å, is presented. The east direction is down in the figures |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig5.ps}
\end{figure}](/articles/aa/full/2001/08/aa9350/Timg76.gif) |
Figure 5:
The signal-to-noise ratio distribution of Hubble V
a) and X b).
The signal-to-noise ratio in the following three emission lines are
shown;
|
| Open with DEXTER | |