2 Observations and results

 

 

Table 1: The integrated line intensities observed towards the centre of NGC 4945; the detections are shown in Fig. 1. Here and in Table 2, the uncertainties are due to $1\sigma$ rms noise fluctuations and the $\approx \pm 5\%$ accuracy of $\eta _{\rm mb}$. The upper limits where obtained by assuming the same velocity range as for the CO (and other molecules), i.e. $\approx$300 km s^-1 to $\approx$800 km s^-1. The H₂CO $J_{\rm K_a, K_c}=2_{0,2}\rightarrow 1_{0,1}$ line is a blend with HC₃N $J=16\rightarrow 15$

Molecule	Transition	$I_{\rm mb}$ [K km s-1]
12CO	$1\rightarrow 0$	$510\pm30$
	$2\rightarrow 1$	$740\pm40$
	$3\rightarrow 2$	$760\pm50$
13CO	$1\rightarrow 0$	$30\pm2$
	$2\rightarrow 1$	$86\pm5$
C18O	$1\rightarrow 0$	$8.4\pm0.8$
	$2\rightarrow 1$	$29\pm2$
C17O	$1\rightarrow 0$	$1.8\pm0.4$
	$2\rightarrow 1$	$5\pm1$
CS	$2\rightarrow 1$	$9.3\pm0.8$
	$3\rightarrow 2$	$11\pm1$
13CS	$2\rightarrow 1$	<2
SO	$3_2\rightarrow 2_1$	$1.2\pm0.3$
	$4_3\rightarrow 3_2$	$1.4\pm0.2$
HCN	$1\rightarrow 0$	$24\pm2$
	$3\rightarrow 2$	$45\pm4$
H13CN	$1\rightarrow 0$	$1.1\pm0.4$
HCO+	$1\rightarrow 0$	$21\pm1$
	$3\rightarrow 2$	$37\pm3$
H13CO+	$1\rightarrow 0$	$2.3\pm0.5$
	$3\rightarrow 2$	<4
H2CO	$2_{1,2}\rightarrow 1_{1,1}$	$6.5\pm0.7$
	$2_{0,2}\rightarrow1_{0,1}$	$5.4\pm0.5$
	$2_{1,1}\rightarrow 1_{1,0}$	$5.9\pm0.6$
	$3_{0,3}\rightarrow2_{0,2}$	<3
	$3_{2,2}\rightarrow2_{2,1}$	<3
	$3_{1,2}\rightarrow2_{1,1}$	<3
CH3C2H	$6\rightarrow5$	<2

 

 

Table 2: The integrated line intensities observed towards the centre of Circinus; the detections are shown in Fig. 2. The CO data are taken from Curran et al. (1998). As in the case of NGC 4945 (Table 1), the integrated intensities were estimated by assuming the same velocity range as for the CO i.e. $\approx$200 km s^-1 to $\approx$650 km s^-1

Molecule	Transition	$I_{\rm mb}$ [K km s-1]
12CO	$1\rightarrow 0$	$180\pm10$
	$2\rightarrow 1$	$220\pm20$
	$3\rightarrow 2$	$230\pm20$
13CO	$1\rightarrow 0$	$12\pm1$
	$2\rightarrow 1$	$24\pm4$
C18O	$1\rightarrow 0$	$4.3\pm0.4$
C17O	$1\rightarrow 0$	$0.9\pm0.1$
CS	$2\rightarrow 1$	$3.2\pm0.3$
	$3\rightarrow 2$	$3.0\pm0.3$
	$5\rightarrow 4$	$1.1\pm0.3$
SO	$3_2\rightarrow 2_1$	$0.8\pm0.2$
HCN	$1\rightarrow 0$	$5.2\pm0.8$
HNC	$1\rightarrow 0$	$3\pm1$
HCO+	$1\rightarrow 0$	$7\pm1$
H2CO	$2_{1,2}\rightarrow 1_{1,1}$	$0.8\pm0.2$

The observations were carried out in June 1989, February 1993, June 1995, June 1998, December 1998, December 1999 and April 2000 with the Swedish-ESO Sub-millimetre Telescope (SEST) at La Silla, Chile. The receiver system consisted of a 3 mm Schottky mixer and cryogenic 1.3 mm, 2 mm and 3 mm SIS mixers. The mixers were tuned to single sideband mode (resulting system temperatures, corrected for the atmosphere, were typically $T_{\rm A}^{*}\approx200{-}550$ K), and connected to low resolution acousto-optical spectrometers (1440 channels, total bandwidth of 1 GHz). Dual beam-switching, with a beam-throw of $\approx$12$^\prime$ in azimuth, was used as observing mode. The intensity calibration was done with the chopper-wheel method. Pointing and focus checks were made towards stellar SiO masers as well as the continuum source in Centaurus A. The pointing offsets were typically 3'' rms in each coordinate. Calibration uncertainties are estimated to be $\pm10, 15 ~{\rm and}~ 20\%$ in the 3, 2 and 1.3 mm bands, respectively.

2.1 Observational results

Figures 1 and 2 show the observed spectra. The observational results are summarised in Tables 1 and 2, where main-beam integrated intensities are given. The total uncertainty in the observed intensities is obtained by adding quadratically the contribution of noise in the spectra to the calibration and pointing uncertainties.

In NGC 4945 most of the molecules have stronger emission in the blue-shifted than in the red-shifted part of the line. An exception to this is CS, whose emission is more evenly distributed over the full spectral profile (this has previously been noted by Henkel et al. 1990). This asymmetry in the spectra may indicate that the chemistries differ in the two regions or that the excitation is varying, e.g. due to differences in the gas density/temperature, electron density or the background infrared radiation. Henkel et al. (1994) have suggested that the differing emission strengths may be due to differences in the exposure to the far-infrared (FIR) radiation. Yet another possible explanation is self-absorption, i.e. some locations suffering a greater degree of saturation (Henkel et al. 1990), perhaps due to a temperature gradient across the molecular ring where the inner edge is expected to be hotter than the outer.

Unlike those of NGC 4945 the profiles in Circinus are fairly symmetric. Again checking against previous observations, the lines are similar to those which have been previously observed i.e. ¹²CO $1\rightarrow 0$(Johansson et al. 1991; Israel 1992; Elmouttie et al. 1997; Elmouttie et al. 1998), ¹³CO $1\rightarrow 0$, ¹²CO $2\rightarrow 1$, ¹³CO $2\rightarrow 1$ (Johansson et al. 1991) and HCO⁺, HCN and HNC, in the $1\rightarrow 0$ transition (Israel 1992).

Figure 1: The observed spectra in NGC 4945. Apart from H2CO $2_{1,1}\rightarrow 1_{1,0}$, which required the removal of a higher order baseline, a constant or first order baseline has been subtracted from each spectra. The spectra have been smoothed to a channel width corresponding to 10 km s-1 (except C17O $2\rightarrow 1$, SO $3_2\rightarrow 2_1$ and SO $4_3\rightarrow 3_2$ to 20 km s-1). The intensity scale is $T_{\rm A}^*$ and the velocity scale is relative to the local standard of rest (l.s.r.)

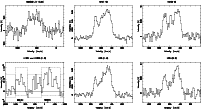Figure 1: continued. The H13CN and H13CO+ $1\rightarrow 0$ transitions lie in the same band, centred on 86.55 GHz, at 86.34 GHz (1280 km s-1) and 86.75 GHz (-140 km s-1), respectively. These spectra are shown with a resolution corresponding to 50 km s-1 (the remainder of the spectra being shown smoothed to 10 km s-1). The weak detections (here and in Fig. 2), are shown with the baseline and moment boxes used to determine their integrated intensities, given in Table 1

Figure 2: The observed spectra in Circinus. A constant or first order baseline has been subtracted from each spectra. The spectra have been smoothed to a channel width corresponding to 10 km s-1(except C17O $1\rightarrow 0$, CS $5\rightarrow 4$, HNC $1\rightarrow 0$ and H2CO ( $2_{1,2}\rightarrow 1_{1,1}$) to 20 km s-1) and SO $3_2\rightarrow 2_1$ to 40 km s-1. The intensity scale is $T_{\rm A}^*$ and the velocity scale is relative to the local standard of rest (l.s.r.)

2.2 Excitation and radiative transfer analysis

In the analysis we use velocity integrated line intensities, $I=\int{T {\rm d}v}$, which have been corrected for beam-dilution due to finite source and beam sizes. This is carried out by assuming that the source distribution on the sky is Gaussian and applying the full-width half-maximum (FWHM) diameter ( $\Theta _{\rm source}$) of the corresponding ¹²CO transition to the various CO isotopomers. The other molecules have transitions of higher excitation requirements and in those cases the CO $2\rightarrow 1$ value of $\Theta _{\rm source}$is applied (Table 3). The resulting corrected intensity ratios are shown in Table 4.

 

 

Table 3: The beam widths, $\Theta _{\rm mb}$, at SEST and source sizes, $\Theta _{\rm source}$, of the various CO transitions. In the case of NGC 4945 the $1\rightarrow 0$ value is from Dahlem et al. (1993); Mauersberger et al. (1996), the $2\rightarrow 1$ value from Dahlem et al. (1993); Mauersberger et al. (1996); Curran (2000) and the $3\rightarrow 2$ value from Mauersberger et al. (1996); Curran (2000). For Circinus all the values are obtained from the maps of Curran et al. (1998). Applying the FWHMs listed to the relation $I=I_{\rm mb}/\eta _{\rm bf}$ (where $\eta _{\rm bf}=\Theta _{\rm source}^{2}/(\Theta _{\rm mb}^{2}+\Theta _{\rm source}^{2}$)), in order to correct for the Gaussian beam-filling factor, we obtain the corrected intensity ratios listed in Table 4

	CO $1\rightarrow 0$	CO $2\rightarrow 1$	CO $3\rightarrow 2$
SEST beam	45''	22''	15''
NGC 4945	29''	20''	15''
Circinus	42''	31''	21''

 

 

Table 4: Integrated line intensity ratios. For the values listed in Table 3 the uncertainties in $\Theta _{\rm source}$ (typically 10%) lead to uncertainties of $\approx$10% in the values of $\eta _{\rm bf}$ $\left(\frac{\Delta\eta}{\eta}=2(1-\eta)\frac{\Delta\Theta}{\Theta}\right)$, or $\sim$20% for ratios involving different source sizes

Molecule(s)	Transitions	I ratio
		NGC 4945	Circinus
12CO	$2\rightarrow 1/1\rightarrow 0$	$1.0\pm0.2$	$1.0\pm0.2$
	$3\rightarrow2/1\rightarrow0$	$0.9\pm0.2$	$0.9\pm0.2$
13CO	$2\rightarrow 1/1\rightarrow 0$	$1.9\pm0.4$	$1.5\pm0.5$
12CO/13CO	$1\rightarrow0/1\rightarrow0$	$17\pm2$	$14\pm2$
	$2\rightarrow1/2\rightarrow1$	$8.3\pm0.8$	$10\pm3$
C18O	$2\rightarrow 1/1\rightarrow 0$	$2.4\pm0.6$	-
12CO/C18O	$1\rightarrow0/1\rightarrow0$	$59\pm9$	$41\pm7$
	$2\rightarrow1/2\rightarrow1$	$25\pm4$	-
C17O	$2\rightarrow 1/1\rightarrow 0$	$1.7\pm0.9$	-
12CO/C17O	$1\rightarrow0/1\rightarrow0$	$300\pm80$	$230\pm50$
	$2\rightarrow1/2\rightarrow1$	$170\pm50$	-
C18O/C17O	$1\rightarrow0/1\rightarrow0$	$5\pm2$	$6\pm2$
	$2\rightarrow1/2\rightarrow1$	$7\pm2$	-
CS	$2\rightarrow1/3\rightarrow2$	$1.7\pm0.3$	$1.8\pm0.6$
	$2\rightarrow1/5\rightarrow4$	-	$7\pm3$
CS/13CS	$2\rightarrow1/2\rightarrow1$	>4	-
SO	$3_2\rightarrow2_1/4_3\rightarrow3_2$	$1.4\pm0.9$	-
CS/SO	$2\rightarrow1/3_2\rightarrow2_1$	$8\pm3$	$3\pm1$
	$3\rightarrow2/4_3\rightarrow3_2$	$7\pm3$	-
HCN	$1\rightarrow0/3\rightarrow2$	$2.6\pm0.4$	-
HCN/H13CN	$1\rightarrow0/1\rightarrow0$	$20\pm10$	-
HCN/HNC	$1\rightarrow0/1\rightarrow0$	-	$1.7\pm0.8$
HCO+	$1\rightarrow0/3\rightarrow2$	$2.7\pm0.4$	-
12CO/CS	$2\rightarrow1/2\rightarrow1$	$23\pm5$	$31\pm6$
	$3\rightarrow2/3\rightarrow2$	$36\pm5$	$52\pm10$
12CO/HCN	$1\rightarrow0/1\rightarrow0$	$7.5\pm0.9$	$17\pm4$
	$3\rightarrow2/3\rightarrow2$	$18\pm3$	-
12CO/HCO+	$1\rightarrow0/1\rightarrow0$	$8\pm1$	$13\pm4$
	$3\rightarrow2/3\rightarrow2$	$20\pm3$	-
HCN/HCO+	$1\rightarrow0/1\rightarrow0$	$1.2\pm0.2$	$0.7\pm0.2$
	$3\rightarrow2/3\rightarrow2$	$1.2\pm0.2$	-
HCO+/H13CO+	$1\rightarrow0/1\rightarrow0$	$9\pm3$	-
HCO+/13CO	$1\rightarrow0/1\rightarrow0$	$2.0\pm0.2$	$1.2\pm0.3$
HCO+/CS	$3\rightarrow2/3\rightarrow2$	$1.7\pm0.3$	-
H13CN	$1\rightarrow0/3\rightarrow2$	>3	-
H2CO	$\frac{2_{1,2}\rightarrow1_{1,1}+2_{1,1}\rightarrow1_{1,0}}{2_{0,2}\rightarrow1_{0,1}}$	$2.3\pm0.7$	-
H2CO	$2_{1,2}\rightarrow1_{1,1}/2_{1,1}\rightarrow1_{1,0}$	$1.2\pm0.2$	-
H2CO	$2_{1,2}\rightarrow1_{1,1}/2_{0,2}\rightarrow1_{0,1}$	$1.3\pm0.2$	-

For both galaxies we find a ¹²CO $2\rightarrow 1/1\rightarrow 0$intensity ratio of $\approx$1 which is typical for star-burst/Seyfert galaxies (Aalto et al. 1991; Dahlem et al. 1993). Also, the CO $1\rightarrow 0$/HCN $1\rightarrow 0$ intensity ratios are similar to those found in (other) Seyfert galaxies; with NGC 4945 showing the same ratio as for the more distant Seyferts and Circinus showing a similar ratio to the near-by sample (see Sect. 1). In NGC 4945 our ¹²CO and ¹³CO $2\rightarrow 1/1\rightarrow 0$ ratio agrees with that previously determined (e.g. Dahlem et al. 1993; Henkel et al. 1994).

In order to estimate the prevailing physical conditions and column densities in the molecular gas, we have performed radiative transfer calculations. In order to complement this, in temperature and column density estimates we have also applied local thermodynamic equilibrium (LTE) calculations. The presented column density estimates are peak values in the sense that the intensities have been corrected for finite source and beam size. However, small-scale (i.e. structures smaller than the assumed source size) beam-filling has not been taken into account. Conversion to beam-averaged quantities is obtained by multiplication by $\eta _{\rm bf}$ (see Table 3 for the definition of this).

2.2.1 The radiative transfer results

The code used here is described in Jansen (1995): The excitation problem involves statistical equilibrium of a multi-level system (incorporating typically 12 rotational levels in the lowest vibrational state of the molecule in question). The radiative transfer is treated in the mean-escape probability (MEP) approximation: like the large velocity gradient (LVG) method (e.g. Leung & Liszt 1976), this uses a local source function in which the optical depth in each transition determines the mean escape probability (Osterbrock 1989) of a photon from a typical location within a cloud. The model gas cloud has a spherical shape and a uniform density and kinetic temperature. The gas density and the temperature are estimated by fitting the observed line ratios of different transitions of CO, CS, HCN and HCO⁺ to the excitation and radiative transfer model. The intensity ratios for each species were constrained by a routine which tested the goodness-of-fit by calculating the $\chi ^2$error of the MEP integrated intensity ratios for each of the observed values. The ¹²CO and C¹⁸O intensity ratios gave limits for the column density whereas ¹³CO was quite specific (e.g. using $2\rightarrow1/1\rightarrow0=1.9$ in NGC 4945). Examining the results we selected, for example, the ¹²CO column density which gave the observed ¹²CO $1\rightarrow 0$ to ¹³CO $1\rightarrow 0$ intensity ratio. This process was repeated for each transition of each isotopomer.

For NGC 4945 this gave $N(^{12}{\rm CO})/N(^{13}{\rm CO})\approx50$ for the relative column densities and solutions could only be found for $T_{\rm kin}\approx100$ K and $n_{{\rm H}_2}\approx3~10^3$ cm^-3, i.e. as Henkel et al. (1994). Constraining the HCN solutions using the $1\rightarrow0/3\rightarrow2$ and the CO/HCN $1\rightarrow0/1\rightarrow0$ and $3\rightarrow2/3\rightarrow2$ line ratios, we could obtain a solution for $n_{{\rm H}_2}\approx10^4-10^5$ cm^-3, regardless of kinetic temperature. For CS at the kinetic temperature defined by the CO, the $2\rightarrow1/3\rightarrow2$ line ratios only permit a value of $n_{{\rm H}_2}\approx10^4$ cm^-3. Note that solutions at this molecular hydrogen density can be found over a range of kinetic temperatures (e.g. $T_{\rm kin}=10$ K, $N_{\rm CS}/\Delta v\approx6~10^{14}$ cm $^{-2}~({\rm km~s}^{-1})^{-1}$ and $T_{\rm kin}=150$ K, $N_{\rm CS}/\Delta v\approx5~10^{13}$ cm $^{-2}~({\rm km~s}^{-1})^{-1}$), but for densities higher than this ( $n_{{\rm H}_2}=10^5$ cm^-3), solutions can only be found for  K (for $n_{{\rm H}_2}=10^6$ cm^-3 there are no solutions). It is important to note that these results apply to the observed intensity ratios (within errors) only, and so still hold if the CS traces a different gas component to the CO. The upper limit for the $1\rightarrow0/3\rightarrow2$ transitions of H¹³CN together with the HCN/H¹³CN $1\rightarrow0/1\rightarrow0$ ratio gives the range of column densities shown in Table 5, where the MEP results are summarised. Note that, as for the CO isotopomers, we obtain a HCN/H¹³CN column density ratio of $\approx$50-200.

 

 

Table 5: The MEP solutions for NGC 4945 for $T_{\rm kin}=100$ K. The column density is derived for a cloud velocity width of $30{\rm ~km~s}^{-1}$, Eq. (1). These solutions satisfy both the observed line ratios for each isotopomer and the line ratios between isotopomers (within uncertainties)

Molecule	$n_{{\rm H}_2}$ [cm-3]	N [cm-2]
12CO	3 103	$\approx$6 1018
13CO	3 103	1.2-1.5 1017
C18O	3 103	$\approx$3 1016
HCN	104	1.5-2.4 1016
	105	$\approx$3 1015
CS	104	1.5-2.4 1015
HCO+	104	1.5-2.1 1015
H13CN	104	1-3 1014

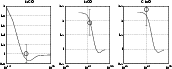Figure 3: MEP solutions for the CO isotopomers per velocity interval at $T_{\rm kin}=100$ K, $n_{{\rm H}_2}=3~10^3$ cm-3 (i.e. for NGC 4945). The plots show the $2\rightarrow 1/1\rightarrow 0$ intensity ratio against the column density per unit line width [cm $^{-2}~({\rm km~s}^{-1})^{-1}$] for each isotopomer, and give N(12CO $)/\Delta v \gtrsim 3~10^{16}$ cm $^{-2}~({\rm km~s}^{-1})^{-1}$, $(N^{13}{\rm CO})/\Delta v\sim 10^{16}$ cm $^{-2}~({\rm km~s}^{-1})^{-1}$ and $N({\rm C}^{18}O)/\Delta v\lesssim 10^{16}$ cm $^{-2}~({\rm km~s}^{-1})^{-1}$. In this and Fig. 4, the circles indicate the nominal observed values with the associated uncertainties shown as bars. Note that these are only the solutions for each isotopomer and are therefore valid over the range of column densities constrained by the error bars. In the case of the final solutions (Tables 5 and 6), however, we also take into account the ratios between different isotopomers

For the CO values in Circinus, solutions could only be found for $T_{\rm kin}\approx50{-}80$ K and $n_{{\rm H}_2}=2~10^3$ cm^-3, i.e. as the warm gas solution of Curran et al. (1998), where we obtained solutions of the CO isotopomers convolved to the ¹²CO $1\rightarrow 0$ beam. The column densities give $N(^{12}{\rm CO})/N(^{13}{\rm CO})=60{-}80$. Since we have only the $1\rightarrow 0$transition available in this galaxy, models for HCN and HCO⁺ are not so easy to constrain. Assuming, however, a similar kinetic temperature between the various tracers and using the ¹²CO/HCN $1\rightarrow0/1\rightarrow0$ and ¹²CO/HCO⁺ $1\rightarrow0/1\rightarrow0$ ratios (i.e. the HCN and CO trace similar regions), solutions may be found for $n_{{\rm H}_2}\sim10^4{-}10^6$ cm^-3. From the $2\rightarrow1/3\rightarrow2$and $2\rightarrow1/5\rightarrow4$ ratios of CS, we could only find a solution at a molecular hydrogen density of $n_{{\rm H}_2}\sim10^5$ cm^-3. Note that solutions using this molecule could only be obtained over a similar temperature range as for the CO. No solutions which satisfy the observed CO/CS ratios at $n_{{\rm H}_2}\approx10^4$ or 10⁶ cm^-3 could be found, regardless of kinetic temperature. The results are summarised in Table 6.

 

 

Table 6: The MEP solutions for Circinus for $T_{\rm kin}=50{-}80$ K. The column density is derived for a cloud velocity width of $10{\rm ~km~s}^{-1}$, Eq. (1). These solutions satisfy both the observed line ratios for each isotopomer and the line ratios between isotopomers (within uncertainties)

Molecule	$n_{{\rm H}_2}$ [cm-3]	N [cm-2]
12CO	2 103	$\approx$2 1018
13CO	2 103	2.5-3 1016
HCN	104	$\approx$1 1015
	105	$\approx$1 1014
	106	<1 1014
CS	105	$\approx$5 1013
HCO+	105	$\approx$3 1013

Figure 4: MEP solutions for the CO isotopomers per velocity interval at $T_{\rm kin}=50$ K, $n_{{\rm H}_2}=2~10^3$cm-3 (i.e. for Circinus). The plots show the $2\rightarrow 1/1\rightarrow 0$ intensity ratio against the column density per unit line width [cm $^{-2}~({\rm km~s}^{-1})^{-1}$] for each isotopomer, and give $N(^{12}{\rm CO})/\Delta v\gtrsim 10^{15}$ cm $^{-2}~({\rm km~s}^{-1})^{-1}$ and $N(^{13}{\rm CO})/\Delta v\lesssim 10^{16}$ cm $^{-2}~({\rm km~s}^{-1})^{-1}$

Using the total observed line emission to estimate an individual cloud velocity width (neglecting effects due to cloud-cloud shielding) from

$$\Delta v = \left(1+\frac{\Theta_{\rm mb}^2}{\Theta_{\rm source}^2}\right) \sqrt{4\ln2 /\pi} \frac{I_{\rm mb}}{T_{\rm MEP}},$$ (1)

where $I_{\rm mb}$ is the total velocity integrated intensity (Tables 1 and 2) and $T_{\rm MEP}$ is the antenna temperature obtained from the MEP analysis, we find velocity widths of $\approx$ $30{\rm ~km~s}^{-1}$ and $\approx$ $10{\rm ~km~s}^{-1}$ for NGC 4945 and Circinus, respectively. These values are applied to the derived column densities per unit line width to give the values shown in Tables 5 and 6.

2.2.2 The LTE results

In order to complement the MEP results, we applied the LTE model to the observed data. Since this method depends only upon the excitation temperature ( $T_{\rm ex}$) and the column density, it is the simplest way to analyse the observed line ratios. Here we have assumed that the excitation temperature is the same for both ¹²CO and ¹³CO.

 

 

Table 7: The minimum $\chi ^2$ LTE solutions. Note that, unlike previously, these are beam averaged column densities (based upon the velocity integrated intensities)

Galaxy	$T_{\rm ex}$ [K]	$N(^{12}{\rm CO})$ [cm-2]	$N(^{12}{\rm CO})/N(^{13}{\rm CO})$
NGC 4945	20	2 1019	40
Circinus	14	2 1018	25

From the solutions (Table 7) we see that the LTE results differ significantly from the solutions obtained from the radiative transfer calculations, although the derived column densities are reasonable, cf. $\approx$8 10¹⁹ cm^-2 for the peak column densities in NGC 4945, obtained by multiplying the ¹²CO column density per unit line width ($\approx$2 10¹⁷ cm $^{-2}~({\rm km~s}^{-1})^{-1}$) over the full line width (Fig. 1). For Circinus the value obtained is closer to that for an individual cloud (see Table 6). Applying the temperatures and column densities from the LTE solutions to the MEP code we can satisfy the observed intensity ratios for $N(^{12}{\rm CO})>6~10^{19}$ cm^-2 and >5 10¹⁹ cm^-2 in NGC 4945 and Circinus, respectively. We cannot, however, reproduce the observed ¹³CO ratios: ¹³CO $2\rightarrow1/1\rightarrow0<1.1$ for NGC 4945 and <0.87 (or $\approx$0.9 for $N(^{13}{\rm CO})>2~10^{18}$ cm^-2) for Circinus using the molecular hydrogen densities obtained from the MEP solutions.