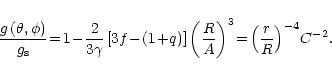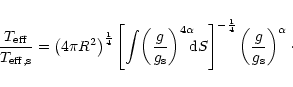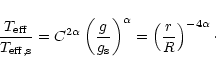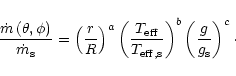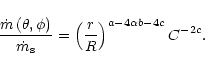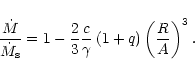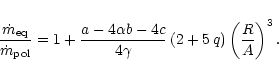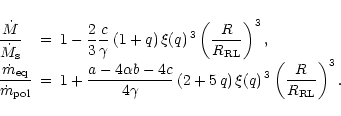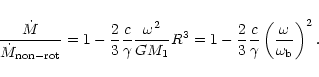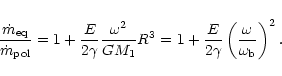A&A 367, 513-520 (2001)
DOI: 10.1051/0004-6361:20000444
On winds from giants in binary systems
A. Frankowski
- R. Tylenda
Nicolaus Copernicus Astronomical Center, Polish Academy of
Sciences, Rabianska 8, 87-100 Torun, Poland
Received 3 July 2000 / Accepted 4 December 2000
Abstract
We explore the influence of a companion on the wind from a giant
in a binary system. We have developed a simple method for estimating the
enhancement and intrinsic non-sphericity of the outflow in this case.
Assuming the Roche model (modified to account for the reduced effective
gravity of the giant), local stellar parameters ( ,
g) are
calculated. This, according to our approach, allows to derive
the local mass loss rate.
The influence of varying the model parameters on the results is studied.
A relation between the ratio of the stellar radius to the Roche lobe radius
and the overall wind enhancement is obtained both numerically and in an
analytical approximation. A similar relation is derived for the
equatorial-to-polar wind intensity contrast.
,
g) are
calculated. This, according to our approach, allows to derive
the local mass loss rate.
The influence of varying the model parameters on the results is studied.
A relation between the ratio of the stellar radius to the Roche lobe radius
and the overall wind enhancement is obtained both numerically and in an
analytical approximation. A similar relation is derived for the
equatorial-to-polar wind intensity contrast.
Key words: binaries: general - stars: mass-loss - stars: late-type -
stars: AGB and post-AGB
Mass loss is known to be a key factor for stellar
evolution in late stages. Matter escapes easily because of
high luminosities and low surface
gravities of evolved, cool giants.
On the Red Giant Branch (RGB) and especially on
the Asymptotic Giant Branch (AGB) the mass loss rate can be larger,
sometimes by orders of
magnitude, than the nuclear burning rate. Therefore it is mass
loss which determines the AGB lifetime and which plays the key
role in the stellar initial-final mass relation. Thanks to the stellar winds
intermediate mass stars avoid supernova explosions. Instead, due to the
copious mass loss terminating the AGB they give
origin to planetary nebulae with their amazing shapes.
The stellar winds also affect the evolution of the interstellar medium by
influencing its dynamics and spreading elements created in the stellar interiors.
It is also believed that interstellar dust has its origin in cool atmospheres
and dense winds blowing from the RGB and AGB stars.
The mass loss process becomes even more important, more interesting and
more complex when it takes place in a binary system.
The most dramatic phenomena occur when an RGB or AGB star
happens to fill its Roche lobe. In this case,
a dynamically unstable mass transfer to the companion takes place. This
leads to the formation of a common envelope and a very rapid
evolution of the entire system.
However, even far from the Roche lobe filling the extended atmosphere of
an RGB or AGB star can be significantly disturbed by binarity.
The gravitational attraction from the companion and the
centrifugal force due to the rotation of the system are expected to increase
the mass loss rate. Mass loss from the star also means mass and angular
momentum loss from the system. Certain mass and angular momentum accretion on the
companion is also possible. The binary
parameters are therefore expected to evolve accordingly which, in turn, will
affect the stellar mass loss. Thus the evolution of the RGB and AGB stars in
binary systems deserves thorough studies as it can be significantly different
from that of the single stars.
In this paper we try to investigate effects of binarity on the mass loss
rate and the wind structure from cool, evolved stars by analysing
intrinsic conditions under which the mass loss process occurs. Generally
speaking, mass loss is driven by physical conditions in the stellar
atmosphere. Physics involved in mass loss from cool, extended atmospheres
is very complex and difficult for theoretical modelling although a
significant progress has recently been made in its understanding (e.g. Bowen
& Willson 1991; Arndt et al. 1997).
In the classical theory of (plane-parallel) stellar atmospheres
the physical structure of the
atmosphere, for a given chemical compositon, is determined by two parameters:
effective temperature,
 ,
and gravity, g.
In the case of the RGB and AGB stars the situation is
certainly more complex. Geometrical extension of the atmosphere and phenomena
generated in the stellar interior, e.g. pulsations and convection,
influence
the structure of the atmosphere. The ratio of the photospheric
scale height,
,
and gravity, g.
In the case of the RGB and AGB stars the situation is
certainly more complex. Geometrical extension of the atmosphere and phenomena
generated in the stellar interior, e.g. pulsations and convection,
influence
the structure of the atmosphere. The ratio of the photospheric
scale height, 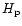 (
(
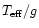 ), to the stellar radius, R,
can be considered as a measure of
the geometrical extension. If we define
), to the stellar radius, R,
can be considered as a measure of
the geometrical extension. If we define 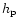 as
as
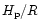 then
it seems reasonable to
adopt, at least to a first approximation, that
then
it seems reasonable to
adopt, at least to a first approximation, that
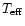 ,
g and
,
g and 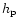 are principal parameters of the RGB and AGB atmospheres and
their winds. This notion finds its support in results of modelling winds from the red
giants. Bowen & Willson (1991) have found that the mass loss rate
from the AGB stars depends first of all on the density scale height in
the atmosphere. Arndt et al. (1997) obtained formulae in which the
AGB wind characteristics are functions of the effective temperature, stellar
mass, and luminosity.
In the famous wind formula for red giants of
Reimers (1975), the mass loss rate depends on the stellar
mass, radius and luminosity.
However, the formulae of Arndt et al. and Reimers can be reduced to
dependencies on local atmospheric parameters,
i.e.
are principal parameters of the RGB and AGB atmospheres and
their winds. This notion finds its support in results of modelling winds from the red
giants. Bowen & Willson (1991) have found that the mass loss rate
from the AGB stars depends first of all on the density scale height in
the atmosphere. Arndt et al. (1997) obtained formulae in which the
AGB wind characteristics are functions of the effective temperature, stellar
mass, and luminosity.
In the famous wind formula for red giants of
Reimers (1975), the mass loss rate depends on the stellar
mass, radius and luminosity.
However, the formulae of Arndt et al. and Reimers can be reduced to
dependencies on local atmospheric parameters,
i.e.
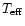 ,
g and
,
g and 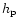 (see next section).
This becomes important in the case of
a binary system, where the mass losing star can be noticeably distorted
by tidal forces. Differences in the local conditions over the stellar
surface may then lead to different
local intensities of the outflow. Thus the wind will show an intrinsic
directivity and may be globally enhanced.
(see next section).
This becomes important in the case of
a binary system, where the mass losing star can be noticeably distorted
by tidal forces. Differences in the local conditions over the stellar
surface may then lead to different
local intensities of the outflow. Thus the wind will show an intrinsic
directivity and may be globally enhanced.
Next section presents details of our approach.
Results of numerical modelling of the wind structure are given and discussed in
Sect. 3. An analytical approximation, which helps to understand and
interpret the results, is developed in Sect. 4. General discussion and
summary are given in Sect. 5.
Preliminary results of this study have been presented
in Frankowski & Tylenda (2000).
Principal assumptions made in our model are the following: 1. the binary orbit is
circular, the giant corotates with the orbital motion, and the gravitational
fields of both components can be
treated as originating from point masses -
hence the Roche model for the effective potential applies; 2. the stellar
surface is defined by the Roche equipotential surface; 3. the local mass
loss rate per unit area, 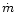 ,
is a function of the
local stellar parameters, namely the effective temperature,
,
is a function of the
local stellar parameters, namely the effective temperature,
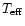 ,
gravity, g, and the ratio of the photospheric scale height
to the stellar radius,
,
gravity, g, and the ratio of the photospheric scale height
to the stellar radius, 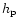 .
.
Our formulae for 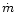 have been derived from relations
obtained by other authors, either from theoretical modelling or observations.
These relations usually link the global mass loss rate,
have been derived from relations
obtained by other authors, either from theoretical modelling or observations.
These relations usually link the global mass loss rate, 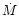 ,
to the global stellar parameters, i.e. stellar mass,
M, radius, R, and luminosity, L.
They can be transformed to dependencies on the
local atmospheric parameters using standard definitions and relations, i.e.
,
to the global stellar parameters, i.e. stellar mass,
M, radius, R, and luminosity, L.
They can be transformed to dependencies on the
local atmospheric parameters using standard definitions and relations, i.e.
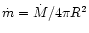 ,
,
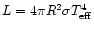 ,
g=GM/R2 and
,
g=GM/R2 and
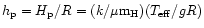 (where
(where 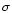 is the
Stefan-Boltzmann constant, G is the gravitational constant, k is the
Boltzmann constant,
is the
Stefan-Boltzmann constant, G is the gravitational constant, k is the
Boltzmann constant, 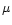 is the mean molecular weight, and
is the mean molecular weight, and  is
the hydrogen atom mass). In this way the Reimers' (1975) law can be
written in the form
is
the hydrogen atom mass). In this way the Reimers' (1975) law can be
written in the form
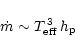 |
(1) |
while Eq. (2) of Arndt et al. (1997) becomes
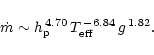 |
(2) |
Later on in this paper we will not use, however, the mass loss formulae in
the form as Eqs. (1) and (2). The reason is that the
dependence on g and
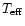 is not there easily seen as it is partially
hidden in
is not there easily seen as it is partially
hidden in 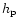 .
We have found that the discussion and
especially the analytical considerations in Sect. 4 become much
more clear if
.
We have found that the discussion and
especially the analytical considerations in Sect. 4 become much
more clear if
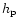 is replaced by
is replaced by
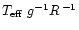 in the mass loss
formulae. Thus the Reimers' law becomes
in the mass loss
formulae. Thus the Reimers' law becomes
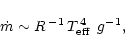 |
(3) |
while the relation of Arndt et al. is now written as
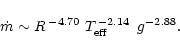 |
(4) |
The stellar radius which appears in Eqs. (3) and (4) is
usually considered as a global stellar parameter. However, for a tidally
distorted star the radius can be interpreted as a "local'' parameter in a
sense that it varies from point to point over the stellar surface.
Now, in general form, we can write:
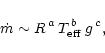 |
(5) |
where the exponents a, b, and c depend on the particular
form of the mass loss formula used.
An important point here is that gravity, as a counteracting factor to
mass loss, appears in the mass loss formulae of this kind with a
negative exponent (see Eqs. (3) and (4)).
Thus the general pattern is:
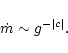 |
(6) |
In order to obtain the surface distribution of the effective temperature for
a tidally distorted star we have applied two approaches.
(A) An explicit relation linking
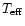 with g of the form:
with g of the form:
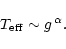 |
(7) |
This
includes the case of a completely uniform temperature distribution (
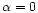 ), the von Zeipel's relation (von Zeipel 1924;
), the von Zeipel's relation (von Zeipel 1924;
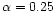 ),
and the Lucy's relation (Lucy 1967), developed as a more suitable
for convective stars variant of the von Zeipel's relation (
),
and the Lucy's relation (Lucy 1967), developed as a more suitable
for convective stars variant of the von Zeipel's relation (
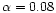 ).
(B) An assumption that the luminosity is spread uniformly over the solid angle,
and therefore the effective temperature depends only on the radius and
the inclination of a given surface element.
For a star deep in its Roche lobe this is equivalent to a relation
).
(B) An assumption that the luminosity is spread uniformly over the solid angle,
and therefore the effective temperature depends only on the radius and
the inclination of a given surface element.
For a star deep in its Roche lobe this is equivalent to a relation
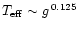 ,
but results in a much flatter temperature
distribution when the giant starts to fill its Roche lobe. In particular,
this allows to avoid the temperature going to zero at the
"sub-companion'' point (where
,
but results in a much flatter temperature
distribution when the giant starts to fill its Roche lobe. In particular,
this allows to avoid the temperature going to zero at the
"sub-companion'' point (where
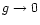 ), what occurs in the (A)
case.
), what occurs in the (A)
case.
We have introduced a free parameter, 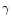 ,
describing the effectiveness
of the Newtonian gravitational force. This has been done to account for
effects of pulsation, radiation pressure, and
convective motions acting to diminish the gravity on the giant's surface.
Thus we assume that the
gravitational acceleration from the giant alone is:
,
describing the effectiveness
of the Newtonian gravitational force. This has been done to account for
effects of pulsation, radiation pressure, and
convective motions acting to diminish the gravity on the giant's surface.
Thus we assume that the
gravitational acceleration from the giant alone is:
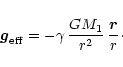 |
(8) |
In the context of early type stars a similar formulation has been proposed
e.g. by Schuerman (1972).
In our calculations, values of 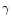 ranging from 1.0 to 0.1 have been used.
ranging from 1.0 to 0.1 have been used.
With the assumptions described above, we have calculated sequences of models,
representing stars filling an
increasing fraction of their Roche lobes for various mass ratios, q.
The filled fraction of the giant's Roche lobe can be represented by the
ratio of the giant's volume radius, R, to the Roche lobe volume radius,
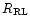 :
:
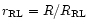 .
(The volume radius is defined as
a radius of a sphere of the same volume as the volume of the considered object.)
For each point of the stellar surface we have computed radius, gravity
and effective temperature (relative to the spherical case). This allowed us
to evaluate the local mass loss rate.
.
(The volume radius is defined as
a radius of a sphere of the same volume as the volume of the considered object.)
For each point of the stellar surface we have computed radius, gravity
and effective temperature (relative to the spherical case). This allowed us
to evaluate the local mass loss rate.
Integrating 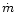 over the
whole surface leads to the total mass loss rate, which can be compared
with the mass loss rate for a single
(spherical) star of the same intrinsic parameters (L, M, R).
Further, an intensity contrast between the equatorial and polar mass loss rates
can be calculated as a ratio of the local mass loss rate averaged along
the stellar equator,
over the
whole surface leads to the total mass loss rate, which can be compared
with the mass loss rate for a single
(spherical) star of the same intrinsic parameters (L, M, R).
Further, an intensity contrast between the equatorial and polar mass loss rates
can be calculated as a ratio of the local mass loss rate averaged along
the stellar equator,
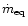 ,
to the polar mass loss rate,
,
to the polar mass loss rate,
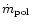 (the latter is usually close to the minimum value of
(the latter is usually close to the minimum value of 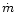 ).
).
3 Results
The most important results of our study are presented in
Figs. 1-4.
Figures 1a-d show the local mass loss rates
represented by grayscale. For each figure black
denotes maximum and white - minimum in the mass loss rate.
The mass loss rate at the dotted line is equal to that of a single,
undistorted (i.e. spherical) star. It marks the border between the polar
regions where the mass loss rate is lower, and the "equatorial strip'' where
it is higher than for the single star. The calculations have been done using
the local mass loss rate according to
the Arndt et al. prescription (Eq. (4)).
The gravity effectiveness factor
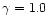 has been adopted.
The effective temperature surface distribution follows from
the assumption of uniform flux distribution over the solid angle (case (B)
described in Sect. 2).
has been adopted.
The effective temperature surface distribution follows from
the assumption of uniform flux distribution over the solid angle (case (B)
described in Sect. 2).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{10070f1.eps}\end{figure}](/articles/aa/full/2001/08/aa10070/Timg42.gif) |
Figure 1:
a-d) The local mass loss rate per unit area across
the surface of a giant in a binary system.
Dark and light regions have, respectively, high and low mass loss rate per
unit area. At the dotted line the local mass loss rate is equal to that of
a single star. The mass loss formula of Arndt et al. has been applied.
The mass ratio is q = 0.5. The gravity effectiveness is
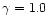 .
Case (B) of the temperature surface distribution is assumed (see text).
a) For the ratio of the stellar radius
to the Roche lobe volume radius .
Case (B) of the temperature surface distribution is assumed (see text).
a) For the ratio of the stellar radius
to the Roche lobe volume radius
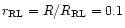 .
b) For .
b) For
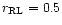 .
c) For .
c) For
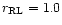 .
d) The same as b), but viewed from the opposite hemisphere .
d) The same as b), but viewed from the opposite hemisphere |
| Open with DEXTER |
Figures 1a-c have been obtained for the mass ratio q=0.5 and
the ratio of the giant's volume radius to the critical Roche surface volume radius
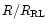 = 0.1, 0.5, 1.0, respectively. The stars are viewed from the
orbital plane, with the hemisphere facing the companion being closer to the
observer. Figure 1d presents for comparison the q = 0.5,
= 0.1, 0.5, 1.0, respectively. The stars are viewed from the
orbital plane, with the hemisphere facing the companion being closer to the
observer. Figure 1d presents for comparison the q = 0.5,
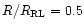 case (the same as in Fig. 1b) viewed from the opposite hemisphere.
case (the same as in Fig. 1b) viewed from the opposite hemisphere.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{10070f2.eps}\end{figure}](/articles/aa/full/2001/08/aa10070/Timg45.gif) |
Figure 2:
a and b) The dependence of the total mass loss rate enhancement,
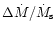 ,
on the ,
on the
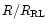 ratio: for the mass
loss formula of Arndt et al. a) and for the Reimers' law b).
The effective temperature surface distribution is uniform.
Results for
ratio: for the mass
loss formula of Arndt et al. a) and for the Reimers' law b).
The effective temperature surface distribution is uniform.
Results for
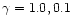 (thick and thin symbols, respectively) and
q = 1.0, 0.1 (full and dashed lines, respectively) are shown. Points
denote numerical results, lines - analytical relations
(thick and thin symbols, respectively) and
q = 1.0, 0.1 (full and dashed lines, respectively) are shown. Points
denote numerical results, lines - analytical relations |
| Open with DEXTER |
Figure 2 plots the enhancement of the total mass loss rate caused by
the presence of the
binary companion,
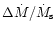 ,
against the
,
against the
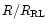 ratio.
Note the logarithmic scale on both axes. Points represent the numerical results,
lines - the analytical relation derived in Sect. 4, i.e.
ratio.
Note the logarithmic scale on both axes. Points represent the numerical results,
lines - the analytical relation derived in Sect. 4, i.e.
Thick lines and symbols correspond to
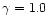 ,
the thin ones - to
,
the thin ones - to
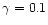 .
Figure 2a has been obtained with
the Arndt et al. mass loss formula,
while Fig. 2b is for the Reimers' law.
.
Figure 2a has been obtained with
the Arndt et al. mass loss formula,
while Fig. 2b is for the Reimers' law.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{10070f3.eps}\end{figure}](/articles/aa/full/2001/08/aa10070/Timg49.gif) |
Figure 3:
a and b)The dependence of the equatorial-to-polar wind intensity contrast,
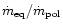 ,
on the ,
on the
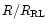 ratio: for the
mass loss formula of Arndt et al. a) and for the Reimers' law b).
The effective temperature surface distribution is uniform.
The same notation as in Fig. 2
ratio: for the
mass loss formula of Arndt et al. a) and for the Reimers' law b).
The effective temperature surface distribution is uniform.
The same notation as in Fig. 2 |
| Open with DEXTER |
Figure 3 presents the wind intensity contrast as a function of the
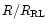 ratio.
For clarity of the functional dependence,
ratio.
For clarity of the functional dependence,
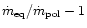 instead of
instead of
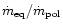 is plotted.
Again, note the logarithmic scale on both axes. As in Fig. 2, points
represent the numerical results, lines - the analytical relation derived in
Sect. 4, i.e.
is plotted.
Again, note the logarithmic scale on both axes. As in Fig. 2, points
represent the numerical results, lines - the analytical relation derived in
Sect. 4, i.e.
The cases of
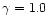 and
and
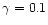 are marked in the same way
as in Fig. 2.
Figure 3a is for the Arndt et al. mass loss formula,
Fig. 3b - for the Reimers' law.
are marked in the same way
as in Fig. 2.
Figure 3a is for the Arndt et al. mass loss formula,
Fig. 3b - for the Reimers' law.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{10070f4.eps}\end{figure}](/articles/aa/full/2001/08/aa10070/Timg52.gif) |
Figure 4:
a and b) The dependence of the equatorial-to-polar wind intensity contrast,
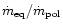 ,
on the ,
on the
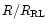 ratio for different
temperature surface distribution laws: a) the
mass loss formula of Arndt et al., b) the Reimers' law.
Results for q = 1.0,
ratio for different
temperature surface distribution laws: a) the
mass loss formula of Arndt et al., b) the Reimers' law.
Results for q = 1.0,
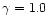 are shown. Points denote numerical
results, lines - analytical relations
are shown. Points denote numerical
results, lines - analytical relations |
| Open with DEXTER |
Figure 4 shows the influence of the temperature distribution
law on the
wind intensity contrast. Results of case (A) with
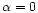 ,
0.08,
0.25 and of case (B) are displayed for q = 1.0 and
,
0.08,
0.25 and of case (B) are displayed for q = 1.0 and
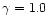 .
As in Figs. 2 and 3, points represent
the numerical results, lines - the derived analytical relation.
Figure 4a is for the Arndt et al. mass loss formula,
Fig. 4b - for the Reimers' law. In the case of the Reimers'
formula, the model with
.
As in Figs. 2 and 3, points represent
the numerical results, lines - the derived analytical relation.
Figure 4a is for the Arndt et al. mass loss formula,
Fig. 4b - for the Reimers' law. In the case of the Reimers'
formula, the model with
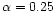 is not shown, because it has a reversed intensity
contrast (the wind is more intense on the poles than at the equator - see
Sect. 5).
is not shown, because it has a reversed intensity
contrast (the wind is more intense on the poles than at the equator - see
Sect. 5).
We have also made analytical considerations in order to obtain
approximate expressions for
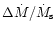 and for
and for
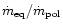 .
As usual,
analytical formulae help to understand and interpret the numerical results.
Our analysis has been done in the limit of small R/A
(which is equivalent to small
.
As usual,
analytical formulae help to understand and interpret the numerical results.
Our analysis has been done in the limit of small R/A
(which is equivalent to small
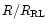 but makes the formulae more clear).
but makes the formulae more clear).
Let us define a corotating spherical coordinate system (
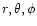 ), with the origin at the center of mass of the giant, with the
), with the origin at the center of mass of the giant, with the
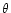 angle measured from the axis parallel to the binary rotation axis,
and with
angle measured from the axis parallel to the binary rotation axis,
and with 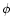 measured in the orbital plane from the axis pointing to the
companion.
measured in the orbital plane from the axis pointing to the
companion.
The stellar surface is then defined as a function
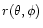 .
In order to use Eq. (5) for the mass loss rate, we need expressions for
.
In order to use Eq. (5) for the mass loss rate, we need expressions for
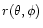 ,
,
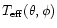 ,
and
,
and
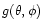 in the considered limit.
Actually, we need only formulae for r and g, because when R/A is small,
in the considered limit.
Actually, we need only formulae for r and g, because when R/A is small,
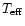 is determined by
is determined by
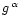 (either in (A) or in (B)
case).
(either in (A) or in (B)
case).
For a given point with coordinates (
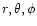 )
in the corotating
frame, the potential function,
)
in the corotating
frame, the potential function,
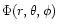 ,
is given by:
,
is given by:
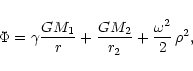 |
(9) |
where 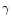 is the giant's gravity effectiveness factor,
M1 and M2 are the masses of the giant and of the
companion, respectively, r2 is the distance to the companion,
is the giant's gravity effectiveness factor,
M1 and M2 are the masses of the giant and of the
companion, respectively, r2 is the distance to the companion,
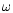 is the angular
velocity of the binary rotation, and
is the angular
velocity of the binary rotation, and 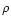 is the distance to the rotation
axis, so:
is the distance to the rotation
axis, so:
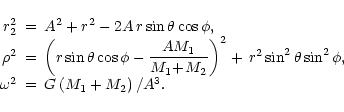 |
(10) |
In a more convenient, dimensionless form (with 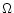 being the
dimensionless potential) one has:
being the
dimensionless potential) one has:
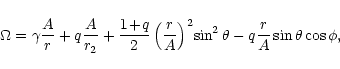 |
(11) |
where q is the mass ratio, M2/M1.
For a fixed value of 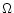 ,
Eq. (11) defines an equipotential
surface. Comparing this with the equation of surface for a single, spherical
star of radius R, i.e.
,
Eq. (11) defines an equipotential
surface. Comparing this with the equation of surface for a single, spherical
star of radius R, i.e.
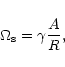 |
(12) |
and expanding into a power series in small r, one gets (up to terms of
order r2):
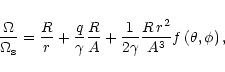 |
(13) |
where we introduced a new symbol,
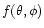 ,
denoting the angular
part of the above expression, i.e.
,
denoting the angular
part of the above expression, i.e.
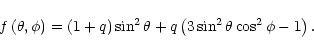 |
(14) |
From this point on, the subscript "s'' denotes quantities characterizing the
single, spherical star of a radius R.
The equation of surface of the giant can be written as:
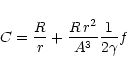 |
(15) |
where the constant C also includes the second term in the right hand side
of Eq. (13). Now it is easy to obtain the shape of
the giant (expanded in R/AC):
![\begin{displaymath}
\frac{r\left(\theta,\phi\right)}{R} =
C^{-1}\left[1+ \frac{1}{2\gamma} f\left(\frac{R}{AC}\right)^3 +
\ldots \right].
\end{displaymath}](/articles/aa/full/2001/08/aa10070/img72.gif) |
(16) |
The specific value of C for the equipotential surface of the volume radius
R can be derived from Eq. (16) and the definition of the volume
radius. As a result one gets:
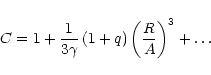 |
(17) |
This leads to a final expression for the radius, i.e.
![\begin{displaymath}
\frac{r\left(\theta,\phi\right)}{R} =
1+\frac{1}{6\gamma}\left[\,3f-2\left(1+q\right)\right]
\left(\frac{R}{A}\right)^3\cdot
\end{displaymath}](/articles/aa/full/2001/08/aa10070/img74.gif) |
(18) |
Note that Eq. (18) approximately describes
a triaxial ellipsoid with semi-axes:
![\begin{displaymath}
\begin{array}{rcl}
a_1 & = & \displaystyle R \left[1+ \left(...
...2+5q\right) \left(\frac{R}{A}\right)^3 \right]. \\
\end{array}\end{displaymath}](/articles/aa/full/2001/08/aa10070/img75.gif) |
(19) |
The effective gravity
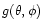 can be obtained from the gradient of the
potential function
can be obtained from the gradient of the
potential function
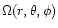 (Eq. (11)), i.e.
(Eq. (11)), i.e.
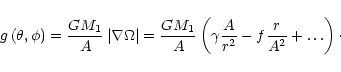 |
(20) |
A comparison with the single star case gives:
![\begin{displaymath}\frac{g\left(\theta,\phi\right)}{g_{\rm s}} =
\left(\frac{r}{...
...\frac{1}{\gamma} f
\left(\frac{R}{A}\right)^3 + \ldots\right],
\end{displaymath}](/articles/aa/full/2001/08/aa10070/img78.gif) |
(21) |
or in a convenient form adequate up to terms of order (R/A)3:
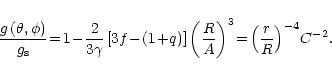 |
(22) |
The proportionality constant in the law linking
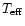 with
g (Eq. (7)) can be derived from a demand that the stellar luminosity
should be the same as in the case of spherical star. This gives:
with
g (Eq. (7)) can be derived from a demand that the stellar luminosity
should be the same as in the case of spherical star. This gives:
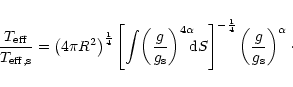 |
(23) |
Integrating the flux over the equipotential surface approximated here by a sphere
(which is justified for small R/A) yields:
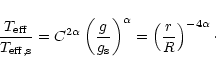 |
(24) |
Our mass loss law in the general form of Eq. (5) can be rewritten as:
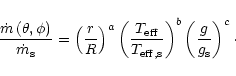 |
(25) |
Substituting Eqs. (22) and (24) into Eq. (25) one obtains:
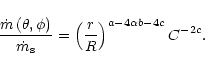 |
(26) |
In the last formula the angular variation of the local mass
loss rate is entirely enclosed in the angular variation of r/R.
C characterizes the given equipotential surface and thus is independent of
the angles. The factor C-2c describes the overall wind enhancement,
resulting from the modified shape of the potential well.
Now (again making use of the fact that for small R/A we can regard the
stellar surface as spherical) an integration of Eq. (26) over
the sphere of radius Ryields an expression for the global mass loss rate:
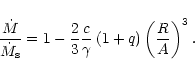 |
(27) |
The equatorial or polar wind intensity,
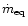 or
or
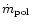 ,
can be obtained by putting the respective radius (equatorial,
,
can be obtained by putting the respective radius (equatorial,
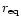 ,
or polar,
,
or polar,
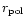 )
into Eq. (26). These radii
result from substituting the appropriate values of
)
into Eq. (26). These radii
result from substituting the appropriate values of 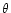 into Eq. (18)
and, in the case of
into Eq. (18)
and, in the case of
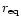 ,
averaging over the
,
averaging over the 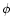 angle.
The equatorial-to-polar intensity contrast is then:
angle.
The equatorial-to-polar intensity contrast is then:
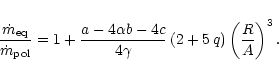 |
(28) |
In order to get formulae dependent on
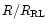 ,
instead of R/A,
one can simply introduce a new factor
,
instead of R/A,
one can simply introduce a new factor
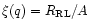 into Eqs. (27) and (28).
However, the dependences on q become then
apparently more complicated:
into Eqs. (27) and (28).
However, the dependences on q become then
apparently more complicated:
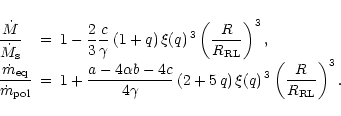 |
(29) |
Equations (29) have been used to derive the analytical lines shown in
Figs. 2-4.
5 Discussion
We have constructed a model of a tidally enhanced wind from a
giant in a binary system.
The model has five parameters. Two of them, the
mass ratio q and the Roche lobe filling factor
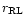 ,
characterize
the binary configuration. The other three - i.e. the gravity effectiveness
factor
,
characterize
the binary configuration. The other three - i.e. the gravity effectiveness
factor 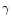 ,
the temperature distribution parameter
,
the temperature distribution parameter 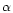 ,
and the
mass loss law - describe the properties of the mass losing giant.
Figures 1-4 and the equations derived in
Sect. 4 show
the influence of these parameters quantitatively. A more general description and
interpretation of the results is given below.
,
and the
mass loss law - describe the properties of the mass losing giant.
Figures 1-4 and the equations derived in
Sect. 4 show
the influence of these parameters quantitatively. A more general description and
interpretation of the results is given below.
At the beginning we note, that
one of the most prominent features of our model (that can be seen from
Sect. 4) is that when the Roche lobe filling factor
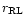 is small, the departures of all the local mass loss related quantities from
their values in the spherical case scale with the third power of R/A (and
therefore also with
is small, the departures of all the local mass loss related quantities from
their values in the spherical case scale with the third power of R/A (and
therefore also with
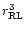 ).
Other model parameters can be thought of as constituting "scaling factors''
for this general dependence.
We shall return to this observation in more detail later on.
).
Other model parameters can be thought of as constituting "scaling factors''
for this general dependence.
We shall return to this observation in more detail later on.
As can be seen from Eq. (27), the global mass loss rate
enhancement depends only on one of three exponents in the mass loss
formula (Eq. (5)), namely on the gravity exponent, c.
The reason for this is evident from Eq. (26), as the
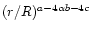 term is averaged to 1 when integrating over the
stellar surface. The angular dependence of the stellar radius contributes
only to the wind intensity contrast.
The sign of c decides whether the overall mass loss from the giant in a binary system
will be greater (negative c) or smaller (positive c) than that of the
single giant. As has been noted in Sect. 2 (see comments on
Eq. (6)), as gravity counteracts matter ejection, it seems natural to
assume c<0. Both mass loss formulae considered in this work
(Eqs. (3) and (4)) indeed have c<0, and so the overall mass
loss rate is enhanced compared to the single, non-rotating star case.
This is also true for the AGB wind formulae of Blöcker (1995)
and for the RGB wind formulae reviewed by Catelan (2000 -
with one exception, when a dependence of mass loss on radius only is assumed).
term is averaged to 1 when integrating over the
stellar surface. The angular dependence of the stellar radius contributes
only to the wind intensity contrast.
The sign of c decides whether the overall mass loss from the giant in a binary system
will be greater (negative c) or smaller (positive c) than that of the
single giant. As has been noted in Sect. 2 (see comments on
Eq. (6)), as gravity counteracts matter ejection, it seems natural to
assume c<0. Both mass loss formulae considered in this work
(Eqs. (3) and (4)) indeed have c<0, and so the overall mass
loss rate is enhanced compared to the single, non-rotating star case.
This is also true for the AGB wind formulae of Blöcker (1995)
and for the RGB wind formulae reviewed by Catelan (2000 -
with one exception, when a dependence of mass loss on radius only is assumed).
The influence of the mass ratio q is clear when R/A is used as a
variable (Eq. (27)) - the higher the mass of the companion, the
stronger is the wind enhanced. However, things may look a bit confusing when
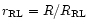 is used (see Eqs. (29) and Fig. 2).
The results shown in Fig. 2 seem to be - at first glance - counterintuitive:
the lines displaying the wind enhancement for q=0.1 lie always above the lines for
q=1.0. But a greater q means a stronger companion's influence, so why should
the global wind enhancement decrease with increasing q? This is just a
result of using
is used (see Eqs. (29) and Fig. 2).
The results shown in Fig. 2 seem to be - at first glance - counterintuitive:
the lines displaying the wind enhancement for q=0.1 lie always above the lines for
q=1.0. But a greater q means a stronger companion's influence, so why should
the global wind enhancement decrease with increasing q? This is just a
result of using
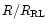 as the abscissa. The ratio of the Roche lobe
radius to the separation,
as the abscissa. The ratio of the Roche lobe
radius to the separation,
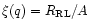 ,
decreases with
increasing q, and this causes the whole expression
,
decreases with
increasing q, and this causes the whole expression
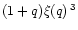 also to decrease. The increasing (1+q) term does not prevail until
also to decrease. The increasing (1+q) term does not prevail until
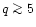 .
Thus - in the range of q considered here -
for a given
.
Thus - in the range of q considered here -
for a given
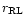 ,
the overall wind
enhancement is in fact greater for a smaller q.
,
the overall wind
enhancement is in fact greater for a smaller q.
The intrinsic structure of the wind in the presence of a companion, as described
by our model, can be outlined as follows. For a star well
inside its Roche lobe the local mass loss rate per unit area is governed by
Eq. (26). This means that maxima and minima of the local mass loss
rate coincide with extrema of the stellar radius. These are easy
to find, as the stellar surface can be approximated by an triaxial ellipsoid
(Eqs. (18) and (19)).
The principal axes of the ellipsoid are defined by: the
direction to the companion (semi-axis a1), the direction in the
orbital plane that is perpendicular to the latter (semi-axis a2), and
the direction perpendicular to the orbital plane (semi-axis a3).
Equation (19) implies also that
a1>a2>a3 for any q>0.
Magnitudes of the local mass loss rates corresponding to the semi-axes
follow this order when the expression
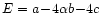 is
positive, but have a reversed order when it is negative
(see Eqs. (26) and (28)). In the first case
the global maxima of the mass loss rate occur in the directions to/from the
companion, and the global minima occur at the poles. There are also two saddle
points, corresponding to the semi-axis a2. These are the minima in the
is
positive, but have a reversed order when it is negative
(see Eqs. (26) and (28)). In the first case
the global maxima of the mass loss rate occur in the directions to/from the
companion, and the global minima occur at the poles. There are also two saddle
points, corresponding to the semi-axis a2. These are the minima in the 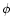 coordinate, but maxima in
coordinate, but maxima in 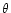 .
The values of
.
The values of 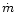 at the saddle points
are higher than (or equal to) the value for the spherical case,
at the saddle points
are higher than (or equal to) the value for the spherical case,
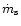 ,
when
,
when
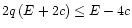 ,
otherwise they are
lower. When comparing
,
otherwise they are
lower. When comparing 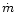 at the saddle points with the average over the whole
stellar surface,
at the saddle points with the average over the whole
stellar surface,
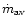 ,
the analogous condition is
,
the analogous condition is 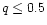 .
Thus not always there is a well-defined "equatorial strip'' of enhanced mass loss. However,
for E>0, and provided that
.
Thus not always there is a well-defined "equatorial strip'' of enhanced mass loss. However,
for E>0, and provided that 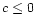 (see above),
the average equatorial mass loss rate,
(see above),
the average equatorial mass loss rate,
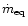 ,
is enhanced
both compared to
,
is enhanced
both compared to
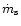 ,
as well as compared to
,
as well as compared to
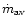 ,
independently of the mass ratio q. (As a matter of fact, the
requirement on c is even less severe, namely
,
independently of the mass ratio q. (As a matter of fact, the
requirement on c is even less severe, namely
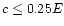 ,
and is needed
only when comparing to
,
and is needed
only when comparing to
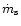 .)
.)
In the case of negative E the mass loss is most intense at
the poles and weakest in the directions to/from the companion. Also the
situation at the saddle points is changed. The condition for
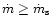 is still
is still
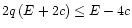 ,
but the
one for
,
but the
one for
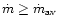 is reversed, i.e.
is reversed, i.e. 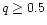 .
Further, if the mass loss from these saddle points is in fact enhanced, then
now a "meridional strip'' of enhanced mass loss is created.
If the opposite is true, there is an equatorial strip of reduced mass
loss.
.
Further, if the mass loss from these saddle points is in fact enhanced, then
now a "meridional strip'' of enhanced mass loss is created.
If the opposite is true, there is an equatorial strip of reduced mass
loss.
Finally, if E=0 the local mass loss rate per unit area is constant over
the stellar surface.
For a given mass loss law (a given set of a,b,c) it is 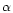 ,
the
temperature distribution parameter, that determines the sign of E.
In the case of the Reimers' mass loss formula E is positive when
,
the
temperature distribution parameter, that determines the sign of E.
In the case of the Reimers' mass loss formula E is positive when
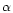 is smaller than 0.1875. For the Arndt et al. prescription
all values of
is smaller than 0.1875. For the Arndt et al. prescription
all values of 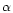 greater than
greater than
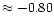 result in positive E.
Since
result in positive E.
Since 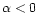 seems unrealistic, all the models with the Arndt et al. mass loss
law have an equatorially enhanced mass loss. However, the case of
Reimers' formula with
seems unrealistic, all the models with the Arndt et al. mass loss
law have an equatorially enhanced mass loss. However, the case of
Reimers' formula with
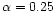 falls in the region of negative E.
The wind intensity contrast,
falls in the region of negative E.
The wind intensity contrast,
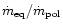 ,
is reversed - the mass
loss rate on the poles becomes greater than at the equator.
For this reason Fig. 4b does not show the case of
,
is reversed - the mass
loss rate on the poles becomes greater than at the equator.
For this reason Fig. 4b does not show the case of
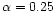 .
Nevertheless, we may conclude that for the values of
.
Nevertheless, we may conclude that for the values of 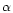 reasonable for
stars with deep convective envelopes, our model always gives the equatorial wind
enhancement, as expected for cool giants.
This holds also for the aforementioned wind formulae of Blöcker
(1995) and Catelan (2000).
reasonable for
stars with deep convective envelopes, our model always gives the equatorial wind
enhancement, as expected for cool giants.
This holds also for the aforementioned wind formulae of Blöcker
(1995) and Catelan (2000).
When the star approaches to fill its Roche lobe, an asymmetry between the
sub-companion and off-companion hemispheres develops. Mass loss
towards the companion becomes more intense than in the opposite
direction. The asymmetry grows until the gravity at the sub-companion point drops to
zero (i.e. when the inner Lagrangian point L1 is reached),
and the local mass loss rate per unit area at this point becomes infinite.
The above picture remains qualitatively the same
independently of the value of 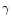 .
The effect of
.
The effect of 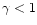 is essentially to cause the "effective Roche lobe''
to shrink. As a result, the giant fills its critical equipotential surface
even while it fits comfortably inside its clasically determined Roche lobe.
The mass loss enhancement/reduction phenomena described
above are more pronounced and the deviations from the ellipsoidal symmetry
occur for smaller values of
is essentially to cause the "effective Roche lobe''
to shrink. As a result, the giant fills its critical equipotential surface
even while it fits comfortably inside its clasically determined Roche lobe.
The mass loss enhancement/reduction phenomena described
above are more pronounced and the deviations from the ellipsoidal symmetry
occur for smaller values of
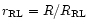 .
The quantitative
differences are evident from Eq. (29) and
Figs. 2-3. For a given
.
The quantitative
differences are evident from Eq. (29) and
Figs. 2-3. For a given
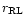 both the global mass loss enhancement and the
equatorial-to-polar intensity contrast enhancement scale as
both the global mass loss enhancement and the
equatorial-to-polar intensity contrast enhancement scale as 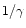 .
.
The use of 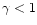 in our modelling can be justified in different ways.
As mentioned in Sect. 2 any kind of motions, like pulsations,
waves, turbulence, which are expected
to be important in the atmospheres of giants will effectively act as a
factor reducing the gravity. In the case of AGB stars there are additional
reasons why
in our modelling can be justified in different ways.
As mentioned in Sect. 2 any kind of motions, like pulsations,
waves, turbulence, which are expected
to be important in the atmospheres of giants will effectively act as a
factor reducing the gravity. In the case of AGB stars there are additional
reasons why 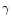 significantly smaller than 1 can be expected.
significantly smaller than 1 can be expected.
The AGB stars have dusty winds and therefore
it seems reasonable to consider, that the intensity of the wind
should strongly depend on the conditions in the dust condensation region,
which lies well above the photosphere. Replacing in our
equations R by the condensation radius,
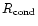 ,
and assuming, say,
,
and assuming, say,
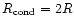 ,
pushes the maximal possible stellar radius back to
,
pushes the maximal possible stellar radius back to
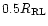 and
increases 8 times the analytical values for the enhancement/reduction
of mass loss related quantities.
Therefore it is roughly equivalent to setting
and
increases 8 times the analytical values for the enhancement/reduction
of mass loss related quantities.
Therefore it is roughly equivalent to setting
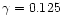 .
In reality, however, it seems more likely that it is a certain combination of
conditions in the stellar atmosphere and in the dust condensation region,
that governs the mass loss.
.
In reality, however, it seems more likely that it is a certain combination of
conditions in the stellar atmosphere and in the dust condensation region,
that governs the mass loss.
The above considerations are
consistent with the results of a study of S stars by
Jorissen & Knapp (1998).
These authors do not find any significant mass loss
enhancement for the so called "extrinsic S stars'' which are believed to be
RGB giants in binary systems. However, they find that among the "intrinsic
S stars'', which are AGB giants, those which
are in binaries tend to have the largest mass loss rates.
The assumption made by Bowen (1988) in his models of dusty
AGB winds, that the ratio of the acceleration due to radiation pressure on
dust to that due to gravity is 0.95, translates into setting
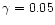 .
The idea of a reduced effective gravity of a mass losing star has also been
remarked by Jorissen et al. (1998) in connection
with short-period Ba stars.
.
The idea of a reduced effective gravity of a mass losing star has also been
remarked by Jorissen et al. (1998) in connection
with short-period Ba stars.
An interesting result has been obtained by Mürset & Schmid (1999)
from their analysis of symbiotic systems. These authors
conclude that the radius of the cool giant in the symbiotic binaries
is limited to
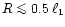 ,
where
,
where 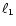 is the distance from the center of
the giant to the inner Lagrangian point.
This translates into
is the distance from the center of
the giant to the inner Lagrangian point.
This translates into
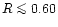 -
-
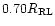 ,
depending on q. Mürset & Schmid suggest that when the giant exceeds this limit, a dynamical
mass transfer ending the symbiotic phenomenon occurs.
All the systems involved are s-type symbiotics so they are expected
to contain an RGB star. Thus Reimers' formula for the mass loss rate can be applied.
The intensity of the outflow from the sub-companion point in our models
with the Reimers' wind exhibits a steep rise
at
,
depending on q. Mürset & Schmid suggest that when the giant exceeds this limit, a dynamical
mass transfer ending the symbiotic phenomenon occurs.
All the systems involved are s-type symbiotics so they are expected
to contain an RGB star. Thus Reimers' formula for the mass loss rate can be applied.
The intensity of the outflow from the sub-companion point in our models
with the Reimers' wind exhibits a steep rise
at
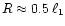 when
when
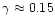 -0.35is adopted, depending on q.
-0.35is adopted, depending on q.
In theoretical modelling of the evolution of binary systems one has to cope
with the fact that
the stellar mass loss rate can be affected by the presence
of the companion. Tout & Eggleton (1988) have suggested
on a heuristic basis that the wind from a star in a binary system is
enhanced by means of tidal forces by a factor of
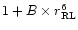 ,
where B is a free parameter. These authors have proposed B=104.
Since then, this prescription has often been invoked in various studies
of the binary evolution (e.g. Miko
,
where B is a free parameter. These authors have proposed B=104.
Since then, this prescription has often been invoked in various studies
of the binary evolution (e.g. Miko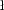 ajewska et al. 1989;
Tout & Hall 1991; Soker 1994, 1998;
Han et al. 1995; Skopal et al. 1997).
However, attempts of establishing a reliable estimate of Bhave not brought a conclusive result. Han et al. (1995) have
preferred B=500, whereas in a later work Han (1998) has adopted B=1000.
Soker et al. (1998) have written the enhancement
factor in a more general form, i.e.
ajewska et al. 1989;
Tout & Hall 1991; Soker 1994, 1998;
Han et al. 1995; Skopal et al. 1997).
However, attempts of establishing a reliable estimate of Bhave not brought a conclusive result. Han et al. (1995) have
preferred B=500, whereas in a later work Han (1998) has adopted B=1000.
Soker et al. (1998) have written the enhancement
factor in a more general form, i.e.
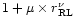 with
with
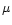 and
and 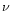 being free parameters. From their modelling of
off-center planetary nebula nuclei they argue for
being free parameters. From their modelling of
off-center planetary nebula nuclei they argue for 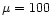 and
and 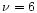 .
.
The numerical and analytical results presented in the present work suggest
a different form of the enhancement factor.
As has already been mentioned, when the Roche lobe filling factor
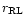 is
small, the enhancement/reduction of all the local mass loss related quantities
scales as
is
small, the enhancement/reduction of all the local mass loss related quantities
scales as
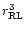 .
Also the formula for the global wind
enhancement is of the form
.
Also the formula for the global wind
enhancement is of the form
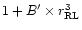 (see Eq. (29)). The value of the scaling factor B' is again uncertain,
but the
(see Eq. (29)). The value of the scaling factor B' is again uncertain,
but the
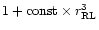 pattern is common for all the
mass loss related quantities. In fact, it stems from the Roche model geometry
and thus should not depend on details of any particular account to the
mass loss description. In this paper
we have concentrated on the winds from red giants of RGB
and AGB, but as we allow for various
pattern is common for all the
mass loss related quantities. In fact, it stems from the Roche model geometry
and thus should not depend on details of any particular account to the
mass loss description. In this paper
we have concentrated on the winds from red giants of RGB
and AGB, but as we allow for various 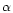 exponents in the
exponents in the
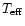 vs. g law and for various wind formulae, our approach is not limited to
the late type stars only.
Our general results should apply to all stars losing mass
in the form of wind, irrespectively of their spectral type.
vs. g law and for various wind formulae, our approach is not limited to
the late type stars only.
Our general results should apply to all stars losing mass
in the form of wind, irrespectively of their spectral type.
It is worth noting, that the applicability of the above pattern also extends
onto single, rotating stars.
Although single red giants are generally expected to be slow rotators, and
therefore the effects of rotation on the wind should be negligible, recently
Heger & Langer (1998) and García-Segura et al. (1999)
conjectured mechanisms that allow single giants at the tip of the AGB to
rotate at considerable rates.
Our results can be applied also in this case.
Indeed, the expression for the global
mass loss enhancement (Eq. (27)) with q = 0 becomes identical
to that for a single star rotating with the angular velocity
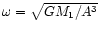 .
For a single star, however, A has a different
physical meaning - it is a break-up radius.
If one defines the break-up velocity as
.
For a single star, however, A has a different
physical meaning - it is a break-up radius.
If one defines the break-up velocity as
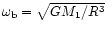 then Eq. (27) can be rewritten in a more
convenient form for single, rotating stars, i.e.
then Eq. (27) can be rewritten in a more
convenient form for single, rotating stars, i.e.
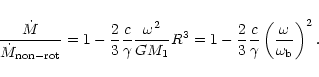 |
(30) |
The same goes for Eq. (28):
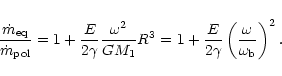 |
(31) |
To the accuracy of our analytical approximation, this functional dependence
of
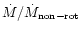 on
on
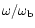 is the same as
that given by Maeder (1999) for radiative winds from rotating
early-type single stars.
is the same as
that given by Maeder (1999) for radiative winds from rotating
early-type single stars.
In this paper we have dealt with the
intrinsic structure of the stellar wind, caused by the local
differences in physical conditions at the origin of the outflow. Further
fate of the ejected matter is beyond the scope of our work. Certainly, the
giant's orbital motion and the still present gravitational influence of the
companion can change the equatorial-to-polar contrast and complicate the
structure of the outflow. Scenarios for such processes have been proposed by
Soker (1994, 1997) and - along with a detailed numerical
modelling - by Mastrodemos & Morris (1998, 1999).
The equatorial compression
of the already ejected matter is possible also in winds from single,
rotating stars, as shown by Bjorkman & Cassinelli (1993) and Asida
& Tuchman (1995).
The picture can be further enriched by introducing magnetic effects
(García-Segura et al. 1999).
Our results could be used as inner boundary conditions for considerations of
these types.
Acknowledgements
This work has been supported from the grant No. 2.P03D.020.17 of the Polish
State Committee for Scientific Research.
- Arndt, T. U., Fleischer, A. J., & Sedlmayr, E. 1997,
A&A, 327, 614
In the text
NASA ADS
- Asida, S. M., & Tuchman, Y. 1995, ApJ, 455, 286
In the text
NASA ADS
- Bjorkman, J. E., & Cassinelli, J. P. 1993, ApJ, 409,
429
In the text
NASA ADS
- Blöcker, T. 1995, A&A, 297, 727
In the text
NASA ADS
- Bowen, G. H. 1988, ApJ, 329, 299
In the text
NASA ADS
- Bowen, G. H., & Willson, L. A. 1991, ApJ, 375, 53
In the text
- Catelan, M. 2000, ApJ, 531, 826
In the text
NASA ADS
- Frankowski, A., & Tylenda, R. 2000, in
ASP Conf. Ser., 199,
Asymmetrical
Planetary Nebulae II: From Origins to Microstructures, ed. J. H. Kastner,
N. Soker, & S. Rappaport, 179
In the text
- García-Segura, G., Langer, N., Rózyczka, M.,
& Franco, J. 1999, ApJ, 517, 767
In the text
NASA ADS
- Han, Z. 1998, MNRAS, 296, 1019
In the text
NASA ADS
- Han, Z., Eggleton, P. P., Podsiadlowski, P., & Tout,
Ch. A. 1995, MNRAS, 277, 1443
In the text
NASA ADS
- Heger, A., & Langer, N. 1998, A&A, 334, 210
In the text
NASA ADS
- Jorissen, A., & Knapp, G. R. 1998, A&AS, 129, 363
In the text
NASA ADS
- Jorissen, A., Van Eck, S., Mayor, M., & Udry, S. 1998,
A&A, 332, 877
In the text
NASA ADS
- Lucy, L. B. 1967, Z. Astrophys., 65, 89
In the text
- Maeder, A. 1999, A&A, 347, 185
In the text
NASA ADS
- Mastrodemos, N., & Morris, M. 1998, ApJ, 497, 303
In the text
NASA ADS
- Mastrodemos, N., & Morris, M. 1999, ApJ, 523, 357
In the text
NASA ADS
- Miko
 ajewska, J., Kenyon, S. J., &
Miko
ajewska, J., Kenyon, S. J., &
Miko ajewski, M. 1989, AJ, 98, 1427
In the text
NASA ADS
ajewski, M. 1989, AJ, 98, 1427
In the text
NASA ADS
- Mürset, U., & Schmid, H. M. 1999, A&AS, 137, 473
In the text
NASA ADS
- Reimers, D. 1975, Mem. Soc. Roy. Sci. Liège, 8, 369
In the text
NASA ADS
- Schuerman, D. W. 1972, Ap&SS, 19, 351
In the text
NASA ADS
- Skopal, A., Vittone, A., Errico, L., et al. 1997,
MNRAS, 292, 703
In the text
NASA ADS
- Soker, N. 1994, MNRAS, 270, 774
In the text
NASA ADS
- Soker, N. 1997, ApJS, 112, 487
In the text
NASA ADS
- Soker, N. 1998, ApJ, 496, 833
In the text
NASA ADS
- Soker, N., Rappaport, S., & Harpaz, A. 1998, ApJ, 496,
842
In the text
NASA ADS
- Tout, Ch. A., & Eggleton, P. P. 1988, MNRAS, 231, 823
In the text
NASA ADS
- Tout, Ch. A., & Hall, D. S. 1991, MNRAS, 253, 9
In the text
NASA ADS
- von Zeipel, H. 1924, MNRAS, 84, 702
In the text
NASA ADS
Copyright ESO 2001
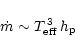
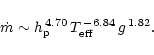
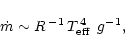
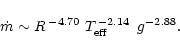
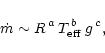
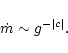
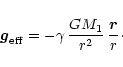
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{10070f1.eps}\end{figure}](/articles/aa/full/2001/08/aa10070/Timg42.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{10070f2.eps}\end{figure}](/articles/aa/full/2001/08/aa10070/Timg45.gif)
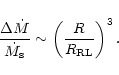
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{10070f3.eps}\end{figure}](/articles/aa/full/2001/08/aa10070/Timg49.gif)
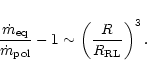
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{10070f4.eps}\end{figure}](/articles/aa/full/2001/08/aa10070/Timg52.gif)
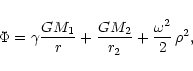
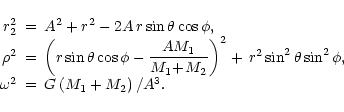
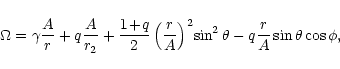
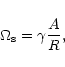
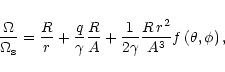
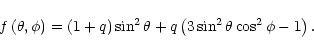
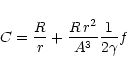
![\begin{displaymath}
\frac{r\left(\theta,\phi\right)}{R} =
C^{-1}\left[1+ \frac{1}{2\gamma} f\left(\frac{R}{AC}\right)^3 +
\ldots \right].
\end{displaymath}](/articles/aa/full/2001/08/aa10070/img72.gif)
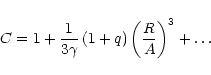
![\begin{displaymath}
\frac{r\left(\theta,\phi\right)}{R} =
1+\frac{1}{6\gamma}\left[\,3f-2\left(1+q\right)\right]
\left(\frac{R}{A}\right)^3\cdot
\end{displaymath}](/articles/aa/full/2001/08/aa10070/img74.gif)
![\begin{displaymath}
\begin{array}{rcl}
a_1 & = & \displaystyle R \left[1+ \left(...
...2+5q\right) \left(\frac{R}{A}\right)^3 \right]. \\
\end{array}\end{displaymath}](/articles/aa/full/2001/08/aa10070/img75.gif)
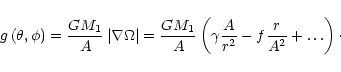
![\begin{displaymath}\frac{g\left(\theta,\phi\right)}{g_{\rm s}} =
\left(\frac{r}{...
...\frac{1}{\gamma} f
\left(\frac{R}{A}\right)^3 + \ldots\right],
\end{displaymath}](/articles/aa/full/2001/08/aa10070/img78.gif)