A&A 367, 605-612 (2001)
DOI: 10.1051/0004-6361:20000407
S. M. Andrievsky1,2 - V. V. Kovtyukh1,2 - S. A. Korotin1,2 - M. Spite3 - F. Spite3
1 - Department of Astronomy, Odessa State University,
Shevchenko Park, 65014, Odessa, Ukraine
2 -
Isaac Newton Institute of Chile, Odessa Branch
3 -
Observatoire de Paris, DASGAL, UMR 8633 du CNRS, 92195 Meudon
Cedex, France
Received 23 June 2000 / Accepted 30 November 2000
Abstract
With an improved method of the LTE abundance analysis for most elements
(Kovtyukh & Andrievsky 1999), the abundances have been re-investigated
in nine F supergiants of the Large Magellanic Cloud. The NLTE calculations
for carbon, oxygen and sodium, based on Kurucz's atmospheric models with
an over-all metal deficiency, were carried out.
The most important results are the following:
- carbon abundance in supergiants is in much better agreement with the
carbon abundance of the LMC H II regions, oxygen remaining in fair
agreement with H II regions. The (C/O) ratio is low, lower than solar
and the H II ratios (a possible sign of the first dredge-up, or another
large-scale mixing event in the supergiant atmospheres);
- the NLTE computations do not show remarkable sodium overabundances in
the LMC supergiants, in contrast with the Galactic supergiants;
- the mean abundance of iron is found to be
![]() ,
slightly
lower than the results of some previous determinations for the LMC, but
in agreement with the recent result obtained by Korn et al. (2000),
who give
,
slightly
lower than the results of some previous determinations for the LMC, but
in agreement with the recent result obtained by Korn et al. (2000),
who give
![]() .
The relative to iron abundance of oxygen
.
The relative to iron abundance of oxygen
![]() derived
from nine F supergiants appears to be in excellent accordance with
predictions based on the smooth model of the LMC evolution;
- the (
derived
from nine F supergiants appears to be in excellent accordance with
predictions based on the smooth model of the LMC evolution;
- the (![]() /Fe) ratios are comparable to those found in
previous analyses. The surprisingly low abundance of Mg is even lower
in the new analysis, but it is in good agreement with the relative
magnesium abundance in LMC B-stars
/Fe) ratios are comparable to those found in
previous analyses. The surprisingly low abundance of Mg is even lower
in the new analysis, but it is in good agreement with the relative
magnesium abundance in LMC B-stars
![]() determined by
Korn et al. (2000). Sulphur in the program supergiants
shows the same abundance within an error bar as in H II regions;
- the iron-group elements follow the solar distribution of the (M/Fe)
ratios;
- the heavy elements show enhanced abundances;
- significantly larger
determined by
Korn et al. (2000). Sulphur in the program supergiants
shows the same abundance within an error bar as in H II regions;
- the iron-group elements follow the solar distribution of the (M/Fe)
ratios;
- the heavy elements show enhanced abundances;
- significantly larger ![]() values were obtained than in a previous study,
resulting in supergiant masses of about
10-20
values were obtained than in a previous study,
resulting in supergiant masses of about
10-20 ![]() ,
which are in excellent agreement with evolutionary
calculations.
,
which are in excellent agreement with evolutionary
calculations.
Key words: stars: abundances - stars: NLTE -analysis - supergiants - Magellanic Clouds
The chemical evolution of the Magellanic Clouds is the subject of many researches. Among the basic data, detailed stellar abundances are especially needed, but currently only the brightest stars are observable. The H II regions also provide an important information about abundances of the light elements in Magellanic Clouds. All these objects are young.
Recent spectroscopic analyses of F supergiants in the LMC have been performed by Hill et al. (1995) - hereafter HAS95, Luck & Lambert (1992) - L L92, and Luck et al. (1998) - LET98. The latter paper gives a thorough discussion of the abundances in yellow supergiants obtained by different authors during the last decade. In brief, the following points can be outlined:
Comparison to the Sun:
| Star | E(B-V) | V0 | (V-R)0 |
|
(V-I)0 |
|
|
||
| G244 | 0.08 | 11.20 | 0.11 | 7200 | 0.21 | 7400 | 7300 | 1.1 | 6.5 |
| G258 | 0.08 | 10.92 | 0.21 | 6500 | 0.41 | 6610 | 6550 | 1.0 | 6.5 |
| G274 | 0.11 | 11.88 | 0.22 | 6450 | 0.44 | 6500 | 6500 | 1.2 | 5.0 |
| G319 | 0.10 | - | - | - | - | - | 7500* | 1.8 | 4.5 |
| G396 | 0.10 | 11.61 | 0.14 | 6950 | 0.26 | 7150 | 7050 | 1.1 | 6.0 |
| G406 | 0.15 | 11.87 | 0.19 | 6600 | 0.38 | 6700 | 6650 | 1.2 | 5.0 |
| G439 | 0.11 | 11.51 | 0.25 | 6250 | 0.45 | 6480 | 6350 | 1.0 | 6.0 |
| G501 | 0.22 | 11.96 | 0.23 | 6380 | 0.45 | 6480 | 6450 | 1.4 | 5.2 |
| G538 | 0.06 | 11.22 | 0.27 | 6140 | 0.53 | 6200 | 6180 | 0.8 | 6.5 |
| G244 | G258 | G274 | G319 | G396 | |||||||||||
| Ion | [El/H] | N | [El/H] | N | [El/H] | N | [El/H] | N | [El/H] | N | |||||
| Mg I | -1.01 | - | 1 | -0.54 | - | 1 | -0.60 | - | 1 | -1.08 | - | 1 | - | - | - |
| Al I | - | - | - | - | - | - | -0.18 | 0.01 | 2 | - | - | - | - | - | - |
| Si I | - | - | - | -0.15 | 0.13 | 14 | -0.21 | 0.14 | 12 | -0.10 | 0.21 | 4 | -0.30 | 0.29 | 5 |
| S I | - | - | - | -0.19 | 0.18 | 2 | -0.27 | 0.02 | 2 | -0.15 | - | 1 | -0.16 | - | 1 |
| Ca I | -0.21 | 0.17 | 9 | -0.34 | 0.11 | 9 | -0.33 | 0.18 | 9 | -0.26 | 0.12 | 9 | -0.19 | 0.22 | 4 |
| Sc II | -0.61 | 0.35 | 4 | -0.50 | 0.37 | 2 | -0.52 | 0.21 | 3 | -0.49 | 0.22 | 7 | -0.81 | 0.17 | 2 |
| Ti I | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - |
| Ti II | -0.51 | - | 1 | -0.34 | - | 1 | -0.33 | - | 1 | -0.49 | 0.11 | 6 | -0.38 | - | 1 |
| Cr II | -0.43 | 0.08 | 9 | -0.28 | 0.10 | 5 | -0.54 | 0.11 | 3 | -0.44 | 0.08 | 11 | - | - | - |
| Mn I | - | - | - | -0.59 | 0.04 | 2 | -0.59 | 0.12 | 2 | - | - | - | - | - | - |
| Fe I | -0.40 | 0.16 | 31 | -0.32 | 0.13 | 85 | -0.40 | 0.15 | 73 | -0.37 | 0.17 | 38 | -0.45 | 0.15 | 33 |
| Fe II | -0.40 | 0.12 | 17 | -0.30 | 0.08 | 21 | -0.37 | 0.12 | 17 | -0.39 | 0.16 | 31 | -0.47 | 0.12 | 12 |
| Ni I | - | - | - | -0.39 | 0.25 | 3 | -0.46 | 0.33 | 3 | - | - | - | -0.49 | - | 1 |
| Y II | -0.79 | - | 1 | -0.20 | 0.23 | 4 | -0.30 | 0.35 | 3 | -0.46 | 0.10 | 3 | -0.04 | - | 1 |
| Zr II | - | - | - | -0.06 | - | 1 | - | - | - | +0.06 | - | 1 | - | - | - |
| Ba II | -0.07 | - | 1 | - | - | - | - | - | - | +0.06 | 0.11 | 2 | - | - | - |
| La II | - | - | - | +0.15 | - | 1 | -0.01 | 0.34 | 2 | - | - | - | -0.07 | - | 1 |
| Ce II | - | - | - | +0.00 | 0.01 | 2 | -0.25 | - | 1 | -0.14 | 0.15 | 2 | - | - | - |
| Pr II | - | - | - | -0.07 | - | 1 | - | - | - | - | - | - | - | - | - |
| Nd II | - | - | - | -0.15 | 0.15 | 5 | - | - | - | - | - | - | - | - | - |
| Eu II | - | - | - | -0.01 | - | 1 | -0.24 | - | 1 | - | - | - | - | - | - |
| G406 | G439 | G501 | G538 | mean | |||||||||||
| Ion | [El/H] | N | [El/H] | N | [El/H] | N | [El/H] | N | n | [El/H] | |||||
| Mg I | -0.53 | - | 1 | -0.63 | - | 1 | -0.60 | - | 1 | -0.62 | - | 1 | 8 | -0.70 | 0.21 |
| Al I | - | - | - | - | - | - | -0.23 | 0.01 | 2 | -0.27 | - | 1 | 3 | -0.22 | 0.05 |
| Si I | -0.10 | 0.12 | 12 | -0.33 | 0.18 | 18 | -0.14 | 0.14 | 11 | -0.26 | 0.12 | 14 | 8 | -0.21 | 0.09 |
| S I | -0.16 | 0.06 | 2 | -0.43 | 0.18 | 2 | -0.27 | 0.17 | 2 | -0.29 | 0.28 | 5 | 8 | -0.26 | 0.25 |
| Ca I | -0.30 | 0.10 | 8 | -0.42 | 0.11 | 9 | -0.39 | 0.07 | 8 | -0.46 | 0.13 | 10 | 9 | -0.33 | 0.09 |
| Sc II | -0.46 | 0.24 | 5 | -0.63 | 0.22 | 3 | - | - | - | -0.63 | 0.21 | 2 | 8 | -0.55 | 0.11 |
| Ti I | - | - | - | -0.11 | - | 1 | - | - | - | -0.43 | - | 1 | 2 | -0.27 | - |
| Ti II | -0.38 | - | 1 | -0.53 | - | 1 | - | - | - | -0.55 | - | 1 | 8 | -0.46 | 0.09 |
| V II | - | - | - | - | - | - | - | - | - | -0.74 | - | 1 | - | - | - |
| Cr I | -0.56 | - | 1 | -0.56 | - | 1 | -0.59 | - | 1 | -0.63 | 0.19 | 2 | - | - | - |
| Cr II | -0.43 | 0.08 | 6 | -0.55 | 0.06 | 6 | -0.45 | 0.09 | 6 | -0.55 | 0.08 | 6 | 8 | -0.45 | 0.09 |
| Mn I | -0.43 | 0.05 | 2 | -0.60 | 0.04 | 2 | -0.53 | 0.04 | 2 | -0.73 | 0.07 | 3 | 6 | -0.58 | 0.10 |
| Fe I | -0.37 | 0.14 | 83 | -0.44 | 0.13 | 74 | -0.29 | 0.12 | 80 | -0.52 | 0.16 | 112 | 9 | -0.40 | 0.12 |
| Fe II | -0.34 | 0.07 | 20 | -0.45 | 0.08 | 15 | -0.29 | 0.12 | 17 | -0.49 | 0.10 | 15 | 9 | -0.39 | 0.07 |
| Co I | - | - | - | - | - | - | - | - | - | -0.36 | - | 1 | - | - | - |
| Ni I | -0.37 | 0.14 | 2 | -0.75 | 0.13 | 3 | -0.57 | 0.03 | 2 | -0.74 | 0.16 | 11 | 7 | -0.61 | 0.16 |
| Cu I | - | - | - | - | - | - | - | - | - | -0.40 | 0.58 | 2 | - | - | - |
| Zn I | - | - | - | - | - | - | - | - | - | -0.17 | - | 1 | - | - | - |
| Y II | -0.16 | - | 1 | -0.19 | - | 1 | -0.17 | - | 1 | -0.43 | 0.17 | 5 | 9 | -0.30 | 0.22 |
| Zr II | - | - | - | - | - | - | - | - | - | -0.44 | 0.08 | 2 | 3 | -0.14 | 0.26 |
| La II | +0.05 | 0.35 | 2 | -0.12 | 0.26 | 2 | -0.05 | 0.23 | 2 | +0.02 | - | 1 | 7 | +0.00 | 0.09 |
| Ce II | -0.03 | 0.08 | 2 | -0.12 | 0.11 | 2 | +0.01 | - | 1 | -0.41 | 0.17 | 5 | 7 | -0.13 | 0.15 |
| Pr II | - | - | - | - | - | - | - | - | - | -0.51 | 0.16 | 2 | - | - | - |
| Nd II | +0.02 | - | 1 | -0.07 | 0.19 | 3 | +0.05 | - | 1 | -0.30 | 0.22 | 10 | 5 | -0.09 | 0.14 |
| Eu II | -0.07 | - | 1 | +0.02 | - | 1 | - | - | - | -0.23 | 0.16 | 2 | 5 | -0.11 | 0.12 |
It is clear that the main problem, in luminous and metal-poor stars, is the overionisation, but Spite et al. (1989) have evaluated the effect of overionisation in the abundance determination in the SMC supergiants, and estimated that the effects were moderate.
Recently, Thévenin & Idiart (1999) showed that the Fe I lines (which are traditionally used as a tool for determination of the atmospheric parameters) are affected by significant NLTE effects, mainly due to overionisation, and the effect is therefore especially important for metal-poor stars.
Recently also, Gratton et al. (1999) confirmed that the Fe I lines can be significantly affected by NLTE effects: their Fig. 11 clearly shows that departure coefficients for some levels of the Fe I model progressively depend upon optical depth. Especially, in the atmospheres of rather warm and luminous stars (similar to our program supergiants), all the levels of Fe I model are underpopulated, when compared with the LTE case, while Fe II is not affected.
HAS95 made an attempt to correct for overionisation, and found that the microturbulent velocity and the gravity have then both to be increased: the effect on abundances is moderate, and is often nearly negligible for abundance ratios.
Kovtyukh & Andrievsky (1999 - hereafter KA99), have shown that using Fe II lines for microturbulent velocity determination, a higher microtubulent velocity and a higher gravity are also obtained, in the analysis of Cepheids. Metal abundances are only slightly changed (even less the abundance ratios), but the abundances of C and O are changed enough for becoming close to the theoretical predictions.
This modification is usable only when a sufficient number of Fe II lines are measurable, but unfortunately, unblended Fe II lines, neither too weak nor too strong are not numerous. Taking advantage of the good quality of the available spectra, we decided in the present work to re-analyze the sample of F-type LMC supergiants studied previously by HAS95, in the way described by KA99. Moreover, the elements C, O and Na are in addition analysed in more detail, using NLTE computations (Korotin et al. 1999) described in Sect. 3.2. The spectra of the program stars and their reduction are described in detail in HAS95.
We used the recent
![]() -(V-R) and
-(V-R) and
![]() -(V-I)calibrations of Castelli et al. (1997) to derive
the effective temperatures for the program stars (the corresponding
electronic tables can be found using the following address:
cfaku5.harvard.edu). These calibrations are built with the aim of being
independent of the metallicity effects. The individual colours and reddenings
for our stars were selected from Grieve & Madore (1986). The temperatures
are given in Table 1. The results on microturbulent velocity and
gravity, determined as described by KA99 (non standard approach: use of
Fe II lines), are also given in Table 1.
-(V-I)calibrations of Castelli et al. (1997) to derive
the effective temperatures for the program stars (the corresponding
electronic tables can be found using the following address:
cfaku5.harvard.edu). These calibrations are built with the aim of being
independent of the metallicity effects. The individual colours and reddenings
for our stars were selected from Grieve & Madore (1986). The temperatures
are given in Table 1. The results on microturbulent velocity and
gravity, determined as described by KA99 (non standard approach: use of
Fe II lines), are also given in Table 1.
The LTE analysis has been made using Kurucz's WIDTH9 code (1992) and the grid of atmosphere models of Castelli et al. (1997) with an over-all metal deficiency of -0.3 dex. The line oscillator strengths used are discussed and presented in KA99 (they are obtained by inverse solar analysis). The broadening values were selected from CD-ROM No. 23 of Kurucz & Bell (1995). In Table 2 we give the results of the determination of elemental abundances (except for carbon, oxygen and sodium abundances, presented in the next section). In Fig. 1 we also show graphically the averaged abundances which will be discussed below.
The NLTE abundances of C, O and Na were found with the help of a modified
version of the MULTI code (Carlsson 1986) described in Korotin
et al. (1999) and Korotin et al. (1999).
In such a modified version, in particular, additional opacity sources
from ATLAS9 code (Kurucz 1992) were included. This was done in
order to calculate the continuum opacity more precisely, and to take into
account the absorption by a great number of spectral lines (especially
within the region of the near-UV). It allows then to calculate more accurately
the intensity distribution in the region 900-1500 Å. In turn, this significantly
affects the determination of the radiative rates of b-f transitions.
A simultaneous solution of the radiative transfer and statistical equilibrium
equations has been performed in the approximation of complete frequency
redistribution for all the lines. All the NLTE calculations were also
based on the Kurucz's grid of atmospheric models.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{F1.EPS}
\end{figure}](/articles/aa/full/2001/08/aa10037/Timg28.gif) |
Figure 1:
Averaged elemental abundances. 2 |
| Open with DEXTER | |
We employed a model of carbon atom consisting of 115 levels: 94 levels of C I, 20 levels of C II and the ground state of C III. Within the described system of the carbon atomic levels, we considered the radiative transitions between the first 47 levels of C I and ground level of C II. Transitions between the remaining levels were not taken into account (they were used only in the equations of particle number conservation). After test calculations, 113 transitions were included in the linearization procedure. These transitions describe quite completely the formation of the lines of interest. The other 155 transitions were treated as those having fixed radiative rates.
In our computations, the oxygen atomic model consists of 75 levels: 72 levels of O I, 3 levels of O II and the ground state of O III (for details see Mishenina et al. 1999). The radiative transitions between the first 23 levels of O I and the ground level of O II were calculated.
The model of sodium atom as described by Sahibullin (1987),
has been modified (see Korotin & Mishenina 1999). It consists of
27 levels of Na I and the ground level of Na II. We considered
the radiative transitions between the first 20 levels of Na I and
the ground level of Na II. Transitions between the remaining levels
were used only in the equations of particle number conservation. Finally,
46 b-b and 20 b-f transitions were included in the linearization procedure.
For 34 transitions the radiative rates were fixed.
| g | log gf | g | log gf | ||
| C I | Na I | ||||
| 4775.91 | 5 | -2.27 | 5682.63 | 2 | -0.70 |
| 5052.17 | 3 | -1.24 | 5688.21 | 4 | -0.46 |
| 5380.34 | 3 | -1.57 | 5688.19 | 4 | -1.39 |
| 6001.12 | 5 | -2.07 | 6154.23 | 2 | -1.53 |
| 6010.68 | 3 | -2.02 | 6160.75 | 4 | -1.23 |
| 6014.83 | 5 | -1.71 | |||
| 6413.55 | 3 | -2.38 | O I | ||
| 6587.61 | 3 | -1.05 | 6155.98 | 3 | -0.67 |
| 6671.85 | 5 | -1.66 | 6156.77 | 5 | -0.45 |
| 7111.48 | 3 | -1.07 | 6158.18 | 7 | -0.31 |
| 7113.18 | 7 | -0.76 | 6363.88 | 3 | -10.30 |
| 7116.99 | 7 | -0.91 | 5577.34 | 5 | -8.24 |
A detailed structure of the multiplets was ignored in the calculations
and each LS multiplet was considered as a single term (with one exception
for the Na I 3
![]() level, whose structure has been taken into
account in detail).
After the combined solution of radiative transfer and statistical
equilibrium equations, the averaged levels have been splitted with respect
to multiplet structure. Then the level populations were redistributed
proportionally to the statistical weights of the corresponding sublevels
and finally the lines of interest were studied.
level, whose structure has been taken into
account in detail).
After the combined solution of radiative transfer and statistical
equilibrium equations, the averaged levels have been splitted with respect
to multiplet structure. Then the level populations were redistributed
proportionally to the statistical weights of the corresponding sublevels
and finally the lines of interest were studied.
For all atomic models, the photoionization cross sections were mainly taken from the Opacity Project (Yan et al. 1987) keeping a detailed structure of their frequency dependence, including resonances. Collisional ionization was described using Seaton's formula (Seaton 1962). For all allowed b-b transitions we used van Regemorter (1962) formula. Collisional rates for the forbidden transitions were calculated with the help of semiempirical formula (Allen 1973), with collisional force of 1. As known, the elastic collisions with hydrogen atoms become rather significant in the atmospheres of cool stars. This effect has been taken into account with the help of Steenbock & Holweger (1984) formula (with correcting factor 1/3).
For the NLTE calculation we used theoretical oscillator strengths from
the catalogue by Hirata & Horaguchi (1994), instead of the "solar''
![]() determined under the LTE approximation from the solar
spectrum. Some
determined under the LTE approximation from the solar
spectrum. Some ![]() for transitions from the ground level were
selected from Verner et al. (1994) and from CD-ROM
No. 23 by Kurucz & Bell (1995). For C I the oscillator
strengths from Biémont et al. (1993) were also used.
for transitions from the ground level were
selected from Verner et al. (1994) and from CD-ROM
No. 23 by Kurucz & Bell (1995). For C I the oscillator
strengths from Biémont et al. (1993) were also used.
Van der Waals C6 constant for the lines of considered
elements was calculated using the classical formula of Unsöld.
For the strong sodium lines the classical C6 values were corrected
by fitting the calculated and observed line wings in the solar spectrum
(this procedure is described in Korotin & Mishenina 1999).
No correction factor to C6 constant was used for the weak carbon and
oxygen lines. In Table 3 we give the list of the carbon, oxygen
and sodium lines and the oscillator strengths used for the NLTE calculations.
| NLTE | LTE | NLTE | LTE | NLTE | LTE | |||||||
| Star | A(C) | A(C) | A(O) | A(O) | A(Na) | A(Na) | ||||||
| G244 | 7.92 | 0.06 | 8.05 | 0.05 | 8.43 | 0.11 | 8.46 | 0.12 | 5.98 | 0.06 | 6.07 | 0.08 |
| G258 | 7.95 | 0.07 | 8.01 | 0.07 | 8.68 | 0.04 | 8.70 | 0.05 | 6.03 | 0.01 | 6.12 | 0.04 |
| G274 | 7.80 | 0.19 | 7.85 | 0.14 | 8.50 | 0.07 | 8.50 | 0.09 | 5.82 | 0.04 | 5.94 | 0.05 |
| G319 | 7.86 | 0.15 | 7.86 | 0.19 | 8.47 | 0.03 | 8.47 | 0.06 | 5.79 | - | 5.87 | - |
| G396 | 7.90 | 0.03 | 7.93 | 0.07 | 8.50 | 0.12 | 8.52 | 0.11 | - | - | - | |
| G406 | 7.94 | 0.15 | 7.99 | 0.09 | 8.45 | 0.08 | 8.46 | 0.09 | 6.05 | 0.04 | 6.15 | 0.06 |
| G439 | 7.67 | 0.17 | 7.75 | 0.14 | 8.46 | 0.08 | 8.46 | 0.07 | 5.79 | 0.08 | 5.88 | 0.08 |
| G501 | 8.04 | 0.04 | 8.08 | 0.06 | 8.60 | 0.08 | 8.60 | 0.08 | 5.96 | 0.14 | 6.05 | 0.13 |
| G538 | 7.94 | 0.12 | 8.01 | 0.16 | 8.53 | 0.06 | 8.54 | 0.07 | 5.78 | 0.01 | 5.88 | 0.04 |
| Mean | 7.89 | 0.11 | 7.95 | 0.11 | 8.51 | 0.08 | 8.52 | 0.08 | 5.90 | 0.12 | 6.01 | 0.11 |
| Sun | 8.55 | 0.05 | 8.90 | 0.04 | 6.25 | 0.03 | ||||||
Table 4 contains the abundances of carbon, oxygen and sodium,
averaged for each star. The abundances of the element
X are given as A(X)
![]() .
The mean abundance of C, O and Na for the sample is provided in the
bottom line, above the solar abundances.
We also give for reference the computed solar NLTE abundances:
they were determined from the lines listed in Table 3. Those lines
were accurately measured from the solar flux spectrum (Kurucz et al.
1984).
The abundances were calculated with Kurucz's solar atmosphere model.
To take into account the chromospheric growth of the temperature, this
model was completed by a model of the solar chromosphere from the work of
Maltby et al. (1986).
Nevertheless, the influence of a chromosphere on the calculated equivalent
widths of the lines considered appeared to be insignificant (less than 2%).
Our calculated solar NLTE abundances of C, O and Na, are in good agreement
with the currently adopted abundances of these elements in the solar
atmosphere. For example,
.
The mean abundance of C, O and Na for the sample is provided in the
bottom line, above the solar abundances.
We also give for reference the computed solar NLTE abundances:
they were determined from the lines listed in Table 3. Those lines
were accurately measured from the solar flux spectrum (Kurucz et al.
1984).
The abundances were calculated with Kurucz's solar atmosphere model.
To take into account the chromospheric growth of the temperature, this
model was completed by a model of the solar chromosphere from the work of
Maltby et al. (1986).
Nevertheless, the influence of a chromosphere on the calculated equivalent
widths of the lines considered appeared to be insignificant (less than 2%).
Our calculated solar NLTE abundances of C, O and Na, are in good agreement
with the currently adopted abundances of these elements in the solar
atmosphere. For example,
1) our solar carbon abundance, A(C) = 8.55, is hardly different from the one given by Biémont et al. (1993) or Grevesse & Sauval (1998): 8.57 and 8.52 respectively;
2) Anders & Grevesse (1989), Grevesse & Sauval (1998)
and Biémont et al. (1991) derive
![]() ,
8.83 and 8.86
respectively, while we find
,
8.83 and 8.86
respectively, while we find
![]() ;
;
3) Our estimate of the sodium content A(Na) = 6.25 agrees well with the determination of Takeda & Takada-Hidai (1994), who give A(Na) = 6.23, while Grevesse & Sauval (1998) give the meteoritic value A(Na) = 6.33.
It has to be noted that, for our program F supergiants, the NLTE corrections lead to slightly lower abundances as compared to the LTE case. The differences between NLTE and LTE abundances are small (about of 0.10 dex) for carbon, oxygen and sodium. As discussed below, the deficiency of these elements, in the LMC supergiants, relative to the Sun, is therefore confirmed.
In this work, some parameters of the supergiants are different from those found in HAS95. But the temperature values are only slightly different from those derived in HAS95. The difference never exceeds 200K, and is much smaller (about 50 K) in the mean.
The abundance differences between both works have to be ascribed
to differences in ![]() ,
,
![]() and
and ![]() and not only to
temperature differences.
The microturbulent velocities found by using the Fe II lines are
from 1 to 3 kms-1 greater than those derived using the Fe I
lines. The surface gravities for the program stars are significantly greater.
In Table 5 we give the masses of program stars estimated using
the usual expression:
and not only to
temperature differences.
The microturbulent velocities found by using the Fe II lines are
from 1 to 3 kms-1 greater than those derived using the Fe I
lines. The surface gravities for the program stars are significantly greater.
In Table 5 we give the masses of program stars estimated using
the usual expression:
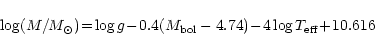 |
(1) |
| This paper | HAS95 | ||||
| Star | Mv |
|
|
||
| G 244 | -7.37 | 1.1 | 12.8 | 0.3 | 2.1 |
| G 258 | -7.65 | 1.0 | 20.3 | 0.1 | 2.6 |
| G 274 | -6.69 | 1.2 | 13.7 | 0.3 | 1.7 |
| G 319 | 1.8 | 1.0 | |||
| G 396 | -6.96 | 1.1 | 10.1 | 0.6 | 3.5 |
| G 406 | -6.70 | 1.2 | 12.6 | 0.5 | 2.8 |
| G 439 | -7.06 | 1.0 | 13.3 | 0.4 | 3.2 |
| G 501 | -6.61 | 1.4 | 20.8 | 0.7 | 4.6 |
| G 538 | -7.35 | 0.8 | 12.2 | 0.1 | 2.4 |
The absolute visual magnitudes were found using the distance modulus for
LMC
(V0-Mv) = 18.57 (Sandage et al. 1999).
We extrapolated the bolometric magnitude corrections for F supergiants of
approximately zero from data of Castelli (1999). The gravities
and masses found here are in agreement with the stellar evolution theory.
This is clearly seen in Fig. 2.
![\begin{figure}
\par\includegraphics[width=6cm,clip]{F2.EPS}\end{figure}](/articles/aa/full/2001/08/aa10037/Timg39.gif) |
Figure 2: Evolutionary tracks and position of program stars in HR diagram. Evolutionary tracks for Z=0.01 are from 1) Pols et al. (1998): standard models - dashed line, and models with overshooting - dotted line, 2) Schaller et al. (1992) - solid line |
| Open with DEXTER | |
Table 6 summarizes the useful ratios of carbon and oxygen abundances
that will be used in the discussion below.
| Ratio | HAS95 | LL92 | H II | Our data |
| [C/H] | -0.46 | -0.58 | -0.65/-0.74 | -0.66 |
| [O/H] | -0.45 | -0.22 | -0.47/-0.53 | -0.39 |
| [Fe/H] | -0.27 | -0.36 | -0.40 | |
| [C/Fe] | -0.19 | -0.22 | -0.26 | |
| [O/Fe] | -0.18 | +0.14 | +0.01 | |
| (C/O) | -0.36 | -0.71 | -0.53/-0.56 | -0.62 |
Previous estimate of carbon abundance in the sample of F supergiants
(HAS95) gave A(C) = 8.10. Our present NLTE mean result for the same sample of
stars gives A(C) = 7.89, in much better agreement with data on carbon abundance
in LMC H II regions (7.90 and 7.81 accordingly to Dufour
![]() and Kurt & Dufour
and Kurt & Dufour
![]() respectively). However, the stellar carbon
abundance may be expected to be lower than the H II abundance in case
of dredge-up or partial mixing due to rotation, for example.
A first dredge-up event in the phase of the red giant should produce the
following effect:
a surface carbon abundance becomes smaller (and nitrogen abundance larger,
while oxygen remains practically unchanged) than that of H II regions,
assumed to be made of the same young matter which formed the young supergiants.
Of course H II regions may illuminate some less evolved matter, not yet
enriched in carbon by intermediate mass stars (and this hypothesis has even
been formalised by Pilyugin 1998), but the strikingly uniform
metallicity of the LMC supergiants (HAS95, see also LET98) suggests on the
contrary an efficient mixing of the young matter in the LMC. And a similar
homogeneity has also been noted for H II regions (e.g.,
Pagel et al. 1978). In addition, it is commonly
accepted that a rotating bar produces a considerable gas streaming in
a galaxy, explaining this homogeneity.
respectively). However, the stellar carbon
abundance may be expected to be lower than the H II abundance in case
of dredge-up or partial mixing due to rotation, for example.
A first dredge-up event in the phase of the red giant should produce the
following effect:
a surface carbon abundance becomes smaller (and nitrogen abundance larger,
while oxygen remains practically unchanged) than that of H II regions,
assumed to be made of the same young matter which formed the young supergiants.
Of course H II regions may illuminate some less evolved matter, not yet
enriched in carbon by intermediate mass stars (and this hypothesis has even
been formalised by Pilyugin 1998), but the strikingly uniform
metallicity of the LMC supergiants (HAS95, see also LET98) suggests on the
contrary an efficient mixing of the young matter in the LMC. And a similar
homogeneity has also been noted for H II regions (e.g.,
Pagel et al. 1978). In addition, it is commonly
accepted that a rotating bar produces a considerable gas streaming in
a galaxy, explaining this homogeneity.
One should also note that another source of the surface alteration of the carbon and nitrogen abundances in supergiant star may be identified with convection induced turbulence (i.e. overshooting into stable regions) during the previous main sequence evolution of the supergiant, when the star was the hot B dwarf. For example, Andrievsky et al. (1999) found among ten main sequence carbon deficient B stars three objects showing an increased nitrogen content.
Thus, the rather low ratio (C/O) found for our stars, which is lower than solar ratio (C/O) = -0.35 and that of H II regions (see Table 6) seems to support the supposition about the first dredge-up (or turbulent mixing) in their history.
On the other hand, the position of the program stars in HR
diagram with evolutionary tracks from Pols et al. (1998)
seems to indicate that they are only on the first way towards the
red giant region (see Fig. 2), because no blue loops are
expected for the models of masses greater than 15 ![]() .
At
least for some program stars this conclusion remains valid with
evolutionary tracks calculated by Schaller et al.
(1992), while several of them occupy the position on
blue loop (see Fig. 2), and an exact direction of their
evolution within the HR is not clear.
.
At
least for some program stars this conclusion remains valid with
evolutionary tracks calculated by Schaller et al.
(1992), while several of them occupy the position on
blue loop (see Fig. 2), and an exact direction of their
evolution within the HR is not clear.
There are only two possibilities to explain an actual position of our program stars in HR diagram: 1) either they (or some of them) are traveling to the red giant region for the first time, and their present atmospheric carbon abundance being unchanged is the same as that inherent to H II regions, or 2) the F supergiants may have already experienced the first dredge-up (or another kind of the large-scale mixing), and their initial carbon abundance was really decreased. In this case the rather low carbon abundance in H II (when compared with the supergiants' mean value) may result from the processes in which some part of the carbon and oxygen atoms are locked into grains in H II regions (owing to their low condensation temperature). Summarizing, we have also to state that based only on the measured carbon abundance and having not investigated the nitrogen content we cannot confidently conclude whether our program supergiants have already experienced the large-scale mixing, or not.
The oxygen abundance obtained for our sample of F supergiants is close
to that of the interstellar medium in LMC, as expected, because the
surface abundance of this element is not significantly changed by
the supergiant evolution. The NLTE mean value of the oxygen abundance
for our sample of F supergiants is A(O) = 8.51 dex: it is higher than
the previous LTE value (8.45 dex), but remains close to that of LMC H II
regions (Dufour 1984; Kurt & Dufour 1998 give 8.43
and 8.37 respectively). Our new value of oxygen abundance, referred to the
mean iron abundance (A(Fe) = 7.10) and then to the corresponding solar ratio
(O/Fe)![]() ,
gives [O/Fe] = +0.01. This ratio is slightly greater than
zero, and anyway larger than previous estimate made by HAS95 (Table 6).
The models of chemical evolution of the Magellanic Clouds (e.g.,
Pagel & Tautvaisiene 1998) predict [O/Fe] values near zero for
continuous formation. This prediction from the bursting and smooth models for
the metallicity [Fe/H] of about -0.40 dex appears to be in the excellent
agreement with our results, especially for the case of smooth evolution (see
Fig. 6 from that paper). To reach an agreement between the theory predictions
and observational data on the oxygen abundance derived in several previous
studies, Pagel & Tautvaisiene (1998) formally shifted data points for
the LMC stars upwards by 0.2 dex. This was supposed to be a correction in order
to adjust the data on LMC supergiants to those of Galactic supergiants.
The latter stars show the mean negative value [O/Fe] of about -0.2 dex
based on the results of some works (e.g., Luck & Lambert 1981,
1985).
,
gives [O/Fe] = +0.01. This ratio is slightly greater than
zero, and anyway larger than previous estimate made by HAS95 (Table 6).
The models of chemical evolution of the Magellanic Clouds (e.g.,
Pagel & Tautvaisiene 1998) predict [O/Fe] values near zero for
continuous formation. This prediction from the bursting and smooth models for
the metallicity [Fe/H] of about -0.40 dex appears to be in the excellent
agreement with our results, especially for the case of smooth evolution (see
Fig. 6 from that paper). To reach an agreement between the theory predictions
and observational data on the oxygen abundance derived in several previous
studies, Pagel & Tautvaisiene (1998) formally shifted data points for
the LMC stars upwards by 0.2 dex. This was supposed to be a correction in order
to adjust the data on LMC supergiants to those of Galactic supergiants.
The latter stars show the mean negative value [O/Fe] of about -0.2 dex
based on the results of some works (e.g., Luck & Lambert 1981,
1985).
Nevertheless, one important note has to be made. As it was shown by KA99,
the oxygen abundances obtained for supergiant stars using the standard method
can be significantly underestimated. Using the high quality multiphase spectra
for famous Cepheid ![]() Cep KA99 obtained with a modified method the value
[O/Fe]
Cep KA99 obtained with a modified method the value
[O/Fe] ![]() 0. Moreover, the similar results were also recently obtained
by us for the number of Galactic Cepheids (results are in preparation for
publications). These results are in agreement with the value [O/Fe] which is
expected from the model of Galactic chemical evolution for [Fe/H]
0. Moreover, the similar results were also recently obtained
by us for the number of Galactic Cepheids (results are in preparation for
publications). These results are in agreement with the value [O/Fe] which is
expected from the model of Galactic chemical evolution for [Fe/H] ![]() 0
(see Wyse 1999).
0
(see Wyse 1999).
Our new analysis provides both a lower metallicity and a higher (O/H) value than previous determinations, providing a value which is closer to what would be expected for this metallicity in the classical and global evolution of abundances in our Galaxy (Edvardsson et al. 1993; Wyse 1999): suggesting that the evolution of the LMC is slightly less different from the Galactic one than previously thought.
High luminosity Galactic stars are known to have enhanced sodium lines,
possibly a real enhancement of Na abundance due to Ne-Na
processed material mixed with the atmospheric gas. Recently, El Eid & Champagne
(
![]() )
proposed a theory in which a sodium overproduction in
supergiants increases with increasing stellar mass. Such an overproduction
does not exceed 0.3-0.4 dex for 10-20
)
proposed a theory in which a sodium overproduction in
supergiants increases with increasing stellar mass. Such an overproduction
does not exceed 0.3-0.4 dex for 10-20 ![]() .
Our mean result for
massive F supergiants indicates an abundance smaller than the LTE
value, resulting in a very small enhancement ([Na/Fe] = +0.05), smaller than
expected within the theory. This result is in agreement with LET98.
The Galactic supergiants have also high (Na/Ca) ratios, and this peculiarity
is not found here. Among several explanations, the difference with the
Galactic supergiants, could be due to the suppression of sodium overproduction
in metal deficient stars.
.
Our mean result for
massive F supergiants indicates an abundance smaller than the LTE
value, resulting in a very small enhancement ([Na/Fe] = +0.05), smaller than
expected within the theory. This result is in agreement with LET98.
The Galactic supergiants have also high (Na/Ca) ratios, and this peculiarity
is not found here. Among several explanations, the difference with the
Galactic supergiants, could be due to the suppression of sodium overproduction
in metal deficient stars.
The ratio (![]() -elements/Fe) is less different from the predictions of
the classical Galactic evolution. Magnesium was previously found without any
enhancement, and even with a slight deficiency relative to iron, but in this
work it is even lower (by a factor of 2). This overdeficiency is surprising,
but let us note that such a NLTE overdeficiency of Mg is also found
in the B-type supergiants of the SMC (Dufton et al. 2000),
but not generally in A-type SMC supergiants (Venn 1999
and references therein).
-elements/Fe) is less different from the predictions of
the classical Galactic evolution. Magnesium was previously found without any
enhancement, and even with a slight deficiency relative to iron, but in this
work it is even lower (by a factor of 2). This overdeficiency is surprising,
but let us note that such a NLTE overdeficiency of Mg is also found
in the B-type supergiants of the SMC (Dufton et al. 2000),
but not generally in A-type SMC supergiants (Venn 1999
and references therein).
Sulphur is one of the elements whose abundance can be also
measured in H II regions. This element is not processed in
the intermediate-to-high mass stars at their early evolutionary
stages, therefore its abundance in the young supergiant
atmospheres should reflect that of the ISM. Our mean S abundance
obtained for a sample of F supergiants is A(S) =
![]() (i.e. [S/H] = -0.26), while from H II regions of LMC
Dufour (1984) found A(S) =
(i.e. [S/H] = -0.26), while from H II regions of LMC
Dufour (1984) found A(S) =
![]() ,
that within
an error bar is practically the same value as ours.
,
that within
an error bar is practically the same value as ours.
It has to be noted that the mean iron abundance determined in the present study is [Fe/H] = -0.40, i.e. slightly lower than the value derived by HAS95, while LL92 and Korn et al. (2000) obtained the metallicity of LMC [Fe/H] = -0.36 and -0.41 respectively. Both these estimates agree with our result. The relative abundances [M/H] of iron-group elements are close to the iron content (see Fig. 1).
Even with an analysis made with different gravities, the abundances of the heavy elements (derived from the lines of ions) remain enhanced. This is clearly seen in Fig. 1. The (hs/ls) ratio is rather high and definitely non-solar.
The elemental abundances have been re-investigated in nine F supergiants of the Large Magellanic Cloud. The mean abundance of iron is found to be [Fe/H] = -0.40, slightly lower than previously adopted for LMC, but in accordance with the recent results obtained by Korn et al. (2000).
The NLTE calculations for carbon, oxygen and sodium, based on Kurucz's atmospheric models with an over-all metal deficiency, were carried out as described in Korotin et al. (1999). Importantly, the NLTE oxygen abundance is found higher and the carbon abundance lower than in previous work. The carbon abundance is in much better agreement with that of the LMC H II regions, oxygen remaining in fair agreement with H II regions. The (C/O) ratio is low, lower than solar and the H II ratio (a possible sign of the first dredge-up). The relative to iron abundance of oxygen [O/Fe] = + 0.01 derived for nine F supergiants appears in excellent accordance with the prediction based on the smooth model of the LMC evolution.
We did not find a remarkable sodium overabundance in the LMC supergiants, at contrast to the Galactic supergiants that could be caused by inefficient sodium overproduction in Ne-Na cycle in the metal deficient stars.
The (![]() /Fe) ratios are comparable to those that were obtained in
previous analyses, with magnesium abundance being significantly lower
in the new analysis. Sulphur abundances in supergiants show a good
agreement with those measured in H II regions.
/Fe) ratios are comparable to those that were obtained in
previous analyses, with magnesium abundance being significantly lower
in the new analysis. Sulphur abundances in supergiants show a good
agreement with those measured in H II regions.
The iron-group elements follow the solar distribution of the (M/Fe) ratios. With a different method of gravity determination, for the elements heavier than iron-group ones, an enhancement remains, in agreement with previous studies.
For the LTE analysis, the non-standard approach, following KA99,
leads to significantly larger ![]() values, and these larger
gravities result in masses of supergiants of about 10-20
values, and these larger
gravities result in masses of supergiants of about 10-20 ![]() ,
that are in the excellent agreement with the evolutionary calculations.
However, the evolutionary status of our program stars is not completely
clear. Depending upon the used evolutionary tracks, our stars can be
considered 1) either as those moving towards the red giant region for the
first time, 2) or having already passed the red giant stage and
experienced the first dredge-up, and now performing their blue loops.
,
that are in the excellent agreement with the evolutionary calculations.
However, the evolutionary status of our program stars is not completely
clear. Depending upon the used evolutionary tracks, our stars can be
considered 1) either as those moving towards the red giant region for the
first time, 2) or having already passed the red giant stage and
experienced the first dredge-up, and now performing their blue loops.
Finally, one can note that an extension of this work to the SMC would be useful. The latter is planned to be presented in our next paper.
Acknowledgements
We thank Dr. O. R. Pols for having put in our disposal an electronic version of the evolutionary models. Our special thanks to Dr. R.-P. Kudritzki and N. Przybilla for the careful inspection of the manuscript and giving us many useful suggestions which significantly improved the initial version of the paper.