A&A 367, 236-249 (2001)
DOI: 10.1051/0004-6361:20000344

A new analysis of the radial velocity variations of the eclipsing and spectroscopic binary EN Lacertae[*]

H. Lehmann1 - P. Harmanec2,3 - C. Aerts4 - H. Bozic5,3 - P. Eenens6 - G. Hildebrandt7 - D. Holmgren8 - P. Mathias9 - G. Scholz7 - M. Slechta3 - S. Yang10


1 - Thüringer Landessternwarte Tautenburg, 07778 Tautenburg, Germany
2 - Institute of Astronomy of the Charles University, V Holesovickách 2, 180 00 Praha 8, Bohemia, Czech Republic
3 - Astronomical Institute, Academy of Sciences, 251 65 Ondrejov, Bohemia, Czech Republic
4 - Institute of Astronomy, Celestijnenlaan 200 B, 3001 Leuven, Belgium
5 - Hvar Observatory, Faculty of Geodesy, University of Zagreb, Kaciceva 26, 10000 Zagreb, Croatia
6 - Departamento de Astronomia, Universidad de Guanajuato, Apartado 144, 36000 Guanajuato, GTO, Mexico
7 - Astrophysikalisches Institut Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany
8 - Dept. of Physics & Astronomy, Brandon University, Brandon, Manitoba, R7A 6A9, Canada
9 - Observatoire de la Côte d'Azur, BP 4229, 06304 Nice Cedex 4, France
10 - Dept. of Physics & Astronomy, University of Victoria, PO Box 3055, Victoria, B.C., V8W 3P6, Canada

Received 9 October 2000 / Accepted 17 November 2000

Abstract
An analysis of 1236 new electronic spectra of the eclipsing binary EN Lac from four observatories and of 994 radial velocities (RV hereafter) from photographic spectra, published by several authors, has allowed us to disentangle the RV variations due to orbital motion and due to pulsations of the star. New, accurate orbital elements as well as precise values of the three pulsation periods, already known from the previous studies, were derived. The accuracy of the orbital solution has been substantially improved after the observed RV changes were properly prewhitened for the short-term oscillations. The amplitude of the dominant RV oscillation with a period of $P_1=0\hbox{$.\!\!^{\rm d}$ }16916703$ was found to vary with a 74 year cycle. The amplitudes of the two other RV oscillations, having periods of $P_3=0\hbox{$.\!\!^{\rm d}$ }18173256$ and $P_2=0\hbox{$.\!\!^{\rm d}$ }17085554$, vary on much shorter time scales of 674 d and 331 d, respectively. The value of P2 derived here does not correspond to a one year alias of the value found by several authors from photometry but appears to be an intrinsic period. The time scales of the amplitude modulations found for P1 and P3 are in good agreement with previous photometric results. For the first time we present evidence of line profile variations of EN Lac. They correlate well with the short-term RV variations but they alternatively occur with periods corresponding either to the fundamental periods or to the first harmonics of P1 to P3. An analysis of the RV scatter along the orbital phase curve for the new spectra, obtained over a relatively short interval of time, gives some indication of a sharp increase of this scatter when the stars are approaching periastron. Since this could be a signature of forced oscillations, the effect is worth further study, though it appears rather marginal at present[*].

Key words: stars: binaries: close - stars: binaries: eclipsing - stars: binaries: spectroscopic - stars: fundamental parameters - stars: oscillations - stars: individual: EN Lac


1 Introduction

One of the topical problems in the current research of early-type stars is to understand the nature of rapid line profile changes observed for many hot stars. Speculations about the crucial role of duplicity for either triggering or at least modifying stellar pulsations are not new. Fitch (1967, 1969) called attention to the fact that many known $\beta $ Cep stars are spectroscopic binaries and demonstrated, on particular examples, that the tide-raising potential does indeed affect the pulsations. Osaki (1971) pointed out that slow periodic changes of the mean ($\gamma$) value of the pulsational ($\beta $ Cep) RV curve need not be due to orbital motion in a binary system but may also be caused by a superposition of two oscillations with similar periods. He suggested this as an explanation for Fitch's (1969) result for $\beta $ Cep. Pigulski & Boratyn (1992) demonstrated, however, that the secular changes in the main pulsational period of $\beta $ Cep are caused by light time effect as the star moves in orbit with a distant binary companion, discovered by speckle interferometry. On the other hand, an archetype line profile variable $\varepsilon $ Per (HD 24760) was found to be a 14.1-d spectroscopic binary in an eccentric orbit, with a possible distant tertiary - see Harmanec (1989), Harmanec & Tarasov (1990), Tarasov et al. (1995) and De Cat et al. (2000). Kato (1974) investigated the conditions under which non-radial oscillations could either be excited or become multi-periodic due to a resonant interaction with the tidal mode in binary systems. One of the principle problems in investigating pulsations in binaries is the disentangling of the variations due to orbital motion and of the short-term oscillations. This disentangling was successfully applied e.g. to the $\beta $ Cep stars $\beta $ Sco A (Holmgren et al. 1997) and ARCas (Holmgren et al. 1999).

2 Current knowledge about EN Lac

EN Lac (HD 216916, 16 Lac, HR 8725, BD+40$^\circ$4949, SAO 52512, HIP 113281, ADS 16381A) is a well-known representative of the class of $\beta $ Cep stars and a member of the visual binary ADS 16381. Its spectral type is B2 IV. RV variations of EN Lac were discovered by Lee (1910). Struve & Bobrovnikoff (1925) demonstrated that the object is a single-lined spectroscopic binary for which they derived a period of 12.$^{\rm d}$3106 and the first set of orbital elements. Daniel obtained series of Allegheny spectra between 1912 and 1916 and considered two possible periods, either 12.$^{\rm d}$093 or its one-day alias of 1.$^{\rm d}$09 but his observations and conclusions have only been published by Beardsley (1969).

Only much later Walker (1951) found that EN Lac is a new $\beta $ Cep variable with light variations up to 0.$^{\rm d}$11 and RV variations of 40 kms-1 (including orbital motion). For the short-term contributions he derived a preliminary period of 0.$^{\rm d}$16900. Walker (1952), Struve et al. (1952) and Miczaika (1952) published extended series of photoelectric and spectral observations and concluded that two short periods, 0.$^{\rm d}$169165 and 0.$^{\rm d}$170845, are excited which produce a beat period of about 17.$^{\rm d}$2. Moreover, Struve et al. (1952) improved the value of the orbital period to 12.$^{\rm d}$097. Fitch (1969) re-analyzed available photometric and RV observations and found that the rapid changes can be better described by three sinusoidal components with periods of 0.$^{\rm d}$16917, 0.$^{\rm d}$17086 and 0.$^{\rm d}$18182.

The interest in EN Lac was revived after Jerzykiewicz et al. (1978) discovered that EN Lac is an eclipsing system. Jarzebowski et al. (1979) analyzed new series of photoelectric observations and concluded that the previous authors identified one-year aliases of the two longer periods. According to them, the correct periods are 0.$^{\rm d}$169170, 0.$^{\rm d}$170793 and 0.$^{\rm d}$181712. Garrido et al. (1983) obtained new photometry, including one complete eclipse, and using also the new orbital elements derived by LeContel et al. (1983), they estimated the basic physical elements of the system. They also concluded that the amplitudes of the two shorter oscillation periods were secularly decreasing. Balona (1985) attempted to explain the amplitude variation by the precession in the binary system. Jerzykiewicz & Pigulski (1996) concluded that the amplitudes of the first two short periods vary in a cycle of about 50 years while the third one is in fact a close doublet with a beat period of 676d. For convenience, the exact values of the periods so far reported by various authors are summarized in Table 1.

 

 
Table 1: Short periods in days of EN Lac reported by various authors from photometry and from spectroscopy, as marked in columns $\triangle m$ and RV, respectively. The errors of the last digits of the periods, given by the respective authors, are in parentheses following the periods

Source		 P1 P2 P3 P4 $\triangle m$ RV Notes

A		 .16900 - - - *    
B .169165 .170845 - - *    
C .16916 .17085 - -   *  
D .169168 .1707 - - *    
E .169166 .170857 .181821+.181885 - * *  
F .1691703(15) .1707932(30) .1817117(29) - *   1965 data
F .169170(16) .170770(30) .181692(24) - *   1977 data
G .169155(11) .170765(20) .181688(19) - *   1977 data
H .169168 .170776 .181734 -   *  
I .169168 .170776 .181734 - *   1977+1979 data
J .16767 .17053 .18173 - * * 1977 data
J .1691677 - - - *   P variable?
K .16917 .17079 .18171 6.05, .139005 *    
L .16915 .17077 .18171 - *    
M - - .181732 - *   P variable
N - - .1816843+.18173312 - *    
N  62 yr  52 yr  676 d - *   modulation time scales
O .1691778 .1707769 .1817331 - *   misprint in P1?
P - - .1814+.1817 - *    
Q .1691651 0.1707775 .18173300(2)+.1816843(3) - *    
Q  71 yr  50 yr  677.9(4) - *   modulation time scales


Details on sources of data and instruments used (column "Source") A: Walker (1951), B: Walker (1952), C: Struve et al. (1952), D: Miczaika (1952), E: Fitch (1969), F: Jarzebowski et al. (1979), G: Jarzebowski et al. (1980), H: LeContel et al. (1983), I: Chapellier et al. (1995), J: Sato & Hayasaka (1986), K: Jerzykiewicz (1993), L: Chapellier et al. 1995, M: Sato (1996), N: Jerzykiewicz & Pigulski (1996), O: González Bedolla et al. (1997), P: Sareyan et al. (1997), Q: Jerzykiewicz & Pigulski (1999).

Most accurate pulsation periods and modulation time scales of EN Lac should be that given by Jerzykiewicz & Pigulski (1999). Their values base on photometric data covering the period of 1950 to 1992.

There has been a continuing controversy on whether the binary nature of EN Lac plays an important role for the character of the $\beta $ Cep variations observed. Fitch (1967) and Fitch (1969) argued in favour of the presence of tidal effects in binaries with pulsating components, including EN Lac. For EN Lac, this possibility was refuted by Jarzebowski et al. (1979). Frolov et al. (1980) argued that the principal short periods of many $\beta $ Cep and other pulsating stars in binary systems are nearly integer submultiples of the orbital periods (or rotational periods). They obtained the period ratio of 71.5 for EN Lac, however. Recently, Chapellier et al. (1995) concluded on the basis of their new observations that the amplitude of the longest of the three short periods of light and RV variations varies with the phase of the orbital period (or rotational period of the primary). This finding was, however, challenged by Jerzykiewicz & Pigulski (1996).

Considering all these developments, we felt that a dedicated study of possible effects of the duplicity of the star on the character and time changes of the rapid variations observed is still desirable.

3 Observation and reduction

3.1 New spectroscopy


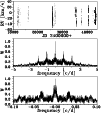  \begin{figure} \par\epsfig{file=FIGS_ORIG/H2483f01r.eps, width=8.8cm}\end{figure} Figure 1: Spectroscopic observations of EN Lac. Top: time sampling. Center: window function. Bottom: window function zoomed at low frequencies
Open with DEXTER


 

 
Table 2: Journal of observations. Authors (A) and instruments (I) are given below. $N_{\rm o}$, $N_{\rm r}$, and $N_{\rm l}$ list the number of observations, the number of runs, and the number of lines used for RV measurements. $w^{\rm w}$ and $w^{\rm s}$ are the calculated weights for the weak and for the strong weighting schemes, $RV_0^{\rm w}$ and $RV_0^{\rm s}$ are the corresponding finally calculated zero-point corrections

set		 A I Epoch $N_{\rm o}$ $N_{\rm r}$ $N_{\rm l}$ Disp. $w^{\rm w}$ $w^{\rm s}$ $RV_0^{\rm w}$ $RV_0^{\rm s}$
      [JD-2400000]       [Åmm-1]     [kms-1] [kms-1]

1		 A I 18542.7-24165.5 31 24 10-17 30 3.2 1.6 +3.3 +3.5
2 B II 19631.8-21109.6 108 108 2-12 40 2.4 1.0 -2.0 -2.5
3 C III 33869.7-33966.8 327 34 13 32 3.0 1.5 +0.6 +0.4
4 C IV 33873.8-33877.0 47 4 13 10 7.0 3.4 -0.9 -1.4
5 C V 33883.7-33925.9 68 43 7 11 6.7 2.7 -1.8 -1.8
6 D V 34253.7-34984.9 36 20 5 11 6.7 2.3 -1.8 -1.8
7 D VI 34258.6-34258.8 14 1 10 37 2.6 1.2    
8 D III 34909.8-34915.0 26 6 13 32 3.0 1.5 +0.6 +0.4
9 E VII 40126.3-40128.4 19 3 23 76 1.0 0.5    
10 F VIII 43055.3-43058.6 51 4 23 12 6.4 3.2 +0.3 $\pm 0.0$
11 F VIII 43417.3-43430.5 118 14 39 12 6.4 3.2 +0.3 $\pm 0.0$
12 G IX 43459.7-44188.7 20 20 7 16.9 5.2 2.1    
13 H X 43738.0-43740.3 82 3 18 10 7.0 3.5 -0.6 -1.3
14 I XI 45623.3-45631.5 47 9 41 9.65 7.1 3.5 -2.7 -2.6

15		 J XII 50279.4-51080.4 4 4 30 10 7.0 13.9 +0.9 +0.7
16 J XIII 51009.5-51483.4 942 16 3 3.2 10.0 10.0 $\pm 0.0$ $\pm 0.0$
17 J XIV 51436.7-51462.0 33 5 1 10 7.0 2.9 $\pm 0.0$ $\pm 0.0$
18 J XV 48450.4-48457.6 205 5 40 8.1 7.7 15.2 +0.9 +0.7
19 J XVI 48456.4-48456.6 45 1 40 5.2 8.9 17.7 +0.9 +0.7
20 J XVII 50289.9-50294.0 7 4 1 10 7.0 2.9 $\pm 0.0$ $\pm 0.0$


Details on sources of data and instruments used. Column "A": A: Frost et al. (1926) (cf. also Lee 1910 and Struve & Bobrovnikoff 1925), B: Beardsley (1969), C: Struve et al. (1952), D: McNamara (1957), E: Bloch et al. (1970), F: LeContel et al. (1983), G: Abt et al. (1990), H: Sato & Hayasaka (1986) I: Chapellier et al. (1995), J: this paper. Column "I": I: Yerkes 1.02-m refractor, Bruce 1-prism spg., II: Allegheny 0.79-m Keeler Memorial reflector, 1-prism Mellon spg., III: Mt. Wilson 1.52-m reflector, Cassegrain spg., IV: Mt. Wilson 2.54-m reflector, coudé grating spg., V: Lick 0.91-m refractor, new Mills 3-prism spg., VI: Lick 0.30-m refractor, 2-prism spg., VII: Haute Provence 1.20-m reflector, prism spg., VIII: Haute Provence 1.52-m reflector, grating spg., IX: Kitt Peak National Observatory 1-m coudé feed grating spg., X: Okayama 1.88-m reflector, coudé grating spg., XI: Haute Provence 1.93-m reflector, grating spg., XII: this paper: Ondrejov 2.0-m reflector, coudé grating spg. with a Reticon RL 1872F/30 detector with 15 $\mu$m pixels, XIII: this paper: Tautenburg 2.0-m reflector, coudé echelle spectrograph with a Tektronix $1024\times1024$ CCD with 24 $\mu$m pixels, XIV: this paper: DAO 1.22-m reflector, coudé grating spg. with a thick Loral $4096\times200$ CCD with 15 $\mu$m pixels, XV, XVI: this paper: OHP 1.52-m reflector, Aurélie coudé grating spg. with a TH 7832 detector with 13 $\mu$m pixels, XVII: this paper: DAO 1.83-m reflector, Cassegrain grating spg.

Table 2 gives the journal of all RV observations at our disposal. Our own observations more than doubled the existing body of the data. Derived RVs are listed in Table 3[*]. New spectra were obtained at four observatories:

1.
The dominant data set consists of 942 echelle spectra from the Thüringer Landessternwarte (TLS) Tautenburg. They were reduced with the help of MIDAS software by HL. The standard MIDAS software was modified for the wavelength calibration to obtain a perfect fit also at the overlapping edges of the echelle orders. RVs were obtained from the comparison of the synthetic and observed line profiles for the three cleanest (least blended) He I lines: 5015, 5875, and 6678 Å;
2.
The second largest set is a series of blue (4400-4700 Å) and green (4750-5050 Å) Aurelie spectra secured with the 1.52-m reflector of the Haute Provence Observatory (OHP) during 8 consecutive nights. Their initial reduction (bias subtraction, flat-fielding) was done by PM. The wavelength calibration and RV measurements were carried out by PH who used the SPEFO program - see Horn et al. (1996) and Skoda (1996). RVs of symmetric and stronger metallic lines (mostly O II, N II and C II), H$\beta $ and He I 4472 and 4923 Å lines were measured. Their wavelengths were derived from measurements of synthetic spectra broadened to the projected rotational velocity of EN Lac. Only lines which were symmetric in the synthetic spectra were used;
3.
Four red (6280-6720 Å) Reticon spectra were obtained in the coudé focus of the Ondrejov 2.0-m reflector. They were completely reduced with SPEFO by PH. RVs were derived from He I 6678 Å, H$\alpha$and several stronger and symmetric metallic lines;
4.
Several red (6100-6750 Å) CCD spectrograms were obtained at the Dominion Astrophysical Observatory (DAO). They were completely reduced within IRAF and MIDAS by SY and DH. Only RV of the He I 6678 Å line was measured.
For all spectra covering the red wavelength region the instrumental RV zero-points were derived with the help of a large set of telluric O2 and H2O lines. This allows us to assume that the above datasets 1, 3 and 4 (sets 15, 16, 17 and 20 of Table 2) are on exactly the same heliocentric wavelength scale. Note that due to the fitting procedures all RVs correspond to the RVs of line centroids and not of line minima.

3.2 Data from literature

We compiled all series of RV observations available in the astronomical literature and used a computer program to derive heliocentric Julian dates (HJDs hereafter) from the tabulated dates of mid-exposures or geocentric Julian dates for all of them. This way we found a few misprints in tabulated JDs for RVs of EN Lac published by Beardsley (1969). For convenience of future investigators, they are summarized in Table 4. For JD 2420038 it is not clear whether the misprint occurred for the date or the Julian date and we omitted this observation from our data set. Figure 1 shows the sampling of all RVs in time and also the window function of the data which will be discussed later.


 

 
Table 4: Misprints detected in tabulated times of observations of EN Lac in Beardsley (1969)

Date (G.M.T.)		 Tabulated JD Correct JD
  -2400000 -2400000

1913 Sep. 27.621		 20038.671 ?
1914 Sep. 22.746 20389.746 20398.746
1916 Sep. 02.631 21107.631 21109.631


3.3 Weighting scheme

Our compilation of RVs is very inhomogeneous. Spectra were observed with different instruments and have very different linear dispersions and resolutions. Also RVs were derived by different authors and rest on different sets of spectral lines. A part of them comes from photographic plates and another one from electronic spectra. So we have a set of RVs of different accuracy and probably also of a slightly different zero point of the RVscale.

To take these differences at least partly into account, we attempted to find out a suitable weighting scheme. This is not simple in our particular case. Due to steady improvements of the observational and reduction techniques, the accuracy, and therefore the weights would, on average, increase with time. We have recent observations of a high accuracy, well suited for precise RV measurements. However, the older, less accurate observations are invaluable to a search for the long-term amplitude changes over the periods of years or even decades.

The trouble is that any weighting scheme with a steep dependence on, say, the dispersion of the spectra (a strong weighting hereafter) almost completely suppresses the older observations. Consequently, we used three different weighting schemes: unweighted data, weak weighting, and strong weighting. Unweighted data will be used to derive a complete multiple-frequency fit and to include long-term amplitude modulation of rapid oscillations. Weighted data will be used to verify and improve the frequencies found in the first step and to derive an accurate orbital solution.

Strong weighting: The error of a RV value derived from a single spectral line profile I(RV)follows from the photon statistics (Butler et al. 1996):

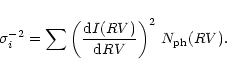\begin{displaymath}\sigma^{-2}_i = \sum{\left(\frac{{\rm d}I(RV)}{{\rm d}RV}\right)^2\,N_{\rm ph}(RV)}. \end{displaymath} (1)

The accuracy of a RV measurement at a certain point of the line profile is determined by the local gradient of the profile and the number of photons $N_{\rm ph}$ collected at this point. The sum extends over all discrete measurements (steps in RV) taken to derive the RV of line i. Assuming a Gaussian line profile and a small central line depth Ai, it follows that

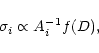\begin{displaymath}\sigma_i \propto A^{-1}_i f(D), \end{displaymath} (2)

where f is a function of the dispersion, but also of $v\sin(i)$ and of the resolution of measurement limited by the projected slit width of the spectrograph, or possibly by the pixel size of the electronic detector or the point spread function of the photographic plates. Petrie (1962) tabulated the mean RV errors found from single-line measurements in photographic spectra of various dispersions. A least squares fit to his values for B-type stars give

 \begin{displaymath}f(D) \propto 1.33 + 0.042\,D, \end{displaymath} (3)

where D is in Åmm-1 and f is in kms-1. If the mean RV, based on measurements of N lines, is computed from unweighted data, as we will assume here, the error of the mean follows as

 \begin{displaymath}\sigma^2 \propto f^2 N^{-2} \sum A^{-2}_i. \end{displaymath} (4)

To estimate the sum in Eq. (4) we will assume that in any spectrum the Nstrongest lines were used. In that case the sum can be estimated from the inverse frequency distribution of line depths in the spectrum. For EN Lac we obtain from an analysis of the TLS spectra an approximate distribution of $A^{-1}_i \propto 0.9+0.1\,i$, where i=1 stands for the strongest metal line (the 11th strongest line of the spectrum has a line depth of about half of the depth of the strongest line).

The weight w of a RV value should be $w \propto \sigma^{-2}$ which leads to the final formula

 \begin{displaymath}w = \frac{Q\,N^2}{(1.33+0.042\,D)^2 \sum(0.9+0.1\,i)^2}\cdot \end{displaymath} (5)

The summation goes over the N lines measured in a given spectrum. The superior S/N ratio of the electronic spectra is taken into account via an additional multiplicative factor Q. We set Q=1 for photographic and Q=4 for electronic spectra.

Since we assumed that unweighted mean RVs are derived by most of the authors, the approximately assumed steadily decrease of line depth with increasing N results in a maximum of the weights for $N \sim 16$. We, therefore, set in Eq. (3) N=16for all RVs derived from more than 16 lines.

Weak weighting: To test the influence of weighting on the obtained results we also used a weak weighting for a comparison. We assumed that the accuracy of RVs depends only on the linear dispersions and use Eq. (3) to calculate the weights, with $w\sim f^{-2}$. The adopted weights for the individual data sets and for both weighting schemes are also given in Table 2. Weights were normalized in such a way that w=10 for the TLS data.

The question of different instrumental RV zero-points will be discussed later in connection with the multiple period search.

4 Disentangling orbital and short-term $\vec {RV}$ changes

4.1 Period finding techniques

Three different computer programs were used to calculate the orbital solution and to search for, and model the short-period changes. The first program derives the orbital solution by the method of differential corrections to the initial orbital elements (Schlesinger 1908; Sterne 1941). The program optimizes the orbital elements including the orbital period. It can handle data with unequal weights, and it is possible to include the apsidal advance among the elements.

The second program uses a multiple period finding technique which is able to optimize arbitrary frequencies and its harmonics. It is based on a least-squares fit of sinusoids. For very low eccentricities, as in the case of EN Lac, the program fits the orbital curve very well using only the fundamental period and its first harmonic. It is, therefore, possible to obtain a simultaneous fit of orbital as well as pulsational periods at one iterative process. All but one of the periods are fixed. To optimize the whole family of frequencies involved, the procedure is iteratively repeated for individual frequencies. In a sense, the program represents an extension of the well-known CLEAN algorithm since not only one single period but also the amplitudes and phases of all included periods are optimized.

The third program computes a modified Scargle periodogram the ordinate of which corresponds to the reduction of the sum of squares by the least squares fit of sinusoids used. A detailed description of the periodogram and a discussion of its statistical properties can be found in Lehmann et al. (1999). The program is used to search in the residuals of an assumed multiple frequency model for possible additional frequencies.

Some principal results were also independently verified with the help of program FOTEL - see Hadrava (1990).

4.2 Orbital solution for the original RVs

When the oscillations show constructive interference, the amplitude of the observed short-term RV variations is nearly comparable to the semi-amplitude of the orbital RV curve. This complicates the determination of truly reliable orbital elements. One can of course make use of the fact that the three periods of oscillations, P1 = 0 $.\!\!^{\rm d}$1691678, P2 = 0 $.\!\!^{\rm d}$1707769, and P3 = 0 $.\!\!^{\rm d}$1817331, have been well established from photometric observations. However, the amplitudes of these oscillations are known to vary with time which represents an extra complication for the frequency analysis.


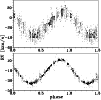  \begin{figure} \par\epsfig{file=FIGS_ORIG/H2483f02r.eps, width=8.8cm}\end{figure} Figure 2: Top: orbital solution I derived from raw data. Bottom: orbital solution II derived from the same data but prewhitened for the short-term variations found in selected data groups
Open with DEXTER


 

 
Table 5: Orbital elements. Epochs are in JD - 2400000
  Solution I Solution II
P [d] 12.096860 $\pm$ 0.000026 12.096844 $\pm$ 0.000010
K [kms-1] 23.66 $\pm$ 0.18 23.818 $\pm$ 0.033
$\gamma$ [kms-1] -12.52 $\pm$ 0.13 -12.289 $\pm$ 0.026
e 0.0347 $\pm$ 0.0090 0.0392 $\pm$ 0.0017
$\omega$ [deg] 65 $\pm$ 12 63.7 $\pm$ 2.1
$T_{\rm periastron}$ 39053.77 $\pm$ 0.41 39053.71 $\pm$ 0.07
$T_{\rm eclipse} $ 39054.55 $\pm$ 0.78 39054.53 $\pm$ 0.14
rms 6.03 kms-1 1.10 kms-1



 

 
Table 6: Periods found within the data groups. Sets are as in Table 2, $N_{\rm s}$ is the total number of spectra, $N_{\rm r}$ the number of runs. P and K give the periods in days and semi-amplitudes in kms-1, respectively. P1 to P3 refer to periods near to the known triplet of short-term variations, all other periods are listed as P4
group set mean JD $N_{\rm s}$ $N_{\rm r}$ P1 K1 P2 K2 P3 K3 P4 K4
1 2 19699.6 39 39 .16918 8.6 .17078 3.0 .18165 2.4    
2 2 20054.0 52 52 .16920 7.9 .17092 3.4 .18169 5.6    
3 3 33923.4 327 15 .16915 15.5 .17070 2.9 .18179 1.6    
4 4 33874.9 47 4 .16865 11.7         1.733 1.9
5 5 33904.9 68 7 .16917 13.7 .17081 4.5 .18106 1.0    
6 6 34795.8 36 4 .16924 15.1 .17078 4.1 .18173 4.2    
7 8 34913.0 26 2 .16961 18.9            
8 10 43057.3 51 4         .18193 4.5 .16961 7.4
9 11 43425.0 118 7 .16931 5.2 .17076 1.9 .18173 2.6    
10 13 43739.3 82 3 .16831 7.5     .18073 4.8 .2896 2.1
11 14 45627.6 47 5 .16916 4.2 .17348 1.0 .18166 5.2    
12 18+19 48453.8 250 6     .16986 5.7 .18179 6.4 .19701 1.1
13 16 51110.4 229 6 .16917 1.9 .17323 4.4     .19545 2.2
14 16 51437.1 714 9 .16917 3.9 .17083 3.1 .18171 2.0 .17258 2.0
15 17 51449.5 33 4 .16921 3.7 .17084 4.0 .18193 0.8    


To disentangle the orbital motion and short-term RV changes, we proceeded in two different ways. In the first step, we derived an initial solution (solution I of Table 5) using all the original RVs of Table 2 and adopting the weak weighting. This is why the scatter around the mean orbital RV curve displayed in the upper panel of Fig. 2 looks larger than the calculated mean rms per one observation: the scatter is mainly caused by low-dispersion data with small weights. A small part of the scatter is also due to the fact that we assumed one joint systemic velocity for all RVs at this stage.

4.3 Investigation of data subsets

To proceed further, we created subsets of RV data, spanning not more than 180 d. Moreover, each subset was formed in such a way that it contains data from only one source and from one spectrograph and also enough RVs with a sufficient sampling in time to allow a separate period search for rapid changes. This way, we formed 15 different subsets which are listed in Table 6. Then we subjected the O-C velocity residuals from solution I for each of the subsets to a period search in the neighbourhood of the known periods P1 to P3. Using a least-squares sinusoidal fit of these three periods within each subset, we prewhitened the original RVs for the rapid changes. Prewhitened RVs from all subsets were then combined and used to calculate a new orbital solution. The process was iterated until convergence was achieved. The final orbital solution is given as solution II in Table 5. No evidence of apsidal motion was found. It is seen that the decrease of the mean rms error per 1 observation between solutions I and II is quite substantial.


  \begin{figure} \par\epsfig{file=FIGS_ORIG/H2483f03r.eps, width=8.8cm}\end{figure} Figure 3: A plot of the semi-amplitude of the P1-variation of Table 6 vs. time. The solid curve is a sinusoid with a period of 23000 d
Open with DEXTER

Table 6 shows that for a few subsets, we arrived at rather peculiar values of the short periods. In some cases, only one or two periods are detectable. A significant result of our analysis is the finding that the amplitude of P1 varies with an apparent cycle of about 23000 d - see Fig. 3. Possible time scales for the amplitude variation of P3 are 237, 473 or 673 d, the latter value being reported already by Jerzykiewicz & Pigulski (1996) from their analysis of photometric data. There is no evidence of a periodic modulation of the amplitude of P2.

4.4 Properties of the triplet of short periods

Note that our approach differs from that used by Jerzykiewicz & Pigulski (1996) who fixed the values of the three short periods at their values known from photometry and fitted only their amplitudes. They concluded that the amplitudes are strongly variable with time. For completeness, we repeated their analysis using all our RVs prewhitened for orbital variation via solution II. The results are compared in Table 7. It is seen that a free fit of the periods leads to much larger semiamplitudes for all three considered periods than a fit with fixed values of the periods from photometry. Moreover, the phase diagram of the data prewhitened for P2 and P3 and folded with P1 shows a clear phase shift between the older, more scattered RVs of higher amplitude and the CCD data with a lower amplitude - see the upper panel in Fig. 4.

If one allows for a free convergence of all three periods, it is possible to arrive at somewhat larger amplitudes and a better phase coherence for P1. There are remaining phase shifts, however, especially for P2 and P3, and it is clear that the three known frequencies are unable to model the large amplitudes of P1 (up to 18 kms-1 during certain epochs) properly. For P2 we arrived at a one-year alias of the reported photometric period. This value was also found by others, as already mentioned in Sect. 2.


 

 
Table 7: Periods and semi-amplitudes of the short-term triplet found in the data prewhitened for orbital solution II
periods fixed periods optimized
P [d] K [kms-1] P [d] K [kms-1]
.1691678 3.8 .16916714 5.7
.1707769 0.9 .17085757 2.6
.1817331 2.1 .18171870 2.7



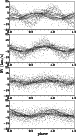  \begin{figure} \par\epsfig{file=FIGS_ORIG/H2483f04r.eps, width=8.8cm}\end{figure} Figure 4: Phase diagrams folded with the periods of P1 to P3 of the data prewhitened for the orbital and the corresponding two other short-term distributions. From top to bottom: P1, all short-term periods fixed to the values from photometry, P1 from optimized short-term periods, P2 optimized, P3 optimized
Open with DEXTER

4.5 A free search for multiperiodicity

At this stage of investigation it is legitimate to ask whether a free search for multiperiodicity, not necessarily restricted to the three known periods, can significantly improve the fit of the RV residuals from the orbit and offer a self-consistent solution, at least comparable to our locally fitted solution presented in Sect. 4.3.

The varying accuracy of the RVs was taken into account through the weighting schemes already described. To check on possible differences in the RVzero-points of individual data sets, we will now include only data sets with large enough RVs, with a good orbital-phase coverage. Applying these requirements, we finally selected all data sets from Table 2 with the exception of subsets 7, 9, and 12. We may assume that the RV zero-point of our own measurements, calibrated via telluric lines (data sets 15, 16, and 17) is identical and equal to zero in the RV residuals. We will further assume that the subsets 3 and 8 have a common zero point, similarly as subsets 5, 6, 3, and 8, 10, 11, and 18, 19. All these groups were obtained with the same instruments and have comparable weights.

We started with prewhitening the selected set of RVs, formed by all of above-mentioned subsets, for orbital solution II. The RV residuals from this prewhitening were then subjected to a period search over the frequency range from 0 to 10 d-1. The frequency corresponding to the strongest peak in the periodogram was then improved via sinusoidal fit and removed from the data. The new residuals were again subjected to a period search and the sinusoidal fit was repeated, now for two free periods. After finding three short periods near to the photometric periods P1 to P3, a multiperiodic fit was applied to the original RVs and allowed to calculate also the orbital frequency and its first harmonics. (Note that this procedure is legitimate as long as there is no detectable apsidal motion present in the system.)

Since the results could be sensitive to possible differences in the RV zero points, parallel analyses were carried out for original data and for data where the zero-point corrections were taken into account. To compute the zero-point corrections the residuals from the multiperiodic fit were averaged within each data subset and the mean value was subtracted from all RVs of the subset in question. As long as the same new frequency was found in both parallel analyses, it was adopted as a real one, i.e. not caused by differing RVzero-points only.


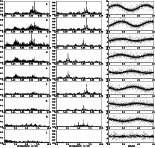  \begin{figure} \par\epsfig{file=FIGS_ORIG/H2483f05r.eps, width=17.9cm, height=17cm}\end{figure} Figure 5: Left column: periodograms obtained during the process of successive prewhitening. The following detected periods of Table 9 are indicated: a) P1, b) P1-, c) P2, d) P3, e) P3+, f) P1+, g) P2+, h) P1++, i) P4. Middle and right column: periodograms and phase diagrams for the same periods are also shown, based on the final solution, after the RVs were prewhitened for all other contributions
Open with DEXTER


 

 
Table 8: Multiple frequency solution valid for all weighting schemes used. Periods P and their semi-amplitudes K are given. Column "Order" gives the order in which the periods were found during the process while $t_{\rm amp}$ contains the probable periods of amplitude changes of the respective periods
  Order P K $t_{\rm amp}$
    [d] [kms-1]  
P1 1 0.16916707 7.6  
P1+ 4 0.16916605 5.0 76.7 y
P1- 2 0.16916809 3.2 76.7 y
P2 7 0.17085553 2.7  
P2+ 3 0.17077074 1.4 344 d
P3 5 0.18173251 2.6  
P3+ 6 0.18168352 2.4 674 d



 

 
Table 9: Periods P and semi-amplitudes K, including the period P1++, which could only be detected in data with strong weighting. P4 is not a significant period but the period corresponding to the largest peak in the residuals. Otherwise, the same notation as in Table 8 was used
  Order P K $t_{\rm amp}$
    [d] [kms-1]  
P1 1 0.16916703 5.9  
P1+ 4 0.16916596 5.2 73.6 y
P1- 2 0.16916810 3.5 73.6 y
P1++ 8 0.16916078 2.3 12.5 y
P2 7 0.17085554 2.2 331 d
P2+ 3 0.17076729 1.6  
P3 5 0.18173256 2.8 674 d
P3+ 6 0.18168357 2.3  
P4 9 1.91985 0.7  


The obtained results are summarized in Tables 8 and 9. The periods which were detected in our analyses and which are very close to the three known photometric periods are denoted here as P1, P2and P3. Newly found periods, which are very close to P1, P2 or P3and which can be responsible for the amplitude modulation of the periods P1, P2 and P3, are denoted $P_i^\pm$ in such a way that

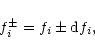\begin{displaymath}f_i^\pm = f_i\pm {\rm d}f_i, \end{displaymath} (6)

where fi are the corresponding frequencies for i = 1, 2, 3and $({\rm d}f_i)^{-1}$ is a period corresponding to the amplitude variation of the respective principal period.

We stopped at the point when different new frequencies were detected from different weighting schemes. Table 8 summarizes the results for this stage of reduction. Beside the values of P1 to P3, two "sidelobes'' of P1, responsible for the amplitude modulation of P1 with a period of 76.7 years, and two frequencies very close to P2 and P3 and corresponding to their amplitude modulation with 344-d and 674-d periods, respectively, were detected.


 

 
Table 10: Final orbital solutions III (corresponding to Table 8) and IV (Table 9) after subtracting all short term contributions. Epochs are in JD-2240000
  Solution III Solution IV
P [d] 12.096867 $\pm$ 0.000010 12.096864 $\pm$ 0.000011
K [kms-1] 23.858 $\pm$ 0.051 23.853 $\pm$ 0.051
$\gamma$ [kms-1] -12.694 $\pm$ 0.039 -12.446 $\pm$ 0.039
e 0.0435 $\pm$ 0.0026 0.0539 $\pm$ 0.0026
$\omega$ [deg] 59.4 $\pm$ 2.9 61.4 $\pm$ 2.1
$T_{\rm periastron}$ 39053.59 $\pm$ 0.10 39053.65 $\pm$ 0.10
$T_{\rm eclipse} $ 39054.54 $\pm$ 0.20 39054.52 $\pm$ 0.17
rms 1.7 kms-1 1.5 kms-1



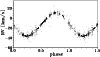  \begin{figure} \par\epsfig{file=FIGS_ORIG/H2483f06r.eps, width=8.8cm}\end{figure} Figure 6: Final orbital solution IV after subtracting all short-term contributions
Open with DEXTER


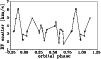  \begin{figure} \epsfig{file=FIGS_ORIG/H2483f07r.eps, width=8.8cm}\end{figure} Figure 7: The RV phase scatter vs. orbital phase with phase zero at periastron passage - see the text for details
Open with DEXTER

No other periods could be detected in the residuals from this solution for the unweighted data. In the weakly weighted data, the strongest peak suggests yet another period of 0 $.\!\!^{\rm d}$202, which, however, does not seem to be significant (semi-amplitude of 0.4 kms-1 and a very unconvincing phase diagram). From the strongly weighted data, another period very close to P1 was indicated. A free fit for all detected periods changes the period of the amplitude modulation of P2 from 344 d to 331 d, however. The solution derived from the strongly weighted data is summarized in Table 9 and the successive periodograms are shown in Fig. 5. Middle panels show the periodograms for each of the periods resulting after subtraction of all other contributions obtained in the final solution. Comparing panels a to g of this column (panels h and i are on enlarged frequency scale) one can recognize the window function of the data shown in Fig. 1. The one-month aliases can clearly be seen. In all periodograms also the one-year alias peaks can be found (not resolved in Fig. 1). Note that the difference of the two frequencies found for the P2 variation corresponds to 331 d so that the two frequencies are not one-year aliases of each other. In the right column of Fig. 5 the phase diagrams of each period, after prewhitening the data for all other periods, are shown.

The orbital solutions, based on RVs prewhitened for all short periods of Tables 8 and 9, are presented in Table 10 as solutions III and IV, respectively. For comparison we also give the calculated epochs of primary mid-eclipse. Pigulski & Jerzykiewicz (1988) derived $P = 12\hbox{$.\!\!^{\rm d}$ }09684$ and $T_{\rm eclipse} = 39054.568$ from the light-curve analysis. Note that the epoch of the primary mid-eclipse from all of our orbital solutions agrees with their epoch within the errors of its determination. A phase diagram corresponding to solution IV is shown in Fig. 6.

Solutions III and IV are based on RVs corrected for the zero-point shifts and on strong weights. The results are almost identical to those derived without the zero-point corrections. In particular, there is only a marginal difference of 0 $.\!\!^{\rm d}$000007 in the orbital period. The adopted zero-point corrections are summarized in Table 2.

4.6 Search for signatures of forced oscillations

To demonstrate that the rapid variations of EN Lac are somehow related to the binary nature of the star is not an easy task, especially given the fact that the amplitude of the strongest mode of oscillations varies secularly. Fortunately, the rich collection of new spectra analyzed here was obtained over a limited period of time and seems suitable to such an analysis.

Using all 1315 original RVs from spectrograms of sets 16 to 20, we formed phase bins 0.$^{\rm P}$07 wide in three sliding representations - similar to three different "covers'' in the phase dispersion minimization method of Stellingwerf (1978). (The width of the bins was chosen in such a way as to ensure numerous enough representation in most of them.) We then calculated mean RV and its rms error within each such phase bin. The rms error characterizes the total scatter at given orbital phase and should be proportional to the total amplitude of rapid changes at that phase. Omitting all bins defined by less than 30 RVs, we plot the phase scatter versus orbital phase calculated from periastron in Fig. 7. There seems to be a rapid increase of the scatter prior and perhaps also after each periastron passage, though the effect is only marginal. Still more data will be needed to verify that it is a real effect dependent on orbital phase and not, e.g., an accidental effect of positive interference of several pulsational modes.

5 Line profile variations

We used the high-resolution spectra obtained with the coudé echelle spectrograph of the Tautenburg 2-m telescope to the study of the He I line profile changes. These spectra (set 16 in Table 2) have a 2-pixel resolution of about 37000, the typical time resolution being about 5 min. The signal-to-noise ratio is of about 200 for the majority of them. In the spectral range covered, from H$\beta $ to 7100 Å, there are 6 He I lines which are much stronger than all metallic lines. Three of them (5015, 5875, and 6678 Å) have almost clean, unblended profiles and were already used for the RVmeasurements. The strongest and cleanest singlet He I 6678 Å line has been used to the study of line profile changes (Fig. 8).


  \begin{figure} \par\hspace{6mm}\epsfig{file=FIGS_ORIG/H2483f08r.eps, width=8.8cm}\end{figure} Figure 8: Mean profiles of the interstellar NaD lines (left) and of the He I 6678 Å line (right)
Open with DEXTER


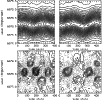  \begin{figure} \par\epsfig{file=FIGS_ORIG/H2483f9a.eps, angle=-90, width=8.8cm, ... ... \epsfig{file=FIGS_ORIG/H2483f9b.eps, angle=-90, width=8.8cm, clip=}\end{figure} Figure 9: Contour plots of two time series of the He I 6678 Å line obtained during JD 2451387 (left) and JD 2451472 (right). Top: line profiles. Bottom: differential profiles. Enhanced parts are shown by solid lines, depleted parts by dashed lines
Open with DEXTER


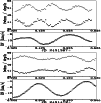  \begin{figure} \par\epsfig{file=FIGS_ORIG/H2483f0ar.eps, width=8.8cm, height=4.5cm}\par\epsfig{file=FIGS_ORIG/H2483f0br.eps, width=8.8cm, height=4.5cm}\end{figure} Figure 10: Variation of central line depth in % (plus signs), of line width in kms-1(crosses), and of RV (circles) of the He I 6678 Å line during two single runs
Open with DEXTER


  \begin{figure} \epsfig{file=FIGS_ORIG/H2483f11r.eps, width=8.8cm}\end{figure} Figure 11: Line depth of the interstellar Na I 5896 Å line, expressed in per cents of the continuum level, vs. line depth of He I, shown for the JD 2451472 run
Open with DEXTER

Examples of two time series are given in Fig. 9. The profiles shown in the upper part of the diagram were properly shifted in wavelength (based on orbital solution IV) and are on the rest frame of the primary star. A variation in the line centers, caused by rapid line profile changes, is seen. Beside the variation of line centers, a clear variation of line depths and an indication of line widths can also be seen.

In the lower part of Fig. 9, residual profiles are shown. They were created in the following way: cross-correlating individual line profiles with the mean profile of the given series, we first shifted all profiles to put them on the laboratory wavelength and then we subtracted the mean profile from the individual ones.

From the pattern seen on JD 2451387, one can estimate a period of about 130 min (0 $.\!\!^{\rm d}$093) which is about a half of the P3 period 0 $.\!\!^{\rm d}$181733, found from RVs. The pattern itself can be simply explained by a periodic variation of the line width which occurs nearly in anti-phase to the variation of the line depth. To prove this, we measured these values on the He I line profiles. The results for the two runs shown in Fig. 9 are displayed in Fig. 10. The periodic changes in both, the line depth and the line width are clearly seen, as well as the anti-phase behaviour of the two. The anti-phase variation of line depth and line width which is shown here for two selected nights is present in the entire data set. The equivalent widths were found to be constant within the limits of accuracy of our measurements.

Line profiles of the sharp and very strong NaD doublet of interstellar origin can be seen in Fig. 8. Figure 11 shows that the line depths of the interstellar lines and of the stellar HeI lines are not correlated, the interstellar line profiles show no variability. So we can be sure that the changes observed in the stellar lines are intrinsic.

It is important to mention that obviously two different kinds of line profile variations were found from different night series. In some series, the frequency of line profile changes was twice the frequency of the RV changes - for instance on JD 2451387 - while in some others, like on JD 2451472, the periods of RV and line profile changes were about the same. Assuming the possible presence of the fundamental periods and the first overtones, we therefore carried out a period search in the variation of the line depth using the technique of successive prewhitening. The periods of the strongest contributions found correspond to the periods P1 to P3 (Table 11).

No correlation between the occurrence of the minima and/or maxima of the line depth and the RV variation was found. Also, no periodic changes of the line asymmetry which could be responsible for the rapid RV variation observed were found.

Line profile variations of ENLac will be studied in much more detail in a forthcoming paper.


 

 
Table 11: Periods of line depth and line width variations found in the He I profiles of TLS spectra. For each contribution, the semi-amplitude of the fundamental period, A0, and its first harmonic, A1, are given
P [d] line depth [%] line width [km s-1]
  A0 A1 A0 A1
0.1691864 0.37 0.71 0.34 0.75
0.1708522 0.63 0.35 0.59 0.35
0.1816000 0.24 1.07 0.25 0.85


6 Discussion

There are two main obstacles in the investigation of the variablity patterns of EN Lac. The first is the need to separate safely the variations due to stellar oscillations from the orbital motion. Whereas the orbital period can be determined very accurately from the narrow eclipses, accurate orbital elements can only be derived from spectroscopy. To do that, a considerable contribution of the short-term RV changes has to be eliminated.

A proper analysis of the pattern of the rapid changes requires a solution of another problem, namely an appropriate modelling of the long-term amplitude modulation of the pulsational periods. Accurate RVs as well as observations covering several decades are needed to this task. The data set at our disposal fullfils these requirements. It consists of numerous recent observations of high quality and of numerous older observations covering a period of about 90 years. Analyzing this sample, we were able to derive

The accuracy of our final multiple-frequency model is limited by the accuracy of the older RVs obtained from photographic spectra. That is why we offer (in Tables 8 and 9) two possible solutions. The first one is based on all data and was obtained by successive prewhitenings. The second solution mainly rests on the recent RVs from electronic spectra which were given large weights. It includes one more period describing the amplitude modulation of P1, and it also slightly modifies the period of the amplitude variation of P2. Only the change in the orbital elements $\gamma$ and e (Table 10) is considerably larger than the errors calculated from the orbital fit itself. Note, however, that the smallest rms error per 1 observation was achieved for solution II where we allowed for local fits of rapid changes. This may indicate that either our description in terms of several sinusoidal terms is not complete or that the variations are not strictly periodic after all.

Pigulski & Jerzykiewicz (1988) derived an eclipse period of 12 $.\!\!^{\rm d}$09684 from photometric data obtained between 1952 and 1981, the epoch of minimum light is JD 2439054.568. The small differences between this period and our spectroscopic periods of orbital solutions II to IV give only rise to a negligible phase shift between the mean epochs of the photometric data and our RVs. So we can directly compare the epochs of minimum light (Tables 4, 9). The agreement is very good: the maximum deviation from the photometric value is of 0 $.\!\!^{\rm d}$048 which is only 13% of the total duration of the eclipse of about 0 $.\!\!^{\rm d}$36.

The pulsation periods derived for P1 and P3 are in good agreement with the periods known from the photometry of ENLac (Jerzykiewicz & Pigulski 1999, see also Table 1). In particular we observe an amplitude modulation period of the P3 variation of the RVs of 674d corresponding to the same modulation period and splitted frequencies as observed by Jerzykiewicz & Pigulski (1999) for the light changes. Also the modulation time scale of P1 of about 75yr is of the same order as observed photometrically. In the RV variation we did not find a modulation time scale of the order of several decades for P2, however.

The 0 $.\!\!^{\rm d}$17085553 period obtained for P2 agrees with the early values reported by Struve et al. (1952), Walker (1952), and Fitch (1969). This value had been revised in all later publications where the authors adopted the new value of 0.17078d and assumed the old one to be a one year alias of this value. In our extended data set the 0 $.\!\!^{\rm d}$170856 period is the dominating period during all reduction steps of successive prewhitening. The value of 0 $.\!\!^{\rm d}$17077 we found as a slight additional contribution in one of the last steps of this procedure. The doublet finally adopted for P2 corresponds to a modulation period of 331d which is significantly different from the value of one year. A word of caution is appropriate, however. The window function (Fig. 1) has a complicated structure and there is also a peak corresponding to about 340 d, though with a smaller amplitude than the one-year alias. One should, therefore, still treat the 674/331-d modulation of the P2 and P3 oscillations with some reservation and perhaps to seek for other possible explanations. On the other hand, our tentative assumption that we deal with real modulation time scales is supported by the agreement of the value for P1 with the value obtained from the light variation, and for P2 by the fact that besides the P2 doublet the exact one-year alias of P2 can be observed in all periodograms.

We were not able to establish a self-consistent multiple frequency model for the line shape variations. Since we are limited to the high resolution data our time basis is too small to resolve frequencies small enough to give rise to modulation time scales of years or decades as it was observed for the RV variations. But we can put all periods into one scheme if we assume that the variations can be described by one fundamental frequency and its first harmonic. The three strongest contributions are near P1, P2, and P3 (Table 11). All three contributions are of comparable total strengths. The fundamental period dominates in the P2 variation, whereas the first harmonics dominate the P1 and P3 variations.

The observed line profile variations show a behaviour which is typical for low degree lmodes of nonradial pulsations: an anti-phase variation of line depth and line width preserving the equivalent width of the lines. There are different methods of mode identification based on line profile and RV analysis (Balona 1999). In general the identification of nrp-modes is much easier done by an analysis of line profile moments (Aerts et al. 1992; Aerts 1996) as by an investigation of the line variation in terms of line widths and depths. Results of this line moments analysis will be presented in a forthcomimg paper as well as the results of an analysis of the light variations of ENLac. By the light curve analysis of the eclipsing binary we will be able to set narrow limits for the physical parameters of ENLac and its secondary. By combining the results with the results of mode identification we should be able to give a physical explanation of most of the RV and line profile variations found and described here.

Acknowledgements
The authors are indebted to the referee, Guillermo Torres, for his comments which helped to improve the paper and for the careful proofreading of the manuscript. Research of P.Har. was partly supported by grants A3003805 of the Granting Agency of the Academy of Sciences of the Czech Republic and M402: Program KONTAKT of the Ministry of Education of the Czech Republic, and in final stages from the research plan J13/98: 113200004.

References

 
Copyright ESO 2001