A&A 367, 86-105 (2001)
DOI: 10.1051/0004-6361:20000479

Chemical abundances in the inner 5kpc of the Galactic disk

S. J. Smartt^1,4 - K. A. Venn² - P. L. Dufton³ - D. J. Lennon⁴ - W. R. J. Rolleston³ - F. P. Keenan³

1 - Institute of Astronomy, University of Cambridge, Madingley Road, Cambridge CB3 0HA, UK
2 - Department of Physics and Astronomy, Macalester College, St. Paul, MN 55101, USA
3 - The Department of Pure and Applied Physics, The Queen's University of Belfast, Belfast BT7 1NN, North Ireland
4 - ING Telescopes, Apartado de Correos 368, Santa Cruz De La Palma, 38780, Canary Islands, Spain

Received 2 August 2000 / Accepted 17 November 2000

Abstract
High-resolution, high signal-to-noise spectral data are presented for four young B-type stars lying towards the Galactic Centre. Determination of their atmospheric parameters from their absorption line profiles, and uvby photometric measurement of the continua indicate that they are massive objects lying slightly out of the plane, and were probably born in the disk between 2.5-5kpc from the Centre. We have carried out a detailed absolute and differential line-by-line abundance analyses of the four stars compared to two stars with very similar atmospheric parameters in the solar neighbourhood. The stars appear to be rich in all the well sampled chemical elements (C, N, Si, Mg, S, Al), except for oxygen. Oxygen abundances derived in the atmospheres of these four stars are very similar to that in the solar neighbourhood. If the photospheric composition of these young stars is reflective of the gaseous ISM in the inner Galaxy, then the values derived for the enhanced metals are in excellent agreement with the extrapolation of the Galactic abundance gradients previously derived by Rolleston et al. (2000) and others. However, the data for oxygen suggests that the inner Galaxy may not be richer than normal in this element, and the physical reasons for such a scenario are unclear.

Key words: stars: early-type - stars: atmospheres - stars: abundances - Galaxy: evolution - Galaxy: center - Galaxy: abundances

1 Introduction

The current metallicity of the Galactic disk represents a fossil record of chemical enrichment since the birth of the Milky Way and during its subsequent evolution. As stars continually enrich the interstellar medium with their nucleosynthetic products, the metallicity of the disk increases over time. By investigating the relative abundance of chemical elements as a function of time and position within the Galaxy, it is possible to constrain models of Galaxy formation and evolution.

Much work has been done on tracking the chemical evolution of the solar neighbourhood as a function of time using age-metallicity relations and element abundance ratios in cool F and G-type stars. The seminal work by Edvardsson et al. (1993) showed the potential of using samples of nearby stars with an age spread to trace the temporal evolution of the disk and the halo, and such work has been extended by, for example, Fuhrmann (1998) and Israelian et al. (1998). These types of metallicity ratios have been modelled by many authors (e.g. Carraro et al. 1998; Pilyugin & Edmunds 1996 and references therein), in order to constrain our Galaxy's history. The photospheric abundances of massive stars (viz. stars with ZAMS $$\mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\displaystyle ...$ $10\, M_{\odot}$ ) do not have the potential to provide us with temporal information as they are by nature short-lived objects (with typical lifetimes of the order of $\sim$ 10-50Myrs). However, their high intrinsic luminosities mean that we can spectroscopically observe them at large distances from the solar neighbourhood; OB-type main-sequence stars are typically 8 $^{\rm m}$ visually brighter than early G-type dwarfs. Their photospheres are representative of the interstellar material from which they were born due to their relative youth. Hence, we can spatially and radially sample the metallicity of the Galactic disk by determining abundances in distant, luminous blue stars. The radial variation of different elements provides a further key constraint on the formation and evolutionary mechanisms of the Galactic disk (Matteucci & Francois 1989; Matteucci & Chiappini 1999; Prantzos & Aubert 1995; Portinari & Chiosi 1999; Pagel & Tautvaisine 1995).

These models require further observational constraints to restrict the possible influence of their many free parameters such as initial mass function, gas fraction variations, star formation rates, infall and outflow rates and metallicity dependent stellar yields. Previous work has shown that the metallicity of the Galactic disk decreases as Galactocentric distance increases. This metallicity gradient has been reproduced quantitatively using a number of different methods. For example, extensive studies of optical emission lines in H II regions by Shaver et al. (1983) and Fich & Silkey (1991) have derived an oxygen abundance gradient of $-0.07 \pm 0.02$ dex kpc^-1; within the region $$6 \mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\displaystyle ...$ kpc (where $R_{\rm g}$ refers to Galactocentric distance throughout this paper). Good agreement was also found by Maciel & Köppen (1994) and Maciel & Quireza (1999) from PN studies, and by Afflerbach et al. (1997) in a study of ultra-compact H II regions. Several studies of B-type main-sequence stars throughout the disk had given discrepant results, and a much shallower gradient than that derived from the nebular studies (e.g Fitzsimmons et al. 1992, and references therein). However Smartt & Rolleston (1997), in a consistent re-analysis of an extensive data-set of B-type stars covering $$6 \mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\displaystyle ...$ kpc, showed that previous B-type star studies produced spurious gradient determinations, and derived an oxygen abundance gradient of $-0.07 \pm 0.02$ dexkpc^-1 in excellent agreement with the nebular studies. As a follow up to this, Rolleston et al. (2000; hereafter RSDR) carried out a more detailed and exhaustive survey of the large data-set gathered by the group at Queen's University and have confirmed this result, while also producing abundance ratios of different elements along the disk. Further work by Gummersbach et al. (1998) also indicates that the nebular and stellar results are in agreement within the errors of measurement.

However, most studies of the chemical composition of the Galactic disk have concentrated on the solar neighbourhood, and the anti-centre direction. Optical extinction rises steeply in the direction toward the Galactic Centre, and restricts the optical observation of disk stars more than a few kiloparsecs away. In the anti-centre direction we have previously probed out to $R_{\rm g}\sim18$ kpc, experiencing $A_v\simeq3$ (Smartt et al. 1996), but have only managed to observe open clusters towards the Centre approximately 2-3kpc away (RSDR) with a reddening of $A_v\simeq2$ . The metallicity within the solar Galactic radius is poorly sampled, with only a few IR studies available. Rudolph et al. (1997) and Afflerbach et al. (1997) have used similar observational methods for far-IR emission lines in H II regions (of differing sizes) as ISM abundance probes. This far-IR technique has allowed observation of some inner Galactic regions. These studies suggest that the abundance gradients for both nitrogen and sulphur do tend to increase towards the Galactic Centre, but both indicate that their oxygen abundance derivations may suffer some uncertainties (see Sect.5.1). Carr et al. (2000) have achieved a first determination of stellar abundances (in an M-type supergiant) directly at the Galactic Centre in the spectacular star forming region within the central few hundred parsecs. They find an Fe abundance close to that of the solar neighbourhood, which at first may seems surprising given the wealth of evidence of a strong abundance gradient in the Milky Way (and also in other spirals). However as we discuss in Sect. 4, this region may be unrelated to the starforming Galactic disk ( $$3 \mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\displaystyle ...$ kpc) as a whole, and its evolution may have proceeded independently.

The metallicity of the inner disk therefore has not been investigated in any great detail, and lacks information on a variety of elemental abundances. Spectra of B-type stars provide the potential to sample many more chemical elements than is possible through emission line studies. As discussed above, massive B-type main-sequence stars are excellent probes of the current interstellar medium and sample particularly well the $\alpha$ -processed elements (O, Mg, and Si) as well as C and N (Smartt et al. 1996). This paper describes observations of metal-rich massive stars lying towards the Galactic Centre together with detailed model atmosphere and abundance analyses. This allows the comparison of abundance ratios in this interesting regime with those in the rest of the disk, as a key probe of the evolution of our Galaxy.

2 Observational data

The main difficulty in optically probing the inner regions of the Galactic disk is of course the high extinction encountered. This section describes how we identified targets for optical photometry and spectroscopy which are in regions of low extinction, but which have probably originated in the inner disk region.

2.1 Selection of targets in regions of low extinctions towards the Galactic centre

The catalogue of Reed (1993) provides a database of published UBV $\beta$ photoelectric photometry for objects in the Stephenson and Sanduleak catalogue Luminous Stars in the Southern Milky Way (1983). This catalogue is a fairly complete record of OB-type stars and A- & F-type supergiants and giants within 10 $^{\circ}$ of the galactic plane and with longitude limits $-174^{\circ} < l < +81^{\circ}$ , down to a limiting photographic magnitude of approximately 12.5. In order to identify OB-type stars near the Galactic Centre, which also have moderate Galactic latitudes and hence suffer from low extinction, stars from the Reed catalogue were selected which satisfied all of the criteria listed below:

1.: Stars within $-40^{\circ} < l < +20^{\circ}$ ; hence restricting the sample to objects towards the Galactic Centre;
2.: Stars which are more than 4 $^{\circ}$ above or below the plane; in order to limit the effects of interstellar extinction;
3.: Stars which are fainter than V = 11.0, to sample the more distant objects;
4.: Stars with a colour factor between -0.90 < Q < -0.66; appropriate for early B-type stars;
where Q = (U - B) - 0.72(B - V);
5.: Stars with a B-V of less than 0.5 - which implies a reddening of $$E(B-V) \mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\displays... ...\offinterlineskip\halign{\hfil$\scriptscriptstyle ...$ (for early B-type intrinsic colours).

The combination of these criteria should produce targets which are potentially normal early B-type dwarfs (or near main-sequence objects) lying within $\sim$ 4kpc of the Galactic Centre and twelve such stars were found.

The database of Reed & Beatty (1995) contains published spectral types for a subset of the objects in Reed (1993). However, the fainter objects of the earlier study (which were the most promising distant B-type stellar candidates) did not have an entry in Reed & Beatty (1995). As a result we had to rely on colours as a primary selector.

2.2 Spectroscopic data

The spectroscopic data presented in this paper were taken on two different runs. All twelve candidates were observed at the Anglo-Australian Telescope in August 1994 at intermediate resolution. The RGO spectrograph along with the 1200B diffraction grating, 82cm camera and the TEK1K CCD were used to give a resolution of approximately 0.7Å (FWHM). Two grating positions were employed with central wavelengths of 4020Å and 4580Å, each giving a wavelength coverage of 240Å. The primary motivation of these observations was to identify normal stars for further, higher resolution observations at a higher signal-to-noise ratio, and to provide reliable H I profiles for the stars which did turn out to be normal. Six of the stars observed appeared to be normal main-sequence early-type B-stars. However one of these was a fast rotator with a lack of metal line features, while another appeared to be a double-lined spectroscopic binary (composed of two early-type components) with the metal lines severely blended. The nature of the other six peculiar stars is discussed in Venn et al. (1998). The four apparently normal stars (see Table 1) were further observed with the ESO 3.6 m telescope using the CASPEC échelle spectrograph during July 1995. The central wavelength was 4500Å with a wavelength coverage of near 1300Å (3920-5240Å) at a resolution of $\sim$ 0.1Å.

Table 1: Photometric details of Galactic Centre B-type main-sequence stars. Our estimated spectral types are quoted
Star SpT V B-V U-B $l^{\circ}$ $b^{\circ}$

LS5130 B2IV 12.09 0.24 -0.53 21.12 -5.63

LS4419 B2IV 11.08 0.08 -0.65 351.78 -5.88

LS4784 B2IV 11.55 0.09 -0.60 1.70 -6.12

LS5127 B3II-III 11.96 0.15 -0.55 16.13 -7.34

**Table 1:** Photometric details of Galactic Centre B-type main-sequence stars. Our estimated spectral types are quoted
Star	SpT	V	B-V	U-B	$l^{\circ}$	$b^{\circ}$
LS5130	B2IV	12.09	0.24	-0.53	21.12	-5.63
LS4419	B2IV	11.08	0.08	-0.65	351.78	-5.88
LS4784	B2IV	11.55	0.09	-0.60	1.70	-6.12
LS5127	B3II-III	11.96	0.15	-0.55	16.13	-7.34

During both observing programmes the observational routine was similar. Each star was observed long enough to accumulate sufficient counts in the continuum to yield a minimum signal-to-noise ratio of $\sim$ 70, and in most cases more than 100. The observations were split into exposures of 1200-1500s to minimize the impact of cosmic-ray contamination and were bracketed by observations of Cu-Ar and/or Cu-Ne wavelength calibration lamps. Flat-field exposures and bias frames were generally taken at both the beginning and the end of the night.

The single order spectra were reduced using the STARLINK package FIGARO (Shortridge et al. 1997) as discussed in Smartt et al. (1996), where further details can be found. The échelle data were reduced using the Image Reduction and Analysis Facility ( IRAF), using standard techniques. When in one dimensional format, all the spectra were transferred for further analysis to the STARLINK program DIPSO (Howarth et al. 1998). Normalization was achieved by carefully selecting continuum regions free from absorption lines, and fitting low order (of degree 3 or 4) polynomials through the noise. Equivalent widths for the metal lines and non-diffuse lines of neutral helium were measured by the non-linear least square fitting of single or multiple Gaussian profiles to the normalised spectra. Each line is assigned an error estimate reflecting the reliability of the equivalent width measurement, viz. a: error less than 10%, b: error less than 20%, c: error greater than 20%. These were assigned by considering the numerical error returned by the DIPSO line fitting computation and the qualitative accuracy of the profile fit. The hydrogen and diffuse helium lines were not measured in this manner, but the normalised profiles were extracted directly for comparison with Galactic standards and with theoretical profiles. The equivalent width measurements for each star can be found in Appendix A (available electronically).

2.3 Photometric data

Strömgren uvby photometry of the four B-type LS stars was obtained in service mode using the People's photometer on the SAAO 0.5-m telescope. Details of the instrumental set-up can be found in Kilkenny et al. (1988) - and the resultant photoelectric aperture photometry is listed in Table 2. Additionally, we attempted to obtain Strömgren CCD uvby data (as a consistency check) on the ESO 1.5-m Danish Telescope in July 1998. For two of the stars (viz. LS4419 and LS5127) we did indeed obtain good quality observations during photometric conditions. However, the data for the other two stars was compromised by high cirrus. Initial CCD reductions were performed using the IRAF CCDRED package (Massey 1992), while subsequent digital aperture and point-spread function photometry was undertaken using tasks within the IRAF package DAOPHOT (Davis 1994). Further details of these methods can be found in Mooney et al. (2000).

In Table 2 we list the individual photometric indices as derived from the SAAO observations. Typical uncertainies in the SAAO photoelectric photometry are 0.01 and 0.005 magnitudes in colours and the individual passbands respectively. The Strömgren reddening free [u-b] index should be accurate to $\pm$ 0.03 mag. The ESO CCD dataset comprised four independent observations per filter per field containing each of the LS stars. Photometric errors were estimated using two methods. First, each set of uvby instrumental magnitudes were independently transformed to the standard system of y and (b-y), m₁, c₁ indicies. These were used to deduce mean values and associated standard errors of the mean. Secondly, values of the arithmetic mean and standard error were deduced for the independent sets of uvby instrumental measurements. The mean values were transformed to the standard magnitude and colour indicies, while the associated photometric uncertainties were deduced by propagating the standard error of the mean values through the transformation equations.

For LS4419, both these methods inferred a photometric accuracy of 0.006 magnitudes in y and 0.011 magnitudes in the colour (b-y). The reddening free [u-b] index should be accurate to $\pm0.02$ mag. Thus, it is not surprising that we find excellent agreement between the SAAO and ESO photometry for LS4419. Photometric uncertainties are somewhat larger for the ESO data obtained for LS5127, viz. 0.015, 0.035 and 0.15 mag in y, colour and [u-b] index respectively. For this star, the SAAO data should be the more reliable. However, it should be noted that the SAAO and ESO measurements agree within the photometric errors - which in turn lead to similar estimates of the stellar effective temperature (see Sect. 3).

Table 2: Strömgren photometric data for stars observed at the SAAO 0.5m, and the ESO 1.5m Danish. Values for $\gamma$ Peg and $\iota$ Her were taken from the SIMBAD database and references therein
Star y (b-y) m₁ c₁ [c₁] [u-b] (SAAO) [u-b] (ESO)

LS 5130 12.038 0.264 -0.025 0.182 0.129 0.248 -

LS 4419 11.089 0.115 0.032 0.105 0.082 0.220 0.204

LS 4784 11.519 0.157 0.035 0.122 0.091 0.261 -

LS 5127 11.883 0.193 0.023 0.233 0.194 0.364 0.456

$\gamma$ Peg 2.84 -0.106 0.093 0.116 0.137 0.255

$\iota$ Her 3.80 -0.064 0.078 0.294 0.307 0.423

**Table 2:** Strömgren photometric data for stars observed at the SAAO 0.5m, and the ESO 1.5m Danish. Values for $\gamma$ Peg and $\iota$ Her were taken from the SIMBAD database and references therein
Star	y	(b-y)	m₁	c₁	[c₁]	[u-b] (SAAO)	[u-b] (ESO)
LS 5130	12.038	0.264	-0.025	0.182	0.129	0.248	-
LS 4419	11.089	0.115	0.032	0.105	0.082	0.220	0.204
LS 4784	11.519	0.157	0.035	0.122	0.091	0.261	-
LS 5127	11.883	0.193	0.023	0.233	0.194	0.364	0.456

$\gamma$ Peg	2.84	-0.106	0.093	0.116	0.137	0.255
$\iota$ Her	3.80	-0.064	0.078	0.294	0.307	0.423

3 Model atmosphere and abundance analyses

The methods employed to derive stellar atmospheric parameters are similar to those described in Smartt et al. (1996) and Rolleston et al. (1997). All results are based on the ATLAS9 grid of line-blanketed model atmospheres of Kurucz (1991). LTE line formation codes were used to derive line profiles leading to determinations of atmospheric parameters and chemical compositions.

As a first attempt to constrain the effective temperatures ( $T_{\rm eff}$ ) of the four LS stars, which were all of spectral type B2/B3, we used the ionization balance of the two stages of silicon; the Si II lines at 4128Å and 4130Å, and the Si III triplet at 4552-4574Å. This method has been previously employed to analyse the bright standard $\gamma$ Pegasi (HR39), and is known to produce anomalous and unsatisfactory results (Ryans et al. 1996; Gies & Lambert 1992; Peters 1976). Absolute abundances (derived using this temperature diagnostic) of N II, O II, Mg II, and S III show systematic underabundances of around 0.4dex with respect to normal B-type stellar values. Further, and more critically, large discrepancies then exist between the abundances derived from other ionization equilibria (C II/C III, S II/S III, and Si III/Si IV) when using this Si II/Si III temperature balance. Using Strömgren photometry as an alternative effective temperature indicator produces more satisfactory results; typically, a value systematically 3000K less than that estimated from the Si II/Si III balance has been obtained which agrees with the other ionization balances, and the metal abundances give normal results. The problem with the Si II lines historically stretches back more than two decades, when Peters (1976) first reported the problem. All stars in the Gies & Lambert (1992) study (which have $T_{\rm eff} \sim 21\,000$ ; from Strömgren indices) appear to produce spurious Si II results and a similar temperature problem has been found by the authors in at least two other stars - 22Ori and $\iota$ Her. In each case the temperature found from the Si II/Si III lines is systematically higher than that produced from the Strömgren indices. Hence, it appears that the Si II/Si III ionization balance is flawed as a temperature diagnostic due to reasons which are, as yet, not well understood. We find that including non-LTE corrections (Brown 1987) in the line formation calculations fails to remove the discrepancy. Cuhna & Lambert (1994) have also reported the same effect when adopting Strömgren temperatures for Orion B-types and their subsequent determination of Si abundances from both ionization stages.

In the rest of this paper we shall adopt the effective temperatures derived from the Strömgren indices listed in Table 2. The colour index [u-b] measures the Balmer jump as a function of $T_{\rm eff}$ and we have primarily used the calibration of Napiwotzki et al. (1993). We also compared the effective temperatures derived using the calibration of Lester et al. (1986), which provides the [u-b] vs. $T_{\rm eff}$ relation as a function of surface gravity; consistent results were found in each case. Table 3 lists the effective temperatures that we have adopted. For the two stars for which we have both SAAO and ESO data, we list the mean of the two temperatures. Excellent agreement was found from the two data sets for LS4419, with temperatures of 21900 and 22300K derived from ESO and SAAO respectively; for LS5127 the temperatures were in poorer agreement, 18700 and 17100K, but consistent with a $17\,900 \pm1000$ K range.

Logarithmic surface gravities ( $\log g$ ) were estimated by fitting model profiles of the Balmer lines from our atmospheric analysis codes to observed H $\epsilon$ , H $\delta$ , and H $\gamma$ depending on which lines were available in the RGO spectra (see Sect.2). In all cases the results from each line were in good agreement. A conservative estimate of the probable random errors in our analyses, given the errors in the measured data are $\pm$ 1000K and $\pm0.2$ dex. A value for microturbulent velocity ( $\xi$ ) was determined for all the B-type stars by requiring that the derived abundances from, primarily, O II were independent of line strength. The O II ion was chosen as it has the richest absorption line spectra in stars of this type. However where a significant number of N II lines were available, $\xi$ was independently estimated and the mean taken. Atmospheric parameters for all the stars are listed in Table 3.

As a final step in defining the model atmosphere appropriate to each star, we determined the helium abundance within this iterative procedure. Helium abundances were calculated from the line strengths of the available non-diffuse lines (3964, 4437, 4713, 5015 & 5047Å) and the profile fitting of the diffuse lines (4009, 4026, 4387, & 4471Å). In each star we found a normal helium composition of approximately 10.9dex (corresponding to $y\simeq0.1$ by fraction). Hence, we did not need to repeat the $T_{\rm eff} - \log g - \xi$ iterations for models with significantly abnormal helium fractions.

Table 3: Atmospheric parameters of the Galactic Centre main-sequence B-type stars and the bright spectroscopic standards used in the differential analysis. $T_{\rm eff}$ was derived from Strömgren photometry; typical random errors on the derived values are $\pm$ 1000K and $\pm$ 0.2dex for $T_{\rm eff}$ and $\log g$ , respectively, and $\pm$ 3kms^-1 for $\xi$ . For LS4419 and LS5127, the values for $T_{\rm eff}$ are the mean of the results from the SAAO and ESO data - and the others are derived from the SAAO photometry only
Star $T_{\rm eff}$ $\log g$ $\xi$ [He] $v\sin i$

(K) (cgs) (kms^-1) dex (kms^-1)

LS5130 21200 3.5 5 $11.05 \pm0.20$ 35

LS4419 22100 3.7 7 $10.92 \pm0.10$ 80

LS4784 20900 3.9 5 $10.92 \pm0.15$ 93

LS5127 17900 3.2 7 $10.87 \pm0.13$ 120

$\gamma$ Peg 21000 3.8 5 $10.87 \pm0.09$ 5

$\iota$ Her 17700 3.9 5 $10.78 \pm0.08$ 10

**Table 3:** Atmospheric parameters of the Galactic Centre main-sequence B-type stars and the bright spectroscopic standards used in the differential analysis. $T_{\rm eff}$ was derived from Strömgren photometry; typical random errors on the derived values are $\pm$ 1000K and $\pm$ 0.2dex for $T_{\rm eff}$ and $\log g$ , respectively, and $\pm$ 3kms^-1 for $\xi$ . For LS4419 and LS5127, the values for $T_{\rm eff}$ are the mean of the results from the SAAO and ESO data - and the others are derived from the SAAO photometry only
Star	$T_{\rm eff}$	$\log g$	$\xi$	[He]	$v\sin i$
	(K)	(cgs)	(kms^-1)	dex	(kms^-1)
LS5130	21200	3.5	5	$11.05 \pm0.20$	35
LS4419	22100	3.7	7	$10.92 \pm0.10$	80
LS4784	20900	3.9	5	$10.92 \pm0.15$	93
LS5127	17900	3.2	7	$10.87 \pm0.13$	120
$\gamma$ Peg	21000	3.8	5	$10.87 \pm0.09$	5
$\iota$ Her	17700	3.9	5	$10.78 \pm0.08$	10

Table 4: Absolute elemental abundances for the star LS5130, together with a line-by-line differential analysis with the "standard'' star $\gamma$ Peg which is a chemically normal star lying within the solar neighbourhood. The abundances quoted are the mean values from results from n lines in each star (where n is the number in brackets after the abundance), and the uncertainties are the sample standard deviations. Also listed are absolute abundances normally associated with bright B-type stars within approximately 500pc of the Sun¹; and values from ISM or H II region studies in the solar neighbourhood². For reference, the actual solar photospheric abundances are listed, and we note (as others have indicated e.g. Snow & Witt 1996) that the Sun appears significantly metal-rich compared to the surrounding ISM and neighbouring PopulationI objects (i.e. young, massive stars) in many elements
Species LS5130 $\gamma$ Peg Differential Nearby Other solar Solar

B-stars¹ neighbourhood

C II $8.47 \pm 0.31$ (11) $8.22 \pm 0.31$ (9) $+0.23 \pm 0.15$ (9)      8.20 8.13 $^{\rm c}$ 8.55

N II $7.96 \pm 0.22$ (25) $7.79 \pm 0.24$ (19) $+0.15 \pm 0.13$ (19)      7.81 7.94 $^{\rm d}$ 7.97

O II $8.69 \pm 0.19$ (43) $8.72 \pm 0.32$ (81) $-0.06 \pm 0.16$ (35)      8.68 8.70 $^{\rm c}$ 8.87

Mg II 7.64          (1) 7.22          (1) +0.42          (1)      7.38 $^{\rm a}$ - 7.58

Al III $6.30 \pm 0.09$ (4) $6.14 \pm 0.05$ (3) $+0.13 \pm 0.10$ (3)      6.45 - 6.47

Si II $6.85 \pm 0.14$ (4) $6.50 \pm 0.10$ (4) $+0.34 \pm 0.04$ (4)      7.28 $^{\rm a}$ - 7.55

Si III $7.66 \pm 0.19$ (5) $7.29 \pm 0.20$ (5) $+0.36 \pm 0.24$ (5)      7.28 $^{\rm a}$ - 7.55

S II $7.39 \pm 0.21$ (2) $6.96 \pm 0.24$ (15) $+0.38 \pm 0.02$ (2)      7.21 7.12 $^{\rm d}$ 7.21

S III 7.29          (1) $7.06 \pm 0.41$ (9) +0.23          (1)      7.21 7.12 $^{\rm d}$ 7.21

Ar II $7.03 \pm 0.6$ 1 (3) $6.75 \pm 0.46$ (3) $+0.28 \pm 0.15$ (3)      - - 6.58

Fe III $6.53 \pm 0.96$ (3) $6.39 \pm 0.82$ (3) $+0.13 \pm 0.18$ (3)      7.36 $^{\rm a}$ - 7.51

**Table 4:** Absolute elemental abundances for the star LS5130, together with a line-by-line differential analysis with the "standard'' star $\gamma$ Peg which is a chemically normal star lying within the solar neighbourhood. The abundances quoted are the mean values from results from n lines in each star (where n is the number in brackets after the abundance), and the uncertainties are the sample standard deviations. Also listed are absolute abundances normally associated with bright B-type stars within approximately 500pc of the Sun¹; and values from ISM or H II region studies in the solar neighbourhood². For reference, the *actual* solar photospheric abundances are listed, and we note (as others have indicated e.g. Snow & Witt 1996) that the Sun appears significantly metal-rich compared to the surrounding ISM and neighbouring PopulationI objects (i.e. young, massive stars) in many elements
Species	LS5130	$\gamma$ Peg	Differential	Nearby	Other solar	Solar
				B-stars¹	neighbourhood
C II	$8.47 \pm 0.31$ (11)	$8.22 \pm 0.31$ (9)	$+0.23 \pm 0.15$ (9)	8.20	8.13 $^{\rm c}$	8.55
N II	$7.96 \pm 0.22$ (25)	$7.79 \pm 0.24$ (19)	$+0.15 \pm 0.13$ (19)	7.81	7.94 $^{\rm d}$	7.97
O II	$8.69 \pm 0.19$ (43)	$8.72 \pm 0.32$ (81)	$-0.06 \pm 0.16$ (35)	8.68	8.70 $^{\rm c}$	8.87
Mg II	7.64 (1)	7.22 (1)	+0.42 (1)	7.38 $^{\rm a}$	-	7.58
Al III	$6.30 \pm 0.09$ (4)	$6.14 \pm 0.05$ (3)	$+0.13 \pm 0.10$ (3)	6.45	-	6.47
Si II	$6.85 \pm 0.14$ (4)	$6.50 \pm 0.10$ (4)	$+0.34 \pm 0.04$ (4)	7.28 $^{\rm a}$	-	7.55
Si III	$7.66 \pm 0.19$ (5)	$7.29 \pm 0.20$ (5)	$+0.36 \pm 0.24$ (5)	7.28 $^{\rm a}$	-	7.55
S II	$7.39 \pm 0.21$ (2)	$6.96 \pm 0.24$ (15)	$+0.38 \pm 0.02$ (2)	7.21	7.12 $^{\rm d}$	7.21
S III	7.29 (1)	$7.06 \pm 0.41$ (9)	+0.23 (1)	7.21	7.12 $^{\rm d}$	7.21
Ar II	$7.03 \pm 0.6$ 1 (3)	$6.75 \pm 0.46$ (3)	$+0.28 \pm 0.15$ (3)	-	-	6.58
Fe III	$6.53 \pm 0.96$ (3)	$6.39 \pm 0.82$ (3)	$+0.13 \pm 0.18$ (3)	7.36 $^{\rm a}$	-	7.51

1. All typical B-type stellar values are taken from Gies & Lambert (1992), apart from

a: Kilian (1994).

2. Solar neighbourhood values taken from:

c: Local ISM abundances from Meyer et al. (1998), Cardelli et al. (1996).

d: Orion nebular abundances from Baldwin et al. (1991).

3. Solar values taken from Grevesse & Noels (1993) and Anders & Grevesse (1989).

Final model atmospheres with parameters which satisfied the above criteria were then calculated in order to allow the metal abundances from each unblended ionic feature to be determined in each star. The elemental abundance associated with a particular line was derived by comparing the observed line strengths and profiles to those predicted from the LTE line formation calculations. A line-by-line differential analysis was performed for each star relative to nearby (i.e. within the solar neighbourhood) spectroscopic standard stars of very similar atmospheric parameters. The atomic data used in the line formation theory were from Jeffery (1991), but this choice is not critical for our purposes of a differential abundance analysis. Tables 4-6 list the absolute and differential abundances derived for each star. The mean absolute abundances are on a logarithmic scale with hydrogen = 12.0 dex (i.e. $[X]= 12 + \log N_{X}/N{\rm _H}$ ), and the errors quoted are the standard deviations about this mean value.

Table 5: Absolute elemental abundances for the stars LS4419 and LS4784, together with a line-by-line differential analysis with the "standard'' star $\gamma$ Peg which is chemically "normal'' with very similar atmospheric parameters. The absolute abundances for $\gamma$ Peg are shown in the previous table
Species LS4419 (absolute) LS4419 (differential) LS4784 (absolute) LS4784 (differential)

C II $8.18 \pm 0.27$ (5) $+0.07 \pm 0.19$ (5)     $8.42 \pm 0.56$ (4) $+0.27 \pm 0.16$ (4)

N II $8.27 \pm 0.52$ (16) $+0.43 \pm 0.25$ (13)     $8.43 \pm 0.37$ (15) $+0.62 \pm 0.29$ (12)

O II $8.76 \pm 0.27$ (28) $-0.06 \pm 0.20$ (23)     $9.06 \pm 0.44$ (26) +0.17 $\pm$ 0.35 (19)

Mg II 7.50           (1) +0.28           (1)     7.70            (1) +0.48           (1)

Al III $6.35 \pm 0.04$ (2) +0.18           (1)     $6.65 \pm 0.03$ (2) +0.47           (1)

Si II 6.90           (1) +0.23           (1)     $6.94 \pm 0.12$ (4) $+0.44 \pm 0.07$ (4)

Si III $7.58 \pm 0.12$ (5) $+0.28 \pm 0.26$ (5)     $8.00 \pm 0.11$ (3) +0.58 $\pm$ 0.18 (3)

S II 7.17           (1) +0.12           (1)     7.51            (1) +0.33           (1)

Ar II 6.59           (1) +0.09           (1)     - -

Fe III 6.45           (1) -0.18           (1)     - -

**Table 5:** Absolute elemental abundances for the stars LS4419 and LS4784, together with a line-by-line differential analysis with the "standard'' star $\gamma$ Peg which is chemically "normal'' with very similar atmospheric parameters. The absolute abundances for $\gamma$ Peg are shown in the previous table
Species	LS4419 (absolute)	LS4419 (differential)	LS4784 (absolute)	LS4784 (differential)
C II	$8.18 \pm 0.27$ (5)	$+0.07 \pm 0.19$ (5)	$8.42 \pm 0.56$ (4)	$+0.27 \pm 0.16$ (4)
N II	$8.27 \pm 0.52$ (16)	$+0.43 \pm 0.25$ (13)	$8.43 \pm 0.37$ (15)	$+0.62 \pm 0.29$ (12)
O II	$8.76 \pm 0.27$ (28)	$-0.06 \pm 0.20$ (23)	$9.06 \pm 0.44$ (26)	+0.17 $\pm$ 0.35 (19)
Mg II	7.50 (1)	+0.28 (1)	7.70 (1)	+0.48 (1)
Al III	$6.35 \pm 0.04$ (2)	+0.18 (1)	$6.65 \pm 0.03$ (2)	+0.47 (1)
Si II	6.90 (1)	+0.23 (1)	$6.94 \pm 0.12$ (4)	$+0.44 \pm 0.07$ (4)
Si III	$7.58 \pm 0.12$ (5)	$+0.28 \pm 0.26$ (5)	$8.00 \pm 0.11$ (3)	+0.58 $\pm$ 0.18 (3)
S II	7.17 (1)	+0.12 (1)	7.51 (1)	+0.33 (1)
Ar II	6.59 (1)	+0.09 (1)	-	-
Fe III	6.45 (1)	-0.18 (1)	-	-

3.1 LS5130

The value of microturbulence adopted for LS5130 and $\gamma$ Peg plays an important role in the derived abundances of oxygen, magnesium and silicon in particular. As the abundance variations of these elements are of particular interest, a short discussion is warranted. From the O II and N II lines of $\gamma$ Peg, the microturbulence is likely to lie in the range of 5 $\pm$ 2 kms^-1. This is consistent with other studies (e.g. Peters 1976; Gies & Lambert 1992) who quote a value at the lower end of this scale (3kms^-1) and Ryans et al. (1996) who estimate a value of 6 $\pm$ 5 kms^-1. It is likely that the latter error bars are too conservative, and from our investigation we believe the result appropriate to our methods to be in the range 3-7kms^-1. For LS5130 we similarly derive a value of $5 \pm3$ kms^-1, which leads to a relatively normal O abundance in this star, but significantly higher Mg and Si abundances. The latter differential abundances would move closer to the value of O (as would generally be expected from a chemical evolution point of view; see discussion in Sect. 5.2), if the value of $\xi$ was increased in LS5130 and decreased in $\gamma$ Peg by about 3kms^-1 in each case. However while such changes are compatible with our random error range quoted, it would be an artificially biased analysis. Indeed our best estimates of $\xi$ for LS5130 tend to suggest that a value of no more than 5kms^-1 is required to flatten the equivalent width - abundance relation for the O II and N II species. One should note that the large number of O II features (a total of 43), which renders this element abundance estimate particularly reliable. The analysis here implies that its abundance is very similar to that of $\gamma$ Peg, i.e. no significant enhancement of this element is observed, and this is a very robust result. The other elements which we believe give reliable results are C, N, Mg, Si and S - and we note that all of these elements show enhanced patterns, particularly Si and Mg. Although the Mg abundance is based on only one line (the doublet at 4481Å), it is a strong, well measured feature which is reliably modelled in B-type stars at this effective temperature. This pattern of a relatively normal oxygen abundance together with enhanced C, N, Mg, Si and S is also reflected in the other B-type stars. The values for Al III, Ar II, and Fe III are based on relatively weak detections of features and should be treated with some caution - this is generally true for each of the four stars, and LS 5130 has the highest "quality'' spectrum available, i.e. it has a high signal-noise-ratio and the star itself has a relatively low projected rotational velocity.

3.2 LS4419

The higher projected rotational velocity of this star results in fewer metal line features being identified. However again the oxygen abundance is well constrained, with 28 features contributing to the final result. Hence, we conclude that LS4419 also shows no evidence for enhanced oxygen (with respect to the solar neighbourhood), and there is certainly no evidence for the large enhancements one might expect to see in inner Galactic regions. It should be noted (and this is true for LS4784 and LS5130 also) that although the absolute Mg abundance derived is close to the "solar'' range of $7.50 \pm 0.2$ dex, the value derived for $\gamma$ Peg by our methods (and indeed any other star of approximately the same spectral type in the solar neighbourhood) is 7.2dex. We believe that a value of 7.5 is +0.3dex above the solar neighbourhood value, and that the absolute abundance discrepancy is possibly due to atomic data uncertainties or non-LTE effects. Again we believe that the C, N, O, Mg, Si, and S differential abundances are reliable for this star, but the others should be treated with caution due to the paucity and weakness of the individual features.

3.3 LS4784

The quality of this spectrum is similar to that of LS4419, and the previous comments about the reliability of the abundances (particularly with reference to O and Mg) are equally applicable here. One should also note that although the absolute abundances derived from the Si II lines are of dubious worth (as discussed above with respect to $T_{\rm eff}$ determinations), in both the standard stars and the LS stars, it is encouraging to see that the differential abundances derived from Si II and Si III are consistent. This suggests that the same effect occurs in each spectra, and that the lines can be quantitatively compared from star to star. Again in this star we see a relatively normal oxygen abundance, but enhanced magnesium and silicon. Nitrogen and sulphur are also enhanced, with carbon showing a mildly enriched abundance.

Table 6: Absolute elemental abundances for the star LS5127, together with a line-by-line differential analysis with the "standard'' star $\iota$ Her (HR6588) which is chemically "normal'' with very similar atmospheric parameters
Ion LS5127 $\iota$ Her Differential

C II $8.82 \pm 0.34$ (2) $8.26 \pm 0.27$ (11) +0.55           (1)

N II $8.29 \pm 0.10$ (7) $7.87 \pm 0.18$ (23) $+0.51 \pm 0.23$ (6)

O II $9.05 \pm 0.19$ (7) $8.79 \pm 0.20$ (54) $+0.21 \pm 0.25$ (6)

Mg II 7.76           (1) $7.23 \pm 0.26$ (6) +0.69           (1)

Al III 6.68           (1) $6.23 \pm 0.05$ (6) +0.36           (1)

Si II $7.45 \pm 0.26$ (3) $6.84 \pm 0.50$ (4) $+0.81 \pm 0.33$ (3)

Si III $8.18 \pm 0.12$ (4) $7.51 \pm 0.20$ (7) $+0.64 \pm 0.08$ (3)

S II $7.44 \pm 0.16$ (5) $6.99 \pm 0.23$ (41) $+0.39 \pm 0.49$ (5)

S III $7.97 \pm 0.34$ (2) $7.14 \pm 0.30$ (5) $+0.76 \pm 0.02$ (2)

Fe III -               (0) $6.97 \pm 0.67$ (8) -                 (0)

**Table 6:** Absolute elemental abundances for the star LS5127, together with a line-by-line differential analysis with the "standard'' star $\iota$ Her (HR6588) which is chemically "normal'' with very similar atmospheric parameters
Ion	LS5127	$\iota$ Her	Differential
C II	$8.82 \pm 0.34$ (2)	$8.26 \pm 0.27$ (11)	+0.55 (1)
N II	$8.29 \pm 0.10$ (7)	$7.87 \pm 0.18$ (23)	$+0.51 \pm 0.23$ (6)
O II	$9.05 \pm 0.19$ (7)	$8.79 \pm 0.20$ (54)	$+0.21 \pm 0.25$ (6)
Mg II	7.76 (1)	$7.23 \pm 0.26$ (6)	+0.69 (1)
Al III	6.68 (1)	$6.23 \pm 0.05$ (6)	+0.36 (1)
Si II	$7.45 \pm 0.26$ (3)	$6.84 \pm 0.50$ (4)	$+0.81 \pm 0.33$ (3)
Si III	$8.18 \pm 0.12$ (4)	$7.51 \pm 0.20$ (7)	$+0.64 \pm 0.08$ (3)
S II	$7.44 \pm 0.16$ (5)	$6.99 \pm 0.23$ (41)	$+0.39 \pm 0.49$ (5)
S III	$7.97 \pm 0.34$ (2)	$7.14 \pm 0.30$ (5)	$+0.76 \pm 0.02$ (2)
Fe III	- (0)	$6.97 \pm 0.67$ (8)	- (0)

Table 7: The errors listed in this table illustrate how the absolute abundances in the B-type stars would vary within the error bars of the atmospheric parameters. A systematic error in both the target LS-star and the standard used in the differential abundance analysis would result in little change in the differential results. The results below are for typical random analysis errors of $\log g\, \pm\, 0.2$ , $T_{\rm eff} \pm 1000$ K and $\xi \, \pm \, 3$ kms^-1. The values were calculated around a model atmosphere with $\log g = 3.6$ , $T_{\rm eff} = 21\,000, \xi = 5$
Species $\log g+0.2$ $\log g-0.2$ $T_{\rm eff}$ +1000 $T_{\rm eff}-$ 1000 $\xi+3$ kms^-1 $\xi-3$ kms^-1

C II
0.01 0.00 0.02 0.03 -0.08 0.11

N II 0.07 -0.05 -0.06 0.12 -0.08 0.11

O II 0.12 -0.11 -0.18 0.23 -0.11 0.15

Mg II -0.05 0.05 0.13 -0.11 -0.22 0.32

Al III 0.05 -0.03 -0.02 0.08 -0.08 0.15

Si II -0.06 0.08 0.20 -0.15 -0.05 0.11

Si III 0.09 -0.09 -0.14 0.18 -0.21 0.24

S II -0.04 0.05 0.16 -0.14 -0.09 0.21

S III 0.13 -0.12 -0.14 0.18 -0.07 0.13

Ar II 0.01 0.02 0.12 -0.06 -0.06 0.14

Fe III 0.09 -0.08 -0.04 0.08 -0.08 0.24

**Table 7:** The errors listed in this table illustrate how the absolute abundances in the B-type stars would vary within the error bars of the atmospheric parameters. A *systematic* error in *both* the target LS-star and the standard used in the differential abundance analysis would result in little change in the differential results. The results below are for typical random analysis errors of $\log g\, \pm\, 0.2$ , $T_{\rm eff} \pm 1000$ K and $\xi \, \pm \, 3$ kms^-1. The values were calculated around a model atmosphere with $\log g = 3.6$ , $T_{\rm eff} = 21\,000, \xi = 5$
Species	$\log g+0.2$	$\log g-0.2$	$T_{\rm eff}$ +1000	$T_{\rm eff}-$ 1000	$\xi+3$ kms^-1	$\xi-3$ kms^-1
C II	0.01	0.00	0.02	0.03	-0.08	0.11
N II	0.07	-0.05	-0.06	0.12	-0.08	0.11
O II	0.12	-0.11	-0.18	0.23	-0.11	0.15
Mg II	-0.05	0.05	0.13	-0.11	-0.22	0.32
Al III	0.05	-0.03	-0.02	0.08	-0.08	0.15
Si II	-0.06	0.08	0.20	-0.15	-0.05	0.11
Si III	0.09	-0.09	-0.14	0.18	-0.21	0.24
S II	-0.04	0.05	0.16	-0.14	-0.09	0.21
S III	0.13	-0.12	-0.14	0.18	-0.07	0.13
Ar II	0.01	0.02	0.12	-0.06	-0.06	0.14
Fe III	0.09	-0.08	-0.04	0.08	-0.08	0.24

3.4 LS5127

This star is cooler than the three previously discussed, and hence we used a different solar neighbourhood star for the differential abundance comparison. The star $\iota$ Her has atmospheric parameters more compatible with that of LS5127 than $\gamma$ Peg (we did in fact carry out the same differential analysis using $\gamma$ Peg, and the results were not significantly different to those in Table 6). The oxygen abundance appears to be slightly above normal, but is not as high as the abundances of both Mg and Si. We find a particularly large magnesium abundance from the 4481Å feature, and a line profile together with a spectral synthesis of the region is shown in Fig. 1. The microturbulence derivation in LS5127 is probably more uncertain than in the previous three stars, due to the fewer O II lines visible at this effective temperature. However, it is unlikely that the particularly large Mg II abundance can be explained by an underestimate of $\xi$ . In Fig. 1 we have used $\xi =7$ kms^-1, but adopting a value of 10kms^-1, and a high abundance for Al III (i.e. >7.00 in order to ensure that the strength of this feature is not due to severe blending with the Al III line at 4479Å) still results in the differential value being >0.5dex. Again we find that both ionization stages of Si give consistently high abundances, consistent with the Mg enhancement.

$\begin{figure} \par\includegraphics[width=8.3cm]{h2371f1.eps}\end{figure}$

Figure 1: The Mg II doublet at 4481Å in LS5127 with synthesised fits. The observed line profile is the solid histogram, together with theoretical fits for magnesium abundances of 7.2, 7.5, 7.8 and 8.1dex (each with a microturbulence of $\xi =7$ kms^-1), convolved with a rotational broadening function $v\sin i = 120$ kms^-1. A value of 7.8dex is required to fit the line properly. Note that there is a Al III line in the blueward wing, and we have also assumed a high Al abundance (6.8 dex) when synthesizing this region

Open with DEXTER

Table 8: Distances, masses, lifetimes, radial velocities and regions of origin for the programme stars. Masses and evolutionary lifetimes were determined from the stellar evolutionary tracks of Schaller et al. (1992)
Star M $T_{\rm ev}$ $d_{\odot}$ z PRV $V_{\rm i}$ $R_{\rm g}$

( $M_\odot$ ) (Myrs) (kpc) (kpc) (kms^-1) (kms^-1) (kpc)

LS5130 $10\pm2$ $24\pm5$ $6.9\pm1.0$ 0.7 -7 64 $3.1\pm1.0$

LS4419 $11\pm2$ $20\pm5$ $5.2\pm1.0$ 0.5 -28 45 $2.9\pm1.0$

LS4784 $8\pm2$ $27\pm5$ $3.8\pm1.0$ 0.4 -30 36 $4.7\pm1.0$

LS5127 $10\pm2$ $25\pm5$ $9.1\pm1.0$ 1.2 -3 98 $2.5\pm1.0$

**Table 8:** Distances, masses, lifetimes, radial velocities and regions of origin for the programme stars. Masses and evolutionary lifetimes were determined from the stellar evolutionary tracks of Schaller et al. (1992)
Star	M	$T_{\rm ev}$	$d_{\odot}$	z	PRV	$V_{\rm i}$	$R_{\rm g}$
	( $M_\odot$ )	(Myrs)	(kpc)	(kpc)	(kms^-1)	(kms^-1)	(kpc)
LS5130	$10\pm2$	$24\pm5$	$6.9\pm1.0$	0.7	-7	64	$3.1\pm1.0$
LS4419	$11\pm2$	$20\pm5$	$5.2\pm1.0$	0.5	-28	45	$2.9\pm1.0$
LS4784	$8\pm2$	$27\pm5$	$3.8\pm1.0$	0.4	-30	36	$4.7\pm1.0$
LS5127	$10\pm2$	$25\pm5$	$9.1\pm1.0$	1.2	-3	98	$2.5\pm1.0$

4 Distances, Galactic positions and evolutionary status

We have calculated distances to the stars as follows. Masses were derived by placing the stars in the effective temperature - surface gravity diagram using the evolutionary tracks of Schaller et al. (1992). This allowed a calculation of the luminosity appropriate to the stars current evolutionary status, rather than assuming that the object is on the zero-age main sequence (ZAMS). The absolute visual magnitude was then determined employing the bolometric corrections of Kurucz (1979). Extinctions were estimated from the measured B-V values taken from Reed (1993), and the intrinsic colours of Deutschman et al. (1976) for stars with these atmospheric parameters. The distance was finally calculated assuming a standard Galactic extinction law, i.e. with R=3.1 (Seaton 1979). We note that although our stars have relatively low $v\sin i$ values, their rotational velocities could be higher depending on the inclination viewing angle. Recent studies of the evolution of rotating stars (e.g. Heger & Langer 2000; Maeder & Meynet 2000) indicate that their main-sequence properties maybe altered by rotation, however the differences predicted in the luminosities are smaller than the uncertainities in the rest of the distance calculation and do not significantly increase the a error bar we calculate on the stellar distances.

The four B-type targets lie at significant distances below the plane of the Galaxy (see Table 8), and it is unlikely that they have formed at their current positions. The probable explanation is that they were born in the Galactic disk, and were then subsequently ejected. This class of early-type stars lying at, in some cases, significant distances from their formation sites (i.e. runaway stars) has been studied extensively, and their existence is well accepted (see Rolleston et al. 1999). In a previous paper (Smartt et al. 1997) we have discussed the analysis of four blue supergiants lying at similar Galactic latitudes, and a full discussion of the possible origins and ejection mechanisms from the disk of these types of objects is presented. Leonard (1993) has presented plausible mechanisms for early-type stars suffering large ejection velocities within massive binary evolution scenarios, or dynamical ejection from clusters. These can result in initial velocity injections of up to $\sim$ 350 kms^-1, easily allowing our objects to reach their current estimated distance from the Galactic plane (z).

In order to constrain the regions of the disk where these stars were formed, we follow the arguments of Smartt et al. (1997). For each of the stellar spectra we have determined a radial velocity, and we compare this velocity to that expected if the stars were co-rotating with the disk at their current projected positions (assuming a flat rotation curve and $R_{\odot}$ = 8.5kpc, $\Theta = 220$ kms^-1 from Kerr & Lynden-Bell 1986). We calculate a peculiar radial velocity (PRV) which is the difference between these two, as a representative measure of the dynamics of the stars with respect to the Galaxy rotation. This PRV is only one component of the total peculiar space velocity, with the other two components unknown (directed along axes mutually perpendicular to the PRV). We assume that the second component of velocity is perpendicular to the Galactic plane (which, given the small Galactic latitudes of these stars is a reasonable assumption). House & Kilkenny (1980) have given an expression for the force field normal to the Galactic plane (K_z), but this is probably only valid for $R_{\rm g} \sim 10$ kpc. Given that these stars have origins closer to the Galactic Centre, we have assumed a simple relation which is an approximation to the shape of the House & Kilkenny form of K_z, but which is always greater in magnitude (with a peak of twice the House & Kilkenny maximum). We assume that within $0 \leq z \leq 700$ pc the force field K_z is approximated by -kz (with k = 2.29 10^-11cms^-2 pc^-1) and for z > 700 pc then K_z = -k. Analytical expressions for the initial velocity ( $V_{\rm i}$ ) and time required for the stars to reach their present z distance, could then be deduced. The initial ejection velocity perpendicular to the Galactic plane needs to be no more than 100kms^-1 (see Table 8) for these stars to reach their present positions, and significantly less for three of the objects. Velocities of this order are well within those plausible for common ejection methods (Leonard 1993). The PRV of each star is also relatively low, indicating that the initial space velocities of these stars were probably directed mostly in the z-direction. However without proper motion information we cannot definitively constrain their space velocity. If we assume that the mean ejection velocity in the sample ( $V_{\rm i} \sim 60$ kms^-1) is indicative of the maximum value of any one velocity component, then we can calculate a circular locus within which the star probably formed. In 20Myrs, a star could have moved 1.7kpc within (or parallel to) the Galactic disk, and this is a reasonable error on the birth sites of the stars.

$\begin{figure} \par\includegraphics[width=6.5cm]{h2371f2.eps} \end{figure}$

Figure 2: a) A schematic view of the Galaxy with the Galactic Centre at (0, 0). The inner dotted circle represents the possible bulge-disk transition with which a rapid decline in the disk stellar density is associated; the outer dashed circle represents the stellar ring proposed by Bertelli et al. (1995) of radius 3.5kpc (they estimate a Gaussian half-width of $\sigma _{\rm ring}=0.5$ kpc). The shaded arc is a schematic representation of the Sagittarius spiral arm at $R_{\rm g}=5.5$ kpc. Also shown are possible birth sites in the disk, together with our error estimates. b) A section through the Galaxy with the current positions of the stars marked, again the Galactic Centre is at (0, 0). The disk scale height for early-type stars is shown (90pc), together with the spheroidal latitude extent assuming a/b=0.8 (Bahcall 1986)

Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm]{h2371f3.eps}\end{figure}$

Figure 3: Galactic abundance gradients and the stellar sample (open circles) of RSDR. Also shown are the four current targets (open stars) at $R_{\rm g} < 5$ kpc, the error bars being the standard deviations in the mean line abundances or conservative $\pm$ 0.2dex for Mg. In a) the abundance gradient plotted is a least squares fit to the data in RSDR only and has a value of -0.07dexkpc^-1; the four stars towards the Galactic Centre clearly lie below this gradient if it were extrapolated towards the centre. In b) and c) the linear least squares gradients are fits to all the points in the plot. The Si and Mg abundances in the Galactic Centre are compatible with a steadily increasing abundance gradient towards the centre, and a re-evaluation of the least-squares fit through all points leads to values of $-0.06 \pm 0.01$ dexkpc^-1 for Si and $-0.09 \pm 0.02$ dexkpc^-1 for Mg. The solid square is the Orion abundance from Cuhna & Lambert (1994), the asterisk is the Local ISM from Meyer et al. (1998), and the solar symbol is the solar abundance from Grevesse & Noels (1993)

Open with DEXTER

Figure 2 illustrates the estimated stellar birth sites and also schematically draws attention to features of Galactic structure in this region. Bertelli et al. (1995) have discussed the possibility that a "stellar ring'' exists, which surrounds the Galactic Centre at a distance of 3.5kpc, with a 0.5kpc half-width. The nature of this ring is still somewhat uncertain, but Bertelli et al. claim that assuming it to be a region of increased stellar disk density would produce synthetic colour-magnitude diagrams closely matching those they have observed in fields towards the Galactic Centre. They suggest that it is associated with active star formation, and that the cross-section through this ring is at a maximum when viewed at $\vert l\vert=23.5^{\rm o}$ . They further suggest that this is consistent with an observed peak in OH maser sources (Blommaert et al. 1994) around $l=25^{\rm o}$ , a signature of relatively recent star formation. Whether this is a complete ring surrounding the inner Galaxy, or part of an inner spiral arm, is still debatable (Ortiz & Lépine 1993). Clemens et al. (1988) have mapped the distribution of molecular gas in the first quadrant of the Galaxy, and found an H₂ring at approximately 4kpc from the Centre. This would appear to correlate with the stellar ring found by Bertelli et al., but the latter suggest that the stellar and molecular ring are not necessarily co-incident. Rather that the molecular ring maybe the result of a "bow-shock of propagating star formation''.

Although some Galaxy models (Bahcall & Soneira 1980; Bahcall 1986) adopt a relation for the number density of disk stars which falls off exponentially with increasing distance from the Galactic Centre, it appears that at $R_{\rm g}\leq2.5$ kpc from the Galactic Centre there is a sharp decrease in the stellar disk density (Bertelli et al. 1995, Paczynski et al. 1994). This has been interpreted as the transition between the disk and the bulge. Figure 2 suggests that the four B-type stars have their origins in this stellar ring, or where the molecular ring dynamics are causing current star formation. Indeed if there is a disk/bulge transition, early-type stars may be relatively rare within this inner region, although current and spectacular star formation is certainly on-going in the inner few hundred parsecs (Serabyn et al. 1998; Najarro et al. 1997). The above indicates that our B-type stars probably formed around $R_{\rm g}\sim3.5$ kpc in the Galactic disk and were subsequently ejected.

$\begin{figure} \par\includegraphics[width=8cm]{h2371f4.eps}\end{figure}$

Figure 4: a) Filled stellar symbols are oxygen abundances of the Galactic Centre objects, together with stars from RSDR with $R_{\rm g} < 11$ kpc. The error bars for the Galactic Centre stars are standard errors of the mean. The dotted line is a least-squares straight-line fit to all the B-stars. It has a gradient of $-0.01 \pm 0.01$ dexkpc^-1. The open symbols are results from H II regions from Afflerbach et al. (1997). Solar and orion points as in Fig. 3. b) Symbols are as in a), but for nitrogen abundances. The gradient derived is $-0.06 \pm 0.02$ dexkpc^-1, on good agreement with the outer gradient as derived in RSDR. Reasonable agreement between the stellar and H II region points is found. b) The $\log$ N/O ratio, from the stars in the above two panels. The straight-line fit is $-0.06 \pm 0.02$ dexkpc^-1, indicating a fairly significant trend in N/O with Galactocentric distance

Open with DEXTER

Carr et al. (2000) have presented IR spectra of a red M-type supergiant (IRS7) lying in the central cluster, and compared the metal line spectra with that of a similar star in the solar neighbourhood. A differential abundance analysis of the star indicates that it has an Fe abundance very close to solar, and certainly does not appear metal enhanced in any significant way (although it does appear to show CNO-abundances typical of severe dredge-up after core H-burning). At first this may seem a surprising result given that one might expect a linear Galactic abundance gradient in the thin disk to keep rising towards the Centre, and that the central regions would thus show super-metal rich abundances. However there is lack of molecular gas, young stars and H II regions within the inner 3.5kpc, until one gets to the central cluster. Hence, whatever the evolutionary history of the massive stellar clusters at the Centre, it seems to have occurred independently of the Milky Way disk ( $R_{\rm g} \mathrel{\hbox{\rlap{\hbox{\lower4pt\hbox{$\sim$ }}}\hbox{$>$ }}}3.5$ kpc). There is no reason therefore too assume that the disk and central cluster are chemically linked, and one should consider them as separate entities in evolutionary scenarios.

5 Discussion

5.1 The oxygen abundance gradient towards the Galactic Centre

As discussed in Sects.3.1-3.4, all four stars have relatively normal oxygen abundances. If the oxygen abundance gradients derived in the solar neighbourhood and outer disk are extrapolated inwards (Smartt & Rolleston 1997, RSDR; -0.07 dexkpc^-1) their O abundances would be 0.3-0.4dex above the solar neighbourhood value. LS5130 and LS4419 show no evidence at all of oxygen-rich photospheres, and both sample the O II line spectra extremely well, with 43 and 28 features measured respectively. If the statistical errors are normally distributed around the mean, then the random error in our mean differential abundance ( $\sigma/\sqrt n$ ; where $\sigma$ is the standard deviation quoted in Tables 4 and 5) may be as small as $\pm$ 0.04 for both these stars. Furthermore, a systematic error in the atmospheric parameters significantly greater than that quoted in Table 7 would be required to make these stars O-rich which would have major consequences for the other elements and for the continuum fitting of the uvby indices. The large number of O II lines well observed in these stars and the possible error sources in Table 7 make this a robust result. The other two stars LS4784 and LS5127 show marginal evidence for oxygen abundances higher than their comparison stars, with standard errors of the mean $\pm$ 0.1dex. However again these results appear to be incompatible with an O abundance that is 0.3-0.4dex above solar. A number of previous authors have speculated that the oxygen abundance gradient (in particular) may steepen towards the Centre (Vílchez & Esteban 1996; Shaver et al. 1983). However, we can find no evidence that this is the case. Figure 3 shows the oxygen abundances of our stars together with those of the large Galactic B-star sample of RSDR. The low metallicity stars in the outer Galaxy ( $R_{\rm g} > 11$ kpc) are clearly evident, but between 6-9kpc there is little evidence of O abundance variations. The four new stellar points toward the Centre accentuate this relation, and it would appear that the O abundance gradient in the Galaxy flattens off at around 9kpc and does not significantly increase at smaller Galactocentric distances.

Afflerbach et al. (1997) have carried out an extensive study of the N, S and O abundances in H II regions with $R_{\rm g}\leq 12$ kpc. In Fig. 4, their O abundances are plotted together with those for our stars and the stellar sample of RSDR with $R_{\rm g}\leq 12$ kpc. The results from the H II regions and the RSDR data-set in the outer Galaxy are in excellent agreement (see RSDR and Smartt 2000 for further details). However differences appear at smaller Galactocentric distances. In particular while the H II region data is consistent with a linear gradient -0.06dexkpc^-1, no significant variations are apparant for the B-stars. One possible explanation is that the zero-points for the two studies is somewhat different. For example, if the Afflerbach et al. data were shifted upwards by $\sim$ 0.2dex (the difference in the mean results within $7.5 < R_{\rm g} < 9.5$ kpc), then good agreement would be found within the solar neighbourhood, but the B-stars towards the Centre would not reflect the H II region results. The cause of this discrepancy is unclear and appears to be limited to oxygen (see Sects. 5.2 and 5.3). We note that Afflerbach et al. is the only H II region study of the inner Galaxy to quote oxygen abundances. Rudolph et al. (1997) were unable to independently determine S and O, while Shaver et al. (1983) point out that their two inner Galaxy objects ( $R_{\rm g}\sim$ 4kpc) are somewhat peculiar, and that their radio and optical sources may not be the same. Afflerbach et al. have recalculated N abundances from the data of Simpson et al. (1995) and find differences of a factor of $\sim$ 2 in some of the highest metallicity regions. Additionally, on average there seems to be a 50% discrepancy in the sulphur abundances. Therefore it appears that the nebular abundances in the inner Galaxy require further study to constrain their absolute values, while a more extensive sample of B-stars is required. Smartt et al. (2000) have discussed the problem of determining reliable absolute nebular abundances in regions of solar abundance and above in M31, and find significant discrepancies across different analysis methods.

$\begin{figure} \par\includegraphics[width=6cm,clip]{h2371f5.eps}\end{figure}$

Figure 5: Oxygen abundances in the Milky Way from our stellar sample (open circles) and the H II region oxygen abundances in NGC2403 from Garnett et al. (1997, solid circles). Both are shown as a function of effective radius. Within $R_{\rm g}/r_{\rm e} \mathrel{\hbox{\rlap{\hbox{\lower4pt\hbox{$\sim$ }}}\hbox{$<$ }}}1.8$ there is little evidence for increasing oxygen abundances in either galaxy, but there are many other well studied spirals which do not show such an effect

Open with DEXTER

In terms of effective radius (where $r_{\rm e}=5.98$ kpc, from de Vaucouleurs & Pence 1978), the break in the observed O abundance gradient occurs at $R_{\rm g}/r_{\rm e} \simeq1.8$ . The spiral galaxy NGC2403 has been studied by Garnett et al. (1997) who estimated H II region abundances at 12 points across the disk. In Fig. 5 the oxygen abundance is plotted as a function of effective radius for both these galaxies. A similar gradient change may be present in NGC2403, although the sampling is relatively sparse. This would imply that a two component model for the radial variation of oxygen is not exclusive to our own Galaxy and suggests indirect evidence that it is a real effect. Certainly the data suggests that for both galaxies, at $R_{\rm g}/r_{\rm e} \mathrel{\hbox{\rlap{\hbox{\lower4pt\hbox{$\sim$ }}}\hbox{$<$ }}}1.8$ , there is little evidence for increasing oxygen abundances. However, the well studied galaxy M33 (Garnett et al. 1997; Henry & Howard 1995; Monteverde et al. 2000) which is similar in size, mass and metallicity to NGC2403 does not appear to show such a break. Additionally, M101 and NGC4303 are other examples of extensively studied galaxies (Kennicutt & Garnett 1996; Martin & Roy 1992), with 30-80 H II region data points sampled in each. Neither show evidence for anything other than a linear relation across the whole disk. As these spirals are much better sampled than the Galaxy or NG2403, we require more data points in the inner Milky Way to confirm that this flattening is a real effect.

5.2 Magnesium, aluminium, silicon and sulphur abundances towards the Galactic Centre

The magnesium and silicon abundances for the Galactic Centre stars and the corresponding RSDR dataset are plotted in Fig. 3. For oxygen and silicon we note that the absolute abundances derived in our two solar neighbourhood standard stars are similar to the mean of the RSDR data set within 1kpc of the Sun. Hence the absolute results of the Galactic Centre stars are on a consistent scale to the rest of the data. However with Mg, the abundance derived in $\gamma$ Peg and $\iota$ Her is 7.2dex, whereas in RSDR the mean local value is 7.85 dex (again estimated from the mean of stellar values within 1kpc of the Sun). The stars analysed in this paper have effective temperatures in the range $17\,700{-}22\,100$ K, while the RSDR sample have a mean temperature of 25275K and it is possible that the modelling of this line is temperature dependent. It is important to use homogeneous datasets when looking for abundance trends and that is indeed what was done in RSDR. They showed that although the zero-point of any particular abundance may be in the error, any gradient biasing is removed by using suitable sub-samples of stars. Hence to put the four Galactic Centre stars onto the same scale as RSDR, we have added 7.85dex to their differential Mg abundances. This assumes that $\gamma$ Peg, $\iota$ Her and the stars within 1kpc of the Sun in RSDR have similar abundances and that any offset is due to temperature dependent modelling inaccuracies. It appears that the Galactic Centre stars are richer in Mg than their local counterparts (see also Sect. 3). From Table 7 an underestimate of the microturbulence ( $\xi$ ) in each star could reduce this Mg overabundance as it is based on a relatively strong line. However an increase in $\xi$ by 5kms^-1 or more in each star would be required. While observational uncertainties might cause a particular determination of $\xi$ to have such an error, there is no evidence that we have systematically underestimated the microturbulence in each star. The Mg abundance gradient in Fig. 3 hence appears to steadily increase towards the Centre. A value of $-0.09 \pm 0.02$ dexkpc^-1 is derived by fitting all points, which is slightly larger the RSDR result, although they agree within the uncertainties.

The silicon abundances of the Galactic centre stars are also plotted in Fig. 3, and again appear compatible with a steadily increasing abundance gradient towards the centre. A fit through all the Si points gives a gradient of $-0.06 \pm 0.01$ dexkpc^-1, again in good agreement with the RSDR value for the outer Galaxy only. The differential abundances derived for each star are between 0.3-0.6dex higher than their respective standards, strongly supporting the idea that these stars are richer in Si than solar neighbourhood material. In Fig. 6 the Al abundances of the galactic Centre stars are plotted again with the data from RSDR. Aluminium appears to increase steadily toward the Centre, and a gradient of $-0.05 \pm 0.01$ dexkpc^-1 is derived from the whole data set, similar to that produced by RSDR for the anti-centre direction.

Sulphur abundances for our stars are also available, although we have no similar data at greater radii from RSDR. In Fig. 6 our stellar abundances are compared with with those from Afflerbach et al. (1997). Reasonable agreement is found with these stars appearing to be S-rich and having abundances similar to those found in nebular studies towards the Centre (although the caveat regarding the nebular absolute values discussed in the previous section may be important).

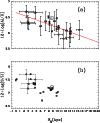$\begin{figure} \par\psfig{file=h2371f6.eps,width=8.8cm}\end{figure}$

Figure 6: a) Asterisk symbols are aluminium abundances of the Galactic Centre objects and circular points are Al abundances from RSDR stars. Error bars for the Galactic Centre stars are taken as typically $\pm$ 0.2 dex. The dotted line is a least-squares straight-line fit for all the B-type stellar data, with a gradient of $-0.05 \pm 0.01$ dexkpc^-1, similar to that derived by RSDR. The solar point comes from Table 4. b) Asterisk symbols are stellar sulphur abundances and filled squares are results from Afflerbach et al. (1997). Little reliable stellar data exists for S in the outer Galaxy

Open with DEXTER

The correlation of of O, Mg, and Si abundances found in the outer Galaxy (see RSDR) and in the low metallicity Magellanic Clouds (Rolleston et al. 1996) is theoretically expected as these elements are all produced and returned to the ISM through supernovae typeII. One would expect that this trend should continue towards the inner Galaxy, and it is surprising that our O abundances show no sign of increase, while Mg and Si appear significantly higher than their comparison stars. The S abundances in these stars are also higher than normal, although the dataset is somewhat less robust given the weakness of the absorption features of this element.

There has been some investigation into the effects of metallicity dependent yields from massive stars. Prantzos et al. (1994) have taken the yields of Maeder 1992) and investigated the the galactic chemical evolution of C and O. These studies suggest that oxygen yields from massive stars tend to decrease towards higher metallicities. This is due to mass loss being higher at high metallicities and significantly more mass is ejected in the stellar wind (which is rich in helium and carbon). This leaves a smaller mass fraction which can be converted into oxygen. However a detailed study of element yields other than C and O, and their subsequent evolution has not yet been done. Hence given the statistically small number of stars we have in the present study, and the lack of metallicity dependent yield calculations for the other elements we cannot interpret the data in any more detail at present. Analysis of more stars in this region of the Galaxy is desirable. The observational findings presented here should provide a stimulus to investigations of the evolution of the Galaxy at high metallicities, given the possibility that stellar yields are highly variable with metallicity. Furthermore, we should attempt to determine the true quantitative variation in the ratios of the $\alpha$ -elements in the inner Galaxy to investigate if this trend is real. The recent chemical evolution models of Portinari & Chiosi (1999, 2000) do indicate that the O abundance gradient may indeed flatten off in the region $$3 \mathrel{\mathchoice {\vcenter{\offinterlineskip\halign{\hfil $\displaystyle ...$ kpc, which is encouraging. However their SN typeII yields would suggest that the other $\alpha$ -processed elements (Mg and Si) should follow a similar trend, which we do not observe. Boissier & Prantzos (1999) also suggest that their evolutionary models for the Milky Way predict a flattening of the metallicity gradient with time, and that saturation is reached in the inner Galaxy. This is in reasonable quantitative agreement with what we find for oxygen abundances, but does not explain the behaviour of the other elements.

5.3 Carbon and nitrogen abundances towards the Galactic Centre

Each of the four stars do appear to have nitrogen abundances significantly higher than their solar neighbourhood counterparts. The result for LS5130 is more marginal than the others, but with 19 features measured an error in the mean ( $\sigma/\sqrt n$ ) of 0.03 dex would suggest that the enrichment is real although small. Figure 4b shows the nitrogen abundances of the Galactic Centre stars plotted along with a sample of stars from RSDR, and the H II regions from Afflerbach et al. (1997). The gradient found in RSDR appears to continue towards the Centre; certainly the abundance estimates do not appear to flatten as for oxygen. Reasonably good agreement with the absolute values of the H II region analyses is found, and we calculate quite a significant gradient for $\log$ N/O. The full sample of RSDR yielded a gradient in N/O of $-0.04\pm0.02$ dexkpc^-1, and this is increased slightly by the inclusion of the four Galactic Centre stars. The latter effect is clearly due to the stars showing enhanced nitrogen in their atmospheres, but normal oxygen. We have previously discussed the possibility of N-rich core gas contaminating the surface of young massive stars, and hence polluting the natal photospheric material (RSDR). However due to the lack of a strong anti-correlation of C and N, RSDR found no evidence for such contamination and the same argument holds for the four stars analysed here.

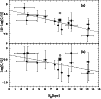$\begin{figure} \par\psfig{file=h2371f7.eps,width=8.8cm}\end{figure}$

Figure 7: a) The Galactic abundance gradient of carbon, composed of the four programme stars and the data from RSDR. A gradient of $-0.07 \pm 0.02$ dexkpc^-1 is found, similar to that reported by RSDR. Three of the four stars in our sample do appear C-rich from their differential abundances. The solar symbol and the solar neighbourhood B-type star value (the large square) are taken from Table 4. b) The $\log$ C/O abundances are plotted and a least-squares gradient of $-0.05\, \pm \, 0.02$ dexkpc^-1 is deduced. This provides stronger evidence than in RSDR that a C/O gradient exists in the Galaxy and is due to the four Galactic Centre stars having normal O abundances, while three are significantly C-rich. The solar and neighbourhood B-type star ratios are again taken from Table 4

Open with DEXTER

An explanation of the N/O gradient was discussed in RSDR, based on the original ideas of Vila-Costas & Edmunds (1993). At metallicities higher than $12 + \log$ O/H $\sim$ 8.3, $\log$ N/O would be proportional to $\log$ O/H, because N enrichment would be dominated by secondary production, i.e. from C and O seed nuclei in the natal interstellar material through the CNO-cycle. Primary production would play a minimal role in contributing to the ISM abundance of N, and simple closed-box models in which the production of N is dominated by secondary production do predict a linear trend. At low metallicities the secondary component becomes less important (due to its inherent dependence on metallicity), and the dominant mechanism for the production of nitrogen is primary. The metallicity at which this happens is around 8.3 dex, close to the value found in the outer most regions of the Galactic disk. These ideas stem from the fact that the N/O ratios in low metallicity dwarf galaxies show a very large scatter, with little discernable trend. As primary nitrogen orginates in low-intermediate mass stars there is a time delay between is enrichment and that of primary oxygen (from short-lived massive stars), hence the scatter at low metallicitities is often interpreted as time dependent delays between oxygen and nitrogen enrichments. However at the high metallicities we are dealing with, it is likely that secondary production (in massive stars is dominant), and there would thus be no delay between N and O production. Our N/O ratios toward the Galactic Centre tend to support the conclusions of RSDR that the N/O gradient in the Galaxy is real, and due to secondary N production dominating across the disk.

In Fig. 7 carbon abundances for the four Galactic Centre stars and from the RSDR compilation are plotted. As three of our new points are C-rich, it is not surprising that the abundances appears to steadily increase toward the Centre. As discussed for nitrogen, because the stars are not rich in oxygen the C/O ratio is greater than normal, hence producing a larger (and statistically more significant) gradient than that given in RSDR. As discussed by Maeder (1992) this would be consistent with C being produced at a greater rate than O in metal-rich stars (Sect. 5.2), due to the increased mass-loss in the post He-burning phase.

6 Conclusions

The analysis of high-quality data for four blue stars lying towards the Galactic Centre, and a comparison with young stars throughout the Galactic disk, leads to the following conclusions

1.

The four stars appear to be normal, young, massive, early B-type stars. They lie slightly out of the Galactic plane and their calculated distances indicate that they are at distances from the disk of 0.4 < z < 1.2 kpc. A kinematic analysis indicates that they were probably born in the disk within 2.5-5 kpc of the Galactic Centre and then subsequently ejected. Comparison with Galactic structure models suggests they may have originated in the stellar or molecular ring at $R_{\rm g}\simeq3$ kpc;

2.

A differential line-by-line abundance analysis of the four stars with two bright stars near the Sun indicates a surprising abundance pattern:

Two of the stars (LS5130 and LS4419) have oxygen abundances very similar to stars in the solar neighbourhood. The other two (LS4784 and LS5130) show only marginal evidence for enhanced oxygen. In all cases any enhancement is significantly below the 0.3-0.4dex that would be expected given the Galactic position of the stars and the gradient from RSDR. Oxygen is a very reliably determined abundance in these particular types of stars;
The relatively well measured abundances of Si, Al, Mg and S however do indicate that these stars have enhanced abundances in most other elements. However, the physical cause of the natal gas having a "normal'' oxygen content and enriched $\alpha$ -processed elements is unclear. The Si and Mg abundances are consistent with the continuation of the linear gradient derived by RSDR for stars in the solar neighbourhood and the outer Galaxy;
The four stars also appear rich in both C and N, again in agreement with a continuation of the RSDR gradients towards the Centre;
We discuss the possible errors in our analysis, and conclude that it is unlikely that these stars have higher oxygen abundances than those typically found in the solar neighbourhood. It is also very likely they are rich in all the other elements studied (C, N, Mg, Si, S, Al) although the physical pocesses that produces such a pattern is unclear.

Acknowledgements

Spectroscopic data were obtained at the Anglo-Australian Observatory in Siding Spring, New South Wales and the ESO 3.6m Telescope on La Silla. We also obtained photoelectric photometry on the 0.5m in South Africa, and CCD photometry on the 1.5m Danish Telescope in La Silla. We are grateful to the staff at all observatories for their assistance. We are particularly grateful to Dave Kilkenny at SAAO who provided urgent initial photometry, which allowed some of this work to be incorporated into S. Smartt's Ph.D. Thesis. Data reduction was performed on the PPARC funded Northern Ireland STARLINK node, and some of the model atmosphere programs were made available through the PPARC supported Collaborative Computational Project No. 7. We made use of the SIMBAD database maintained at CDS, Strasbourg. We acknowledge financial support for this work from the British Council and the Deutscher Akademischer Austauschdienst in the context of the British-German Academic Research Collaboration initiative, and also the Visiting Fellowship program at Queen's University which allowed travel for SJS to further discussions. SJS and WRJR acknowledge funding from the PPARC. KAV would like to acknowledge travel and observing support by ESO, and to thank the Henry Luce Foundation for research funds through a Clare Boothe Luce professorship award.

Appendix A:

Tables 9 and 10 are the lists of equivalent widths of all metal lines measured in the spectra of the Galactic centre stars and the standards $\iota$ Her, and $\gamma$ Peg and are also available in electronic form at CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via
http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/367/86

Table 9: Equivalent widths (mÅ) of the non-diffuse helium lines and the metal lines in the stars LS5130, LS4419, LS4784 and the spectroscopic standard $\gamma$ Peg. Each equivalent width has been assigned error estimates as follows - a: error less than 10% - b: error less than 20% - c: error greater than 20%
Species and Line LS5130 LS4419 LS4784 $\gamma$ Peg

O II 3911.96 57a 96c 76b 50a

C II 3918.98 138a 130a 261a⁷ -

N II 3919.01

O II 3919.28

C II 3920.69 127a 113a - -

O II 3945.04 30b 63b 58c -

O II 3954.37 51a 63b 74b 48a

He I 3964.73 177a 187a 188a 155a

O II 3982.72 29c 72b¹ 60a¹ 31a

S III 3983.77 28c - - 14a

Table 9: continued
Species and Line LS5130 LS4419 LS4784 $\gamma$ Peg

N II 3995.00 102a 104a 93a 78a

N II 4035.08 35b 46a 42c 25a

N II 4041.31 44b 51a 60b 37a

O II 4069.62 95a 115a 97b 94

O II 4069.89

O II 4072.16 62a 75a 43c 65a

C II 4074.48 48b 147a² 141b² 42a

C II 4074.85

C II 4075.85

O II 4075.86 124a - - -

C II 4076.53

N II 4076.91

O II 4078.84 24c 19c - 26a

O II 4085.11 32c 39b 34b 26a

O II 4087.15 22c - - 12a

Si IV 4088.85 37c 44b 61a -

O II 4089.28

Si IV 4116.10 20c - - -

O II 4119.22 62a - - -

O II 4120.28 291a - - -

He I 4120.81

He I 4120.99

O II 4121.46

Si II 4128.07 53a 38c 65b 33a

Si II 4130.89 54a 86c³ 70c³ 34a

Ar II 4131.71 38b - - 17a

O II 4132.80 33b - 54c³ 30a

Al III 4149.50 - 56b 64a -

Al III 4150.14 -

S II 4153.10 60a 125b 105a -

O II 4153.30

S II 4162.70 47b - - -

Fe III 4164.79 45c 32b -

Fe III 4166.86 26c - - 13a

He I 4168.97 99a 99a 104a -

O II 4169.22

Table 9: continued
Species and Line LS5130 LS4419 LS4784 $\gamma$ Peg

S II 4174.24 40b 28c - -

N II 4179.67 14c 21c - -

O II 4185.45 36b 43b - 30a

O II 4189.79 46b 54b 65b -

P III 4222.15 21c 20c - 21a

N II 4227.74 30b 55b 61b 18a

N II 4236.86 51a 55a 66c 28a

N II 4236.98

N II 4241.78 49a 86a 105b -

S III 4253.59 - 118a - -

O II 4253.90

O II 4254.13

C II 4267.02 262a 245a 305a -

C II 4267.27

O II 4267.71

O II 4275.56 - 97b 123a⁸ -

O II 4277.40 - 72b - 16a

S III 4284.99 - - 47c 28a

S II 4294.43 35b 50b 37c -

O II 4294.79

O II 4303.84 30c 62a 54c 26a

C II 4313.30 17c - - -

O II 4317.14 58a 76a 64b 56a

C II 4317.26

O II 4319.63 48a 78a 63b 52a

O II 4325.76 40b 23b 29c 20a

O II 4345.56 30c - - 24a

O II 4347.42 26c - - 21a

Ar II 4348.11 32c - - -

O II 4349.43 66b - - 63a

O II 4351.26 31c - - 41a

O II 4366.89 60a 61a 32c 48a

O II 4369.27 - - - 14a

Table 9: continued
Species and Line LS5130 LS4419 LS4784 $\gamma$ Peg

C II 4372.49 52a 91a 67c⁹ -

C II 4374.27 32b - - -

Fe III 4395.78 40b 60a 58b -

O II 4395.94

C II 4411.20 38b 63b - -

C II 4411.52

O II 4414.90 84a 95a 52c 75a

O II 4416.97 64a 76a 28c 61a

Fe III 4419.59 44b 32c 35c 34a

Fe III 4430.95 33c - 39c 24a

N II 4432.74 38c - 51c 20a

He I 4437.55 126a 103a 135a 118a

N II 4442.02 - - 38c 9a

N II 4447.03 60a - 72b 15a

O II 4448.19

O II 4452.37 31c - 29c 25a

Al III 4479.89 55a - - 38a

Al III 4479.89

Mg II 4481.13 202a 196a 265a 160a

Mg II 4481.33

Al III 4512.54 57a 65a 63a 39a

Al III 4528.91 73a 144a¹⁰ 135a¹⁰ 66a

Al III 4529.20

N II 4530.40 29c - - 25a

N II 4552.53 174a 199a 187a 114a

Si III 4552.62

Si III 4567.82 150a 152a 151a 102a

Si III 4574.76 81a 97a 90a 69a

O II 4590.97 52a 87a 67a -

O II 4596.18 59a 74a 52a 47a

N II 4601.48 62b 107a 90a 37a

O II 4602.13 15a

N II 4607.16 56a 64a 68a 35a

O II 4609.44 41b 63a 50a 30a

Table 9: continued
Species and Line LS5130 LS4419 LS4784 $\gamma$ Peg

N II 4613.87 55a 79a 56a 27a

C II 4618.40 137c 82a 213a¹¹ -

C II 4619.23

N II 4621.29 41b 73a - 26a

N II 4630.54 92a 122a 123a

O II 4638.86 61b 81a 71a 54a

O II 4641.82 74b 171a⁴ 172a⁴ 76a

N II 4643.09 58b - - 42a

C III 4647.42 - 230a ⁵ 192a⁵ -

O II 4649.14 90a - - 92a

O II 4650.84 64b - - 52a

O II 4661.63 67a 94a 75a 54a

O II 4673.74 26c - - 19a

O II 4676.24 44c 45c - 46a

N II 4678.10 24c - - -

N II 4694.70 15c - - 9a

O II 4696.35 15c - - 12a

O II 4699.00 42a 69c 37a -

O II 4699.22

O II 4703.16 - 66a⁵ 53a⁵ -

O II 4705.35 47b - - -

O II 4710.01 30b 40c - 20a

He I 4713.14 289a 283a 250a 271a

He I 4713.37

Si III 4716.65 41b 52b - 12a

N II 4779.67 18c 36c 44b 10a

C II 4802.70 28c - - 15a

N II 4803.29 37c 61a 74a 18a

Ar II 4806.07 29c 21c - 18a

Si III 4813.30 31b 41a 75b¹² 21a

S II 4815.52 54b 27b - 27a

Si III 4819.72 55b 55a 50a 40a

**Table 9:** continued
Species and Line	LS5130	LS4419	LS4784	$\gamma$ Peg

N II 4613.87	55a	79a	56a	27a

C II 4618.40	137c	82a	213a¹¹	-
C II 4619.23

N II 4621.29	41b	73a	-	26a

N II 4630.54	92a	122a	123a

O II 4638.86	61b	81a	71a	54a

O II 4641.82	74b	171a⁴	172a⁴	76a

N II 4643.09	58b	-	-	42a

C III 4647.42	-	230a ⁵	192a⁵	-

O II 4649.14	90a	-	-	92a

O II 4650.84	64b	-	-	52a

O II 4661.63	67a	94a	75a	54a

O II 4673.74	26c	-	-	19a

O II 4676.24	44c	45c	-	46a

N II 4678.10	24c	-	-	-

N II 4694.70	15c	-	-	9a

O II 4696.35	15c	-	-	12a

O II 4699.00	42a	69c	37a	-
O II 4699.22
O II 4703.16	-	66a⁵	53a⁵	-

O II 4705.35	47b	-	-	-

O II 4710.01	30b	40c	-	20a

He I 4713.14	289a	283a	250a	271a
He I 4713.37
Si III 4716.65	41b	52b	-	12a

N II 4779.67	18c	36c	44b	10a

C II 4802.70	28c	-	-	15a

N II 4803.29	37c	61a	74a	18a

Ar II 4806.07	29c	21c	-	18a

Si III 4813.30	31b	41a	75b¹²	21a

S II 4815.52	54b	27b	-	27a

Si III 4819.72	55b	55a	50a	40a

Table 9: continued
Species and Line LS5130 LS4419 LS4784 $\gamma$ Peg

S II 4824.07 12c - 18c -

Si III 4828.96 44b 64a 59a -

Ar II 4879.14 28b - 19c -

O II 4890.93 21c 22b - 11a

O II 4906.83 38b - 29b -

O II 4941.07 25b 38b 14c 15a

O II 4943.00 39b 52b 45c 28a

S II 4991.94 16c - 24c 22a

N II 4994.36 31b 55a 59b -

S II 5009.62 32b - - -

N II 5010.62 40b 40c - -

S II 5014.03 52b - - -

He I 5015.68 322a 319a 354a -

S II 5032.41 66b 56a 91a -

Si II 5041.03 24c - 30c 15a

N II 5045.09 54b 59a 47c -

He I 5047.74 207a 163a 179b -

Si II 5055.98 35c - 56b 22a

Si II 5056.31

S II 5103.30 - - 20c -

C II 5132.96 97a 74a 99a -

C II 5133.29

Notes:

1. Blend of O II 3982.72 and S III 3983.77.

2. Includes the O II, N II and C II lines at 4075-4076AA.

3. Blended with Ar II 4131.71.

4. Blended with N II 4643.09.

5. Blended with O II 4649.14 & 4650.84.

6. Blended with O II 4705.35.

7. Also includes C II 3920.69.

8. Blended with O II 4277.40.

9. Blended with C II 4374.27.

10. Blended with N II 4530.40.

11. Blended with N II 4621.29.

12. Blended with S II 4815.52.

Table 10: Equivalent widths (mÅ) of the non-diffuse helium lines and the metal lines in the stars LS5127 and $\iota$ Her
Species and Line LS5127 $\iota$ Her

O II 3911.96 50c 12a

C II 3918.98 340b 72a

N II 3919.01 -

O II 3919.28 8a

C II 3920.69 88a

O II 3954.37 44c 20a

He I 3964.73 210c 132a

N II 3995.00 108a 40a

N II 4041.31 57b 19a

N II 4043.53 59b 9a

O II 4069.62 182a 16a

O II 4069.89 19a

O II 4072.16 27a

C II 4074.48 185a 15a

C II 4074.85 9a

O II 4075.86 32a

C II 4076.53 -

N II 4076.91 -

O II 4119.22 324a -

O II 4120.28

He I 4120.81

He I 4120.99

O II 4121.46

Fe III 4122.06

Fe III 4122.98

He I 4168.97 70b 81a

N II 4241.78 67a 16a

S III 4253.59 69a 13a

O II 4253.90 4a

O II 4254.13 2a

C II 4267.02 338a 184a

C II 4267.27

O II 4267.71

Si III 4267.80 26a

S II 4294.43 43a 24a

O II 4294.79 3a

O II 4303.84 39a 9a

**Table 10:** Equivalent widths (mÅ) of the non-diffuse helium lines and the metal lines in the stars LS5127 and $\iota$ Her
Species and Line	LS5127	$\iota$ Her

O II 3911.96	50c	12a

C II 3918.98	340b	72a
N II 3919.01		-
O II 3919.28		8a
C II 3920.69		88a

O II 3954.37	44c	20a

He I 3964.73	210c	132a

N II 3995.00	108a	40a

N II 4041.31	57b	19a

N II 4043.53	59b	9a

O II 4069.62	182a	16a
O II 4069.89		19a
O II 4072.16		27a

C II 4074.48	185a	15a
C II 4074.85		9a
O II 4075.86		32a
C II 4076.53		-
N II 4076.91		-

O II 4119.22	324a	-
O II 4120.28
He I 4120.81
He I 4120.99
O II 4121.46
Fe III 4122.06
Fe III 4122.98

He I 4168.97	70b	81a

N II 4241.78	67a	16a

S III 4253.59	69a	13a
O II 4253.90		4a
O II 4254.13		2a

C II 4267.02	338a	184a
C II 4267.27
O II 4267.71
Si III 4267.80		26a
S II 4294.43	43a	24a
O II 4294.79		3a

O II 4303.84	39a	9a

Table 10: continued
Species and Line LS5127 $\iota$ Her

O II 4325.76 55c 6a

C II 4325.83 -

C II 4326.16 -

S III 4361.53 39c 4a

O II 4366.89 42c 16a

C II 4372.49 48c -

Fe III 4395.78 43b 15a

O II 4414.90 101b 28a

O II 4416.97 23a

Fe III 4419.59 53a 23a

He I 4437.55 101a 102a

N II 4447.03 65b 18a

S II 4463.58 36b 14a

Mg II 4481.13 423a 205a

Mg II 4481.33

Al III 4512.54 60a 20a

S II 4524.95 47b 22a

Al III 4528.91 100b 6a

Al III 4529.20 28a

N II 4530.40 7a

Fe II 4549.47 49b -

S II 4552.38 191a 71a

Si III 4552.62

Si III 4567.82 156a 59a

Si III 4574.76 93a 27a

Fe II 4583.83 39b 12a

O II 4590.97 39c 17a

O II 4596.18 32c 12a

**Table 10:** continued
Species and Line	LS5127	$\iota$ Her

O II 4325.76	55c	6a
C II 4325.83		-
C II 4326.16		-

S III 4361.53	39c	4a

O II 4366.89	42c	16a

C II 4372.49	48c	-

Fe III 4395.78	43b	15a

O II 4414.90	101b	28a
O II 4416.97		23a

Fe III 4419.59	53a	23a

He I 4437.55	101a	102a

N II 4447.03	65b	18a

S II 4463.58	36b	14a

Mg II 4481.13	423a	205a
Mg II 4481.33

Al III 4512.54	60a	20a

S II 4524.95	47b	22a

Al III 4528.91	100b	6a
Al III 4529.20		28a
N II 4530.40		7a

Fe II 4549.47	49b	-

S II 4552.38	191a	71a
Si III 4552.62

Si III 4567.82	156a	59a

Si III 4574.76	93a	27a

Fe II 4583.83	39b	12a

O II 4590.97	39c	17a

O II 4596.18	32c	12a

Table 10: continued
Species and Line LS5127 $\iota$ Her

N II 4601.48 49c 15a

N II 4607.16 47c 14a

C II 4618.40 114c -

C II 4619.23

N II 4621.29

Si II 4621.42

Si II 4621.72

Fe II 4629.34 107a -

N II 4630.54

O II 4638.86 43a 21a

O II 4641.82 108a 24a

N II 4643.09 17a

S II 4648.17 170a 5a

O II 4649.14 34a

O II 4650.84 17a

S II 4656.74 26b 10a

O II 4661.63 65b 15a

Al III 4663.05 13a

He I 4713.14 306a 239a

He I 4713.37

Si III 4813.30 81b 8a

S II 4815.52 40a

Si III 4819.72 47c -

S II 5014.03
522a 38a

He I 5015.68 233a

S II 5032.41 128a 47a

Si II 5041.03 85a 42a

N II 5045.09 190a

S II 5047.28

He I 5047.74

Si II 5055.98 182a 82a

Si II 5056.31

References

Afflerbach A., Churchwell E., Werner M.W., 1997 478, 190 In the text
Anders E., Grevesse N., 1989, Geochim. Cosmochim. Acta 53, 197 In the text NASA ADS
Bahcall J.N., 1986, ARA&A 24, 577
Bahcall J.N., Soneira R.M., 1980, ApJS 44, 73 NASA ADS
Baldwin J.A., Ferland G.A., Martin P.G., et al. 1991, ApJ 374, 580 NASA ADS
Bertelli G., Bressan A., Chiosi C., Ng Y.K., Ortolani S., 1995, A&A 301, 381 In the text NASA ADS
Blommaert J.A.D.L., Langevelde van H.J., Michiels W., 1994, A&A 287, 479 In the text NASA ADS
Brown P.J.F., 1987, PhD Thesis, Queens University of Belfast
Boissier S., Prantzos N., 1999, MNRAS 307, 857 In the text NASA ADS
Cardelli J.A., Meyer D.M., Jura M., Savage B.D., 1996, ApJ 467, 334 In the text NASA ADS
Carr J.S., Sellgren K., Balachandran S.C., 2000, ApJ 530, 307 In the text NASA ADS
Carraro G., Ng Y.K., Portinari L., 1998, MNRAS 296, 1054
Clemens D.P., Sanders D.B., Scoville N.Z., 1988, ApJ 327, 139 In the text NASA ADS
Cunha K., Lambert D., 1994, ApJ 426, 170 In the text NASA ADS
Davis L.E., 1994, A Reference Guide to the IRAF/DAOPHOT Package, NOAO Laboratory In the text
Deutschman W.A., Davis R.J., Schild R.E., 1976, ApJS 30, 97 In the text NASA ADS
de Vaucouleurs G., Pence W. D., 1978, AJ 83, 1163 In the text NASA ADS
Edvardsson B., Andersen J., Gustafsson B., et al. 1993, A&A 75, 101 In the text
Fich M., Silkey M., 1991, ApJ 366, 107 In the text NASA ADS
Fitzsimmons A., Dufton P.L., Rolleston W.R.J., 1992, MNRAS 259, 489 In the text NASA ADS
Fuhrmann K., 1998, A&A 338, 161 In the text NASA ADS
Garnett D.R., Shields G.A. Skillman E.D., Sagan S.P., Dufour R.J., 1997, ApJ 489, 63 In the text NASA ADS
Gies D.R., Lambert D.L., 1992, ApJ 387, 673 NASA ADS
Grevesse N., Noels A., 1993 in Origin and Evolution of the Elements, ed. N. Prantzos, E. Vangioni-Flam, & M. Casse (Cambridge: Cambridge Univ. Press), 14 In the text
Gummersbach C.A., Kaufer A., Shäfer D.R., Szeifert T., Wolf B., 1998, A&A 338, 881 In the text NASA ADS
Henry R. B. C., Howard J. W., 1995, ApJ 438, 170 In the text NASA ADS
Heger A., Langer N., 2000, ApJ in press, (astro-ph/0005110). In the text
House F., Kilkenny D., 1980, A&A 81, 251 In the text
Howarth I.D., Murray J., Mills D., Berry D.S., 1998 Starlink User Notice, No.50.21 In the text
Israelian G., Garcia Lopez R.J., Rebolo R., 1998, ApJ 507, 805 In the text NASA ADS
Jeffery C.S., 1991, in: Newsletter on Analysis of Astronomical Spectra No. 16, pg. 17 In the text
Kennicutt R.C., Garnett D.R., 1996, ApJ 456, 504 In the text NASA ADS
Kerr F.J., Lynden-Bell D., 1986, MNRAS 221, 1023 In the text NASA ADS
Kilian J., 1994, A&A 282, 867 In the text NASA ADS
Kilkenny D., Balona L.A., Carter D.B., Ellis D.T., Woodhouse G.F.W., 1998, MNASSA 47, 69 In the text
Kurucz R.L., 1979, ApJS 40, 1 In the text NASA ADS
Kurucz R.L., 1991, in Precision Photometry: Astrophysics of the Galaxy, ed. A.G. Davis-Philip, A.R. Upgren, & P.L. Janes (Schenectady:Davis) In the text
Leonard P. J. T., 1993, in Luminous High-Latitude stars, ed. D. Sasselov (San Francisco:ASP) In the text
Lester J.B., Gray R.O., Kurucz R.L., 1986, ApJS 61, 509 In the text NASA ADS
Maciel W.J., Köppen J., 1994, A&A 282, 43 In the text
Maciel W. J., Quireza 1999, A&A 345, 629 In the text NASA ADS
Maeder A., 1992, A&A 264, 105 In the text
Maeder A., & Meynet G., 2000, astro-ph/0006405 In the text
Martin P., Roy J.-R., 1992, ApJ 397, 63 In the text
Massey P., 1992, A User's Guide to CCD Reductions with IRAF, NOAO Laboratory In the text
Matteucci F., Chiappini C., 1999, in Proc. ESO Conf. on Chemical Evolution from Zero to High Redshift, Springer Conference Series, eds. J. Walsh & M. Rosa In the text
Matteucci F., Francois P., 1989, MNRAS 239, 885 In the text NASA ADS
Meyer D. M., Jura M., Cardelli J. A., 1998, ApJ 493, 222 In the text NASA ADS
Monteverde I., Herrero A.H., Lennon D.J., 2000, ApJ, submitted In the text
Mooney C.J., Rolleston W.R.J., Keenan F.P., et al. 2000, A&A 357, 553 In the text NASA ADS
Najarro F., Krabbe A., Genzel R., et al. 1997, A&A 325, 700 NASA ADS
Napiwotzki R., Schonberner D., Wenske V., 1993, A&A 268, 653 In the text NASA ADS
Ortiz R., Lépine J.R.D., 1993, A&A 279, 90 In the text NASA ADS
Paczynski B., Stanek K.Z., Udalski A., et al. 1994, AJ 107, 2060 In the text NASA ADS
Pagel B.E.J., Tautvaisine G., 1995, MNRAS 276, 505 In the text
Peters G.J., 1976, ApJS 30, 551 In the text NASA ADS
Pilyugin L.S., Edmunds M.G., 1996 A&A 313, 792 NASA ADS
Portinari L., Chiosi C., 1999, A&A 350, 827 In the text NASA ADS
Portinari L., Chiosi C., 2000, A&A 355, 929 In the text NASA ADS
Prantzos N., Aubert O., 1995, A&A 302, 69 In the text NASA ADS
Prantzos N., Vangioni-Flam E., Chauveau S., 1994, A&A 285, 132 In the text NASA ADS
Reed B.C., 1993, ApJS, 87, 367 In the text NASA ADS
Reed B.C., Beatty A.E., 1995, ApJS 97, 189 In the text NASA ADS
Rolleston W.R.J., Brown P.J.F., Dufton P.L., Howarth I.D., 1996, A&A 315, 95 In the text NASA ADS
Rolleston W.R.J., Hambly N.H, Dufton P.L., et al. 1997, MNRAS 290, 422 NASA ADS
Rolleston W.R.J., Hambly N.C., Keenan F.P., Dufton P.L., Saffer R.A., 1999, A&A 347, 69 In the text NASA ADS
Rolleston W.R.J., Smartt S.J., Dufton P.L., Ryans R.S.I., 2000, A&A, in press In the text
Ryans R.S.I, Hambly N.C., Dufton P.L., Keenan F.P., 1996, MNRAS 278, 132 NASA ADS
Rudolph A.L., Simpson J.P., Haas M.R., Erickson E.F., Fich M., 1997, ApJ 489, 94 In the text NASA ADS
Seaton M.J., 1979, MNRAS 187, 73 In the text
Serabyn E., Shupe D., Figer D., 1998, Nat. 394, 448 NASA ADS
Schaller G., Schaerer D., Meynet G., Maeder A., 1992, A&AS 96, 269 In the text NASA ADS
Shaver P.A., McGee R.X., Newton M.P., Danks A.C., Pottasch S.R., 1983, MNRAS 204, 53 In the text NASA ADS
Shortridge K., Meyerdierks H., Currie M., Clayton M., Lockley J., 1997, Starlink User Note 86.14 In the text
Simpson J. P., Colgan S. W. J., Rubin R. H., Erickson E. F., Haas M. R., 1995, ApJ 444, 721 In the text NASA ADS
Smartt S.J., 2000, in The Chemical Evolution of the Milky Way: Stars vs. Clusters, Rome-Trieste Workshop, es F. Matteucci, F. Giovanelli In the text
Smartt S.J., Rolleston W.R.J., 1997, ApJ 481, L47 In the text NASA ADS
Smartt S.J., Dufton P.L., Rolleston W.R.J. 1996, A&A 305, 164 In the text NASA ADS
Smartt S.J., Dufton P.L., Lennon D.J., 1997, A&A 326, 763 In the text NASA ADS
Smartt S.J., Crowther P.A., Dufton P.L.,, Lennon D.J., Kudritzki R.P., Herrero A., Mcarthy J., Bresolin F., 2000, MNRAS submitted, astro-ph/0009156 In the text
Snow T.P., Witt A.N., 1996, ApJ 468, L65 In the text NASA ADS
Stephenson C.B., Sanduleak N., 1971, Publ. Warner & Swasey Obs., 1, 1 In the text NASA ADS
Venn K.A, Smartt S.J., Lennon D.J., Dufton P.L., 1998, A&A 334, 987 In the text NASA ADS
Vílchez J. M., Esteban C., 1996, MNRAS 280, 720 In the text NASA ADS
Vila-Costas M. B., Edmunds M. G., 1993, MNRAS 265, 199 In the text NASA ADS