A&A 367, 339-346 (2001)
DOI: 10.1051/0004-6361:20010016

The topological behaviour of 3D null points in the Sun's corona

D. S. Brown - E. R. Priest

Mathematical Institute, University of St Andrews, St Andrews KY16 9SS, UK

Received 27 July 2000 / Accepted 17 November 2000

Abstract
Many traditional two-dimensional models of flares and other reconnective events rely on an X-point in the corona which collapses to form a current sheet where reconnection takes place. However, the Sun's corona is three-dimensional and the X-point is only a two-dimensional artifact. Three-dimensional models can instead make use of 3D null points in the corona, and Priest & Titov (1996) have studied how reconnection may take place at such locations. This paper aims to study possible conditions for coronal nulls to occur, and how they can be born. It starts with three negative sources and a positive source that is weaker than the sum of the negative sources. As the positive source moves inwards towards the negative sources, there is a local double-separator bifurcation of the topology to a new state, referred to as a Coronal Null state, which contains a null point above the photosphere.

Key words: Sun: corona, magnetic fields


1 Introduction

Many dynamic events in the Sun's corona are largely dominated by the magnetic field. Often, three-dimensional models of such events need to incorporate considerations of the topology of the magnetic field, for example, flares (Sweet 1969; Machado 1983; Lau 1993; Aulanier et al. 1998), jets (Yokoyama & Shibata 1996; Shibata et al. 1996) and reconnection in general (Schindler et al. 1988; Hesse & Schindler 1988; Hornig & Rastätter 1997,1998; Priest & Forbes 2000). To understand these phenomena, it is helpful to consider the topological structure of their magnetic fields.

The topological structure, or skeleton, of a magnetic field is defined by the configuration of the flux sources (which are not necessarily balanced), the null points (where the magnetic field vanishes) and the network of spine field lines and separatrix surfaces (Priest et al. 1997).

For each null the eigenvalues of the magnetic field can be calculated. Since $\nabla . {\vec B}=0$ the sum of the eigenvalues must be zero (Cowley 1973; Fukao et al. 1975; Greene 1988; Lau & Finn 1991; Parnell et al. 1996), so this will normally mean that two eigenvalues are of one sign (say, negative) and the other is of opposite sign (say, positive). In the plane of the eigenvectors corresponding to the two negative eigenvalues there is a fan of field lines which converge into the null (or radiate out from it when the eigenvalues are positive) and make up a separatrix surface. In the direction of the eigenvector corresponding to the lone positive eigenvalue there is a spine field line, which comes out of the null (or goes in when the eigenvalue is negative) (Priest & Titov 1996; Lau & Finn 1990). An example of this is shown in Fig. 1.

  \begin{figure} \par\includegraphics[width=5.8cm,clip]{H2357F1.ps} \par\end{figure} Figure 1: The structure of a three-dimensional magnetic field near a linear null point
Open with DEXTER

The separatrix surfaces divide the volume into regions where all the field lines have the same connectivity between flux sources. For example, a single separatrix surface will divide the volume into two regions of connectivity, each region on either side of the separatrix surface. So the magnetic topology describes how regions of field line connectivity are positioned relative to one another and which regions border one another.

It is convenient when studying solar coronal magnetic topology to work with potential fields (i.e., static fields with $\nabla \times {\vec B} = {\vec 0}$) and to adopt the magnetic charge topology method described by Longcope (1996). Here the flux sources in the photosphere are modelled as point sources lying on a plane and the coronal volume is normally taken to be the upper half plane. This formulation gives the simple analytical expression

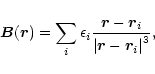
\begin{displaymath}% {\vec B}({\vec r}) = \sum_{i} \epsilon_{i} \frac{{\vec r} -... ...c r}_{i}}{\left\vert {\vec r} - {\vec r}_{i} \right\vert^{3}}, \end{displaymath}

for the resulting magnetic field, where ri is the position of the ith source and $\epsilon_{i}$ is its strength.

It should be noted that the approximation of coronal magnetic fields by equilibrium models such as potential fields is valid when the plasma velocities are much smaller than the Alfvén speed so that the coronal field evolves through a series of equilibria. This is, for example, fine during the usual evolution of active regions, although often force-free models are more appropriate than potential models, especially during the slow storage of excess energy before a solar flare. It certainly fails during the rapid phase of an eruptive flare when speeds are no longer much smaller than the Alfvén speed. Furthermore, it should be noted that the strength of single magnetic sources can change either by their fragmentation into two or more sources, by the merging of two or more sources, or by the appearance (or disappearance) by flux emergence (or submergence) of a positive-negative bipolar pair.

Modelling photospheric flux sources (of radius $\delta$, say) by point sources of zero radius is a reasonable approximation provided one is further than a distance $\delta$ from the source. This would be typically $200\,$km for an intense photospheric flux tube, a few megametres for a pore and about $10\,$Mm for a sunspot. A possible way to avoid the singularity would be to place a source below the photosphere, but this has the disadvantage of making flux pass through the whole photosphere. Preferable would be to model a source by a circular region of radius $\delta$ in the photosphere at which the normal field is uniform and outside which it vanishes (Lothian & Browning 1995). At distances much larger than $\delta$ from the source, this would give a field structure that is very similar to the structure due to a point source.

Generally, in a finite region of the solar surface the magnetic flux does not balance, since flux leaves (or enters) the region to (or from) other sources at large distances (R, say). Therefore, this paper usually considers an unbalanced set of sources by essentially putting the balancing source at infinity (e.g., Inverarity & Priest 1999). This is a good approximation at distances that are small compared to R, since, when viewed from such a distance the group of unbalanced sources resembles the uni-polar field due to a single source of strength equal to the imbalance.

(Brown & Priest 1999a) have used this approach to classify completely the topological behaviour resulting from three sources. They described the key bifurcation behaviour that occurs when one topological state is perturbed and changes into different state. One particular bifurcation, called the global separator bifurcation, describes how two separatrix surfaces can interact and give birth to a separator.

A separator is the field line that marks the intersection of two separatrix surfaces and borders four regions of different connectivity. Separators are believed to be locations where current ribbons form and reconnection can take place (Longcope 1996; 1996). The topological behaviour of separators has been investigated further by Brown & Priest (1999b). They study how four unbalanced sources can give rise to multiple separators in the corona, and how these separators can interact. In particular, they describe how two separators can merge to form a single separator (although this technically involves three other separators lying in the photosphere).

Figure 2 shows a topological state, which will be referred to as the double-intersecting-detached state, due to four sources.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{H2357F2.ps} \par\end{figure} Figure 2: Three-dimensional field line plot showing the double-intersecting-detached topological state due to three negative sources (labelled 1, 2 and 3) and a positive source (labelled 4). The solid lines show the fan field lines, the thick lines show the spine field lines, the dashed lines represent separators, the asterisks are sources and the dots are null points
Open with DEXTER

Three of the sources are negative and the fourth is positive. The three negative sources outweigh the positive source. There are three null points and these give rise to three separatrix surfaces. One of the surfaces forms a separatrix dome which has the three negative sources and three null points lying on its boundary, while the positive source is completely enclosed by the dome. There are also two separatrix walls which divide the interior of the dome into three segments. Each segment contains field lines which connect the positive source to one of the negative sources (a different source for each segment). The separatrix walls continue outside the dome, and divide the external region into three subregions, where the remaining flux from each of the negative sources radiates out to infinity (or other "hypothetical'' sources a large distance away). Figure 3 shows the intersection of the separatrices with the z=0 plane, which clearly shows the different regions of connectivity and how they border one another.
  \begin{figure} \par\includegraphics[width=7cm,clip]{H2357F3.ps} \par\end{figure} Figure 3: Field line plot showing the intersection of the separatrix dome and walls of the double-intersecting-detached topological state with the z=0 plane. The solid lines show the fan field lines, the thicker lines show the spine field lines, the dashed lines represent the projection of the separators onto the z=0 plane, the asterisks are sources and the dots are null points
Open with DEXTER

The two separatrix walls intersect the separatrix dome in two separators, both of which begin at one of the null points and end up at the remaining null points.

The long-term goal is to understand the complex topology of coronal magnetic fields due to many sources (Seehafer 1985,1986), by constructing the skeletons of the different topologies and understanding the bifurcations from one topology to another. Although the potential field due to three sources is fully understood (Brown & Priest 1999a), the four-source case has no complete understanding, even though several authors have investigated various aspects.

For example, Molodenskii & Syrovatskii (1977) discussed the existence of null points out of the z=0 plane, and suggested that their number and position are determined by the number of sources and their positions, though they generally considered balanced fields. Topologies incorporating null points out of the z=0 plane were also considered by Lau (1993) for a class of solar flare models. However, to obtain these nulls the magnetic sources were set at different levels beneath the z=0 plane

Gorbachev et al. (1988) considered how topologies due to four balanced sources (arranged as two bipoles) can produce separators, the formation of which may act as a trigger for a solar flare. They examined how the sources can be perturbed from a topological configuration without a separator to a state where a separator is present. They also considered how the magnetic field along the separator can reverse direction as the sources pass through critical configurations. This work was continued by Gorbachev & Somov (1988) who studied the effect that varying the source strengths of these bipoles has on the shape of the polarity inversion line (PIL). Fixing the positions of the sources they demonstrated that, by varying the relative source strengths, the curvature of the S-like shape of the PIL would change. They also showed that a separator can appear and they related the field structure about the separator to the plasma structure seen during two-ribbon flares.

Bungey et al. (1996) considered two, three and four source cases where the sources are placed at different heights beneath the z=0 plane in such a way that bald patches, places where a field line grazes the z=0 plane, are present. They investigated the behaviour of bald patches in an evolving configuration similar to that used by Gorbachev & Somov (1988), particularly how a bald patch can appear and split into two separate bald patches. Together, these works give only a partial understanding of the complexity of four-source configurations.

Inverarity & Priest (1999) modelled the magnetic structure of the quiet Sun by placing magnetic sources and sinks on a hexagonal network of supergranule cells. In particular, they considered a simple three-cell network configuration of twelve unit sources and the effect of increasing the strength of a central source and moving it around. They found many null points in the plane of the sources and out of the plane when the central (negative) source is smaller in magnitude than the sum of the (positive) strengths of the surrounding sources. The main results of the study were to show how complex the topology of the coronal field is and to use Euler characteristics to relate the numbers of null points and sources.

The aim of this paper is two-fold. Firstly, it will continue to explore the nature of the topology due to four sources as one of the building blocks of even more complex configurations. Secondly, in view of the potential importance of null points in the corona, which were demonstrated in one particular quiet-Sun configuration by Inverarity & Priest (1999), the object is to explore in detail the nature of the simplest configuration with a coronal null and a bifurcation that causes such a null point to be born or die. Such a configuration may form part of many more structures than just the simple network configuration.

2 Null points in the corona

2.1 Analytical example of a coronal null

Often, null points of topological states due to three or four sources lie in the plane z=0 (Brown & Priest 1999a). This is not always the case, however, and it is possible for null points to lift off from the z=0 plane. However, in general it has not been established how common coronal nulls are in the solar corona. For example, the particular quiet-Sun network configuration of Inverarity & Priest (1999) of three hexagonal cells of unit positive sources with a central negative source had at most one coronal null and between 12 and 20 photospheric nulls.

Consider now, a simple example with three sources of equal strength, $\epsilon_{\rm s} = -1$, positioned equidistant from each other in an triangular formation. Now place a positive source of unit strength in the centre of the triangular formation, as shown in Fig. 4.

  \begin{figure} \par\includegraphics[width=5.2cm,clip]{H2357F4.ps} \par\end{figure} Figure 4: Diagram showing a possible configuration of sources that can produce a null point out of the plane
Open with DEXTER

Taking the origin at the positive source and each negative source a unit distance away from it in directions $\pi/2$, $7\pi/6$ and $11\pi/6$, the magnetic field is given by
Bx(x,y,z) = $\displaystyle \frac{x}{\left(x^{2} + y^{2} + z^{2}\right)^{3/2}}$  
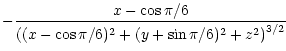    $\displaystyle - \frac{x-\cos{\pi/6}}{\left((x-\cos{\pi/6})^{2} + (y+\sin{\pi/6})^{2} + z^{2}\right)^{3/2}}$  
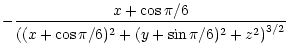    $\displaystyle - \frac{x+\cos{\pi/6}}{\left((x+\cos{\pi/6})^{2} + (y+\sin{\pi/6})^{2} + z^{2}\right)^{3/2}}$  
    $\displaystyle - \frac{x}{\left(x^{2} + (y-1)^{2} + z^{2}\right)^{3/2}}$ (1)


 
By(x,y,z) = $\displaystyle \frac{y}{\left(x^{2} + y^{2} + z^{2}\right)^{3/2}}$  
    $\displaystyle - \frac{y+\sin{\pi/6}}{\left((x-\cos{\pi/6})^{2} + (y+\sin{\pi/6})^{2} + z^{2}\right)^{3/2}}$  
    $\displaystyle - \frac{y+\sin{\pi/6}}{\left((x+\cos{\pi/6})^{2} + (y+\sin{\pi/6})^{2} + z^{2}\right)^{3/2}}$  
    $\displaystyle - \frac{y-1}{\left(x^{2} + (y-1)^{2} + z^{2}\right)^{3/2}}$ (2)


 
Bz(x,y,z) = $\displaystyle \frac{z}{\left(x^{2} + y^{2} + z^{2}\right)^{3/2}}$  
    $\displaystyle - \frac{z}{\left((x-\cos{\pi/6})^{2} + (y+\sin{\pi/6})^{2} + z^{2}\right)^{3/2}}$  
    $\displaystyle - \frac{z}{\left((x+\cos{\pi/6})^{2} + (y+\sin{\pi/6})^{2} + z^{2}\right)^{3/2}}$  
    $\displaystyle - \frac{z}{\left(x^{2} + (y-1)^{2} + z^{2}\right)^{3/2}}$ (3)

in Cartesian geometry. By symmetry, it is clear that there is a null point lying on the y-axis (i.e., x=0 and z=0). Along this line Bx = Bz = 0 and By is given by Eq. (2) as
$\displaystyle B_{y}(0,y,0) = \frac{y}{\vert y\vert^{3}} - \frac{2y+1}{\left(y^{2}+y+1\right)^{3/2}} - \frac{y-1}{\vert y-1\vert^{3}},$     (4)

which vanishes at $y \approx -0.91$. By rotational symmetry there are two further nulls at a distance $\approx$0.91 from the origin, along the lines $y = x \cos{\pi/6}$ and $y = x \cos{5\pi/6}$.

However, this does not account for all of the nulls. Along the z-axis (x=y=0) Bx=By=0, and Eq. (3) becomes

$\displaystyle B_{z}(0,0,z) = \frac{z}{\vert z\vert^{3}} - \frac{3z}{\left(1+z^{2}\right)^{3/2}}\cdot$     (5)

Setting this to zero produces exactly one null point above the plane z=0 satisfying
8z6 - 3z4 - 3z2 - 1 = 0,     (6)

which gives $z \approx 0.962$.

The topology is shown in Fig. 5.

  \begin{figure} \par\includegraphics[width=8.4cm,clip]{H2357F5.ps} \par\end{figure} Figure 5: Three-dimensional field line plot showing a topological state which has a null out of the z=0 plane. The solid lines show the fan field lines, the thick lines show the spine field lines, the dashed lines represent separators, the asterisks are sources and the dots are null points
Open with DEXTER

There are three vertical separatrix walls which meet at the spine of the null out of the plane. This spine is connected to the central positive source. Each of the separatrix walls includes one of the null points which lie in the z=0 plane. Enclosing the central positive source there is a separatrix dome on which lie the remaining three sources and all of the nulls. The three separatrix walls intersect the separatrix dome at separators (shown dashed in Fig. 5). These separators meet at the null out of the plane and connect it to each of the three nulls in the z=0 plane. The null point which lies out of the plane marks the point where all three of the separatrix walls and the separatrix dome meet.

2.2 Varying the central source strength

Suppose now that the central positive source has a strength of $\epsilon_{\rm p}$ rather than 1 and the negative sources each have strength $-\epsilon_{\rm n}$ instead of -1. The position of the null point out of the plane on the z-axis is then given by:

$\displaystyle B_{z}(0,0,z) = \frac{\epsilon_{\rm p}}{z^{2}} - \frac{3\epsilon_{\rm n}z}{\left(1+z^{2}\right)^{3/2}}=0,$     (7)

which can be rearranged to give
 
$\displaystyle z=\pm \frac{1}{\left( \left(\frac{3\epsilon_{n}}{\epsilon_{p}}\right)^{2/3} -1\right)^{1/2}}\cdot$     (8)

This has the property that $z \longrightarrow \infty$ as $\epsilon_{\rm p} \longrightarrow 3\epsilon_{\rm n}$ from below. Thus, as the sum of the sources tends to zero, the null point out of the z=0 plane moves out to infinity. When $\epsilon_{\rm p}/\epsilon_{\rm n}$ exceeds 3 the null point out of the plane no longer exists (since solutions to Eq. (8) are complex) and some of the field lines from the positive source open out. This could occur by negative flux interacting and being cancelled by external positive flux.

2.3 Bifurcation behaviour

In the previous example, it was possible to calculate the null points analytically due to the three-fold degree of symmetry. Nevertheless, one has to be careful in making general deductions from symmetric systems since many such examples can possess topologically unstable non-generic behaviour (Brown & Priest 2000). However, the topology of this configuration, with its null out of the plane is structurally stable and so does continue to exist when the system is perturbed and the symmetry is broken. An example of this is given in Fig. 6.

  \begin{figure} \par\includegraphics[width=7cm,clip]{H2357F6.ps} \par\end{figure} Figure 6: Three-dimensional field line plot showing a particular Coronal-Null state - an asymmetric topological state generated by sources at (0,0), (0,1), (-0.7,-0.6) and (0.9,-0.4) with respective strengths 1.5, -0.9, -0.8 and -1.1 and a null out of the z=0 plane. The solid lines show the fan field lines, the thick lines show the spine field lines, the dashed lines represent separators, the asterisks are sources and the dots are null points
Open with DEXTER

Figure 7 shows where the topological state with a null out of the plane (henceforth referred to as the Coronal-Null state or CN state for short) exists in parameter space.
  \begin{figure} \par\includegraphics[width=7cm,clip]{H2357F7.ps} \par\end{figure} Figure 7: Bifurcation diagram showing the region in parameter space where there is a null point out of the plane. The horizontal and vertical axes represent the locations of a positive source of strength 1.5. Fixed negative sources are located at (0,1), (-0.7,-0.6) and (0.9,-0.4) with strengths -0.9, -0.8 and -1.1. The topological states are (CN) coronal-null state, (2ID) double-intersecting-detached state
Open with DEXTER

The negative sources in Fig. 6 are fixed and the position of the positive source is varied. Eventually, the coronal-null state bifurcates into the so called double-intersecting-detached state shown in Fig. 2, in which there are two separators, one separatrix dome and two separatrix walls.

To understand how this bifurcation occurs, the behaviour of the null points must be analysed. The paths of the null points as the positive source is moved are shown in Fig. 8.

  \begin{figure} \par\includegraphics[width=7cm,clip]{H2357F8.ps} \par\end{figure} Figure 8: Plot showing the evolution of the null points as the topology bifurcates between the coronal-null state and the double-intersecting-detached state. The large dots indicate the initial position of the nulls. The path of the varying source is indicated by a dashed line
Open with DEXTER

The initial configuration is the one shown in Fig. 6 and, as the positive source is moved along the dashed line, the nulls move along the solid curves.

The null which is out of the z=0 plane can be seen to approach the plane and merge with one of the null points already in the plane. This behaviour seems strange at first, until one remembers that the behaviour in the unphysical region below the z=0 plane is the mirror image of the behaviour above the plane. Thus, there is also a null point below the plane which approaches the plane and merges with the null in the plane and the one that approaches from above at the same time.

In other words, the three nulls merge to form a third-order null point at the moment of bifurcation. Two of the solutions then become complex and the third-order null becomes a first-order null (part of the double-intersecting-detached state). This is a three-dimensional version of a pitchfork bifurcation, which is referred to here as a local double-separator bifurcation.

Previously (for example Brown & Priest 1999a), local bifurcations of the magnetic field have involved the appearance of a second-order null which splits into two first-order nulls, or the reverse process where two first-order nulls coalesce to form a second-order null which is annihilated. In both cases the second-order null only exists for critical values of the parameters, and is therefore topologically unstable (as small perturbations of the parameters will cause it either to disappear or to spilt into two first-order nulls).

Pitchfork-type bifurcations of the magnetic field have been demonstrated by Priest et al. (1997) with three sources. However, their example only occurs between topologically unstable three-source states which have high symmetry and is a non-generic example. Also, the three null points involved in their bifurcation remain in the z=0 plane at all times.

2.4 Analytical model for local double-separator bifurcation

An analytical model for the magnetic field of this process can be described by the equation

 
$\displaystyle {\vec B}({\vec r}) = \left( \begin{array}{c} -x \left(3z^{2} + \l... ...ght) \\ (2\lambda +a)y \\ z \left( z^{2}-\lambda \right) \end{array} \right),$     (9)

where $\lambda$ is the parameter to be varied and a is a constant which is fixed so that $\lambda+a > 0$ and $2\lambda+a > 0$ near the bifurcation point ( $\lambda =0)$.

Equation (9) has null points where x=y=0 and z=0 or $z=\pm \sqrt{\lambda}$. When $\lambda<0$ the system has two complex roots and the only physical null point is at (0,0,0). When $\lambda=0$ the system has a triple root at (0,0,0) which is a third-order null point. As $\lambda$ increases, the third-order null splits into three first-order nulls, as shown in Fig. 9.

  \begin{figure} \par\includegraphics[width=8.4cm,clip]{H2357F9a.ps}\\ % \includegraphics[width=8.4cm,clip]{H2357F9b.ps} \par\end{figure} Figure 9: Plots illustrating a local-double-separator bifurcation. The field initially has one null point with a separatrix surface. At bifurcation this null becomes a third-order null and splits into three first-order nulls, which give birth to two new separatrix surfaces and the corresponding spines
Open with DEXTER

Before bifurcation the single null point has an associated separatrix surface. At bifurcation, this actually becomes two different surfaces in the plane x=0 that meet along the line x=z=0 (which becomes a spine field line). As the nulls split, a new separatrix surface is formed between the spines of the two nulls that leave the z=0 plane (Fig. 9). This surface is perpendicular to the other two separatrix surfaces.

3 Simulated magnetograms for coronal nulls

This paper has examined lower-order cases that produce coronal nulls utilising point sources. However, the flux surface seen in magnetograms, taken by instruments such as SOHO/MDI, are more complex than this, so what type of configurations in a magnetogram would give rise to nulls in the corona? Antiochos (1998) discuss a possible theoretical setup where a negative flux patch is completely surrounded by positive flux. This possesses a coronal null above the negative flux patch.

Figure 10 shows contour plots of Bz for the coronal-null state and the double intersecting-detached state.

  \begin{figure} \par\includegraphics[width=7cm,clip]{H2357F10a.ps}\\ % \includegraphics[width=7cm,clip]{H2357F10b.ps} \par\end{figure} Figure 10: Contour plots of the magnetic field in the z-direction, Bz at a height z=0.1, for (top) the coronal-null state in Fig. 6. and (bottom) the double-intersecting-detached state, where the positive null has been perturbed to the position (0.7, 0.5). The dashed curves are negative contours, the solid curves are positive contours and the thick curve is the polarity inversion line. The plusses and asterisks show the xy-positions of the positive and negative sources
Open with DEXTER

These plots are used to simulate how magnetogram data for these configurations might appear. The plots are taken at a height z=0.1 so that Bz has a non-zero component almost everywhere (small perturbations of this height do not change the qualitative nature of the field, so long as it does not approach or exceed the height of the coronal null).

These cases are quite simple representations of what happens in the solar corona and photosphere and a more complex example is shown in Fig. 11 along with the topological skeleton it produces.

  \begin{figure} \par\includegraphics[width=7cm,clip]{H2357F11a.ps}\\ % \includegraphics[width=7cm,clip]{H2357F11b.ps} \par\end{figure} Figure 11: (Top) Contour plot of the magnetic field in the z-direction, Bz at a height z=0.1, for a complex thirteen source case where a coronal null exists. (Bottom) The skeleton of this topology showing where the coronal null lies
Open with DEXTER

This is more akin to the type of magnetogram observable when a small bipole emerges between a larger bipole (such as those observed by Wang & Wang 1996; Filippov 1999; Aulanier et al. 2000), and one of the smaller flux patches interacts and embeds itself within a larger patch. For this case, the total flux is balanced (although the small bipole and the large bipole are individually unbalanced) and the coronal null is located above the positive source which is embedded within the ring of negative sources. There are nine separators connecting the coronal null to nulls in the z=0 plane and these lie on a separatrix dome which incorporates the ring of negative sources and their associated nulls and encloses the small positive source completely.

4 Conclusions and discussion

To be able to understand coronal phenomena, it is important to develop a theory for magnetic topology of the corona. As the solar magnetic field is extremely complex, it is vital to study local structures, such as the one that has been described in this paper, in order to be able to comprehend the global field in which it may be embedded. Coronal nulls may be a vital topological feature for reconnective events and so it is necessary to understand how they are born and the magnetic field evolves.

Researchers such as Inverarity & Priest (1999) have demonstrated the theoretical existence of stable coronal nulls, but have not discussed in detail the mechanisms which cause them to be born through a bifurcation. When a source of one polarity (say, positive) is surrounded by sources of the opposite polarity (say, negative), and the sum of the negative sources locally outweighs the strength of the positive source, then a null point will be present in the region z>0. This paper has illustrated such behaviour with three surrounding sources, but, it is expected to hold also with four or more sources or as part of a more complex topology (such as in Fig. 11).

Such a coronal null is connected to the other nulls in the z=0 plane by separators. These separators would probably play an important role in a more dynamic situation since they are regions where current ribbons can form and reconnection can take place (Longcope & Cowley 1996). Adding more negative sources to the surrounding ring would create more null points in the z=0 plane which could be connected to the coronal null by a separator. The example shown in Fig. 11 has eight null points in the z=0 plane which are all connected to the coronal null by separators. This provides plenty of locations for reconnection to take place.

It has also been demonstrated how a coronal null can bifurcate out of or back into the z=0 plane. At a critical source configuration, a linear null lying in the z=0 plane becomes a third-order null, which splits into three linear nulls, one of which stays in the z=0 plane, one rises into the region z>0 and the third moves into the unphysical region z<0. This is known as a local double-separator bifurcation, which is a three-dimensional version of a pitchfork bifurcation. Previous local bifurcations of the magnetic field have involved the appearance of second-order nulls which split into two first-order nulls (or the reverse process) (Brown & Priest 1999a). An example of the appearance of a third-order null was given by Priest et al. (1997), but this was a non-generic case due to the symmetry of the system, where a second-order null appeared at the same location as an existing first-order null.

Varying the relative strength of the flux sources causes the null point to rise and lower in the z-direction. As the sources approach flux balance, the null point moves out to infinity. Such a mechanism causes closed field lines to open in response to a finite motion of the sources and may be the basis of a flux break-out model for solar flares and other eruptions (Bungey 1995; Antiochos 1998; Antiochos et al. 1999). The idea of having topological triggers for confined flares rather than eruptions has been previously suggested by Lau (1993) and Gorbachev et al. (1988). Furthermore, the flux configuration of a magnetic fragment being surrounded by fragments of opposite polarity has been observed by Démoulin et al. (1994); Filippov (1999); Aulanier et al. (2000) in photospheric magnetograms, and their coronal magnetic structures (whether computed or sketched) were related to a coronal null. Also (2000) have recently proposed a model using a topological structure of this form and demonstrated that field lines may reconnect through the coronal null when flux cancellation (or emergence) occurs.

The presence of a coronal null may then form a basis for an explanation of why regions with so-called parasitic polarities or delta spots (e.g., Zirin 1988) are likely to produce flares.

Acknowledgements
The authors wish to thank the referee for his valuable comments which improved the content of this paper. Also, the Particle Physics and Astronomy Research Council and the Engineering and Physical Science Research Council for financial support.

References

 

Copyright ESO 2001