A&A 367, 362-370 (2001)
DOI: 10.1051/0004-6361:20000339
M. Gai1 - D. Carollo1 - M. Delbò 2 - M. G. Lattanzi1 - G. Massone1 - F. Bertinetto3 - G. Mana3 - S. Cesare4
1 - Osservatorio Astronomico di Torino, Str. Osservatorio
20, 10025 Pino T.se (TO), Italy
2 -
Deutsches Zentrum für Luft- und Raumfahrt, Berlin, Germany
3 -
Istituto Metrologico "G. Colonnetti" del CNR, Str. delle Cacce 73,
10135 Torino, Italy
4 -
Alenia Spazio, C.so Marche 41, 10146 Torino, Italy
Received 27 September 2000 / Accepted 28 November 2000
Abstract
The accurate measurement of the position of celestial objects is a
fundamental step for several astrophysical investigations. For
ground based instruments, the atmosphere is considered the basic
limiting factor; in space, the knowledge of the instrumental
parameters and/or of their stability define the performance
limits, but CCD cameras operated in time delay integration may
take advantage of their operating mode to reduce significantly the
calibration problem. We implemented a low-cost laboratory
experiment aimed at assessing the precision achievable in the
location determination with a CCD camera, by evaluating the
measurement repeatability throughout a set of images of a
simulated stellar field. Our experiment provides an initial
location dispersion of the order of 1/100 of the CCD pixel, with
clear evidence of dominant common mode effects. After removing
such terms with straightforward numerical procedures, we achieve a
final location precision of 1/700 pixel on individual images, or
1/1300 pixel on co-added images. The scaling of precision with
target magnitude is in quite good agreement with theoretical
expectations. The initial common mode systematics appear to be
induced by the thermal control of the CCD camera head, which
degrades the structural stability. In actual implementations, such
problems can be greatly reduced by proper design. Finally, our
results show that residual effects, which could hamper the final
astrometric accuracy, can be calibrated out with simple
procedures.
Key words: instrumentation: detectors - methods: data analysis - space vehicles - techniques: image processing - astrometry
Astrometric measurements of celestial objects are often based on images obtained with CCDs. These measurements allow accurate determination of relative positions as well as, through the direct determination of parallaxes, of the tri-dimensional perspective of regions within our Galaxy, which are becoming increasingly large as measurement precision increases. With the success of the ESA astrometric mission Hipparcos (Perryman 1997), space astrometry has come of age, establishing itself as the most appropriate means for exploiting future micro-arcsec precision measurement capabilities.
Both ESA and NASA are funding three ambitious initiatives in global space astrometry. The measurement principle of the Space Interferometry Mission (SIM, Shao 1998), is somewhat different from that used on Hipparcos, requiring the combination of afocal beams from a single source at one time (Michelson interferometry) rather than the simultaneous imaging of a star field. The other two missions, FAME (Horner et al. 1998) and GAIA (Gilmore 1998), are direct evolutions of the Hipparcos measurement concept; basic location measurements are accomplished on focal planes with large angular size, using mosaics of CCDs. As we are more familiar with the GAIA mission, we will reference to that for some of the practical implications of our findings; details on the focal plane architecture of the GAIA detector have been presented recently (Saint Pé 1999). However, we believe that many of the results presented in this article should also be of interest to the FAME community.
The GAIA measurement concept is, as for Hipparcos, the complete
and repeated coverage of the sky by a scanning satellite,
providing accurate astrometry by reduction of the endless strip
obtained by its CCD detectors operating in Time Delay Integration
(TDI) mode. Given ideal optics, attitude and detectors, the
location accuracy of the targets within the image, and therefore
of the angular position on the sky, is limited only by photon
statistics. In particular, for a given imaging system, in stable
conditions, the expected location dispersion ![]() for a
point-like target image is (Lindegren 1978):
for a
point-like target image is (Lindegren 1978):
At the bright end of the measured objects (actual values depend on
the saturation level of the detection system adopted), the
intrinsic data dispersion appears to be a very small fraction of
the detector pixel size, or of the image size (![]()
![]() ), as a natural consequence of the very high SNR. In order to
ensure photon-limited performances to GAIA, neglecting other error
sources (as, e.g., attitude disturbances), the elementary image
location process should provide an intrinsic dispersion of better
than 1/1000 of the CCD pixel for the brightest targets (
), as a natural consequence of the very high SNR. In order to
ensure photon-limited performances to GAIA, neglecting other error
sources (as, e.g., attitude disturbances), the elementary image
location process should provide an intrinsic dispersion of better
than 1/1000 of the CCD pixel for the brightest targets (
![]() ). It is reasonable to raise the suspicion that, at this
level, the discrepancy between the physical behavior of the device
and the simple geometric model assumed in the above analysis
becomes significant.
). It is reasonable to raise the suspicion that, at this
level, the discrepancy between the physical behavior of the device
and the simple geometric model assumed in the above analysis
becomes significant.
Indeed, ground based observations quote, in favorable conditions, a location accuracy on individual images of the order of 1/100 pixels (Smart et al. 1999), although such precision is believed to be limited mainly by atmospheric effects. It is therefore important to address the problem of the kind of accuracy attainable in a real system which is not dominated by atmospheric turbulence, thus approximating operations in space. Real-world CCD characteristics (like deviation from uniformity or from linear pixel response) are in many cases sufficiently well known to allow a more detailed device modeling than required herein. This would provide further insight into the ultimate performance achievable, and, more importantly, would help define operation and calibration requirements for optimal astrometric results. Such a higher level of CCD modeling, and above all the calibration issues, will be the subject of further investigations.
Hereafter, Sect. 2 describes the equipment we used to generate sets of frames, on which the statistics of Eq. (1) can be directly evaluated; Sect. 3 describes the operating concepts of GAIA leading to our design; in Sect. 4, the data treatment is described; Sect. 5 investigates on the systematic effects evidenced in our simple set-up; in Sect. 6, the implications of our findings for the operation of the GAIA focal plane are described; finally, in Sect. 7, we draw our conclusions.
| |
Figure 1: Schematic of the experimental set-up: from the left, the source system generating the simulated stellar field, imaged by the doublet on the CCD camera |
| Open with DEXTER | |
 |
Figure 2: The experimental set-up: bottom-left to top-right, the CCD camera head, the doublet optics and aperture stop, the shutter (decoupled from the bench), the source system with target mask, frosted glass diffuser and LEDs. Baffling has been removed |
| Open with DEXTER | |
The key concept under investigation is the limiting location accuracy of a CCD camera when acquiring the image of a set of point-like sources. Therefore, we minimize by design the sensitivity to system perturbations, i.e. optical aberrations, mechanical and thermal disturbances. Figure 1 illustrates the experiment in its essential parts, mounted on an optical bench to ensure some degree of stability to the optical system, whereas Fig. 2 shows the set-up as installed in the laboratory. The simulated stellar field produced by the equipment is shown in Fig. 3. Seven significant sources are imaged on the detector. Reference to individual sources is done below according to the numbers in Fig. 3. The experiment was mounted in the Alenia Spazio laboratories (Torino). The data sets analyzed herein were collected on December 2nd, 1998, and some preliminary results have been recently presented (Gai et al. 1999).
The light source is a light emitting diode (LED) circuit.
A frosted glass flat generates a uniformly scattered light beam,
illuminating the artificial stellar field, a mask of pinholes,
each simulating a point-like source at infinity.
The pinhole separation s is large compared to diameter d,
to provide a field with limited star density and well separated
images.
The distance to the CCD camera is r = 1 m, the pinhole diameter
is
![]() m, and the typical pinhole separation is
m, and the typical pinhole separation is
![]() mm.
Therefore,
mm.
Therefore,
![]() ;
the intrinsic angular size of
the sources at the camera is
;
the intrinsic angular size of
the sources at the camera is
![]() ,
and
their angular separation is
,
and
their angular separation is
![]() .
.
We find that sources {1, 2, 3} are brightest, with comparable
magnitude, No. 4 is the faintest, whereas sources
{5, 6, 7} have intermediate intensity. Table 1
provides the intensity and magnitude values, the X and Y source
position (in pixels, averaged over the frame set) and the image
width (in pixels, for sequence No. 1). The brightest source, No. 2, has been set to magnitude 0, whereas the relative
intensity is referred to the star No. 4, for convenience; the
measured magnitude spread is
![]() mag.
mag.
| Star | I | Mag. | X | Y | ||
| [pixel] | [pixel] | [pixel] | [pixel] | |||
| 1 | 14.58 | 0.02 | 197.321 | 283.297 | 1.453 | 1.398 |
| 2 | 14.82 | 0.00 | 249.322 | 191.296 | 1.460 | 1.418 |
| 3 | 13.63 | 0.09 | 315.330 | 292.275 | 1.432 | 1.369 |
| 4 | 1.00 | 2.93 | 317.571 | 428.218 | 1.396 | 1.357 |
| 5 | 3.76 | 1.49 | 103.547 | 305.166 | 1.430 | 1.381 |
| 6 | 3.23 | 1.65 | 218.529 | 101.113 | 1.469 | 1.426 |
| 7 | 3.53 | 1.56 | 434.523 | 222.105 | 1.472 | 1.419 |
The aperture stop diameter of the camera system is D = 2 mm,
resulting in an Airy disk diameter
![]() ;
the simulated stars are therefore completely unresolved, as
;
the simulated stars are therefore completely unresolved, as
![]() .
Due to the small aperture, the matching optics (a doublet) is used
in a small region close to its optical axis, reducing
the sensitivity to aberrations and mechanical tolerances.
The internal shutter of the CCD camera is replaced by an external
device, decoupled from the optical bench, to suppress a
potential source of vibrations within the equipment.
.
Due to the small aperture, the matching optics (a doublet) is used
in a small region close to its optical axis, reducing
the sensitivity to aberrations and mechanical tolerances.
The internal shutter of the CCD camera is replaced by an external
device, decoupled from the optical bench, to suppress a
potential source of vibrations within the equipment.
 |
Figure 3: The simulated star field; sources numbered counterclockwise from the center. In the text, these labels are used as reference for the individual sources |
| Open with DEXTER | |
The CCD camera used in our experiment is model HR 1600 from DTA
(Italy), using a Kodak KAF-1600 chip, with
![]() m pixels,
cooled by a Peltier cell to an operating temperature of -5
m pixels,
cooled by a Peltier cell to an operating temperature of -5 ![]() C.
The detector is a thick, front illuminated CCD with format
C.
The detector is a thick, front illuminated CCD with format
![]() pixels; its quantum efficiency is
pixels; its quantum efficiency is
![]() in the spectral region of interest.
The read-out electronics is based on a 16 bits analog to digital
converter (pixel period 20
in the spectral region of interest.
The read-out electronics is based on a 16 bits analog to digital
converter (pixel period 20 ![]() s), with correlated double sampling.
This camera was adopted because readily available, and because of
its geometric similarity with the selected detectors for the
baseline option of GAIA (Saint Pé 1999).
s), with correlated double sampling.
This camera was adopted because readily available, and because of
its geometric similarity with the selected detectors for the
baseline option of GAIA (Saint Pé 1999).
In TDI, the motion of the image on the focal plane must be matched
by the CCD clock rate: each potential well follows the current
position of the associated point in object space, observed
by the optical system.
The continuous motion is matched to a step-by-step process, since
the CCD potential well is displaced by one pixel per clock cycle.
Ideally, the conventional CCD pixel, associated to a specific device
location, is replaced by a logical pixel generated by the
superposition of the contributions from all subsequent steps of
elementary exposure.
Each logical pixel scans all physical electrodes along one CCD column,
averaging all local variations over the whole device.
The sensitivity of both photometric and astrometric performance
to local device parameters is therefore reduced.
The geometric calibration of a CCD used for pointed observation,
in principle, requires characterization of every pixel, which is
an heavy task for the large logical format
![]() of most
modern devices.
For a CCD in TDI mode, thanks to the uniformity of logical pixels
from each CCD column, the number of individual parameters drops from
the order N2 to
of most
modern devices.
For a CCD in TDI mode, thanks to the uniformity of logical pixels
from each CCD column, the number of individual parameters drops from
the order N2 to ![]() ,
i.e. the linear size of the device.
,
i.e. the linear size of the device.
A relevant case of effects due to local CCD characteristics has
recently been investigated in detail (Anderson & King 1999), concerning
the astrometric and photometric calibration of the Wide
Field/Planetary Camera 2 (WFPC2) on board the Hubble Space
Telescope (HST).
The detector is affected by a manufacturing defect, so that one row
out of every 34 is 3% narrower than the design value.
The smaller pixels collect less light, and the reconstructed
image is compressed; the irregular effect is due to the pointed
observations.
For drift scanning observations, the resulting image would be
composed of equal logical pixels with equivalent width
![]() 1-3%/
34 = 0.999912 of the nominal value, effectively
suppressing the lack of uniformity to a very high degree.
The localized astrometric error of the pointed case is spread out
uniformly in TDI observation, allowing accurate calibration thanks
to the measurement technique: for GAIA, images of the same targets
in subsequent revolutions must superpose each other, providing the
image scale and therefore the correction to the actual value of the
logical pixel size.
Given the large number of bright stars on each scan circle, very
accurate calibration of the pixel scale is achievable: using 103
bright stars, with average precision 1/300 pixels, the precision is
1-3%/
34 = 0.999912 of the nominal value, effectively
suppressing the lack of uniformity to a very high degree.
The localized astrometric error of the pointed case is spread out
uniformly in TDI observation, allowing accurate calibration thanks
to the measurement technique: for GAIA, images of the same targets
in subsequent revolutions must superpose each other, providing the
image scale and therefore the correction to the actual value of the
logical pixel size.
Given the large number of bright stars on each scan circle, very
accurate calibration of the pixel scale is achievable: using 103
bright stars, with average precision 1/300 pixels, the precision is
![]()
![]() .
.
We based our experiment on the acquisition of static images, as this represents a worst case, able to provide a conservative evaluation of the potential performance of a CCD in TDI mode. Pointed exposures may be limited by irregularity of the pixel geometry (e.g. due to the CCD manufacturing process) or by pixel to pixel response variation, requiring very good detector calibration from a geometric standpoint. Assuming uniform pixel size and response, local variation effects are cumulated in the residual errors, which provide an upper limit to the potential performance achievable either in TDI operation (which benefits of pixel equalization) or by a pointed instrument with very good detector characterization. In this sense, a simple set-up is sufficient to yield the desired information, at least concerning the geometric aspects of the CCD and the trend with SNR; implementation of a TDI test is much more complex and expensive, and it is affected by potential limitations which are beyond the scope of our current investigation. For example, requirements for the timing of focal plane electronics have been evaluated by the authors (Gai et al. 1997); the additional performance penalty due to real device limitations (e.g. charge transfer efficiency, CTE, and its progressive degradation for radiation damage in the space environment) are under study with special reference to GAIA (Lindegren, private communication). The trap/hot pixel map should be updated frequently; hot pixels can be reduced or removed by warming up the CCD (Holtzman et al. 1995), whereas the effect of traps can be reduced by the "fat zero" techniques if low signal sensitivity is not critical. For the HST WFPC2, CTE induces signal losses which require correction dependent on the X and Y position of the target in the frame (Whitmore et al. 1999). TDI observation remove the effect on the along scan direction, as all pixels are transferred over the whole array. In principle, TDI only equalizes the CCD response in the along scan direction, which is the fundamental measurement direction in the Hipparcos-like concept used by both GAIA and FAME. The requirements on across scan direction are much less stringent, because we need to separate different nearby sources and possibly to provide a first-order position for data reduction and attitude reconstruction. Calibration is eased by the redundant mosaic structure of the focal plane: every target crosses several CCDs, providing independent values of position associated to the satellite motion and to the detector geometry, which become measurable. Detailed modeling of the detector, its operation and of the available options for data quality assessment are crucial aspects of calibration and data reduction.
For seven different signal levels, sets of 50 frames are
collected, providing a statistically significant sample of
images in the same nominal conditions.
Each image is approximated by a bidimensional Gaussian profile;
a least-squares fit provides estimates of background, intensity,
characteristic width ![]() ,
and center coordinates.
Given the mismatch in the fitting function with respect to the Point
Spread Function (PSF) of the unobstructed circular aperture, and
the sampling resolution of
,
and center coordinates.
Given the mismatch in the fitting function with respect to the Point
Spread Function (PSF) of the unobstructed circular aperture, and
the sampling resolution of ![]() 7 pixels per Airy disk, the
location performance is degraded by approximately 11%
(Gai et al. 1998). Since several parameters are estimated from the
image, the location process is not optimal, so that the
positional accuracy is further degraded, as discussed below.
For GAIA, independent measurements of star brightness and position
are taken in each transit.
The diameter of the PSF Airy disk is
7 pixels per Airy disk, the
location performance is degraded by approximately 11%
(Gai et al. 1998). Since several parameters are estimated from the
image, the location process is not optimal, so that the
positional accuracy is further degraded, as discussed below.
For GAIA, independent measurements of star brightness and position
are taken in each transit.
The diameter of the PSF Airy disk is ![]() 5 times the variance
5 times the variance
![]() of the image profile; the latter is used hereafter as the
characteristic width of the image. Its average value for
the frame sequence No. 1 is listed in Table 1.
We do not apply corrections for dark current, bias, and flat field:
this gives a worst case result.
Figure 4 shows, for a set of 50 frames obtained
with 18 s exposures, a typical behavior of the system: the
positions of the three central sources (labeled in Fig. 3 as 1, 2 and 3) are plotted by the solid, dotted and
dashed line, respectively; the X and Y coordinates are shown in
the top and bottom plot, respectively. The three source positions
are shown after subtraction of their average value within the
frame set, in order to display them on the same plot; a
significant correlation among the target coordinates is evident on
both axis, as all the targets are affected by a common mode
disturbance and feature a much smaller dispersion with respect to
the common trend. Also, the X and Y coordinates do not appear to
have a linear correlation, but they feature similar time scale and
amplitude.
The same considerations apply to the other four stars (4, 5, 6 and 7 in Fig. 3), not shown here for clarity.
We restrict temporarily our analysis to the central three stars.
of the image profile; the latter is used hereafter as the
characteristic width of the image. Its average value for
the frame sequence No. 1 is listed in Table 1.
We do not apply corrections for dark current, bias, and flat field:
this gives a worst case result.
Figure 4 shows, for a set of 50 frames obtained
with 18 s exposures, a typical behavior of the system: the
positions of the three central sources (labeled in Fig. 3 as 1, 2 and 3) are plotted by the solid, dotted and
dashed line, respectively; the X and Y coordinates are shown in
the top and bottom plot, respectively. The three source positions
are shown after subtraction of their average value within the
frame set, in order to display them on the same plot; a
significant correlation among the target coordinates is evident on
both axis, as all the targets are affected by a common mode
disturbance and feature a much smaller dispersion with respect to
the common trend. Also, the X and Y coordinates do not appear to
have a linear correlation, but they feature similar time scale and
amplitude.
The same considerations apply to the other four stars (4, 5, 6 and 7 in Fig. 3), not shown here for clarity.
We restrict temporarily our analysis to the central three stars.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10309f4.eps}
\end{figure}](/articles/aa/full/2001/07/aa10309/Timg33.gif) |
Figure 4: Frame positions for the three central artificial stars versus frame number; data set No. 2, 18 s exposures. The individual positions are referred to the mean location computed by averaging over the whole set of frames, to allow superposition of the plots. Sources Nos. 1, 2, and 3 are represented by the solid, dotted and dashed lines, respectively; top: X coordinate; bottom: Y coordinate |
| Open with DEXTER | |
For each frame (
n = 1, ..., 50), we compute the Gaussian center
coordinates (
![]() ,
,
![]() )
of the three stars (
T = 1,
2, 3), as described above; the standard deviation of the raw data
is slightly above 1% of the pixel size.
We evaluate the average "center of mass" of the three stars over
the 50 frames, with equal weights, as
)
of the three stars (
T = 1,
2, 3), as described above; the standard deviation of the raw data
is slightly above 1% of the pixel size.
We evaluate the average "center of mass" of the three stars over
the 50 frames, with equal weights, as
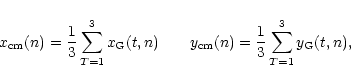
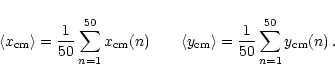
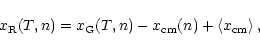
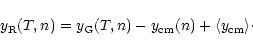
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10309f5.eps}
\end{figure}](/articles/aa/full/2001/07/aa10309/Timg42.gif) |
Figure 5: Reduced coordinates of stars 1, 2, and 3 (represented by the solid, dotted and dashed lines, respectively) vs. frame number, for the same data set as in previous Fig. 4; top: X; bottom: Y. Common mode is strongly suppressed and the residual fluctuations are reduced by about one order of magnitude |
| Open with DEXTER | |
The photo-center evaluation factors out a fraction of the intrinsic
motion of each target.
With comparable standard deviation of the parent data, as justified
by the similar source intensity, i.e.
![]() ,
where
m = 1, 2, 3 refers to the stars and
n=1, 2, ..., 50refers to the frames, we get the dispersion of the reduced
coordinates:
,
where
m = 1, 2, 3 refers to the stars and
n=1, 2, ..., 50refers to the frames, we get the dispersion of the reduced
coordinates:
![]() .
The same holds on Y axis.
The measured standard deviation of the reduced coordinates
is associated to a standard deviation of the parent data
.
The same holds on Y axis.
The measured standard deviation of the reduced coordinates
is associated to a standard deviation of the parent data
![]() 1/700 pixel.
1/700 pixel.
For the case of N sources of comparable brightness, the two sets of
coordinates have quite similar precision, because the transformation
factor is
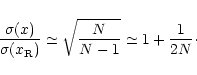
It is possible to reverse Eq. (1), using the measured
position dispersion, image size and SNR to deduce the instrumental
degradation factor:
The choice of the magnitude scale is in approximate agreement with
the baseline GAIA design parameters: the elementary exposure of a
target of magnitude V=15 and near-solar type provides a signal
of ![]() 3.9 104 photo-electrons at the focal plane, and
our magnitude is scaled accordingly.
Throughout the measurement range, the scaling of location accuracy
with SNR (or magnitude) is reasonably linear, in spite of comparably
large variations of the environment and of some operating parameters.
3.9 104 photo-electrons at the focal plane, and
our magnitude is scaled accordingly.
Throughout the measurement range, the scaling of location accuracy
with SNR (or magnitude) is reasonably linear, in spite of comparably
large variations of the environment and of some operating parameters.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10309f6.eps}
\end{figure}](/articles/aa/full/2001/07/aa10309/Timg53.gif) |
Figure 6:
Accuracy of reduced coordinates vs. instrumental
magnitude (logarithmic plot of the location standard deviation).
All targets and data sets are included, and the reduced
coordinates are evaluated by subtraction of the photo-center
motion, defined by the weighted average of the star positions in
each set. The weight is the target intensity. The solid line
represents the best linear fit of the experimental values:
|
| Open with DEXTER | |
To explore a larger parameter space, we implement two tests, frame
binning and coadding.
In the former case, we reduce the image resolution by summing
the pixels inside each
![]() box; the
box; the
![]() frame is reduced to
frame is reduced to
![]() larger pixels.
Each star is now sampled over little more than
larger pixels.
Each star is now sampled over little more than
![]() pixels,
and the same location process is applied, with an expected dispersion
corresponding to a smaller fraction of the larger pixels.
The degradation due to reduced resolution is about 35%.
The evaluation of the new data set provides at best a centering
accuracy of 1/1030 new pixels, consistent with the scaled geometry.
pixels,
and the same location process is applied, with an expected dispersion
corresponding to a smaller fraction of the larger pixels.
The degradation due to reduced resolution is about 35%.
The evaluation of the new data set provides at best a centering
accuracy of 1/1030 new pixels, consistent with the scaled geometry.
We also compress the data set by generating a new set of 25 frames,
each obtained by the sum of two original frames, pixel by pixel,
retaining the original resolution.
This process is similar, in principle, to doubling the exposure time,
with a net increase of the SNR by a factor ![]() .
The location accuracy achieved by the new set of coadded frames
reaches 1/1100 (X) and 1/1300 (Y) pixels.
The instrumental factors are quite compatible with the original
values: the instrumental magnitude becomes
.
The location accuracy achieved by the new set of coadded frames
reaches 1/1100 (X) and 1/1300 (Y) pixels.
The instrumental factors are quite compatible with the original
values: the instrumental magnitude becomes
![]() ,
and the scaling factor is
,
and the scaling factor is
![]() .
The instrument degradation factor is now
.
The instrument degradation factor is now
![]() .
.
The evolution of the experimental conditions is monitored by the
system: in particular, the X and Y image widths are evaluated on
each image.
Within each image set, the variation of the
image width is of the order of 1/100 pixel or smaller, comparable
with the estimate error.
A significant variation of the X image width after the third frame
sequence seems to be due to a system transition, associated
to the air conditioning system, off during the first three
sequences, and switched on at that point, with an interruption of
one hour to allow for temperature settling. No similar variation
is observed for the Y coordinate, and this may be due to the
mounting geometry.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10309f7.eps}
\end{figure}](/articles/aa/full/2001/07/aa10309/Timg62.gif) |
Figure 7: Frame positions for the three central stars versus frame number; data set No. 5, 25 s exposures. Individual positions are referred to the average star location. Sources 1, 2, and 3 are represented by the solid, dotted and dashed lines, respectively; top: X coordinate; bottom: Y coordinate |
| Open with DEXTER | |
An insight on the variation origin is offered by the data:
Fig. 7 shows the X (top) and Y (bottom)
center coordinates of stars 1, 2 and 3 (solid, dotted and dashed
line, respectively) throughout frame sequence no. five, taken
after turning on the air conditioning system.
Again, we subtract the average value of position to each source,
to superpose the plot. The standard deviation of the target positions
is ![]() 2% pixel, with large common mode perturbations. The
residuals (after subtraction of the common mode motion, evaluated
on the seven stars) are at the level of 1/600 pixels.
Oscillating fluctuations with a period of approximately 11 frames
(about eight minutes) are evident, whereas without the air
conditioning system (Fig. 4) we perceive a
settling phase of approximately 18 frames (
2% pixel, with large common mode perturbations. The
residuals (after subtraction of the common mode motion, evaluated
on the seven stars) are at the level of 1/600 pixels.
Oscillating fluctuations with a period of approximately 11 frames
(about eight minutes) are evident, whereas without the air
conditioning system (Fig. 4) we perceive a
settling phase of approximately 18 frames (![]() 15 min),
before reaching a stationary regime, still affected by fluctuations
and a slow drift.
All sequences observed with air conditioning on are affected by
similar oscillations, with comparable time constant; also, all
frame sets taken with air conditioning off feature a slow drift.
Therefore, the air conditioner interacts with the source of the
perturbations.
15 min),
before reaching a stationary regime, still affected by fluctuations
and a slow drift.
All sequences observed with air conditioning on are affected by
similar oscillations, with comparable time constant; also, all
frame sets taken with air conditioning off feature a slow drift.
Therefore, the air conditioner interacts with the source of the
perturbations.
The most likely origin of the perturbations is the CCD camera head itself, which is the only subsystem featuring significant increase in activity during operation. This hypothesis is analyzed in more detail in the next section, deriving a few numbers which can be compared with the requirements for GAIA.
The time scale of the images is between 30 s and one minute per frame. High frequency disturbances, with period significantly shorter than the elementary exposure time, are averaged out by the analog integration; only noise acting on a time scale comparable with the single exposure, i.e. with characteristic frequency <10-1 Hz, may provide a significant residual.
The mechanical set-up has been designed for high stiffness,
to achieve high stability; the proper frequencies of
individual components are of order of hundreds of Hz,
and it is reasonable to expect for the lowest global proper
frequency a value of a few tens of Hz.
The time scale of ![]() 102 s is typical of the thermal
evolution of a small size system, sensitive to any parameter
affecting the conduction, convection and radiative transfer
properties toward the environment.
Usually, analysis can not be carried on explicitly except for very
simple systems, and the designer is forced to work on a
finite-element model (FEM) and evaluate the system behavior by
means of numerical simulators.
Some effort have been spent in our design to reduce the coupling
within the set-up and with the external world, by means of some
shielding, and by mounting the equipment over an optical bench
with large thermal mass.
102 s is typical of the thermal
evolution of a small size system, sensitive to any parameter
affecting the conduction, convection and radiative transfer
properties toward the environment.
Usually, analysis can not be carried on explicitly except for very
simple systems, and the designer is forced to work on a
finite-element model (FEM) and evaluate the system behavior by
means of numerical simulators.
Some effort have been spent in our design to reduce the coupling
within the set-up and with the external world, by means of some
shielding, and by mounting the equipment over an optical bench
with large thermal mass.
The generation of small oscillations is often associated to
digital control systems, because of the finite resolution
associated with the quantization levels.
Hereafter, we describe a simplified model of an heating system,
sufficient to illustrate the mechanism; for the CCD head,
the sign of heat flow is reversed, because it is a
cooling system.
The system, shown in Fig. 8, is represented by
the thermal mass M, to be stabilized at temperature
![]() ;
the environmental conditions are such that in the temperature
interval around
;
the environmental conditions are such that in the temperature
interval around ![]() the average power dissipation to the
environment is
the average power dissipation to the
environment is ![]() .
The thermometer measures the current temperature T(M), compared
with two threshold values (high,
.
The thermometer measures the current temperature T(M), compared
with two threshold values (high, ![]() ,
and low,
,
and low, ![]() ), and the
heater changes its power output between P1, if
), and the
heater changes its power output between P1, if
![]() ,
and
P2, if
,
and
P2, if
![]() ,
where P1 < P2 are the nearest digital
approximations to PE.
The minus sign in Fig. 8 is due to the negative
feedback used for stabilization: if the system temperature increases,
the output power is decreased, and vice versa.
,
where P1 < P2 are the nearest digital
approximations to PE.
The minus sign in Fig. 8 is due to the negative
feedback used for stabilization: if the system temperature increases,
the output power is decreased, and vice versa.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{MS10309f8.eps} %\end{figure}](/articles/aa/full/2001/07/aa10309/Timg66.gif) |
Figure 8:
A simple thermal control system: the actuator can switch
its output between the power levels P1 and P2, heating the
mass M which loses an intermediate amount of power |
| Open with DEXTER | |
The condition for static thermal equilibrium requires that the power
loss ![]() is equal to one of the power output states of the heater,
P1 or P2.
In all other cases, an oscillating steady state is reached.
When the current temperature is higher than the lower threshold
is equal to one of the power output states of the heater,
P1 or P2.
In all other cases, an oscillating steady state is reached.
When the current temperature is higher than the lower threshold ![]() ,
the input power is P1, and the mass suffers a net power loss
,
the input power is P1, and the mass suffers a net power loss
![]() ;
therefore, its temperature decreases at a
rate depending upon its thermal capacity
;
therefore, its temperature decreases at a
rate depending upon its thermal capacity ![]() .
After some time, the descending temperature reaches the threshold
value
.
After some time, the descending temperature reaches the threshold
value ![]() ,
so that the heater switches to output power P2, and
the system, now heated by a constant flux of energy
,
so that the heater switches to output power P2, and
the system, now heated by a constant flux of energy
![]() ,
begins to warm up until reaching temperature
,
begins to warm up until reaching temperature
![]() .
After that, the heater switches to P1 again and the cycle is
repeated.
The variation between
.
After that, the heater switches to P1 again and the cycle is
repeated.
The variation between ![]() and
and ![]() is associated to an amount of
energy
is associated to an amount of
energy
![]() ,
where
,
where
![]() ,
in both warm-up and cool-down phase, i.e.
,
in both warm-up and cool-down phase, i.e.
![]() .
This defines the rise and fall time,
.
This defines the rise and fall time,
![]() and
and
![]() ,
respectively, as well as the
oscillation period:
,
respectively, as well as the
oscillation period:
![]() .
The period becomes indefinitely long as one of the power output
levels approaches
.
The period becomes indefinitely long as one of the power output
levels approaches ![]() ,
i.e. stationary thermal equilibrium.
The average temperature of the system is
,
i.e. stationary thermal equilibrium.
The average temperature of the system is
![]() ,
as P1 and P2 are
the best digital approximations to the desired value
,
as P1 and P2 are
the best digital approximations to the desired value ![]() .
.
The simple model can be applied to our CCD camera head.
We assume a rigid detector, displaced from its nominal position
due to the deformation of its metal supporting structure, having
a thermal expansion coefficient about five times larger than
silicon.
The Peltier cell resolution is
![]()
![]() C, and we
assume for the cold node a thermal capacity of
C, and we
assume for the cold node a thermal capacity of ![]()
![]() C
(equivalent to 0.02 kg of iron or copper, or 0.01 kg of aluminum).
The energy involved in the thermal cycle is
C
(equivalent to 0.02 kg of iron or copper, or 0.01 kg of aluminum).
The energy involved in the thermal cycle is
![]() J; we assume
J; we assume
![]() ,
so that the rise and fall time are equal.
With a full-range cooling power of 2.5 W, and 8 bit resolution,
the output step is
,
so that the rise and fall time are equal.
With a full-range cooling power of 2.5 W, and 8 bit resolution,
the output step is
![]() mW.
Then, the rise/fall time is
mW.
Then, the rise/fall time is
![]() s,
corresponding to an oscillation period
s,
corresponding to an oscillation period
![]() s, or
little more than 6 min, consistent with the observed time scale.
s, or
little more than 6 min, consistent with the observed time scale.
Moreover, the linear expansion coefficient is
![]() parts per million per degree (ppm/
parts per million per degree (ppm/![]() C) for some steels and
C) for some steels and
![]() 17 ppm/
17 ppm/![]() C for copper; therefore, the linear
deformation of a metallic component in the cold head, with length
l = 0.05 m, is
C for copper; therefore, the linear
deformation of a metallic component in the cold head, with length
l = 0.05 m, is
![]() m, quite consistent with the measured fluctuations
in the raw data: 1% of the 9-
m, quite consistent with the measured fluctuations
in the raw data: 1% of the 9-![]() m pixel is actually 90 nm!
Therefore, our simple model provides qualitative agreement with
the systematic effects observed in the raw data, considering only
the thermal behavior of the CCD head.
m pixel is actually 90 nm!
Therefore, our simple model provides qualitative agreement with
the systematic effects observed in the raw data, considering only
the thermal behavior of the CCD head.
The GAIA detection system will be endowed with a large mosaic composed of several hundred CCDs, each with a dedicated analog output line. The CCD output circuit is usually an on-chip MOS source follower, with a DC operating point defined by the bias network, and the charge packet from each CCD pixel appears as a modulation of the output voltage level. In static conditions, the power dissipation on the detector is stable; however, GAIA operates in continuous readout mode, because of the TDI observation. Since the star density and brightness are extremely variable over the sky, the signal level at the CCD output is not stable. The readout of a bright star signal corresponds to a perturbation of the power dissipation on the CCD, which usually consists in a net transfer of energy from the output amplifier to the external load.
This small internal dissipation is the only term to be taken into
account for GAIA, as the design includes passive cooling for the
CCD mosaic and provides a very stable thermal environment. For a
single target, assuming a charge responsivity of ![]() V/e- and
a peak signal of 105 electrons, the output voltage swing is
0.4 V. With a DC bias current of 0.5 mA, and in the simplified
assumption of a sinusoidal signal, the modulated power is
V/e- and
a peak signal of 105 electrons, the output voltage swing is
0.4 V. With a DC bias current of 0.5 mA, and in the simplified
assumption of a sinusoidal signal, the modulated power is
![]() mW. As the readout time for a single
star is
mW. As the readout time for a single
star is ![]() 50
50 ![]() s (five pixels), the energy contributed is 5 10-9 J, to be
compared with the value of
s (five pixels), the energy contributed is 5 10-9 J, to be
compared with the value of ![]() 1 J for
the simple laboratory model described in the previous section.
Even for the limiting case of a sky region with "infinite" object
density, the energy perturbation contributed by each CCD on
GAIA will be 100 times smaller than those experienced in
our laboratory: 0.1 mW vs. 10 mW.
1 J for
the simple laboratory model described in the previous section.
Even for the limiting case of a sky region with "infinite" object
density, the energy perturbation contributed by each CCD on
GAIA will be 100 times smaller than those experienced in
our laboratory: 0.1 mW vs. 10 mW.
The focal plane perturbation is therefore reduced from ![]() 1%
to the order of 10-4 of the
1%
to the order of 10-4 of the ![]() m pixels, i.e. to about
1 nm, even assuming the same structure stability as for our
commercial CCD camera. With a plate scale of 4 arcsec/mm (as
currently planned), this perturbation is then 4
m pixels, i.e. to about
1 nm, even assuming the same structure stability as for our
commercial CCD camera. With a plate scale of 4 arcsec/mm (as
currently planned), this perturbation is then 4 ![]() arcsec, i.e.
below the final mission accuracy specification of 10
arcsec, i.e.
below the final mission accuracy specification of 10 ![]() arcsec.
Moreover, an infinite star density is not a realistic case, and
the focal plane structure can be designed with much better
dimensional stability than our commercial CCD camera, so that the
geometry sensitivity to the thermal variation may be further
depressed. Therefore, thermal effects onto the detector probably
can be excluded as limiting factors for the final mission accuracy
of GAIA.
arcsec.
Moreover, an infinite star density is not a realistic case, and
the focal plane structure can be designed with much better
dimensional stability than our commercial CCD camera, so that the
geometry sensitivity to the thermal variation may be further
depressed. Therefore, thermal effects onto the detector probably
can be excluded as limiting factors for the final mission accuracy
of GAIA.
Within the limits of our experiment, the operating principle of GAIA is not refuted: the measurement of relative positions on individual images from a CCD focal plane appears compatible with the precision level desired for bright stars, even without the advantage of TDI operation. The limiting accuracy in the determination of target positions in CCD images does not appear to be limited by the finite pixel size, at least down to the level of 1/1000 of its value, and the underlying mathematical framework seems to be adequate at this level. The one-dimensional coordinate can then be translated into global astrometric positions through the observations of either a double instrument with relative orientation strictly monitored, or a single telescope fed by a beam combiner, repeatedly covering the whole sky for a few years, as in the Hipparcos scheme. At least in our set-up, which limits by design most of the known CCD limitations, a relative centering precision comparable with the requirements of GAIA, i.e. a dispersion of 1/700 pixel for individual frames or 1/1300 pixel for co-added images.
The paramount importance of an intrinsically stable design, within a quiet environment, is confirmed; in particular, temperature excursions of the order of 1 mK over the focal plane would provide system errors comparable with the desired mission accuracy of GAIA, if the structure sensitivity is comparable to that of our experiment. The effects evidenced in our data are common mode image displacements (about 1/100 pixel), which in real cases may be related to perturbations of the satellite attitude or of the instrument optics. Correction for the common mode motion provide suppression of the disturbances by up to an order of magnitude. Therefore, simple calibration procedures promise to be effective.
Acknowledgements
The experiment concept and rationale benefitted from discussions with members of the Scientific Advisory Group appointed by ESA in support to refinement of the GAIA mission concept. C.O.M.P. (Cusano Milanino, MI, Italy) helped in development of the pinhole mask and supplying engineering information on some optical components. The engineers of Alenia Spazio contributed to the set-up implementation. Funding of our experiment was granted by the Italian Space Agency (ASI, contracts ASI ARS 96-77 and ASI ARS 98-92) for preliminary study of the GAIA mission. We also acknowledge a contribution from the National Council for Astronomy and Astrophysics (CNAA, contract CNAA 16/97) for part of the laboratory equipment. The layout of this paper benefits of the corrections and suggestions of our Referee.We wish to express our thanks to all of them, as well as to the staff of the Observatory and the other institutes involved.