Most of our clusters have too few galaxies to accurately determine the shape of the LF. Instead, we can combine all individual LFs to construct the composite LF of the whole sample. In doing so, vagaries of individual LFs are washed out and only the underlying possibly universal LF is enhanced. We adopt the method used by GMA99, consisting of a modified version of the formula introduced by Colless (=C89, 1989). In practice, the composite LF is obtained by weighting each cluster against the relative number of galaxies in a magnitude range that takes into account the variations in the completeness limit of our data.
Ostriker & Hausman (1977) have shown that giant galaxies in clusters may be the result of peculiar accretion processes. For this reason we took care to remove from each cluster the Brightest Cluster Member (BCM).
The final composite LF is shown in Fig. 6 for the g, rand i bands.
The fit of the composite luminosity functions to a Schechter (1976)
function![]()
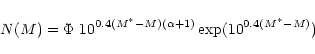
| Band | M* | ||
| g | -1.07+0.09-0.07 | -21.72+0.13-0.17 | 9.4/13 |
| r | -1.11+0.09-0.07 |
|
10.2/13 |
| i | -1.09+0.12-0.11 |
|
11.4/12 |
The faint end of the composite LF (g:
-1.07+0.09-0.07, r:
-1.11+0.09-0.07, i:
-1.09+0.12-0.11) is, in all bands, shallower than the
traditional value,
![]() (cf. Schechter 1976),
but still compatible within the 99% level in the r and i bands.
The best fit values of
(cf. Schechter 1976),
but still compatible within the 99% level in the r and i bands.
The best fit values of ![]() in the three bands are almost identical, while M*increases from the blue to the red band as it is expected from the color of the dominant
population in clusters (taken, for example, from Fukugita et al. 1995).
in the three bands are almost identical, while M*increases from the blue to the red band as it is expected from the color of the dominant
population in clusters (taken, for example, from Fukugita et al. 1995).
In order to test if our background is measured too near the
cluster, we re-computed the LF by adopting the g and r field counts derived
by Weir et al. (1995b), from the same photographic
material and using the same software. We also adopt our
direct measure of the background fluctuations, because these
are not provided in Weir et al. The newly found best fit
parameters differ by less than ![]() from those previously determined,
thus suggesting that cluster members that are more than 3 Mpc away from
the clusters (and that therefore fall in our control field direction) have
null impact on the composite LF. A definitive assessment of the effects
of this assumption on the outer LF,
which is much more sensitive to a small error on the background correction,
calls, however, for a larger sample of clusters.
from those previously determined,
thus suggesting that cluster members that are more than 3 Mpc away from
the clusters (and that therefore fall in our control field direction) have
null impact on the composite LF. A definitive assessment of the effects
of this assumption on the outer LF,
which is much more sensitive to a small error on the background correction,
calls, however, for a larger sample of clusters.
| Band | M* | ||
g |
|
|
9.7/13 |
| r |
|
|
11.2/13 |
We stress that for the time being we prefer to use the local background for an aesthetic reason: the use of the far field implicitly assumes that all galaxy overdensities near the cluster belong to the cluster, including superclusters and filaments. From a technical point of view, the problem is similar to the well understood problem of performing accurate photometry of non isolated objects: when an object in embedded in (or simply superposed to) a much larger one as it happens, for instance, in the case of HII regions or globular clusters on a galaxy or in that of a small galaxy projected on the halo of a larger one. It makes no sense to measure the background very far from the source of interest, since such a procedure ignores the non negligible background contributor. By using a "far distant" background field, we would produce perfectly empty regions at the location of clusters in superclusters, for HII regions in galaxies, and at every locations in the Universe where there are superposed structures of different sizes.
Our composite g and r LFs can be easily compared with those obtained from
photographic material by C89 in the ![]() band and by
Lugger (=L86, 1986) in the R band, as shown in Fig. 7.
Conversions between their photometric systems
and our own has been performed using the color conversions given in the original
papers and those by Fukugita et al. (1995).
We found that the characteristic magnitudes
agree very well (within 1
band and by
Lugger (=L86, 1986) in the R band, as shown in Fig. 7.
Conversions between their photometric systems
and our own has been performed using the color conversions given in the original
papers and those by Fukugita et al. (1995).
We found that the characteristic magnitudes
agree very well (within 1![]() )
while the faint end slopes
are compatible within 2
)
while the faint end slopes
are compatible within 2![]() (
(
![]() and
and
![]() ). At bright magnitudes our LF matches
the Lugger one well, but not the Colless one, which includes the BCMs in the LF.
Anyway, our LF extends more than one magnitude further both at the
bright and faint end: the bright end, which includes rare objects, is better
sampled due to the large area coverage of our survey, whereas fainter
magnitudes are reached due to our deeper magnitude limit.
). At bright magnitudes our LF matches
the Lugger one well, but not the Colless one, which includes the BCMs in the LF.
Anyway, our LF extends more than one magnitude further both at the
bright and faint end: the bright end, which includes rare objects, is better
sampled due to the large area coverage of our survey, whereas fainter
magnitudes are reached due to our deeper magnitude limit.
Evidence in favor of a flat LF has been presented by many authors (cf. Gaidos 1997 for 20 Abell clusters and GMA99 for 65 clusters). A comparison with GMA99 is of particular interest since, in addition to adopting our same photometric system, they use a completely different method for removing possible interlopers. GMA99 exploit the fact that the observed colors of the galaxies change with redshift due to the k-correction, which moves the background objects in a locus of the color-color plane different from that occupied by the cluster galaxies. We compare our r band LF with GMA99 in Fig. 8. The agreement is impressive considering not only that the background correction is made using different approaches, but also the different total magnitude corrections (FOCAS "total" in this work, aperture magnitude corrected to total in GMA99). Moreover, our sample is independent from theirs, except for a few clusters wich are anyway sampled in different regions due to the different field of view.
We find that both the slope and the characteristic magnitude of their best-fit function
are in good agreement with ours and are compatible within the errors (within
![]() ).
This agreement tends to confirm that our choice of using a local
background determination instead of the "average'' one leads to a good estimate of the number of interlopers contaminating cluster galaxy counts.
).
This agreement tends to confirm that our choice of using a local
background determination instead of the "average'' one leads to a good estimate of the number of interlopers contaminating cluster galaxy counts.
In the comparison with GMA99, a few more facts are worth mentioning:
![\begin{figure}
\par\includegraphics[width=8cm,clip]{MS10293f11.ps} \end{figure}](/articles/aa/full/2001/07/aa10293/Timg52.gif) |
Figure 8: Comparison between our composite LF and the Garilli et al. (1999) LF obtained from CCD data and adopting a different method to remove interlopers (see discussion in text) |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{MS10293f12.ps} \end{figure}](/articles/aa/full/2001/07/aa10293/Timg53.gif) |
Figure 9: Comparison between our composite LF (filled dots) and the Trentham (1997) LF (shaded region) based on CCD data |
Our result disagrees with the steep (
![]() )
LF found by Valotto et al. (1997). Their work
is based on photographic data taken from the APM cluster survey
and they adopt, as we do, "local'' background counts
measured in annuli surrounding each cluster.
Nevertheless, their completeness limit is 1.5 magnitudes shallower than ours,
so that they are sampling the brighter portion of the LF, and therefore the slope
is subject to large errors.
)
LF found by Valotto et al. (1997). Their work
is based on photographic data taken from the APM cluster survey
and they adopt, as we do, "local'' background counts
measured in annuli surrounding each cluster.
Nevertheless, their completeness limit is 1.5 magnitudes shallower than ours,
so that they are sampling the brighter portion of the LF, and therefore the slope
is subject to large errors.
At first glance, our claim that a Schechter function is a good fit to
our data (
![]() )
seems in contradiction with
various claims of a non-universal LF produced by the various morphological
composition of clusters and by the non-homology of the LFs of the morphological types
(e.g. Sandage et al. 1985; Jerjen
& Tammann 1997; Andreon 1998) or because of the variable dwarf content of clusters
(Secker & Harris 1996; Trentham 1997, 1998).
)
seems in contradiction with
various claims of a non-universal LF produced by the various morphological
composition of clusters and by the non-homology of the LFs of the morphological types
(e.g. Sandage et al. 1985; Jerjen
& Tammann 1997; Andreon 1998) or because of the variable dwarf content of clusters
(Secker & Harris 1996; Trentham 1997, 1998).
| Band | ||||||
| g | r | i | ||||
| Prob. |
Prob. |
Prob. |
||||
| R>1 vs. |
22.98/16 | 0.11 | 6.58/15 | 0.97 | 11.38/14 | 0.66 |
| BM I+I-II vs. II+II-III | 21.91/15 | 0.11 | 13.18/12 | 0.36 | 11.43/11 | 0.41 |
| BM I+I-II vs. III | 22.66/14 | 0.07 | 20.81/12 | 0.05 | 13.29/11 | 0.27 |
| BM II+II-III vs. III | 9.45/15 | 0.85 | 9.37/14 | 0.80 | 4.18/12 | 0.98 |
| Compact vs. Elongated | 20.47/14 | 0.12 | 11.78/14 | 0.62 | 14.59/13 | 0.33 |
| Compact vs. Multiple | 17.74/17 | 0.41 | 6.92/15 | 0.96 | 17.97/14 | 0.21 |
| Elongated vs. Multiple | 20.03/14 | 0.12 | 11.49/14 | 0.65 | 10.13/12 | 0.60 |
Trentham (1997), for instance, showed that the cluster LF rises steeply at
faint magnitudes (
![]() )
and thus a simple Schechter function cannot
properly describe the whole distribution.
Nevertheless, as shown in Fig. 9, for magnitudes between -22 and -17 the LF is
quite flat and in good agreement with our data.
In fact, in our magnitude range the contribution of dwarf galaxies is visible
only in the faintest bins, as suggested by the fact that in Fig. 6 the
last points lie systematically above the best-fit function. This trend (a flattening of
the distribution around M=-21 and a steepening over M=-19.5) is also confirmed
by the comparison with GMA99, whose LF shows a similar behavior.
At bright magnitudes, instead, the act of averaging over the cluster region can mask the
environmental effects.
)
and thus a simple Schechter function cannot
properly describe the whole distribution.
Nevertheless, as shown in Fig. 9, for magnitudes between -22 and -17 the LF is
quite flat and in good agreement with our data.
In fact, in our magnitude range the contribution of dwarf galaxies is visible
only in the faintest bins, as suggested by the fact that in Fig. 6 the
last points lie systematically above the best-fit function. This trend (a flattening of
the distribution around M=-21 and a steepening over M=-19.5) is also confirmed
by the comparison with GMA99, whose LF shows a similar behavior.
At bright magnitudes, instead, the act of averaging over the cluster region can mask the
environmental effects.
We must note that while in Fig. 9 the two LFs differ substantially at the bright end, our data are in very good agreement with L86 and GMA99, thus suggesting that Trentham is underestimating the contribution of bright galaxies to the LF. This can be due to various reasons, including the small area and the specific portions of the clusters sampled, or the different morphological composition of his clusters. Moreover, due to our larger number of clusters, we can sample the LF at twice the resolution in magnitude.
We compared the LFs obtained dividing our sample into rich (Abell class
R > 1) and poor (![]() )
clusters. Table 4 shows that
the LFs of these two classes are consistent within the
errors. GMA99 found instead that the slope of the LF computed in the
central regions of the clusters depends on the cluster central
density, while they found mild differences, statistically
significant, between rich and poor clusters.
Our result differs from the GMA99 finding that
the giant to dwarf ratio is higher in rich clusters than in poor ones,
but only in the statistical significance:
we find that poor clusters have a faint-end slope steeper than
rich clusters (
)
clusters. Table 4 shows that
the LFs of these two classes are consistent within the
errors. GMA99 found instead that the slope of the LF computed in the
central regions of the clusters depends on the cluster central
density, while they found mild differences, statistically
significant, between rich and poor clusters.
Our result differs from the GMA99 finding that
the giant to dwarf ratio is higher in rich clusters than in poor ones,
but only in the statistical significance:
we find that poor clusters have a faint-end slope steeper than
rich clusters (
![]() )
by
a quantity that is compatible within
)
by
a quantity that is compatible within ![]() to those
derived by GMA99 in their poor-rich comparison.
The dependence of the slope on richness is
more evident in the g band, as shown in Fig. 10.
to those
derived by GMA99 in their poor-rich comparison.
The dependence of the slope on richness is
more evident in the g band, as shown in Fig. 10.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{MS10293f13.ps} \end{figure}](/articles/aa/full/2001/07/aa10293/Timg59.gif) |
Figure 10:
The 68% and 99% confidence levels relative to the fit
of the rich (R>1, continuous line) and poor ( |
We also explored the influence of the cluster dynamical state, as indicated by the Bautz-Morgan type (Bautz & Morgan 1970), on the LF. We divided the sample in three subsamples: BM I + BM I-II, BM II + BM II-III and BM III in order to have a similar number of clusters in each group. We find that early and late BM types have LFs which are compatible within 95%, in agreement with GMA99 and Lugger (1986).
Moreover, we divided our sample into 3 morphological classes based on
visual inspection of density profiles (cf. Sect. 4.1). We classified
clusters into "compact'', showing a single strong density peak within the
1.5![]() isodensity contour above background; "elongated'' if the
cluster is irregularly spread across the field with a weak density peak, and
"multiple'' if it shows multiple peaks. Again, we find
no significant differences between the LFs of these classes of clusters.
isodensity contour above background; "elongated'' if the
cluster is irregularly spread across the field with a weak density peak, and
"multiple'' if it shows multiple peaks. Again, we find
no significant differences between the LFs of these classes of clusters.
In interpreting this result we note that when our sample is divided in subsamples
the number of objects may not be large enough for a ![]() test to reveal differences in the distribution,
as in the case of the poor-rich comparison, so that a conclusive statement
calls for a larger sample.
test to reveal differences in the distribution,
as in the case of the poor-rich comparison, so that a conclusive statement
calls for a larger sample.
As already shown in GMA99, we find that the cluster LF is compatible with the field
LF. This result does not rule out environmental influence on galaxy
formation and/or evolution, but rather indicates that either evidence for such
effects must be investigated at fainter magnitudes than those reached
by DPOSS data, or that the effect is smaller than what the data
allows us to detect.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{MS10293f14.ps} \end{figure}](/articles/aa/full/2001/07/aa10293/Timg60.gif) |
Figure 11: Comparison between our composite LF (filled dots) and the LF obtained by Andreon & Cuillandre (2000), (shaded region) |
It could be argued that our (and also most literature) LF are flatter than they should be since compact galaxies are misclassified as stars. For the most distant cluster even normal galaxies are badly classified due to the low angular resolution of the available images and/or to errors in the star/galaxy classifiers (see, for example Drinkwater et al. 1999). In our case, the comparison with the LF of the Coma cluster obtained by Andreon & Cuillandre (2000) settles this issue, because their determination is not affected from this problem since it does not use any star/galaxy classification. Figure 11 shows the good agreement between the two LFs and confirms that we are not missing any large population of compact galaxies.
Copyright ESO 2001