A&A 367, 282-296 (2001)
DOI: 10.1051/0004-6361:20000419
Helium-like triplet density diagnostics
Applications to CHANDRA-LETGS X-ray
observations of Capella and Procyon
J.-U. Ness1 -
R. Mewe2 -
J. H. M. M. Schmitt1 -
A. J. J. Raassen2,3 -
D. Porquet4 - J. S. Kaastra2 -
R. L. J. van der Meer2 -
V. Burwitz5 -
P. Predehl5
1 -
Universität Hamburg, Gojenbergsweg 112, 21029 Hamburg, Germany
2 -
Space Research Organization Netherlands (SRON),
Sorbonnelaan 2, 3584 CA Utrecht, The Netherlands
3 -
Astronomical Institute "Anton Pannekoek", Kruislaan 403,
1098 SJ Amsterdam, The Netherlands
4 -
CEA/DSM/DAPNIA, Service d'Astrophysique, CEA Saclay, 91191 Gif-sur-Yvette Cedex, France
5 -
Max-Planck-Institut für Extraterrestrische Physik (MPE), Postfach 1603,
85740 Garching, Germany
Received 18 September 2000 / Accepted 1 December 2000
Abstract
Electron density diagnostics based on the triplets of helium-like C V, N VI,
and O VII are applied to the X-ray spectra of Capella and Procyon measured with
the Low Energy Transmission Grating Spectrometer (LETGS) on board
the Chandra X-ray Observatory.
New theoretical models for the calculation of the line ratios between the
forbidden (f), intercombination (i), and the resonance (r) lines of the
helium-like triplets are used. The (logarithmic) electron densities
(in cgs units) derived from the f/i ratios for Capella are
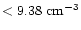 for O VII (2
for O VII (2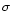 upper limit)
(
upper limit)
(
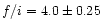 ),
),
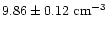 for N VI (
for N VI (
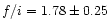 ),
and
),
and
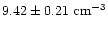 for C V (
for C V (
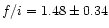 ), while for Procyon we obtain
), while for Procyon we obtain
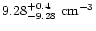 for O VII (
for O VII (
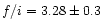 ),
),
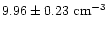 for N VI (
for N VI (
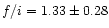 ),
and <8.92
),
and <8.92
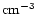 for C V (
for C V (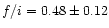 ).
These densities are quite typical of densities found
in the solar active regions, and also pressures and temperatures
in Procyon's and Capella's corona at a level of
).
These densities are quite typical of densities found
in the solar active regions, and also pressures and temperatures
in Procyon's and Capella's corona at a level of
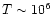 K are quite
similar. We find no evidence for densities as high
as measured in solar flares. Comparison of our Capella and Procyon
measurements with the Sun shows little difference in the physical properties
of the layers producing the C V, N VI, and O VII emission.
Assuming the X-ray emitting plasma to be confined in magnetic loops, we
obtain typical loop length scales of
K are quite
similar. We find no evidence for densities as high
as measured in solar flares. Comparison of our Capella and Procyon
measurements with the Sun shows little difference in the physical properties
of the layers producing the C V, N VI, and O VII emission.
Assuming the X-ray emitting plasma to be confined in magnetic loops, we
obtain typical loop length scales of
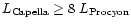 from the loop scaling laws, implying that the magnetic structures
in Procyon and Capella are quite different.
The total mean surface fluxes emitted in the helium- and
hydrogen-like ions are quite similar for Capella and Procyon, but
exceed typical solar values by one order of magnitude.
We thus conclude that Procyon's and Capella's coronal filling factors
are larger than corresponding solar values.
from the loop scaling laws, implying that the magnetic structures
in Procyon and Capella are quite different.
The total mean surface fluxes emitted in the helium- and
hydrogen-like ions are quite similar for Capella and Procyon, but
exceed typical solar values by one order of magnitude.
We thus conclude that Procyon's and Capella's coronal filling factors
are larger than corresponding solar values.
Key words: atomic data - atomic processes - techniques: spectroscopic -
stars: individual: Capella & Procyon - stars: coronae - stars: late-type - stars: activity -
X-rays: stars
The hot plasma in the corona of the Sun and of other stars is thought to be
in "coronal equilibrium''. Atomic excitations occur through collisions
with electrons. The excited atoms decay radiatively and the emitted
radiation escapes without any further interaction with the emitting plasma.
As a consequence, the emission is optically thin, and the total flux
emitted in some spectral band or in a given emission line is proportional
to the emission measure EM, defined as the integral
of the square of the plasma density n over the emitting volume elements
dV through
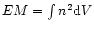 .
Thus, observationally, the contributions of
density and volume to a given observed value of EM cannot be disentangled.
.
Thus, observationally, the contributions of
density and volume to a given observed value of EM cannot be disentangled.
Stellar X-ray surveys carried out with the Einstein and ROSAT satellites
have shown an enormous range of X-ray luminosity (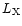 )
for stars of given spectral type (cf., Vaiana et al. 1981; Schmitt 1997).
Typically, one observes star to star variations in
)
for stars of given spectral type (cf., Vaiana et al. 1981; Schmitt 1997).
Typically, one observes star to star variations in 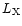 of up to four orders
of magnitude, with the largest X-ray luminosities found among the stars
with the largest rotation rates. While one definitely finds a correlation
between mean coronal temperature and X-ray luminosity
(Schmitt et al. 1985; Schmitt 1997), it is also clear that the single-most
important factor contributing to the large variations in
of up to four orders
of magnitude, with the largest X-ray luminosities found among the stars
with the largest rotation rates. While one definitely finds a correlation
between mean coronal temperature and X-ray luminosity
(Schmitt et al. 1985; Schmitt 1997), it is also clear that the single-most
important factor contributing to the large variations in 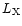 is the
variation in emission measure. The conclusion therefore is that active stars
(can) have a couple of orders of magnitude higher coronal emission measure,
while maintaining the same optical output as low-activity stars like our Sun.
is the
variation in emission measure. The conclusion therefore is that active stars
(can) have a couple of orders of magnitude higher coronal emission measure,
while maintaining the same optical output as low-activity stars like our Sun.
The emission measure is directly linked to the structure of stellar coronae,
if we assume, going along with the solar analogy, that the X-ray emitting
plasma of a stellar corona is confined in magnetic loops.
The observed values of EM and 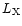 for a given star could
be accounted for either by the existence of
more loops than typically visible on the solar surface, by higher density
loops or by longer, more voluminous loops. Thus the question is reduced to the
following: if
for a given star could
be accounted for either by the existence of
more loops than typically visible on the solar surface, by higher density
loops or by longer, more voluminous loops. Thus the question is reduced to the
following: if
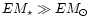 for an active
star, one wants to know whether this is due to
for an active
star, one wants to know whether this is due to
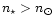 or
or
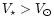 or both.
or both.
Spatially resolved solar observations allow to disentangle density and volume
contributions to the overall emission measure.
One finds the total X-ray output of the Sun dominated - at least under maximum
conditions - by the emission from rather small, dense loops.
Stellar coronae always appear as point sources. The only way to infer
structural information in these unresolved point sources has been via
eclipse studies in suitably chosen systems where one tries
to constrain the emitting plasma volume from the observed light curve.
Another method to infer structure in spatially unresolved data
are spectroscopic measurements of density.
The emissivity
of plasma in coronal equilibrium in carefully selected lines does depend
on density.
Some lines may be present in low-density plasmas and
disappear in high-density plasmas such as the forbidden lines
in He-like triplets, while other lines may appear in high-density
plasmas and be absent in low-density plasmas (such as lines formed following
excitations from excited levels).
With the high-resolution spectroscopic facilities onboard Chandra it is
possible to carry out such studies for a wide range of X-ray sources.
The purpose of this paper is to present and discuss some key density
diagnostics
available in the high-resolution grating spectra obtained with
Chandra. We will specifically discuss the spectra obtained
with the Low Energy Transmission Grating Spectrometer (LETGS)
for the stars Capella and Procyon.
Table 1:
Properties of Procyon and Capella:
mass M, radius R, effective temperature
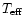 ,
log g and
the limb darkening coefficient
,
log g and
the limb darkening coefficient 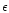
| |
Procyon |
Capella |
| d/pc |
3.5 |
13 |
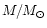 |
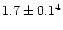 |
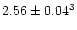 |
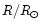 |
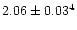 |
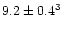 |
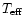 /K /K |
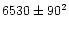 |
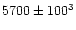 |
| log g |
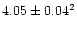 |
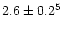 |
| Spectr. type |
F5 IV-V |
Ab: G1 III |
| |
|
(Aa: G8/K0 III) |
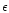 |
0.7241 |
0.831 |
| References: | |
|
1 Díaz-Cordovés et al. (1995). | |
|
2 Fughrman et al. (1997). | |
|
3 Hummel et al. (1994). | |
|
4 Irwin et al. (1992). | |
|
5 Kelch et al. (1978). | |
|
|
Both Capella and Procyon are known to be relative steady and strong X-ray
sources; no signatures of flares from these stars
have ever been reported in the literature.
Both Capella and Procyon are rather close to the Sun at distances
of 13 pc and 3.5 pc (Table 1),
so that effects of interstellar absorption are very
small. Both of them have been observed with virtually all
X-ray satellites flown so far. Capella was first detected
as an X-ray source by Catura et al. (1975), and confirmed by Mewe et al. (1975), Procyon by Schmitt et al. (1985).
The best coronal spectra of Capella were obtained with the
Einstein Observatory FPCS and OGS (Vedder et al. 1983; Mewe et al. 1982), the
EXOSAT transmission grating (Mewe et al. 1986; Lemen et al. 1989) and EUVE
(Dupree et al. 1993; Schrijver et al. 1995),
while high-spectral resolution spectral
data for Procyon have been presented by Mewe et al. (1986) and Lemen et al. (1989) using EXOSAT
transmission grating data and Drake et al. (1995) and Schrijver et al. (1995) using EUVE data. Note that
Schmitt et al. (1996b) and Schrijver et al. (1995) investigated the coronal density of Procyon using
a variety of density sensitive lines from Fe X to Fe XIV in the EUV range
and found Procyon's coronal density consistent with that of solar active
region densities.
The plan of our paper is as follows: We first briefly review the atomic
physics of He-like ions as applicable to solar (and our stellar)
X-ray spectra. We briefly describe the spectrometer used to obtain
our data, and discuss in quite some detail the specific procedures
used in the data analysis, since we plan to use these methods in all
our subsequent work on Chandra and XMM-Newton spectra. We then proceed
to analyze the extracted spectra and describe in detail how we dealt
with the special problem of line blending with higher dispersion orders. Before
presenting our results we estimate the formation temperatures of the lines, the
influence of the stellar radiation field and the influence of optical depth
effects followed by detailed interpretation. The results
will then be compared to measurements of the Sun and we
close with our conclusions.
The theory of the atomic physics of helium-like triplets has been
extensively described in the literature
(Gabriel & Jordan 1969; Blumenthal et al. 1972; Mewe & Schrijver 1978; Pradhan et al. 1981; Pradhan & Shull 1981; Pradhan1982; Pradhan 1985, and recently Porquet & Dubau 2000; Mewe et al. 2000a).
Basically, the excited states (1s2l) split up into the terms 2 1P,
2 3P, 2 1S, and 2 3S, out of which the levels with  decay to the
ground state 1 1S through the
resonance line (abbreviated by r), the intercombination line
(i) and the forbidden line (f), respectively; the latter two lines
involve spin changes and therefore violate the selection
rules for electric dipole radiation.
Although the radiative transition rate for the forbidden line
is quite small, in a low-density plasma collisional
depopulation processes are so rare, that
the excited 2 3S state does
decay radiatively. In a high-density plasma collisional deexcitations
dominate and hence the forbidden line disappears.
Complications arise from other competing processes populating and depopulating
the 3P and 3S levels. These are in particular radiative transitions
induced by the underlying photospheric stellar radiation field (discussed in
Sect. 5.2) as well as ionization and recombination processes from
the Li-like and H-like ions.
decay to the
ground state 1 1S through the
resonance line (abbreviated by r), the intercombination line
(i) and the forbidden line (f), respectively; the latter two lines
involve spin changes and therefore violate the selection
rules for electric dipole radiation.
Although the radiative transition rate for the forbidden line
is quite small, in a low-density plasma collisional
depopulation processes are so rare, that
the excited 2 3S state does
decay radiatively. In a high-density plasma collisional deexcitations
dominate and hence the forbidden line disappears.
Complications arise from other competing processes populating and depopulating
the 3P and 3S levels. These are in particular radiative transitions
induced by the underlying photospheric stellar radiation field (discussed in
Sect. 5.2) as well as ionization and recombination processes from
the Li-like and H-like ions.
It is customary to describe the measured line intensities r, i and f in
terms of the ratios
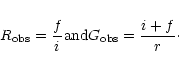 |
(1) |
In this paper we use the notation used in e.g. Pradhan & Shull (1981). In other
contexts (e.g. calculating ions of higher ionization stages) another notation
labeling r as w, f
as z and i as x+yis often used pointing out that the intercombination
line separates via M2 and E1 transitions into two components.
Theory describes the density sensitivity of the R ratio by the functional
dependence
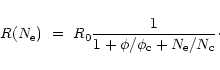 |
(2) |
Densities are inferred from equating
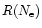 with
with
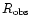 .
For convenience, we follow here the expressions as given by (1972).
The low-density limit
.
For convenience, we follow here the expressions as given by (1972).
The low-density limit 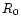 ,
which applies for
,
which applies for
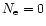 and
and
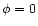 ,
is given by
,
is given by
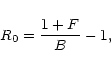 |
(3) |
with the radiative branching parameter B averaged over the two
components of the intercombination line.
The parameter 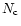 ,
the so-called critical density (cf.,
Table 2), above which the observed line ratio is density-sensitive,
is given by
,
the so-called critical density (cf.,
Table 2), above which the observed line ratio is density-sensitive,
is given by
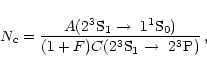 |
(4) |
where
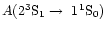 is the radiative transition probability of the forbidden line,
is the radiative transition probability of the forbidden line,
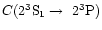 is the electron collisional rate coefficient
for the transition from
is the electron collisional rate coefficient
for the transition from
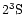 to
to
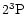 ,
and F is the ratio of the collision rates from the
ground to the levels
,
and F is the ratio of the collision rates from the
ground to the levels
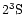 and
and
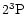 ,
respectively
(including cascade effects from upper levels through radiative transitions
after excitation or recombination).
Finally, the parameters
,
respectively
(including cascade effects from upper levels through radiative transitions
after excitation or recombination).
Finally, the parameters 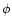 (the radiative absorption rate from
(the radiative absorption rate from
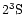 to
2 3P induced by an external
radiation field) and
to
2 3P induced by an external
radiation field) and
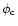 describe the additional
possible influence of the stellar radiation field on the depopulation of the
3S state (cf., Sect. 5.2). The latter is insignificant
especially for the He-like triplets of higher ionization stages than C V.
Values for
describe the additional
possible influence of the stellar radiation field on the depopulation of the
3S state (cf., Sect. 5.2). The latter is insignificant
especially for the He-like triplets of higher ionization stages than C V.
Values for 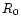 and
and 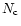 used in this paper are listed in
Table 2.
Obviously, for very large densities or large radiation fields the forbidden
line and hence R disappears. The ratio
used in this paper are listed in
Table 2.
Obviously, for very large densities or large radiation fields the forbidden
line and hence R disappears. The ratio
a measure of the relative strength
of the resonance line, depends on the electron temperature, 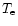 (e.g., Mewe et al. 2000a).
G can be used to derive temperatures for the lines used for
density diagnostics that can be compared to the maximum formation temperature
(e.g., Mewe et al. 2000a).
G can be used to derive temperatures for the lines used for
density diagnostics that can be compared to the maximum formation temperature
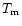 .
.
The Low Energy Transmission Grating Spectrometer (LETGS) on board the Chandra Observatory
is a diffraction grating spectrometer covering the wavelength range between
2-175 Å (0.07-6 keV). 540 individual grating elements are mounted
onto a toroidal ring structure. Each of the elements consists of a
freestanding
gold grating with 1 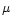 m grating period. The fine gold wires are held by two
different support structures, a linear grid with 25.4
m grating period. The fine gold wires are held by two
different support structures, a linear grid with 25.4 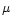 m and a coarse
triangular mesh
with 2 mm spacing. The whole grating ring can be inserted into the convergent
beam just behind the High Resolution Mirror Assembly (HRMA) thereby dispersing
the light of any X-ray source in the field of view into its spectrum.
The efficiency of the grating
spectrometer is of the order of 10% on average but is enhanced by a
factor of two around 2 keV due to partial transparency effects;
a more detailed description of the instrument is presented by Predehl et al. (1997).
Both sides of the spectrum are recorded with a microchannel plate detector
(HRCS), placed behind the transmission grating. In contrast to CCD based
detectors, the HRCS detector provides essentially no intrinsic energy
resolution, the energy information for individually recorded events is
solely contained in the events' spatial location.
m and a coarse
triangular mesh
with 2 mm spacing. The whole grating ring can be inserted into the convergent
beam just behind the High Resolution Mirror Assembly (HRMA) thereby dispersing
the light of any X-ray source in the field of view into its spectrum.
The efficiency of the grating
spectrometer is of the order of 10% on average but is enhanced by a
factor of two around 2 keV due to partial transparency effects;
a more detailed description of the instrument is presented by Predehl et al. (1997).
Both sides of the spectrum are recorded with a microchannel plate detector
(HRCS), placed behind the transmission grating. In contrast to CCD based
detectors, the HRCS detector provides essentially no intrinsic energy
resolution, the energy information for individually recorded events is
solely contained in the events' spatial location.
Table 3:
List of the data sets with start and stop times and durations used in this paper
| Obs. |
time |
Observation date [UT] |
| ID. |
[ksec] |
start |
end |
| Capella |
|
|
| 62435 |
22.34 |
09-06-1999 00:35:40 |
09-06-1999 06:48:01 |
| 01167 |
15.36 |
09-09-1999 13:10:06 |
09-09-1999 17:26:08 |
| 01244 |
12.37 |
09-09-1999 17:42:27 |
09-09-1999 21:08:36 |
| 62410 |
11.33 |
09-09-1999 23:43:57 |
09-10-1999 02:52:48 |
| 01246 |
15.00 |
09-10-1999 03:06:06 |
09-10-1999 07:16:08 |
| 62422 |
11.68 |
09-12-1999 18:26:42 |
09-12-1999 21:41:20 |
| 62423 |
14.80 |
09-12-1999 23:37:44 |
09-13-1999 03:44:28 |
| 01420 |
30.30 |
10-29-1999 22:49:29 |
10-30-1999 07:14:27 |
| 01248 |
85.36 |
11-09-1999 13:42:24 |
11-10-1999 13:25:05 |
| total: |
218.54 |
|
|
| Procyon |
|
|
| 00063 |
70.39 |
11-06-1999 21:24:31 |
11-07-1999 16:57:38 |
| 01461 |
70.36 |
11-07-1999 17:04:55 |
11-08-1999 12:37:39 |
| total: |
140.75 |
|
|
The data described and analyzed in this paper were gathered during the
calibration phase of the Chandra LETGS.
Part of the data has already been presented by Brinkman et al. (2000).
The individual observation intervals used in our analysis are listed in
Table 3. As is clear
from Table 3, the observations extend over two days for
Procyon and over two months for Capella.
Our analysis refers to the mean properties of Procyon and Capella; the subject
of possible time variations is not subject of this paper.
The total on source integration times are 218.54 ksec for Capella and
140.75 ksec for Procyon.
Since the sources are among the strongest coronal X-ray sources
(cf., Hünsch et al. 1998a,b), it is also evident that these spectra
belong to the highest quality coronal X-ray spectra
reasonably obtainable with the Chandra LETGS.
All the HRCS datasets analyzed in this paper (see Table 3)
were processed using the standard pipeline processing.
The incoming X-rays are diffracted by the grating, dispersing the
different energy photons to different detector positions
along the dispersion direction.
Therefore the spectral information obtained with the LETGS has to be
extracted spatially.
The pulse heights with which the HRC detector records registered
events contains some very modest energy information, which was,
however, not used.
At each wavelength, the photons have to be integrated in cross-dispersion direction.
Because of the spectrograph's astigmatism, the width of the spectral
trace in cross-dispersion direction is wavelength dependent.
For wavelengths below 75 Å we choose a 3.6
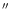 wide extraction
box around the spectral trace which includes almost all of the source signal while
keeping the background level low. For wavelengths greater than 75 Å the extraction box widens in cross dispersion direction to 8.4
wide extraction
box around the spectral trace which includes almost all of the source signal while
keeping the background level low. For wavelengths greater than 75 Å the extraction box widens in cross dispersion direction to 8.4
 at
175 Å. In addition the photons in four background regions of identical shape
to that of the object extraction region where selected. These regions are
displaced 12
at
175 Å. In addition the photons in four background regions of identical shape
to that of the object extraction region where selected. These regions are
displaced 12
 and 24
and 24
 above and below the source extraction box
in order to check for any spatial variation of the background in
cross-dispersion direction.
above and below the source extraction box
in order to check for any spatial variation of the background in
cross-dispersion direction.
![\begin{figure}
\par\includegraphics[width=6cm,clip]{MS10283f1.eps}
\end{figure}](/articles/aa/full/2001/07/aa10283/Timg60.gif) |
Figure 1:
Comparison of fit results from left side (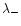 )
and right side ( )
and right side (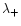 )
of the spectrum )
of the spectrum |
| Open with DEXTER |
For the purpose of verifying the symmetry of the dispersed spectra,
we determined
empirical wavelengths of ten strong emission lines recorded on both sides
of the middle detector plate (i.e.
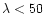 Å). For the example of
Capella we plot the wavelength difference
Å). For the example of
Capella we plot the wavelength difference
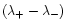 against the mean wavelength
against the mean wavelength
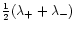 in Fig. 1. As can be seen from Fig. 1,
the wavelength values obtained from the right and left side agree to within
less than the instrumental resolution of
in Fig. 1. As can be seen from Fig. 1,
the wavelength values obtained from the right and left side agree to within
less than the instrumental resolution of  0.06 Å (cf.
0.06 Å (cf. 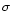 -values in Table 4) Both spectra can thus
be added for the analysis in order to increase the SNR of the data.
In the following we will always consider co-added spectra.
-values in Table 4) Both spectra can thus
be added for the analysis in order to increase the SNR of the data.
In the following we will always consider co-added spectra.
4.4 Method of analysis
4.4.1 Treatment of background
Before determining the flux of any emission line, the spectral
background must be modeled.
This background consists of essentially two components: instrumental
background and source background, which may consist of continuum radiation
and weak lines.
The instrumental background is also present on those parts of the microchannel
plate not illuminated by X-rays from the target source.
We checked for any variation of the instrumental background perpendicular
to the dispersion direction and found none. We then
modeled this instrumental background bg along the dispersion
direction by a low-order polynomial and
found acceptable fits for almost the whole spectrum.
A far more difficult task is the determination of a reliable source
background sbg. The source background is by definition present only
on the extracted spectral trace; it is formed by continuum radiation from
the source, and possibly by weak, unrecognized spectral lines and/or higher
order contamination.
For the determination of the fluxes of individual emission lines, the source
background is required only in the vicinity of the line(s) under consideration
and is approximated by a single number. Our numerical procedures
can, however, scope with arbitrary source background models.
In order to estimate this source background, we adopted the following
procedure. We first subtracted the instrumental background from the spectral
trace on the source, and calculated the median of the thus obtained count values
for all bins within the investigated (small) part of the spectrum.
The median is a statistically robust estimate of the background (which we
assume to be flat over the considered part of the
spectrum) as long as more than 50% of
all bins belong to the source background, i.e. the spectrum contains not too
many lines.
For each bin i we thus obtain a background value of sbg+bgiin the studied wavelength range.
The emission line spectra are fitted with a maximum likelihood technique
similar to that used by Schmitt et al. (1996a) for their EUVE spectra.
The spectrum is assumed to consist of the background b and of M discrete
emission lines. The treatment of the background b is described in
Sect. 4.4.1.
Each line j is assumed to be represented by a normalized profile
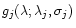 ,
e.g. a Gaussian profile
,
e.g. a Gaussian profile
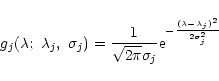 |
(6) |
with the dispersion
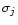 and the central wavelength
and the central wavelength 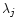 .
The assumption
of a Gaussian line profile is of course arbitrary. Strong isolated
emission lines (like O VIII
Ly
.
The assumption
of a Gaussian line profile is of course arbitrary. Strong isolated
emission lines (like O VIII
Ly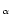 )
can be fitted quite well with such a model,
and other analytical models can easily be incorporated into our
scheme.
Let the observed spectrum be given on a grid of N bins with wavelength
values
)
can be fitted quite well with such a model,
and other analytical models can easily be incorporated into our
scheme.
Let the observed spectrum be given on a grid of N bins with wavelength
values
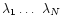 .
The number of expected
counts ci in the
.
The number of expected
counts ci in the 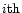 bin can then be calculated as
bin can then be calculated as
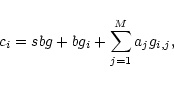 |
(7) |
where aj is the total number of counts of line j and gi,j is the
value of the profile function for line j in bin i.
In order to compare the modeled
spectrum ci with a measured spectrum ni, we assume ni to be a
Poisson realization of ci. The total probability of the observations
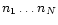 is then given by
is then given by
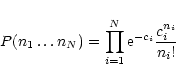 |
(8) |
and the likelihood function
 is defined as
is defined as
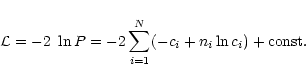 |
(9) |
The best-fit values of the parameters
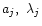 and
and 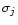 (j=1 ... N) are
determined by finding extremal values of
(j=1 ... N) are
determined by finding extremal values of 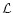 through:
through:
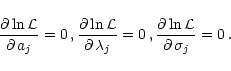 |
(10) |
The physical meaning of the fit parameters aj, 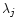 and
and 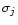 is quite different.
is quite different. 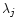 and
and 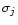 are in principle
fixed by the wavelengths of the considered lines and the instrumental
resolution, complications arise from possible wavelength calibration errors
and line blends. On the other hand, the amplitudes aj, proportional
to the line flux, are the genuine interesting parameters. Analysis of
the likelihood equations shows that
for the amplitude aj a fixed point equation can be derived for each
line j with
are in principle
fixed by the wavelengths of the considered lines and the instrumental
resolution, complications arise from possible wavelength calibration errors
and line blends. On the other hand, the amplitudes aj, proportional
to the line flux, are the genuine interesting parameters. Analysis of
the likelihood equations shows that
for the amplitude aj a fixed point equation can be derived for each
line j with 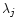 and
and 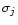 assumed to be given:
assumed to be given:
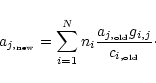 |
(11) |
Equation (11) can be efficiently solved by iteration.
In order to find optimum values for the wavelengths
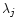 and line-widths
and line-widths 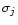 ,
we seek minimal values of
,
we seek minimal values of
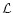 by ordinary minimization procedures. In this process
the wavelengths
by ordinary minimization procedures. In this process
the wavelengths 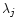 can vary either freely, or - if the wavelengths
of the lines to be fitted are all known - the wavelength differences between
the individual lines in a multiplet can be kept fixed in order to
account for possible shifts of the overall wavelength scale.
Similarly, the line widths
can vary either freely, or - if the wavelengths
of the lines to be fitted are all known - the wavelength differences between
the individual lines in a multiplet can be kept fixed in order to
account for possible shifts of the overall wavelength scale.
Similarly, the line widths 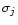 can either vary freely or be fixed,
and in such a way blended lines can be described.
In this fashion
an optimal value for
can either vary freely or be fixed,
and in such a way blended lines can be described.
In this fashion
an optimal value for 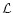 is obtained, and the parameters
aj,
is obtained, and the parameters
aj,
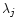 (if fitted) and
(if fitted) and 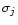 (if fitted) represent our
best fit measurements of these values.
(if fitted) represent our
best fit measurements of these values.
Measurement errors are determined by assuming the likelihood
curve
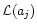 to be parabolic and finding the value of
to be parabolic and finding the value of
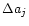 where
where
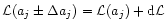 resulting in
resulting in
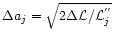 with
with
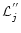 being the second derivative of
being the second derivative of 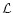 with respect to aj known from
Eqs. (9) and (7).
We choose
with respect to aj known from
Eqs. (9) and (7).
We choose
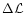 =1 which yields formal
=1 which yields formal 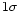 errors.
errors.
Similarly the errors for 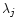 and
and 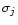 are calculated. We
determine the errors in d
are calculated. We
determine the errors in d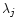 and d
and d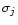 numerically from
numerically from
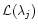 and
and
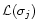 ,
respectively with
,
respectively with
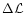 =1, i.e. errors being given within 68.3%.
Thus formally we treat all other parameters as "uninteresting''.
=1, i.e. errors being given within 68.3%.
Thus formally we treat all other parameters as "uninteresting''.
![\begin{figure}
\par\includegraphics[width=12.4cm,clip]{MS10283f2a.eps}\par\inclu...
...0283f2b.eps}\par\includegraphics[width=12.4cm,clip]{MS10283f2c.eps} \end{figure}](/articles/aa/full/2001/07/aa10283/Timg90.gif) |
Figure 2:
Spectrum (line-dotted) and fitted (solid) curve for the O VII, N VI,
and C V triplet for Procyon. The dotted line represents the total background.
The binsize is 0.02 Å for O VII and 0.03 Å for C V and N VI |
| Open with DEXTER |
With the procedure described in Sect. 4.4 we analyzed the spectra of
the He-like
triplets of O VII, N VI, and C V for the two stars Capella and Procyon.
In Figs. 2 and 3 the measured spectra are
plotted with bold line-dotted lines and the best-fit model curve is indicated
by a thin solid line.
The total background, i.e. the instrumental background and the assumed
source continuum background, is shown with a dotted line.
The derived best-fit parameters are given in Table 4,
where we list, for both Capella and Procyon, the derived
empirical wavelengths, the line widths and the line strengths (in counts).
For reference purposes we also list the source background values used.
Extrapolating the instrumental background onto the spectral trace shows
that Procyon's source background must be quite small as expected for a
low coronal temperature X-ray source. It will therefore be neglected for the
purpose of line flux modeling. In Table 4 we also list the ratios
between forbidden and intercombination line, and that of the
sum of intercombination and forbidden line to the resonance line, which
are needed for subsequent analysis. Since no significant
rotational or orbital line broadening is expected given the even high spectral
resolution of our Chandra data, the line-width 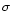 was kept fixed
for all models assuming that this value described the instrumental resolution.
Starting values for the wavelengths were taken from Mewe et al. (1985).
was kept fixed
for all models assuming that this value described the instrumental resolution.
Starting values for the wavelengths were taken from Mewe et al. (1985).
![\begin{figure}
\par\includegraphics[width=12.4cm,clip]{MS10283f3a.eps}\par\inclu...
...10283f3b.eps}\par\includegraphics[width=12.4cm,clip]{MS10283f3c.eps}\end{figure}](/articles/aa/full/2001/07/aa10283/Timg91.gif) |
Figure 3:
Spectrum (line-dotted) and fitted (solid) curve for the O VII, N VI,
and C V triplet for Capella. The dotted line represents the total background.
The binsize is 0.02 Å for O VII and 0.03 Å for C V and N VI |
| Open with DEXTER |
The O VII triplet has the best signal to noise ratio in both stars and is
unaffected by any significant contamination from higher orders
as can be seen from
Figs. 2 and 3 in the top panel.
As far as the N VI triplet is concerned, it
is not as isolated as the O VII triplet and requires further
analysis. In both Procyon (Fig. 2) and Capella
(Fig. 3) additional lines appear.
At 28.44 Å a line attributed to C VI is evident for both Capella and
Procyon. In order to minimize any possible
cross talk, this line was included in the fit.
The line at 30 Å seen in the Capella spectrum
is interpreted as the second order of the strong Fe XVII line at 15.013 Å;
Fe XVII is strong in Capella, but essentially absent in Procyon.
A somewhat strange feature can be seen only in the N VI
spectrum of Procyon at about
29.3 Å. This is not a line but an instrumental effect which is present
only on the negative side of the spectrum.
Contamination with higher order lines makes the
analysis of the C V triplet for Capella particularly difficult (cf.,
Fig. 3). This is clear since the Capella spectrum contains
strong emission in the band between 13-14 Å, which appears in third
order in the 39-42 Å band under consideration for the C V triplet.
Specifically, the interfering lines are Ne IX (13.44 Å 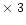 = 40.32 Å), Fe XIX (13.52 Å
= 40.32 Å), Fe XIX (13.52 Å 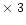 = 40.56 Å), Ne IX (13.7 Å
= 40.56 Å), Ne IX (13.7 Å 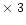 = 41.1 Å), Fe XIX (13.795 Å
= 41.1 Å), Fe XIX (13.795 Å 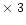 = 41.385 Å)
and Fe XVII (13.824 Å
= 41.385 Å)
and Fe XVII (13.824 Å 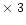 = 41.472 Å). We modeled the
contamination from these five lines by first determining their
first order contributions, transforming the fit results to third order.
In the transformation the first order intensities are reduced by a factor
of 14.1. This reduction factor is obtained by comparison of first and third
order of the isolated 15.013 Å line (Fe XVII). Since the contaminating
photons are rather energetic, we expect essentially the same reduction factor
in the range 13-14 Å. The first order fit result is plotted in
Fig. 4 and the resulting fit values are listed in
Table 5. Technically
the higher order contamination was treated as an additional nonconstant
contribution to the instrumental background. In addition to the
C V triplet, another line, Si XII at 40.91 Å, appearing strong in
Capella but weaker in Procyon, had to be modeled.
The source background was estimated by requiring the lowest count bins to
be adequately modeled. The median function could not
be applied since there are too many lines in the considered wavelength range.
The result of this
modeling exercise is shown in Fig. 3 in the bottom panel,
where the dotted line, representing the background, is not constant,
but heavily influenced by higher order lines. We emphasise that
the errors listed in Table 4 do not include errors from the fits
in the 13 Å band. We point out in particular
that the forbidden C V line lies on top of the third order Fe XVII
13.824 Å line, so that any derivation of the forbidden line flux
does require an appropriate modeling of the third order contamination. This
is especially difficult because the Fe XVII 13.824 Å line is blended
with the Fe XIX 13.795 Å line in first order, while
in third order this blend is resolved.
= 41.472 Å). We modeled the
contamination from these five lines by first determining their
first order contributions, transforming the fit results to third order.
In the transformation the first order intensities are reduced by a factor
of 14.1. This reduction factor is obtained by comparison of first and third
order of the isolated 15.013 Å line (Fe XVII). Since the contaminating
photons are rather energetic, we expect essentially the same reduction factor
in the range 13-14 Å. The first order fit result is plotted in
Fig. 4 and the resulting fit values are listed in
Table 5. Technically
the higher order contamination was treated as an additional nonconstant
contribution to the instrumental background. In addition to the
C V triplet, another line, Si XII at 40.91 Å, appearing strong in
Capella but weaker in Procyon, had to be modeled.
The source background was estimated by requiring the lowest count bins to
be adequately modeled. The median function could not
be applied since there are too many lines in the considered wavelength range.
The result of this
modeling exercise is shown in Fig. 3 in the bottom panel,
where the dotted line, representing the background, is not constant,
but heavily influenced by higher order lines. We emphasise that
the errors listed in Table 4 do not include errors from the fits
in the 13 Å band. We point out in particular
that the forbidden C V line lies on top of the third order Fe XVII
13.824 Å line, so that any derivation of the forbidden line flux
does require an appropriate modeling of the third order contamination. This
is especially difficult because the Fe XVII 13.824 Å line is blended
with the Fe XIX 13.795 Å line in first order, while
in third order this blend is resolved.
The strong emission in the 13 Å regime is mostly due to iron in
excitation stages Fe XVII and Fe XIX.
Since there is no significant emission from iron in these high excitation stages
in the spectrum of Procyon, there is no blending with
third order lines in this case. From Fig. 2 it can be seen
that the modeling is straightforward for Procyon.
![\begin{figure}
\par\includegraphics[width=12.4cm,clip]{MS10283f4.eps}\end{figure}](/articles/aa/full/2001/07/aa10283/Timg120.gif) |
Figure 4:
First order spectrum responsible for third order contamination
of the C V triplet of Capella; shown are the data (dash-dotted histogram) as well as the best fit (solid line). Note that the feature near 13.8 Å is actually
a line blend (consisting of Fe XIX and Fe XVII contributions) resolved in third order |
| Open with DEXTER |
Inspection of our Chandra spectra of Capella and Procyon shows the O VII
and N VI forbidden lines to be present in both cases. The C V forbidden line
is very weak but present for Procyon, it is also present in Capella despite
being significantly contaminated by third order radiation. The observed
f/i-ratios for O VII are very close to the expected low-density limit 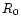 for both Procyon and Capella, while the measured f/i-ratios for N VI and
C V are definitely below the respective values of
for both Procyon and Capella, while the measured f/i-ratios for N VI and
C V are definitely below the respective values of 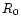 in both cases.
Before giving a quantitative interpretation of the observed line ratios we must
first consider the formation temperature of the studied He-like lines.
Especially for the C V triplet the stellar radiation field can contribute
significantly to the depopulation of the atomic level from which the forbidden
line originates. Low forbidden line intensities can thus also indicate
large radiation fields and not necessarily high densities.
in both cases.
Before giving a quantitative interpretation of the observed line ratios we must
first consider the formation temperature of the studied He-like lines.
Especially for the C V triplet the stellar radiation field can contribute
significantly to the depopulation of the atomic level from which the forbidden
line originates. Low forbidden line intensities can thus also indicate
large radiation fields and not necessarily high densities.
For the purpose of density diagnostics it is customary to assume
that all of the emission is produced at a single temperature 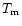 (cf., Table 2), which corresponds
to the peak of the contribution function of the considered line, the so-called
formation temperature. It should
be kept in mind, however, that He-like ions are present over a relatively
broad temperature range, and therefore this assumption might be poor
if steep emission measure gradients are present. The measured value of
G is also a temperature diagnostics, although optical depth effects in the
resonance line may contribute (cf., Acton 1978);
the relevance of optical depth effects to our results is analyzed in
Sect. 5.4.
In Table 6 we show the temperatures T(G) determined from converting
the observed
(cf., Table 2), which corresponds
to the peak of the contribution function of the considered line, the so-called
formation temperature. It should
be kept in mind, however, that He-like ions are present over a relatively
broad temperature range, and therefore this assumption might be poor
if steep emission measure gradients are present. The measured value of
G is also a temperature diagnostics, although optical depth effects in the
resonance line may contribute (cf., Acton 1978);
the relevance of optical depth effects to our results is analyzed in
Sect. 5.4.
In Table 6 we show the temperatures T(G) determined from converting
the observed
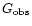 values into temperatures according to Mewe et al. (2000a)
using an electron density of
values into temperatures according to Mewe et al. (2000a)
using an electron density of
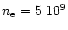 cm-3.
We also determined temperatures by studying the line ratio between the observed
Ly
cm-3.
We also determined temperatures by studying the line ratio between the observed
Ly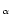 lines of O VIII, N VII, and C VI and the r-lines of O VII, N VI, and C V
respectively by assuming isothermal plasma emission. We assume plasma
emissivities as calculated in the codes MEKAL (Mewe et al. 1985; Mewe et al. 1995)
and SPEX (Kaastra et al. 1996). The thus obtained fluxes are multiplied with
effective areas (cf., Table 7) before comparison with the measured
ratios. The results are listed in Table 6 as T(H-He).
lines of O VIII, N VII, and C VI and the r-lines of O VII, N VI, and C V
respectively by assuming isothermal plasma emission. We assume plasma
emissivities as calculated in the codes MEKAL (Mewe et al. 1985; Mewe et al. 1995)
and SPEX (Kaastra et al. 1996). The thus obtained fluxes are multiplied with
effective areas (cf., Table 7) before comparison with the measured
ratios. The results are listed in Table 6 as T(H-He).
As can be seen from Table 6, the temperatures T(G) and
T(H-He) do not agree. This is not surprising given the fact that we are
likely dealing with a temperature distribution. For Procyon the
temperatures T(H-He) agree quite well with 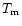 ,
while
T(G) agrees with
,
while
T(G) agrees with 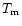 only for N VI. For Capella the respective
temperatures T(H-He) always exceed those found for Procyon, while
the T(G) temperature derived from N VI is below that found for Procyon.
We tentatively conclude that the observed N VI and O VII
emission in Capella has significant contributions from plasma at
temperatures away from the peak in the line emissivity curve, while for
Procyon the emission appears to come from rather close to the
line emissivity peak.
only for N VI. For Capella the respective
temperatures T(H-He) always exceed those found for Procyon, while
the T(G) temperature derived from N VI is below that found for Procyon.
We tentatively conclude that the observed N VI and O VII
emission in Capella has significant contributions from plasma at
temperatures away from the peak in the line emissivity curve, while for
Procyon the emission appears to come from rather close to the
line emissivity peak.
5.2 Influence of the stellar radiation field
The observed C V line ratios are particularly interesting. While
the observed value for Capella agrees well with the solar observations
(cf., Austin et al. 1966; Freeman & Jones 1970), the observed value for Procyon is
rather small. The important point to keep in mind in this context
is that Procyon
and Capella are stars with different properties compared to the Sun. Procyon
is of spectral type F5V-IV (cf., Table 1) with an effective
temperature of 6500 K, Capella is a spectroscopic binary,
the components of which are of spectral type G1 and G8; occasionally
the brighter component is also classified as F9.
Strictly speaking, what really
matters is the effective temperature of the radiation field at the
wavelength corresponding
to the energy difference between forbidden and intercombination line
levels, i.e., 2272 Å for C V (cf., Table 8) for the
transition 2
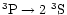 .
We investigated the stellar
surface radiation fluxes from measurements obtained with the International
Ultraviolet Explorer satellite (IUE). We first determined continuum
fluxes from archival IUE data, and converted these fluxes into
intensities using the expression
.
We investigated the stellar
surface radiation fluxes from measurements obtained with the International
Ultraviolet Explorer satellite (IUE). We first determined continuum
fluxes from archival IUE data, and converted these fluxes into
intensities using the expression
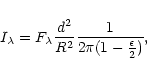 |
(12) |
where 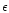 is the (linear) limb darkening coefficient.
It is determined
from (1995) using log g and
is the (linear) limb darkening coefficient.
It is determined
from (1995) using log g and
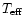 listed in
Table 1; d and R are distance and radius of the sample
stars as listed in Table 1.
For the case of the binary system Capella we assumed the worst case and
attributed all emission to the Ab component, i.e., the star with the higher
radiation temperature. The other component Aa (G8/K0 III) is about equally
bright in the corona as G1 III (cf., Linsky et al. 1998),
but much weaker in the chromosphere and transition region.
From the thus obtained value for the intensity a radiation temperature
listed in
Table 1; d and R are distance and radius of the sample
stars as listed in Table 1.
For the case of the binary system Capella we assumed the worst case and
attributed all emission to the Ab component, i.e., the star with the higher
radiation temperature. The other component Aa (G8/K0 III) is about equally
bright in the corona as G1 III (cf., Linsky et al. 1998),
but much weaker in the chromosphere and transition region.
From the thus obtained value for the intensity a radiation temperature
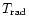 can be inferred from the appropriate Planck curve, expressed as
can be inferred from the appropriate Planck curve, expressed as
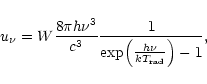 |
(13) |
where W is the dilution factor of the radiation field (we take
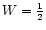 close to the stellar
surface).
The results derived from these data are listed in Table 8.
close to the stellar
surface).
The results derived from these data are listed in Table 8.
In order to compute the dependence of
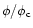 ,
required
in Eq. (2), on
,
required
in Eq. (2), on
 we use the
calculations by Blumenthal et al. (1972), who derive the expression
we use the
calculations by Blumenthal et al. (1972), who derive the expression
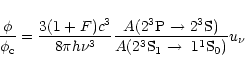 |
(14) |
with
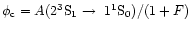 ,
transition
probabilities
,
transition
probabilities
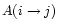 ,
and
,
and 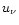 the spectral energy density
at the appropriate
the spectral energy density
at the appropriate
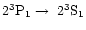 frequency
frequency 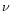 .
The factor 3 is the ratio of the statistical weights of the levels
.
The factor 3 is the ratio of the statistical weights of the levels
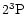 and
and
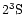 .
F is approximated by Blumenthal et al. (1972) through
.
F is approximated by Blumenthal et al. (1972) through
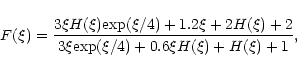 |
(15) |
where
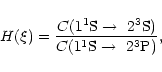 |
(16) |
with
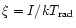 and the collisional excitation rate coefficients
and the collisional excitation rate coefficients
 .
The ionization potentials
.
The ionization potentials
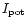 for the
ions C V, N VI, and O VII are taken from Pradham & Shull (1981).
The collisional excitation rate coefficients
for the
ions C V, N VI, and O VII are taken from Pradham & Shull (1981).
The collisional excitation rate coefficients
 were taken
from Pradhan et al. (1981)
for C V and O VII while the rate coefficients for N VI
were obtained by interpolation from these values.
were taken
from Pradhan et al. (1981)
for C V and O VII while the rate coefficients for N VI
were obtained by interpolation from these values.
From Eq. (14) we determine the values used in Eq. (2)
for the calculation of the theoretical curves in Fig. 5.
They are also listed in Table 8.
For comparison, we also give in Table 8 the values derived from
recent calculations by Mewe et al. (2000a) considering a
multi-level model previously used by Porquet & Dubau (2000),
and taking into account the effect of temperature on G and
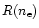 (Mewe et al. 2000a, see also Porquet & Dubau 2000).
(Mewe et al. 2000a, see also Porquet & Dubau 2000).
In Fig. 5 we show for Procyon and Capella
the expected line ratio f/i as a function of the electron density 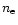 in comparison with the observed line ratio
in comparison with the observed line ratio
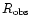 (corrected for detector
efficiencies) and its 1
(corrected for detector
efficiencies) and its 1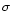 error.
The expected curves are plotted for the radiation temperature range estimated
for the two stars as listed in Table 8; for O VII the
stellar radiation field does not significantly influence the f/i ratio as
expected. We used the formation
temperatures T(G) calculated from the G ratios as listed in
Table 6, thus assuming all the emission being produced at a single
temperature. In Table 9 we
summarize the derived densities and their 1
error.
The expected curves are plotted for the radiation temperature range estimated
for the two stars as listed in Table 8; for O VII the
stellar radiation field does not significantly influence the f/i ratio as
expected. We used the formation
temperatures T(G) calculated from the G ratios as listed in
Table 6, thus assuming all the emission being produced at a single
temperature. In Table 9 we
summarize the derived densities and their 1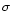 errors for Procyon and
Capella not accounting for errors in T(G).
No density values could be determined for the C V triplet in Procyon
and for the O VII triplet in Capella. Instead we give upper limits
for the two cases (Table 9); for Capella only a 2
errors for Procyon and
Capella not accounting for errors in T(G).
No density values could be determined for the C V triplet in Procyon
and for the O VII triplet in Capella. Instead we give upper limits
for the two cases (Table 9); for Capella only a 2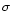 upper limit could be determined.
upper limit could be determined.
Obviously, for both stars the measured line ratios are within (Capella)
and very close to (Procyon)
the low-density limit 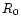 .
At any rate, the measured f/i ratio is
larger for Capella than for Procyon, so one arrives at the somewhat unexpected
conclusion that the coronal density in the active star
Capella should be smaller than in the inactive star Procyon.
.
At any rate, the measured f/i ratio is
larger for Capella than for Procyon, so one arrives at the somewhat unexpected
conclusion that the coronal density in the active star
Capella should be smaller than in the inactive star Procyon.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{MS10283f5a.eps}\includegra...
...p]{MS10283f5e.eps}\includegraphics[width=6.5cm,clip]{MS10283f5f.eps}\end{figure}](/articles/aa/full/2001/07/aa10283/Timg174.gif) |
Figure 5:
Theoretical curves in the radiation temperature range given in
Table 8 in comparison with the measured value of
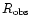 for the O VII, N VI and the C V triplet for Capella and Procyon. The measured
R values from Table 4 are corrected for detector efficiencies for the O VII, N VI and the C V triplet for Capella and Procyon. The measured
R values from Table 4 are corrected for detector efficiencies |
| Open with DEXTER |
5.4 Optical depth effects
In all of the above analysis we assumed all triplet lines to be optically thin.
In the following section we show this assumption to be consistent with our
results. Let us therefore assume that the optical depth in the resonance lines
is not small. This leads to a reduction of the measured resonance
line flux due to radiative scattering. At line center the optical depth is given
by the equation
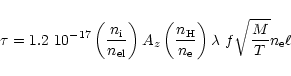 |
(17) |
(Schrijver et al. 1994) with the fractional ionization is denoted by
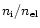 ,
the elemental abundances by Az,
the ratio of hydrogen to electron density is
,
the elemental abundances by Az,
the ratio of hydrogen to electron density is
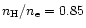 ,
the oscillator strength f=0.7 for all ions, the atomic number is M, the
wavelength is measured in Å, the temperature in K, the electron density
,
the oscillator strength f=0.7 for all ions, the atomic number is M, the
wavelength is measured in Å, the temperature in K, the electron density 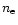 in cm-3 and the mean free path is denoted by
in cm-3 and the mean free path is denoted by 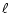 .
In Eq. (17) we adopt a value of unity for the fractional ionization and use
the solar abundances. We further assume T at the peak line formation and
note, that
.
In Eq. (17) we adopt a value of unity for the fractional ionization and use
the solar abundances. We further assume T at the peak line formation and
note, that 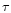 is rather insensitive to the precise value of T. We can
determine - for each resonance line - that value of
is rather insensitive to the precise value of T. We can
determine - for each resonance line - that value of
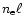 which yields
an optical depth of unity. Adopting a maximum value of
which yields
an optical depth of unity. Adopting a maximum value of 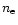 of 1010cm-3 (cf. Table 9), we determine lower values of
of 1010cm-3 (cf. Table 9), we determine lower values of 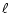 of
of
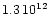 cm,
cm,
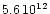 cm and
cm and
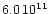 cm, for
O VII, N VI and C V, respectively. Assuming a geometry most
suitable for resonance scattering, we can compute the respective emission
measures of
cm, for
O VII, N VI and C V, respectively. Assuming a geometry most
suitable for resonance scattering, we can compute the respective emission
measures of
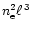 respectively. Comparing these emission measures with those
derived from the measured line fluxes
respectively. Comparing these emission measures with those
derived from the measured line fluxes 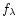
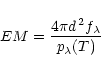 |
(18) |
with the line cooling function
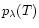 and the distance d(cf. Table 1), shows the former to be larger by a few orders of
magnitude for both stars. This inconsistency shows that the assumption of a
non-negligible optical depth is invalid and we conclude that optical depth
effects are irrelevant for the analysis of He-like triplets in Procyon and
Capella.
and the distance d(cf. Table 1), shows the former to be larger by a few orders of
magnitude for both stars. This inconsistency shows that the assumption of a
non-negligible optical depth is invalid and we conclude that optical depth
effects are irrelevant for the analysis of He-like triplets in Procyon and
Capella.
Both Capella and Procyon are considered to be solar-like stars.
In the solar context the He-like triplets of oxygen, nitrogen and carbon have
been known for a long time and in fact the He-like ion density diagnostics have
been first developed to interpret these solar data. Many solar observations
are available for the O VII triplet, while only very few observations have
been made for the N VI and C V triplets. The first observations of
the C V triplet are reported by Austin et al. (1966), who obtained an f/i-ratio of 1.9,
while Freeman & Jones (1970) found an f/i-ratio of 1.0. The latter authors also
observed the N VI triplet, but failed to detect the intercombination line
and hence deduced f/i > 1.9. Brown et al. (1986) observed the C V and N VI triplets
during a flare and found a mean value of
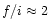 with large scatter
between 0.1-4 around this mean for N VI and a value of 0.21 (with a scatter
between 0.17-0.25) for C V. In consequence, little can be said about the solar
N VI line ratios because of the large measurement errors. The measured ratios for
both Capella and Procyon are certainly consistent
with the range of N VI f/i values quoted by Brown et al. (1986). As far as
C V is concerned, the flare data yield very low f/i ratios indicative of
high densities. The C V f/i ratio observed for Capella is higher, and that for
Procyon - still higher than that observed for the Brown et al. (1986) flare -
we argue is due to large photospheric radiation fluxes. We therefore conclude
that the layers contributing the C V emission in Capella and Procyon are at
lower density than those encountered in solar flares, and the same applies to
the layers emitting N VI.
with large scatter
between 0.1-4 around this mean for N VI and a value of 0.21 (with a scatter
between 0.17-0.25) for C V. In consequence, little can be said about the solar
N VI line ratios because of the large measurement errors. The measured ratios for
both Capella and Procyon are certainly consistent
with the range of N VI f/i values quoted by Brown et al. (1986). As far as
C V is concerned, the flare data yield very low f/i ratios indicative of
high densities. The C V f/i ratio observed for Capella is higher, and that for
Procyon - still higher than that observed for the Brown et al. (1986) flare -
we argue is due to large photospheric radiation fluxes. We therefore conclude
that the layers contributing the C V emission in Capella and Procyon are at
lower density than those encountered in solar flares, and the same applies to
the layers emitting N VI.
Observations of the O VII triplet in the solar corona are reported by
Freeman & Jones (1970); McKenzie et al. (1978); McKenzie et al. (1982), all of which
refer to the quiescent corona, while some of the observations
from McKenzie et al. (1982) and Brown et al. (1986) refer to flares and those
of Parkinson (1975) refer to active regions. In addition we considered
some data points collected from various sources cited by
Doyle (1980). In Fig. 6 we plot G vs. R of these solar observations
and compare these solar data with our Chandra measurements for
Procyon and Capella. For clarity we omitted individual error bars, which
are typically 0.1-0.3 for the solar measurements. As can be seen from
Fig. 6, most of the solar measurements yield R value between 3 and 4.
A few values are significantly lower around
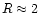 ,
with all
them referring to flares or active regions. Our Chandra measurements
(3.28 for Procyon, 4.0 for Capella) thus fall into the bulk part of the solar
data. Unfortunately, the solar data are by no means unambiguous. It is
not always
clear which regions the data refer to (except for the flare observations
by Brown et al. 1986, and further, most of the observations are relatively old
and have not been taken with high spatial resolution; they are comparable
in some sense to our full disk observations of stellar X-ray sources.
In addition, the instrumentation used in
different experiments is quite different and each experiment is affected
by its own specific difficulties. Nevertheless it seems fair to state
that most O VII measurements referring to quiescent conditions are close
to the low density limit, thus indicating that the physical properties
of the O VII emitting layers
in Capella and Procyon
should not be that different from those in the Sun; a little
puzzling in this context is the large scatter of the solar G data.
In contrast, the solar flare data (
,
with all
them referring to flares or active regions. Our Chandra measurements
(3.28 for Procyon, 4.0 for Capella) thus fall into the bulk part of the solar
data. Unfortunately, the solar data are by no means unambiguous. It is
not always
clear which regions the data refer to (except for the flare observations
by Brown et al. 1986, and further, most of the observations are relatively old
and have not been taken with high spatial resolution; they are comparable
in some sense to our full disk observations of stellar X-ray sources.
In addition, the instrumentation used in
different experiments is quite different and each experiment is affected
by its own specific difficulties. Nevertheless it seems fair to state
that most O VII measurements referring to quiescent conditions are close
to the low density limit, thus indicating that the physical properties
of the O VII emitting layers
in Capella and Procyon
should not be that different from those in the Sun; a little
puzzling in this context is the large scatter of the solar G data.
In contrast, the solar flare data (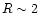 )
is much lower than any of the
other measurements, consistent with a high density plasma.
)
is much lower than any of the
other measurements, consistent with a high density plasma.
![\begin{figure}
\par\includegraphics[width =7.5cm,clip]{MS10283f6.eps}
\end{figure}](/articles/aa/full/2001/07/aa10283/Timg195.gif) |
Figure 6:
Measurements of solar values for He-like ratios of O VII: Freeman & Jones (1970) (dotted open box),
McKenzie et al. (1982): quiescent (diamond), flare (asterix),
McKenzie et al. (1978) (dotted diamond),
Doyle (1980) (filled triangle upside down),
Parkinson (1975): active region (plus symbol),
Brown et al. (1986): flare (cross).
Encircled are our measurements of Procyon (open triangle) and Capella (open box) |
| Open with DEXTER |
Inspection of Table 9 suggests that
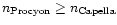 for the densities derived from C V, N VI, and O VII; there is definitely no
evidence for
for the densities derived from C V, N VI, and O VII; there is definitely no
evidence for
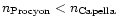 .
These findings are in
contradiction to the claims made by Dupree et al. (1993), who argue on the
basis of Fe XXI line ratios measured with the EUVE satellite that
.
These findings are in
contradiction to the claims made by Dupree et al. (1993), who argue on the
basis of Fe XXI line ratios measured with the EUVE satellite that
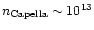 cm-3. A recent analysis of the
long wavelength part (
cm-3. A recent analysis of the
long wavelength part (
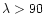 Å) of the LETGS spectrum of
Capella by Mewe et al. (2000b), however, yielded plasma densities of
5 1012 cm-3 at most for the plasma emitting in the
Fe XXI lines with no evidence for any deviations from the low density
limit. Of course, these values refer to
those plasma layers emitting in the Fe XXI line, which ought to be at
far higher temperature (
Å) of the LETGS spectrum of
Capella by Mewe et al. (2000b), however, yielded plasma densities of
5 1012 cm-3 at most for the plasma emitting in the
Fe XXI lines with no evidence for any deviations from the low density
limit. Of course, these values refer to
those plasma layers emitting in the Fe XXI line, which ought to be at
far higher temperature (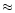 8 MK) than
those emitting in the C V, N VI, and O VII lines (1-2 MK).
If we assume all the observed emissions to come from the same
magnetically confined structures (loops), one expects the gas pressure
to be more or less constant and hence the density at lower temperatures even
higher. However, plasma densities (for Capella) of
8 MK) than
those emitting in the C V, N VI, and O VII lines (1-2 MK).
If we assume all the observed emissions to come from the same
magnetically confined structures (loops), one expects the gas pressure
to be more or less constant and hence the density at lower temperatures even
higher. However, plasma densities (for Capella) of
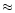 1013 cm-3 at temperatures of 2 MK are clearly inconsistent
with our LETGS spectra. Therefore the plasma emitting in the Fe XXI line
is either at the low density limit or the Fe XXI emission comes from
different structures than the emissions from He-like ions.
1013 cm-3 at temperatures of 2 MK are clearly inconsistent
with our LETGS spectra. Therefore the plasma emitting in the Fe XXI line
is either at the low density limit or the Fe XXI emission comes from
different structures than the emissions from He-like ions.
Our temperature measurements of the line forming regions (cf.,
Table 6) are not fully conclusive, although they suggest that the same
lines of C V, N VI, and O VII respectively are
formed at a somewhat higher temperature (at most a factor of 2)
in Capella as compared to Procyon. As a consequence we must have
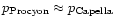 for the gas pressures in the respective
line forming regions.
Capella's peak coronal temperature is clearly much higher than
Procyon's.
If we again assume - going along with the solar analogy - that for both
Procyon and Capella (all of) the X-ray emission originates from magnetically
confined plasma loops, the loop top temperatures in Capella must be
higher than in Procyon. The loop scaling laws then imply for the
typical loop length scales L for Procyon and Capella
for the gas pressures in the respective
line forming regions.
Capella's peak coronal temperature is clearly much higher than
Procyon's.
If we again assume - going along with the solar analogy - that for both
Procyon and Capella (all of) the X-ray emission originates from magnetically
confined plasma loops, the loop top temperatures in Capella must be
higher than in Procyon. The loop scaling laws then imply for the
typical loop length scales L for Procyon and Capella
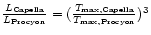 .
A conservative estimate
yields
.
A conservative estimate
yields
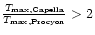 ,
thus
,
thus
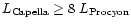 .
The conclusion then appears
inescapable that the typical sizes of the magnetic structures in
Procyon and Capella are quite different by probably at least one order
of magnitude.
.
The conclusion then appears
inescapable that the typical sizes of the magnetic structures in
Procyon and Capella are quite different by probably at least one order
of magnitude.
Next, it is instructive to compare the total mean surface fluxes emitted in
the helium- and
hydrogen-like ions of carbon, nitrogen and oxygen for Procyon and Capella.
Using the measured count ratios and correcting for the effects of distance,
exposure times and the surface areas of the
stars we find for the C V, C VI, N VI, N VII,
O VII, and O VIII lines values of (Capella)/(Procyon) of 0.96,
1.37, 1.09, 4.9, 1.87, and 9.71 respectively. Therefore up to those
temperatures where the C V, C VI, and N VI lines are
formed, the mean surface fluxes in the two stars hardly differ at all;
pressures and temperatures are also quite similar. We therefore conclude
that the physical characteristics and global properties (such as filling factor)
of Procyon's and Capella's corona at a level of
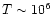 K are very similar.
K are very similar.
It is interesting to again perform a comparison to the Sun.
Freeman & Jones (1970) quote - for their SL801 rocket flight on Nov. 20 1969 -
resonance line fluxes of 4.2 10-3, 2.1 10-3, and 3.1 10-3erg/(cm2s) for O VII, N VI, and C V respectively.
Correcting for the distance between Earth and Sun we find average surface
fluxes of 200, 100, and 150 erg/cm2/s for O VII, N VI,
and C V respectively on the
solar surface. Carrying out the same calculation for our Chandra
data, we find - using the effective areas given in Table 7 -
mean surface fluxes in O VII of 3700 and 1980 erg/(cm2s),
in N VI of 480 and 430 erg/(cm2s),
and in C V of 830 and 860 erg/(cm2s)
for Capella and Procyon respectively. We therefore recover our
previous finding that Capella's and Procyon's surface fluxes are quite
similar, and determine in addition that both stars exceed typical¹ (?)
solar values by one order of magnitude. Since the physical conditions of the
line emitting regions are quite similar, we conclude that the coronal
filling factors are larger.
Evaluating now the coronal pressure for Procyon we find - using the
densities and temperatures derived from
N VI - p(N VI) = 4.4 dyn/cm2, a value also very
typical for solar active regions. From the loop scaling law (Rosner et al. (1978))
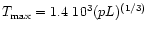 we deduce a typical length
of 2.7 108 cm using
we deduce a typical length
of 2.7 108 cm using
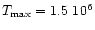 K.
This value must be considered as a lower limit to the
probable length scale because of the unfortunate sensitive dependence of L on
K.
This value must be considered as a lower limit to the
probable length scale because of the unfortunate sensitive dependence of L on
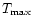 through
through
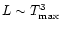 ;
;
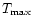 is likely somewhat higher than
is likely somewhat higher than
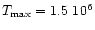 K as suggested by the temperatures derived from the
O VIII data. At any rate, however, the conclusion is, that the X-ray
emission originates from low-lying loops and hence also our Chandra data
support the view that Procyon's corona has an appearance very similar to the
Sun's, just like
the conclusion drawn by Schmitt et al. (1996b) from their EUVE spectra. It then
follows that the sizes of the magnetic loops in Procyon's corona are similar
to the loops found in the solar corona.
Adopting - for argument's sake -
a characteristic length of
K as suggested by the temperatures derived from the
O VIII data. At any rate, however, the conclusion is, that the X-ray
emission originates from low-lying loops and hence also our Chandra data
support the view that Procyon's corona has an appearance very similar to the
Sun's, just like
the conclusion drawn by Schmitt et al. (1996b) from their EUVE spectra. It then
follows that the sizes of the magnetic loops in Procyon's corona are similar
to the loops found in the solar corona.
Adopting - for argument's sake -
a characteristic length of
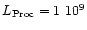 cm, we then find
for Capella
cm, we then find
for Capella
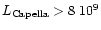 cm, and possibly even
a significant
fraction of Capella's radius. This result is somewhat puzzling. On the Sun,
loop structures, i.e., magnetically closed topologies, are occasionally
found at larger heights, but they are always of low density and
they never contribute significantly to the
overall X-ray emission. It will be interesting to see whether this
behavior is typical for active stars in general, or whether it applies
only to Capella. After all, Capella may not be the prototypical active star.
Its corona is not as hot as that of other stars, it does not produce flares
and its radio emission is very weak.
cm, and possibly even
a significant
fraction of Capella's radius. This result is somewhat puzzling. On the Sun,
loop structures, i.e., magnetically closed topologies, are occasionally
found at larger heights, but they are always of low density and
they never contribute significantly to the
overall X-ray emission. It will be interesting to see whether this
behavior is typical for active stars in general, or whether it applies
only to Capella. After all, Capella may not be the prototypical active star.
Its corona is not as hot as that of other stars, it does not produce flares
and its radio emission is very weak.
Acknowledgements
J.-U. N. acknowledges financial support from Deutsches Zentrum für Luft- und
Raumfahrt E. V. (DLR) under 50OR98010. The Space Research Organization Netherlands (SRON) is supported financially by NWO. We thank
Tom Ayres, U/COLORADO (CASA), for very useful discussion.
- Acton, L. W. 1978, ApJ, 255, 1069
In the text
- Austin, W. E., Purcell, J. D., Tousey, R., & Widing, K. G., ApJ , 145, 373
In the text
NASA ADS
- Blumenthal, G. R., Drake, G. W., &
Tucker, W. H. 1972 ApJ, 172, 205
In the text
NASA ADS
- Brinkman, A. C., Gunsing, C. J. T.,
Kaastra, J. S., et al. 2000, ApJ, 530, L111
In the text
NASA ADS
- Brown, W. A., Bruner, M. E., Acton, L. W.,
et al. 1986 ApJ, 301, 981
In the text
NASA ADS
- Catura, R. C., Acton, L. W., & Johnson, H. M. 1975, ApJL, 196, L47
In the text
NASA ADS
- Díaz-Cordovés, J., Claret, A., & Giménez, A. 1995, A&AS, 110, 329
In the text
NASA ADS
- Doyle, J. G. 1980, A&A, 87, 183
In the text
NASA ADS
- Drake, J. J., Laming, J. M., & Widing, K. G. 1995, ApJ, 443, 393
In the text
NASA ADS
- Dupree, A. K., Brickhouse, N. S., Doschek, G. A., et al. 1993, ApJL, 418, L41 In the text
- Freeman, F. F., & Jones, B. B. 1970, Sol. Phys., 15, 288
In the text
- Fuhrman, K., Pfeiffer, M., Frank, C., et al. 1997, A&A, 323, 909
In the text
NASA ADS
- Gabriel, A. H., & Jordan, C. 1969, MNRAS, 145, 241
In the text
NASA ADS
- Hummel, C. A., Armstrong, J. T., Quirrenbach, A., et al. 1994, ApJ, 107(5), 1859
In the text
- Hünsch, M., Schmitt, J. H. M. M., & Voges, W. 1998a, A&A, 127, 251
In the text
- Hünsch, M., Schmitt, J. H. M. M., & Voges, W. 1998b, A&A, 132, 155
- Irwin, A. W., Fletcher, J. M., Yang, S. L. S., et al. 1992, PASP, 104, 489
In the text
NASA ADS
- Kaastra, J. S., Mewe, R., & Nieuwenhijzen, H. 1996, in UV and X-ray Spectroscopy of Astrophysical and Laboratory Plasmas, ed. K. Yamashita, & T. Watanabe (Tokyo, Universal Academy Press, Inc.), 411 (SPEX)
In the text
- Kelch, W. L., Linsky, J. L., Basri, G. S., et al. 1978, ApJ, 220, 962
In the text
NASA ADS
- Lemen, J. R., Mewe, R., Schrijver, C. J., et al. 1989, ApJ, 341, 474
In the text
NASA ADS
- Linsky, L. L., Wood, B. E., Brown, A., et al. 1998, ApJ, 492, 767
In the text
NASA ADS
- McKenzie, D. L., Rugge, H. R.,
Underwood, J. H., et al. 1978, ApJ, 221, 342
In the text
NASA ADS
- McKenzie, D. L., & Landecker, P. B. 1982, ApJ, 259, 372
In the text
NASA ADS
- Mewe, R., & Schrijver, J. 1978, A&A 65, 114
In the text
- Mewe, R., Heise, J., Gronenschild, E. H. B. M., et al. 1975, ApJL, 202, L67
In the text
NASA ADS
- Mewe, R., Gronenschild, E. H. B. M., Westergaard, N. J., et al. 1982, ApJ, 260, 233
In the text
NASA ADS
- Mewe, R., Gronenschild, E. H. B. M., & van den Oord, G. H. J. 1985, A&AS, 62, 197
In the text
NASA ADS
- Mewe, R., Schrijver, C. J., Lemen, J. R., et al. 1986, Adv. Space Res., 6, 133
In the text
NASA ADS
- Mewe, R., Kaastra, J. S., & Liedahl, D. A. 1995, Legacy, 6, 16 (MEKAL)
In the text
- Mewe, R., Porquet, D., Raassen, A. J. J., & Kaastra, J. S. 2000a, in preparation
In the text
- Mewe, R., Raassen, A. J. J., Brickhouse, N. S., et al. 2000b, A&A, submitted
In the text
- Parkinson, J. H. 1975, Sol. Phys., 42, 183
In the text
NASA ADS
- Porquet, & Dubau 2000, A&AS, 143, 495
In the text
NASA ADS
- Pradhan, A. K. 1982, ApJ, 263, 477
In the text
NASA ADS
- Pradhan, A. K. 1985, ApJ, 288, 824
In the text
NASA ADS
- Pradhan, A. K., Norcross, D. W., &
Hummer, D. G. 1981, ApJ, 246, 1031
In the text
NASA ADS
- Pradhan, A. K., & Shull, J. M.
1981, ApJ, 249, 821
In the text
NASA ADS
- Predehl, P., Braeuninger, H.,
Brinkman, A., et al. 1997, Proc. SPIE, 3113, 172
In the text
- Rosner, R., Tucker, W. H., & Vaiana, G. S. 1978, ApJ, 220, 643
In the text
NASA ADS
- Schmitt, J. H. M. M., Harnden, F. R., Jr., Rosner, R., et al. 1985, ApJ, 288, 751
In the text
NASA ADS
- Schmitt, J. H. M. M., Haisch, B. M., & Drake, J. J. 1994, Science, 265, 1420
NASA ADS
- Schmitt, J. H. M. M., Drake, J. J., Stern, R. A., et al. 1996a, ApJ, 457, 882
In the text
NASA ADS
- Schmitt, J. H. M. M., Drake, J. J., Haisch, B. M., et al. 1996b, ApJ, 467, 841
In the text
NASA ADS
- Schmitt, J. H. M. M. 1997, A&A, 318, 215
In the text
NASA ADS
- Schrijver, C. J., van den Oord, G. H. J., & Mewe, R. 1994, A&A, 289, L23
In the text
NASA ADS
- Schrijver, C. J., van den Oord, G. H. J., Mewe, R., et al. 1995, A&A, 302, 438
In the text
NASA ADS
- Vaiana, G. S., Cassinelli, J. P., & Giacconi, R. 1981, ApJ, 244, 163
In the text
- Vedder, P. W., & Canizares, C. R. 1983, ApJ, 270, 666
In the text
NASA ADS
Copyright ESO 2001
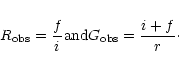
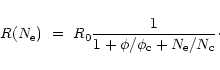
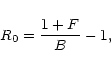
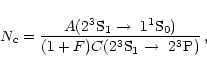
![\begin{figure}
\par\includegraphics[width=6cm,clip]{MS10283f1.eps}
\end{figure}](/articles/aa/full/2001/07/aa10283/Timg60.gif)
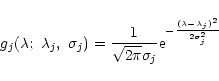
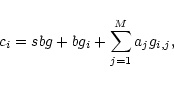
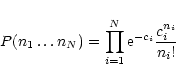
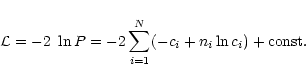
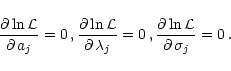
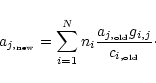
![\begin{figure}
\par\includegraphics[width=12.4cm,clip]{MS10283f2a.eps}\par\inclu...
...0283f2b.eps}\par\includegraphics[width=12.4cm,clip]{MS10283f2c.eps} \end{figure}](/articles/aa/full/2001/07/aa10283/Timg90.gif)
![\begin{figure}
\par\includegraphics[width=12.4cm,clip]{MS10283f3a.eps}\par\inclu...
...10283f3b.eps}\par\includegraphics[width=12.4cm,clip]{MS10283f3c.eps}\end{figure}](/articles/aa/full/2001/07/aa10283/Timg91.gif)
![\begin{figure}
\par\includegraphics[width=12.4cm,clip]{MS10283f4.eps}\end{figure}](/articles/aa/full/2001/07/aa10283/Timg120.gif)
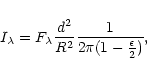
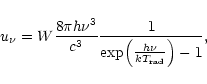
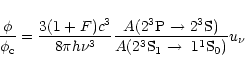
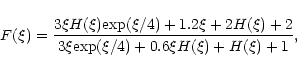
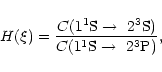
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{MS10283f5a.eps}\includegra...
...p]{MS10283f5e.eps}\includegraphics[width=6.5cm,clip]{MS10283f5f.eps}\end{figure}](/articles/aa/full/2001/07/aa10283/Timg174.gif)
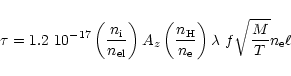
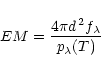
![\begin{figure}
\par\includegraphics[width =7.5cm,clip]{MS10283f6.eps}
\end{figure}](/articles/aa/full/2001/07/aa10283/Timg195.gif)