A&A 367, 18-26 (2001)
DOI: 10.1051/0004-6361:20000406
T. Hamana1![]() - S. Colombi1,2 - Y. Suto3,4
- S. Colombi1,2 - Y. Suto3,4
1 - Institut d'Astrophysique de Paris, CNRS, 98bis Boulevard Arago, 75014 Paris, France
2 - NIC (Numerical Investigations in Cosmology) Group, CNRS
3 - Department of Physics, University of Tokyo, Tokyo 113-0033, Japan
4 - Research Center for the Early Universe (RESCEU),
School of Science, University of Tokyo, Tokyo 113-0033, Japan
Received 5 July 2000 / Accepted 29 November 2000
Abstract
We examine the light-cone effect on the two-point correlation
functions using numerical simulations for the first time.
Specifically, we generate several sets of dark matter particle
distributions on the light-cone up to z=0.4 and z=2 over the
field-of-view of ![]() degree2 from cosmological N-body
simulations. Then we apply the selection function to the dark matter
distribution according to the galaxy and QSO luminosity functions.
Finally we compute the two-point correlation functions on the
light-cone both in real and in redshift spaces using the pair-count
estimator and compare with the theoretical predictions. We find
that the previous theoretical modeling for nonlinear gravitational
evolution, linear and nonlinear redshift-distortion, and the
light-cone effect including the selection function is in good
agreement with our numerical results, and thus is an accurate and
reliable description of the clustering in the universe on the
light-cone.
degree2 from cosmological N-body
simulations. Then we apply the selection function to the dark matter
distribution according to the galaxy and QSO luminosity functions.
Finally we compute the two-point correlation functions on the
light-cone both in real and in redshift spaces using the pair-count
estimator and compare with the theoretical predictions. We find
that the previous theoretical modeling for nonlinear gravitational
evolution, linear and nonlinear redshift-distortion, and the
light-cone effect including the selection function is in good
agreement with our numerical results, and thus is an accurate and
reliable description of the clustering in the universe on the
light-cone.
Key words: cosmology: theory - dark matter - large-scale structure of universe - galaxies: general - quasars: general
In the proper understanding of on-going redshift surveys of galaxies and quasars, in particular the Two-degree Field (2dF) and the Sloan Digital Sky Survey (SDSS), it is essential to establish a theory of cosmological statistics on the light cone. This project has been undertaken in a series of our previous papers (Matsubara et al. 1997; Yamamoto & Suto 1999; Nishioka & Yamamoto 1999; Suto et al. 1999; Yamamoto et al. 2000; Suto et al. 2000). Those papers have formulated the light-cone statistics in a rigorous manner, described approximations to model the clustering evolution in the redshift space, and presented various predictions in canonical cold dark matter (CDM) universes. Their predictions, however, have not yet been tested quantitatively, for instance, against numerical simulations. This is not surprising since it is fairly a demanding task to construct a reliable sample extending over the light-cone from the conventional simulation outputs at a specified redshift, z.
In the present paper, we examine, for the first time, the validity and limitation of the above theoretical framework to describe the cosmological light-cone effect against the mock catalogues on the light-cone. Such catalogues from cosmological N-body simulations have been originally constructed for the study of the weak lensing statistics (Hamana et al. 2000, in preparation). Applying the same technique (Sect. 3.1), we generate a number of different realizations for the light-cone samples up to z=0.4 and z=2, evaluate the two-point correlation functions directly, and compare with the theoretical predictions.
In order to predict quantitatively the two-point statistics of objects
on the light cone, one must take account of (i) nonlinear
gravitational evolution, (ii) linear redshift-space distortion, (iii)
nonlinear redshift-space distortion, (iv) weighted averaging over the
light-cone, (v) cosmological redshift-space distortion due to the
geometry of the universe, and (vi) object-dependent clustering bias.
The effect (v) comes from our ignorance of the correct cosmological
parameters, and (vi) is rather sensitive to the objects which one has
in mind. Thus the latter two effects will be discussed in a separate
paper, and we focus on the effects of (i) ![]() (iv) throughout the
present paper.
(iv) throughout the
present paper.
| Model | h | Box size | Force resolution |
|
|||
|
|
[h-1 Mpc] | ||||||
| SCDM small box | 1 | 0 | 0.5 | 0.6 |
|
0.31 | 0.4 |
| SCDM large box | 1 | 0 | 0.5 | 0.6 |
|
0.94 | 2 |
| 0.3 | 0.7 | 0.7 | 0.9 |
|
0.45 | 0.4 | |
| 0.3 | 0.7 | 0.7 | 0.9 |
|
1.4 | 2 |
Nonlinear gravitational evolution of mass density fluctuations is now
well understood, at least for two-point statistics. In practice, we
adopt an accurate fitting formula (Peacock & Dodds 1996) for the
nonlinear power spectrum
![]() in terms of its
linear counterpart.
in terms of its
linear counterpart.
Then the nonlinear power spectrum in redshift space is given as
| = | ![$\displaystyle \! \left[{H_0 \over H(z)}\right]^2 \, (1+z)^3 \Omega_0 ,$](/articles/aa/full/2001/07/aa10074/img21.gif) |
(3) | |
| = | ![$\displaystyle \! \left[{H_0 \over H(z)}\right]^2 \, \lambda_0 ,$](/articles/aa/full/2001/07/aa10074/img23.gif) |
(4) | |
| = | (5) |
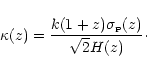 |
(8) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS10074f1.eps}\end{figure}](/articles/aa/full/2001/07/aa10074/Timg31.gif) |
Figure 1: Pairwise peculiar velocity dispersions of dark matter particles at z=0, 1 and 2. Dashed lines indicate the values predicted from the formula of MJB (Eq. (9)), while solid lines indicate our adopted fit (Eq. (10)) |
| Open with DEXTER | |
On large scales,
![]() can be well
approximated by a fitting formula proposed by Mo et al. (1997):
can be well
approximated by a fitting formula proposed by Mo et al. (1997):
| = | 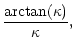 |
(12) | |
| = | ![$\displaystyle {3\over\kappa^2}
\left[1-{{\arctan}(\kappa) \over \kappa}\right] ,$](/articles/aa/full/2001/07/aa10074/img43.gif) |
(13) | |
| = | ![$\displaystyle {5\over3\kappa^2}\left[1-{3\over\kappa^2} +
{3 \, {\arctan}(\kappa) \over \kappa^3} \right] .$](/articles/aa/full/2001/07/aa10074/img45.gif) |
(14) |
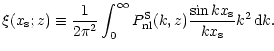 |
(16) |
![\begin{displaymath}{\rm d}s^2 = -{\rm d}t^2 + a(t)^2
\{{\rm d}\chi^2 + S_K(\chi)^2 [{\rm d}\theta^2 + \sin^2\theta {\rm d}\phi^2 ] \} ,
\end{displaymath}](/articles/aa/full/2001/07/aa10074/img50.gif) |
(17) |
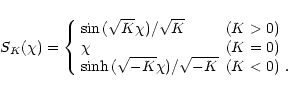 |
(18) |
| = | 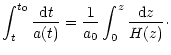 |
(19) |
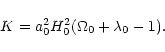 |
(20) |
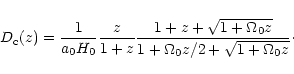 |
(21) |
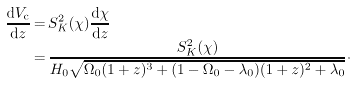 |
(22) |
We test the theoretical modeling against simulation results, we focus
on two spatially-flat cold dark matter models, SCDM and ![]() CDM,
adopting a scale-invariant primordial power spectral index of n=1.
Their cosmological parameters are listed in Table
1.
While SCDM are known to have several problems
in reproducing the recent observations (e.g., de Bernardis et al.
2000), this model is suitable for testing the theoretical formula
since the clustering evolution on the light-cone is more significant.
We use a series of N-body simulations originally constructed for the
study of weak lensing statistics (Hamana et al. 2000, in preparation).
These simulations were generated with a vectorized PM code (Moutarde
at al. 1991) modified to run in parallel on several processors of a
CRAY-98 (Hivon 1995). They use
CDM,
adopting a scale-invariant primordial power spectral index of n=1.
Their cosmological parameters are listed in Table
1.
While SCDM are known to have several problems
in reproducing the recent observations (e.g., de Bernardis et al.
2000), this model is suitable for testing the theoretical formula
since the clustering evolution on the light-cone is more significant.
We use a series of N-body simulations originally constructed for the
study of weak lensing statistics (Hamana et al. 2000, in preparation).
These simulations were generated with a vectorized PM code (Moutarde
at al. 1991) modified to run in parallel on several processors of a
CRAY-98 (Hivon 1995). They use
![]() particles and the
same number of force mesh in a periodic rectangular comoving box. We
use both the small and large boxes (Table 1).
particles and the
same number of force mesh in a periodic rectangular comoving box. We
use both the small and large boxes (Table 1).
The initial conditions are generated adopting the transfer function of
Bond & Efstathiou (1984, see also Jenkins et al. 1998) with the shape
parameter
![]() .
The amplitude of the power
spectrum is normalized by the cluster abundance (Eke et al. 1996; Kitayama & Suto 1997).
.
The amplitude of the power
spectrum is normalized by the cluster abundance (Eke et al. 1996; Kitayama & Suto 1997).
Using the above simulation data, we generated light-cone samples as
follows; first, we adopt a distance observer approximation and assume
that the line-of-sight direction is parallel to Z-axis regardless
with its (X,Y) position (Fig. 2).
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{MS10074f2.eps}\end{figure}](/articles/aa/full/2001/07/aa10074/Timg67.gif) |
Figure 2:
Schematic geometry of our light-cone samples.
The comoving distances denoted in the figure are for SCDM model.
In the case of |
| Open with DEXTER | |
In practice, we apply the above procedure separately in real and
redshift spaces by using
![]() and
and
![]() of each
particle (see Eq. (25) below). The total numbers of
particles in those realizations are listed in Table 3.
of each
particle (see Eq. (25) below). The total numbers of
particles in those realizations are listed in Table 3.
Two-point correlation function is estimated by the conventional
pair-count adopting the estimator proposed by Landy & Szalay (1993):
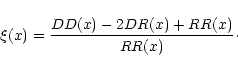 |
(23) |
The comoving separation x12 of two objects located at z1 and
z2 with an angular separation
![]() is given by
is given by
| x122 | = | ||
| (24) |
|
|
k1 | k2 |
|
||||
| 1 | 0 | 3.45 | 1.63 | -20.59 | 1.31 | -0.26 | 0.80 10-5 |
| 0.3 | 0.7 | 3.41 | 1.58 | -21.14 | 1.36 | -0.27 | 2.88 10-6 |
In redshift space, the observed redshift
![]() for each object
differs from the "real'' one
for each object
differs from the "real'' one
![]() due to
the velocity distortion effect:
due to
the velocity distortion effect:
| s122 | = | ||
| (26) |
| Model | Realization | Total | Random selection | LF based selection | LF based with random selection |
| SCDM small box | 1 | 8193106/8216016 | 10258/10282 | 125477/125289 | 8546/8540 |
| 2 | 8291309/8311402 | 10388/10413 | 168363/168999 | 11444/11497 | |
| 3 | 8448034/8479865 | 10591/10627 | 165217/165192 | 11221/11218 | |
| 4 | 9181442/9250736 | 11533/11618 | 175769/175773 | 11927/11927 | |
| 5 | 8263119/8324278 | 10340/10434 | 178135/177348 | 12075/12025 | |
| SCDM large box | 1 | 6253827/6254790 | 10481/10482 | 2037314/2041146 | 10348/10363 |
| 2 | 6321816/6319899 | 10591/10582 | 2077216/2077310 | 10552/10552 | |
| 3 | 6346239/6342617 | 10626/10623 | 2090246/2090222 | 10622/10622 | |
| 4 | 6423700/6417089 | 10767/10757 | 2102122/2099505 | 10671/10664 | |
| 5 | 6298022/6300195 | 10546/10552 | 2077854/2079776 | 10553/10564 | |
| 1 | 3253963/3224663 | 7589/7512 | 43377/42960 | 8760/8666 | |
| 2 | 4326797/4341618 | 10025/10050 | 48690/48581 | 9808/9791 | |
| 3 | 4429032/4423464 | 10263/10258 | 62073/62274 | 12517/12553 | |
| 4 | 4859939/4842481 | 11245/11201 | 59105/59022 | 11903/11890 | |
| 5 | 4993640/4988234 | 11532/11517 | 72490/72674 | 14608/14635 | |
| 1 | 5358865/5370894 | 9834/9863 | 1427660/1429062 | 9588/9593 | |
| 2 | 5277031/5286441 | 9665/9681 | 1415712/1418226 | 9498/9516 | |
| 3 | 5625180/5631157 | 10322/10326 | 1507183/1507424 | 10174/10175 | |
| 4 | 5630820/5631761 | 10326/10326 | 1511963/1511565 | 10219/10218 | |
| 5 | 5606636/5612974 | 10287/10300 | 1507176/1508490 | 10174/10187 |
In properly predicting the power spectra on the light cone, the selection function should be specified. In this subsection, we describe the selection functions appropriate for galaxies and quasars samples.
For galaxies, we adopt a B-band luminosity function of the APM galaxies
(Loveday et al. 1992) fitted to the Schechter function:
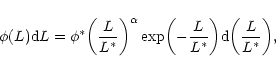 |
(27) |
| = | 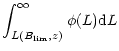 |
||
| = | (28) |
![\begin{displaymath}x(B_{\rm lim},z) \equiv {L(B_{\rm lim},z) \over L^*}
= \left[...
...\over 1\, h^{-1}~{\rm Mpc}}\right]^2 10^{2.2-0.4 B_{\rm lim}},
\end{displaymath}](/articles/aa/full/2001/07/aa10074/img96.gif) |
(29) |
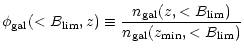 |
(30) |
For quasars, we adopt the B-band luminosity recently determined by
Boyle et al. (2000) from the 2dF QSO survey data:
| MB*(z) = MB*(0) - 2.5 (k1 z + k2 z2) , | (32) |
To compute the B-band apparent magnitude from a quasar of absolute
magnitude MB at z (with the luminosity distance
dL(z)), we applied the K-correction:
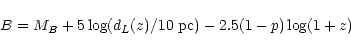 |
(33) |
Then the comoving number density of
QSOs at z which are brighter than the limiting magnitude
![]() is given by
is given by
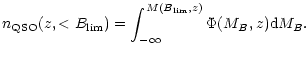 |
(34) |
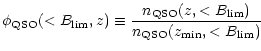 |
(35) |
In practice, we adopt the galaxy selection function
![]() with
with
![]() and
and
![]() for
the small box realizations, while the QSO selection function
for
the small box realizations, while the QSO selection function
![]() with
with
![]() and
and
![]() for the large box realizations. We do not introduce the
spatial biasing between selected particles and the underlying dark
matter, which will be discussed elsewhere. For comparison, we also
select the similar number of particles randomly but independently of
their redshifts. It should be emphasized here that our simulated data
are constructed to match the shape of the above selection
functions but not the amplitudes of the number densities. The
field-of-view of our simulated data,
for the large box realizations. We do not introduce the
spatial biasing between selected particles and the underlying dark
matter, which will be discussed elsewhere. For comparison, we also
select the similar number of particles randomly but independently of
their redshifts. It should be emphasized here that our simulated data
are constructed to match the shape of the above selection
functions but not the amplitudes of the number densities. The
field-of-view of our simulated data, ![]() degree2, is
substantially smaller than those of 2dF and SDSS, and we sample
particles much more densely than the realistic number density.
degree2, is
substantially smaller than those of 2dF and SDSS, and we sample
particles much more densely than the realistic number density.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{MS10074f3.eps}\end{figure}](/articles/aa/full/2001/07/aa10074/Timg110.gif) |
Figure 3: Selection function of galaxies in a case of SCDM model on the basis of the B-band luminosity function of APM galaxies (Loveday et al. 1992) |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{MS10074f4.eps}\end{figure}](/articles/aa/full/2001/07/aa10074/Timg111.gif) |
Figure 4: Selection function of QSOs in a case of SCDM model on the basis of the 2dF QSO sample (Boyle et al. 2000) |
| Open with DEXTER | |
In order to examine the robustness of the estimates from the simulated
data, we randomly selected
![]() particles from the entire
light-cone volume (independently of their redshifts). The resulting
correlation functions are plotted in the right panels. It is
remarkable that the estimates on scales larger than
particles from the entire
light-cone volume (independently of their redshifts). The resulting
correlation functions are plotted in the right panels. It is
remarkable that the estimates on scales larger than ![]()
![]() are almost the same. This also indicates that the error-bars in
our data are dominated by the sample-to-sample variation among the
different realizations.
are almost the same. This also indicates that the error-bars in
our data are dominated by the sample-to-sample variation among the
different realizations.
![\begin{figure}
\par\includegraphics[width=11cm,height=10.5cm,clip]{MS10074f5.eps}\end{figure}](/articles/aa/full/2001/07/aa10074/Timg113.gif) |
Figure 5: Mass two-point correlation functions on the light cone without redshift-dependent selection functions in SCDM model. Upper: z<0.4, Lower: 0<z<2.0. Left: all particles on the light cone, Right: randomly selected particles |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=11cm,clip]{MS10074f6.eps}\end{figure}](/articles/aa/full/2001/07/aa10074/Timg114.gif) |
Figure 6:
Same as Fig. 5 but for |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=12cm,height=10.5cm,clip]{MS10074f7.eps}\end{figure}](/articles/aa/full/2001/07/aa10074/Timg115.gif) |
Figure 7:
Mass two-point correlation functions on the light cone for
particles with redshift-dependent selection functions in SCDM model.
Upper: z<0.4, Lower: 0.2<z<2.0.
Left: with selection function whose shape
is the same as that of the B-band magnitude limit of
19 for galaxies (upper) and 21 for QSOs (lower).
Right: randomly selected
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=11cm,height=10.5cm,clip]{MS10074f8.eps}\end{figure}](/articles/aa/full/2001/07/aa10074/Timg116.gif) |
Figure 8:
Same as Fig. 7 but for |
| Open with DEXTER | |
We have presented detailed comparison between the theoretical modeling
and the direct numerical results of the two-point correlation
functions on the light-cone. In short, we have quantitatively shown
that the previous theoretical models by Yamamoto & Suto (1999) and
Yamamoto et al. (1999) are quite accurate on scales
![]() where the numerical
simulations are reliable. It is also encouraging that this conclusion
remains true even for the particle number of around 104. In fact,
the error-bars in our estimates of the two-point correlation functions
are dominated by the sample-to-sample variance due to the limited
angular-size (
where the numerical
simulations are reliable. It is also encouraging that this conclusion
remains true even for the particle number of around 104. In fact,
the error-bars in our estimates of the two-point correlation functions
are dominated by the sample-to-sample variance due to the limited
angular-size (![]() -degree2) and thus the limited volume.
-degree2) and thus the limited volume.
In order for the more realistic evaluation of the statistical and systematic uncertainties, one needs mock light-cone data samples with a much wider sky coverage. More importantly such datasets enable one to access the effect of biasing on the two-point correlation functions on the light-cone. Since our present study indicated that all the physical effects except for the biasing are well described by the existing theoretical models, it is very interesting to examine in detail how to extract the effect of the galaxy/QSO biasing from the upcoming redshift survey on the basis of the above mock samples. We plan to come back to these issues with larger simulation datasets in near future.
Acknowledgements
This research was supported in part by the Direction de la Recherche du Ministère Français de la Recherche and the Grant-in-Aid by the Ministry of Education, Science, Sports and Culture of Japan (07CE2002) to RESCEU. The computational resources (CRAY-98) for the present numerical simulations were made available to us by the scientific council of the Institut du Développement et des Ressources en Informatique Scientifique (IDRIS).