of the 3.4
A&A 367, 347-354 (2001)
DOI: 10.1051/0004-6361:20000341
G. M. Muñoz Caro 1 - R. Ruiterkamp 1 - W. A. Schutte 1 - J. M. Greenberg 1 - V. Mennella2
1 - Raymond and Beverly Sackler Laboratory for Astrophysics at Leiden
Observatory, 2300 RA Leiden, The Netherlands
2 - Osservatorio Astronomico di Capodimonte, via Moiariello 16, 80131 Napoli, Italy
Received 26 June 2000 / Accepted 28 November 2000
Abstract
Experiments simulating the processing of various hydrocarbon species under
diffuse and dense cloud conditions by UV irradiation were performed.
The results indicate that
such molecules will be efficiently dehydrogenated in interstellar space.
It is argued that the presence of hydrogen in the aliphatic grain material
in diffuse clouds results from an equilibrium between dehydrogenation by
UV processing and re-hydrogenation by the impinging atomic gas.
In dense clouds, the presence of the ice layer will prevent the
re-hydrogenation process, causing the carbonaceous grain material to be
gradually de-hydrogenated if UV photons are able to penetrate into
the dense medium. The implications of this study for the evolution of the
carbonaceous component of dust in the interstellar medium are discussed.
Key words: ISM: dust, extinction - infrared: ISM: lines and bands - methods: laboratory
The composition of the carbonaceous dust in various galactic regions
has mainly been probed from the 3.4 ![]() m band due to the aliphatic C-H
stretching mode. Observations show that, relative to the 9.7
m band due to the aliphatic C-H
stretching mode. Observations show that, relative to the 9.7 ![]() m silicate feature,
the 3.4
m silicate feature,
the 3.4 ![]() m band is reduced in the spectra of dense cloud dust as compared
to that of diffuse medium dust (Allamandola et al. 1992,
1993; Brooke et al. 1996; Chiar et al. 1996). This difference
led to the suggestion that carbonaceous dust material
is destroyed inside dense clouds (Pendleton 1999). In view of the
continuous cycling of material between the dense and diffuse phases of
the interstellar medium (Greenberg 1985; McKee 1989),
this would imply that there must
be a highly efficient mechanism to form organic species in the ISM to
counterbalance the destruction.
m band is reduced in the spectra of dense cloud dust as compared
to that of diffuse medium dust (Allamandola et al. 1992,
1993; Brooke et al. 1996; Chiar et al. 1996). This difference
led to the suggestion that carbonaceous dust material
is destroyed inside dense clouds (Pendleton 1999). In view of the
continuous cycling of material between the dense and diffuse phases of
the interstellar medium (Greenberg 1985; McKee 1989),
this would imply that there must
be a highly efficient mechanism to form organic species in the ISM to
counterbalance the destruction.
To investigate how the cycling of the dust from the dense to the diffuse medium would affect the chemical evolution of the carbonaceous dust material,
this article reports on laboratory experiments involving UV processing
of simple hydrocarbon species under simulated dense and
diffuse cloud conditions. Observations of interstellar dust suggest
that the 3.4 ![]() m band is due to short aliphatic chains attached to aromatic
structures (Sandford et al. 1991; Pendleton et al. 1994).
Hexane (C6H14) was adopted as it fulfils the
-CH2-/-CH3 ratio of 2-2.5 suggested by the observations
(Furton et al. 1999).
Ethane (C2H6) was used to investigate the effect of the chain length
on the photodestruction rate.
Ethylbenzene (C6H5-C2H5) was used to study the
case of an aliphatic chain attached to an aromatic structure.
Since the carbonaceous dust material is probably characterized by
polyaromatic structures (Furton et al. 1999; Mennella et al. 1998;
Schnaiter et al. 1999), ethylbenzene is not a fully adequate
analog material. However, this study focuses
on the aliphatic component of the interstellar organics, and is therefore only
concerned with the influence of an attached aromatic ring structure on the
destruction efficiency of the aliphatic chain.
m band is due to short aliphatic chains attached to aromatic
structures (Sandford et al. 1991; Pendleton et al. 1994).
Hexane (C6H14) was adopted as it fulfils the
-CH2-/-CH3 ratio of 2-2.5 suggested by the observations
(Furton et al. 1999).
Ethane (C2H6) was used to investigate the effect of the chain length
on the photodestruction rate.
Ethylbenzene (C6H5-C2H5) was used to study the
case of an aliphatic chain attached to an aromatic structure.
Since the carbonaceous dust material is probably characterized by
polyaromatic structures (Furton et al. 1999; Mennella et al. 1998;
Schnaiter et al. 1999), ethylbenzene is not a fully adequate
analog material. However, this study focuses
on the aliphatic component of the interstellar organics, and is therefore only
concerned with the influence of an attached aromatic ring structure on the
destruction efficiency of the aliphatic chain.
In the next paper of this series (Mennella et al. 2001; henceforth Paper II) amorphous carbon grains are the material submitted to photoprocessing, which should be more representative of the carbonaceous matter of interstellar grains. Nevertheless, we wanted to study the processing of a number of well defined species to investigate the dependence on such parameters as the molecular size, the presence of aromatic structures and the thickness of the sample. These results will be used in Paper II to assess the robustness of the results for the more realistic but chemically more complex analog material.
The layout of this paper is as follows:
in Sect. 2 of this paper we derive upper limits for
the strength of the 3.4 ![]() m feature of the dense medium and compare
these to the 3.4
m feature of the dense medium and compare
these to the 3.4 ![]() m feature which is observed in
the diffuse medium. The experimental protocol is described in Sect. 3.
The experimental results are presented in Sect. 4, and discussed
in Sect. 5. Section 6 reviews the astrophysical implications.
Finally, our conclusions are reported in Sect. 7.
m feature which is observed in
the diffuse medium. The experimental protocol is described in Sect. 3.
The experimental results are presented in Sect. 4, and discussed
in Sect. 5. Section 6 reviews the astrophysical implications.
Finally, our conclusions are reported in Sect. 7.
While the reduction of the strength of the interstellar 3.4 ![]() m feature
in dense interstellar regions was already noted by Allamandola et al. (1993), no upper limits have yet been derived quantitatively. Such upper limits
are of major importance as a criterion to test any model proposed
for this reduction.
m feature
in dense interstellar regions was already noted by Allamandola et al. (1993), no upper limits have yet been derived quantitatively. Such upper limits
are of major importance as a criterion to test any model proposed
for this reduction.
![\begin{figure}
\par\includegraphics[width=13cm,clip]{10042_f1.ps}\end{figure}](/articles/aa/full/2001/07/aa10042/Timg8.gif) |
Figure 1:
Sequential addition of the 3.4 |
| Open with DEXTER | |
A direct integration of the optical depth of the 3.4 ![]() m
band towards embedded protostars is difficult, due to the presence
of broad absorption features in this region, such as the 3.05
m
band towards embedded protostars is difficult, due to the presence
of broad absorption features in this region, such as the 3.05 ![]() m H2O
band, the "diamond'' feature at 3.47
m H2O
band, the "diamond'' feature at 3.47 ![]() m (Allamandola et al. 1992;
Chiar et al. 1996; Brooke et al. 1999),
the 3.25
m (Allamandola et al. 1992;
Chiar et al. 1996; Brooke et al. 1999),
the 3.25 ![]() m band with frozen PAHs as possible carrier
(Sellgren et al. 1994, 1995), the CH stretch modes of solid CH3OH at
3.48
m band with frozen PAHs as possible carrier
(Sellgren et al. 1994, 1995), the CH stretch modes of solid CH3OH at
3.48 ![]() m and 3.54
m and 3.54 ![]() m (Grim et al. 1991; Allamandola et al. 1992;
Schutte et al. 1996; d'Hendecourt et al. 1996;
Dartois et al. 1999) and the "long wavelength shoulder'' of the 3.05
m (Grim et al. 1991; Allamandola et al. 1992;
Schutte et al. 1996; d'Hendecourt et al. 1996;
Dartois et al. 1999) and the "long wavelength shoulder'' of the 3.05 ![]() m
feature centered around 3.4
m
feature centered around 3.4 ![]() m (Willner et al. 1982; Smith et al. 1988).
Instead, we obtained upper limits of the 3.4
m (Willner et al. 1982; Smith et al. 1988).
Instead, we obtained upper limits of the 3.4 ![]() m feature in the dense
medium by sequential addition of the 3.4
m feature in the dense
medium by sequential addition of the 3.4 ![]() m feature as observed
towards a diffuse interstellar medium source,
GC IRS6E (adopted from Pendleton et al. 1994), to the spectra of four
YSOs, namely GL 2136, MonR2/IRS2, W33A (Brooke et al. 1999),
NGC 7538/IRS9 (Allamandola et al. 1992), as well as the background field
star Elias 16 (Chiar et al. 1996).
This approach can be elucidated in the following
way. If a 3.4
m feature as observed
towards a diffuse interstellar medium source,
GC IRS6E (adopted from Pendleton et al. 1994), to the spectra of four
YSOs, namely GL 2136, MonR2/IRS2, W33A (Brooke et al. 1999),
NGC 7538/IRS9 (Allamandola et al. 1992), as well as the background field
star Elias 16 (Chiar et al. 1996).
This approach can be elucidated in the following
way. If a 3.4 ![]() m feature is present in the absorption spectrum towards
a source obscured by dense cloud material, the spectrum is given by
m feature is present in the absorption spectrum towards
a source obscured by dense cloud material, the spectrum is given by
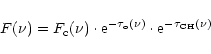 |
(1) |
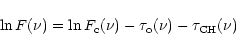 |
(2) |
After addition of the 3.4 ![]() m feature as observed in the diffuse
interstellar medium, multiplied by a variable factor C, to the observed
spectrum
m feature as observed in the diffuse
interstellar medium, multiplied by a variable factor C, to the observed
spectrum ![]() )
this becomes
)
this becomes
| = | |||
| (3) |
In order to compare the composition of the dust particles in the dense and
the diffuse medium, Table 1 lists the ratios of the intensity of the 3.4 ![]() m feature over the 9.7
m feature over the 9.7 ![]() m silicate feature depth.
The 9.7
m silicate feature depth.
The 9.7 ![]() m optical depth towards the YSOs, corrected for the underlying
emission feature, was calculated using
m optical depth towards the YSOs, corrected for the underlying
emission feature, was calculated using
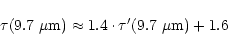 |
(4) |
From the values of
![]() listed in Table 1, it
can be concluded that
listed in Table 1, it
can be concluded that ![]() 55% of the 3.4
55% of the 3.4 ![]() m carrier is destroyed
for GL 2136,
m carrier is destroyed
for GL 2136, ![]() 50% for NGC 7538/IRS9 and
50% for NGC 7538/IRS9 and ![]() 30% for W33A. For
MonR2/IRS2 and Elias 16 the upper
limits are less stringent, and could be
consistent with no destruction of the 3.4
30% for W33A. For
MonR2/IRS2 and Elias 16 the upper
limits are less stringent, and could be
consistent with no destruction of the 3.4 ![]() m band.
However, the results for GL 2136, NGC 7538/IRS9 and W33A show that,
at least towards some embedded sources, the
3.4
m band.
However, the results for GL 2136, NGC 7538/IRS9 and W33A show that,
at least towards some embedded sources, the
3.4 ![]() m feature is substantially reduced.
m feature is substantially reduced.
| Source | Type |
|
|
|
| GL 2136 | YSO, dense | 5.07b | ||
| NGC 7538/IRS9 | YSO, dense | 4.46b | ||
| MonR2/IRS2 | YSO, dense | 1c | ||
| W33A | YSO, dense | 7.84b | ||
| Elias 16 | field, dense | 0.81e | ||
| GC IRS 6E | field, diffuse | 0.21a | 3.6 |
0.058 |
| a Pendleton et al. (1994). |
| b Willner et al. (1982). |
| c Beckwith et al. (1976). |
| d Roche & Aitken (1984). |
| e Bowey et al. (1998). |
Details of the experimental set-up have been
described earlier (Gerakines et al. 1995). In summary, the set-up
consists of a high vacuum chamber (![]()
![]() mbar)
with an IR transparent substrate mounted on a cold finger which is
cooled to
mbar)
with an IR transparent substrate mounted on a cold finger which is
cooled to ![]() 12 K. Samples can be controllably deposited
(
12 K. Samples can be controllably deposited
(![]() 1014 molec
1014 molec
![]()
![]() )
through
a narrow tube. A hydrogen flow discharge lamp
provides vacuum UV photons
(
)
through
a narrow tube. A hydrogen flow discharge lamp
provides vacuum UV photons
(![]() 5
5
![]() photons
photons
![]()
![]() ;
;
![]()
![]() 6 eV).
The evolution of the sample is monitored by infrared transmission
spectroscopy.
6 eV).
The evolution of the sample is monitored by infrared transmission
spectroscopy.
The carbonaceous component of interstellar grains was simulated by deposition
of a thin layer (typically 0.01 ![]() m or
m or
![]() cm-2) of various aliphatic and aromatic compounds.
Aliphatics were deposited on a CsI substrate window,
while ethylbenzene was deposited both on the CsI and a quartz substrate
window. The reason for this was that quartz does not adsorb molecules as readily as
CsI, thus providing a cleaner substrate and smooth background in the
important CH stretching region. This is especially important for
experiments using aromatic species, which have relatively weak C-H stretching
bands. For quartz substrates the infrared range is limited to 4000-2200 cm-1.
The species used were hexane
(C6H12, Merck,
cm-2) of various aliphatic and aromatic compounds.
Aliphatics were deposited on a CsI substrate window,
while ethylbenzene was deposited both on the CsI and a quartz substrate
window. The reason for this was that quartz does not adsorb molecules as readily as
CsI, thus providing a cleaner substrate and smooth background in the
important CH stretching region. This is especially important for
experiments using aromatic species, which have relatively weak C-H stretching
bands. For quartz substrates the infrared range is limited to 4000-2200 cm-1.
The species used were hexane
(C6H12, Merck, ![]() 97%), ethane (C2H6,
Praxair, 99.99%) and
ethylbenzene (C6H5-C2H5, Merck-Schuchardt, >99%).
A layer thickness of 0.01
97%), ethane (C2H6,
Praxair, 99.99%) and
ethylbenzene (C6H5-C2H5, Merck-Schuchardt, >99%).
A layer thickness of 0.01 ![]() m corresponds to typical dimensions of the
carbonaceous component of interstellar dust
(Mathis et al. 1977; Li & Greenberg 1997).
To emulate the icy mantle accreting in dense clouds, the carbonaceous
layer was covered by an H2O ice cap, triply distilled,
of typically
m corresponds to typical dimensions of the
carbonaceous component of interstellar dust
(Mathis et al. 1977; Li & Greenberg 1997).
To emulate the icy mantle accreting in dense clouds, the carbonaceous
layer was covered by an H2O ice cap, triply distilled,
of typically ![]() 0.01
0.01 ![]() m (N(H2O) = 3 1016 cm-2).
This is consistent with mantle thicknesses
expected for grains in dense clouds (Schutte & Greenberg 1991;
Kim & Martin 1996). The ice
mixture
m (N(H2O) = 3 1016 cm-2).
This is consistent with mantle thicknesses
expected for grains in dense clouds (Schutte & Greenberg 1991;
Kim & Martin 1996). The ice
mixture ![]() :CO:
:CO:![]() = 5:2:1 (CO, Praxair, 99.997%;
NH3, Praxair, 99.9995%) was also employed. To reproduce diffuse medium
conditions, the hydrocarbon layer was sandwiched in
argon (Praxair, 99.9997%), layer thickness
= 5:2:1 (CO, Praxair, 99.997%;
NH3, Praxair, 99.9995%) was also employed. To reproduce diffuse medium
conditions, the hydrocarbon layer was sandwiched in
argon (Praxair, 99.9997%), layer thickness ![]() 0.5
0.5 ![]() m, to isolate
it from the background gas in the
vacuum set-up (mostly H2O; Gerakines et al. 1996). Both the diffuse
and dense medium analog samples were exposed to UV radiation, with infrared
spectra taken at regular intervals. Experimental parameters are listed in
Table 3.
The carbon column density of the sample, N(C), and the column
density of the ice cap on top of the carbon layer, N(ice), were obtained by
integration of the spectral features:
m, to isolate
it from the background gas in the
vacuum set-up (mostly H2O; Gerakines et al. 1996). Both the diffuse
and dense medium analog samples were exposed to UV radiation, with infrared
spectra taken at regular intervals. Experimental parameters are listed in
Table 3.
The carbon column density of the sample, N(C), and the column
density of the ice cap on top of the carbon layer, N(ice), were obtained by
integration of the spectral features:
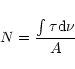 |
(5) |
| Species | Feature | Position | Position | A | Ref. |
| cm-1 | cm mol-1 | ||||
| H2O | OH stretch | 3.05 | 3279 | 2.0 10-16 | a |
| C2H6 | CH stretch | 3.4 | 2940 | 1.0 10-17 | b |
| C6H14 | CH stretch | 3.4 | 2940 | 3.5 10-17 | b |
| Ethylb. | aliph. CH st. | 3.4 | 2940 | 1.7 10-17 | c |
| a Hagen et al. (1981). | |
| Open with DEXTER | |
| b Wexler (1967). | |
| c Obtained from strength relative to the aromatic feature. | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{10042_f2.ps}\end{figure}](/articles/aa/full/2001/07/aa10042/Timg39.gif) |
Figure 2: Infrared spectrum of a layer of hexane covered by H2O ice, corresponding to Exp. No. 2 in Table 3, before and after irradiation. For clarity, the spectra have been offset |
Figure 2 shows a spectroscopic record of the photochemical
evolution of a dense medium analog sample consisting of a hexane layer covered
by water ice (Exp. No. 2, Table 3). The
spectrum shows that, as a result of the photolysis, the CH stretching
mode at 2940
![]() (3.4
(3.4 ![]() m) and the CH bending
modes around 1400 cm-1 (7.1
m) and the CH bending
modes around 1400 cm-1 (7.1 ![]() m) are strongly reduced.
Although features due to CO and
m) are strongly reduced.
Although features due to CO and ![]() develop during irradiation, it was
found by means of control experiments, where only water was deposited and
irradiated, that accretion and
photolysis of background gases, i.e. contamination, can fully account for
the formation of these features.
develop during irradiation, it was
found by means of control experiments, where only water was deposited and
irradiated, that accretion and
photolysis of background gases, i.e. contamination, can fully account for
the formation of these features.
Figure 3 traces the evolution of the 3.4 ![]() m feature as
a function of irradiation dose for three
samples with similar thickness of the hexane layer but with varying ice
thickness (see Table 3). Error bars were obtained by performing
the integration of the feature with polynomial baselines of different order.
It shows that the destruction of the CH bond decreases somewhat for thicker
ice caps, apparently due to absorption of the UV by the ice.
Figure 4 compares the destruction of the 3.4
m feature as
a function of irradiation dose for three
samples with similar thickness of the hexane layer but with varying ice
thickness (see Table 3). Error bars were obtained by performing
the integration of the feature with polynomial baselines of different order.
It shows that the destruction of the CH bond decreases somewhat for thicker
ice caps, apparently due to absorption of the UV by the ice.
Figure 4 compares the destruction of the 3.4 ![]() m feature for
samples with different hexane thickness but similar ice cap.
Clearly, the destruction rate of the 3.4
m feature for
samples with different hexane thickness but similar ice cap.
Clearly, the destruction rate of the 3.4 ![]() m feature is higher for thinner
carbon layers. No significant difference was found
between the destruction of the 3.4
m feature is higher for thinner
carbon layers. No significant difference was found
between the destruction of the 3.4 ![]() m feature of ethane and hexane,
indicating that the length of the aliphatic chain is not relevant
(Fig. 5). Furthermore, the composition of the ice
cap, whether pure H2O or H2O:CO:NH3 = 5:2:1, does not appreciably
affect the evolution of the 3.4
m feature of ethane and hexane,
indicating that the length of the aliphatic chain is not relevant
(Fig. 5). Furthermore, the composition of the ice
cap, whether pure H2O or H2O:CO:NH3 = 5:2:1, does not appreciably
affect the evolution of the 3.4 ![]() m band under photolysis.
m band under photolysis.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{10042_f3.ps}\end{figure}](/articles/aa/full/2001/07/aa10042/Timg42.gif) |
Figure 3:
Destruction of the 3.4 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{10042_f4.ps}\end{figure}](/articles/aa/full/2001/07/aa10042/Timg43.gif) |
Figure 4:
Destruction of the 3.4 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{10042_f5.ps}\end{figure}](/articles/aa/full/2001/07/aa10042/Timg44.gif) |
Figure 5:
Destruction of the 3.4 |
| Open with DEXTER | |
To quantify these results, we calculated the destruction
cross section
![]() for aliphatic CH bonds using
for aliphatic CH bonds using
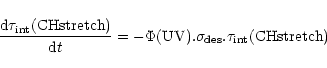 |
(6) |
| Exp. No. | Species | N(C) | N(icea) |
|
| cm-2 | cm-2 | cm2 | ||
| 1 | Hexane | 3.4 1017 | 2.3 1016 | 3.6 10-19 |
| 2 | Hexane | 7.1 1016 | 2.8 1016 | 8.4 10-19 |
| 3 | Hexane | 6.8 1016 | 5.3 1016 | 8.6 10-19 |
| 4 | Hexane | 6.5 1016 | 2.9 1015 | 9.0 10-19 |
| 5 | Hexane | 3.5 1016 | 3.1 1016 | 3.2 10-18 |
| 6 | Hexane | 2.4 1016 | 3.7 1016 | 2.6 10-18 |
| 7 | Hexane | 9.5 1016 | 3.8 1016b | 6.4 10-19 |
| 8 | Hexane | 6.1 1016 | -c | 2.2 10-18 |
| 9 | Ethane | 1.4 1017 | 3.1 1016 | 8.2 10-19 |
| 10 | Ethylb. | 3.8 1016 | 7.1 1016 | 5.0 10-19 |
| a H2O ice, unless otherwise noted. |
| b Ice mixture H2O:CO:NH3 = 5:2:1. |
| c Sandwiched in Ar. |
Figure 6 shows the destruction of the 3.4 ![]() m feature of
ethylbenzene capped by water ice as function of the irradiation dose
(Exp. No. 10, Table 3). Note that the applied irradiation dose is
higher than it was for the pure hydrocarbons (cf., Figs. 3 and 4).
Even though the destruction of the aliphatic 3.4
m feature of
ethylbenzene capped by water ice as function of the irradiation dose
(Exp. No. 10, Table 3). Note that the applied irradiation dose is
higher than it was for the pure hydrocarbons (cf., Figs. 3 and 4).
Even though the destruction of the aliphatic 3.4 ![]() m band of ethylbenzene
is less rapid than for pure aliphatic molecules such as hexane, still 40% is
destroyed after 3 hr of
irradiation (5 1018 photons cm-2) and 80% after 15 hr
(2.5 1019 photons cm-2).
The difference might be due to the presence of the aromatic ring giving more
stability to the molecule by allowing distribution of the UV induced
excitation.
m band of ethylbenzene
is less rapid than for pure aliphatic molecules such as hexane, still 40% is
destroyed after 3 hr of
irradiation (5 1018 photons cm-2) and 80% after 15 hr
(2.5 1019 photons cm-2).
The difference might be due to the presence of the aromatic ring giving more
stability to the molecule by allowing distribution of the UV induced
excitation.
The decrease of the 3.4 ![]() m band of the carbon-based materials upon
irradiation may result from a number of mechanisms. First,
the material may be destroyed by highly oxidizing species
formed by photolysis of the ice cap, such as OH radicals. Second, reactions
with ice photofragments may insert oxygen containing groups like
hydroxy and carbonyl into the carbon skeleton. Such
groups strongly decrease the intensity
of nearby CH stretching modes (Wexler 1967). Finally, because
the UV photon energy is larger than the bond enthalpy (
m band of the carbon-based materials upon
irradiation may result from a number of mechanisms. First,
the material may be destroyed by highly oxidizing species
formed by photolysis of the ice cap, such as OH radicals. Second, reactions
with ice photofragments may insert oxygen containing groups like
hydroxy and carbonyl into the carbon skeleton. Such
groups strongly decrease the intensity
of nearby CH stretching modes (Wexler 1967). Finally, because
the UV photon energy is larger than the bond enthalpy (![]() 4.3 eV for aliphatic CH bonds),
photolysis may break CH bonds and dehydrogenate the carbonaceous sample.
4.3 eV for aliphatic CH bonds),
photolysis may break CH bonds and dehydrogenate the carbonaceous sample.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{10042_f6.ps}\end{figure}](/articles/aa/full/2001/07/aa10042/Timg50.gif) |
Figure 6:
Destruction of the 3.4 |
| Open with DEXTER | |
The experimental results suggest that dehydrogenation is the main cause of
the decrease of the CH stretching mode. First, it is clear that
destruction is higher with thinner ice caps (Table 3),
arguing against any mechanism in which the
interaction with water ice photoproducts causes the reduction.
Indeed, the highest destruction is obtained when the hydrocarbon layer
is covered only with argon. Second, if the carbonaceous layer is broken up
by the attack of, say, OH radicals, the growth of features of new species,
e.g. CO, CO2, HCO, should be observed. Although some CO and ![]() is formed during the photolysis (Fig. 2), comparison with blank
experiments shows this can be explained by accretion and photolysis of
background gases, indicating that breakdown of the carbon skeleton
accounts for less than
is formed during the photolysis (Fig. 2), comparison with blank
experiments shows this can be explained by accretion and photolysis of
background gases, indicating that breakdown of the carbon skeleton
accounts for less than ![]() 2% of the decrease of the 3.4
2% of the decrease of the 3.4 ![]() m band.
Third, the spectrum of the residue, obtained
from Experiment 1 (Table 3) after 3 hours of irradiation (
m band.
Third, the spectrum of the residue, obtained
from Experiment 1 (Table 3) after 3 hours of irradiation (![]() 5 1018 photon cm-2) of a hexane/ice
sample and subsequent warm-up to 200 K, shows
little evidence of oxygen containing groups (Fig. 7). Perhaps the broad band
underlying the CH stretching mode centered at
5 1018 photon cm-2) of a hexane/ice
sample and subsequent warm-up to 200 K, shows
little evidence of oxygen containing groups (Fig. 7). Perhaps the broad band
underlying the CH stretching mode centered at ![]() 3300
3300
![]() could derive from the OH stretch of hydroxy (-OH) groups,
although another possibility is the presence of some residual
could derive from the OH stretch of hydroxy (-OH) groups,
although another possibility is the presence of some residual ![]() locked inside the residue (this possibility is supported by
the trapping of some
locked inside the residue (this possibility is supported by
the trapping of some ![]() in the residue).
Furthermore, while
the position of the feature at 1645
in the residue).
Furthermore, while
the position of the feature at 1645
![]() is indicative of
unsaturated C=C bonds, a weak shoulder at
is indicative of
unsaturated C=C bonds, a weak shoulder at ![]() 1700
1700
![]() may indicate the presence of carbonyl (C=O) groups in the residue. The
weakness of these bands shows that less than 20% of the C atoms are
bound to O-containing groups, too little to explain the reduction of
the CH stretching mode. Finally, the strong features in the residue
spectrum of unsaturated C-C bonds constitute direct evidence for the
importance of dehydrogenation. The residue spectra of ice capped irradiated
ethylbenzene (Exp. No. 10) at 200 K shows no significant features.
For the C=O stretching mode at
may indicate the presence of carbonyl (C=O) groups in the residue. The
weakness of these bands shows that less than 20% of the C atoms are
bound to O-containing groups, too little to explain the reduction of
the CH stretching mode. Finally, the strong features in the residue
spectrum of unsaturated C-C bonds constitute direct evidence for the
importance of dehydrogenation. The residue spectra of ice capped irradiated
ethylbenzene (Exp. No. 10) at 200 K shows no significant features.
For the C=O stretching mode at ![]() 1700 cm-1 we obtained
N(C=O)/N(CH) < 0.1, where N(CH) refers to the column density obtained from
integration of the CH stretch after deposition.
For the -OH deformation mode at
1700 cm-1 we obtained
N(C=O)/N(CH) < 0.1, where N(CH) refers to the column density obtained from
integration of the CH stretch after deposition.
For the -OH deformation mode at ![]() 1350 cm-1 it was found
N(OH)/N(CH) < 0.1.
We thus conclude that dehydrogenation by interaction with UV photons
is responsible for the decrease of the CH stretching features in our
experiments.
1350 cm-1 it was found
N(OH)/N(CH) < 0.1.
We thus conclude that dehydrogenation by interaction with UV photons
is responsible for the decrease of the CH stretching features in our
experiments.
 |
Figure 7: Residue spectrum of a layer of hexane covered by H2O ice after 3 hr of UV-irradiation (5 1018 photon cm-2) and warm-up to 200 K to evaporate the ice cap |
| Open with DEXTER | |
Our experimental results show that hydrocarbon molecules will be
dehydrogenated in the diffuse medium. We derive that for aliphatic chains,
like hexane, dehydrogenation by
![]() 80% requires a dose of 5 1018 UV photon
80% requires a dose of 5 1018 UV photon
![]() (Fig. 4). With a UV field 8 107 photon
(Fig. 4). With a UV field 8 107 photon
![]()
![]() (
(
![]() eV) in the
diffuse galactic medium (Mathis et al. 1983), this corresponds to
2
eV) in the
diffuse galactic medium (Mathis et al. 1983), this corresponds to
2 ![]() yr. The aliphatic component of ethylbenzene requires a
yr. The aliphatic component of ethylbenzene requires a
![]() 5 times higher dose to achieve an 80% dehydrogenation (Fig. 6),
corresponding to
5 times higher dose to achieve an 80% dehydrogenation (Fig. 6),
corresponding to
![]() 1 104 yr.
In Paper II it will be reported that the dehydrogenation of more complex
carbonaceous materials, which are likely more analogous to interstellar
dust, also proceeds efficiently.
1 104 yr.
In Paper II it will be reported that the dehydrogenation of more complex
carbonaceous materials, which are likely more analogous to interstellar
dust, also proceeds efficiently.
Our results suggest that aliphatic solids can only survive
in the diffuse interstellar medium if a hydrogenation mechanism
is active (Mennella et al. 1999). Such a mechanism was earlier proposed to
explain the "turn-on'' of the 3.4 ![]() m feature in proto-planetary nebula (Schnaiter et al. 1999).
A bountiful stock of atomic hydrogen is present in
the gas phase in the diffuse ISM. If the loss of hydrogen is balanced by the
formation of aliphatic groups between solid carbon and gaseous hydrogen,
the following applies:
m feature in proto-planetary nebula (Schnaiter et al. 1999).
A bountiful stock of atomic hydrogen is present in
the gas phase in the diffuse ISM. If the loss of hydrogen is balanced by the
formation of aliphatic groups between solid carbon and gaseous hydrogen,
the following applies:
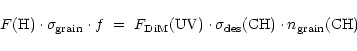 |
(7) |
![\begin{displaymath}\left[\frac{n_{\rm grain}({\rm CH})}{\sigma_{\rm grain}}\righ...
...n_{\rm grain}({\rm CH})}{n_{\rm grain}({\rm C})}\right]\!\cdot
\end{displaymath}](/articles/aa/full/2001/07/aa10042/img60.gif) |
(8) |
![]() is obtained from:
is obtained from:
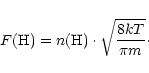 |
(9) |
Inside dense clouds grains will be covered by an ice cap,
consisting primarily of ![]() with in addition CO,
with in addition CO, ![]() ,
probably
,
probably ![]() ,
etc. (Gibb et al. 2000; and references therein).
This cap has a thickness of
,
etc. (Gibb et al. 2000; and references therein).
This cap has a thickness of
![]() 0.01
0.01 ![]() m, i.e.,
m, i.e., ![]() 30 molecular layers (Schutte &
Greenberg 1991). It seems unlikely that any atomic hydrogen
would be able to penetrate the ice mantle and reach the
carbonaceous material. First, hydrogen atoms can be immobilized in ice
at
30 molecular layers (Schutte &
Greenberg 1991). It seems unlikely that any atomic hydrogen
would be able to penetrate the ice mantle and reach the
carbonaceous material. First, hydrogen atoms can be immobilized in ice
at ![]() 12 K, for example, in Ar (van Ijzendoorn et al. 1983).
Second, in the presence of frozen CO, a ubiquitous component of
interstellar ice, formation of HCO
could scavenge diffusing H atoms (van Ijzendoorn et al. 1983).
Third, atomic hydrogen is scarce in the dense cloud environment,
since most of the hydrogen will be in the form of H2.
It therefore seems likely that hydrogenation of carbonaceous grain
material will cease inside dense clouds. However, in spite of the
ice cover, our experiments show that dehydrogenation
of the carbonaceous material will proceed as long as some UV is
present (Sect. 4). Therefore the carbonaceous grain material inside
dense clouds will be dehydrogenated gradually.
12 K, for example, in Ar (van Ijzendoorn et al. 1983).
Second, in the presence of frozen CO, a ubiquitous component of
interstellar ice, formation of HCO
could scavenge diffusing H atoms (van Ijzendoorn et al. 1983).
Third, atomic hydrogen is scarce in the dense cloud environment,
since most of the hydrogen will be in the form of H2.
It therefore seems likely that hydrogenation of carbonaceous grain
material will cease inside dense clouds. However, in spite of the
ice cover, our experiments show that dehydrogenation
of the carbonaceous material will proceed as long as some UV is
present (Sect. 4). Therefore the carbonaceous grain material inside
dense clouds will be dehydrogenated gradually.
The results in Sect. 4 indicate that the UV fluence necessary to achieve
80% dehydrogenation (the reduction consistent with the observational
constraints; Sect. 2) equals ![]() 2.5 1019 photons
2.5 1019 photons
![]() (Fig. 6). Very similar requirements for the amount of processing will be reported in Paper II, based on experiments with the more realistic analog material.
The internal UV field cannot provide such a processing in dense clouds.
Thus, the penetration of the galactic
radiation field, involving intense short term exposures of grains during
a fraction of the lifetime of an interstellar cloud when they reside in the outer regions, should be the driving factor for the reduction of the 3.4
(Fig. 6). Very similar requirements for the amount of processing will be reported in Paper II, based on experiments with the more realistic analog material.
The internal UV field cannot provide such a processing in dense clouds.
Thus, the penetration of the galactic
radiation field, involving intense short term exposures of grains during
a fraction of the lifetime of an interstellar cloud when they reside in the outer regions, should be the driving factor for the reduction of the 3.4 ![]() m feature (see an extended discussion in Paper II). Whether this scenario is realistic depends on the nature of the circulation
of matter in dense clouds. Theoretical modelling of this effect as well as
of the penetration of radiation into filamentary clouds is required to
better understand the extent to which grains in dense regions may be
UV-processed.
m feature (see an extended discussion in Paper II). Whether this scenario is realistic depends on the nature of the circulation
of matter in dense clouds. Theoretical modelling of this effect as well as
of the penetration of radiation into filamentary clouds is required to
better understand the extent to which grains in dense regions may be
UV-processed.
It is intriguing that the dose estimated from the reduction of the 3.4 ![]() m feature is very similar to the dose required to produce the amount of
CO2 ice which is observed in Taurus towards the field star Elias 16
(3 1019 photons cm-2; Whittet et al. 1998). Thus, the present results may point to the importance of UV processing for the chemical evolution of dense
cloud ices.
m feature is very similar to the dose required to produce the amount of
CO2 ice which is observed in Taurus towards the field star Elias 16
(3 1019 photons cm-2; Whittet et al. 1998). Thus, the present results may point to the importance of UV processing for the chemical evolution of dense
cloud ices.
In this scenario, the observed decrease of the CH stretching mode under dense cloud conditions can be achieved without destroying the carbonaceous grain material. This alleviates the requirement of highly efficient formation of carbonaceous matter in the ISM.
The astrophysical implications of our results are independent of the exact morphology of the carbonaceous dust material. They equally apply to all of the grains mentioned in Sect. 1, i.e., the physically separate populations of silicate and carbon grains, and the silicate core/carbonaceous mantle particles.
Acknowledgements
We thank T. Y. Brooke and J. E. Chiar for kindly providing us with their observational data files. One of us, G.M.M.C., thanks the Max-Planck-Institut für Aeronomie at Katlenburg-Lindau, in particular the COSAC-Rosetta group, for a fellowship. One of us, V. M., has been supported by ASI and MURST research contracts.