

Up: The orbital period of
Subsections
The object shows multi-scale time variability with a range of 0.3
magnitudes (see Fig. 1). Four pronounced eclipse-like
depressions obviously shape the light curve. Strong flickering with
optical pulse amplitude (semi-amplitude) of about 0.1 magnitude is also
obvious in the light curve detected and identified earlier (Israel et
al. 1998; Uslenghi et al. 2000) as spin related
modulations. The photometric data of 1WGAJ1958.2+3232 were analyzed for
periodicities using the Discrete Fourier Transform (DFT) code (Deeming
1975) with a CLEAN procedure (Roberts et
al. 1987). The CLEANed power spectrum (Fig. 2) of
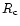 photometric data shows a clear peak at
photometric data shows a clear peak at
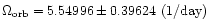 ,
corresponding to
,
corresponding to
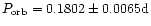 .
This peak
is caused by the above mentioned eclipses in the light curve and clearly
marks the orbital period of the system.
.
This peak
is caused by the above mentioned eclipses in the light curve and clearly
marks the orbital period of the system.
We also found a significant peak at the spin period
 of the WD corresponding to
of the WD corresponding to
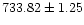 s.
This period is in excellent agreement with that recently discovered
by ASCA X-ray pulsations (Israel et al. 1999). The beat
frequencies at
s.
This period is in excellent agreement with that recently discovered
by ASCA X-ray pulsations (Israel et al. 1999). The beat
frequencies at
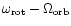 ,
,
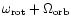 are also present in the
CLEANed power spectrum but with a smaller number of iterations (see
insert in the upper right corner of the Fig. 2). The
harmonics of the basic frequencies
are also present in the
CLEANed power spectrum but with a smaller number of iterations (see
insert in the upper right corner of the Fig. 2). The
harmonics of the basic frequencies
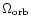 and
and
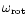 are detected as well. Besides these, there are
comparably significant peaks at the periods of 727.78 s and 1.36 h.
The former was detected also by Uslengi et al. (2000) and
is probably the one-day alias of
are detected as well. Besides these, there are
comparably significant peaks at the periods of 727.78 s and 1.36 h.
The former was detected also by Uslengi et al. (2000) and
is probably the one-day alias of
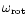 ,
while for
the latter we could not find any reasonable explanation.
,
while for
the latter we could not find any reasonable explanation.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H2429F3.eps}
\par\end{figure}](/articles/aa/full/2001/06/aah2429/Timg31.gif) |
Figure 3:
The diagnostic diagrams for the
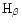 emission
lines. The radial velocity semi-amplitude K, the ratio
emission
lines. The radial velocity semi-amplitude K, the ratio
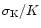 are plotted as a function of the
Gaussian separation, obtained for a period of 0.18152 days
are plotted as a function of the
Gaussian separation, obtained for a period of 0.18152 days |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H2429F4.eps}\par\end{figure}](/articles/aa/full/2001/06/aah2429/Timg32.gif) |
Figure 4:
The radial velocity curves for the emission lines of
H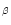 1 and He1II 4686 phased on the spectroscopic
orbital period (0.18152 days) are presented upper and middle panels
respectively. The filled circles corresponds to 4 Aug., filled
rectangulars and open diamonds are 5 and 6 Aug., respectively. Binning
time is 700 s. 1 and He1II 4686 phased on the spectroscopic
orbital period (0.18152 days) are presented upper and middle panels
respectively. The filled circles corresponds to 4 Aug., filled
rectangulars and open diamonds are 5 and 6 Aug., respectively. Binning
time is 700 s. 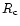 light curve of 1WGAJ1958.2+3232 is presented in the
lower panel. The binning time is 120 s
light curve of 1WGAJ1958.2+3232 is presented in the
lower panel. The binning time is 120 s |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H2429F5.eps}\end{figure}](/articles/aa/full/2001/06/aah2429/Timg33.gif) |
Figure 5:
The power spectrum of the 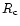 light curve and the
He1II 4686 and H
light curve and the
He1II 4686 and H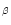 1 radial velocity curves are
presented. They are scaled to the amplitude
of the 1 radial velocity curves are
presented. They are scaled to the amplitude
of the  power spectrum. The
maximum peak of frequency corresponds to the orbital period of the
system
power spectrum. The
maximum peak of frequency corresponds to the orbital period of the
system
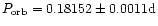
|
The spectrum of 1WGAJ1958.2+3232 shows features characteristic for
Cataclysmic Variables. We refer to Negueruela et
al. (2000), who obtained a spectrum of the object in a
wider spectral range and with better spectral resolution. We also obtained time-resolved spectroscopy of 1WGAJ1958.2+3232 around the
emission lines of H 1#912#>
and He1II, covering
several orbits. Thus, we were able to examine periodical variations
in the spectrum of the object, primarily in the emission lines. The
simple stacking of consecutive spectra onto the trailed spectrum
showed strong variability in the lines. It is distinct in the Balmer lines and
in the higher excitation lines of ionized Helium. The Balmer lines
are double-peaked with an S-wave moving inside, which makes it hard to
see the periodic pattern. In the He1II 4686 line the central
narrow component dominates in most of the phases, and it shows clear
sinusoidal variation.
1#912#>
and He1II, covering
several orbits. Thus, we were able to examine periodical variations
in the spectrum of the object, primarily in the emission lines. The
simple stacking of consecutive spectra onto the trailed spectrum
showed strong variability in the lines. It is distinct in the Balmer lines and
in the higher excitation lines of ionized Helium. The Balmer lines
are double-peaked with an S-wave moving inside, which makes it hard to
see the periodic pattern. In the He1II 4686 line the central
narrow component dominates in most of the phases, and it shows clear
sinusoidal variation.
In order to determine the orbital elements we measured the radial
velocities (RV) of H 1 applying the double Gaussian
deconvolution method introduced by Schneider & Young
(1980), and further developed by Shafter (1983).
This method is especially efficient for measurements of the orbital
motion of CVs with a prominent spot at the edge of the accretion
disk, contaminating the central parts of the emission lines. It
allows us to measure RV variations using the wings of the lines. The
width of the Gaussians were chosen to be slightly larger than our
spectral resolution (8.5 Å), where deconvolution was reached at all
orbital phases. The radial velocities were measured as a function of
distance a between the Gaussians, and then the diagnostic
diagrams were constructed using an initial guess for the orbital
period, derived from photometry and from preliminary radial velocity
measurements via Gaussian fits to the lines. The optimal value of
separation (a= 1175 km
1 applying the double Gaussian
deconvolution method introduced by Schneider & Young
(1980), and further developed by Shafter (1983).
This method is especially efficient for measurements of the orbital
motion of CVs with a prominent spot at the edge of the accretion
disk, contaminating the central parts of the emission lines. It
allows us to measure RV variations using the wings of the lines. The
width of the Gaussians were chosen to be slightly larger than our
spectral resolution (8.5 Å), where deconvolution was reached at all
orbital phases. The radial velocities were measured as a function of
distance a between the Gaussians, and then the diagnostic
diagrams were constructed using an initial guess for the orbital
period, derived from photometry and from preliminary radial velocity
measurements via Gaussian fits to the lines. The optimal value of
separation (a= 1175 km
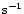 )
was determined from the diagnostic
diagrams, and the RV values measured for these Gaussian separations
were again subjected to a power spectrum analysis in order to refine
the period. The spectroscopic period peaked at a slightly longer
value, than the photometric period (however within the errors of the photometric
period). This method quickly converged and after two iterations no
further improvement was achieved. The diagnostic diagrams for
H
)
was determined from the diagnostic
diagrams, and the RV values measured for these Gaussian separations
were again subjected to a power spectrum analysis in order to refine
the period. The spectroscopic period peaked at a slightly longer
value, than the photometric period (however within the errors of the photometric
period). This method quickly converged and after two iterations no
further improvement was achieved. The diagnostic diagrams for
H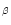 1 are shown in Fig. 3. Figure 4
(top) shows the H
1 are shown in Fig. 3. Figure 4
(top) shows the H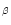 1 radial velocity curve.
1 radial velocity curve.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H2429F6.eps}\end{figure}](/articles/aa/full/2001/06/aah2429/Timg34.gif) |
Figure 6:
The inclination angle of the system vs. q=M2/M1 is
shown (solid line). The mass of WD in the system M1 vs. q for
M2=0.41 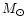 is given by the dot-dashed line. "Best fit''
parameters from the secondary star position and the ballistic
trajectory of the gas stream on the Doppler maps are marked
is given by the dot-dashed line. "Best fit''
parameters from the secondary star position and the ballistic
trajectory of the gas stream on the Doppler maps are marked |
A narrow single Gaussian profile was fitted to the prominent emission
features in the profile of He1II
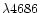 Å, and the
measured line centers were used to determine the radial velocity
solution for 1WGAJ1958.2+3232. The radial velocity curve for
He1II
Å, and the
measured line centers were used to determine the radial velocity
solution for 1WGAJ1958.2+3232. The radial velocity curve for
He1II
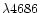 line is presented in the middle panel of
Fig. 4. These measurements were also subjected to the power
spectrum analysis. The obtained orbital period is in good agreement
with the values derived from the photometry and the H
line is presented in the middle panel of
Fig. 4. These measurements were also subjected to the power
spectrum analysis. The obtained orbital period is in good agreement
with the values derived from the photometry and the H 1
line radial velocities. The power spectra around the values
corresponding to the orbital period from these three independent
determinations are plotted in Fig. 5. One can see the
excellent match of the central peak. We adopted
1
line radial velocities. The power spectra around the values
corresponding to the orbital period from these three independent
determinations are plotted in Fig. 5. One can see the
excellent match of the central peak. We adopted
 as the final value for the orbital period of 1WGAJ1958.2+3232
from our observations. Longer time base observations are needed to
improve this value.
as the final value for the orbital period of 1WGAJ1958.2+3232
from our observations. Longer time base observations are needed to
improve this value.
Each of the radial velocity curves was fitted using a
least-squares routine of the form
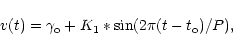 |
(1) |
where
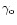 is the systematic velocity of the system, and K1is the semi-amplitude of radial velocity, both in km
is the systematic velocity of the system, and K1is the semi-amplitude of radial velocity, both in km
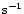 .
The
observation time is t, the epoch
.
The
observation time is t, the epoch
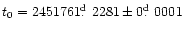 corresponds to the
corresponds to the 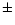 zero crossing of the
zero crossing of the
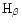 radial velocity
curve, and therefore is a superior conjunction of the binary system
(secondary located between observer and the WD).
Accordingly the phase value at t0 was set to 0.0.
Table 2 gives a summary of the radial velocity fits for
H
radial velocity
curve, and therefore is a superior conjunction of the binary system
(secondary located between observer and the WD).
Accordingly the phase value at t0 was set to 0.0.
Table 2 gives a summary of the radial velocity fits for
H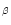 1 and He1II 4686 emission line.
1 and He1II 4686 emission line.
After refining the orbital period from spectroscopy, and determining
the phase 0.0, the photometric light curve was folded by the
corresponding parameters and presented in the lower panel of
Fig. 4.
![\begin{figure}
\par\includegraphics[clip]{H2429F7.ps}\end{figure}](/articles/aa/full/2001/06/aah2429/Timg46.gif) |
Figure 7:
Trailed, continuum-subtracted, spectra of 1WGAJ1958.2+3232
plotted in two cycles. Doppler maps of the emission lines
H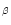 1 (left panel), He1II (right panel) in velocity
space (Vx,Vy) are given. A schematic overlay
marks the Roche lobe of the secondary, the ballistic trajectory and
the magnetically funneled horizontal part of the accretion stream.
The secondary star and gas-stream trajectory are plotted for K=74km 1 (left panel), He1II (right panel) in velocity
space (Vx,Vy) are given. A schematic overlay
marks the Roche lobe of the secondary, the ballistic trajectory and
the magnetically funneled horizontal part of the accretion stream.
The secondary star and gas-stream trajectory are plotted for K=74km
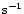 and q=0.46
and q=0.46 |
Several conclusions can be made after considering the three curves in
Fig. 4 in conjunction with and taking into account common
knowledge of Intermediate Polar systems (Patterson 1994;
Warner 1995):
- The double peaked Balmer lines are due to the presence of an
accretion disk or ring orbiting the primary WD in this IP. RV
variations in the wings of lines describe the rotation of the primary
of the binary system;
- The S-wave present in the Balmer and He1II emission lines
is evidence for a hot compact region on the accretion disk;
- From the difference of phases and amplitudes of radial
velocities of the wings of H
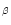 1 and the narrow component of
He1II we can conclude that the S-wave producing hot spot is
located at
1 and the narrow component of
He1II we can conclude that the S-wave producing hot spot is
located at  0.1-0.2 phase ahead of the superior
conjunction. It is difficult to estimate the location more precisely,
because the matter in the spot has an intrinsic velocity. It is the
usual location of the spot originating from the impact of the mass
transfer stream with the accretion disk. However it is also the area
which is most commonly heated by the energetic X-ray beam from the
magnetically accreting pole on the surface of the WD in IPs (see the
sketch in Hellier et al. 1989);
0.1-0.2 phase ahead of the superior
conjunction. It is difficult to estimate the location more precisely,
because the matter in the spot has an intrinsic velocity. It is the
usual location of the spot originating from the impact of the mass
transfer stream with the accretion disk. However it is also the area
which is most commonly heated by the energetic X-ray beam from the
magnetically accreting pole on the surface of the WD in IPs (see the
sketch in Hellier et al. 1989);
- The hot spot itself is eclipsed by the accretion ring as follows
from the phasing of the light curve, the dips in the light curve
centered at the phase
 0.12
0.12
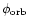 .
The primary at
this phase starts to move toward the observer and the hot spot is on
the opposite side of the ring approaching maximum velocity.
.
The primary at
this phase starts to move toward the observer and the hot spot is on
the opposite side of the ring approaching maximum velocity.
From our spectroscopic radial velocity solution, we can determine
preliminary values for the basic system parameters of 1WGAJ1958.2+3232.
First, from the mass-period and radius-period
relations of Echevarría (1983)
we estimate the mass and radius of the secondary star as
M2 = 0.41 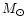 and R2=0.47
and R2=0.47 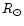 .
.
On the other hand, we can constrain the relation between inclination angle i
versus mass ratio q:
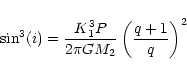 |
(3) |
if the mass ratio of the system is known (see Downes et al. 1986; Dobrzycka & Howel 1992). The
dependence of i versus
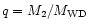 in the range 0.4 up to 0.75 is
shown in Fig. 6 for the above determinated values of
in the range 0.4 up to 0.75 is
shown in Fig. 6 for the above determinated values of
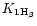 ,
,
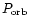 and
and
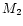 .
.
Meanwhile, the mean mass estimate of 76 white dwarfs in CVs is
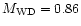
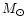 (Sion 1999). Webbink
(1990) gives statistically average white dwarf masses ratios
(q = 0.29) and average masses for all systems (
(Sion 1999). Webbink
(1990) gives statistically average white dwarf masses ratios
(q = 0.29) and average masses for all systems (
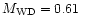
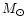 )
below the period gap and (q = 0.64,
)
below the period gap and (q = 0.64,
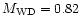
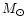 )
above the period gap. Thus, the possible solutions lie in
the narrow range of values.
)
above the period gap. Thus, the possible solutions lie in
the narrow range of values.
We attempted to refine these values for 1WGAJ1958.2+3232 by constraining
Doppler tomograms from observed emission line profiles.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H2429F8.ps}\end{figure}](/articles/aa/full/2001/06/aah2429/Timg66.gif) |
Figure 8:
Doppler maps of the emission line blend
C1III/N1III in velocity space
(Vx,Vy) is given. A schematic overlay marks the
Roche lobe of the secondary, the ballistic trajectory and the
magnetically funneled horizontal part of the accretion stream. The
secondary star and gas-stream trajectory are plotted for K=74 km s-1and q=0.46 |
Doppler tomography is a useful tool to extract further information on
CVs from trailed spectra. This method, which was developed by Marsh
& Horne (1988), uses the velocity profiles of emission-lines
at each phase to create a two-dimensional intensity image in
velocity-space coordinates (Vx,Vy). Therefore,
the Doppler tomogram can be interpreted as a projection of emitting
regions in cataclysmic variables onto the plane perpendicular to the
observers view. We used the code developed by Spruit (1998)
to constrain Doppler maps of 1WGAJ1958.2+3232 with the maximum entropy
method. The resulting Doppler maps (or tomogram) of emission lines of
H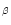 1, He1II and the blend of
C1III/N1III are displayed as a gray-scale image in
Figs. 7 and 8. Also in Fig. 7
are displayed trailed spectra of H
1, He1II and the blend of
C1III/N1III are displayed as a gray-scale image in
Figs. 7 and 8. Also in Fig. 7
are displayed trailed spectra of H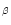 1 and He1II in
phase space and their corresponding reconstructed counterparts. Two
features in the maps are distinct: an accretion disk seen as a dark
circle extending to up to
1 and He1II in
phase space and their corresponding reconstructed counterparts. Two
features in the maps are distinct: an accretion disk seen as a dark
circle extending to up to 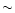 -700 kms-1 on H
-700 kms-1 on H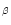 doppler
tomogram and a bright spot detected in all three maps to the left and
below the center of mass at velocities
doppler
tomogram and a bright spot detected in all three maps to the left and
below the center of mass at velocities
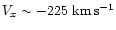 ,
,
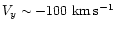 in He1II 4686. Apart from the spot a cometary tail linked to
it and extending to
in He1II 4686. Apart from the spot a cometary tail linked to
it and extending to
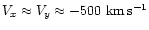 can be clearly seen on the He1II
map. These we identify with the mass transfer stream and its shape was
essential for our selection of the ballistic trajectory. A help
in interpreting Doppler maps are additional inserted plots
which mark the position of the secondary star and the ballistic
trajectory of the gas stream. Here we used our estimates of
can be clearly seen on the He1II
map. These we identify with the mass transfer stream and its shape was
essential for our selection of the ballistic trajectory. A help
in interpreting Doppler maps are additional inserted plots
which mark the position of the secondary star and the ballistic
trajectory of the gas stream. Here we used our estimates of
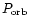 and
and 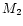 with various combinations of iand q from Fig. 6 in order to obtain the "best fit'' (by
simple eye inspection) of the calculated stream trajectory with the gray
scale image. Our preferred solution for the inclination is
with various combinations of iand q from Fig. 6 in order to obtain the "best fit'' (by
simple eye inspection) of the calculated stream trajectory with the gray
scale image. Our preferred solution for the inclination is
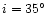 .
It
is marked in Fig. 6 and given in Table 3. Of
course other close solutions are applicable. Comparing the location
of spots in Doppler maps of He1II and H
.
It
is marked in Fig. 6 and given in Table 3. Of
course other close solutions are applicable. Comparing the location
of spots in Doppler maps of He1II and H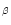 1 we can
actually distinguish two hot spots on the disk (Fig. 7).
The elongated spot coinciding in both emission lines is probably caused
by the mass transfer stream and the shock of impact with the
disk, while the compact dense spot toward negative Vy's,
seen much better in H
1 we can
actually distinguish two hot spots on the disk (Fig. 7).
The elongated spot coinciding in both emission lines is probably caused
by the mass transfer stream and the shock of impact with the
disk, while the compact dense spot toward negative Vy's,
seen much better in H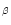 1 than in the two other lines, is a
result of heating
of the disk by the X-ray beam. The
C1III/N1III pattern mostly
repeats that of He1II,
with lower intensity though (Fig. 8).
1 than in the two other lines, is a
result of heating
of the disk by the X-ray beam. The
C1III/N1III pattern mostly
repeats that of He1II,
with lower intensity though (Fig. 8).


Up: The orbital period of
Copyright ESO 2001
![]() photometric data shows a clear peak at
photometric data shows a clear peak at
![]() ,
corresponding to
,
corresponding to
![]() .
This peak
is caused by the above mentioned eclipses in the light curve and clearly
marks the orbital period of the system.
.
This peak
is caused by the above mentioned eclipses in the light curve and clearly
marks the orbital period of the system.
![]() of the WD corresponding to
of the WD corresponding to
![]() s.
This period is in excellent agreement with that recently discovered
by ASCA X-ray pulsations (Israel et al. 1999). The beat
frequencies at
s.
This period is in excellent agreement with that recently discovered
by ASCA X-ray pulsations (Israel et al. 1999). The beat
frequencies at
![]() ,
,
![]() are also present in the
CLEANed power spectrum but with a smaller number of iterations (see
insert in the upper right corner of the Fig. 2). The
harmonics of the basic frequencies
are also present in the
CLEANed power spectrum but with a smaller number of iterations (see
insert in the upper right corner of the Fig. 2). The
harmonics of the basic frequencies
![]() and
and
![]() are detected as well. Besides these, there are
comparably significant peaks at the periods of 727.78 s and 1.36 h.
The former was detected also by Uslengi et al. (2000) and
is probably the one-day alias of
are detected as well. Besides these, there are
comparably significant peaks at the periods of 727.78 s and 1.36 h.
The former was detected also by Uslengi et al. (2000) and
is probably the one-day alias of
![]() ,
while for
the latter we could not find any reasonable explanation.
,
while for
the latter we could not find any reasonable explanation.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H2429F3.eps}
\par\end{figure}](/articles/aa/full/2001/06/aah2429/Timg31.gif)
![]() 1#912#>
and He1II, covering
several orbits. Thus, we were able to examine periodical variations
in the spectrum of the object, primarily in the emission lines. The
simple stacking of consecutive spectra onto the trailed spectrum
showed strong variability in the lines. It is distinct in the Balmer lines and
in the higher excitation lines of ionized Helium. The Balmer lines
are double-peaked with an S-wave moving inside, which makes it hard to
see the periodic pattern. In the He1II 4686 line the central
narrow component dominates in most of the phases, and it shows clear
sinusoidal variation.
1#912#>
and He1II, covering
several orbits. Thus, we were able to examine periodical variations
in the spectrum of the object, primarily in the emission lines. The
simple stacking of consecutive spectra onto the trailed spectrum
showed strong variability in the lines. It is distinct in the Balmer lines and
in the higher excitation lines of ionized Helium. The Balmer lines
are double-peaked with an S-wave moving inside, which makes it hard to
see the periodic pattern. In the He1II 4686 line the central
narrow component dominates in most of the phases, and it shows clear
sinusoidal variation.
![]() 1 applying the double Gaussian
deconvolution method introduced by Schneider & Young
(1980), and further developed by Shafter (1983).
This method is especially efficient for measurements of the orbital
motion of CVs with a prominent spot at the edge of the accretion
disk, contaminating the central parts of the emission lines. It
allows us to measure RV variations using the wings of the lines. The
width of the Gaussians were chosen to be slightly larger than our
spectral resolution (8.5 Å), where deconvolution was reached at all
orbital phases. The radial velocities were measured as a function of
distance a between the Gaussians, and then the diagnostic
diagrams were constructed using an initial guess for the orbital
period, derived from photometry and from preliminary radial velocity
measurements via Gaussian fits to the lines. The optimal value of
separation (a= 1175 km
1 applying the double Gaussian
deconvolution method introduced by Schneider & Young
(1980), and further developed by Shafter (1983).
This method is especially efficient for measurements of the orbital
motion of CVs with a prominent spot at the edge of the accretion
disk, contaminating the central parts of the emission lines. It
allows us to measure RV variations using the wings of the lines. The
width of the Gaussians were chosen to be slightly larger than our
spectral resolution (8.5 Å), where deconvolution was reached at all
orbital phases. The radial velocities were measured as a function of
distance a between the Gaussians, and then the diagnostic
diagrams were constructed using an initial guess for the orbital
period, derived from photometry and from preliminary radial velocity
measurements via Gaussian fits to the lines. The optimal value of
separation (a= 1175 km
![]() )
was determined from the diagnostic
diagrams, and the RV values measured for these Gaussian separations
were again subjected to a power spectrum analysis in order to refine
the period. The spectroscopic period peaked at a slightly longer
value, than the photometric period (however within the errors of the photometric
period). This method quickly converged and after two iterations no
further improvement was achieved. The diagnostic diagrams for
H
)
was determined from the diagnostic
diagrams, and the RV values measured for these Gaussian separations
were again subjected to a power spectrum analysis in order to refine
the period. The spectroscopic period peaked at a slightly longer
value, than the photometric period (however within the errors of the photometric
period). This method quickly converged and after two iterations no
further improvement was achieved. The diagnostic diagrams for
H![]() 1 are shown in Fig. 3. Figure 4
(top) shows the H
1 are shown in Fig. 3. Figure 4
(top) shows the H![]() 1 radial velocity curve.
1 radial velocity curve.
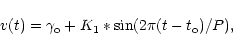
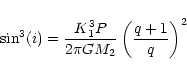
![]()
![]() (Sion 1999). Webbink
(1990) gives statistically average white dwarf masses ratios
(q = 0.29) and average masses for all systems (
(Sion 1999). Webbink
(1990) gives statistically average white dwarf masses ratios
(q = 0.29) and average masses for all systems (
![]()
![]() )
below the period gap and (q = 0.64,
)
below the period gap and (q = 0.64,
![]()
![]() )
above the period gap. Thus, the possible solutions lie in
the narrow range of values.
)
above the period gap. Thus, the possible solutions lie in
the narrow range of values.