Transient spectral absorption events monitored now for years towards the star
A&A 366, 945-964 (2001)
DOI: 10.1051/0004-6361:20000353
H. Beust - C. Karmann - A.-M. Lagrange
Laboratoire d'Astrophysique de l'Observatoire de Grenoble,
Université J. Fourier,
BP 53,
38041 Grenoble Cedex 9, France
Received 19 April 2000 / Accepted 24 November 2000
Abstract
Transient spectral absorption events monitored now for years towards
the star ![]() Pictoris have been interpreted as resulting from the transit across
the line of sight of evaporating star-grazing kilometer-sized bodies
(Falling Evaporating Bodies, or FEBs). Several Herbig Ae/Be stars
of various ages have been observed to exhibit somehow
similar absorption events that have been attributed to similar FEB events.
We investigate here this question from a modeling point of view.
Adapting the FEB simulation code
we had developed earlier specifically for
Pictoris have been interpreted as resulting from the transit across
the line of sight of evaporating star-grazing kilometer-sized bodies
(Falling Evaporating Bodies, or FEBs). Several Herbig Ae/Be stars
of various ages have been observed to exhibit somehow
similar absorption events that have been attributed to similar FEB events.
We investigate here this question from a modeling point of view.
Adapting the FEB simulation code
we had developed earlier specifically for ![]() Pic to the case of typical
Herbig Ae/Be stars, we try to derive in which
conditions FEB-like objects may generate
detectable transient absorption events. We compare these conditions
with those found in the case of
Pic to the case of typical
Herbig Ae/Be stars, we try to derive in which
conditions FEB-like objects may generate
detectable transient absorption events. We compare these conditions
with those found in the case of ![]() Pic. A major difference with
Pic. A major difference with ![]() Pic is that Herbig Ae/Be stars have strong stellar winds
(10-9-
Pic is that Herbig Ae/Be stars have strong stellar winds
(10-9-
![]() yr-1). Those winds
appear to have a drastic interaction with the gaseous material
escaped from the FEBs. With the presence of such stellar winds,
the spectral signatures of FEBs are not detectable, unless their
mass loss rate is huge. This translates into very large
bodies (
yr-1). Those winds
appear to have a drastic interaction with the gaseous material
escaped from the FEBs. With the presence of such stellar winds,
the spectral signatures of FEBs are not detectable, unless their
mass loss rate is huge. This translates into very large
bodies (![]() 100 km size), instead
of
100 km size), instead
of ![]() 15 km for
15 km for ![]() Pic FEBs. This appears unrealistic in
terms of amount of planetesimal mass needed in the disks surrounding
these stars.
We discuss then the validity of the
FEB hypothesis for specific example stars. It turns out that for
the younger (a few
Pic FEBs. This appears unrealistic in
terms of amount of planetesimal mass needed in the disks surrounding
these stars.
We discuss then the validity of the
FEB hypothesis for specific example stars. It turns out that for
the younger (a few ![]() yr old) Herbig Ae/Be stars like AB Aur,
with well identified winds
yr old) Herbig Ae/Be stars like AB Aur,
with well identified winds
![]() yr-1,
the variable features sometimes observed are not likely to
be due to FEBs, unless produced in wind free cavities.
For older (
yr-1,
the variable features sometimes observed are not likely to
be due to FEBs, unless produced in wind free cavities.
For older (
![]() yr old)
stars Herbig Ae/Be like HD 100546, the FEB scenario could still explain
the spectral events observed, but either the wind must to be weaker
than
yr old)
stars Herbig Ae/Be like HD 100546, the FEB scenario could still explain
the spectral events observed, but either the wind must to be weaker
than ![]() 10
10
![]() yr-1 (which cannot be excluded
so far), or the FEBs approach the star in wind free cavities.
yr-1 (which cannot be excluded
so far), or the FEBs approach the star in wind free cavities.
Key words: stars: circumstellar matter - stars: early-type - stars: ![]() Pic -
methods: numerical -
Pic -
methods: numerical -
techniques: spectroscopic
The presence of kilometer-sized bodies was first introduced to explain
the numerous spectral absorption events reported in the spectrum of ![]() Pictoris.
The survey of various spectral lines (Ca II, Mg II, Fe II, etc.)
towards this star revealed that
transient absorption features, usually redshifted, frequently
appear in addition a deep central stable component.
These additional features evolve
within one day or even less (Boggess et al. 1991, Vidal-Madjar et al. 1994, Lagrange et al. 1996, and refs. therein).
Pictoris.
The survey of various spectral lines (Ca II, Mg II, Fe II, etc.)
towards this star revealed that
transient absorption features, usually redshifted, frequently
appear in addition a deep central stable component.
These additional features evolve
within one day or even less (Boggess et al. 1991, Vidal-Madjar et al. 1994, Lagrange et al. 1996, and refs. therein).
These repeated spectral events have been successfully modeled as the signature of the evaporation of kilometer-sized bodies crossing the line of sight in the vicinity of the star, on star-grazing orbits (i.e. FEBs; Beust et al. 1990, 1996, 1998 [hereafter Paper XXV]).
A key issue concerning this scenario was the identification of
a triggering dynamical mechanism capable to bring numerous bodies
on star-grazing orbits, out of a Keplerian rotating disk on
quasi-circular orbits. Various mechanisms were proposed, all of them
involving the gravitational perturbations
by at least one planet. As of yet, the most convincing mechanism was
proposed by Beust & Morbidelli (1996, 2000): The star-grazers are generated from
bodies initially orbiting the star on low eccentricity orbits, but
trapped in a mean-motion resonance (the 4:1 one is by far the most
powerful one) with a massive, Jovian-like planet orbiting the star
on a moderately eccentric orbit (
![]() -0.1). Under such
conditions, the trapped particles are able to become star-grazers
within
-0.1). Under such
conditions, the trapped particles are able to become star-grazers
within ![]() 104 revolutions of the planet. This scenario reproduces
fairly well from a statistical point of view the dynamical characteristics
of the FEBs that were deduced from the observation of variable
features.
104 revolutions of the planet. This scenario reproduces
fairly well from a statistical point of view the dynamical characteristics
of the FEBs that were deduced from the observation of variable
features.
Apart from these stars, redshifted (and less frequently blueshifted)
features and spectral variations
have been now observed for years towards several
Herbig Ae/Be stars. From a strictly stellar point of view, Herbig Ae/Be stars
are pre-main-sequence objects that may be regarded
as ![]() Pic precursors (see the reviews by Grady et al. 1996a, 2000).
These observations are based on UV spectroscopic data gathered
with IUE. In some cases, the Fe II lines as observed with IUE
appeared asymmetrical with extended red wings
(Grady et al. 1993, 1996b),
indicating possible circumstellar components,
sometimes redshifted by several hundreds of kms-1. Over-ionized
species indicating collisional ionization, like in the
Pic precursors (see the reviews by Grady et al. 1996a, 2000).
These observations are based on UV spectroscopic data gathered
with IUE. In some cases, the Fe II lines as observed with IUE
appeared asymmetrical with extended red wings
(Grady et al. 1993, 1996b),
indicating possible circumstellar components,
sometimes redshifted by several hundreds of kms-1. Over-ionized
species indicating collisional ionization, like in the
![]() Pic case are frequently observed. Moreover,
whenever circumstellar
components are observed towards doublet lines like Mg II k and h,
the ratio between the two variable components
often appears close to 1, indicating
that the absorption is caused by opaque but clumpy material in front
of the star (e.g. 51 Oph: Grady & Silvis 1993; Lecavalier et al. 1997).
This characteristic is shared with
Pic case are frequently observed. Moreover,
whenever circumstellar
components are observed towards doublet lines like Mg II k and h,
the ratio between the two variable components
often appears close to 1, indicating
that the absorption is caused by opaque but clumpy material in front
of the star (e.g. 51 Oph: Grady & Silvis 1993; Lecavalier et al. 1997).
This characteristic is shared with ![]() Pic, for which it was
considered as a strong argument in favor of the
FEB scenario. We shall now focus on three specific examples.
Pic, for which it was
considered as a strong argument in favor of the
FEB scenario. We shall now focus on three specific examples.
ISO spectroscopy revealed the presence of circumstellar
dust around this star (van den Ancker 2000; Bouwman et al. 2000)
and an accretion disk detected by interferometric observations.
HST/STIS imaging (Grady et al. 1999b) reveals the presence of circumstellar dust
scattering the stellar light. As the scattered-light distribution
is symmetric, Grady et al. (1999b) conclude that AB Aur is probably
viewed close to pole-on, with an inclination with respect to
the plane of the sky in any case less than
![]() (and more probably than 20-
(and more probably than 20-
![]() ). The fact that
the star is viewed close to pole-on also explains why the wind can
easily be modelled as spherically symmetric; this however allows us
to question whether the wind is actually spherically symmetric or
only axisymmetric, concentrated at high stellar latitudes.
). The fact that
the star is viewed close to pole-on also explains why the wind can
easily be modelled as spherically symmetric; this however allows us
to question whether the wind is actually spherically symmetric or
only axisymmetric, concentrated at high stellar latitudes.
Despite their complex structure which makes components identification difficult, the spectral lines of AB Aur exhibit short-term variations on their red wing that have been interpreted by Grady et al. (1999) as resulting from a FEB phenomenon.
| |
Figure 1:
Two IUE spectra of the k and h Mg II doublet (
|
| Open with DEXTER | |
HD 100546 exhibits
a very important infrared excess (IRAS), later on confirmed
by ISO (Waelkens et al. 1996). Recently, a possible disk of circumstellar
dust has been imaged around this star (Augereau et al. 2001; Pantin & Lagage 2001).
Observations of the near-infrared spectrum of
HD 100546 gathered with the ISO satellite (Malfait et al. 1998) reveal
emission features characteristic for crystalline silicates,
comparable to those of comets and also those observed towards
![]() Pic itself
(and also recently towards two younger systems; Sitko et al. 1999).
Polarimetric variability has been reported and interpreted as resulting
from light scattering by dust within the circumstellar environment
(Clarke et al. 1999).
Pic itself
(and also recently towards two younger systems; Sitko et al. 1999).
Polarimetric variability has been reported and interpreted as resulting
from light scattering by dust within the circumstellar environment
(Clarke et al. 1999).
Striking spectral variable absorption components,
redshifted by several hundreds of kms-1 are reported
in Grady et al. (1997) and Viera et al. (1999),
towards several lines including those of over-ionized species,
and also towards lines of more fragile elements like C I.
We display here the Mg II IUE data taken from Grady et al. (1997)
(Fig. 1), as these are data we will try to
model.
We note in Fig. 1 the presence in one of the
two spectra of a deep variable feature appearing
in both lines at ![]() 150 kms-1 redshift with respect to the central
absorption. 100-300 kms-1 is indeed a typical velocity range
for variable absorption features observed towards Herbig Ae/Be stars.
150 kms-1 redshift with respect to the central
absorption. 100-300 kms-1 is indeed a typical velocity range
for variable absorption features observed towards Herbig Ae/Be stars.
Note however
that the characteristic time-scale of these variations is
very poorly constrained by the observations presented in these papers. The
spectra were indeed taken at different epochs separated by
at least several months; one of the most striking characteristics of
the FEB spectral variations towards ![]() Pic is that they appear or disappear
within one day or even less. The spectroscopic database available as of
yet does not allow to test such variability time-scales.
Pic is that they appear or disappear
within one day or even less. The spectroscopic database available as of
yet does not allow to test such variability time-scales.
Grady et al. (1997) show ratios equal to 1 between the variable
components occurring in doublets, implying as for ![]() Pic saturated clouds that do not mask the whole stellar disk.
They derive filling factors of the stellar disk ranging
between 40 and 50%. A rough estimate of the relative abundances
of the metallic species
in the variable lines shows consistency with a cometary-like
chemical composition (with however more volatiles and magnesium
than for
Pic saturated clouds that do not mask the whole stellar disk.
They derive filling factors of the stellar disk ranging
between 40 and 50%. A rough estimate of the relative abundances
of the metallic species
in the variable lines shows consistency with a cometary-like
chemical composition (with however more volatiles and magnesium
than for ![]() Pic), and the authors estimate the amount of material
in front of the line of sight to the one corresponding to
the entire evaporation of a 1 km sized body. Note however that
the abundance estimate was performed assuming a close-box model
which we showed not to be accurate in permanently refilled
gaseous environments like FEB comas (Lagrange et al. 1998).
Pic), and the authors estimate the amount of material
in front of the line of sight to the one corresponding to
the entire evaporation of a 1 km sized body. Note however that
the abundance estimate was performed assuming a close-box model
which we showed not to be accurate in permanently refilled
gaseous environments like FEB comas (Lagrange et al. 1998).
In the case of ![]() Pic, we developed in the past years
a code able to simulate the dynamics of the gaseous material
escaped from an evaporating body in the vicinity of the star,
together with the absorption components it generates when crossing
the line of sight (Beust et al. 1990, 1996; Paper XXV). This theoretical tool helped
us understanding the various aspects of the scenario, such as the
ability to generate different kinds of variable features
depending on the distance between the passing body and the star,
or the behavior differences between various species.
Pic, we developed in the past years
a code able to simulate the dynamics of the gaseous material
escaped from an evaporating body in the vicinity of the star,
together with the absorption components it generates when crossing
the line of sight (Beust et al. 1990, 1996; Paper XXV). This theoretical tool helped
us understanding the various aspects of the scenario, such as the
ability to generate different kinds of variable features
depending on the distance between the passing body and the star,
or the behavior differences between various species.
We want now to adapt this modeling to the case of Herbig Ae/Be stars, in order to investigate in which conditions the FEB scenario can account for the observations. This parametric study is intended to generally apply for any Herbig star. We shall apply afterwards this study to AB Aur and HD 100546.
In Sect. 2, we describe into more details
the model we assume for Herbig stars. We point
out the differences we need to assume between such a star and ![]() Pic, in
particular the role of the stellar wind. In Sect. 3, we describe
the simulations relevant to FEBs around Herbig stars. In Sect. 4,
we discuss our results and their application to the quoted examples
of Herbig stars. Our conclusions are presented in Sect. 5.
Pic, in
particular the role of the stellar wind. In Sect. 3, we describe
the simulations relevant to FEBs around Herbig stars. In Sect. 4,
we discuss our results and their application to the quoted examples
of Herbig stars. Our conclusions are presented in Sect. 5.
![\begin{figure}
{
\includegraphics[angle=-90,origin=br,width=8.8cm]{ms9851f2} }
\end{figure}](/articles/aa/full/2001/06/aa9851/Timg27.gif) |
Figure 2:
The radiation pressure ( |
| Open with DEXTER | |
| |
Figure 3:
Sublimation region for dusty "astronomical silicates''
grains as a function of their size, in the vicinity of |
| Open with DEXTER | |
Along the path of the evaporating body, the simulation
releases continuously fresh particles close to the nucleus. These
new particles are first assumed to be dust particles chosen
with a convenient Hanner distribution function
(see Paper XXV for details). At each time step, the stellar
spectrum is used to compute the equilibrium temperature of the dust
grains via Mie theory (depending on their stellar distance), and
the strength of the stellar radiation acting on each of them.
The radiation pressure itself is described as usual by a its
ratio ![]() to stellar gravity;
to stellar gravity; ![]() does not depend on
the distance to the star, but for dust grains it depends on
their size. Also the evaporation rate (function of the equilibrium
temperature) is computed for each grain, together with its radius
decrease within the considered time-step. The
does not depend on
the distance to the star, but for dust grains it depends on
their size. Also the evaporation rate (function of the equilibrium
temperature) is computed for each grain, together with its radius
decrease within the considered time-step. The ![]() ratio is used
to compute the motion of the grain during the same time-step.
ratio is used
to compute the motion of the grain during the same time-step.
We model our dust particles as "astronomical silicates'', assuming
the optical constants of Draine & Lee (1984), revised in Laor & Draine (1993).
Once a given dust particle has reached zero radius, it is then assumed
to represent metallic ions. Its dynamics is then computed taking
into account i) the radiation pressure (i.e. the ![]() ratio) acting
on it, eventually reduced by a shielding effect from the other
ions located closer to the star, and ii) the drag force by the
neutral gas escaped from the nucleus. This is described extensively
in Beust et al. (1990, 1996). Finally,
the spectral absorption of the ions passing in front
of the star is computed, and a synthetic spectrum is produced.
ratio) acting
on it, eventually reduced by a shielding effect from the other
ions located closer to the star, and ii) the drag force by the
neutral gas escaped from the nucleus. This is described extensively
in Beust et al. (1990, 1996). Finally,
the spectral absorption of the ions passing in front
of the star is computed, and a synthetic spectrum is produced.
As a template model for a Herbig Ae/Be, we assume
a B9 type star with
![]() ,
,
![]() ,
,
![]() K,
K,
![]() ,
,
![]() kms-1and compute an ATLAS9 Kurucz synthetic spectrum (Kurucz 1979)
relevant for these parameters. These parameters correspond actually
to a model for HD 100546 (van den Ancker 1998), but may be considered as typical
for any Herbig Ae/Be star. For AB Aur (A0 type star), a more exact
set of parameters is (van den Ancker 1998)
kms-1and compute an ATLAS9 Kurucz synthetic spectrum (Kurucz 1979)
relevant for these parameters. These parameters correspond actually
to a model for HD 100546 (van den Ancker 1998), but may be considered as typical
for any Herbig Ae/Be star. For AB Aur (A0 type star), a more exact
set of parameters is (van den Ancker 1998)
![]() ,
,
![]() K,
K,
![]() ,
,
![]() .
Assuming the latter
set of parameters instead of the former appears to only
slightly affect the numerical results of this study
and does not change the conclusions
we derive below. Consequently, we will not present separate
results for both sets of parameters. We will only present those
corresponding to the B9 type star model, considering they are typical
for Herbig Ae/Be star in general.
.
Assuming the latter
set of parameters instead of the former appears to only
slightly affect the numerical results of this study
and does not change the conclusions
we derive below. Consequently, we will not present separate
results for both sets of parameters. We will only present those
corresponding to the B9 type star model, considering they are typical
for Herbig Ae/Be star in general.
Figure 2 plots the ![]() value as a function of grain
size, for two values of grain porosity: 0
(a solid grain), and 0.95 (a more realistic cometary grain value), and
for three stellar cases: a B9 star,
value as a function of grain
size, for two values of grain porosity: 0
(a solid grain), and 0.95 (a more realistic cometary grain value), and
for three stellar cases: a B9 star, ![]() Pic, and the Sun. In the case
of
Pic, and the Sun. In the case
of ![]() Pic, the parameters assumed are (Crifo et al. 1997):
Pic, the parameters assumed are (Crifo et al. 1997):
![]() ,
,
![]() K,
K,
![]() .
The spectrum is
a Kurucz model computed with the quoted
value for
.
The spectrum is
a Kurucz model computed with the quoted
value for
![]() and
and
![]() .
.
The curve corresponding to ![]() Pic and porosity 0 is to be compared
to that published by Artymowicz (1988). We first see that the shapes
of all curves are similar: smaller grains undergo a much stronger
radiation pressure than larger ones, and tend to be blown away
by the star (
Pic and porosity 0 is to be compared
to that published by Artymowicz (1988). We first see that the shapes
of all curves are similar: smaller grains undergo a much stronger
radiation pressure than larger ones, and tend to be blown away
by the star (![]() ). For smaller grains, the radiation pressure
tends to be
). For smaller grains, the radiation pressure
tends to be ![]() 5 times larger in a B9 star environment than
around
5 times larger in a B9 star environment than
around ![]() Pic, while for larger grains, the difference tends to decrease.
Pic, while for larger grains, the difference tends to decrease.
In all cases, grains with porosity 0.95 undergo a radiation pressure at least one order of magnitude larger than the grains with no porosity. We will assume in the numerical simulations that the porosity of the grains is 0.95 as it is a a more realistic cometary value.
A more striking difference shows up in Fig. 3. Here the region of dust sublimation in the various stellar environments is shown as a function of the grain radius. More precisely, the grey zone corresponds to the stellar distance range where the lifetime of the grains lies between 0.1day and 10days. Most of the sublimation of the dust escaped from FEBs is expected to occur in this area.
We first see, as noted in Beust et al. (1998), that smaller grains tend
to evaporate further away from the star(s) than larger ones. In
the case of a B9 star, the grains evaporate at larger
distances that around ![]() Pic, and that around the Sun, the refractory grains
are expected to evaporate only in the immediate vicinity of the star.
This is a direct consequence of the difference in effective
temperature between the various stars. The difference is more important
for smaller grains (radius
Pic, and that around the Sun, the refractory grains
are expected to evaporate only in the immediate vicinity of the star.
This is a direct consequence of the difference in effective
temperature between the various stars. The difference is more important
for smaller grains (radius
![]()
![]() m). Note that the FEBs are supposed
to release grains of all sizes, with a given size distribution. They
can generate transient absorption events as soon as some of these
grains begin to evaporate. Hence FEBs are expected to be observable
around
m). Note that the FEBs are supposed
to release grains of all sizes, with a given size distribution. They
can generate transient absorption events as soon as some of these
grains begin to evaporate. Hence FEBs are expected to be observable
around ![]() Pic as soon as they get a periastron
Pic as soon as they get a periastron
![]() 0.5AU, while
in the environment of a B9 star, this limit jumps up to
0.5AU, while
in the environment of a B9 star, this limit jumps up to
![]() 2AU, i.e., 4 times further away. This is a major difference
that tends to indicate that active FEBs around Herbig
stars can be more frequent than around
2AU, i.e., 4 times further away. This is a major difference
that tends to indicate that active FEBs around Herbig
stars can be more frequent than around ![]() Pic, but whether these FEBs
can generate detectable signatures still needs to be investigated.
Note conversely that the dust sublimation region around the Sun does
not exceed 0.1AU.
Pic, but whether these FEBs
can generate detectable signatures still needs to be investigated.
Note conversely that the dust sublimation region around the Sun does
not exceed 0.1AU.
| Element | Element | ||||
| ( |
(B9 star) | ( |
(B9 star) | ||
| Ca II | 35.1 | 318.9 | Fe I | 19.1 | 90.9 |
| Mg II | 5.0 | 84.4 | Fe II | 4.9 | 46.4 |
| Mn II | 11.0 | 62.2 | Ni II | 1.39 | 15.0 |
| Al II | 0.56 | 132.9 | Zn II | 6.1 | 47.64 |
| Al III | 15.6 | 108.1 | Cr II | 3.4 | 23.9 |
| Si I | 10.1 | 136.1 | S I | 1.52 | 63.7 |
| Si II | 0.15 | 13.9 | C I | 0.095 | 41.4 |
| H I | 0.43 | Na I | 42.8 | 477.1 |
Let us now compare in both stellar environments the behavior of the
metallic ions that are produced by the dust evaporation. Basically the
main parameter is the radiation pressure, which is computed for
a given element by the adding the contribution of all its
spectral resonance lines (see Lagrange et al. 1998, 1996 for details),
and described as for dust grains with a ![]() ratio.
ratio. ![]() values for
values for ![]() Pic a B9 star
are given for some important species in Table 1. The B9 star
values are significantly larger than the corresponding
Pic a B9 star
are given for some important species in Table 1. The B9 star
values are significantly larger than the corresponding ![]() Pic ones.
This is clearly due to the more important stellar flux of
a B9 star. The difference is even more striking for some elements
like C I or H I. In that case, most of the contributing spectral lines
are located fairly far in the UV spectrum (
Pic ones.
This is clearly due to the more important stellar flux of
a B9 star. The difference is even more striking for some elements
like C I or H I. In that case, most of the contributing spectral lines
are located fairly far in the UV spectrum (
![]() Å).
Downwards these wavelengths, the
Å).
Downwards these wavelengths, the ![]() Pic flux drops sharply, while
this is not the case for a hotter star.
Pic flux drops sharply, while
this is not the case for a hotter star.
In any case, we can stress that two identical FEBs,
with similar evaporation rates, located at the same stellar distance,
one in the vicinity of ![]() Pic and the other one in the vicinity of
a Herbig star, will probably generate ionic clouds with different
sizes. The size of a ionic cloud in front of the star is roughly fixed
by the distance to the nucleus where the radiation pressure
exactly balances the drag force from the surrounding neutral medium
(see Beust et al. 1990; Papier XXV). In the B9 star case, as the radiation pressure
is significantly larger than for
Pic and the other one in the vicinity of
a Herbig star, will probably generate ionic clouds with different
sizes. The size of a ionic cloud in front of the star is roughly fixed
by the distance to the nucleus where the radiation pressure
exactly balances the drag force from the surrounding neutral medium
(see Beust et al. 1990; Papier XXV). In the B9 star case, as the radiation pressure
is significantly larger than for ![]() Pic, we expect this balance to occur
closer to the nucleus, and consequently the resulting ionic clouds
to be smaller. As the projected size of the cloud directly controls
the maximum depth of the variable spectral component it can generate,
we thus expect the spectral components generated by identical FEBs
to be fainter in the case of a Herbig star than for
Pic, we expect this balance to occur
closer to the nucleus, and consequently the resulting ionic clouds
to be smaller. As the projected size of the cloud directly controls
the maximum depth of the variable spectral component it can generate,
we thus expect the spectral components generated by identical FEBs
to be fainter in the case of a Herbig star than for ![]() Pic, and therefore
more difficult to observe.
Pic, and therefore
more difficult to observe.
![\begin{figure}
{
\includegraphics[angle=-90,origin=br,width=8.8cm]{ms9851f4} }
\end{figure}](/articles/aa/full/2001/06/aa9851/Timg46.gif) |
Figure 4:
Surface sublimation rate for a large ice sphere as a function of
stellar distance, in the environment of i) |
| Open with DEXTER | |
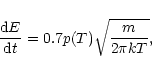 |
(2) |
The equilibrium temperature itself is derived from
the energy balance between the stellar radiation flux,
the thermal energy re-radiated by the body, and the
sublimation energy (see Beust et al. 1998). The absorption efficiency is
obtained via Mie theory, but for a large body as we assume
here (we use a typical size of 1 km), we are well inside the
geometrical optics regime, so that the equilibrium temperature,
and consequently
![]() (as long as it may be assumed homogeneous) are virtually
independent from the size of the body. The latent heat for ice sublimation
and the vapor pressure are taken from Lamy (1974), and are listed
in Paper XXV.
(as long as it may be assumed homogeneous) are virtually
independent from the size of the body. The latent heat for ice sublimation
and the vapor pressure are taken from Lamy (1974), and are listed
in Paper XXV.
Figure 4 gives the computed value
of
![]() as a function of stellar distance, for the
three stellar environments of
as a function of stellar distance, for the
three stellar environments of ![]() Pic, our template B9 type star, and
the Sun. In addition, we have superimposed (dotted line) the g(r)profile, once rescaled to our computed Solar curve. The agreement
is very good.
Pic, our template B9 type star, and
the Sun. In addition, we have superimposed (dotted line) the g(r)profile, once rescaled to our computed Solar curve. The agreement
is very good.
We first note that, as expected for a given stellar distance, the hotter
the star, the larger the sublimation rate. Basically for stellar
distances less than 1AU,
![]() is 11 times larger in
the
is 11 times larger in
the ![]() Pic environment that around the Sun, and it is 3 times larger
around a B9 star than around
Pic environment that around the Sun, and it is 3 times larger
around a B9 star than around ![]() Pic. We also note that the sublimation
of ice begins at much larger stellar distances for hotter stars.
For Solar comets, the sublimation rate drops sharply further
than
Pic. We also note that the sublimation
of ice begins at much larger stellar distances for hotter stars.
For Solar comets, the sublimation rate drops sharply further
than ![]() 2AU from the Sun. Around
2AU from the Sun. Around ![]() Pic, this limits jumps
up to
Pic, this limits jumps
up to ![]() 10AU, and for a B9 star, it reaches
10AU, and for a B9 star, it reaches ![]() 15AU.
This means that we should expect FEBs around Herbig stars
i) to have more important outgassing rates than
15AU.
This means that we should expect FEBs around Herbig stars
i) to have more important outgassing rates than ![]() Pic one, and
ii) to start activity further away from the star.
Pic one, and
ii) to start activity further away from the star.
The actual sublimation rate of a given body may
be somewhat different than predicted in Fig. 4.
It can depend on the surface characteristics
of the body, such as for instance its Bond albedo. Moreover, this
is only a rate per unit surface. The whole production rate of
a given FEB should in fact also depend on its size. We may nevertheless
stress that two identical bodies located at the same stellar
distance from ![]() Pic and a B9 star respectively, should present
outgassing rates within a factor
Pic and a B9 star respectively, should present
outgassing rates within a factor ![]() 3,
provided they are close enough to their stars (
3,
provided they are close enough to their stars (
![]() 1AU).
1AU).
In our simulation runs, our strategy concerning production
rates will thus be the following: once a FEB orbit is chosen,
we give as input the dust and gas production rates, taking care that
the dust/gas mass production rate is of order unity. We assume these
values to apply at periastron, and we scale the production rates
at larger stellar distances according to the
![]() law
plotted in Fig. 4, relevant for the stellar environment
under consideration. The
law
plotted in Fig. 4, relevant for the stellar environment
under consideration. The ![]() Pic spectral events are well
simulated assuming typical dust and gas production rates of
Pic spectral events are well
simulated assuming typical dust and gas production rates of
![]()
![]() mol.s-1 and
mol.s-1 and ![]()
![]() kms-1respectively, for a body passing at 0.2AU. These values may be
considered as accurate within a factor 3 or 4 only. We will nevertheless
assume them as a starting point of our analysis in the environment
of a B9type star, first multiplying them by 3 according to
Fig. 4.
kms-1respectively, for a body passing at 0.2AU. These values may be
considered as accurate within a factor 3 or 4 only. We will nevertheless
assume them as a starting point of our analysis in the environment
of a B9type star, first multiplying them by 3 according to
Fig. 4.
Perhaps the most striking difference between the environment of
a main-sequence A-type star like ![]() Pic and a Herbig Ae/Be star
is the presence of a strong stellar wind. No stellar wind has been
detected so far originating from
Pic and a Herbig Ae/Be star
is the presence of a strong stellar wind. No stellar wind has been
detected so far originating from ![]() Pic. From
a theoretical point of view, A-type stars are expected to have
radiatively driven winds made only of metals (those which indeed
suffer most of the radiation pressure), with a mass-loss rate
less than
Pic. From
a theoretical point of view, A-type stars are expected to have
radiatively driven winds made only of metals (those which indeed
suffer most of the radiation pressure), with a mass-loss rate
less than
![]() yr-1 (Babel 1995).
Conversely, towards pre-main-sequence objects like T Tauri and Herbig Ae/Be stars, there are spectroscopic evidences for strong stellar winds
characterized by terminal velocities ranging between 100 and
500 kms-1, with global mass-loss rates of
yr-1 (Babel 1995).
Conversely, towards pre-main-sequence objects like T Tauri and Herbig Ae/Be stars, there are spectroscopic evidences for strong stellar winds
characterized by terminal velocities ranging between 100 and
500 kms-1, with global mass-loss rates of
![]() -
-
![]() yr-1 (see reviews by Bertout 1989; Catala 1989).
yr-1 (see reviews by Bertout 1989; Catala 1989).
Focusing now to our two example stars, we note first that
the stellar wind of AB Aur has been well studied and modeled.
Bouret & Catala (1998) derive a mass loss rate of
![]() yr-1, which falls in the quoted range. There
is so far no specific measurement on the mass loss rate of HD 100546,
but Viera et al. (1999),
on the basis of the analysis of the H
yr-1, which falls in the quoted range. There
is so far no specific measurement on the mass loss rate of HD 100546,
but Viera et al. (1999),
on the basis of the analysis of the H![]() profile of the star,
conclude to the presence of a stable wind at velocity
profile of the star,
conclude to the presence of a stable wind at velocity
![]() 400 kms-1, in addition to more or less variable
accretion episodes.
400 kms-1, in addition to more or less variable
accretion episodes.
Obviously the presence of a strong stellar wind should drastically affect the coma of the suspected FEBs, and modify their spectroscopic signatures with respect to what should be expected without any noticeable wind. Hence any proper modeling of the FEB scenario around Herbig Ae/Be stars must take the interaction with the stellar wind into account.
It is first necessary to state which model we should assume for a stellar wind of such a star. This is in fact not straightforward as the origin of Herbig Ae/Be winds is still unclear, if not controversial. Basically, three major mechanisms are able to push a stellar wind:
The first one is
a solar-like hot isothermal (![]() K) coronal wind (Parker 1958).
Once the temperature is fixed, this model depends only on one
single parameter, namely the mass loss rate
K) coronal wind (Parker 1958).
Once the temperature is fixed, this model depends only on one
single parameter, namely the mass loss rate ![]() .
The
wind velocity profile has to pass through the sonic critical point,
which location is fixed by the value of
.
The
wind velocity profile has to pass through the sonic critical point,
which location is fixed by the value of ![]() .
The velocity
law v(r) then assumes the form
.
The velocity
law v(r) then assumes the form
![\begin{displaymath}v(r)\exp\left[-\left(\frac{v(r)}{c_{{\rm s}}}\right)^2\right]
={\rm Cst.}\;,
\end{displaymath}](/articles/aa/full/2001/06/aa9851/img59.gif) |
(3) |
The second model will assume is the semi-empirical model introduced
by C87 for Herbig Ae/Be stellar winds.
They assume the following temperature
profile T(r), depending on the four parameters
![]() :
:
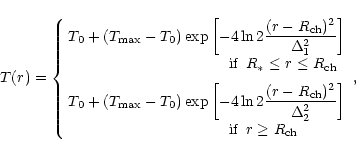 |
(4) |
Using this model to fit the chromospheric wind
lines they observed, Bouret & Catala (1998) gave estimates for all these parameters
for four typical Herbig Ae/Be stars, including AB Aur. Schematically,
the typical values they get are
![]() ,
,
![]() ,
,
![]() ,
and
,
and
![]() ,
depending on the peculiar star under
consideration. In the following we will assume in our tests the values
quoted by Bouret & Catala (1998) for AB Aur, namely
,
depending on the peculiar star under
consideration. In the following we will assume in our tests the values
quoted by Bouret & Catala (1998) for AB Aur, namely
![]() ,
,
![]() ,
,
![]() and
and
![]() .
Note that in any case, the temperature remains considerably less than
the one we assume in the coronal wind model (
.
Note that in any case, the temperature remains considerably less than
the one we assume in the coronal wind model (![]() K).
K).
![\begin{figure}
{
\includegraphics[angle=-90,origin=br,width=8.8cm]{ms9851f5} }
\end{figure}](/articles/aa/full/2001/06/aa9851/Timg78.gif) |
Figure 5: The two velocity profiles assumed in our wind models. The dashed line is the coronal wind profile, and the solid line is a piecewise linear function taken from C87. The velocity gradient of the latter is much steeper in the first stellar radii above the surface, but the terminal velocity is less |
| Open with DEXTER | |
![\begin{figure}
{
\includegraphics[angle=-90,origin=br,width=8.8cm]{ms9851f6.eps} }
\end{figure}](/articles/aa/full/2001/06/aa9851/Timg79.gif) |
Figure 6: Schematic representation of the global interaction between the stellar wind and the cometary atmosphere |
| Open with DEXTER | |
Once the velocity profile is fixed, the density profile ![]() is obtained from the continuity equation
is obtained from the continuity equation
In presence of a strong stellar wind, we expect the dynamics of the gaseous material escaped from the nucleus of the FEBs to be drastically affected. Similarly, the flow of the wind around the FEB nucleus should also be affected, like for the solar wind around comets.
The interaction of comets with the solar wind has been described
by several authors (see e.g. Galeev et al. 1985; Flammer 1991; Flammer et al. 1997); it
is sketched in Fig. 6. Basically, the solar wind is
affected because the gaseous material escaped from the nucleus
tends to be ionized by the ultraviolet radiation field or
by charge exchange interaction with the wind particles.
The new ions produced are then incorporated to the wind.
This mass loading process decelerates the wind in front
of the comet. If the deceleration is strong enough (which is
usually the case), then a bow shock forms. The supersonic
wind becomes subsonic after the shock. Closer to the nucleus,
the wind is then stopped along a stagnation surface (or
tangential discontinuity). Inside this surface we find only
cometary plasma, which undergoes itself an inner shock before
reaching the tangential discontinuity. This picture was
confirmed by in-situ measurements. For typical solar comets
at ![]() 1AU from the Sun, the first shock forms at
1AU from the Sun, the first shock forms at
![]() 5 105 km from the nucleus, while the wind stagnation
takes place at
5 105 km from the nucleus, while the wind stagnation
takes place at ![]() 104 km.
104 km.
In our description, we will assume that the flows is axisymmetric around the line comet - star. Following Krankowsky (1991), we will assume for simplicity that the gaseous material escaped from the nucleus is made of water vapor with a number abundance of 80%, and that the 20% left consist of carbon monoxide (CO). In the environment of a Herbig Ae/Be star, we expect the water molecules to be quickly photo-dissociated. The resulting H and O atoms should not be subject to stellar photoionization (the star is not hot enough), so that they do not take part to the interaction with the wind. Conversely, CO molecules are able to resist a long time enough to allow the formation of CO+ ions which may interact with the stellar wind. As a matter of fact, water photodissociation and CO photoionization were listed by Huebner et al. (1991) as the most important chemical reactions expected in the coma of a comet.
We also assume
that inside the tangential discontinuity
there is no wind, and that the neutral flow is not perturbed.
The details of the dynamics of the wind flow before
and after the bow shock are described in the appendix, as well
as the shape of the shock and of the tangential discontinuity.
The wind is assumed to come from infinity in a plan-parallel
geometry; we neglect the transversal motion
of the wind around the nucleus. The basic parameters
are the velocity and the density of the wind at infinity,
which depend on the distance between the comet and the star,
via the wind model assumed; the volatile production rate Q,
outflow velocity
![]() ,
ionization time
,
ionization time ![]() ,
and recombination rate
,
and recombination rate ![]() .
For solar comets,
.
For solar comets,
![]() is usually about
1 kms-1 and
is usually about
1 kms-1 and
![]() (Flammer et al. 1997), where d is the distance to the star. We will
assume the same values. The recombination
rate
(Flammer et al. 1997), where d is the distance to the star. We will
assume the same values. The recombination
rate ![]() does not depend sharply on the temperature. Following
Gombosi et al. (1983), we assumed
does not depend sharply on the temperature. Following
Gombosi et al. (1983), we assumed
![]() .
From these input parameters, we are able to
derive the characteristics of the wind flow at any point within the
cometary coma.
.
From these input parameters, we are able to
derive the characteristics of the wind flow at any point within the
cometary coma.
The present description holds in fact for a comet which does not
move very fast with respect to the wind. This is justified for
Solar comets at 1AU from the Sun which have an orbital velocity
![]() 40 kms-1 while the Solar wind velocity is more than
400 kms-1. This is far less justified for FEBs passing
at periastron at a few stellar radii from the stellar surface:
closer to the star, the orbital velocity is larger while
the wind velocity is less. At
40 kms-1 while the Solar wind velocity is more than
400 kms-1. This is far less justified for FEBs passing
at periastron at a few stellar radii from the stellar surface:
closer to the star, the orbital velocity is larger while
the wind velocity is less. At ![]() 10 or 20 stellar radii
from the surface (depending on the wind model and of the stellar parameters),
both velocities turn out to be comparable.
10 or 20 stellar radii
from the surface (depending on the wind model and of the stellar parameters),
both velocities turn out to be comparable.
A convenient way to (partially) solve this problem is to take
into account the velocity of the comet when computing the
velocity of the wind at infinity
![]() (see Appendix).
If the comet is located at distance
(see Appendix).
If the comet is located at distance
![]() from the star,
where the wind velocity is
from the star,
where the wind velocity is
![]() ,
and moves
with velocity
,
and moves
with velocity
![]() ,
we may just assume
(vectorially)
,
we may just assume
(vectorially)
| (7) |
We want to point out here that even with this refinement, the present description is probably a fairly crude approximation of the stellar wind flow around a more or less star-grazing comet. If the comet is close enough to the star, the approximation of a plan-parallel wind flow coming from infinity is very bad. One should consider the actual shape of the (spherical) wind expansion around the star, and compute how it is modified in presence of a FEB. Moreover, as the FEB passes near perihelion, it turns quickly around the star. This causes centrifugal terms to appear when the dynamics of the flow is computed in a referential frame bound to the nucleus. These effects are indeed taken into account in our simulation code when we compute the dynamics of individual metallic ions escaped from the FEB (Beust et al. 1996). Taking them nevertheless into a 3-dimensional hydrodynamical computation of the wind flow around the star-grazing comet is far beyond the scope of the present work, as this would require a specific study, probably highly computing time consuming. The purpose of this paper is only to seek the first-order effects of the introduction of a strong stellar wind. Moreover, our knowledge of the structure and the geometry of Herbig Ae/Be winds is so rough that getting into more details in the description of the interaction with the cometary medium would probably not be relevant. We decided however arbitrarily to consider that if the comet is located at distance d from the star, the zone of perturbed wind, as computed from the present model should not extend further away than 2d from the star. Beyond this limit, we assume that the wind recovers its unperturbed geometry.
Now, we need to describe the interaction between a wind flow
(perturbed or not) and the individual metallic
ions escaped from the FEB, and supposed to be responsible for
the transient spectral events observed. We recall that once
escaped from the FEB nucleus, the metallic ions are basically
subject to two major conflicting actions, i) the radiation
pressure that tends to blow them away in the anti-star direction,
and ii) the drag (or collision) force due to the surrounding
volatile medium that tends to retain them around the nucleus.
Now we must add an interaction force with the wind, i.e.
a ionized flow. We had already described this interaction in Beust et al. (1989).
It results from classical Coulomb scattering theory. Let us
consider one ion of mass m and charge q, moving at velocity
v in a field of protons (charge e). After one collision,
the impulsion change in the direction parallel to the unperturbed
velocity reads
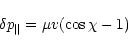 |
(8) |
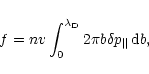 |
(10) |
![\begin{figure}
\captwidth=55truemm
\figwidth=12truecm
\hbox to\textwidth{
\parbo...
...,width=\figwidth]{ms9851f7b.eps}}
\hfill\parbox[b]{\captwidth}{
} }
\end{figure}](/articles/aa/full/2001/06/aa9851/Timg101.gif) |
Figure 7:
Schematic plots of two simulation outputs, for
a FEB passing at |
| Open with DEXTER | |
In the FEB scenario, the bulk redshift velocity v of a variable
absorption corresponds to the projection onto the line of sight
of the orbital velocity of the corresponding FEB. This results
from the fact that most of the absorption is due to the ionic coma
that surrounds the nucleus, and not to the tail.
Assuming a Keplerian formalism, we easily derive
this velocity v (Beust et al. 1996) as a function of the periastron value
of the FEB (or its stellar distance d when crossing the line of sight),
its eccentricity e and its longitude of periastron ![]() with respect to the line of sight:
with respect to the line of sight:
| v | = | 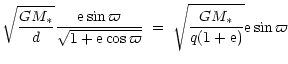 |
|
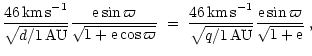 |
(12) |
In order to reproduce
![]() kms-1 in the B9 star
environment, we must then assume a FEB passing closer to the star
than 0.05AU and with orbital orientation more or less perpendicular
(
kms-1 in the B9 star
environment, we must then assume a FEB passing closer to the star
than 0.05AU and with orbital orientation more or less perpendicular
(
![]() )
to the line of sight. If we assume an even smaller
periastron value, then the constraint on
)
to the line of sight. If we assume an even smaller
periastron value, then the constraint on ![]() is weaker, but this does
not change anything to the results presented below.
We will then take in all
the following simulations a typical FEB orbit with
is weaker, but this does
not change anything to the results presented below.
We will then take in all
the following simulations a typical FEB orbit with ![]() AU
and
AU
and
![]() .
.
As mentioned above, in any simulation run, we must fix the
outgassing and dust production rates at periastron. We start from the
values fitted at 0.2AU in the ![]() Pic environment, first multiplying
them by 3 according to Fig. 4 to take into account the
difference between the stellar environments, and multiplying them
once again by
(0.2/0.04)2=25 to take into account the
closer periastron value. This yields a volatile outgassing rate
of
Pic environment, first multiplying
them by 3 according to Fig. 4 to take into account the
difference between the stellar environments, and multiplying them
once again by
(0.2/0.04)2=25 to take into account the
closer periastron value. This yields a volatile outgassing rate
of
![]() mol.s-1 and a dust production rate
of
mol.s-1 and a dust production rate
of
![]() kgs-1. These will constitute
our reference values, intended to be valid for a FEB identical
to those assumed around
kgs-1. These will constitute
our reference values, intended to be valid for a FEB identical
to those assumed around ![]() Pic, but located at 0.04AU from a
B9 type star. Remember that all throughout the simulation run,
the instantaneous production rates of the body under consideration
are computed according to Fig. 4 with respect to the values
at periastron given as input.
Pic, but located at 0.04AU from a
B9 type star. Remember that all throughout the simulation run,
the instantaneous production rates of the body under consideration
are computed according to Fig. 4 with respect to the values
at periastron given as input.
| |
Figure 8: A close up view of the cometary head zone corresponding to Fig. 7b. The location of the bow shock and the tangential discontinuity are now displayed on this enlargement. The flow of Mg II ions is severely constrained by the interaction with the wind |
| Open with DEXTER | |
![\begin{figure}
\captwidth=55truemm
\figwidth=12truecm
\hbox to\textwidth{
\inclu...
...igin=br,width=\figwidth]{ms9851f9}\hfill\parbox[b]{\captwidth}{
} }
\end{figure}](/articles/aa/full/2001/06/aa9851/Timg119.gif) |
Figure 9:
A simulation of the same FEB than in Fig. 7b, but
in the |
| Open with DEXTER | |
![\begin{figure}
\captwidth=55truemm
\figwidth=12truecm
\hbox to\textwidth{
\par\i...
...gin=br,width=\figwidth]{ms9851f10}\hfill\parbox[b]{\captwidth}{
} }
\end{figure}](/articles/aa/full/2001/06/aa9851/Timg121.gif) |
Figure 10:
Same as Fig. 7b, but now with a stellar wind mass
loss rate
|
| Open with DEXTER | |
| |
Figure 11: The spectral signature in the Mg II k line of the same FEB as in Figs. 7 and 10, for different stellar wind mass loss values |
| Open with DEXTER | |
We first note that there are very few differences between the
two plots displayed, though the wind models are different.
This is due to the fact that the structure of the wind flow
around the nucleus (i.e., the location of the shocks) is
essentially a function of the impulsion flux of the
wind
![]() only, which is itself directly related
to the mass loss rate
only, which is itself directly related
to the mass loss rate ![]() by the continuity Eq. (6). Thus, the global action of the wind on
the FEB at a given stellar distance is to first order controlled
by the mass loss rate, irrespective of the wind model
assumed. Note that this is only valid for a spherically
symmetric wind. In the following, we will then not distinguish
furthermore between the results for the Parker (1958) wind
model and those for the C87 one, as in any case we
checked that both were very similar. We will only present
results corresponding to the C87 model, as this
represents a more realistic wind model for a Herbig Ae/Be star.
by the continuity Eq. (6). Thus, the global action of the wind on
the FEB at a given stellar distance is to first order controlled
by the mass loss rate, irrespective of the wind model
assumed. Note that this is only valid for a spherically
symmetric wind. In the following, we will then not distinguish
furthermore between the results for the Parker (1958) wind
model and those for the C87 one, as in any case we
checked that both were very similar. We will only present
results corresponding to the C87 model, as this
represents a more realistic wind model for a Herbig Ae/Be star.
Second, we note that the ionic cloud around the FEB is very thin. This is in fact due to interaction with the wind, and shows up clearly in Fig. 8, which is an enlargement of the cometary head zone for the Fig. 7b case (the C87 wind case), and where the location of the shock surfaces with the wind (bow shock and tangential discontinuity) has been superimposed to the plot for clarity. Note the inclination of these surfaces with respect to the star-FEB axis. This is due to the velocity of the FEB, which is comparable to the wind velocity. Now, the dynamics of the Mg II ions appears obviously strongly affected by the interaction with the wind. They indeed hardly expand further away than the tangential discontinuity (recall that there is no wind inside this area) before flowing along it. In fact, the size of the cloud appears in the present case fully controlled by the wind.
The major consequence of the small size of the ionic cloud is that the
transient absorption event generated by the FEB is not detectable.
Independently from line saturation, the cloud cannot absorb more flux
than its relative projected size onto the stellar surface. Here this
size is so small that the variable absorption is unobservable.
This is the striking difference with the situation for
identical FEBs orbiting ![]() Pic.
As a matter of fact, if we simulate the same FEB around
Pic.
As a matter of fact, if we simulate the same FEB around ![]() Pic, and adding
a small wind of
Pic, and adding
a small wind of
![]() yr-1, the wind appears to
have virtually no role, as the shocks appear much further away from
the nucleus than the typical size of the ionic cloud as it is
sculpted by radiation pressure. In the
yr-1, the wind appears to
have virtually no role, as the shocks appear much further away from
the nucleus than the typical size of the ionic cloud as it is
sculpted by radiation pressure. In the ![]() Pic case, a
strong transient event can be observed (Fig. 9).
Pic case, a
strong transient event can be observed (Fig. 9).
The net effect of a strong stellar wind on the FEB phenomenon is thus
to render it unobservable, as far as we consider mass loss rates
of
![]() yr-1, and FEBs identical
to those assumed in the
yr-1, and FEBs identical
to those assumed in the ![]() Pic case, just scaling the evaporation
parameters according to Fig. 4. These hypotheses need now
to be discussed.
Pic case, just scaling the evaporation
parameters according to Fig. 4. These hypotheses need now
to be discussed.
The value assumed in the simulations
of Fig. 7 (
![]() yr-1) falls in
the range of values commonly assumed for Herbig Ae/Be stars. Of course,
assuming higher values (such as
yr-1) falls in
the range of values commonly assumed for Herbig Ae/Be stars. Of course,
assuming higher values (such as
![]() yr-1,
a still common value for such stars) leads to an even
more drastic situation, the Mg II cloud becoming even thinner.
Conversely, it is of valuable interest to find the maximum
mass loss rate that would allow the FEBs to generate
detectable variable components. This is illustrated
in Figs. 10 and 11. Figure 10 is the same as
Fig. 7b, but
with
yr-1,
a still common value for such stars) leads to an even
more drastic situation, the Mg II cloud becoming even thinner.
Conversely, it is of valuable interest to find the maximum
mass loss rate that would allow the FEBs to generate
detectable variable components. This is illustrated
in Figs. 10 and 11. Figure 10 is the same as
Fig. 7b, but
with
![]() yr-1. Figure 11 displays only
the Mg II k spectral signature of the FEB for various other
yr-1. Figure 11 displays only
the Mg II k spectral signature of the FEB for various other ![]() values less than
values less than
![]() yr-1. The lower the
mass loss rate, the further away the wind shock surfaces
are located from the FEB nucleus, and thus the deeper the variable
components appear. Note that in all these runs, the production rate
of the FEB was unchanged. The depth of the variable component
appears in fact fully controlled by the wind.
yr-1. The lower the
mass loss rate, the further away the wind shock surfaces
are located from the FEB nucleus, and thus the deeper the variable
components appear. Note that in all these runs, the production rate
of the FEB was unchanged. The depth of the variable component
appears in fact fully controlled by the wind.
Basically, for
![]() yr-1,
a detectable component is observable. The wind shock surfaces around
the nucleus are located sufficiently far away from the FEB nucleus to
allows the Mg II cloud to be large enough to have a significant
spectral signature. The variable component turns out to be very deep for
yr-1,
a detectable component is observable. The wind shock surfaces around
the nucleus are located sufficiently far away from the FEB nucleus to
allows the Mg II cloud to be large enough to have a significant
spectral signature. The variable component turns out to be very deep for
![]() yr-1, up to
yr-1, up to
![]() 75% of the continuum (Fig. 11).
The size of the Mg II clouds
is controlled by the wind, i.e. by the location of the
tangential discontinuity, down to
75% of the continuum (Fig. 11).
The size of the Mg II clouds
is controlled by the wind, i.e. by the location of the
tangential discontinuity, down to
![]() yr-1;
for weaker winds, the radiation
pressure blows them away before they feel the wind, so that the
spectral signature of the cloud does no longer grow. In this regime,
we are back to a
yr-1;
for weaker winds, the radiation
pressure blows them away before they feel the wind, so that the
spectral signature of the cloud does no longer grow. In this regime,
we are back to a ![]() Pic-like situation.
Pic-like situation.
This
![]() yr-1 wind threshold (valid for
the FEB production rate assumed) is well below
the usual range for Herbig Ae/Be stellar winds, so that we may conclude
that the FEBs under consideration should not generate observable
transient absorption events like those observed, at least in the
environments of spherically symmetrical winds.
yr-1 wind threshold (valid for
the FEB production rate assumed) is well below
the usual range for Herbig Ae/Be stellar winds, so that we may conclude
that the FEBs under consideration should not generate observable
transient absorption events like those observed, at least in the
environments of spherically symmetrical winds.
![\begin{figure}
\captwidth=55truemm
\figwidth=12truecm
\hbox to\textwidth{
\par\i...
...gin=br,width=\figwidth]{ms9851f12}\hfill\parbox[b]{\captwidth}{
} }
\end{figure}](/articles/aa/full/2001/06/aa9851/Timg131.gif) |
Figure 12: Same as Fig. 7b, but now with dust and volatiles production rates multiplied by 1000. A deep transient absorption component is generated |
| Open with DEXTER | |
| |
Figure 13: The spectral signature in the Mg II k line of the same FEB as in Figs. 7 and 10, for production rates multiplied by 10 (left) and 100 (right) with respect to the case of Fig. 7b |
| Open with DEXTER | |
Figure 13 shows the resulting Mg II k feature for intermediate
cases, i.e. for production rates multiplied by 10 and 100 with respect to
Fig. 7b. We note that a small feature is present in the ![]() case, but that it becomes really observable in the
case, but that it becomes really observable in the
![]() case.
This result holds for a wind mass loss rate
case.
This result holds for a wind mass loss rate
![]() yr-1. For
yr-1. For
![]() yr-1, we must now multiply the production
rates by 10000 to get observable features, and only by 10 for
yr-1, we must now multiply the production
rates by 10000 to get observable features, and only by 10 for
![]() yr-1.
yr-1.
This model appears to fit well the data for ![]() Pic, but we want to
point out that the proposed
mechanism is extremely generic and should be active as soon as
a planet on a moderately eccentric orbit (
Pic, but we want to
point out that the proposed
mechanism is extremely generic and should be active as soon as
a planet on a moderately eccentric orbit (
![]() )
is present, which
is not in itself a strong requirement. The key point here for our
purpose is that the process that brings the bodies from low-eccentricity
to star-grazing orbits is gradual. In this scenario, a given body is
able to become a star-grazer within
)
is present, which
is not in itself a strong requirement. The key point here for our
purpose is that the process that brings the bodies from low-eccentricity
to star-grazing orbits is gradual. In this scenario, a given body is
able to become a star-grazer within ![]() 104 revolutions of the
perturbing planet, i.e. typically
a few
104 revolutions of the
perturbing planet, i.e. typically
a few ![]() yr depending on the orbital period of the planet. Hence
if the dust begins to evaporate at
yr depending on the orbital period of the planet. Hence
if the dust begins to evaporate at ![]() 2AU from the star, then
a body seen with a periastron of 0.04AU
should have already undergone
typically a few thousands of periastron passages within the dust
evaporating zone before reaching this periastron value. It is not
obvious whether it should survive to all these passages.
2AU from the star, then
a body seen with a periastron of 0.04AU
should have already undergone
typically a few thousands of periastron passages within the dust
evaporating zone before reaching this periastron value. It is not
obvious whether it should survive to all these passages.
| |
Figure 14:
The minimum periastron that a body can reach before
being fully evaporated, as a function of its radius, in the |
| Open with DEXTER | |
In Beust & Morbidelli (2000), we investigated this question in the ![]() Pic context,
i.e. with a dust evaporating zone limited to
Pic context,
i.e. with a dust evaporating zone limited to ![]() 0.5AU and
appropriate evaporation rates. The conclusion was that the FEBs
need to be initially
0.5AU and
appropriate evaporation rates. The conclusion was that the FEBs
need to be initially ![]() 15 km large (or more) in order to resist down to
genuine star-grazing periastron values, as some observations (HVFs) seem
to require. This of course does not exclude the presence of (numerous) smaller
bodies, but they do not penetrate very deep into the dust evaporating
zone, as they fully evaporate before. Now, in the Herbig Ae/Be case,
the situation is even more drastic, as the dust evaporation zone
extends 4 times further away from the star, and that the mere
observation of variable features despite the presence of a
strong wind seems to require the evaporation rates to be at least
100 times larger that the expected
15 km large (or more) in order to resist down to
genuine star-grazing periastron values, as some observations (HVFs) seem
to require. This of course does not exclude the presence of (numerous) smaller
bodies, but they do not penetrate very deep into the dust evaporating
zone, as they fully evaporate before. Now, in the Herbig Ae/Be case,
the situation is even more drastic, as the dust evaporation zone
extends 4 times further away from the star, and that the mere
observation of variable features despite the presence of a
strong wind seems to require the evaporation rates to be at least
100 times larger that the expected ![]() Pic ones at the same stellar
distances.
Pic ones at the same stellar
distances.
We apply here the same analysis to the B9 star case, i.e.
with a dust evaporating limit of 1.8AU and evaporation rates 100 times
larger as for ![]() Pic. The compared result with
Pic. The compared result with ![]() Pic is illustrated in
Fig. 14, which is similar to Fig. 7 of Beust & Morbidelli (2000).
Assuming a dynamical evolution given by numerical integration of
a particle trapped in 4:1 mean-motion resonance with a perturbing
Jovian-like planet (located at 10AU), we compute the mass loss
of bodies of various initial radii at each periastron passage,
as soon as they get into the
dust evaporation zone. For various body radii, we thus compute
the minimum periastron reached, which is is the periastron
the body assumes when it turns out to be fully evaporated. Of course, larger
bodies are expected to resist down to smaller periastron values,
and the same body resists much less in the environment of a B9 star than
around
Pic is illustrated in
Fig. 14, which is similar to Fig. 7 of Beust & Morbidelli (2000).
Assuming a dynamical evolution given by numerical integration of
a particle trapped in 4:1 mean-motion resonance with a perturbing
Jovian-like planet (located at 10AU), we compute the mass loss
of bodies of various initial radii at each periastron passage,
as soon as they get into the
dust evaporation zone. For various body radii, we thus compute
the minimum periastron reached, which is is the periastron
the body assumes when it turns out to be fully evaporated. Of course, larger
bodies are expected to resist down to smaller periastron values,
and the same body resists much less in the environment of a B9 star than
around ![]() Pic.
This shows up in Fig. 14. As a matter of fact, we note
from Fig. 14 that in the
Pic.
This shows up in Fig. 14. As a matter of fact, we note
from Fig. 14 that in the ![]() Pic environment, bodies
larger than
Pic environment, bodies
larger than ![]() 15 km are indeed able to get periastron values
significantly less than the dust evaporation limit, while smaller
bodies do not. In the B9 type star environment, this threshold turns
out to be
15 km are indeed able to get periastron values
significantly less than the dust evaporation limit, while smaller
bodies do not. In the B9 type star environment, this threshold turns
out to be ![]() 100 km (Fig. 14).
Therefore, for a FEB to be able
to generate an absorption event when crossing the line
of sight at 0.04AU from the star, it
needs to be at least 100 km large, otherwise it is destroyed before.
The constraint is even more drastic if we consider wind mass loss
values in the range 10-8-
100 km (Fig. 14).
Therefore, for a FEB to be able
to generate an absorption event when crossing the line
of sight at 0.04AU from the star, it
needs to be at least 100 km large, otherwise it is destroyed before.
The constraint is even more drastic if we consider wind mass loss
values in the range 10-8-
![]() yr-1.
yr-1.
In the peculiar case of HD 100546, if we assume similar winds,
the evaporation rate
of the FEB needs to be ![]() 500 times as large as for
500 times as large as for ![]() Pic in order
to reproduce the observed variable features (Fig. 1).
This leads to a minimum size of
Pic in order
to reproduce the observed variable features (Fig. 1).
This leads to a minimum size of ![]() 200 km instead of
100 km.
200 km instead of
100 km.
Assuming we observe towards Herbig Ae/Be FEBs that are at least
![]() 100 km-sized instead of
100 km-sized instead of ![]() 15 km
in the case of
15 km
in the case of ![]() Pic may help understanding the discrepancy concerning
the evaporation
rates. The
Pic may help understanding the discrepancy concerning
the evaporation
rates. The
![]() values plotted in Fig. 4 are the
evaporation rates per unit surface, i.e. they compare the
global evaporation rates between the various stellar environments
for identical bodies. Between a B9 star and
values plotted in Fig. 4 are the
evaporation rates per unit surface, i.e. they compare the
global evaporation rates between the various stellar environments
for identical bodies. Between a B9 star and ![]() Pic, the ratio is 3.
Now, if the typical Herbig Ae/Be FEB is
100 km-sized, while the one for
Pic, the ratio is 3.
Now, if the typical Herbig Ae/Be FEB is
100 km-sized, while the one for ![]() Pic is 15 km, the global evaporation
rate ratio between the two bodies should by
Pic is 15 km, the global evaporation
rate ratio between the two bodies should by
![]() ,
which is comparable to what we have deduced from our simulations.
,
which is comparable to what we have deduced from our simulations.
The problem with this scenario is the number of
such bodies, and consequently the amount of mass in the disk that
should be necessary in order to maintain a statistically
detectable spectral FEB activity. Note also that if there are many
100 km-sized bodies, there should also be many more smaller ones.
We investigated the relevance of this question to the ![]() Pic case
in Beust & Morbidelli (2000), coming to the conclusion that the total mass of
planetesimals necessary in the disk for sustaining the present FEB
activity (several hundreds of events per year) while refilling the
4:1 resonance by mutual collisions among planetesimals or planet
migration was at least
Pic case
in Beust & Morbidelli (2000), coming to the conclusion that the total mass of
planetesimals necessary in the disk for sustaining the present FEB
activity (several hundreds of events per year) while refilling the
4:1 resonance by mutual collisions among planetesimals or planet
migration was at least
![]() per AU . This is only
marginally compatible with realistic estimates. Obviously a more
refined study of this question is necessary.
per AU . This is only
marginally compatible with realistic estimates. Obviously a more
refined study of this question is necessary.
In the present case of Herbig Ae/Be stars, it is almost impossible
to derive any comparable reliable estimate, as we still do not know
the spectral events frequency. All we can say is that the events are
not rare, as they have been observed. In the case of HD 100546, we can
point out that variable events have been observed more than once
(Grady et al. 1997; Viera et al. 1999). On the basis of observed variation time-scales
of a few tens of hours, Grady et al. (2000) give nevertheless tentative
events frequency estimates for some stars else than HD 100546, with
results ranging between one event per day and one every five days.
This is ![]() 10 times less than the estimates for
10 times less than the estimates for ![]() Pic.
In Beust & Morbidelli (2000), we inferred from dynamical simulations a population
of bodies
Pic.
In Beust & Morbidelli (2000), we inferred from dynamical simulations a population
of bodies
![]() -109 bodies per AU in the vicinity of the
4:1 resonance. The mass density
-109 bodies per AU in the vicinity of the
4:1 resonance. The mass density
![]() within the disk then reads
within the disk then reads
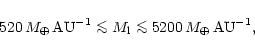 |
(14) |
In the case of AB Aur, Grady et al. (1999) stress that the infall activity is
even higher than for ![]() Pic and HD 100546, arguing that signatures of infalling
gas was detected in all high-resolution UV spectra of AB Aur from 1978
to 1996. Consequently, the disk population and mass
estimates will be even higher than for HD 100546, which turns out
to be even more unrealistic.
Pic and HD 100546, arguing that signatures of infalling
gas was detected in all high-resolution UV spectra of AB Aur from 1978
to 1996. Consequently, the disk population and mass
estimates will be even higher than for HD 100546, which turns out
to be even more unrealistic.
We may then stress that even if we cannot derive any precise events frequency estimate, if we assume that these events are due to 100 km-sized bodies, the inferred "planetesimal'' disk mass turns out to be truly unrealistic.
In the case of AB Aur, where the wind has been successfully modeled
as spherically symmetric with a mass loss rate of
![]() yr-1, the conclusion is
straightforward: FEBs, if present, could probably not be observed
in absorption lines. This conclusion holds in fact for all stars
where similar mass loss rates have been measured, such as those
modeled together with AB Aur by Bouret & Catala (1998). It can in fact be extended
to all Herbig Ae/Be stars of comparable ages (a few 106yr), as they
are all expected to have strong winds. This conclusion is independently
supported by recent observation of an accretion episode towards UX Ori by
Natta et al. (2000), showing that the infalling gas is compatible with
solar rather than cometary (i.e., volatile depleted) composition.
For such stars, this suggests to attribute the accretion episodes observed
to magnetically driven accretion columns
(see e.g. models by Hatman et al. 1994) rather than to FEBs. For AB Aur however, we mentioned
above that the wind might not actually be spherically symmetric,
but only modeled as spherically symmetric thanks to its high viewing
latitude from the Earth.
But even if this is true, in that case this means that we are
actually viewing the star across the wind, so that the main conclusion
concerning the detectability of FEB signatures still holds.
yr-1, the conclusion is
straightforward: FEBs, if present, could probably not be observed
in absorption lines. This conclusion holds in fact for all stars
where similar mass loss rates have been measured, such as those
modeled together with AB Aur by Bouret & Catala (1998). It can in fact be extended
to all Herbig Ae/Be stars of comparable ages (a few 106yr), as they
are all expected to have strong winds. This conclusion is independently
supported by recent observation of an accretion episode towards UX Ori by
Natta et al. (2000), showing that the infalling gas is compatible with
solar rather than cometary (i.e., volatile depleted) composition.
For such stars, this suggests to attribute the accretion episodes observed
to magnetically driven accretion columns
(see e.g. models by Hatman et al. 1994) rather than to FEBs. For AB Aur however, we mentioned
above that the wind might not actually be spherically symmetric,
but only modeled as spherically symmetric thanks to its high viewing
latitude from the Earth.
But even if this is true, in that case this means that we are
actually viewing the star across the wind, so that the main conclusion
concerning the detectability of FEB signatures still holds.
This conclusion does not straightforwardly extend to older Herbig Ae/Be stars (![]() 107yr) such as HD 100546. For HD 100546 specifically, Viera et al. (1999)
conclude on the basis of H
107yr) such as HD 100546. For HD 100546 specifically, Viera et al. (1999)
conclude on the basis of H![]() profiles
to the presence of at least three distinct components in the circumstellar
envelope
of the star: a discrete, variable accretion close to the star, a
more stable one in the remote envelope, and a wind that appeared
stable during the period they observed the star. They however do
not derive any mass loss rate. In fact, modeling this structure appears
here more complex than for P-Cygni class Herbig Ae/Be stars like AB Aur,
for which the wind component dominates the line profile.
profiles
to the presence of at least three distinct components in the circumstellar
envelope
of the star: a discrete, variable accretion close to the star, a
more stable one in the remote envelope, and a wind that appeared
stable during the period they observed the star. They however do
not derive any mass loss rate. In fact, modeling this structure appears
here more complex than for P-Cygni class Herbig Ae/Be stars like AB Aur,
for which the wind component dominates the line profile.
On this simple basis, we may stress that the mass loss rate of
HD 100546 should not exceed that of AB Aur. Based on a statistical
study of T Tauri stars, Muzerolle et al. (2000) showed recently that
accretion rates drop by 2 orders of magnitude between ages
of 106 and ![]() yr. This holds for T Tauri stars,
and for accretion. If we were to believe this to be still true for
Herbig Ae/Be stars, and to similarly apply for wind mass loss
rates, then scaling from measured values for young Herbig Ae/Be stars like AB Aur, we would derive a mass loss rate estimate for HD 100546 of a few
yr. This holds for T Tauri stars,
and for accretion. If we were to believe this to be still true for
Herbig Ae/Be stars, and to similarly apply for wind mass loss
rates, then scaling from measured values for young Herbig Ae/Be stars like AB Aur, we would derive a mass loss rate estimate for HD 100546 of a few
![]() yr-1. This is close to the limit under
which FEB signatures begin to be observable. We may consider
this value as a lower limit.
Therefore, provided this lower limit applies,
FEBs could be marginally observable
around stars like HD 100546, although strong components like those
of Fig. 1 are hardly reproduced with
yr-1. This is close to the limit under
which FEB signatures begin to be observable. We may consider
this value as a lower limit.
Therefore, provided this lower limit applies,
FEBs could be marginally observable
around stars like HD 100546, although strong components like those
of Fig. 1 are hardly reproduced with
![]() yr-1.
yr-1.
Up to now, we have considered a spherically symmetric wind geometry. If this approximation may be considered as valid for young Herbig Ae/Be stars like AB Aur, it is far from being obvious to apply for older stars like HD 100546. Viera et al. (1999) suggest conversely that the regions of the stellar environment of HD 100546 with wind activity should be limited to the higher latitudes, while lower latitude regions should be wind free, accretion of matter taking place close to the equatorial plane. In some specific cases such as HD163296, there is observational evidence for a collimated outflow, i.e., far from spherically symmetric (Devine et al. 2000).
Such non-spherically symmetric geometries can be generated magnetically. This is especially the case if the stars holds a dipole-like fossil magnetic field. In that case, models by Paatz & Camenzind (1996) and Strafella et al. (1998) show that in the first few stellar radii above the stellar surface, the dipole-like magnetic field is expected to co-rotate with the star, leaving a wind free cavity at low latitude, while at higher latitudes the lines should be open and thus transport matter away.
If this picture is correct for HD 100546, then we should expect to potentially
observe spectral signatures of FEBs if they cross the line of sight inside
the wind free cavity, i.e., at low latitude. As a matter of fact,
the mean-motion resonance model invoked at the source for the
FEB phenomenon towards ![]() Pic predicts that most of the FEBs should
remain at moderate orbital inclination with respect
to the equatorial plane of the star.
Pic predicts that most of the FEBs should
remain at moderate orbital inclination with respect
to the equatorial plane of the star.
Besides, we know now that HD 100546 is not viewed edge-on. Pantin & Lagage (2001)
and Augereau et al. (2001) report recently and independently the detection
of a dusk disk surrounding the star, in thermal emission for
Pantin & Lagage (2001) and in scattered light for Augereau et al.(2001).
Both detections agree for a disk inclination of
![]() with respect to
pole-on, based on the shape of the circumstellar nebulosity. This means
that the line of sight is located at
with respect to
pole-on, based on the shape of the circumstellar nebulosity. This means
that the line of sight is located at ![]()
![]() stellar latitude.
It is thus far from being obvious to state whether at
stellar latitude.
It is thus far from being obvious to state whether at
![]() latitude
we are viewing the stellar surface across the wind or not. Moreover,
even if the wind is not strong enough to prevent FEB detection,
it is still not obvious whether FEBs at
latitude
we are viewing the stellar surface across the wind or not. Moreover,
even if the wind is not strong enough to prevent FEB detection,
it is still not obvious whether FEBs at ![]()
![]() inclination
can be dynamically generated. This specific issue will be addressed
in forthcoming work.
inclination
can be dynamically generated. This specific issue will be addressed
in forthcoming work.
In this framework, even a mass loss rate measurement does not allow to state whether FEBs can be observed or not towards such a star, as this depends on the geometry of the wind. Specific, more sophisticated modeling of this stellar environment is therefore required. Moreover, a more regular survey of the spectrum of stars like HD 100546 would help to refine the statistics on the occurrence of these FEB-like events.
This assumption immediately raises the question whether the amount of mass that should be involved in this process is realistic or not. It is still impossible to definitely answer this question, because of the lack of observational statistics on each of these stars. The first events frequency estimates on some of them lead nevertheless to unrealistic masses. A more detailed analysis and a better observational coverage will help solving this question.
It is nevertheless possible to stress that for young Herbig Ae/Be stars
like AB Aur with well identified spherically symmetric winds
with mass loss rates of ![]() 10
10
![]() yr-1 or above,
the FEB hypothesis is probably not realistic to account for variable
accretion events.
yr-1 or above,
the FEB hypothesis is probably not realistic to account for variable
accretion events.
For older Herbig Ae/Be stars like HD 100546 however, the conclusion is not so straightforward, as winds could be close to the limit under which FEB signatures begin to be observable, and because various observations and modeling suggest that the wind is confined to higher stellar latitudes. Hence FEBs could still be observed despite a strong stellar wind if they cross a the line of sight at low stellar latitude. Investigating this issue will require i) more precise measurements of mass loss rates, ii) more extensive modeling adapted to each stellar case, and iii) a more regular survey of the variable spectral events occurring towards such stars.
 |
= | 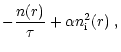 |
(A.6) |
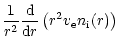 |
= | 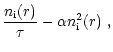 |
(A.7) |
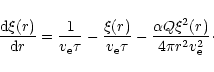 |
(A.8) |
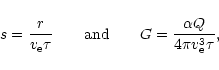 |
(A.9) |
If we set G=0 (no recombination), the solution of this equation
is
![]() .
If we did not
consider the zone inside the tangential discontinuity where
recombination is able to take place, we would add the boundary condition
.
If we did not
consider the zone inside the tangential discontinuity where
recombination is able to take place, we would add the boundary condition
![]() (we neglect the physical radius of the nucleus), i.e.
(we neglect the physical radius of the nucleus), i.e.
![]() ,
add this would bring us
back to Eq. (A.5). Here the constant will be fixed by continuity
with the solution inside the tangential discontinuity at the stagnation
point of the wind
,
add this would bring us
back to Eq. (A.5). Here the constant will be fixed by continuity
with the solution inside the tangential discontinuity at the stagnation
point of the wind
![]() (or
(or
![]() ).
).
Inside the ionopause, where ![]() ,
the solution of Eq. (A.10)
is more complex. As shown by Gombosi et al. (1983),
the general solution to this equation involves the Whittaker function,
but with the boundary condition
,
the solution of Eq. (A.10)
is more complex. As shown by Gombosi et al. (1983),
the general solution to this equation involves the Whittaker function,
but with the boundary condition ![]() ,
the solution may be expressed
as
,
the solution may be expressed
as
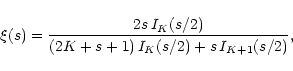 |
(A.11) |
The solution outside the ionopause then reads by continuity
The continuity
Eq. (A.1) can be now integrated. For linear comets first, we find
![\begin{displaymath}(\hat{\rho}\hat{u})_{{\rm s}}=\frac{\gamma^2}{\gamma-1}
\frac{M^2\left[M^2(\gamma^2-1)+1\right]}{(M^2\gamma+1)^2}\;.
\end{displaymath}](/articles/aa/full/2001/06/aa9851/img210.gif) |
(A.17) |
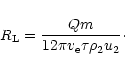 |
(A.21) |
This description holds for the flow along the comet - star axis.
Now we want to describe the flow off the axis. We first assume
an axial symmetry of the flow around that axis, so that any planar
description is valid. We choose to describe the flow in a plane
containing the comet - star axis, and we define a referential frame
(OXY) centered on the nucleus where the OX axis points towards
the star and where OY is perpendicular to that direction.
We will also neglect for simplicity any motion of the gas
that is not parallel to OX, assuming in fact that the
radial motion dominates the transversal one. We will then describe
the flow along an axis parallel to OX, passing at distance yfrom the nucleus. In the supersonic part of the flow,
Eqs. (A.1)-(A.3) still apply, provided
![]() must be replaced by
must be replaced by
![]() .
The density of
neutrals now reads for non-linear comets:
.
The density of
neutrals now reads for non-linear comets:
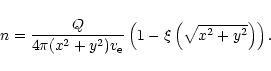 |
(A.23) |
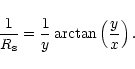 |
(A.26) |
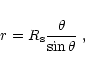 |
(A.27) |
![\begin{displaymath}u(x)=u_2\left[1-\frac{R_{{\rm L}}}{x}\left(
\frac{x}{y}\arctan\left(\frac{y}{x}\right)-\frac{x}{R_{{\rm s}}}\right)
\right]^4.
\end{displaymath}](/articles/aa/full/2001/06/aa9851/img235.gif) |
(A.28) |
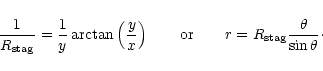 |
(A.29) |