Four Turbo-Rogue GPS receivers owned by the Los Alamos National
Laboratory were set up at the VLA site, one at the array center and
one at the end of each of the three VLA arms, i.e. in an approximately
equilateral triangle with sides of ![]() 35 km. The data from a
single receiver are sufficient to determine the model discussed above,
but it was hoped that comparison of the phase-TEC between the central
receiver and the receivers at the ends of the arms would allow better
estimates of the phase gradients along the arms. The receivers were
removed after a set of test observations that were conducted in
June-August, 1995. During these test observations we attempted to
correct the A-configuration interferometer phases at 327 MHz by
comparison of the phase-TEC data from the appropriately located
receivers. For Faraday rotation experiments at later times, the
central receiver was reinstalled at the VLA site.
35 km. The data from a
single receiver are sufficient to determine the model discussed above,
but it was hoped that comparison of the phase-TEC between the central
receiver and the receivers at the ends of the arms would allow better
estimates of the phase gradients along the arms. The receivers were
removed after a set of test observations that were conducted in
June-August, 1995. During these test observations we attempted to
correct the A-configuration interferometer phases at 327 MHz by
comparison of the phase-TEC data from the appropriately located
receivers. For Faraday rotation experiments at later times, the
central receiver was reinstalled at the VLA site.
The receivers were set with integration times of 30 s and, as discussed below, the data are used to determine a model ionosphere. When models are generated for each integration, the fitted parameters are rather noisy. If the data are averaged for more than about 15 min between fits, the quality of the fitting deteriorates, presumably because of satellite motion and possible variations of ionospheric structure during the averaging period. The best compromise between the poor signal-to-noise of short integrations and data variations during long integrations was found to be about five minutes, and this averaging time was adopted for the analysis.
Instrumental time delays between the L1 and L2 carriers cause a bias, or offset, in the derived slant TEC determined from each satellite. The offsets tend to be large; they cause errors that amount to a substantial fraction of the total TEC and they represent one of the most troublesome aspects of GPS TEC determination. For the example shown in Fig. 1 a negative TEC would occur if no correction were applied. In addition, each receiver has its own offset. We have developed a method for determining these offsets, which we now describe.
We first averaged together published estimates of the satellite offsets and used these for the initial model-fitting. As we had no valid information concerning the offsets of the four receivers we developed a method of determining the receiver offsets from the data alone using a method which is similar to that used by astronomers to correct for atmospheric extinction. In this method, the apparent flux density of a star is measured at various zenith distances, then the measurements are fitted to an air mass extinction curve and extrapolated to zero air mass. In our case, the GPS data for the satellites at various zenith distances were fitted to our ionospheric model and the receiver offset that produced the best average fit was adopted.
The following procedure was employed: the receiver offset was first
assumed to be zero. Then the slant TEC data from each visible
satellite was averaged over the 5 min integration period. The data
were discarded for satellites below 10![]() elevation and, in the
fitting process, the averaged data were weighted according to their
standard deviations. This also discriminated against noisy,
low-elevation data.
elevation and, in the
fitting process, the averaged data were weighted according to their
standard deviations. This also discriminated against noisy,
low-elevation data.
In order to fit a model to the data, the slant TEC in the direction of
each satellite was predicted in terms of the three model parameters
discussed in Sect. 3; the vertical TEC at the observer's location,
![]() ,
the magnitude of its horizontal gradient,
,
the magnitude of its horizontal gradient,
![]() ,
and the azimuth of this gradient,
,
and the azimuth of this gradient,
![]()
![]() . As discussed in Sect. 3,
the average height, h, and thickness, d, of the ionosphere were fixed
at 400 km and 175 km, respectively.
. As discussed in Sect. 3,
the average height, h, and thickness, d, of the ionosphere were fixed
at 400 km and 175 km, respectively.
We must first determine the slant pathlength through the ionosphere
for a ray path to a satellite of zenith distance, ![]() ,
and
azimuth
,
and
azimuth
![]() .
Consider the diagram shown in
Fig. 2; let P be an arbitrary point at a height
.
Consider the diagram shown in
Fig. 2; let P be an arbitrary point at a height ![]() above the Earth's surface on the rectilinear ray path OP
above the Earth's surface on the rectilinear ray path OP
![]() . Consider the triangle formed by the center of the
Earth, E, the observers position, O, and the point, P. Let the angle
at E between the lines EO and EP be
. Consider the triangle formed by the center of the
Earth, E, the observers position, O, and the point, P. Let the angle
at E between the lines EO and EP be ![]() .
Applying the Law of
Sines to the triangle EOP we have:
.
Applying the Law of
Sines to the triangle EOP we have:
![\begin{displaymath}\alpha = \arcsin\left[\frac{r_{\rm o}}{r_{\rm o} + \delta
r}\sin(z_{\rm S})\right]
\end{displaymath}](/articles/aa/full/2001/06/aa10277/img27.gif) |
(3) |
| = | |||
| (4) |
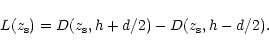 |
(5) |
![\begin{displaymath}T_{\rm P}=[T_{\rm o} + G_{\rm o}\times C(z_{\rm s},
h)\times \cos(\phi_{\rm g} - \phi_{\rm s})]
\end{displaymath}](/articles/aa/full/2001/06/aa10277/img35.gif) |
(6) |
The total electron content in each satellite's direction, i.e. the
slant-TEC
![]() ,
is then fitted to the data for each
satellite of zenith distance,
,
is then fitted to the data for each
satellite of zenith distance, ![]() ,
and azimuth,
,
and azimuth,
![]() ,
where:
,
where:
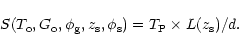 |
(7) |
The three model parameters,
![]() ,
and
,
and
![]() ,
are found for each integration period through a
three dimensional grid search procedure in which the
,
are found for each integration period through a
three dimensional grid search procedure in which the ![]() of the
fit to the data from all of the visible satellites is minimized. A
sample of the output from this grid search procedure is shown in
Fig. 3.
of the
fit to the data from all of the visible satellites is minimized. A
sample of the output from this grid search procedure is shown in
Fig. 3.
In order to estimate the receiver offset this process was repeated for
a 24-hour long section of data and the average ![]() was found for
this entire period. Next, different receiver offsets were tried until
the offset that minimized this average
was found for
this entire period. Next, different receiver offsets were tried until
the offset that minimized this average ![]() was found and this
value of the offset was adopted.
was found and this
value of the offset was adopted.
We found that the model parameters independently derived from each of
the receivers agreed with each other to about 0.3 TU when the
corrections are made for the differences in receiver locations (using
the estimated gradients). We also obtained data from the GPS receiver
which was operated by the JPL and located on the VLBA site at Pietown,
NM. An estimate of this receiver's offset was provided by the JPL.
Our procedure applied to the Pietown data produced the same offset
value to an accuracy of 0.4 TU. The Pietown model parameters
were also used to estimate the vertical TEC at the VLA and these
estimates agreed with our determinations to about
![]() .
.
As a final step, all of the GPS data from the different receivers were
averaged together and the average differences between each satellite's
data and the model predictions for it were found. Minor changes in
the satellite offset values were made to set these average differences
to zero. When a final fit was done for all of the data using the new
values for the satellite offsets, it was found that the average
![]() was slightly reduced. The final values of the satellite
offsets that we determined are given in Table 1.
was slightly reduced. The final values of the satellite
offsets that we determined are given in Table 1.
| Sat. # | Offset | Sat.# | Offset | Sat.# | Offset |
| (TU) | (TU) | (TU) | |||
| PRN 1 | -4.94 | PRN 15 | -3.51 | PRN 23 | -4.99 |
| PRN 2 | -2.82 | PRN 16 | -1.77 | PRN 24 | -2.77 |
| PRN 4 | -10.56 | PRN 17 | -3.77 | PRN 25 | -12.64 |
| PRN 5 | -8.19 | PRN 18 | -7.76 | PRN 26 | -11.81 |
| PRN 6 | -8.64 | PRN 19 | -5.99 | PRN 27 | -7.85 |
| PRN 7 | -3.48 | PRN 20 | -3.45 | PRN 28 | -11.98 |
| PRN 9 | -9.90 | PRN 21 | -3.88 | PRN 29 | -12.81 |
| PRN 12 | +5.02 | PRN 22 | -6.73 | PRN 31 | -10.36 |
| PRN 14 | -3.94 |
Sardón et al. (1994) have developed a method of estimating the TEC and offsets that is somewhat similar to the our method. They make use of GPS data from several stations distributed world-wide and they assume a world-wide ionospheric model that is quasi-stationary in a coordinate system referenced to the sub-solar point on the Earth. Over each GPS station they assume that the ionospheric parameters are linear so their model is, locally, essentially identical to ours. Since their ionospheric parameters vary slowly in their reference system and since the transmitter and receiver offsets are also slowly varying, they can apply a Kalman filter to determine the ionospheric parameters and offsets that best fit the set of GPS observations taken over a 48-hour period. Their method provides values for the parameters that appear to have similar accuracies to those provided by our method. We did not have world-wide GPS data readily available when we conducted our 1995 experiments so we developed a method that requires only locally-derived data.
Copyright ESO 2001