1 - Astronomy Department, University of Maryland, College Park, MD 20742, USA
2 - National Radio Astronomy Observatory
3 - Code 7215, Remote Sensing Division, Naval Research Laboratory
A&A 366, 1071-1080 (2001)
DOI: 10.1051/0004-6361:20000359
W. C. Erickson 1 - R. A. Perley 2 - C. Flatters 2 - N. E. Kassim 3
1 - Astronomy Department, University of Maryland, College Park,
MD 20742, USA
2 - National Radio Astronomy Observatory![]() , Socorro, NM 87801, USA
, Socorro, NM 87801, USA
3 - Code 7215, Remote
Sensing Division, Naval Research Laboratory![]() , Washington, DC 20375-5351, USA
, Washington, DC 20375-5351, USA
Received 15 September 2000 / Accepted 27 November 2000
Abstract
We have conducted an experiment to evaluate the usefulness of
ionospheric data produced using the Global Positioning System (GPS)
for making Faraday rotation and interferometer phase corrections at
the NRAO Very Large Array (VLA). Four GPS receivers were installed at
the VLA site - one at the array center and one at the end of each
arm. A simple ionospheric model consisting of a vertical TEC, a
horizontal gradient, and the azimuth of that gradient was developed
and fitted to the GPS Total Electron Content (TEC) data from each
receiver. The model was then used to predict the TEC in the observing
direction. Ionospheric Faraday rotation and phase gradients were then
estimated and compared with VLA measurements taken at frequencies of
322 and 333 MHz. We find that we can normally make Faraday rotation
corrections that are accurate to
![]() ,
although one
unexplained discrepancy remains. The interferometer phase shifts
caused by large-scale (
,
although one
unexplained discrepancy remains. The interferometer phase shifts
caused by large-scale (
![]() km) ionospheric structures can be
predicted by our model. However the phase shifts caused by smaller
(
km) ionospheric structures can be
predicted by our model. However the phase shifts caused by smaller
(
![]() km) structures can be estimated only when the direction of
observation lies within a few degrees of one of the GPS satellites.
km) structures can be estimated only when the direction of
observation lies within a few degrees of one of the GPS satellites.
Key words: astronomical techniques: interferometric - atmospheric effects - polarimetric techniques
Radio astronomical and ionospheric measurements interact in two ways. Radio astronomical data can be used to infer ionospheric structures, and ionospheric data can be used for the correction of radio data. The first of these processes has been relatively successful. Before the advent of sounding rockets and satellites, only celestial sources provided the required signals for trans-ionospheric propagation studies. These signals have been exploited by many researchers beginning with Hewish (1951). Many of these classic investigations were described by Lawrence et al. (1964). When artificially-produced signals and direct sampling became possible, the use of natural sources for investigating the ionosphere became less important. However, radio astronomical measurements are still useful for the study of certain phenomena such as acoustic gravity waves (Mercier 1986; Mercier et al. 1989; Kelder & Spoelstra 1987; Jacobson & Erickson 1992).
The second process, the correction of ionospheric effects upon radio astronomical measurements using ionospheric data, has been less successful. This is because the effects are often very large - hundreds of wavelengths of delay or several turns of Faraday rotation at meter wavelengths (Hagfors 1976; Thompson et al. 1986) - and ionospheric data of the required accuracy were simply not available. Often the available ionospheric data pertained only to the direction of a single satellite, or the data were obtained from ionosondes separated geographically by hundreds of kilometers. Using ionosonde data, Komesaroff (1960) was able to successfully correct 19.7 MHz source positions for ionospheric refraction. Spoelstra (1983) has presented a refraction correction procedure for WSRT observations employing both topside and bottom-side sounders. However, the use of sounder profiles is often rather tedious and cumbersome because the data must be obtained from several different organizations, resulting in limited application of this method.
Much more convenient and powerful techniques that employ only the radio astronomical data themselves involve closure phases and self-calibration. These techniques (as described by Thompson et al. 1986) are now widely used at wavelengths of a meter or less. They are particularly useful because they pertain to the direction of observation rather than to some other arbitrary direction in the sky. Unfortunately, these techniques are severely limited at low frequencies by poor signal-to-noise, due partly to very rapid phase variations which require short integrations, and partly to dilution of the target object's signal amongst the large number of background sources. Furthermore, self-calibration techniques cannot recover the absolute position of astronomical sources, nor correct for the rotation of the plane of polarization by Faraday rotation in the ionosphere.
The GPS (Global Positioning System, see Dixon 1992; Logsdon 1992; Hofmann-Wellenhof et al. 1993) now allows an observer to conveniently and continuously obtain ionospheric data of unprecedented accuracy with a relatively simple and inexpensive GPS receiver installed at the radio telescope site. With such a receiver, ionospheric parameters over the whole sky can be monitored for the local site 24 hours per day, which opens the possibility of making all-sky ionospheric corrections to both total phase and Faraday rotation. To test these possibilities, we have designed an experiment to evaluate the usefulness of GPS data for making such corrections for the VLA at frequencies near 327 MHz.
Conkright et al. (1997) have compared GPS-derived TEC data with TEC data obtained from the Faraday rotation of signals from geostationary satellites. They found good agreement between the TEC estimates obtained by these two methods. For their study they employed a very simple ionospheric model consisting of a thin, uniform, spherically-symmetrical shell at a height of 400 km.
Campbell (1999) has suggested the use of the United States Air Force Parameterized Ionospheric Model (PIM) for the correction of radio data. The PIM is a theoretical model of global ionospheric climatology. Campbell's approach may be useful, especially if locally determined data are incorporated into the global model. We have not attempted this procedure but present a method for making corrections using locally derived data only.
Ros et al. (2000) have employed GPS data for the correction of VLBI observations. They use only locally-derived data obtained from a GPS receiver located near the VLBI telescope and assume a "frozen" ionosphere that moves over the Earth following the Sun. They use the GPS-TEC measured at one longitude to estimate the TEC at the longitude where the line-of-sight to the radio source pierces the ionosphere. They accomplish this by assuming a frozen ionosphere and an appropriate time correction. Since the time corrections are small, the assumption of a frozen ionosphere should be valid. However, they also neglect North-South ionospheric gradients. This is puzzling because the North-South gradients at mid-latitudes are normally larger than the East-West gradients.
Chatterjee (1999) and Walker & Chatterjee (1999) have discussed the use of various world-wide and regional ionospheric models for the correction of Very Long Baseline Interferometer (VLBI) data.
Our initial observations were made between June and August, 1995. They involved the use of four GPS receivers installed at the VLA site along with simultaneous interferometric observations of radio source phases and Faraday rotation at 330 MHz. An ionospheric model was developed in order to predict the interferometer phase and the rotation of the position angle of polarized flux in the direction of the observed radio source from satellite data in other directions. It was found that this model could also be used to determine GPS receiver and transmitter offsets. This work is discussed in Sects. 2 through 6. Our 1995 data were not useful for determining the ionospheric rotation because the observed sources displayed low polarizations and little variation in rotation occurred during the rather short periods of observation that were available. By the time these intitial observations were reduced, the GPS receivers had been removed, so it was necessary to reinstall a GPS receiver (at the VLA's center) and to obtain rather long allocations of VLA observing time in order to produce useful data. Three successful observing sessions were eventually scheduled during 1997, 1998, and 1999, and their results are covered in Sect. 7.
Each of the GPS satellites transmits on two L-band carrier
frequencies, L1 at 1575.42 MHz and L2 at 1227.60 MHz. A third
carrier, L3 at 1381.05 MHz, is not intended for GPS users. All of
these carriers are phase locked to harmonics of a fundamental, 5.115
MHz, oscillator. By measurement of the time delay between the
modulation on the L1 and L2 carriers, the ionospheric-induced delay
and hence an absolute measure of the total electron content (TEC)
along the line-of-sight to each visible satellite, i.e. the slant-TEC,
can be determined through the simple relation
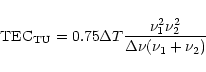 |
(1) |
The relative phases of the carriers can also be measured to obtain a
much more accurate determination of the TEC (the so-called phase-TEC)
via the relation
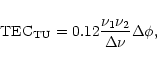 |
(2) |
Typically, our receivers would obtain data from six to nine satellites at any time, but some of these satellites were at such low elevations that their data were of little use for the correction of high elevation radio source observations. Therefore, useful data were normally obtained in about four to seven directions. Because the satellites are typically a radian or more from the astronomical source of interest, it is necessary to model the ionosphere using the GPS data and to then employ this model to estimate the TEC in the direction of the source.
In order to decide between possible ionospheric models which might be
used to fit the GPS TEC data, we compared the zenith distance
variation of TEC and angular refraction as predicted by
spherically-stratified models employing actual ionospheric profiles,
parabolic layers, and a simple, uniform layer. We found that, with
appropriate values for the ionospheric height and layer thickness, a
simple, uniform-layer model for the ionosphere provides a prediction
of the TEC and of ionospheric refraction that is as accurate as models
involving more complicated profiles of the electron density with
height for elevations greater than 15![]() .
See, for example, Thompson
et al. (1986, p. 445) for a comparison of such models. A
uniform model has thus been adopted. This conclusion differs from
that of Spoelstra (1983) who found that the inclusion of
vertical profiles of ionospheric density improved his estimates. This
is probably because Spoelstra was forced to work with top- and
bottom-side sounder observations in order to estimate the TEC while we
are able to determine the TEC directly from the GPS observations.
.
See, for example, Thompson
et al. (1986, p. 445) for a comparison of such models. A
uniform model has thus been adopted. This conclusion differs from
that of Spoelstra (1983) who found that the inclusion of
vertical profiles of ionospheric density improved his estimates. This
is probably because Spoelstra was forced to work with top- and
bottom-side sounder observations in order to estimate the TEC while we
are able to determine the TEC directly from the GPS observations.
However, horizontal gradients of the ionospheric density are extremely
important for the prediction of refraction and TEC. Under typical
conditions, the refraction caused by horizontal gradients exceeds that
caused by the spherical (Earth curvature) component for source
elevations above 10![]() .
This is illustrated by an example of the
data from an individual satellite pass as shown in
Fig. 1 where it is evident that the TEC in the south
considerably exceeds that in the north at similar elevations.
.
This is illustrated by an example of the
data from an individual satellite pass as shown in
Fig. 1 where it is evident that the TEC in the south
considerably exceeds that in the north at similar elevations.
![\begin{figure}
\par\includegraphics[angle=-90,width=12cm,clip]{NewFig1.ps}\end{figure}](/articles/aa/full/2001/06/aa10277/Timg15.gif) |
Figure 1:
An example of the raw data obtained in this project.
These data were obtained by the center receiver from satellite PRN
#6. The lower panel shows the elevation (solid line) and azimuth
divided by 4 (dashed line). In this case the satellite was acquired
in the northwest at an elevation of 30 |
| Open with DEXTER | |
Such data show that a uniform spherical component alone cannot fit the TEC data. Therefore, we have adopted an ionospheric model which has a constant electron density over a thickness, d, centered at a height, h, and which has a constant horizontal gradient of electron density at an arbitrary azimuth. For simplicity we have used fixed values of 175 km and 400 km for d and h, respectively. This simplification does not adversely affect the accuracy of the model, as it is easily shown that the calculated parameters of the model are only weakly dependent upon the height and thickness of the refractive layer. In fact, the GPS data can be fit equally well with an infinitesimally thin layer. We retained a finite thickness layer because it is more physically plausible and also because we were guided in the choice of a model by angular refraction data. A very thin layer does not give a satisfactory fit to the available refraction data.
Therefore, data are fitted to a three parameter model: the vertical TEC at the location of the receiver, the magnitude of the horizontal gradient at this location and the azimuth of this gradient. When fitting the averaged tau-TEC data once every few minutes we find that this simple model usually fits the data to better than ten percent. The accuracy of the fit is demonstrated in the upper panel of Fig. 1.
At a wavelength of one meter, the ionospheric Faraday rotation is
expected to be at most a few turns in the daytime and less than one
turn at night. The rotation depends only on the magnitude of the
ionospheric electron density and upon the angle between the source
direction and the Earth's magnetic field. Since our model fits the
TEC data well, and the Earth's magnetic field is known accurately, we
should expect to be able to correct for the Faraday rotation to
![]() at a wavelength of 1 m, and
at a wavelength of 1 m, and
![]() at a wavelength of
20 cm. Travelling ionospheric disturbances will cause a smaller-scale
spatial gradient in the observed plane of rotation of the polarized
emission - this phenomenon is probably responsible for the residuals
in the fits to our simple model. Under normal ionospheric conditions,
these disturbances will differentially rotate the plane of
polarization across the VLA by only a few degrees in the largest
configuration at a wavelength of one meter, and thus are not expected
to limit the applicability of our method.
at a wavelength of
20 cm. Travelling ionospheric disturbances will cause a smaller-scale
spatial gradient in the observed plane of rotation of the polarized
emission - this phenomenon is probably responsible for the residuals
in the fits to our simple model. Under normal ionospheric conditions,
these disturbances will differentially rotate the plane of
polarization across the VLA by only a few degrees in the largest
configuration at a wavelength of one meter, and thus are not expected
to limit the applicability of our method.
On the other hand, ionospheric refractive effects and interferometer
phase correction at meter wavelengths present far greater difficulties
because these effects are very large. At a wavelength of one meter,
ionospheric delays of hundreds of wavelengths are common in daytime.
Also, the refractive effects depend more critically upon the
horizontal gradient of the TEC than on the vertical TEC itself. With
TEC data from only a limited number of satellites we cannot expect to
model these gradients with great accuracy. The lines of sight to the
satellites puncture the ionosphere at points separated by about 1000
km so we should expect to only model ionospheric structures on similar
scale sizes; we cannot hope to model the smaller-scale, ![]() 100 km,
structures. These smaller structures also cause important refractive
effects and cannot be modeled unless the observed radio source and one
of the satellites are nearly coincident in the sky and we sample the
smaller scale structures in this area of the sky with receivers
separated at appropriate spacings.
100 km,
structures. These smaller structures also cause important refractive
effects and cannot be modeled unless the observed radio source and one
of the satellites are nearly coincident in the sky and we sample the
smaller scale structures in this area of the sky with receivers
separated at appropriate spacings.
Four Turbo-Rogue GPS receivers owned by the Los Alamos National
Laboratory were set up at the VLA site, one at the array center and
one at the end of each of the three VLA arms, i.e. in an approximately
equilateral triangle with sides of ![]() 35 km. The data from a
single receiver are sufficient to determine the model discussed above,
but it was hoped that comparison of the phase-TEC between the central
receiver and the receivers at the ends of the arms would allow better
estimates of the phase gradients along the arms. The receivers were
removed after a set of test observations that were conducted in
June-August, 1995. During these test observations we attempted to
correct the A-configuration interferometer phases at 327 MHz by
comparison of the phase-TEC data from the appropriately located
receivers. For Faraday rotation experiments at later times, the
central receiver was reinstalled at the VLA site.
35 km. The data from a
single receiver are sufficient to determine the model discussed above,
but it was hoped that comparison of the phase-TEC between the central
receiver and the receivers at the ends of the arms would allow better
estimates of the phase gradients along the arms. The receivers were
removed after a set of test observations that were conducted in
June-August, 1995. During these test observations we attempted to
correct the A-configuration interferometer phases at 327 MHz by
comparison of the phase-TEC data from the appropriately located
receivers. For Faraday rotation experiments at later times, the
central receiver was reinstalled at the VLA site.
The receivers were set with integration times of 30 s and, as discussed below, the data are used to determine a model ionosphere. When models are generated for each integration, the fitted parameters are rather noisy. If the data are averaged for more than about 15 min between fits, the quality of the fitting deteriorates, presumably because of satellite motion and possible variations of ionospheric structure during the averaging period. The best compromise between the poor signal-to-noise of short integrations and data variations during long integrations was found to be about five minutes, and this averaging time was adopted for the analysis.
Instrumental time delays between the L1 and L2 carriers cause a bias, or offset, in the derived slant TEC determined from each satellite. The offsets tend to be large; they cause errors that amount to a substantial fraction of the total TEC and they represent one of the most troublesome aspects of GPS TEC determination. For the example shown in Fig. 1 a negative TEC would occur if no correction were applied. In addition, each receiver has its own offset. We have developed a method for determining these offsets, which we now describe.
We first averaged together published estimates of the satellite offsets and used these for the initial model-fitting. As we had no valid information concerning the offsets of the four receivers we developed a method of determining the receiver offsets from the data alone using a method which is similar to that used by astronomers to correct for atmospheric extinction. In this method, the apparent flux density of a star is measured at various zenith distances, then the measurements are fitted to an air mass extinction curve and extrapolated to zero air mass. In our case, the GPS data for the satellites at various zenith distances were fitted to our ionospheric model and the receiver offset that produced the best average fit was adopted.
The following procedure was employed: the receiver offset was first
assumed to be zero. Then the slant TEC data from each visible
satellite was averaged over the 5 min integration period. The data
were discarded for satellites below 10![]() elevation and, in the
fitting process, the averaged data were weighted according to their
standard deviations. This also discriminated against noisy,
low-elevation data.
elevation and, in the
fitting process, the averaged data were weighted according to their
standard deviations. This also discriminated against noisy,
low-elevation data.
In order to fit a model to the data, the slant TEC in the direction of
each satellite was predicted in terms of the three model parameters
discussed in Sect. 3; the vertical TEC at the observer's location,
![]() ,
the magnitude of its horizontal gradient,
,
the magnitude of its horizontal gradient,
![]() ,
and the azimuth of this gradient,
,
and the azimuth of this gradient,
![]()
![]() . As discussed in Sect. 3,
the average height, h, and thickness, d, of the ionosphere were fixed
at 400 km and 175 km, respectively.
. As discussed in Sect. 3,
the average height, h, and thickness, d, of the ionosphere were fixed
at 400 km and 175 km, respectively.
| |
Figure 2: A diagram of the geometry used for modeling |
| Open with DEXTER | |
We must first determine the slant pathlength through the ionosphere
for a ray path to a satellite of zenith distance, ![]() ,
and
azimuth
,
and
azimuth
![]() .
Consider the diagram shown in
Fig. 2; let P be an arbitrary point at a height
.
Consider the diagram shown in
Fig. 2; let P be an arbitrary point at a height ![]() above the Earth's surface on the rectilinear ray path OP
above the Earth's surface on the rectilinear ray path OP
![]() . Consider the triangle formed by the center of the
Earth, E, the observers position, O, and the point, P. Let the angle
at E between the lines EO and EP be
. Consider the triangle formed by the center of the
Earth, E, the observers position, O, and the point, P. Let the angle
at E between the lines EO and EP be ![]() .
Applying the Law of
Sines to the triangle EOP we have:
.
Applying the Law of
Sines to the triangle EOP we have:
![\begin{displaymath}\alpha = \arcsin\left[\frac{r_{\rm o}}{r_{\rm o} + \delta
r}\sin(z_{\rm S})\right]
\end{displaymath}](/articles/aa/full/2001/06/aa10277/img27.gif) |
(3) |
| = | |||
| (4) |
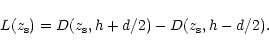 |
(5) |
![\begin{displaymath}T_{\rm P}=[T_{\rm o} + G_{\rm o}\times C(z_{\rm s},
h)\times \cos(\phi_{\rm g} - \phi_{\rm s})]
\end{displaymath}](/articles/aa/full/2001/06/aa10277/img35.gif) |
(6) |
The total electron content in each satellite's direction, i.e. the
slant-TEC
![]() ,
is then fitted to the data for each
satellite of zenith distance,
,
is then fitted to the data for each
satellite of zenith distance, ![]() ,
and azimuth,
,
and azimuth,
![]() ,
where:
,
where:
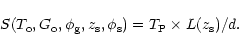 |
(7) |
The three model parameters,
![]() ,
and
,
and
![]() ,
are found for each integration period through a
three dimensional grid search procedure in which the
,
are found for each integration period through a
three dimensional grid search procedure in which the ![]() of the
fit to the data from all of the visible satellites is minimized. A
sample of the output from this grid search procedure is shown in
Fig. 3.
of the
fit to the data from all of the visible satellites is minimized. A
sample of the output from this grid search procedure is shown in
Fig. 3.
In order to estimate the receiver offset this process was repeated for
a 24-hour long section of data and the average ![]() was found for
this entire period. Next, different receiver offsets were tried until
the offset that minimized this average
was found for
this entire period. Next, different receiver offsets were tried until
the offset that minimized this average ![]() was found and this
value of the offset was adopted.
was found and this
value of the offset was adopted.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{NewFig2.ps}\end{figure}](/articles/aa/full/2001/06/aa10277/Timg45.gif) |
Figure 3:
An example of the output from the model fitting program.
The upper panel shows the fitted value of the vertical TEC (in
|
| Open with DEXTER | |
We found that the model parameters independently derived from each of
the receivers agreed with each other to about 0.3 TU when the
corrections are made for the differences in receiver locations (using
the estimated gradients). We also obtained data from the GPS receiver
which was operated by the JPL and located on the VLBA site at Pietown,
NM. An estimate of this receiver's offset was provided by the JPL.
Our procedure applied to the Pietown data produced the same offset
value to an accuracy of 0.4 TU. The Pietown model parameters
were also used to estimate the vertical TEC at the VLA and these
estimates agreed with our determinations to about
![]() .
.
As a final step, all of the GPS data from the different receivers were
averaged together and the average differences between each satellite's
data and the model predictions for it were found. Minor changes in
the satellite offset values were made to set these average differences
to zero. When a final fit was done for all of the data using the new
values for the satellite offsets, it was found that the average
![]() was slightly reduced. The final values of the satellite
offsets that we determined are given in Table 1.
was slightly reduced. The final values of the satellite
offsets that we determined are given in Table 1.
| Sat. # | Offset | Sat.# | Offset | Sat.# | Offset |
| (TU) | (TU) | (TU) | |||
| PRN 1 | -4.94 | PRN 15 | -3.51 | PRN 23 | -4.99 |
| PRN 2 | -2.82 | PRN 16 | -1.77 | PRN 24 | -2.77 |
| PRN 4 | -10.56 | PRN 17 | -3.77 | PRN 25 | -12.64 |
| PRN 5 | -8.19 | PRN 18 | -7.76 | PRN 26 | -11.81 |
| PRN 6 | -8.64 | PRN 19 | -5.99 | PRN 27 | -7.85 |
| PRN 7 | -3.48 | PRN 20 | -3.45 | PRN 28 | -11.98 |
| PRN 9 | -9.90 | PRN 21 | -3.88 | PRN 29 | -12.81 |
| PRN 12 | +5.02 | PRN 22 | -6.73 | PRN 31 | -10.36 |
| PRN 14 | -3.94 |
Sardón et al. (1994) have developed a method of estimating the TEC and offsets that is somewhat similar to the our method. They make use of GPS data from several stations distributed world-wide and they assume a world-wide ionospheric model that is quasi-stationary in a coordinate system referenced to the sub-solar point on the Earth. Over each GPS station they assume that the ionospheric parameters are linear so their model is, locally, essentially identical to ours. Since their ionospheric parameters vary slowly in their reference system and since the transmitter and receiver offsets are also slowly varying, they can apply a Kalman filter to determine the ionospheric parameters and offsets that best fit the set of GPS observations taken over a 48-hour period. Their method provides values for the parameters that appear to have similar accuracies to those provided by our method. We did not have world-wide GPS data readily available when we conducted our 1995 experiments so we developed a method that requires only locally-derived data.
Our model provides valid estimates of large-scale ionospheric
gradients, i.e. gradients with scale sizes of 1000 km or more. By
ray-tracing through the model ionosphere that is determined every few
minutes, we can estimate the refraction that the model ionosphere
would cause and predict the resulting phase shifts on the various VLA
interferometer baselines. Two examples of 327 MHz phases in the A configuration are shown in Figs. 4 and 5.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{NewFig3.ps}\end{figure}](/articles/aa/full/2001/06/aa10277/Timg47.gif) |
Figure 4: An example of the large-scale phase corrections generated by our ionospheric modeling. The small dots are the raw phases; the solid line is the phase predicted by ray tracing through ionospheric models produced at 5 min intervals; the large dots are the phases after correction by the model predictions. These data were taken on a long N-S baseline between telescope 26 located at VLA Station N72 and telescope 14 located at N16 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{NewFig4.ps}\end{figure}](/articles/aa/full/2001/06/aa10277/Timg48.gif) |
Figure 5: Same as Fig. 4 except that these data were taken on a long SW baseline between telescope 21 located at VLA Station W72 and telescope 14 located at N16 |
| Open with DEXTER | |
The predictions follow the general trends of the measured phases quite well. Therefore, we are able to correct for the effects of large-scale ionospheric structures. This may be important over longer, VLBI baselines, where the effects of large-scale structures strongly dominate those of smaller-scale structures. However, over VLA baselines, the measured phases display many short period variations, caused by unmodeled small-scale structures, that are of similar magnitude to the slower variations caused by large-scale structures. When the measured phases are corrected by the model predictions, the phase fluctuations are appreciably decreased, but the correction is far from being perfect. The standard deviations of the corrected phases are 20 to 50% lower than those of the original phases. This rather modest reduction in phase fluctuations corresponds to a reduction in phase noise power by a factor of 1.5 to 4.
Correction of the small-scale phase fluctuations was attempted by
measuring the phase gradients along each arm of the VLA and applying
the appropriate corrections. Previous studies (Jacobson
& Erickson 1992) have shown that the 327 MHz phase gradients
along each arm of the array are very nearly linear, so it should be
possible to estimate the phase at each VLA telescope by interpolation
between phase-TEC measurements at the ends of the arms. We recognized
that the principal problem in making any correction would be caused by
the angular separation between the source under observation and any of
the GPS satellites. To alleviate this problem and to determine the
angular separation over which the correction would remain useful, we
choose an observation in which the source was nearly aligned with a
GPS satellite (see Fig. 6).
![\begin{figure}
\par\includegraphics[angle=-90,width=7cm,clip]{NewFig5.ps}\end{figure}](/articles/aa/full/2001/06/aa10277/Timg49.gif) |
Figure 6:
A horizon plot showing the tracks of the various
satellites in the sky along with the track of the radio source for
which the corrections in Figs. 7 and 8 were made. North
is at the top and the circles are at 0 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{NewFig6.ps}\end{figure}](/articles/aa/full/2001/06/aa10277/Timg50.gif) |
Figure 7: The measured and predicted phases for a long SE-arm baseline are shown in the top panel. The dots are the measured phases; the solid line is the prediction. The vertical line represents the point of closest approach between 3C 461 and PRN 27. The middle panel shows the angular separations in degrees (dots) and the linear separations between the satellite and radio source ionospheric puncture points in units of 10 km (dashed line). The bottom panel gives the position angles of the satellite-to-source lines |
| Open with DEXTER | |
When making a correction by means of a simple interpolation of the
phase gradients, we find, as illustrated in the middle panels of
Figs. 7 and 8, that the correction is good when the source
and satellite lie within the same isoplanatic patch, i.e. within about
4![]() of each other. For larger separations the correction, as
illustrated in the upper panels of Figs. 7 and 8, quickly
becomes useless.
of each other. For larger separations the correction, as
illustrated in the upper panels of Figs. 7 and 8, quickly
becomes useless.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{NewFig7.ps}\end{figure}](/articles/aa/full/2001/06/aa10277/Timg51.gif) |
Figure 8: The same as Fig. 7 but for a long NS-arm |
| Open with DEXTER | |
The lines-of-sight to the satellite being used for correction from the four receivers puncture the ionosphere at four points in the vicinity of the source line-of-sight. The data at these four points can be fit with a model that has not only a linear component but a parabolic component as well, and it was hoped that this model would be valid over larger separations between the source and satellite. We attempted to fit the data with such a model and to use this model to predict the observed phases. However, we found that only four data points are not sufficient to accurately define the parabolic component and that results obtained from these more sophisticated models were no better than those obtained by simple, linear interpolation. A network of GPS receivers spread over a large area would be required to provide many more puncture points and adequately characterize the relevant ionospheric structures in the general direction of the source. We could then hope to extend the corrections over a larger fraction of the sky.
The simple model described above gives fits to the data with a typical
residual of
![]() .
An elementary calculation shows that with
such a residual, and a reasonable model of the Earth's magnetic field,
we should be able to calculate the ionospheric rotation measure with a
typical accuracy of about 0.2
.
An elementary calculation shows that with
such a residual, and a reasonable model of the Earth's magnetic field,
we should be able to calculate the ionospheric rotation measure with a
typical accuracy of about 0.2
![]() at 327 MHz. Such a
capability would permit correction of the ionospherically-induced
rotation of the plane of polarization to better than 10
at 327 MHz. Such a
capability would permit correction of the ionospherically-induced
rotation of the plane of polarization to better than 10![]() - more
than sufficient to permit meaningful polarimetry. However, tests of
this capability were difficult to schedule because of observing
pressure at the VLA and the need to reinstall a GPS receiver to obtain
simultaneous GPS data. In particular, a valid test requires
observation of a strongly polarized source over an extended period
during which the Faraday rotation of the plane of polarization changes
fairly quickly. The validity of the method is most convincingly
demonstrated if the rate of change of the observed position angle
dramatically changes during the observation period - such as would
normally occur during sunrise or sunset.
- more
than sufficient to permit meaningful polarimetry. However, tests of
this capability were difficult to schedule because of observing
pressure at the VLA and the need to reinstall a GPS receiver to obtain
simultaneous GPS data. In particular, a valid test requires
observation of a strongly polarized source over an extended period
during which the Faraday rotation of the plane of polarization changes
fairly quickly. The validity of the method is most convincingly
demonstrated if the rate of change of the observed position angle
dramatically changes during the observation period - such as would
normally occur during sunrise or sunset.
To test the validity of our method, we obtained eight test
observations between October 1996 and June 1999 of the strong and
highly polarized pulsar PSR 1932+109. Of these eight trials, five
showed insufficient change in the observed position angle of the
pulsar over the duration of the observation to permit a useful test of
the method. The three successful tests are summarized in Table 2.
| Date | Time Range | VLA Config. | RMS Fit |
| MST | Deg. | ||
| 04 Apr. 1997 | 04:00-10:30 | B | 4
|
| 27 Aug. 1998 | 16:00-21:30 | B | 8
|
| 24 Jun. 1999 | 02:00-07:30 | A | 9
|
The results of our first useful test are shown in Fig. 9. Observations began at 4 AM local time, well before sunrise, and continued until 10:30 AM. This time span permitted observations for a significant period before sunrise and through the majority of the sunrise period in during which the ionosphere's TEC greatly increases. The observations were taken in the gated pulsar mode so as to ensure maximum SNR, although this pulsar's emission is sufficiently strong that the experiment can be run in a normal ungated mode.
In Fig. 9 for the first 1.5 hours, essentially no change is
seen in either the predicted or observed plane of polarization,
reflecting the fact that these data were taken before dawn. At 5:30
AM local time, both observed and predicted position angle suddenly
begin to increase, with this trend continuing steadily until the end
of the experiment. In Fig. 9 we plot single five-minute
integrations of the observed and modeled position angles. The data
were taken in B-configuration (maximum arm length ![]() 6 km),
which at times can be difficult to calibrate if the ionosphere is in a
disturbed state. However, no disturbances were noted, and the
calibration (using nearby point-like objects) of the phase, amplitude,
and polarization of the antennas proceeded smoothly. Images of the
pulsar in Stokes' I, Q, and U were made every 5 min to permit
detailed tracking of the ionospheric rotation measure. The linear
polarization of the pulsar is
6 km),
which at times can be difficult to calibrate if the ionosphere is in a
disturbed state. However, no disturbances were noted, and the
calibration (using nearby point-like objects) of the phase, amplitude,
and polarization of the antennas proceeded smoothly. Images of the
pulsar in Stokes' I, Q, and U were made every 5 min to permit
detailed tracking of the ionospheric rotation measure. The linear
polarization of the pulsar is ![]() ,
and it does not rotate
appreciably during the each pulse, making measurement of the pulsar's
polarized emission very straightforward.
,
and it does not rotate
appreciably during the each pulse, making measurement of the pulsar's
polarized emission very straightforward.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{04Apr97.eps}\end{figure}](/articles/aa/full/2001/06/aa10277/Timg57.gif) |
Figure 9:
The change of observed and predicted plane of polarization
of the pulsar PSR 1932+109 through dawn on 4 April 1997. The
standard deviation between the observation and the model for a single
5-min integration is 4
|
| Open with DEXTER | |
The data from the GPS receiver located at the VLA site were processed through two special AIPS programs, LDGPS, and APGPS. The former program loads the GPS data into a GP table which is attached to the AIPS database containing the visibility data. This table contains the time, satellite PRN number, satellite azimuth and elevation, and the observed TECTAU and TECPHS. The latter program does the model fit, and calculates the ionospheric rotation measure (RM) for every source in the AIPS database, the results of which are then written into the AIPS CL table.
It was felt that more data were needed and two more successful tests
were made using essentially the same setup. The second test was made
on 27 August 1998 (see Fig. 10). This test ran through
sunset, however, quite abnormal ionospheric conditions occurred. The
TEC began to decrease as normally happens at sunset but then, about an
hour after sunset, it increased to above its daytime level and a very
strong north-south gradient set in. This unusual behavior was
mirrored satisfactorily in both the predicted and observed Faraday
rotation except for a large spike in the model prediction at
03:55 IAT. This was caused by the fact that the North-South gradient
was extremely high, the highest that we have ever observed, while at
the same time the GPS satellites were mostly east and west of the VLA
site, making the modeling of this gradient rather unstable.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{26Aug98.eps}\end{figure}](/articles/aa/full/2001/06/aa10277/Timg58.gif) |
Figure 10:
Same as Fig. 9 but for 27 August 1998. In this case the
standard deviation for single integrations is 8
|
| Open with DEXTER | |
A third test was run through sunrise on 24 June 1999 (see
Fig. 11). In this case the ionospheric measurements were
completely normal with the TEC being low and constant until sunrise,
and then rising rapidly. The Faraday rotation predicted by the model
reflected this situation. However, the observed rotation was about
30![]() above the prediction at the beginning of the test, some four
hours before sunrise. The observed rotation then decreased and came
into agreement with the prediction about an hour before sunrise, and
the predicted and observed rotations then rose together after sunrise.
Also plotted in Fig. 11 are the calculated values using
values of the TEC taken from archived data stored at the Crustal
Dynamics Data Information Center at the Goddard Space Flight Center.
We downloaded the JPL Global Ionospheric Model Maps, and used these to
calculate the predicted Faraday rotation, using the AIPS program
TECOR
above the prediction at the beginning of the test, some four
hours before sunrise. The observed rotation then decreased and came
into agreement with the prediction about an hour before sunrise, and
the predicted and observed rotations then rose together after sunrise.
Also plotted in Fig. 11 are the calculated values using
values of the TEC taken from archived data stored at the Crustal
Dynamics Data Information Center at the Goddard Space Flight Center.
We downloaded the JPL Global Ionospheric Model Maps, and used these to
calculate the predicted Faraday rotation, using the AIPS program
TECOR![]() .
.
The two models are in excellent agreement during the pre-dawn hours,
but diverge significantly about two hours after sunrise. We note that
the pulsar was at very low elevations after this time (25![]() at IAT =
13, dropping to 9
at IAT =
13, dropping to 9![]() at the end of the experiment), so the
differences may be related to the differing geometries utilized by
these models. Because the global data are heavily averaged,
travelling ionospheric disturbances, including sharp ionization waves,
will be smoothed out. This explains the smoothness of the JPL model
predictions. On the other hand, our model, utilizing data averaged
only on 5 min timescales, is sensitive to TIDs and other localized
disturbances, and this shows in the fluctuations in our model
predictions. We note that neither model is in agreement with the
observed data prior to sunrise - we have no viable explanation for the
discrepancy at the beginning of this test.
at the end of the experiment), so the
differences may be related to the differing geometries utilized by
these models. Because the global data are heavily averaged,
travelling ionospheric disturbances, including sharp ionization waves,
will be smoothed out. This explains the smoothness of the JPL model
predictions. On the other hand, our model, utilizing data averaged
only on 5 min timescales, is sensitive to TIDs and other localized
disturbances, and this shows in the fluctuations in our model
predictions. We note that neither model is in agreement with the
observed data prior to sunrise - we have no viable explanation for the
discrepancy at the beginning of this test.
More low-frequency observations of highly polarized objects will be
needed for a better understanding of the limitations of our, and of
the global, models.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{24Jun99JPL.eps}\end{figure}](/articles/aa/full/2001/06/aa10277/Timg59.gif) |
Figure 11:
Same as Fig. 9 but for 24 June 1999. From
11:00 IAT until the end of the test, the standard deviation of the
single integrations was 9
|
| Open with DEXTER | |
We have performed an experiment to evaluate the usefulness of local
GPS data for the correction of ionospheric Faraday rotation and
interferometric phase fluctuations in 327 MHz VLA data. Data from GPS
receivers installed at the VLA site have been fitted to a simple
ionospheric model, and this fitting process has been used to determine
the receiver and transmitter offsets. The parameters derived from the
model fits can be used to determine the interferometer phase and Faraday
rotation caused by the ionosphere along any line of sight towards an
astronomical source. We find that a single GPS receiver in the
vicinity of the VLA site provides data that are sufficient to correct
for Faraday effects to
![]() at 327 MHz and to predict the
phase fluctuations caused by large-scale (
at 327 MHz and to predict the
phase fluctuations caused by large-scale (![]() km) ionospheric
structures. A comparison of our model to one using archived global
data shows good agreement.
km) ionospheric
structures. A comparison of our model to one using archived global
data shows good agreement.
A grid of four GPS receivers was used to predict the phase
fluctuations caused by small-scale (![]() km) structures, but
this prediction could be made only when the ray path from the radio
source under observation and ray paths from one of the GPS satellites
to the receivers punctured the ionosphere within the same isoplanatic
patch - about four degrees for our experiment. A large grid of GPS
receivers at 50 to 100 km spacings surrounding the site would be
required to provide the large number of puncture points required to
characterize isoplanatic patches throughout the whole sky and all
small-scale ionospheric structures. Such a grid of receivers is
impractical at the present time.
km) structures, but
this prediction could be made only when the ray path from the radio
source under observation and ray paths from one of the GPS satellites
to the receivers punctured the ionosphere within the same isoplanatic
patch - about four degrees for our experiment. A large grid of GPS
receivers at 50 to 100 km spacings surrounding the site would be
required to provide the large number of puncture points required to
characterize isoplanatic patches throughout the whole sky and all
small-scale ionospheric structures. Such a grid of receivers is
impractical at the present time.
Acknowledgements
The GPS receivers for this experiment were provided by the Atmospheric Sciences Group of the Los Alamos National Laboratory and we especially wish to thank Mr. Jason Payne of that group who supervised their installation and operation.